Breaking the Kolmogorov Barrier in Model Reduction of Fluid Flows
Abstract
:1. Introduction
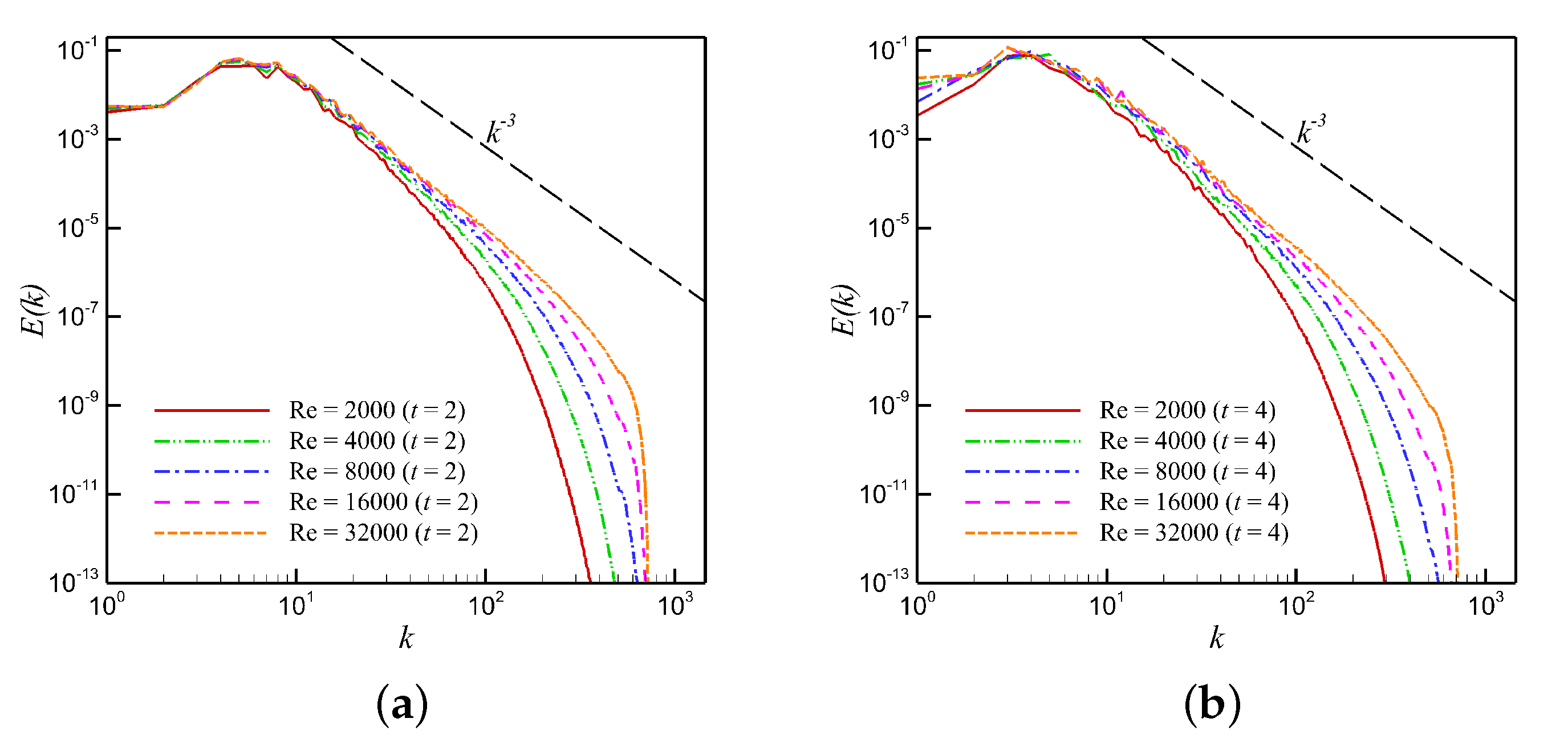
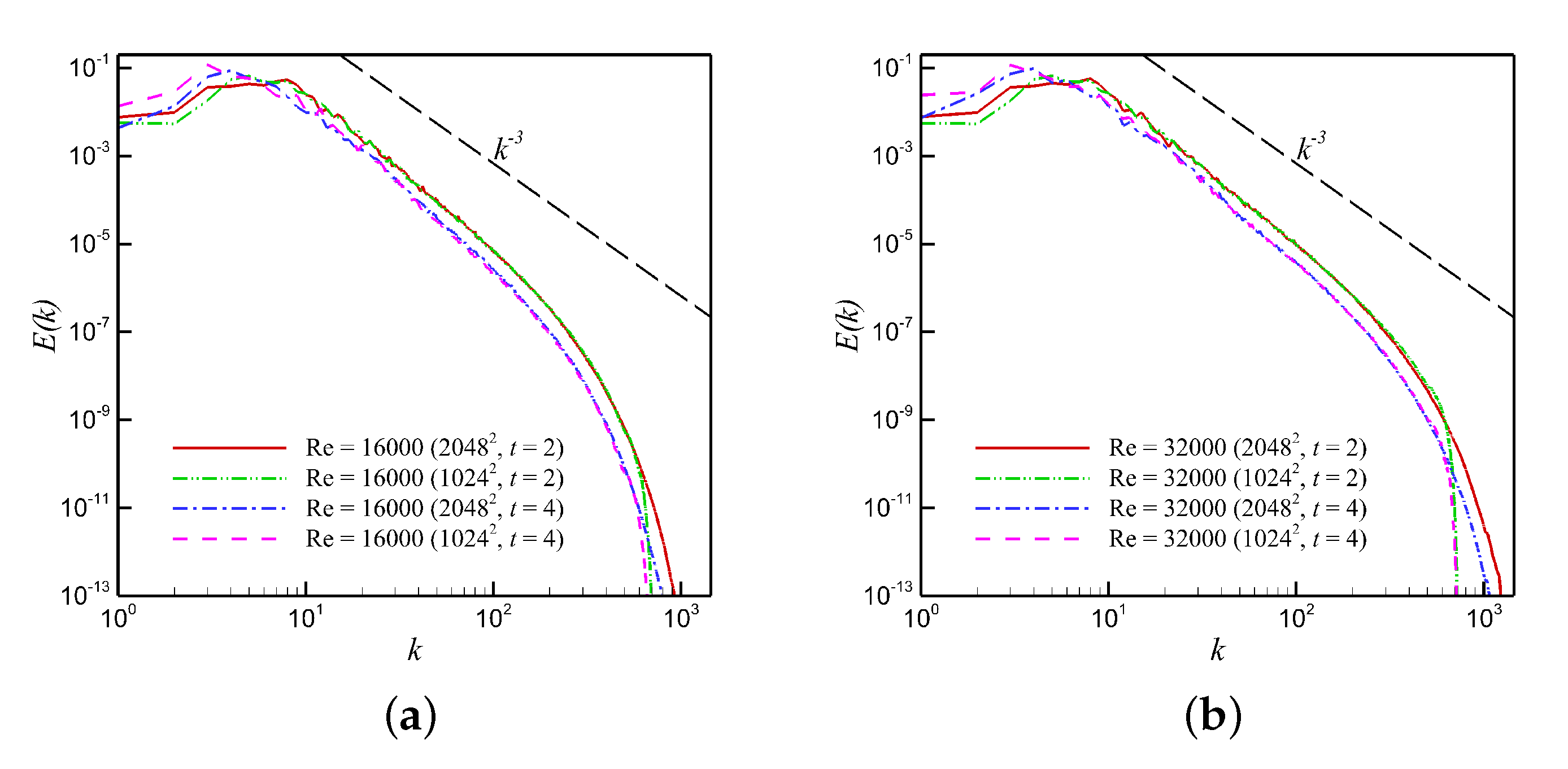
2. Two-Dimensional Kraichnan Turbulence
3. Reduced Order Modeling
3.1. Proper Orthogonal Decomposition
3.2. Galerkin Projection
4. Partitioned ROM
5. Results
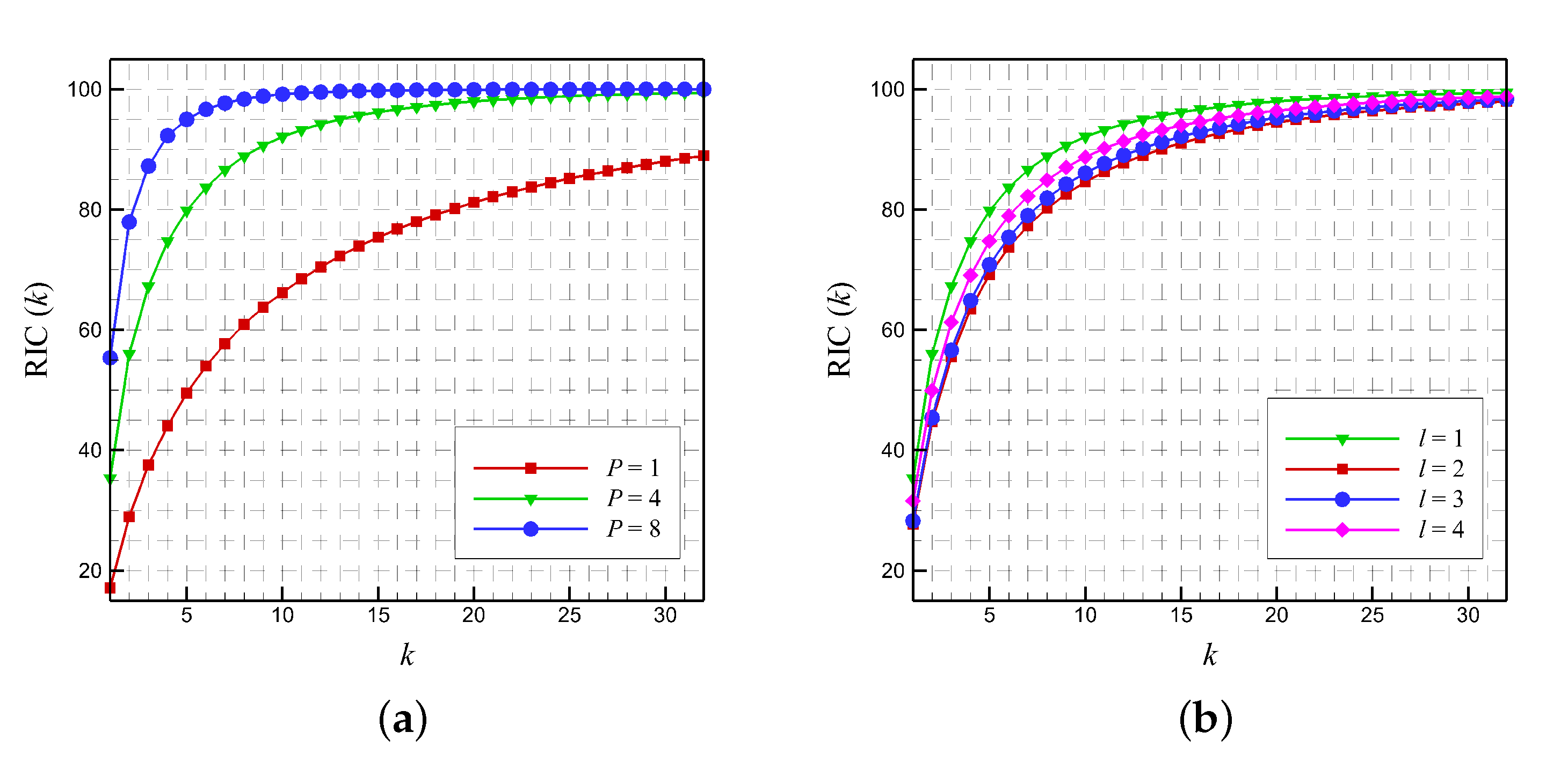
5.1. Kolmogorov n-Width and Relative Information Content
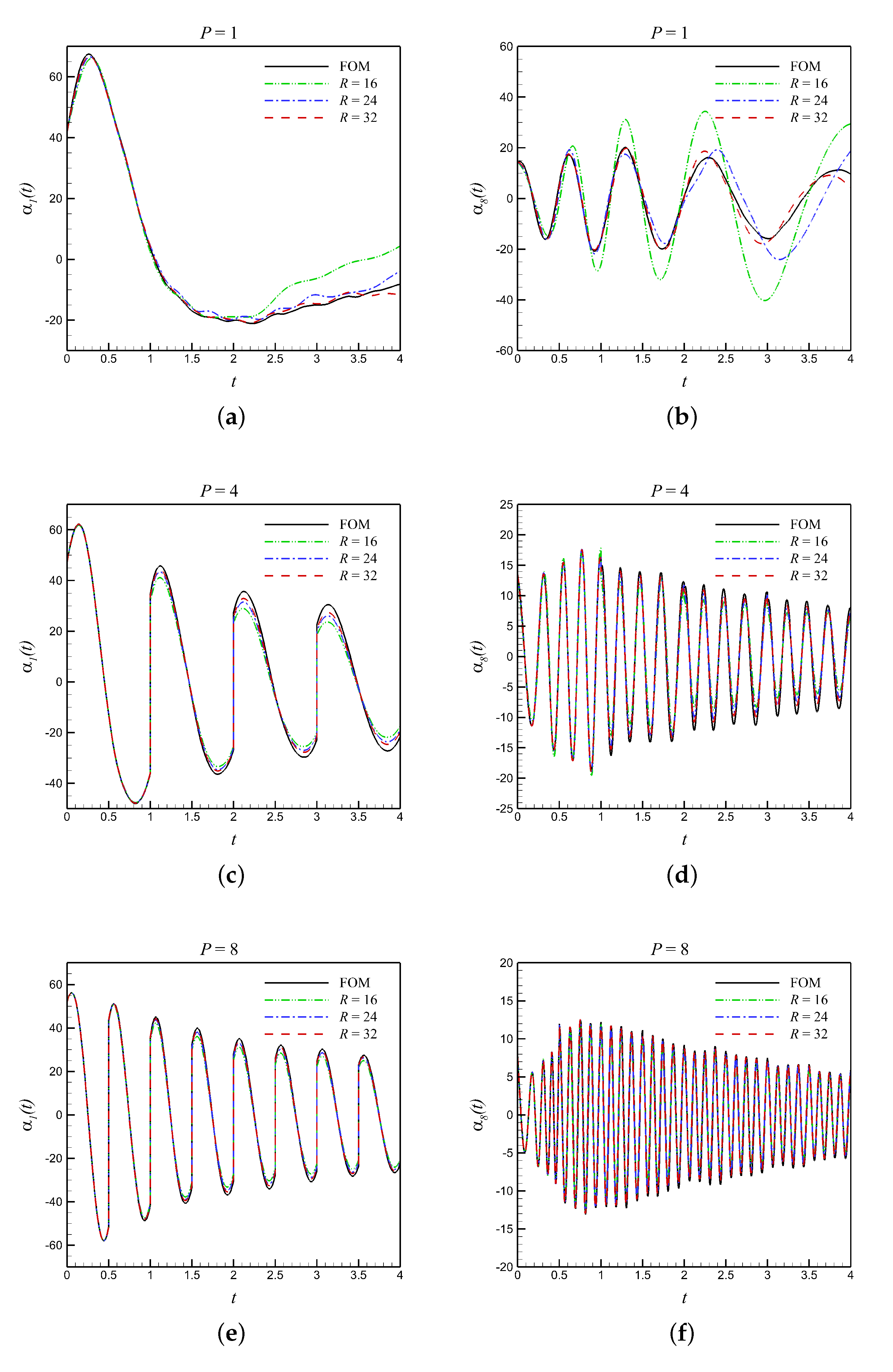
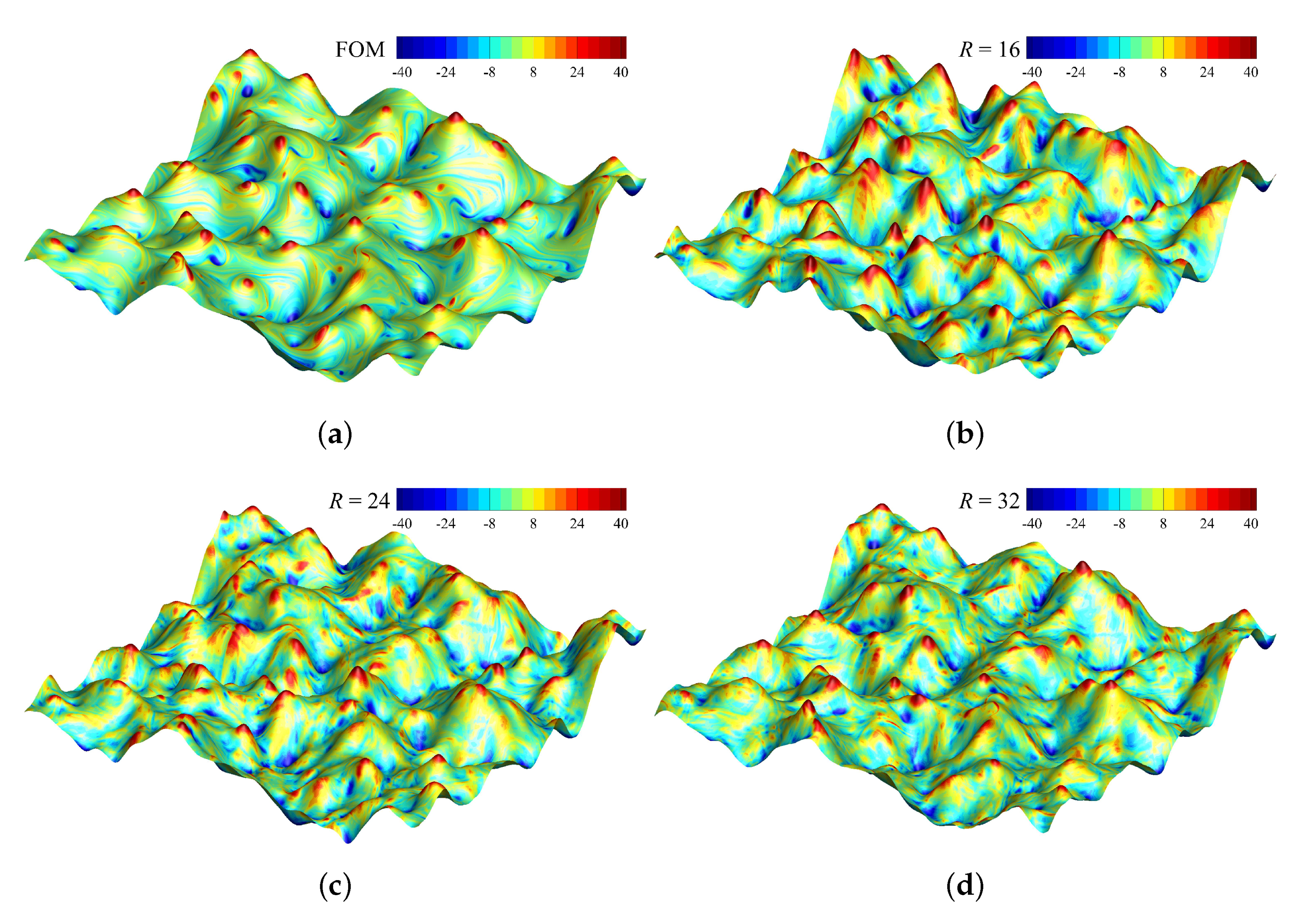
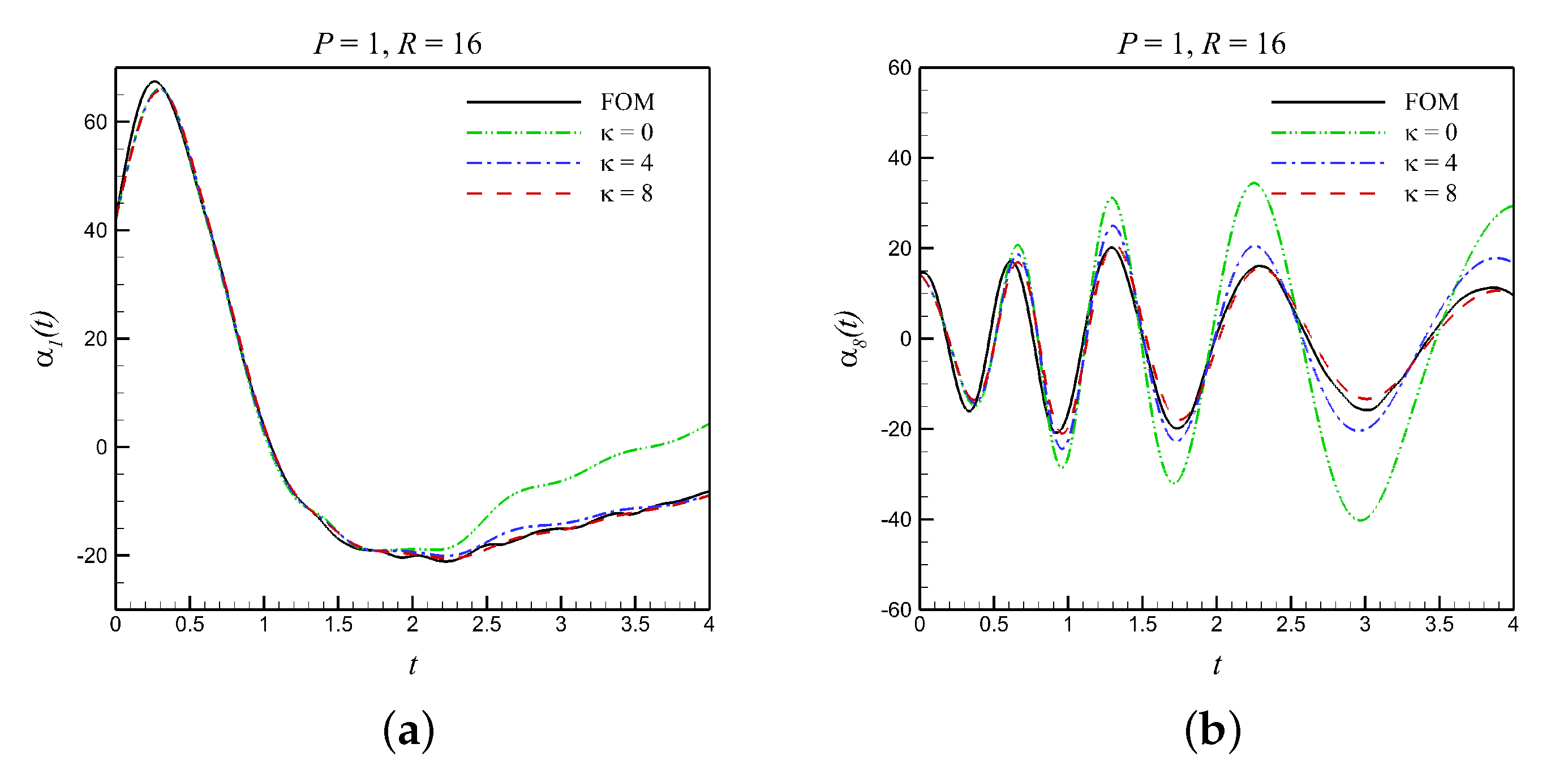
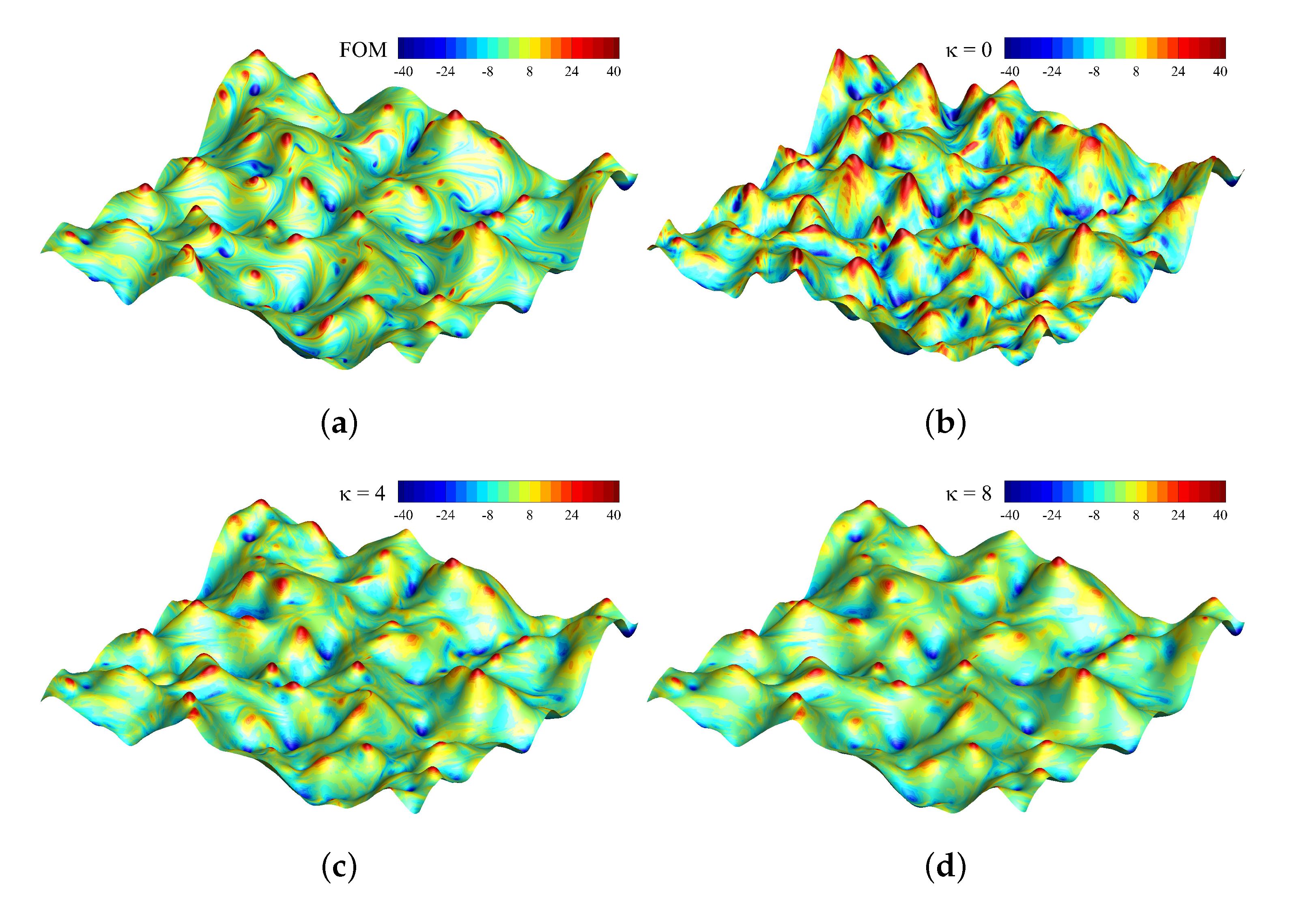
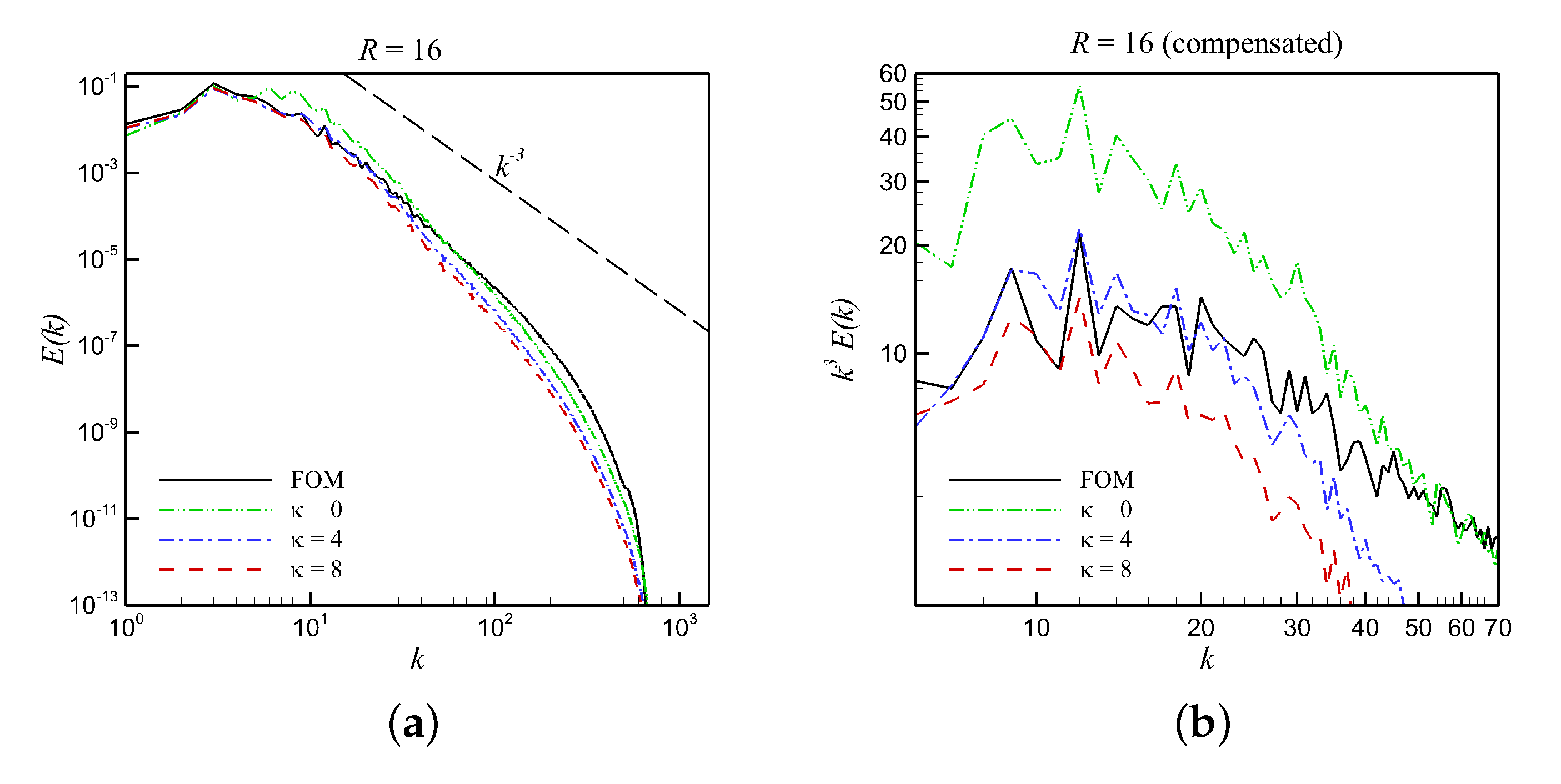
5.2. Closure Modeling
5.3. Computational Cost
6. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Powell, J.R. The quantum limit to Moore’s law. Proc. IEEE 2008, 96, 1247–1248. [Google Scholar] [CrossRef]
- Waldrop, M.M. The chips are down for Moore’s law. Nat. News 2016, 530, 144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, S. The end of Moore’s law and reinventing computing. In High-Speed and Lower Power Technologies: Electronics and Photonics; Choi, J.H., Ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Taira, K.; Brunton, S.L.; Dawson, S.T.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef] [Green Version]
- Puzyrev, V.; Ghommem, M.; Meka, S. pyROM: A computational framework for reduced order modeling. J. Comput. Sci. 2019, 30, 157–173. [Google Scholar] [CrossRef]
- Rasheed, A.; San, O.; Kvamsdal, T. Digital Twin: Values, Challenges and Enablers. arXiv 2019, arXiv:1910.01719. [Google Scholar]
- Grieves, M.; Vickers, J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In Transdisciplinary Perspectives on Complex Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 85–113. [Google Scholar]
- Boschert, S.; Rosen, R. Digital twin—The simulation aspect. In Mechatronic Futures; Springer: Berlin/Heidelberg, Germany, 2016; pp. 59–74. [Google Scholar]
- Tao, F.; Cheng, J.; Qi, Q.; Zhang, M.; Zhang, H.; Sui, F. Digital twin-driven product design, manufacturing and service with big data. Int. J. Adv. Manuf. Technol. 2018, 94, 3563–3576. [Google Scholar] [CrossRef]
- Uhlemann, T.H.J.; Lehmann, C.; Steinhilper, R. The digital twin: Realizing the cyber-physical production system for industry 4.0. Procedia CIRP 2017, 61, 335–340. [Google Scholar] [CrossRef]
- Glaessgen, E.; Stargel, D. The digital twin paradigm for future NASA and US Air Force vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012; p. 1818. [Google Scholar]
- Kapteyn, M.G.; Willcox, K.; Knezevic, D.J. Toward predictive digital twins via component-based reduced-order models and interpretable machine learning. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0418. [Google Scholar]
- Singh, V.; Willcox, K.E. Engineering Design with Digital Thread. AIAA J. 2018, 56, 4515–4528. [Google Scholar] [CrossRef]
- Hartmann, D.; Herz, M.; Wever, U. Model order reduction a key technology for digital twins. In Reduced-Order Modeling (ROM) for Simulation and Optimization; Springer: Berlin/Heidelberg, Germany, 2018; pp. 167–179. [Google Scholar]
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer: Berlin/Heidelberg, Germany, 2011; Volume 528. [Google Scholar]
- Ito, K.; Ravindran, S.S. Reduced basis method for optimal control of unsteady viscous flows. Int. J. Comput. Fluid Dyn. 2001, 15, 97–113. [Google Scholar] [CrossRef]
- McNamara, A.; Treuille, A.; Popović, Z.; Stam, J. Fluid control using the adjoint method. ACM Trans. Graph. 2004, 23, 449–456. [Google Scholar] [CrossRef]
- Bergmann, M.; Cordier, L. Optimal control of the cylinder wake in the laminar regime by trust-region methods and POD reduced-order models. J. Comput. Phys. 2008, 227, 7813–7840. [Google Scholar] [CrossRef] [Green Version]
- Ravindran, S.S. A reduced-order approach for optimal control of fluids using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 2000, 34, 425–448. [Google Scholar] [CrossRef]
- Graham, W.; Peraire, J.; Tang, K. Optimal control of vortex shedding using low-order models. Part I–open-loop model development. Int. J. Numer. Methods Eng. 1999, 44, 945–972. [Google Scholar] [CrossRef]
- Graham, W.; Peraire, J.; Tang, K. Optimal control of vortex shedding using low-order models. Part II–model-based control. Int. J. Numer. Methods Eng. 1999, 44, 973–990. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R. Closed-loop turbulence control: Progress and challenges. Appl. Mech. Rev. 2015, 67, 050801. [Google Scholar] [CrossRef]
- Daescu, D.N.; Navon, I.M. Efficiency of a POD-based reduced second-order adjoint model in 4D-Var data assimilation. Int. J. Numer. Methods Fluids 2007, 53, 985–1004. [Google Scholar] [CrossRef] [Green Version]
- Navon, I.M. Data assimilation for numerical weather prediction: A review. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S.K., Xu, L., Eds.; Springer: New York, NY, USA, 2009; pp. 21–65. [Google Scholar]
- Cao, Y.; Zhu, J.; Navon, I.M.; Luo, Z. A reduced-order approach to four-dimensional variational data assimilation using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 2007, 53, 1571–1583. [Google Scholar] [CrossRef]
- He, J.; Sarma, P.; Durlofsky, L.J. Use of reduced-order models for improved data assimilation within an EnKF context. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 21–23 February 2011; Society of Petroleum Engineers: Richardson, TX, USA, 2011. [Google Scholar]
- Houtekamer, P.L.; Mitchell, H.L. Data assimilation using an ensemble Kalman filter technique. Mon. Weather. Rev. 1998, 126, 796–811. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather. Rev. 2001, 129, 123–137. [Google Scholar] [CrossRef]
- Bennett, A.F. Inverse Modeling of the Ocean and Atmosphere; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Law, K.J.; Stuart, A.M. Evaluating data assimilation algorithms. Mon. Weather. Rev. 2012, 140, 3757–3782. [Google Scholar] [CrossRef] [Green Version]
- Buljak, V. Inverse Analyses with Model Reduction: Proper Orthogonal Decomposition in Structural Mechanics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Xiao, D.; Du, J.; Fang, F.; Pain, C.; Li, J. Parameterised non-intrusive reduced order methods for ensemble Kalman filter data assimilation. Comput. Fluids 2018, 177, 69–77. [Google Scholar] [CrossRef]
- Navon, I. Practical and theoretical aspects of adjoint parameter estimation and identifiability in meteorology and oceanography. Dyn. Atmos. Ocean. 1998, 27, 55–79. [Google Scholar] [CrossRef] [Green Version]
- Fu, H.; Wang, H.; Wang, Z. POD/DEIM reduced-order modeling of time-fractional partial differential equations with applications in parameter identification. J. Sci. Comput. 2018, 74, 220–243. [Google Scholar] [CrossRef] [Green Version]
- Boulakia, M.; Schenone, E.; Gerbeau, J.F. Reduced-order modeling for cardiac electrophysiology. Application to parameter identification. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 727–744. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kramer, B.; Peherstorfer, B.; Willcox, K. Feedback control for systems with uncertain parameters using online-adaptive reduced models. SIAM J. Appl. Dyn. Syst. 2017, 16, 1563–1586. [Google Scholar] [CrossRef] [Green Version]
- Galbally, D.; Fidkowski, K.; Willcox, K.; Ghattas, O. Non-linear model reduction for uncertainty quantification in large-scale inverse problems. Int. J. Numer. Methods Eng. 2010, 81, 1581–1608. [Google Scholar] [CrossRef] [Green Version]
- Biegler, L.; Biros, G.; Ghattas, O.; Heinkenschloss, M.; Keyes, D.; Mallick, B.; Tenorio, L.; Waanders, B.V.B.; Willcox, K.; Marzouk, Y. Large-Scale Inverse Problems and Quantification of Uncertainty; Wiley Online Library: Chichester, UK, 2011. [Google Scholar]
- Mathelin, L.; Hussaini, M.Y.; Zang, T.A. Stochastic approaches to uncertainty quantification in CFD simulations. Numer. Algorithms 2005, 38, 209–236. [Google Scholar] [CrossRef]
- Smith, R.C. Uncertainty Quantification: Theory, Implementation, and Applications; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Najm, H.N. Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Zahr, M.J.; Carlberg, K.T.; Kouri, D.P. An efficient, globally convergent method for optimization under uncertainty using adaptive model reduction and sparse grids. SIAM/ASA J. Uncertain. Quantif. 2019, 7, 877–912. [Google Scholar] [CrossRef]
- Fairbanks, H.R.; Jofre, L.; Geraci, G.; Iaccarino, G.; Doostan, A. Bi-fidelity approximation for uncertainty quantification and sensitivity analysis of irradiated particle-laden turbulence. J. Comput. Phys. 2020, 402, 108996. [Google Scholar] [CrossRef] [Green Version]
- Kevlahan, N.R.; Hunt, J.; Vassilicos, J. A comparison of different analytical techniques for identifying structures in turbulence. Appl. Sci. Res. 1994, 53, 339–355. [Google Scholar] [CrossRef] [Green Version]
- Holmes, P.; Lumley, J.L.; Berkooz, G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Rowley, C.W.; Colonius, T.; Murray, R.M. Model reduction for compressible flows using POD and Galerkin projection. Phys. D Nonlinear Phenom. 2004, 189, 115–129. [Google Scholar] [CrossRef]
- Ma, Z.; Ahuja, S.; Rowley, C.W. Reduced-order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 2011, 25, 233–247. [Google Scholar] [CrossRef] [Green Version]
- Rowley, C.W. Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurc. Chaos 2005, 15, 997–1013. [Google Scholar] [CrossRef] [Green Version]
- Willcox, K.; Peraire, J. Balanced model reduction via the proper orthogonal decomposition. AIAA J. 2002, 40, 2323–2330. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data–driven approximation of the koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef] [Green Version]
- Peterson, J.S. The reduced basis method for incompressible viscous flow calculations. SIAM J. Sci. Stat. Comput. 1989, 10, 777–786. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Rim, D.; Peherstorfer, B.; Mandli, K.T. Manifold Approximations via Transported Subspaces: Model reduction for transport-dominated problems. arXiv 2019, arXiv:1912.13024. [Google Scholar]
- Lai, X.; Wang, X.; Nie, Y.; Li, Q. Characterizing complex flows via adaptive sparse dynamic mode decomposition with error approximation. Int. J. Numer. Methods Fluids 2019. [Google Scholar] [CrossRef]
- Kastian, S.; Reese, S. An Adaptive Way of Choosing Significant Snapshots for Proper Orthogonal Decomposition. In Proceedings of the IUTAM Symposium on Model Order Reduction of Coupled Systems, Stuttgart, Germany, 22–25 May 2018; Springer: Berlin/Heidelberg, Germany, 2020; pp. 67–79. [Google Scholar]
- Aubry, N.; Holmes, P.; Lumley, J.L.; Stone, E. The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 1988, 192, 115–173. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef] [Green Version]
- Protas, B.; Noack, B.R.; Östh, J. Optimal nonlinear eddy viscosity in Galerkin models of turbulent flows. J. Fluid Mech. 2015, 766, 337–367. [Google Scholar] [CrossRef] [Green Version]
- Stabile, G.; Ballarin, F.; Zuccarino, G.; Rozza, G. A reduced order variational multiscale approach for turbulent flows. Adv. Comput. Math. 2019, 45, 2349–2368. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Heaney, C.; Mottet, L.; Fang, F.; Lin, W.; Navon, I.; Guo, Y.; Matar, O.; Robins, A.; Pain, C. A reduced order model for turbulent flows in the urban environment using machine learning. Build. Environ. 2019, 148, 323–337. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Heaney, C.; Fang, F.; Mottet, L.; Hu, R.; Bistrian, D.; Aristodemou, E.; Navon, I.; Pain, C. A domain decomposition non-intrusive reduced order model for turbulent flows. Comput. Fluids 2019, 182, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Kolmogoroff, A. Über die beste Annäherung von Funktionen einer gegebenen Funktionenklasse. Ann. Math. 1936, 37, 107–110. [Google Scholar] [CrossRef]
- Pinkus, A. N-Widths in Approximation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 7. [Google Scholar]
- Taddei, T. A registration method for model order reduction: Data compression and geometry reduction. arXiv 2019, arXiv:1906.11008. [Google Scholar]
- Greif, C.; Urban, K. Decay of the Kolmogorov N-width for wave problems. Appl. Math. Lett. 2019, 96, 216–222. [Google Scholar] [CrossRef] [Green Version]
- IJzerman, W. Signal Representation and Modeling of Spatial Structures in Fluids. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2000. [Google Scholar]
- Borggaard, J.; Hay, A.; Pelletier, D. Interval-based reduced order models for unsteady fluid flow. Int. J. Numer. Anal. Model. 2007, 4, 353–367. [Google Scholar]
- San, O.; Borggaard, J. Principal interval decomposition framework for POD reduced-order modeling of convective Boussinesq flows. Int. J. Numer. Methods Fluids 2015, 78, 37–62. [Google Scholar] [CrossRef]
- Ahmed, M.; San, O. Stabilized principal interval decomposition method for model reduction of nonlinear convective systems with moving shocks. Comput. Appl. Math. 2018, 37, 6870–6902. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Rahman, S.M.; San, O.; Rasheed, A.; Navon, I.M. Memory embedded non-intrusive reduced order modeling of non-ergodic flows. Phys. Fluids 2019, 31, 126602. [Google Scholar] [CrossRef] [Green Version]
- Charney, J.G. Geostrophic turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef] [Green Version]
- Kraichnan, R.H.; Montgomery, D. Two-dimensional turbulence. Rep. Prog. Phys. 1980, 43, 547. [Google Scholar] [CrossRef]
- Boffetta, G.; Ecke, R.E. Two-dimensional turbulence. Annu. Rev. Fluid Mech. 2012, 44, 427–451. [Google Scholar] [CrossRef]
- Rempfer, D. On low-dimensional Galerkin models for fluid flow. Theor. Comput. Fluid Dyn. 2000, 14, 75–88. [Google Scholar] [CrossRef]
- Zhang, M.; Stevens, R.J. Characterizing the Coherent Structures Within and Above Large Wind Farms. Bound.-Layer Meteorol. 2019, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Shah, S.; Bou-Zeid, E. Very-large-scale motions in the atmospheric boundary layer educed by snapshot proper orthogonal decomposition. Bound.-Layer Meteorol. 2014, 153, 355–387. [Google Scholar] [CrossRef]
- Östh, J.; Noack, B.R.; Krajnović, S.; Barros, D.; Borée, J. On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J. Fluid Mech. 2014, 747, 518–544. [Google Scholar] [CrossRef] [Green Version]
- Grimberg, S.; Farhat, C.; Youkilis, N. On the stability of projection-based model order reduction for convection-dominated laminar and turbulent flows. arXiv 2020, arXiv:2001.10110. [Google Scholar]
- Carlberg, K.; Barone, M.; Antil, H. Galerkin v. least-squares Petrov–Galerkin projection in nonlinear model reduction. J. Comput. Phys. 2017, 330, 693–734. [Google Scholar] [CrossRef] [Green Version]
- Kraichnan, R.H. Inertial ranges in two-dimensional turbulence. Phys. Fluids 1967, 10, 1417–1423. [Google Scholar] [CrossRef] [Green Version]
- Batchelor, G.K. Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 1969, 12, II-233. [Google Scholar] [CrossRef]
- Leith, C. Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 1971, 28, 145–161. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Staples, A.E. High-order methods for decaying two-dimensional homogeneous isotropic turbulence. Comput. Fluids 2012, 63, 105–127. [Google Scholar] [CrossRef] [Green Version]
- Arakawa, A. Computational design for long-term numerical integration of the equations of fluid motion: Two-dimensional incompressible flow. Part I. J. Comput. Phys. 1966, 1, 119–143. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.W. Total variation diminishing Runge-Kutta schemes. Math. Comput. 1998, 67, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Rowley, C.W.; Dawson, S.T. Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.K.; Tu, J.H.; Rowley, C.W. Variants of dynamic mode decomposition: Boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 2012, 22, 887–915. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in FORTRAN; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Chaturantabut, S.; Sorensen, D.C. Discrete empirical interpolation for nonlinear model reduction. In Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai, China, 16–18 December 2009; pp. 4316–4321. [Google Scholar]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Everson, R.; Sirovich, L. Karhunen–Loeve procedure for gappy data. JOSA A 1995, 12, 1657–1664. [Google Scholar] [CrossRef] [Green Version]
- Astrid, P.; Weiland, S.; Willcox, K.; Backx, T. Missing point estimation in models described by proper orthogonal decomposition. IEEE Trans. Autom. Control. 2008, 53, 2237–2251. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, R.; Willcox, K. An accelerated greedy missing point estimation procedure. SIAM J. Sci. Comput. 2016, 38, A2827–A2850. [Google Scholar] [CrossRef] [Green Version]
- Ştefănescu, R.; Sandu, A.; Navon, I.M. Comparison of POD reduced order strategies for the nonlinear 2D shallow water equations. Int. J. Numer. Methods Fluids 2014, 76, 497–521. [Google Scholar] [CrossRef] [Green Version]
- Dimitriu, G.; Ştefănescu, R.; Navon, I.M. Comparative numerical analysis using reduced-order modeling strategies for nonlinear large-scale systems. J. Comput. Appl. Math. 2017, 310, 32–43. [Google Scholar] [CrossRef]
- Cazemier, W.; Verstappen, R.; Veldman, A. Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Phys. Fluids 1998, 10, 1685–1699. [Google Scholar] [CrossRef] [Green Version]
- Amsallem, D.; Zahr, M.J.; Farhat, C. Nonlinear model order reduction based on local reduced-order bases. Int. J. Numer. Methods Eng. 2012, 92, 891–916. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K. Online adaptive model reduction for nonlinear systems via low-rank updates. SIAM J. Sci. Comput. 2015, 37, A2123–A2150. [Google Scholar] [CrossRef]
- Taddei, T.; Perotto, S.; Quarteroni, A. Reduced basis techniques for nonlinear conservation laws. ESAIM Math. Model. Numer. Anal. 2015, 49, 787–814. [Google Scholar] [CrossRef]
- Dihlmann, M.; Drohmann, M.; Haasdonk, B. Model reduction of parametrized evolution problems using the reduced basis method with adaptive time-partitioning. In Proceedings of the International Conference on Adaptive Modeling and Simulation (ADMOS 2011), Paris, France, 6–8 June 2011; pp. 156–167. [Google Scholar]
- Ahmed, S.E.; San, O.; Bistrian, D.A.; Navon, I.M. Sampling and resolution characteristics in reduced order models of shallow water equations: Intrusive vs non-intrusive. arXiv 2019, arXiv:1910.07654. [Google Scholar] [CrossRef] [Green Version]
- Gunzburger, M.D. Flow Control; Springer: Berlin, Gemany, 2012. [Google Scholar]
- Rempfer, D. Kohärente Strukturen und Chaos beim Laminar-Turbulenten Grenzschichtumschlag. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 1997. [Google Scholar]
- San, O.; Iliescu, T. Proper orthogonal decomposition closure models for fluid flows: Burgers equation. INternational J. Numer. Anal. Model. Ser. B 2014, 5, 217–237. [Google Scholar]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Two-level discretizations of nonlinear closure models for proper orthogonal decomposition. J. Comput. Phys. 2011, 230, 126–146. [Google Scholar] [CrossRef]
- Borggaard, J.; Iliescu, T.; Wang, Z. Artificial viscosity proper orthogonal decomposition. Math. Comput. Model. 2011, 53, 269–279. [Google Scholar] [CrossRef]
- Akhtar, I.; Wang, Z.; Borggaard, J.; Iliescu, T. A new closure strategy for proper orthogonal decomposition reduced-order models. J. Comput. Nonlinear Dyn. 2012, 7, 034503. [Google Scholar] [CrossRef]
- Iliescu, T.; Wang, Z. Variational multiscale proper orthogonal decomposition: Navier-stokes equations. Numer. Methods Part. Differ. Equations 2014, 30, 641–663. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Wells, D.; Wang, Z.; Iliescu, T. Approximate deconvolution reduced order modeling. Comput. Methods Appl. Mech. Eng. 2017, 313, 512–534. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Wells, D.; Wang, Z.; Iliescu, T. Numerical analysis of the Leray reduced order model. J. Comput. Appl. Math. 2018, 328, 12–29. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Mohebujjaman, M.; Rebholz, L.G.; Iliescu, T. Data-driven filtered reduced order modeling of fluid flows. SIAM J. Sci. Comput. 2018, 40, B834–B857. [Google Scholar] [CrossRef] [Green Version]
- Rahman, S.M.; Ahmed, S.E.; San, O. A dynamic closure modeling framework for model order reduction of geophysical flows. Phys. Fluids 2019, 31, 046602. [Google Scholar] [CrossRef] [Green Version]



| Model | ||
|---|---|---|
| Model with 16 Modes (P = 1) | ||
|---|---|---|
| Model with 16 Modes () | ||
|---|---|---|
| online | |||
| offline | |||
| online | |||
| offline | |||
| online | |||
| offline | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.E.; San, O. Breaking the Kolmogorov Barrier in Model Reduction of Fluid Flows. Fluids 2020, 5, 26. https://doi.org/10.3390/fluids5010026
Ahmed SE, San O. Breaking the Kolmogorov Barrier in Model Reduction of Fluid Flows. Fluids. 2020; 5(1):26. https://doi.org/10.3390/fluids5010026
Chicago/Turabian StyleAhmed, Shady E., and Omer San. 2020. "Breaking the Kolmogorov Barrier in Model Reduction of Fluid Flows" Fluids 5, no. 1: 26. https://doi.org/10.3390/fluids5010026
APA StyleAhmed, S. E., & San, O. (2020). Breaking the Kolmogorov Barrier in Model Reduction of Fluid Flows. Fluids, 5(1), 26. https://doi.org/10.3390/fluids5010026






