Changes in Vertical Distribution of Zooplankton under Wind-Induced Turbulence: A 36-Year Record
Abstract
:1. Introduction
2. Materials and Methods
2.1. Biological Parameters
2.2. Physical Parameters
2.3. Statistical Analyses
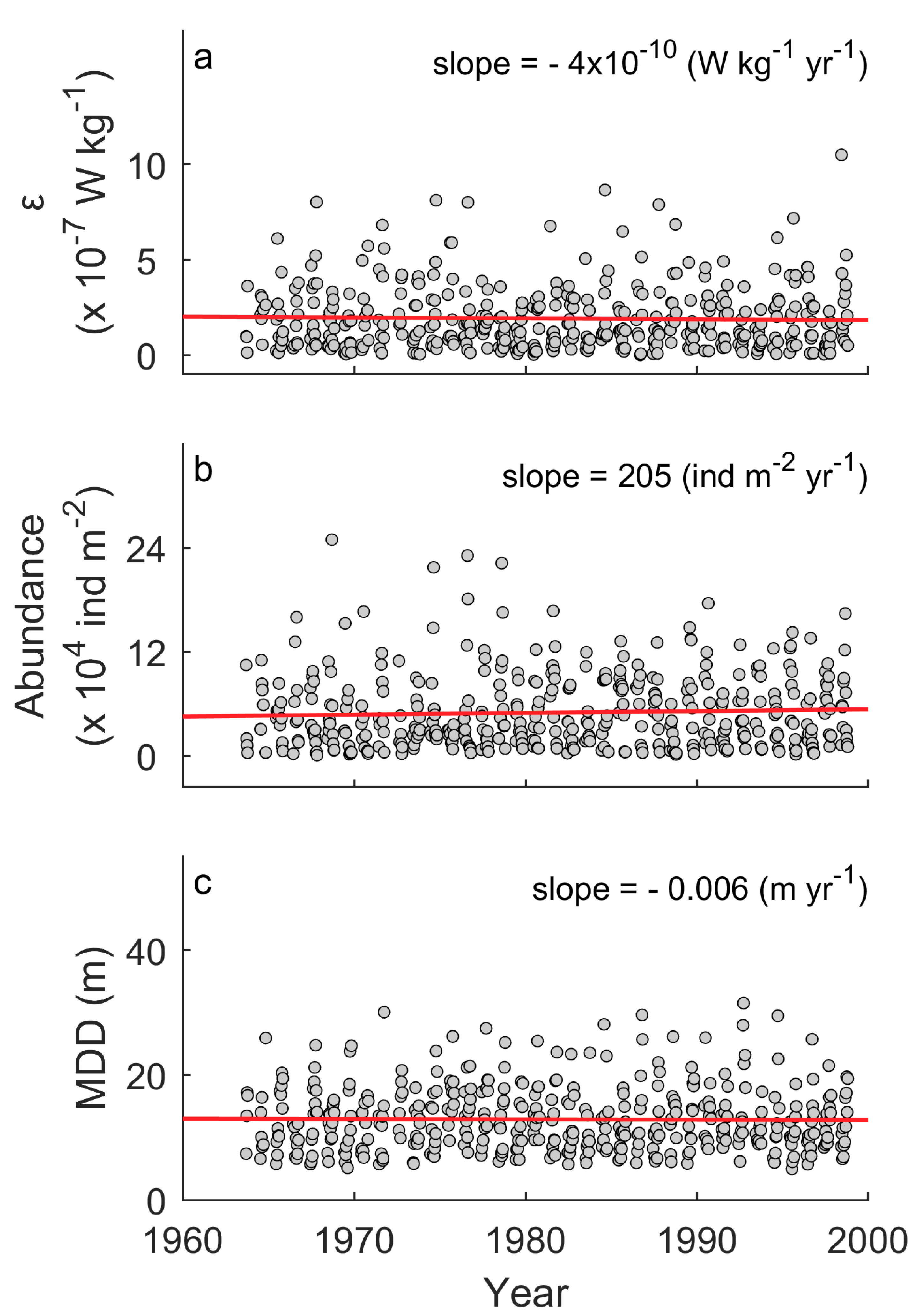
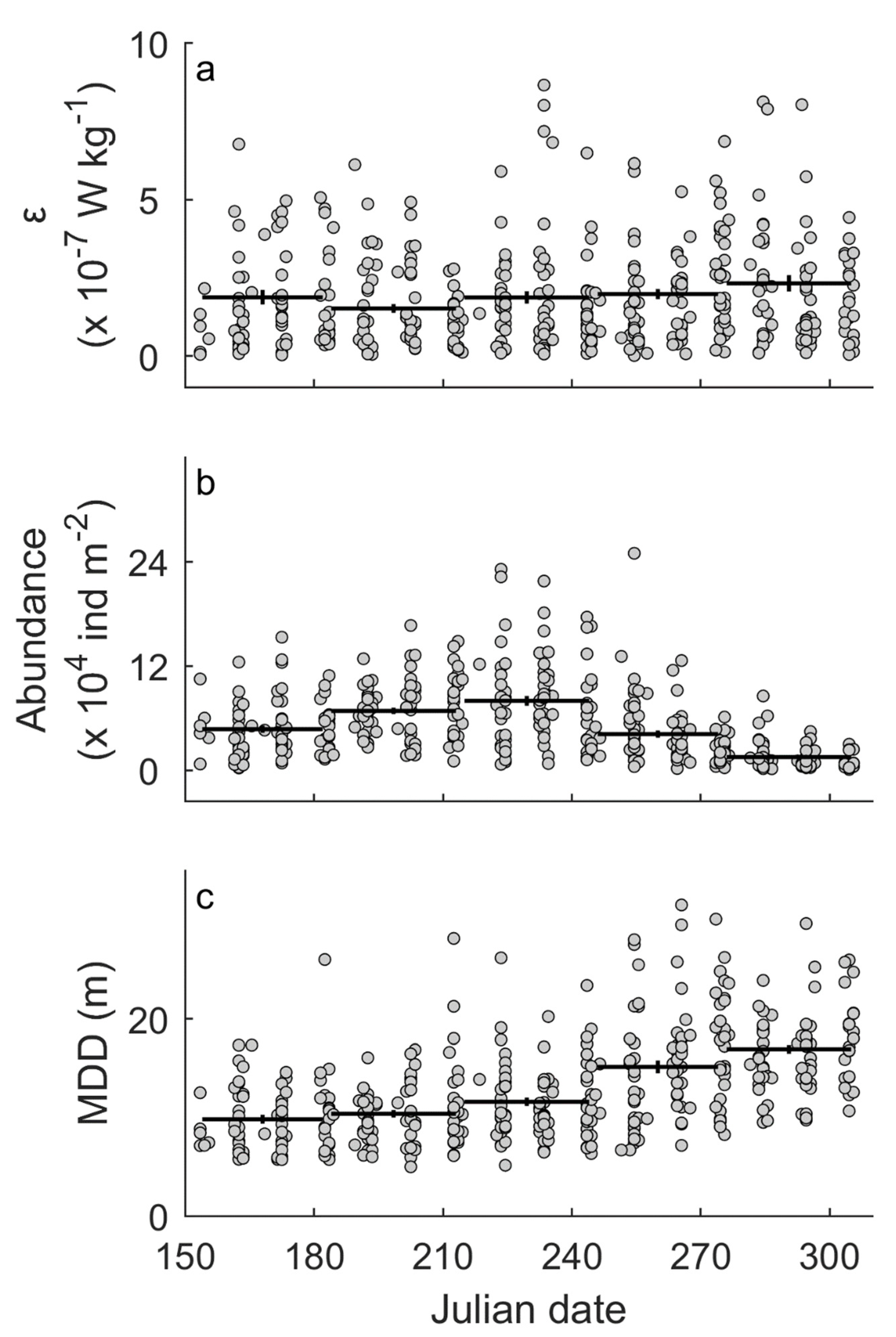
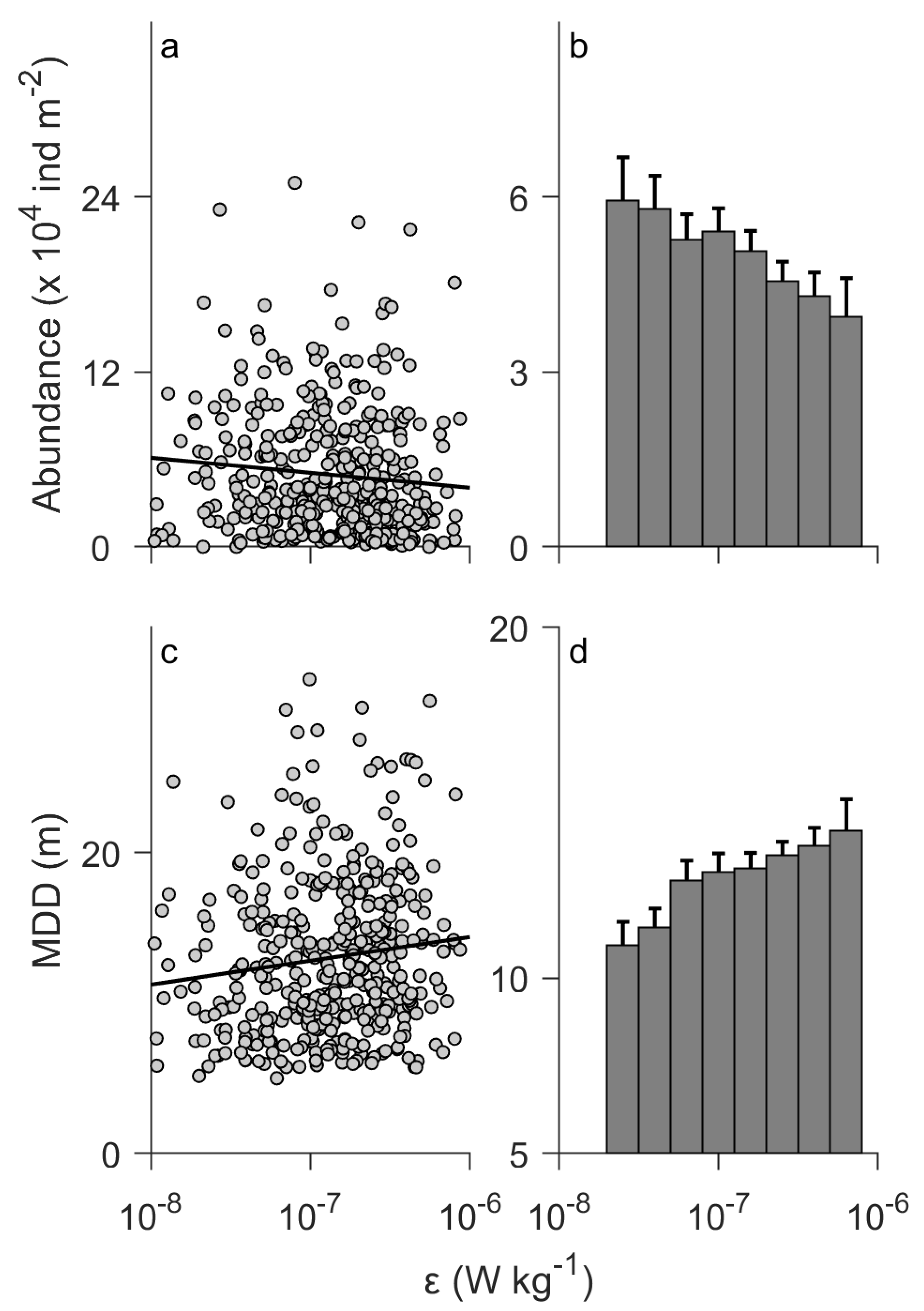
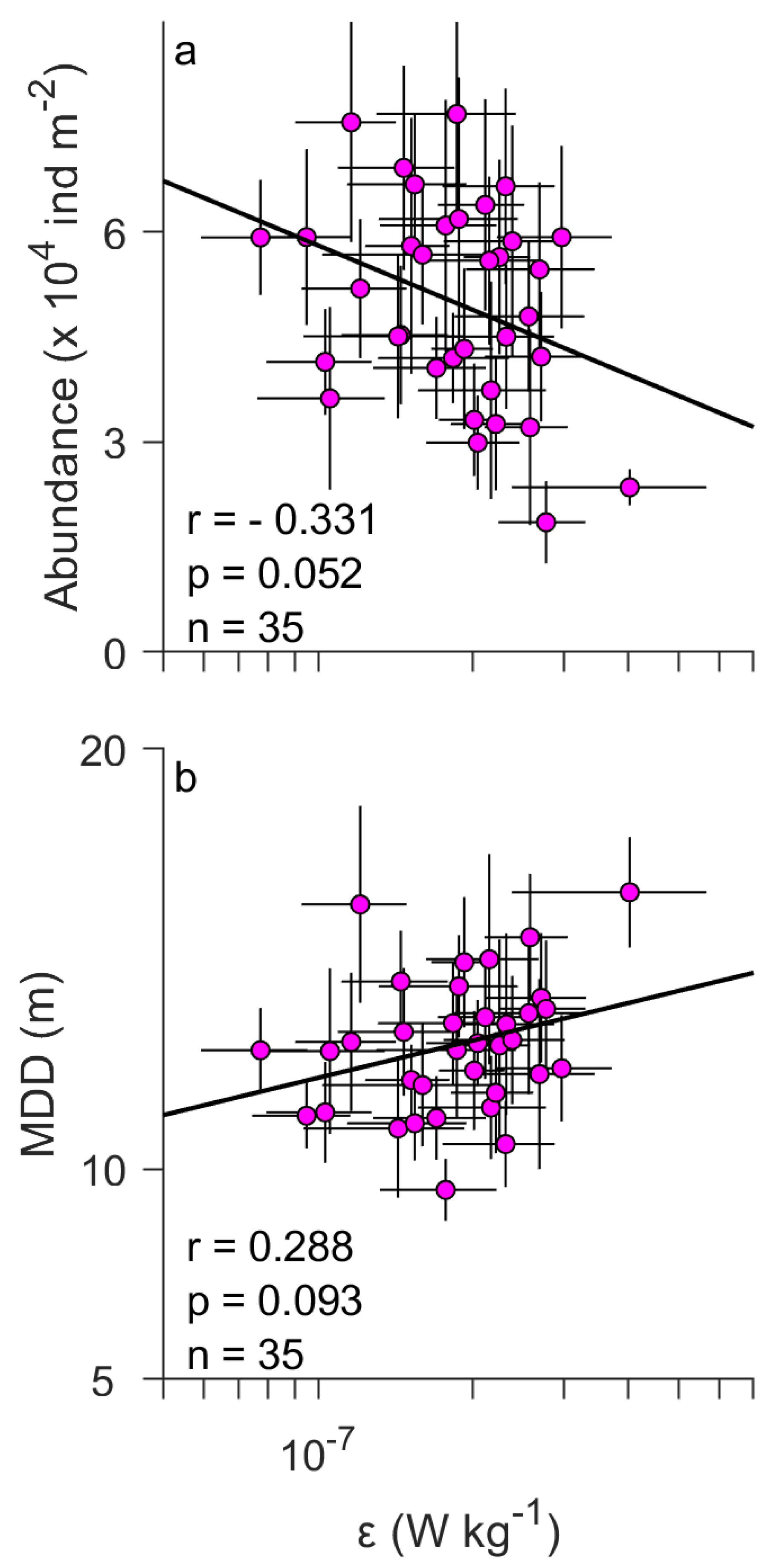
3. Results
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Steinberg, D.K.; Landry, M.R. Zooplankton and the ocean carbon cycle. Annu. Rev. Mar. Sci. 2017, 9, 413–444. [Google Scholar] [CrossRef] [PubMed]
- Thorpe, S.A. The Turbulent Ocean; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kiørboe, T. A Mechanistic Approach to Plankton Ecology; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Yamazaki, H.; Osborn, T.R.; Squires, K.D. Direct numerical simulation of planktonic contact in turbulent flow. J. Plankton Res. 1991, 13, 629–643. [Google Scholar] [CrossRef]
- Gilbert, O.M.; Buskey, E.J. Turbulence decreases the hydrodynamic predator sensing ability of the calanoid copepod Acartia tonsa. J. Plankton Res. 2005, 27, 1067–1071. [Google Scholar] [CrossRef]
- Visser, A.W.; Mariani, P.; Pigolotti, S. Swimming in turbulence: Zooplankton fitness in terms of foraging efficiency and predation risk. J. Plankton Res. 2009, 31, 121–133. [Google Scholar] [CrossRef]
- Seuront, L.; Yamazaki, H.; Souissi, S. Hydrodynamic disturbance and zooplankton swimming behavior. Zool. Stud. 2004, 43, 376–387. [Google Scholar]
- Lagadeuc, Y.; Boulé, M.; Dodson, J.J. Effect of vertical mixing on the vertical distribution of copepods in coastal waters. J. Plankton Res. 1997, 19, 1183–1204. [Google Scholar] [CrossRef]
- Incze, L.S.; Hebert, D.; Wolff, N.; Oakey, N.; Dye, D. Changes in copepod distributions associated with increased turbulence from wind stress. Mar. Ecol. Prog. Ser. 2001, 213, 229–240. [Google Scholar] [CrossRef]
- Visser, A.W.; Saito, H.; Saiz, E.; Kiørboe, T. Observations of copepod feeding and vertical distribution under natural turbulent conditions in the North Sea. Mar. Biol. 2001, 138, 1011–1019. [Google Scholar] [CrossRef]
- Maar, M.; Visser, A.W.; Nielsen, T.G.; Stips, A.; Saito, H. Turbulence and feeding behaviour affect the vertical distributions of Oithona similis and Microsetella norwegica. Mar. Ecol. Prog. Ser. 2006, 313, 157–172. [Google Scholar] [CrossRef]
- 36-Year Time Series (1963–1998) of Zooplankton, Temperature, and Salinity in the White Sea. Available online: https://www.nodc.noaa.gov/OC5/WH_SEA/index1.html (accessed on 20 November 2019).
- The ERA-40 archive. Available online: https://www.ecmwf.int/node/10595 (accessed on 20 November 2019).
- MacKenzie, B.R.; Leggett, W.C. Wind-based models for estimating the dissipation rates of turbulent energy in aquatic environments: Empirical comparisons. Mar. Ecol. Prog. Ser. 1993, 94, 207–216. [Google Scholar] [CrossRef]
- Prairie, Y.T.; Bird, D.F. Some misconceptions about the spurious correlation problem in the ecological literature. Oecologia 1989, 81, 285–288. [Google Scholar] [CrossRef] [PubMed]
- Pertsova, N.M.; Kosobokova, K.N. Zooplankton of the White Sea: Features of the composition and structure, seasonal dynamics, and the contribution to the formation of matter fluxes. Oceanol. C/C Okeanol. 2003, 43, S108–S122. [Google Scholar]
- Flood, P.R. House formation and feeding behaviour of Fritillaria borealis (Appendicularia: Tunicata). Mar. Biol. 2003, 143, 467–475. [Google Scholar] [CrossRef]
- Tönnesson, K.; Tiselius, P. Diet of the chaetognaths Sagitta setosa and S. elegans in relation to prey abundance and vertical distribution. Mar. Ecol. Prog. Ser. 2005, 289, 177–190. [Google Scholar] [CrossRef]
- Brun, P.; Payne, M.R.; Kiørboe, T. A trait database for marine copepods. Earth Syst. Sci. Data 2017, 9, 99–113. [Google Scholar] [CrossRef]
- Saiz, E.; Kiørboe, T. Predatory and suspension feeding of the copepod Acartia tonsa in turbulent environments. Mar. Ecol. Prog. Ser. 1995, 122, 147–158. [Google Scholar] [CrossRef]
- Saiz, E.; Calbet, A.; Broglio, E. Effects of small-scale turbulence on copepods: The case of Oithona davisae. Limnol. Oceanogr. 2003, 48, 1304–1311. [Google Scholar] [CrossRef]
- Pécseli, H.L.; Trulsen, J.K.; Stiansen, J.E.; Sundby, S.; Fossum, P. Feeing of plankton in turbulent oceans and lakes. Limnol. Oceanogr. 2019, 64, 1034–1046. [Google Scholar] [CrossRef]
- Oakey, N.S.; Elliott, J.A. Dissipation within the surface mixed layer. J. Phys. Oceanogr. 1982, 12, 171–185. [Google Scholar] [CrossRef]
- Shay, T.J.; Gregg, M.C. Convectively driven turbulent mixing in the upper ocean. J. Phys. Oceanogr. 1986, 16, 1777–1798. [Google Scholar] [CrossRef]
- Smyth, W.D.; Moum, J.N. 3D Turbulence. In Encyclopedia of Ocean Sciences, 3rd ed.; Cochran, J.K., Bokuniewicz, H.J., Yager, P.L., Eds.; Elsevier Ltd.: London, UK, 2019; Volume 3, pp. 486–496. [Google Scholar]
- Drost, E.J.F.; Lowe, R.J.; Ivey, G.N.; Jones, N.L. Wave-current interactions in the continental shelf bottom boundary layer of the Australian North West Shelf during tropical cyclone conditions. Cont. Shelf Res. 2018, 165, 78–92. [Google Scholar] [CrossRef]
- Kokubu, Y.; Yamazaki, H.; Nagai, T.; Gross, E.S. Mixing observations at a constricted channel of a semi-closed estuary: Tokyo Bay. Cont. Shelf Res. 2013, 69, 1–16. [Google Scholar] [CrossRef]
- Downing, J.A.; Pérusse, M.; Frenette, Y. Effect of interreplicate variance on zooplankton sampling design and data analysis. Limnol. Oceanogr. 1987, 32, 673–680. [Google Scholar] [CrossRef]
- Yamazaki, H.; Squires, K.D. Comparison of oceanic turbulence and copepod swimming. Mar. Ecol. Prog. Ser. 1996, 144, 299–301. [Google Scholar] [CrossRef]
- Buskey, E.J.; Swift, E. Behavioral responses of oceanic zooplankton to simulated bioluminescence. Biol. Bull. 1985, 168, 263–275. [Google Scholar] [CrossRef]

| Surface Abundance (×103 ind m−2) | MDD (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| t-Test | t-Test | |||||||||
| Feeding Mode | Turbulence Level | Mean ± Standard Error | df | t-Value | p-Value | Mean ± Standard Error | df | t-Value | p-Value | |
| Copepod | ||||||||||
| Acartia longiremis | Ambush/suspension | Low | 3.13 ± 0.30 | 417 | 0.76 | 0.449 | 12.45 ± 0.58 | 405 | −0.50 | 0.619 |
| High | 2.87 ± 0.32 | 13.05 ± 0.60 | ||||||||
| Microstella norvegica | Particle | Low | 0.43 ± 0.10 | 417 | 1.06 | 0.290 | 13.47 ± 0.73 | 199 | −0.17 | 0.864 |
| High | 0.52 ± 0.11 | 13.17 ± 0.61 | ||||||||
| Oithona similis | Ambush | Low | 35.53 ± 2.19 | 417 | 3.50 | 0.001 | 11.98 ± 0.34 | 417 | −2.55 | 0.011 |
| High | 26.96 ± 1.96 | 13.10 ± 0.35 | ||||||||
| Temora longicornis | Suspension | Low | 7.36 ± 1.05 | 417 | −0.29 | 0.771 | 13.36 ± 0.59 | 378 | −1.99 | 0.047 |
| High | 6.86 ± 1.08 | 14.54 ± 0.55 | ||||||||
| Chaetognath | ||||||||||
| Saggita elegans | Ambush | Low | 0.53 ± 0.08 | 417 | 2.85 | 0.005 | 24.53 ± 0.85 | 401 | −2.54 | 0.011 |
| High | 0.42 ± 0.09 | 27.78 ± 0.84 | ||||||||
| Cladoceran | ||||||||||
| Evadne nordmanni | Suspension | Low | 4.35 ± 0.57 | 417 | 1.71 | 0.088 | 7.64 ± 0.40 | 353 | −0.97 | 0.335 |
| High | 2.98 ± 0.42 | 7.83 ± 0.33 | ||||||||
| Appendiclarian | ||||||||||
| Fritillaria borealis | Suspension | Low | 3.98 ± 0.55 | 417 | 1.42 | 0.156 | 9.68 ± 0.45 | 361 | −1.35 | 0.179 |
| High | 3.66 ± 0.83 | 10.66 ± 0.52 | ||||||||
| y = ax + b | ||||
|---|---|---|---|---|
| n | a | b | p-Value | |
| ε | 419 | −4 × 10–10 | 1 × 10–6 | 0.639 |
| Abundance | 419 | 205 | −4 × 105 | 0.324 |
| MDD | 419 | −0.006 | 24 | 0.822 |
| Source | df | SS | MS | F | p-Value | |
|---|---|---|---|---|---|---|
| ε | Month | 4 | 3 × 10–13 | 8 × 10–14 | 2.2 | 0.073 |
| Abundance | Month | 4 | 2 × 1011 | 6 × 1010 | 42.7 | <0.001 |
| MDD | Month | 4 | 3271 | 818 | 42.5 | <0.001 |
| Linear Regression Model | ANOVA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| y = ax + b | |||||||||||
| n | a | b | r | p-Value | Source | df | SS | MS | F | p-Value | |
| Abundance | 419 | −1 × 104 | 3 × 104 | −0.12 | 0.012 | ε | 7 | 3 × 1010 | 4 × 109 | 2.2 | 0.004 |
| MDD | 419 | 1.57 | 23.8 | 0.14 | 0.003 | ε | 7 | 510 | 73 | 2.7 | 0.010 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanaka, M. Changes in Vertical Distribution of Zooplankton under Wind-Induced Turbulence: A 36-Year Record. Fluids 2019, 4, 195. https://doi.org/10.3390/fluids4040195
Tanaka M. Changes in Vertical Distribution of Zooplankton under Wind-Induced Turbulence: A 36-Year Record. Fluids. 2019; 4(4):195. https://doi.org/10.3390/fluids4040195
Chicago/Turabian StyleTanaka, Mamoru. 2019. "Changes in Vertical Distribution of Zooplankton under Wind-Induced Turbulence: A 36-Year Record" Fluids 4, no. 4: 195. https://doi.org/10.3390/fluids4040195




