Molecular Dynamics Simulation of the Superspreading of Surfactant-Laden Droplets. A Review
Abstract
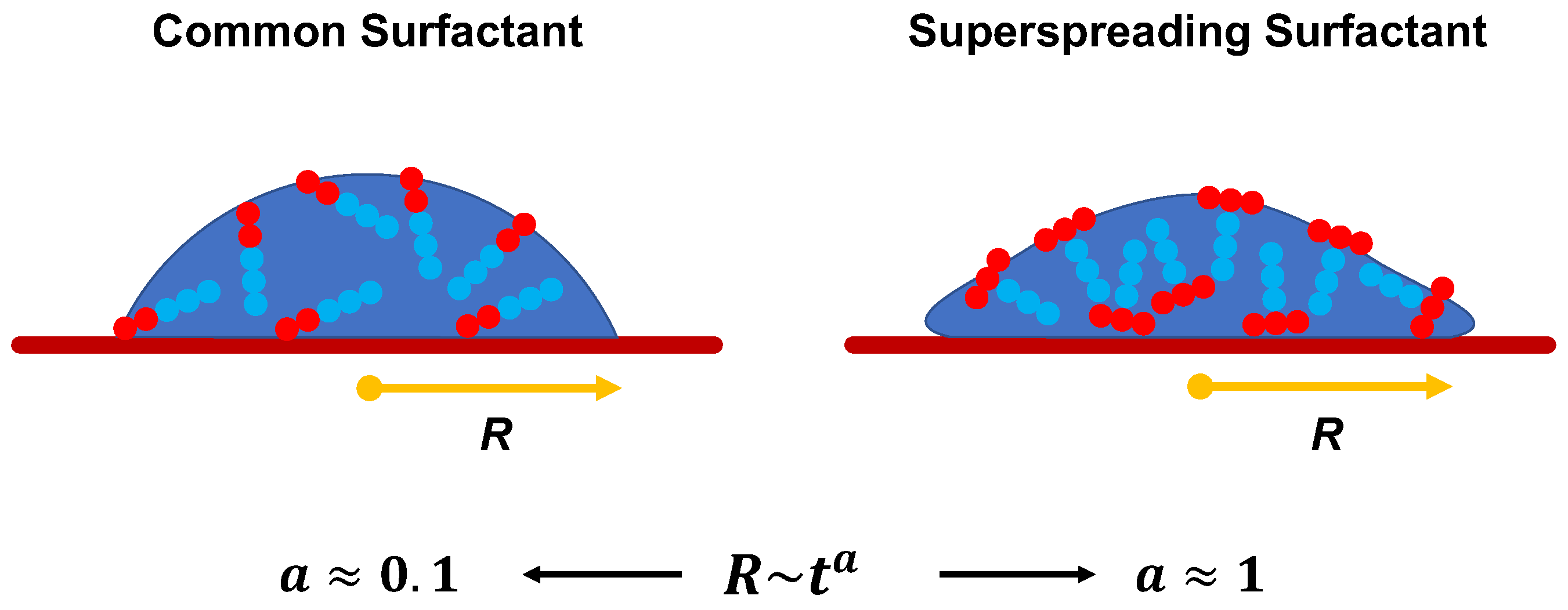
:1. Introduction
2. Methods
2.1. All-Atom Models
2.2. Bead–Spring Models
2.3. MARTINI Model
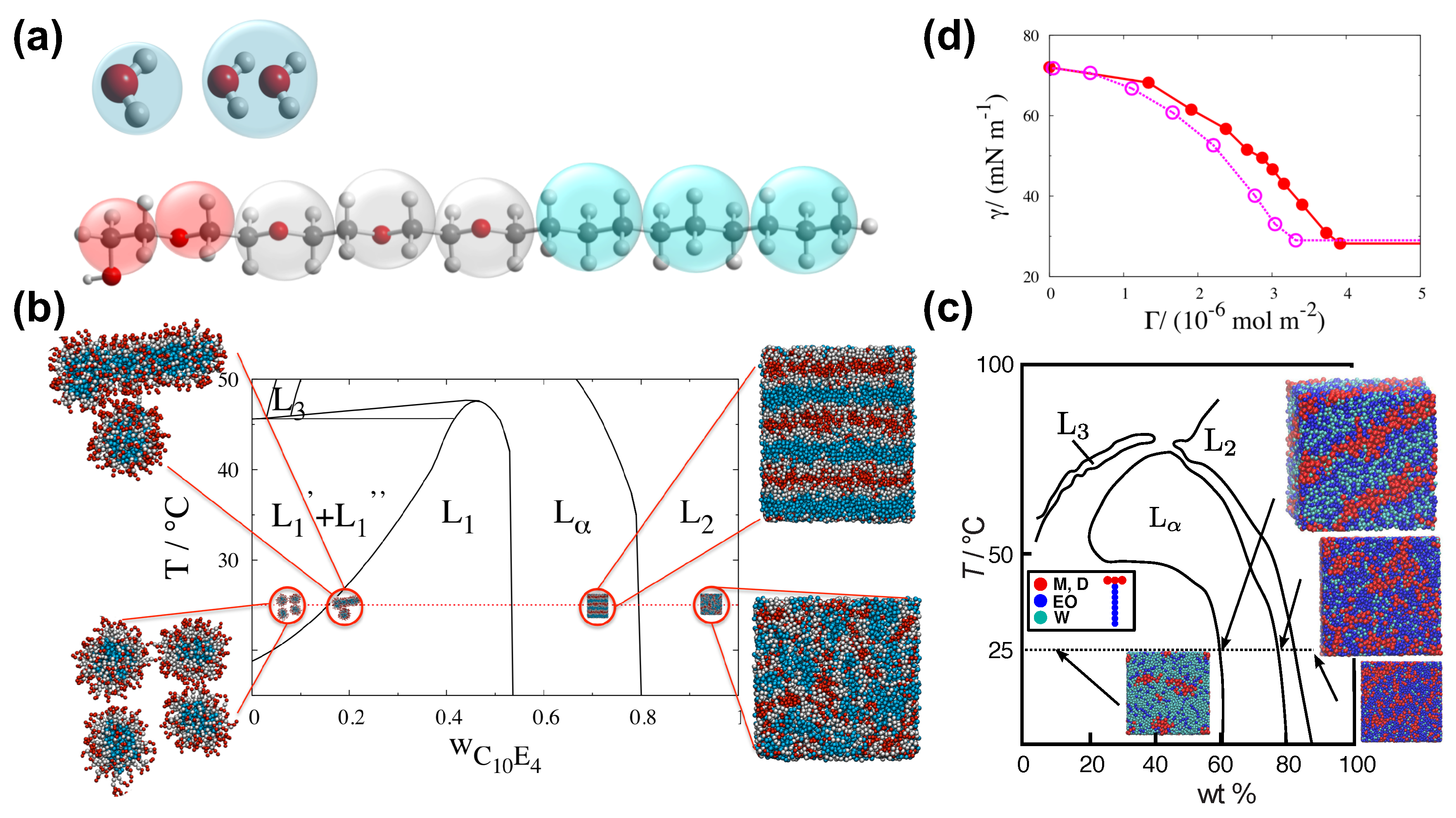
2.4. Statistical Associating Fluid Theory Model
3. Results and Discussion
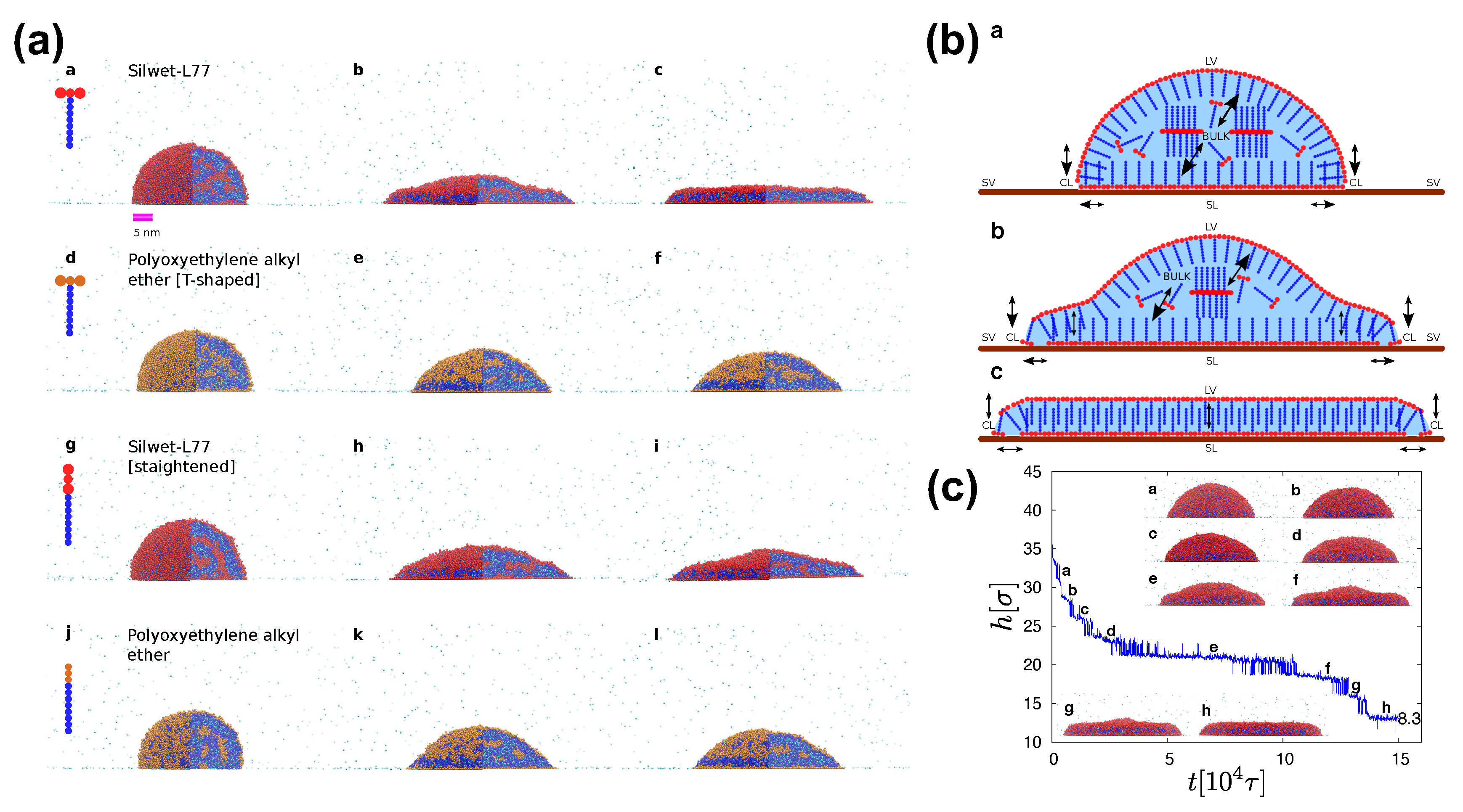
3.1. All-Atom Models
3.2. Bead–Spring Models
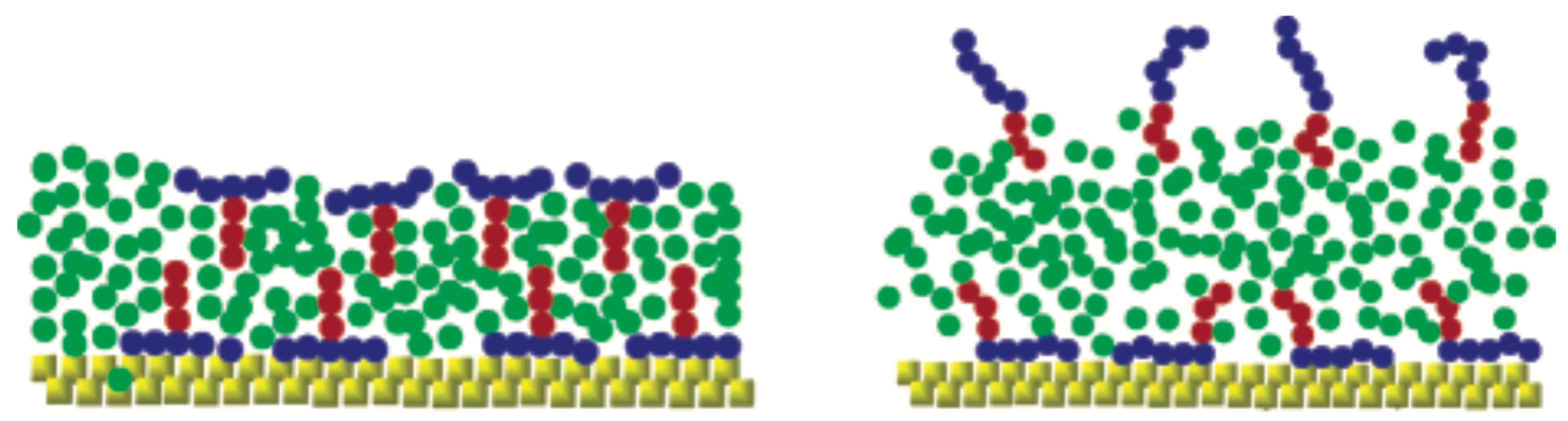
3.3. MARTINI Model
3.4. SAFT Model
3.5. On the Length and Time Scales of Superspreading
4. Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwarz, E.G.; Reid, W.G. Surface active agents—Their behavior and industrial use. Ind. Eng. Chem. 1964, 56, 26–35. [Google Scholar] [CrossRef]
- Hill, R.M. Superspreading. Curr. Opin. Colloid Interface Sci. 1998, 3, 247–254. [Google Scholar] [CrossRef]
- Nikolov, A.; Wasan, D. Superspreading mechanisms: An overview. Eur. Phys. J. Spec. Top. 2011, 197, 325–341. [Google Scholar] [CrossRef]
- Venzmer, J. Superspreading—20 years of physicochemical research. Curr. Opin. Colloid Interface Sci. 2011, 16, 335–343. [Google Scholar] [CrossRef]
- Theodorakis, P.E.; Müller, E.A.; Craster, R.V.; Matar, O.K. Insights into surfactant-assisted superspreading. Curr. Opin. Colloid Interface Sci. 2014, 19, 283–289. [Google Scholar] [CrossRef]
- Sankaran, A.; Karakashev, S.I.; Soumyadip, S.; Grozev, N.; Yarin, A.L. On the nature of the superspreaders. Adv. Colloid Interface Sci. 2019, 263, 1–18. [Google Scholar] [CrossRef]
- Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J.; Rolley, E. Wetting and spreading. Rev. Mod. Phys. 2009, 81, 739–805. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. Dynamics and stability of thin liquid films. Rev. Mod. Phys. 2009, 81, 1131–1198. [Google Scholar] [CrossRef]
- Matar, O.K.; Craster, R.V. Dynamics of surfactant-assisted spreading. Soft Matter 2009, 5, 3801–3809. [Google Scholar] [CrossRef]
- Rosen, M.J.; Kunjappu, J.T. Surfactants and Interfacial Phenomena, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 600. [Google Scholar]
- Stoebe, T.; Lin, Z.; Hill, R.M.; Ward, M.D.; Davis, H.T. Surfactant-enhanced spreading. Langmuir 1996, 12, 337–344. [Google Scholar] [CrossRef]
- Stoebe, T.; Hill, R.M.; Ward, M.D.; Davis, H.T. Enhanced spreading of aqueous films containing ionic surfactants on solid substrates. Langmuir 1997, 13, 7276–7281. [Google Scholar] [CrossRef]
- Stoebe, T.; Lin, Z.; Hill, R.M.; Ward, M.D.; Davis, H.T. Enhanced spreading of aqueous films containing ethoxylated alcohol surfactants on solid substrates. Langmuir 1997, 13, 7270–7275. [Google Scholar] [CrossRef]
- Stoebe, T.; Lin, Z.; Hill, R.M.; Ward, M.D.; Davis, H.T. Superspreading of aqueous films containing trisiloxane surfactant on solid substrates. Langmuir 1997, 13, 7282–7286. [Google Scholar] [CrossRef]
- Kovalchuk, N.M.; Trybala, A.; Starov, V.; Matar, O.; Ivanova, N. Fluoro- vs hydrocarbon surfactants: Why do they differ in wetting performance? Adv. Colloid Interface Sci. 2014, 210, 65–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kovalchuk, N.M.; Matar, O.K.; Craster, R.V.; Starov, V.M. The effect of adsorption kinetics on the rate of surfactant-enhanced spreading. Soft Matter 2016, 12, 1009–1013. [Google Scholar] [CrossRef]
- Kovalchuk, N.M.; Trybala, A.; Arjmandi-Tash, O.; Starov, V. Surfactant-enhanced spreading: Experimental achievements and possible mechanisms. Adv. Colloid Interface Sci. 2016, 233, 155–160. [Google Scholar] [CrossRef]
- Lee, K.S.; Starov, V.M.; Muchatuta, T.J.P.; Srikantha, S.I.R. Spreading of trisiloxanes over thin aqueous layers. Colloid J. 2009, 71, 365–369. [Google Scholar] [CrossRef] [Green Version]
- Theodorakis, P.E.; Müller, E.A.; Craster, R.V.; Matar, O.K. Modelling the superspreading of surfactant-laden droplets with computer simulation. Soft Matter 2015, 11, 9254–9261. [Google Scholar] [CrossRef] [Green Version]
- Theodorakis, P.E.; Müller, E.A.; Craster, R.V.; Matar, O.K. Superspreading: Mechanisms and molecular design. Langmuir 2015, 31, 2304–2309. [Google Scholar] [CrossRef]
- Isele-Holder, R.E.; Ismail, A.E. Atomistic Potentials for Trisiloxane, Alkyl Ethoxylate, and Perfluoroalkane-Based Surfactants with TIP4P/2005 and Application to Simulations at the Air–Water Interface. J. Phys. Chem. B 2014, 118, 9284–9297. [Google Scholar] [CrossRef]
- Isele-Holder, R.E.; Berkels, B.; Ismail, A.E. Smoothing of contact lines in spreading droplets by trisiloxane surfactants and its relevance for superspreading. Soft Matter 2015, 11, 4527–4539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Badra, A.T.; Zahaf, H.; Alla, H.; Roques-Carmes, T. A numerical model of superspreading surfactants on hydrophobic surface. Phys. Fluids 2018, 30, 092102. [Google Scholar] [CrossRef]
- Wei, H.H. Marangoni-enhanced capillary wetting in surfactant-driven superspreading. J. Fluid Mech. 2018, 855, 181–209. [Google Scholar] [CrossRef]
- Karapetsas, G.; Craster, R.V.; Matar, O.K. On surfactant-enhanced spreading and superspreading of liquid drops on solid surfaces. J. Fluid Mech. 2011, 670, 5–37. [Google Scholar] [CrossRef] [Green Version]
- Theodorakis, P.E.; Smith, E.R.; Müller, E.A. Dynamics of trisiloxane wetting: Effects of diffusion and surface hydrophobicity. Colloids Surf. A 2019, 581, 123810. [Google Scholar] [CrossRef]
- Tanner, L.H. The spreading of silicone oil drops on horizontal surfaces. J. Phys. D 1979, 12, 1473–9615. [Google Scholar] [CrossRef]
- Radulovic, J.; Sefiane, K.; Shanahan, E.R. Spreading of aqueous droplets with common and superspreading surfactants. A molecular dynamics study. J. Phys. Chem. C 2010, 114, 13620–13629. [Google Scholar] [CrossRef]
- Semenov, S.; Trybala, A.; Agogo, H.; Kovalchuk, N.; Ortega, F.; Rubio, R.G.; Starov, V.M.; Velarde, M.G. Evaporation of droplets of surfactant solutions. Langmuir 2013, 29, 10028–10036. [Google Scholar] [CrossRef]
- Ivanova, N.A.; Zhantenova, Z.B.; Starov, V.M. Wetting dynamics of polyoxyethylene alkyl ethers and trisiloxanes in respect of polyoxyethylene chains and properties of substrates. Colloids Surf. A 2012, 413, 307–313. [Google Scholar] [CrossRef] [Green Version]
- Radulovic, J.; Sefiane, K.; Shanahan, M.E. On the effect of pH on spreading of surfactant solutions on hydrophobic surfaces. J. Colloid Interface Sci. 2009, 332, 497–504. [Google Scholar] [CrossRef]
- Ivanova, N.; Starov, V.; Rubio, R.; Ritacco, H.; Hilal, N.; Johnson, D. Critical wetting concentrations of trisiloxane surfactants. Colloids Surf. A 2010, 354, 143–148. [Google Scholar] [CrossRef] [Green Version]
- Svitova, T.; Hill, R.M.; Smirnova, Y.; Stuermer, A.; Yakubov, G. Wetting and interfacial transitions in dilute solutions of trisiloxane surfactants. Langmuir 1998, 14, 5023–5031. [Google Scholar] [CrossRef]
- Radulovic, J.; Sefiane, K.; Shanahan, M.E.R. Ageing of trisiloxane solutions. Chem. Eng. Sci. 2010, 65, 5251–5255. [Google Scholar] [CrossRef]
- Rosen, M.J.; Wu, Y. Superspreading of trisiloxane surfactant mixtures on hydrophobic surfaces. 1. Interfacial adsorption of aqueous trisiloxane surfactant-N-alkyl-pyrrolidinone mixtures on polyethylene. Langmuir 2001, 17, 7296–7305. [Google Scholar] [CrossRef]
- Rosen, M.J.; Wu, Y. Superspreading of trisiloxane surfactant mixtures on hydrophobic surfaces 2. Interaction and spreading of aqueous trisiloxane surfactant-N-alkyl-pyrrolidinone mixtures in contact with polyethylene. Langmuir 2002, 18, 2205–2215. [Google Scholar]
- Radulovic, J.; Sefiane, K.; Shanahan, M.E.R. Spreading and Wetting Behaviour of Trisiloxanes. J. Bionic Eng. 2009, 6, 341–349. [Google Scholar] [CrossRef]
- Ivanova, N.A.; Starov, V.M. Wetting of low free energy surfaces by aqueous surfactant solutions. Curr. Opin. Colloid Interface Sci. 2011, 16, 285–291. [Google Scholar] [CrossRef]
- Hautman, J.; Klein, M.L. Microscopic wetting phenomena. Phys. Rev. Lett. 1991, 67, 1763–1766. [Google Scholar] [CrossRef]
- Mar, W.; Klein, M.L. A molecular-dynamics study of n-hexadecane droplets on a hydrophobic surface. J. Phys. Condens. Matter 1994, 6, A381–A388. [Google Scholar] [CrossRef]
- Fan, C.F.; Caǧin, T. Wetting of crystalline polymer surfaces: A molecular dynamics simulation. J. Chem. Phys. 1995, 103, 9053–9061. [Google Scholar] [CrossRef] [Green Version]
- Lane, J.M.D.; Chandross, M.; Lorenz, C.D.; Stevens, M.J.; Grest, G.S. Water penetration of damaged self-assembled monolayers. Langmuir 2008, 24, 5734–5739. [Google Scholar] [CrossRef] [PubMed]
- Saville, G. Computer simulation of the liquid-solid-vapour contact angle. J. Chem. Soc. Faraday Trans. 2 1977, 73, 1122–1132. [Google Scholar] [CrossRef]
- Sikkenk, J.; Indekeu, J.; van Leeuwen, J.; Vossnack, E.; Bakker, A. Simulation of wetting and drying at solid-fluid interfaces on the Delft Molecular Dynamics Processor. J. Stat. Phys. 1988, 52, 23–44. [Google Scholar] [CrossRef]
- Nijmeijer, M.; Bruin, C.; Bakker, A.; Leeuwen, J.V. A visual measurement of contact angles in a molecular-dynamics simulation. Phys. A 1989, 160, 166–180. [Google Scholar] [CrossRef]
- Nijmeijer, M.J.P.; Bruin, C.; Bakker, A.F.; van Leeuwen, J.M.J. Wetting and drying of an inert wall by a fluid in a molecular-dynamics simulation. Phys. Rev. A 1990, 42, 6052–6059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nieminen, J.A.; Ala-Nissila, T. Dynamics of Spreading of Small Droplets of Chainlike Molecules on Surfaces. EPL 1994, 25, 593. [Google Scholar] [CrossRef]
- Nieminen, J.A.; Ala-Nissila, T. Spreading dynamics of polymer microdroplets: A molecular-dynamics study. Phys. Rev. E 1994, 49, 4228–4236. [Google Scholar] [CrossRef]
- de Ruijter, M.J.; Blake, T.D.; De Coninck, J. Dynamic Wetting Studied by Molecular Modeling Simulations of Droplet Spreading. Langmuir 1999, 15, 7836–7847. [Google Scholar] [CrossRef]
- Blake, T.; Clarke, A.; Coninck, J.D.; de Ruijter, M.; Voué, M. Droplet spreading: A microscopic approach. Colloids Surf. A 1999, 149, 123–130. [Google Scholar] [CrossRef]
- Blake, T.; Decamps, C.; Coninck, J.D.; de Ruijter, M.; Voué, M. The dynamics of spreading at the microscopic scale. Colloids Surf. A Physicochem. Eng. Asp. 1999, 154, 5–11. [Google Scholar] [CrossRef]
- Voué, M.; Semal, S.; De Coninck, J. Dynamics of Spreading on Heterogeneous Substrates in a Complete Wetting Regime. Langmuir 1999, 15, 7855–7862. [Google Scholar] [CrossRef]
- Voué, M.; Rovillard, S.; De Coninck, J.; Valignat, M.P.; Cazabat, A.M. Spreading of Liquid Mixtures at the Microscopic Scale: A Molecular Dynamics Study of the Surface-Induced Segregation Process. Langmuir 2000, 16, 1428–1435. [Google Scholar] [CrossRef]
- Voué, M.; Coninck, J.D. Spreading and wetting at the microscopic scale: Recent developments and perspectives. Acta Mater. 2000, 48, 4405–4417. [Google Scholar] [CrossRef]
- Coninck, J.D.; de Ruijter, M.J.; Voué, M. Dynamics of wetting. Curr. Opin. Colloid Interface Sci. 2001, 6, 49–53. [Google Scholar] [CrossRef]
- Lundgren, M.; Allan, N.L.; Cosgrove, T.; George, N. Wetting of water and water/ethanol droplets on a non-polar surface: A molecular dynamics study. Langmuir 2002, 18, 10462–10466. [Google Scholar] [CrossRef]
- Lundgren, M.; Allan, N.L.; Cosgrove, T.; George, N. Molecular Dynamics Study of Wetting of a Pillar Surface. Langmuir 2003, 19, 7127–7129. [Google Scholar] [CrossRef]
- Heine, D.R.; Grest, G.S.; Webb, E.B. Spreading dynamics of polymer nanodroplets. Phys. Rev. E 2003, 68, 061603. [Google Scholar] [CrossRef] [Green Version]
- Werder, T.; Walther, J.H.; Jaffe, R.L.; Halicioglu, T.; Koumoutsakos, P. On the water–carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. 2003, 107, 1345–1352. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Tomassone, M.S.; Couzis, A.; Maldarelli, C.M.; Banavar, J.R.; Koplik, J. Molecular dynamics simulation of gaseous–liquid phase transitions of soluble and insoluble surfactants at a fluid interface. J. Chem. Phys. 2001, 115, 8634–8642. [Google Scholar] [CrossRef]
- Tomassone, M.S.; Couzis, A.; Maldarelli, C.M.; Banavar, J.R.; Koplik, J. Phase transitions of soluble surfactants at a liquid–vapor interface. Langmuir 2001, 17, 6037–6040. [Google Scholar] [CrossRef]
- Shinoda, W.; DeVane, R.; Klein, M.L. Multi-property fitting and parameterization of a coarse grained model for aqueous surfactants. Mol. Simul. 2007, 33, 27–36. [Google Scholar] [CrossRef]
- Shinoda, W.; DeVane, R.; Klein, M.L. Coarse-grained molecular modeling of non-ionic surfactant self-assembly. Soft Matter 2008, 4, 2454–2462. [Google Scholar] [CrossRef]
- Herdes, C.; Santiso, E.E.; James, C.; Eastoe, J.; Müller, E.A. Modelling the interfacial behaviour of dilute light-switching surfactant solutions. J. Colloid Interface Sci. 2015, 445, 16–23. [Google Scholar] [CrossRef] [PubMed]
- Lobanova, O.; Mejía, A.; Jackson, G.; Müller, E.A. SAFT-γ force field for the simulation of molecular fluids 6: Binary and ternary mixtures comprising water, carbon dioxide, and n-alkanes. J. Chem. Thermodyn. 2016, 93, 320–336. [Google Scholar] [CrossRef]
- Lobanova, O. Development of Coarse-grained Force Fields from a Molecular Based Equation of State for Thermodynamic and Structural Properties of Complex Fluids. Ph.D. Thesis, Imperial College London, London, UK, 2014. [Google Scholar]
- Shen, Y.; Couzis, A.; Koplik, J.; Maldarelli, C.; Tomassone, M.S. Molecular dynamics study of the influence of surfactant structure on surfactant-facilitated spreading of droplets on solid surfaces. Langmuir 2005, 21, 12160–12170. [Google Scholar] [CrossRef]
- Kim, H.Y.; Yin, Q.; Fichthorn, K.A. Molecular dynamics simulation of nanodroplet spreading enhanced by linear surfactants. J. Chem. Phys. 2006, 125, 174708. [Google Scholar] [CrossRef]
- Halverson, J.D.; Maldarelli, C.; Couzis, A.; Koplik, J. Wetting of hydrophobic substrates by nanodroplets of aqueous trisiloxane and alkyl polyethoxylate surfactant solutions. Chem. Eng. Sci. 2009, 64, 4657–4667. [Google Scholar] [CrossRef]
- Sergi, D.; Scocchi, G.; Ortona, A. Coarse-graining MARTINI model for molecular-dynamics simulations of the wetting properties of graphitic surfaces with non-ionic, long-chain, and T-shaped surfactants. J. Chem. Phys. 2012, 137, 094904. [Google Scholar] [CrossRef] [Green Version]
- Smith, E.; Theodorakis, P.E.; Craster, R.V.; Matar, O.K. Moving contact lines: Linking molecular dynamics and continuum-scale modeling. Langmuir 2018, 34, 12501–12518. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, D.A.; Case, D.A.; Singh, U.C.; Ghio, C.; Alagona, G.; Profeta, S.; Weiner, P. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 1984, 106, 765–784. [Google Scholar] [CrossRef]
- Nikolov, A.D.; Wasan, D.T.; Chengara, A.; Koczo, K.; Policello, G.A.; Kolossvary, I. Superspreading driven by Marangoni flow. Adv. Colloid Interface Sci. 2002, 96, 325–338. [Google Scholar] [CrossRef]
- Halverson, J.D.; Maldarelli, C.; Couzis, A.; Koplik, J. Atomistic simulations of the wetting behavior of nanodroplets of water on homogeneous and phase separated self-assembled monolayers. Soft Matter 2010, 6, 1297–1307. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6645. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Optimized intermolecular potential functions for liquid alcohols. J. Am. Chem. Soc. 1986, 90, 1276–1284. [Google Scholar] [CrossRef]
- Sok, R.M.; Berendsen, H.J.C.; van Gunsteren, W.F. Molecular dynamics simulation of the transport of small molecules across a polymer membrane. J. Chem. Phys. 1992, 96, 4699–4704. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Rigby, D. Polysiloxanes: Ab initio force field and structural, conformational and thermophysical properties. Spectrochim. Acta Part A 1997, 8539, 1301–1323. [Google Scholar] [CrossRef]
- Frischknecht, A.L.; Curro, J.G. Improved United Atom force field for poly(dimethylsiloxane). Macromolecules 2003, 36, 2122–2129. [Google Scholar] [CrossRef]
- Abascal, J.; Vega, C.A. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Vega, C.A.; Abascal, J. Simulating water with rigid nonpolarizable models: A general perspective. Phys. Chem. Chem. Phys. 2011, 13, 19663–19688. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulation of liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; van Gusteren, W.F.A. Biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, L.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-Atom description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Sorensen, R.A.; Liau, W.B.; Kesner, L.; Boyd, R.H. Prediction of polymer crystal structures and properties. Polyethylene and poly(oxymethylene). Macromolecules 1988, 21, 200–208. [Google Scholar] [CrossRef]
- Borodin, O.; Smith, G.D. Development of quantum chemistry-based force fields for poly(ethylene oxide) with many-body polarization itneractions. J. Phys. Chem. B 2003, 107, 6801–6812. [Google Scholar] [CrossRef]
- Borodin, O.; Smith, G.D.; Bedrov, D. A quantum chemistry based force field for perfluoroalkanes and poly(tetrafluoroethylene). J. Phys. Chem. B 2002, 106, 9912–9922. [Google Scholar] [CrossRef]
- Smith, J.; Borodin, O.; Smith, G.A. A quantum chemistry based force-field for poly(dimethoxysiloxane. J. Phys. Chem. B 2004, 108, 20340–20350. [Google Scholar] [CrossRef]
- Isele-Holder, R.E.; Mitchell, W.; Hammond, J.R.; Kohlmeyer, A.; Ismail, A.E. Reconsidering dispersion potentials: Reduced cutoffs in mesh-based Ewald solvers can be faster than truncation. J. Chem. Theory Comput. 2013, 9, 5412–5420. [Google Scholar] [CrossRef] [PubMed]
- Müller, E.A.; Jackson, G. Force field parameters from the SAFT-γ equation of state for use in coarse-grained molecular simulations. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 405–427. [Google Scholar] [CrossRef] [PubMed]
- Frederix, P.W.J.; Patmanidis, I.; Marrink, S.J. Molecular simulations of self-assembling bio-inspired supramolecular systems and their connection to experiments. Chem. Soc. Rev. 2018, 47, 3470–3489. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingólfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational modeling of realistic cell membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef] [PubMed]
- GROMACS Package. 2019. Available online: http://www.gromacs.org (accessed on 29 September 2019).
- MARTINI Force-Field. 2019. Available online: http://cgmartini.nl (accessed on 29 September 2019).
- Poma, A.B.; Cieplak, M.; Theodorakis, P.E. Combining the MARTINI and structure-based coarse-grained approaches for the molecular dynamics studies of conformational transitions in proteins. J. Chem. Theory Comput. 2017, 13, 1366–1374. [Google Scholar] [CrossRef]
- Lobanova, O.; Avendaño, C.; Lafitte, T.; Müller, E.A.; Jackson, G. SAFT-γ force field for the simulation of molecular fluids. 4. A single-site coarse-grained model of water applicable over a wide temperature range. Mol. Phys. 2015, 113, 1228–1249. [Google Scholar] [CrossRef]
- Rahman, S.; Lobanova, O.; Jiménez-Serratos, G.B.C.; Raptis, V.; Müller, E.A.; Jackson, G.; Avendaño, C.; Galindo, A. SAFT-γ force field for the simulation of molecular fluids. 5. Hetero-group coarse-grained models of linear alkanes and the importance of intracmolecular interactions. J. Phys. Chem. B 2018, 122, 9161–9177. [Google Scholar] [CrossRef]
- Morgado, P.; Lobanova, O.; Müller, E.A.; Jackson, G.; Almeida, M.; Filipe, E.J.M. SAFT-γ force field for the simulation of molecular fluids: 8. Hetero-segmented coarse-grained models of perfluoroalkylalkanes assessed with new vapour–liquid interfacial tension data. Mol. Phys. 2016, 114, 2597–2614. [Google Scholar] [CrossRef]
- Papaioannou, V.; Lafitte, T.; Avendaño, C.; Adjiman, C.S.; Jackson, G.; Müller, E.A.; Galindo, A. Group contribution methodology based on the statistical associating fluid theory for heteronuclear molecules formed from Mie segments. J. Chem. Phys. 2014, 140, 054107. [Google Scholar] [CrossRef]
- Lafitte, T.; Apostolakou, A.; Avendaño, C.; Galindo, A.; Adjiman, C.S.; Müller, E.A.; Jackson, G. Accurate statistical associating fluid theory for chain molecules formed from Mie segments. J. Chem. Phys. 2013, 139, 154504. [Google Scholar] [CrossRef] [PubMed]
- Avendaño, C.; Lafitte, T.; Galindo, A.; Adjiman, C.S.; Jackson, G.; Müller, E.A. SAFT-γ Force Field for the Simulation of Molecular Fluids. 1. A Single-Site Coarse Grained Model of Carbon Dioxide. J. Phys. Chem. B 2011, 115, 11154–11169. [Google Scholar] [CrossRef] [PubMed]
- Avendaño, C.; Lafitte, T.; Galindo, A.; Adjiman, C.S.; Müller, E.A.; Jackson, G. SAFT-γ Force Field for the Simulation of Molecular Fluids: 2. Coarse-Grained Models of Greenhouse Gases. J. Phys. Chem. B 2013, 117, 2717–2733. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Serratos, G.; Herdes, C.; Haslam, A.J.; Jackson, G.; Müller, E.A. Group Contribution Coarse-Grained Molecular Simulations of Polystyrene Melts and Polystyrene Solutions in Alkanes Using the SAFT-γ Force Field. Macromolecules 2017, 50, 4840–4853. [Google Scholar] [CrossRef]
- Herdes, C.; Ervik, A.; Mejía, A.; Müller, E. Prediction of the water/oil interfacial tension from molecular simulations using the coarse-grained SAFT-γ Mie force field. Fluid Phase Equilibria 2017, 476, 9–15. [Google Scholar] [CrossRef]
- Hill, R.M.; He, M.; Davis, H.T.; Scriven, L.E. Comparison of the Liquid Crystal Phase Behavior of Four Trisiloxane Superwetter Surfactants. Langmuir 1994, 10, 1724–1734. [Google Scholar] [CrossRef]
- Eastoe, J.; Dalton, J.S.; Rogueda, P.G.A.; Crooks, E.R.; Pitt, A.R.; Simister, E.A. Dynamic surface tensions of nonionic surfactant solutions. J. Colloid Interface Sci. 1997, 188, 423–430. [Google Scholar] [CrossRef]
- Ramrattan, N.; Avendaño, C.; Müller, E.; Galindo, A. A corresponding-states framework for the description of the Mie family of intermolecular potentials. Mol. Phys. 2015, 113, 932–947. [Google Scholar] [CrossRef] [Green Version]
- Forte, E.; Haslam, A.J.; Jackson, G.; Müller, E.A. Effective coarse-grained solid-fluid potentials and their application to model adsorption of fluids on heterogeneous surfaces. Phys. Chem. Chem. Phys. 2014, 16, 19165–19180. [Google Scholar] [CrossRef]
- Ruckenstein, E. Effect of short range interactions on spreading. J. Colloid Interface Sci. 1996, 179, 136–142. [Google Scholar] [CrossRef]
- Ritacco, H.A.; Fainerman, V.B.; Ortega, F.; Rubio, R.G.; Ivanova, N.; Starov, V.M. Equilibrium and dynamic surface properties of trisiloxane aqueous solutions. Colloids Surf. A 2010, 365, 204–209. [Google Scholar] [CrossRef]
- McNamara, S.; Koplik, J.; Banavar, J.R. Simulation of surfactant-enhanced spreading. Lect. Notes Comput. Sci. 2001, 2073, 551–559. [Google Scholar]
- Theodorakis, P.E.; Egorov, S.A.; Milchev, A. Stiffness-guided motion of a droplet on a solid substrate. J. Chem. Phys. 2017, 146, 244705. [Google Scholar] [CrossRef] [PubMed]
- Starov, V.M.; Kosvintsev, S.R.; Velarde, M.G. Spreading of surfactant solutions over hydrophobic substrates. J. Colloid Interface Sci. 2000, 227, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Couzis, A.; Maldarelli, C. Measurement of the kinetic rate constants for the adsorption of superspreading trisiloxanes to an air/aqueous interface and the relevance of these measurements to the mechanism of superspreading. J. Colloid Interface Sci. 2003, 267, 272–285. [Google Scholar] [CrossRef]
- Churaev, N.V.; Esipova, N.E.; Hill, R.M.; Sobolev, V.D.; Starov, V.M.; Zorin, Z.M. The Superspreading Effect of Trisiloxane Surfactant Solutions. Langmuir 2001, 17, 1338–1348. [Google Scholar] [CrossRef]
- Rafaï, S.; Dipak, S.; Bergeron, V.; Meunier, J.; Bonn, D. Superspreading: Aqueous surfactant drops spreading on hydrophobic surfaces. Langmuir 2002, 18, 10486–10488. [Google Scholar] [CrossRef]
- Tiberg, F.; Cazabat, C.M. Self-assembly and spreading of non-ionic trisiloxane surfactants. Europhys. Lett. 1994, 25, 205–210. [Google Scholar] [CrossRef]
- Ruckenstein, E. Superspreading: A possible mechanism. Colloids Surf. A 2012, 412, 36–37. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Ingólfsson, H.I.; Böckmann, R.A.; Tieleman, D.P.; Marrink, S.J. Computational lipidomics with insane: A versatile tool for generating custom membranes for molecular simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. [Google Scholar] [CrossRef]
- O’Connell, S.T.; Thompson, P.A. Molecular dynamics-continuum hybrid computations: A tool for studying complex fluid flow. Phys. Rev. E 1995, 52, R5792. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, K.M.; Mohamad, A.A. A review of the development of hybrid atomistic-continuum methods for dense fluids. Microfluid. Nanofluid. 2009, 8, 283. [Google Scholar] [CrossRef]
- Groen, D.; Knap, J.; Neumann, P.; Suleimenova, D.; Veen, L.; Leiter, K. Mastering the scales: A survey on the benefits of multiscale computing software. Philos. Trans. R. Soc. Lond. A 2019, 377, 20180147. [Google Scholar] [CrossRef] [PubMed]




| Case 1 | ||||
| type 1 | type 2 | type 3 | type 4 | |
| type 1 | 0.1 | 0.1 | 3.0 | 2.0 |
| type 2 | 0.2 | 0.8 | 2.0 | |
| type 3 | 1.15 | 0.8 | ||
| type 4 | 1.0 | |||
| Case 2 | ||||
| type 1 | type 2 | type 3 | type 4 | |
| type 1 | 0.1 | 0.1 | 2.0 | 2.0 |
| type 2 | 0.2 | 0.8 | 2.0 | |
| type 3 | 1.15 | 0.8 | ||
| type 4 | 1.0 | |||
| Group of Atoms | Mass [m] |
|---|---|
| W | 0.8179 |
| M | 1.8588 |
| D | 1.6833 |
| EO | 1.0000 |
| CM | 0.9552 |
| i–j | |||
|---|---|---|---|
| W–W | 0.8584 | 0.8129 | 8.00 |
| W–M | 1.0491 | 0.8132 | 13.72 |
| W–D | 0.9643 | 0.6311 | 10.38 |
| W–EO | 0.8946 | 0.9756 | 11.94 |
| W–CM | 0.9292 | 0.5081 | 10.75 |
| M–M | 1.2398 | 0.8998 | 26.00 |
| M–D | 1.1550 | 0.7114 | 18.83 |
| M–EO | 1.0853 | 0.8262 | 22.18 |
| M–CM | 1.1199 | 0.7800 | 19.61 |
| D–D | 1.0702 | 0.5081 | 13.90 |
| D–EO | 1.0004 | 0.6355 | 16.21 |
| D–CM | 1.0351 | 0.5953 | 14.43 |
| EO–EO | 0.9307 | 0.8067 | 19.00 |
| EO–CM | 0.9653 | 0.7154 | 16.86 |
| CM–CM | 1.0000 | 0.7000 | 15.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Theodorakis, P.E.; Smith, E.R.; Craster, R.V.; Müller, E.A.; Matar, O.K. Molecular Dynamics Simulation of the Superspreading of Surfactant-Laden Droplets. A Review. Fluids 2019, 4, 176. https://doi.org/10.3390/fluids4040176
Theodorakis PE, Smith ER, Craster RV, Müller EA, Matar OK. Molecular Dynamics Simulation of the Superspreading of Surfactant-Laden Droplets. A Review. Fluids. 2019; 4(4):176. https://doi.org/10.3390/fluids4040176
Chicago/Turabian StyleTheodorakis, Panagiotis E., Edward R. Smith, Richard V. Craster, Erich A. Müller, and Omar K. Matar. 2019. "Molecular Dynamics Simulation of the Superspreading of Surfactant-Laden Droplets. A Review" Fluids 4, no. 4: 176. https://doi.org/10.3390/fluids4040176






