A Simple Analytical Model for Estimating the Dissolution-Driven Instability in a Porous Medium †
Abstract
:1. Introduction
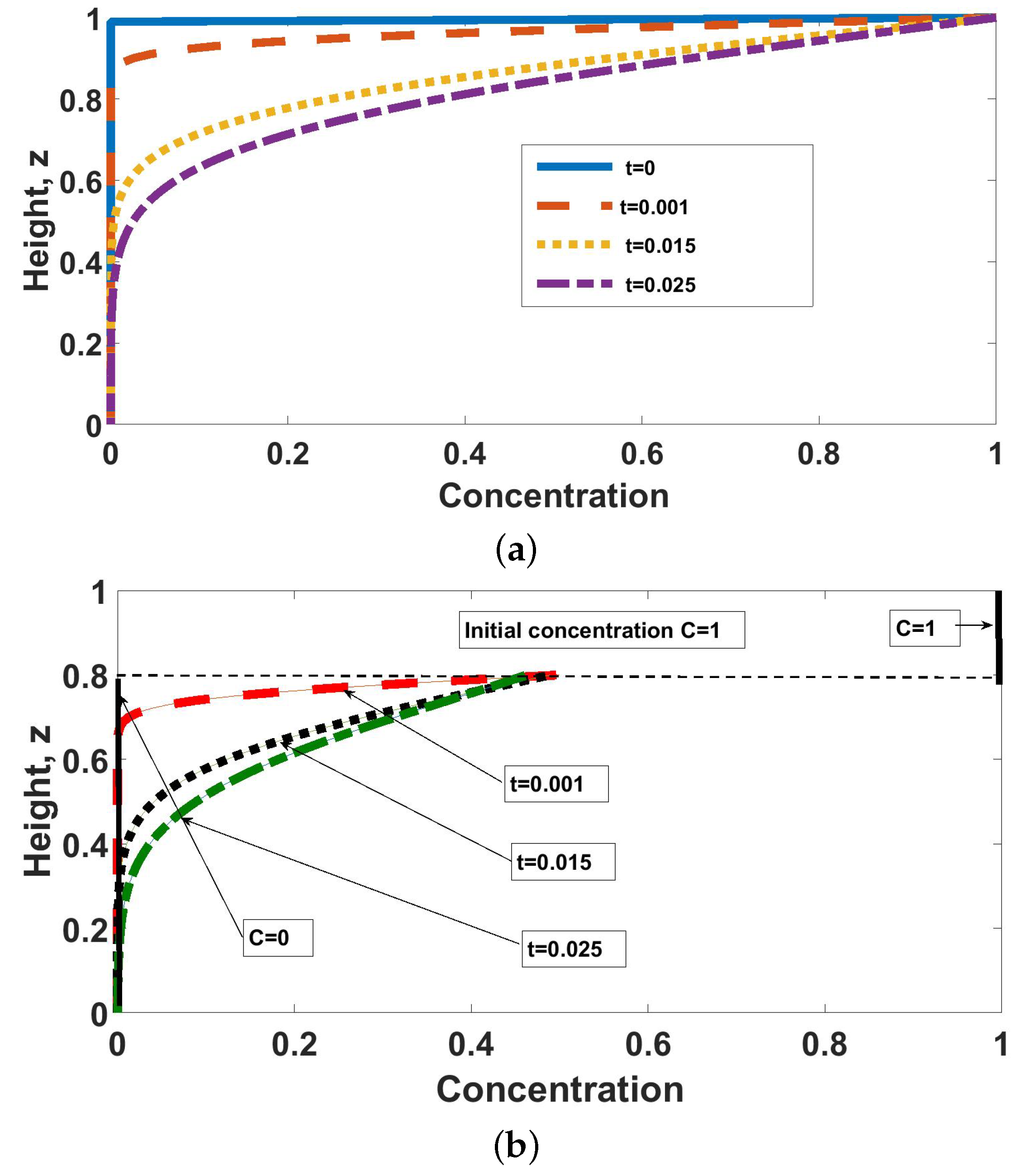
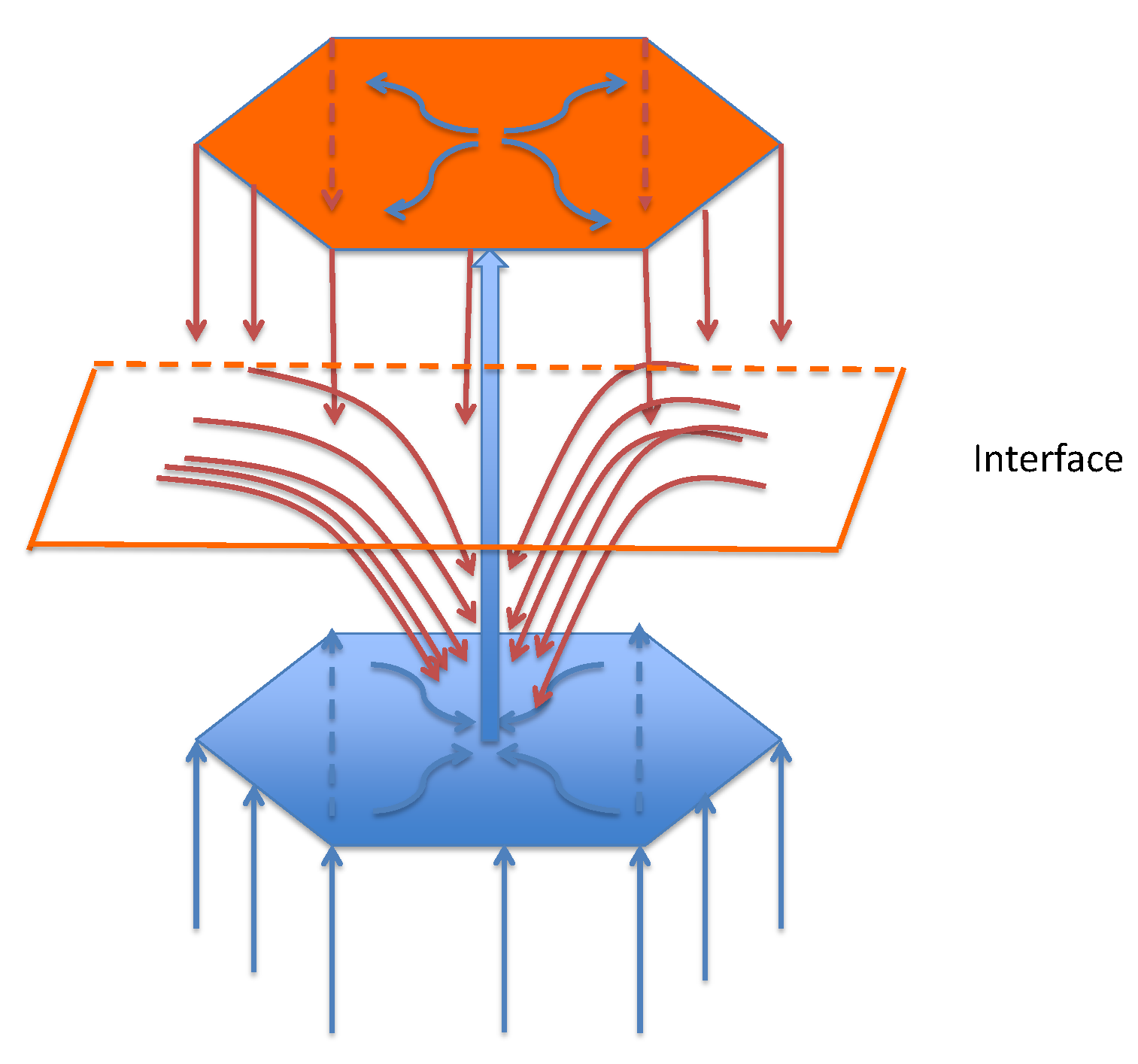
2. The Base State
3. Mathematical Model
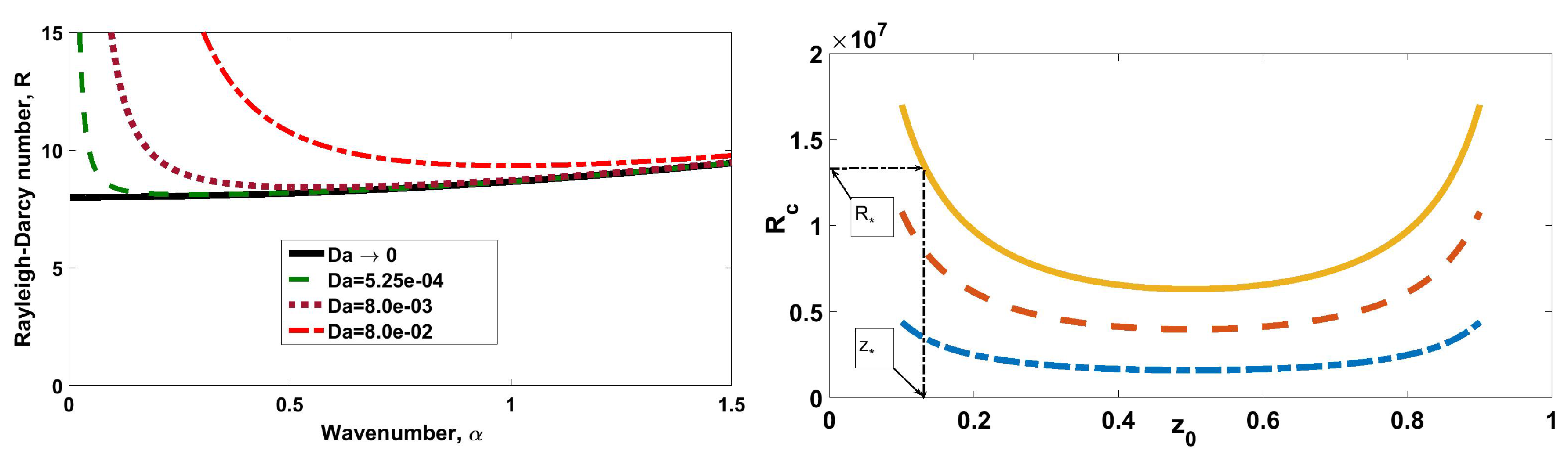
4. Stability Analysis
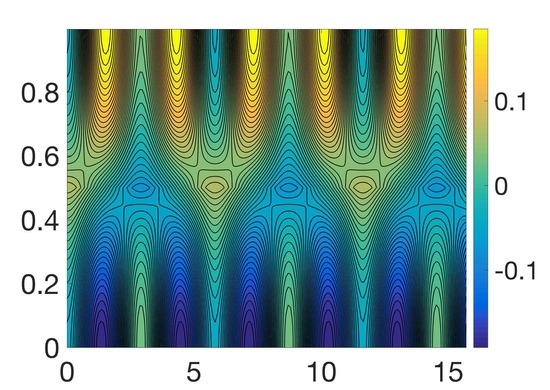
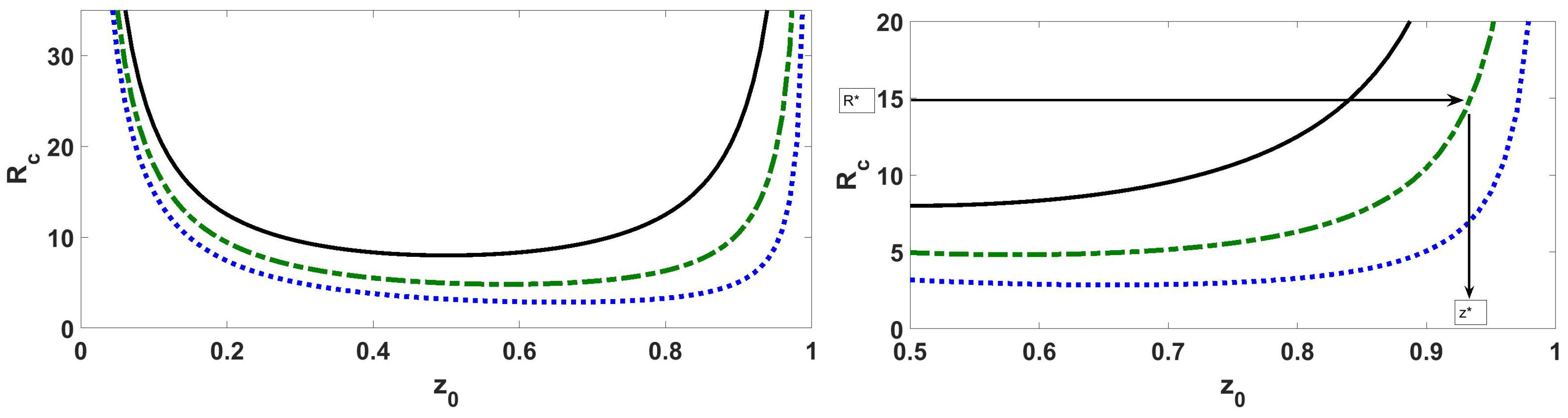
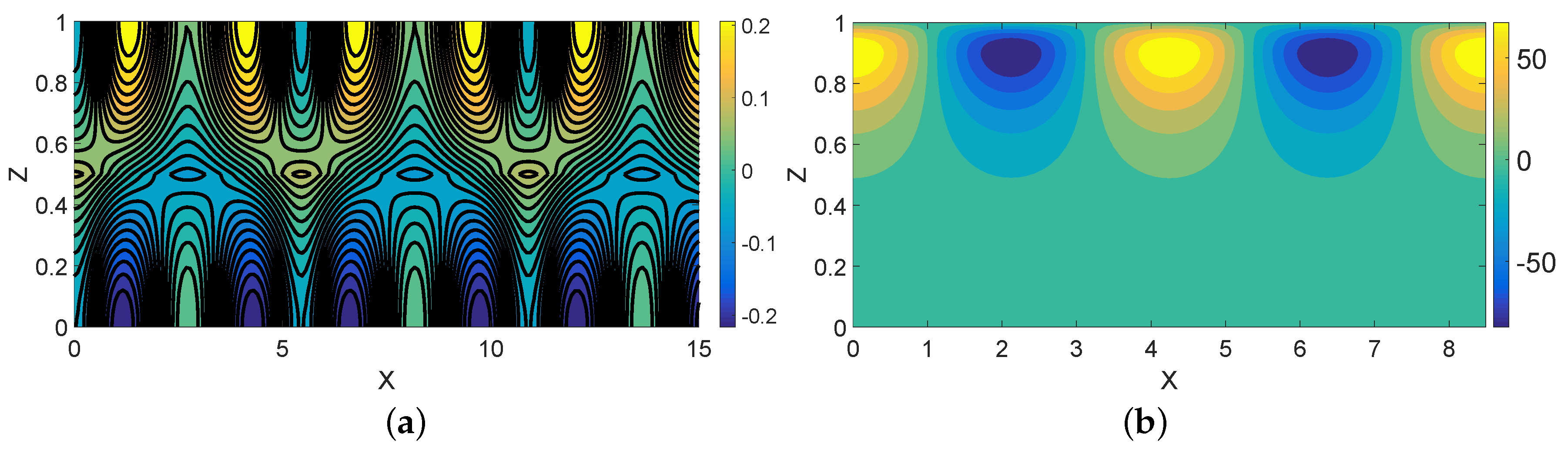
5. Two-Dimensional Results
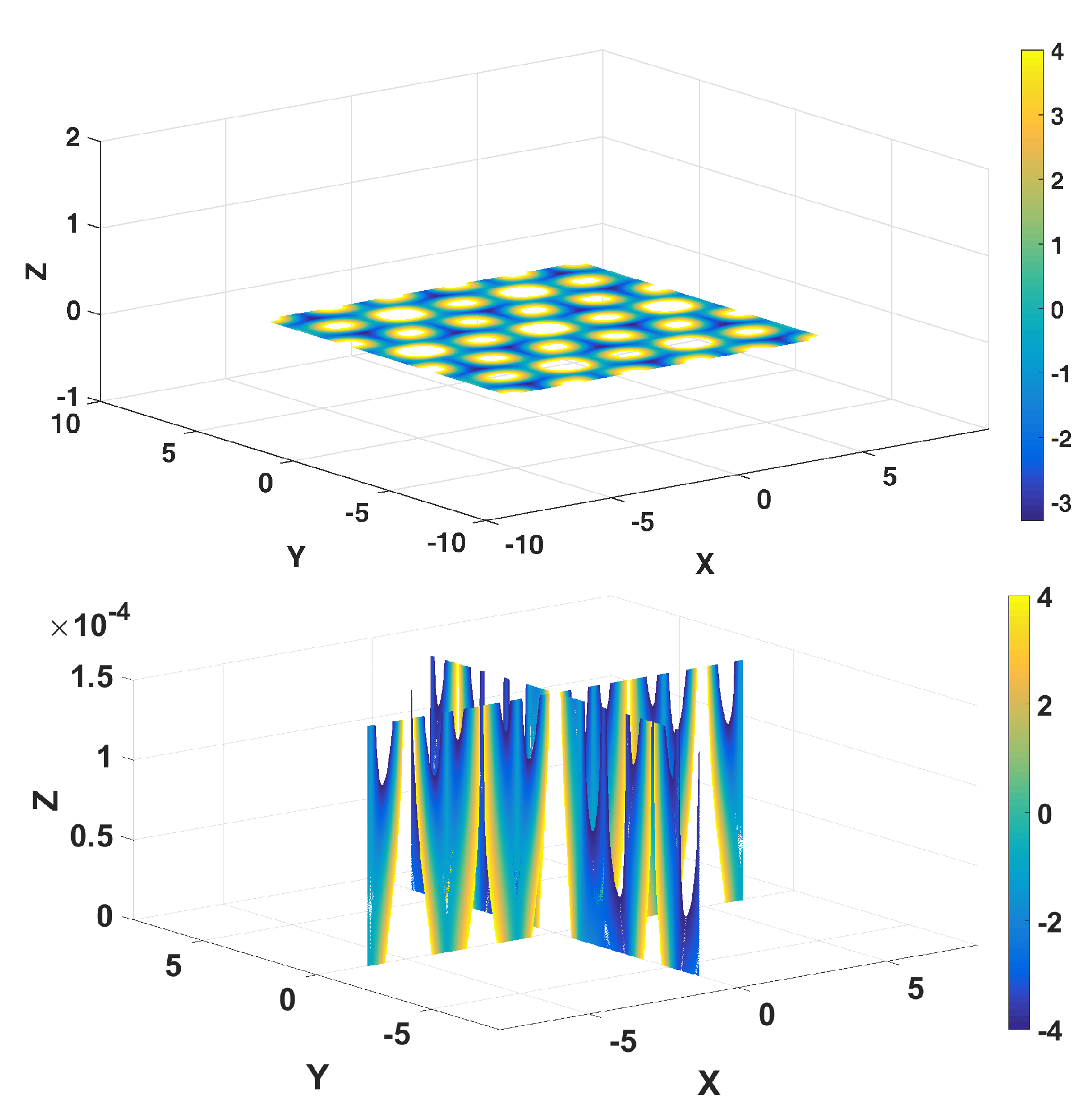
6. Three-Dimensional Results
7. Conclusions
Funding
Conflicts of Interest
References
- Sedjo, R.; Sohngen, B. Carbon sequestration in forests and soils. Annu. Rev. 2012, 4, 127–144. [Google Scholar] [CrossRef]
- Bachu, S. Sequestration of CO2 in geological media in response to climate change: road map for site selection using the transform of the geological space into the CO2 phase space. Energy Convers. Manag. 2002, 43, 87–102. [Google Scholar] [CrossRef]
- Bachu, S. Sequestration of CO2 in geological media: Criteria and approach for site selection in response to climate change. Energy Convers. Manag. 2000, 41, 953–970. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Carbon Sequestration Key R&D Programs and Initiatives. Available online: https://www.energy.gov/fe/science-innovation/carbon-capture-and-storage-research (accessed on 23 August 2018).
- International Panel on Climate Change. Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Huppert, H.E.; Neufeld, J.A. The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 2014, 46, 255–272. [Google Scholar] [CrossRef]
- Vo, L.; Hadji, L. Weakly nonlinear convection induced by the sequestration of CO2 in a perfectly impervious geological formation. Phys. Fluids 2017, 29, 127101. [Google Scholar] [CrossRef]
- Wanstall, C.T.; Hadji, L. A step function density profile model for the convective stability of CO2 geological sequestration. J. Eng. Math. 2018, 108, 53–71. [Google Scholar] [CrossRef]
- De Paoli, M.; Zonta, F.; Soldati, A. Influence of anisotropic permeability on convection in porous media: Implications for geological CO2 sequestration. Phys. Fluids 2016, 28, 056601. [Google Scholar] [CrossRef]
- Meybodi, H.M.; Hassanzadeh, H. Stability analysis of two-phase buoyancy-driven flow in the presence of a capillary transition zone. Phys. Rev. E 2013, 87, 033009. [Google Scholar] [CrossRef]
- Meybodi, H.M. Stability analysis of dissolution-driven convection in porous media. Phys. Fluids 2017, 29, 014102. [Google Scholar] [CrossRef]
- Ennis-King, J.P.; Paterson, L. Role of convective mixing in the long-term storage of carbon dioxide in deep saline formulations. Soc. Pet. Eng. 2005, 10, 349–356. [Google Scholar]
- Foster, T. Onset of convection in a layer of fluid cooled from above. Phys. Fluids 1965, 8, 1770–1774. [Google Scholar] [CrossRef]
- Foster, T. Onset of manifest convection in a layer of fluid with time-dependent surface temperature. Phys. Fluids 1969, 12, 2482–2487. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Batchelor, G.; Nitsche, J. Instability of stationary unbounded stratified fluid. J. Fluid Mech. 1991, 227, 357–391. [Google Scholar] [CrossRef]
- Hill, A.; Morad, M. Convective stability of carbon sequestration in anisotropic porous media. Proc. R. Soc. A 2014, 470, 2170. [Google Scholar] [CrossRef]
- Klinkenberg, K. The permeability of porous media to liquids and gases. In Drilling and Production Practice, American Petroleum Institute; American Petroleum Institute: Washington, DC, USA, 1941. [Google Scholar]
- Riaz, A.; Hesse, M.; Tchelepi, H.A.; Orr, F.M. Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 2006, 548, 87–111. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S.; Zhang, D. Convective stability analysis of the long-term storage of carbon dioxide in deep saline aquifers. Adv. Water Resour. 2006, 29, 397–407. [Google Scholar] [CrossRef]
- Neufeld, J.; Hesse, M.; Riaz, A.; Hallworth, M.; Techelepi, H.; Huppert, H. Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 2010, 37, L22404. [Google Scholar] [CrossRef]
- Riahi, N. Nonlinear convection in a porous layer with finite conducting boundaries. J. Fluid Mech. 1983, 129, 153–171. [Google Scholar] [CrossRef]
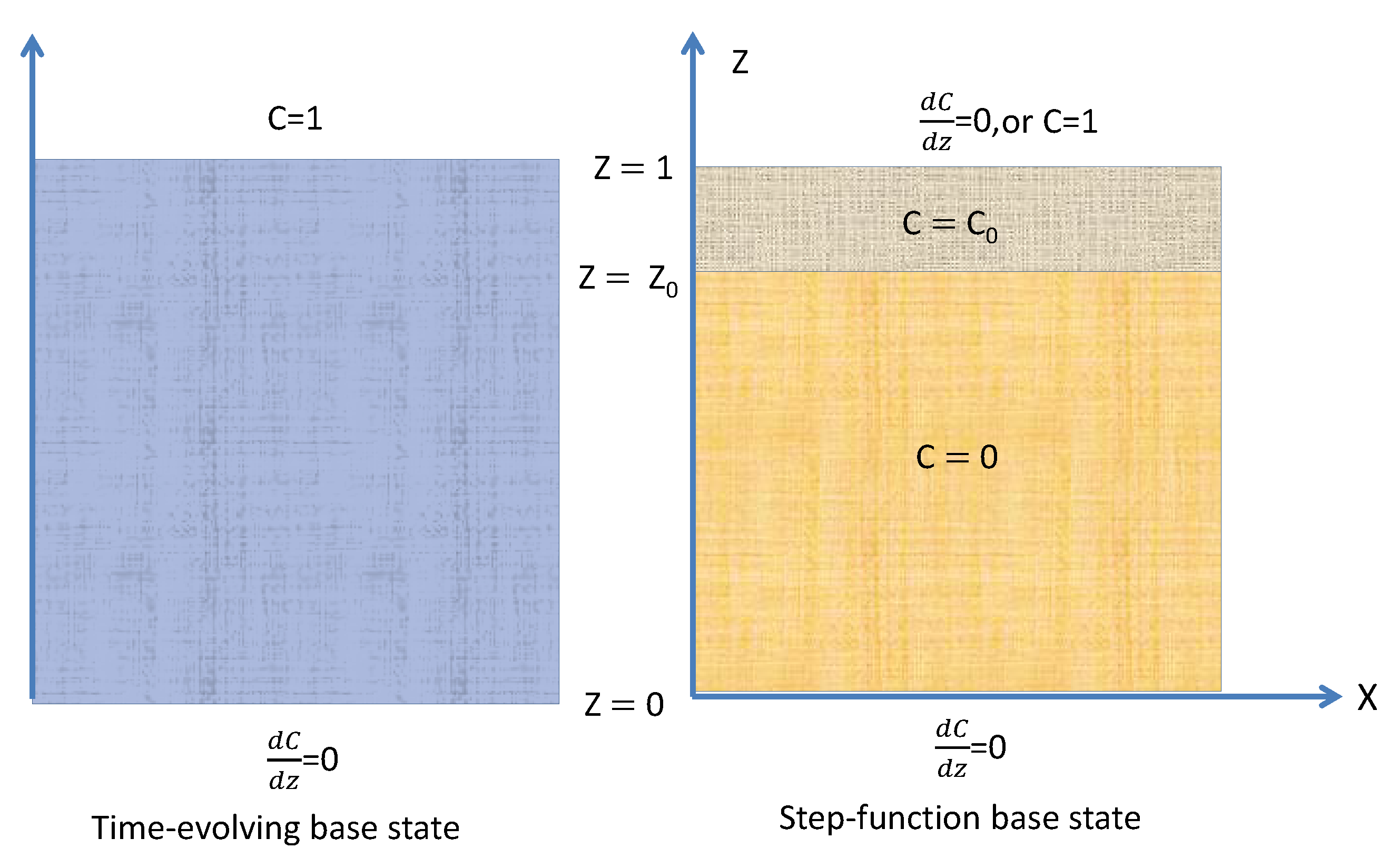
| Time-Evolving Base State | Step-Function Base Profile |
|---|---|
| Onset as function of time | Onset as function of boundary layer thickness |
| Lack of a precise definition of stability | Mathematically precise definition of stability |
| Stability of a time-dependent state | Steady analysis via normal modes |
| Requires refined numerical techniques | Paper-and-pencil analysis |
| Numerical tracking of the interface fluxes | Closed-form expressions for the interface fluxes |
| Numerical extension to nonlinear regime | Analytically tractable weakly nonlinear convection state |
| Challenging extension to three-dimensional case | Analytically tractable pattern formation study |
| Approximate instability threshold values | Conservative instability threshold values |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadji, L. A Simple Analytical Model for Estimating the Dissolution-Driven Instability in a Porous Medium. Fluids 2018, 3, 60. https://doi.org/10.3390/fluids3030060
Hadji L. A Simple Analytical Model for Estimating the Dissolution-Driven Instability in a Porous Medium. Fluids. 2018; 3(3):60. https://doi.org/10.3390/fluids3030060
Chicago/Turabian StyleHadji, Layachi. 2018. "A Simple Analytical Model for Estimating the Dissolution-Driven Instability in a Porous Medium" Fluids 3, no. 3: 60. https://doi.org/10.3390/fluids3030060