A Comparison of Energy Recovery by PATs against Direct Variable Speed Pumping in Water Distribution Networks
Abstract
:1. Introduction
2. Methodology
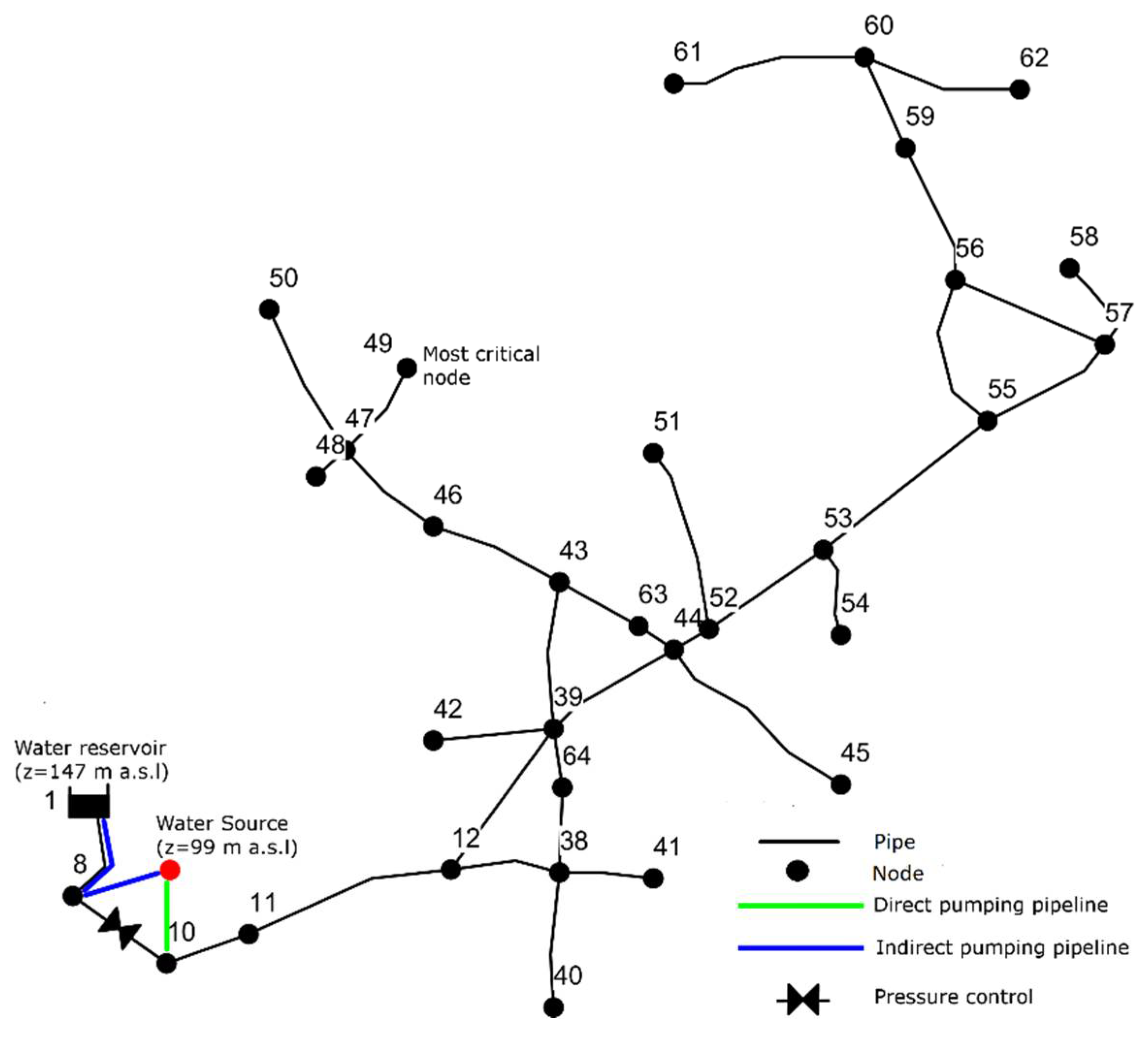
2.1. Study Area
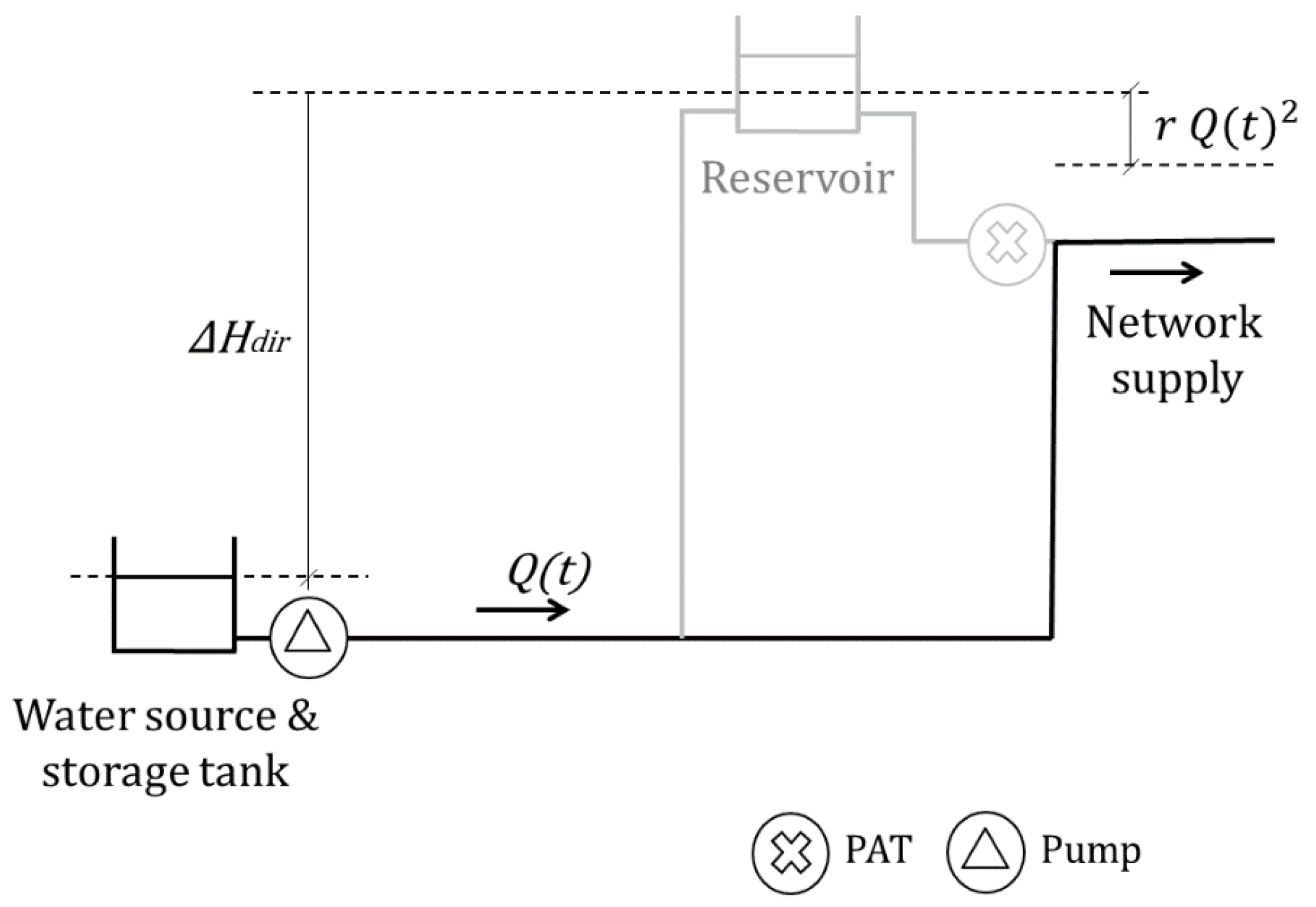
2.2. Direct and Indirect Pumping
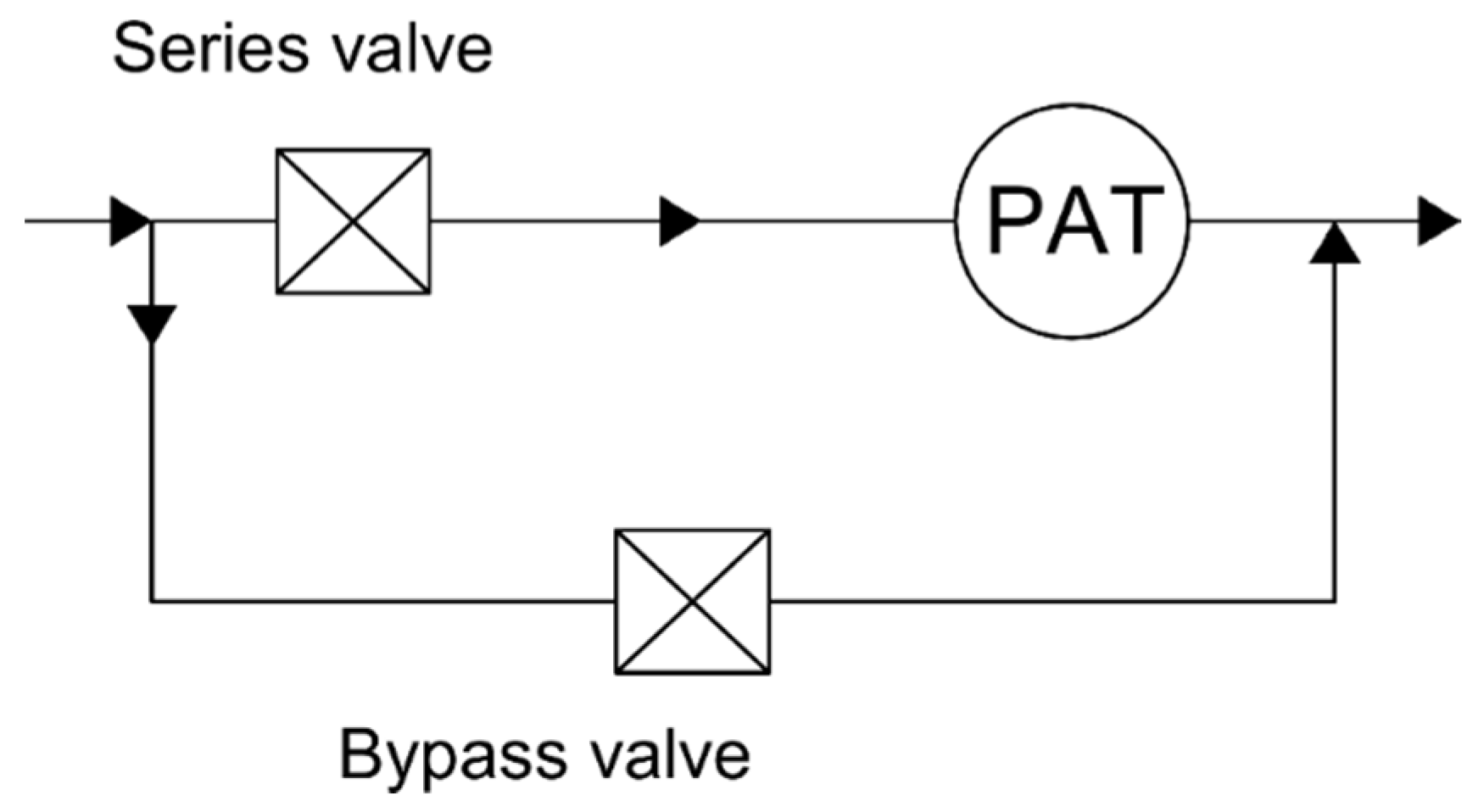
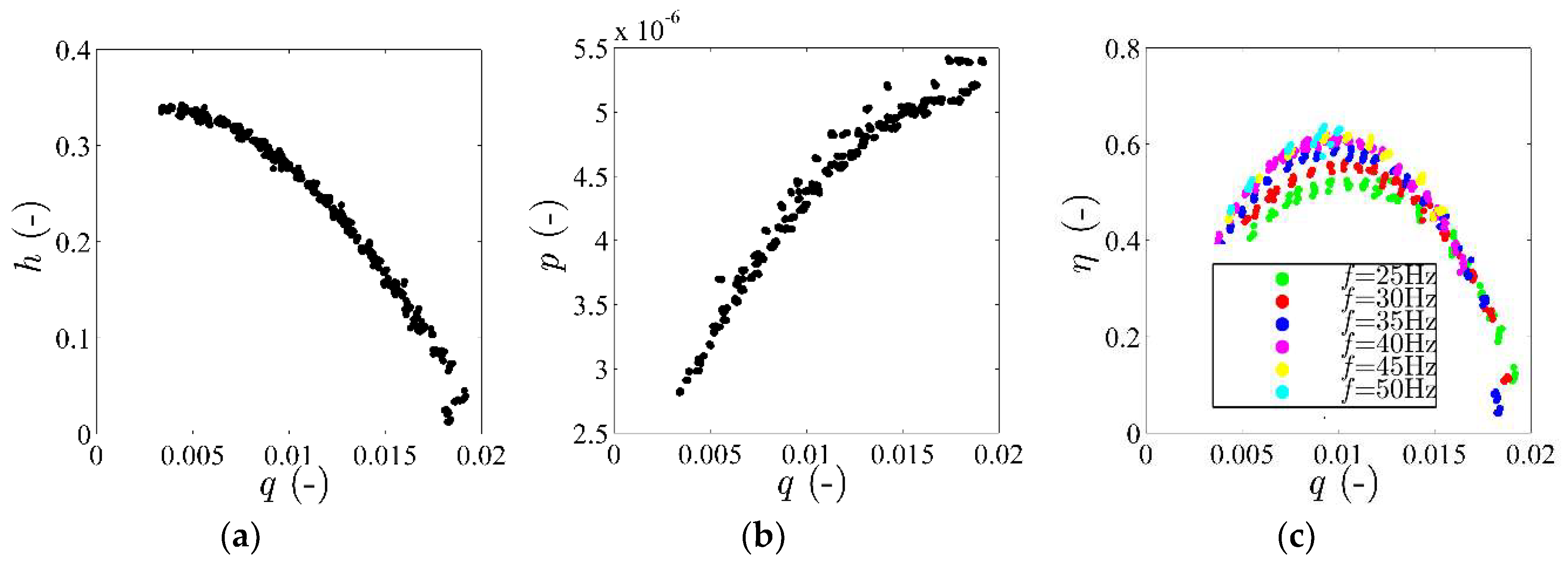
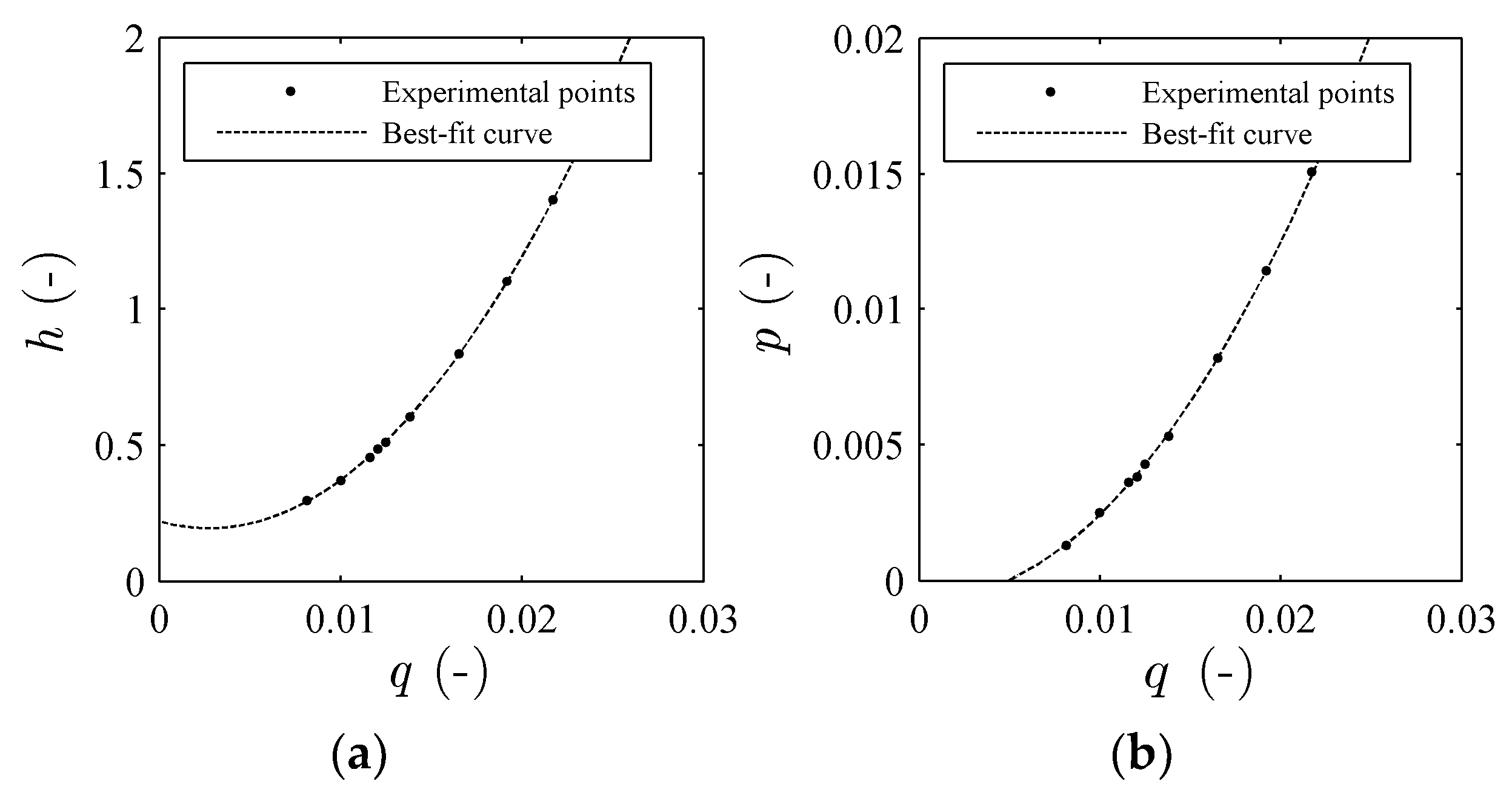
2.3. PAT and Microturbine Design/Operation
2.4. Pressure Management and Energy Recovery
3. Experimental Investigation
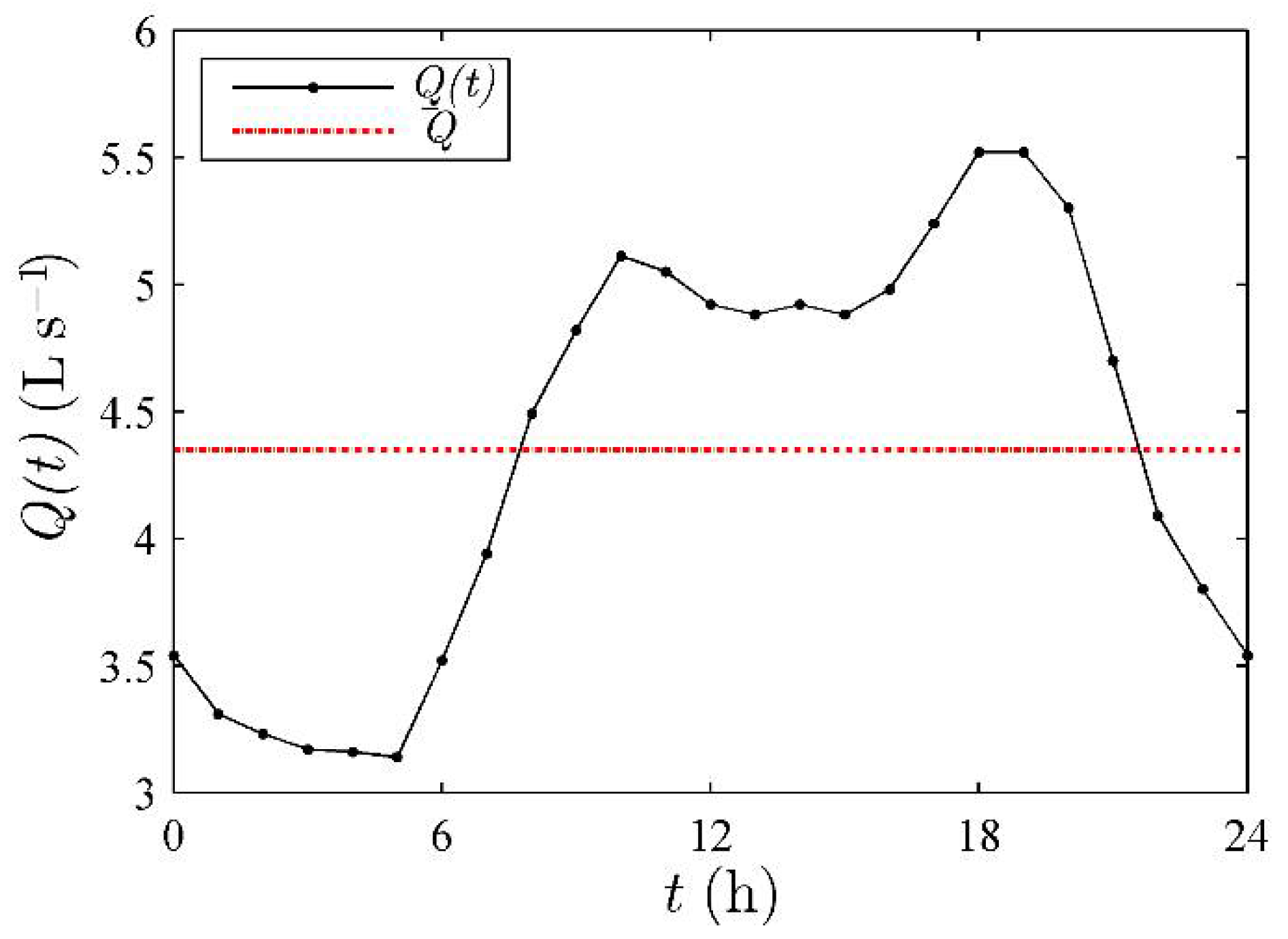
Pump under Variable Speed
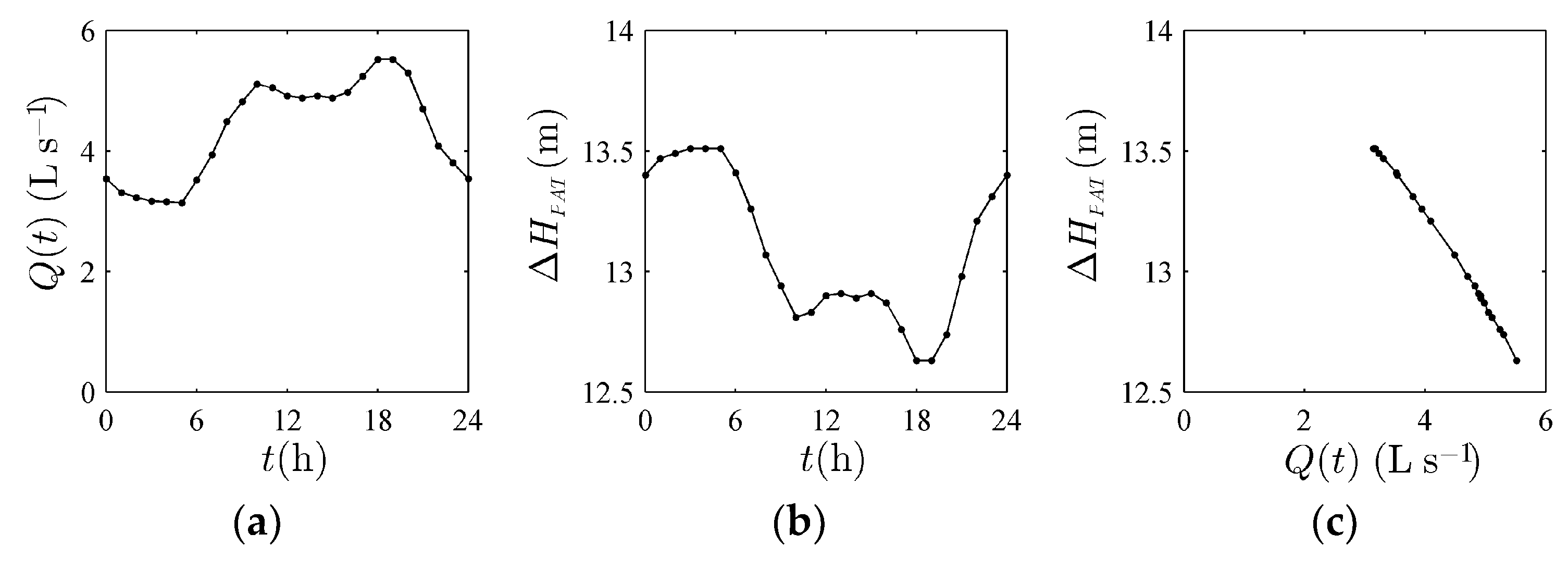
4. Application to the Case Study Network
4.1. Indirect Pumping
4.2. Pressure Management
4.3. Direct Pumping
5. Results
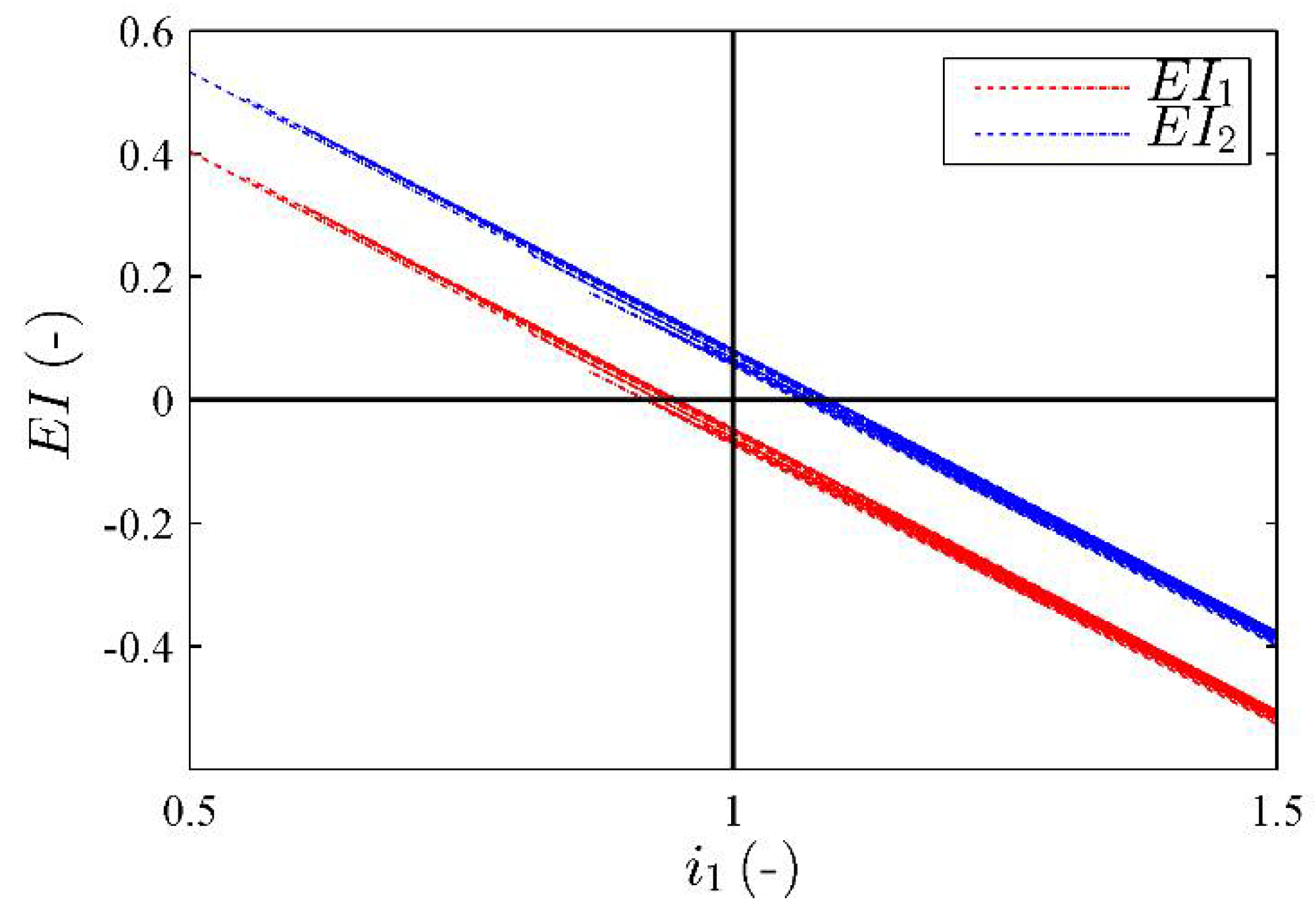
5.1. Energy Indices under Differing Boundary Conditions
5.2. Previously Reported Energy Indices for Different Boundary Conditions
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Abbott, M.; Cohen, B. Productivity and efficiency in the water industry. Util. Policy 2009, 17, 233–244. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy recovery in existing water networks: Towards greater sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Colombo, A.F.; Karney, B.W. Energy and Costs of Leaky Pipes: Toward Comprehensive Picture. J. Water Resour. Plan. Manag. 2002, 128, 441–450. [Google Scholar] [CrossRef]
- Ramos, H.M.; Vieira, F.; Covas, D.I.C. Energy efficiency in a water supply system: Energy consumption and CO2 emission. Water Sci. Eng. 2010, 3, 331–340. [Google Scholar] [CrossRef]
- Gallagher, J.; Styles, D.; McNabola, A.; Williams, A.P.P. Life cycle environmental balance and greenhouse gas mitigation potential of micro-hydropower energy recovery in the water industry. J. Clean. Prod. 2015, 99, 152–159. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Tamburino, V.; Zimbone, S.M. A simple method to evaluate the technical and economic feasibility of micro hydro power plants in existing irrigation systems. Renew. Energy 2016, 85, 498–506. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C.; Vetrano, L. Calibration of Proportional Controllers for the RTC of Pressures to Reduce Leakage in Water Distribution Networks. J. Water Resour. Plan. Manag. 2012, 138, 377–384. [Google Scholar] [CrossRef]
- Stokes, J.R.; Horvath, A.; Sturm, R. Water loss control using pressure management: Life-cycle energy and air emission effects. Environ. Sci. Technol. 2013, 47, 10771–10780. [Google Scholar] [CrossRef] [PubMed]
- Schwaller, J.; van Zyl, J.E. Modeling the Pressure-Leakage Response of Water Distribution Systems Based on Individual Leak Behavior. J. Hydraul. Eng. 2014, 141, 04014089. [Google Scholar] [CrossRef]
- Cabrera, E.; Pardo, M.A.; Cobacho, R.; Cabrera, E.J. Energy Audit of Water Networks. J. Water Resour. Plan. Manag. 2010, 136, 669–677. [Google Scholar] [CrossRef]
- Eliades, D.G.; Polycarpou, M.M. Leakage fault detection in district metered areas of water distribution systems. J. Hydroinform. 2012, 14, 992. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Khalifa, A.; Mansour, R.B.; Habib, M.A. Acoustic Detection of Leaks in Water Pipelines Using Measurements inside Pipe. J. Pipeline Syst. Eng. Pract. 2012, 3, 47–54. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, Q.; Ma, J.; Blanckaert, K. Optimal pipe replacement strategy based on break rate prediction through genetic programming for water distribution network. J. Hydro-Environ. Res. 2013, 7, 134–140. [Google Scholar] [CrossRef]
- Fontanazza, C.; Freni, G.; Loggia, G.; Notaro, V.; Puleo, V. Evaluation of the Water Scarcity Energy Cost for Users. Energies 2013, 6, 220–234. [Google Scholar] [CrossRef] [Green Version]
- Mushtaq, S.; Maraseni, T.N.; Reardon-Smith, K.; Bundschuh, J.; Jackson, T. Integrated assessment of water-energy-GHG emissions tradeoffs in an irrigated lucerne production system in eastern Australia. J. Clean. Prod. 2015, 103, 491–498. [Google Scholar] [CrossRef] [Green Version]
- Filion, Y.R.; Maclean, H.L.; Asce, A.M.; Karney, B.W.; Asce, M. Life-Cycle Energy Analysis of a Water Distribution System. J. Infrastruct. Syst. 2004, 10, 120–130. [Google Scholar] [CrossRef]
- Arriaga, M. Pump as turbine—A pico-hydro alternative in Lao People’s Democratic Republic. Renew. Energy 2010, 35, 1109–1115. [Google Scholar] [CrossRef]
- Ramos, H.M.; Mello, M.; De, P.K. Clean power in water supply systems as a sustainable solution: From planning to practical implementation. Water Sci. Technol. Water Supply 2010, 10, 39. [Google Scholar] [CrossRef]
- Carravetta, A.; Antipodi, L.; Golia, U.; Fecarotta, O. Energy saving in a water supply network by coupling a pump and a Pump As Turbine (PAT) in a turbopump. Water 2017, 9, 62. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Golia, U.M.; La Rocca, M.; Martino, R.; Padulano, R.; Tucciarelli, T. Optimization of Osmotic Desalination Plants for Water Supply Networks. Water Resour. Manag. 2016, 30, 3965–3978. [Google Scholar] [CrossRef] [Green Version]
- Fiuzat, A.A.; Akerkar, B.P. Power outputs of two stages of cross-flow turbine. J. Energy Eng. 1991, 117, 57–70. [Google Scholar] [CrossRef]
- Sammartano, V.; Aricò, C.; Carravetta, A.; Fecarotta, O.; Tucciarelli, T. Banki-Michell optimal design by computational fluid dynamics testing and hydrodynamic analysis. Energies 2013, 6, 2362–2385. [Google Scholar] [CrossRef] [Green Version]
- Sammartano, V.; Sinagra, M.; Filianoti, P.; Tucciarelli, T. A Banki–Michell turbine for in-line water supply systems. J. Hydraul. Res. 2017, 55, 686–694. [Google Scholar] [CrossRef]
- Sopian, K.; Razak, J.A. Pico hydro: Clean power from small streams. In Proceedings of the 3rd World Scientific and Engineering Academy and Society International Conference on Renewable Energy Sources, Tenerife, Spain, 1–3 July 2009. [Google Scholar]
- Gaius-obaseki, T. Hydropower opportunities in the water industry. Int. J. Environ. Sci. 2010, 1, 392–402. [Google Scholar] [CrossRef]
- Punys, P.; Dumbrauskas, A.; Kvaraciejus, A.; Vyciene, G. Tools for Small Hydropower Plant Resource Planning and Development: A Review of Technology and Applications. Energies 2011, 4, 1258–1277. [Google Scholar] [CrossRef] [Green Version]
- Fecarotta, O.; McNabola, A. Optimal Location of Pump as Turbines (PATs) in Water Distribution Networks to Recover Energy and Reduce Leakage. Water Resour. Manag. 2017. [Google Scholar] [CrossRef]
- Mcnabola, A.; Coughlan, P.; Williams, A.P. The technical and economic feasibility of energy recovery in water supply networks. In Proceedings of the International Conference on Renewable Energy and Power Quality, Las Palmas, Spain, 13–15 April 2011. [Google Scholar]
- Carravetta, A.; Derakhshan Houreh, S.; Ramos, H.M. Introduction. In Pumps as Turbines: Fundamentals and Applications; Springer: Cham, Switzerland, 2018; pp. 3–26. ISBN 9783319675060. [Google Scholar]
- Vilanova, M.R.N.; Balestieri, J.A.P. Modeling of hydraulic and energy efficiency indicators for water supply systems. Renew. Sustain. Energy Rev. 2015, 48, 540–557. [Google Scholar] [CrossRef]
- Fecarotta, O.; Ramos, H.M.; Derakhshan, S.; Del Giudice, G.; Carravetta, A. Fine Tuning a PAT Hydropower Plant in a Water Supply Network to Improve System Effectiveness. J. Water Resour. Plan. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Pelli, T.; Hitz, H.U. Energy indicators and savings in water supply. J. Am. Water Work. Assoc. 2000, 92, 55–62. [Google Scholar] [CrossRef]
- Emec, S.; Bilge, P.; Seliger, G. Design of production systems with hybrid energy and water generation for sustainable value creation. Clean Technol. Environ. Policy 2015, 17, 1807–1829. [Google Scholar] [CrossRef] [Green Version]
- Gómez, E.; Cabrera, E.; Balaguer, M.; Soriano, J. Direct and indirect water supply: An energy assessment. Procedia Eng. 2015, 119, 1088–1097. [Google Scholar] [CrossRef]
- Cabrera, E.; Gomez, E.; Cabrera, E., Jr.; Soriano, J.; Espert, V. Energy Assessment of Pressurized Water Systems. J. Water Resour. Plan. Manag. 2015, 141, 1–12. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Energy Production in Water Distribution Networks: A PAT Design Strategy. Water Resour. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Martino, R.; Antipodi, L. PAT efficiency variation with design parameters. Procedia Eng. 2014, 70, 285–291. [Google Scholar] [CrossRef]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef] [Green Version]
- Simpson, A.R.; Marchi, A. Evaluating the Approximation of the Affinity Laws and Improving the Efficiency Estimate for Variable Speed Pumps. J. Hydraul. Eng. 2013, 139, 1314–1317. [Google Scholar] [CrossRef] [Green Version]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An improved affinity model to enhance variable operating strategy for pumps used as turbines. J. Hydraul. Res. 2016, 1686, 1–10. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H.M. A new low-cost installation scheme of PATs for pico-hydropower to recover energy in residential areas. Renew. Energy 2018. [Google Scholar] [CrossRef]
- Nautiyal, H.; Varun; Kumar, A. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An Interior Point Algorithm for Large-Scale Nonlinear Programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef] [Green Version]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. Ser. B 2000, 89, 149–185. [Google Scholar] [CrossRef] [Green Version]



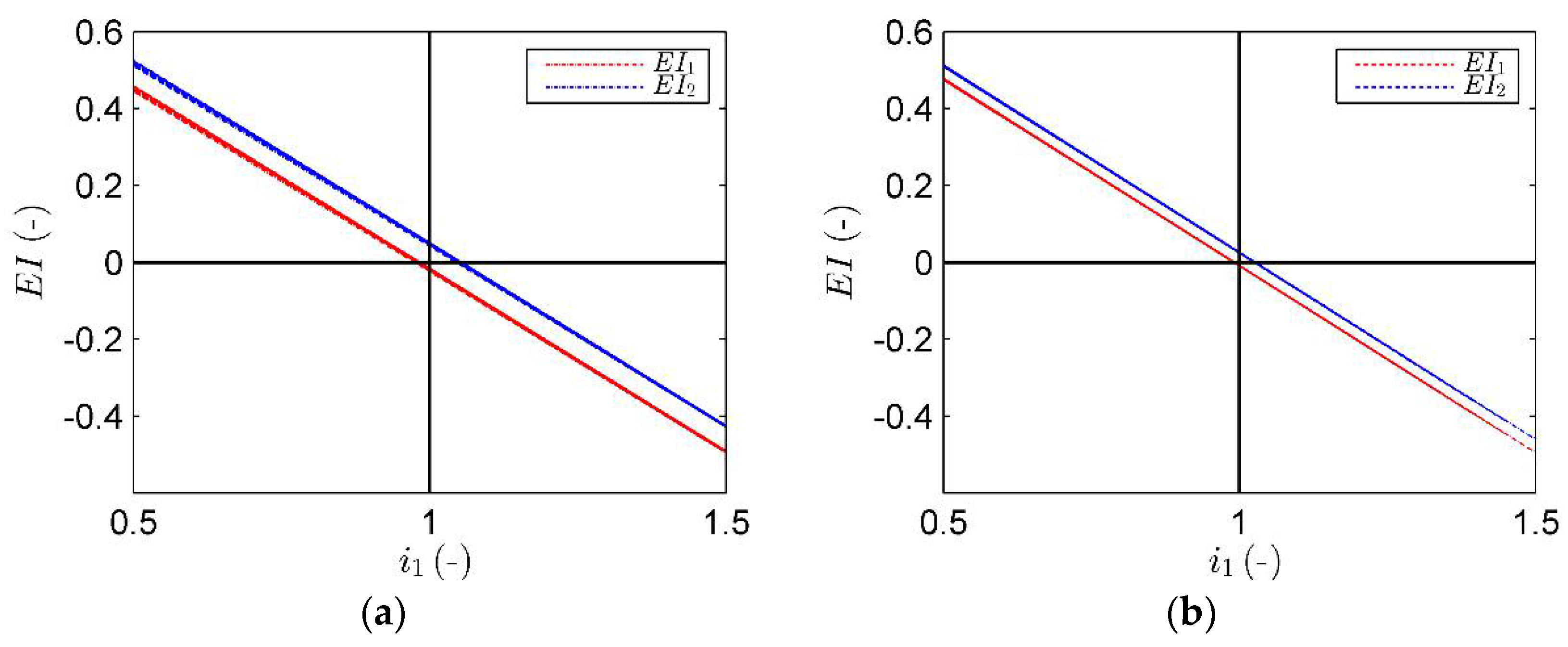
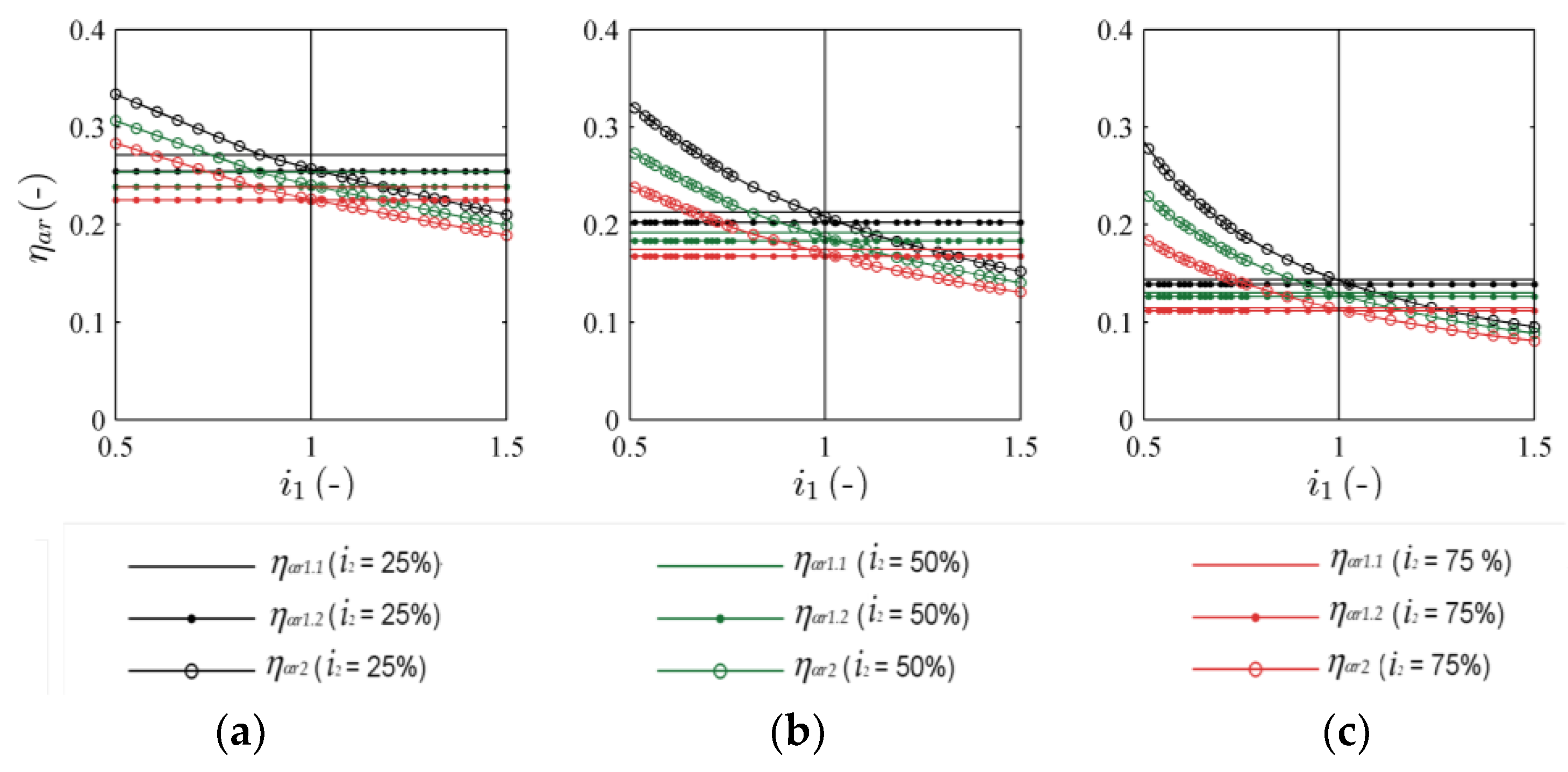
| Scenario | Pumping Head (m) | Energy (kWh/Year) | Efficiency Index EI1 | Efficiency Index EI2 | Recovered Energy (kWh/Year) |
|---|---|---|---|---|---|
| Indirect | 48.14 | 32,420 | 0.24 | 0.31 | 2234 |
| Direct | 34.88 | 22,327 | - |
| (m) | Energy Recovery | No Energy Recovery | ||
|---|---|---|---|---|
| Saving (%) | Direct Scenario Cutoff | Saving (%) | Direct Scenario Cutoff | |
| 25 | 5 | 0.94 | 8 | 1.09 |
| 50 | 2 | 0.98 | 5 | 1.04 |
| 100 | 0.5 | 0.99 | 3 | 1.02 |
| Scenario | ||||
|---|---|---|---|---|
| Indirect | 0.37 | 0.24 | 0.22 | - |
| Direct | 0.46 | - | - | 0.30 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morani, M.C.; Carravetta, A.; Del Giudice, G.; McNabola, A.; Fecarotta, O. A Comparison of Energy Recovery by PATs against Direct Variable Speed Pumping in Water Distribution Networks. Fluids 2018, 3, 41. https://doi.org/10.3390/fluids3020041
Morani MC, Carravetta A, Del Giudice G, McNabola A, Fecarotta O. A Comparison of Energy Recovery by PATs against Direct Variable Speed Pumping in Water Distribution Networks. Fluids. 2018; 3(2):41. https://doi.org/10.3390/fluids3020041
Chicago/Turabian StyleMorani, Maria Cristina, Armando Carravetta, Giuseppe Del Giudice, Aonghus McNabola, and Oreste Fecarotta. 2018. "A Comparison of Energy Recovery by PATs against Direct Variable Speed Pumping in Water Distribution Networks" Fluids 3, no. 2: 41. https://doi.org/10.3390/fluids3020041