1. Introduction
Nematic liquid crystals are classical examples of partially ordered complex liquids for which the constituent molecules have translational freedom but exhibit a degree of long-range orientational ordering or certain preferred directions of averaged molecular alignment, that vary in space and time [
1]. The nematic hydrodynamics is particularly rich because of the intrinsic coupling between fluid motion and nematic molecular orientations i.e., the fluid motion influences the nematic orientational ordering and equally, the inhomogeneities in the orientational ordering have a kick-back effect on the fluid flow, a phenomenon known as “backflow” [
2]. Backflow has no counterpart in conventional isotropic Newtonian fluids. Consequently, nematics can offer unusual mechanical and rheological properties compared to their Newtonian counterparts, such as complex wetting transitions, surface effects and stable topological defects. Backflow is of fundamental scientific interest and equally, has practical consequences on switching rates of liquid crystal display devices and their refresh times [
3,
4].
There are two popular hydrodynamic theories for nematic liquid crystals in the literature—the Ericksen–Leslie theory [
5,
6] and the Beris–Edwards model [
7]. In the Ericksen–Leslie framework, we have two variables—the flow field and the nematic director, which is interpreted as the direction of preferred averaged molecular alignment in space. The typical mathematical framework comprises the incompressibility constraint and evolution equations for the flow field and the nematic director. The evolution equations for the flow field and the nematic director are intrinsically coupled with new anisotropic stresses, compared to the isotropic Newtonian counterpart, and the solution landscapes depend on flow parameters (such as the pressure gradient) and nematic parameters (nematic material constants, temperature, boundary conditions for the nematic director and nematic viscosities) [
8]. The Ericksen–Leslie theory for nematodynamics is based on the premise that the nematic is purely uniaxial, with one single distinguished direction of orientational ordering, referred to as “director”, with a constant degree of orientational order. As said before, the director is interpreted as the single preferred direction of molecular alignment in the sense that all directions perpendicular to the director are physically equivalent. Hence, the Ericksen–Leslie theory is hugely successful for modelling situations that are expected to have a uniform degree of nematic ordering; this usually holds for defect-free situations or for certain choices of material constants that promote perfect nematic ordering such as the vanishing elastic constant limit of the Landau-de Gennes theory studied in [
9]. However, the Ericksen–Leslie theory cannot capture sharp variations in the degree of nematic ordering, complicated topological defects and biaxiality, for which there is a primary and secondary direction of preferred molecular alignment, since the Ericksen–Leslie theory only has two dependent variables. The Beris–Edwards theory is more general than the Ericksen–Leslie since it employs the Landau-de Gennes
-tensor order parameter to describe the nematic orientational ordering. The Landau-de Gennes
-tensor order parameter is a symmetric, traceless
matrix that contains information about the preferred directions of nematic molecular alignment and the degree of ordering about these directions within its eigenvectors and eigenvalues respectively [
9,
10,
11]. The Landau-de Gennes
-tensor can capture both uniaxial and biaxial states, along with variable orientational order and is hence better suited to capture finer structural details and topological defects. The evolution equations for the flow field and the
-tensor are again coupled through “coupling stresses”. A detailed discussion of the Beris–Edwards model and its connections to closely related models can be found in the literature [
12,
13,
14].
We work in a reduced Beris–Edwards framework to model a microfluidic channel, with an applied pressure gradient to induce fluid flow, and different types of boundary conditions for a reduced
-tensor on the channel walls with the usual no-slip boundary conditions for the flow field. We use a reduced
-tensor, which only has two degrees of freedom, in contrast to the usual five degrees of freedom in a three-dimensional approach. This reduced approach has been successfully used for severely confined systems elsewhere [
15,
16] and can be related to the usual Landau-de Gennes
-tensor explicitly [
17]. In particular, we model the microfluidic channel as a two-dimensional domain and this reduced approach is successful in capturing the in-plane system characteristics. The two degrees of freedom of the reduced
-tensor are an angle
that describes the preferred in-plane alignment of the nematic molecules or the direction of the nematic director
in the plane, and a scalar order parameter
s, that is a measure of the degree of orientational order about the director
. We note that the Ericksen–Leslie framework does not include the order parameter
s. The Beris–Edwards system can be recast as a coupled system for
s,
and the flow field parameterised by
u (since we assume unidirectional channel flow). We study the effects of certain key variables on the long-time or equilibrium profiles for
s,
and
u. Namely, we look at the effects of the pressure gradient
, the nematic elastic constant, the nematic material constants and viscosities (modelled by
) and the anchoring conditions for
(modelled by either the winding number
or the surface anchoring coefficient
B). For small
, the evolution equation for the flow field effectively reduces to the Navier–Stokes equation and we recover the usual Poiseuille flow. However, the flow field does influence the
profiles in this regime and we carry out some explicit analysis to compute the
s and
profiles in this limit, for both small and large
. The analysis captures both continuous and discontinuous solution profiles for
; the discontinuous profiles are featured by domain walls with layered structures such that
jumps abruptly across an interface. Again, the discontinuous solutions cannot be captured by the Ericksen–Leslie approach. The discontinuous solutions are the analogue of the well studied “order-reconstruction” solutions [
18], with the novel feature of flow effects. For small
, the flow is negligible as expected. The most interesting regime is when
and
are of comparable magnitude and there is two-way coupling between the flow and nematic order, where the effects of backflow are most pronounced. We expect the asymptotic analysis in this paper to be useful for subsequent detailed analysis of the Beris–Edwards system in this interesting regime.
There is a large body of existing literature on the Ericksen–Leslie theory and the Beris–Edwards theory. For example, an extensive review of existence and regularity results in the Ericksen–Leslie framework can be found in [
19]. In [
20], the authors use perturbation methods in the Ericksen–Leslie framework to study the effects of backflow on defect dynamics. In parallel, there are several papers that focus on the role of backflow in the hydrodynamics of defects, in the Beris–Edwards framework, see for example [
12,
21,
22]. In recent years, there are rigorous existence and regularity results for the Beris–Edwards framework too [
11,
14,
23] and numerical simulations for microfluidic set-ups in [
24,
25]. The various dynamical theories of nematic liquid crystals and the key results are surveyed in [
26] and in [
27]; the authors rigorously derive the Ericksen–Leslie equations from the Beris–Edwards model. In [
28], the authors use a lattice-Boltzmann algorithm to study nematodynamics in a microfluidic channel, in the Beris–Edwards framework, with both Dirichlet and mixed boundary conditions on the channel walls. The emphasis is on the flow rate as a function of the applied pressure gradient and the qualitative effects of the boundary conditions on the director profiles. Our setting is similar but not the same as in [
28]. For example, our Dirichlet conditions are inhomogeneous i.e., different fixed boundary conditions on the two bounding surfaces, whereas the authors employ the same Dirichlet condition on both surfaces in [
28]. A large part of the elegant asymptotics in [
28] is carried out in the
limit, for which we expect a uniform degree of nematic order or
almost everywhere. This limit cannot capture the discontinuous solutions for
described above. Importantly, our emphasis is on “flow reversal" as a function of the pressure gradient, the material and temperature-dependent parameter
and the re-scaled elastic constant
and this is not addressed in [
28]. In fact, flow reversal or flow in the direction of increasing pressure gradient is a distinct manifestation of backflow, only observable for
large enough; this warrants further study in the future.
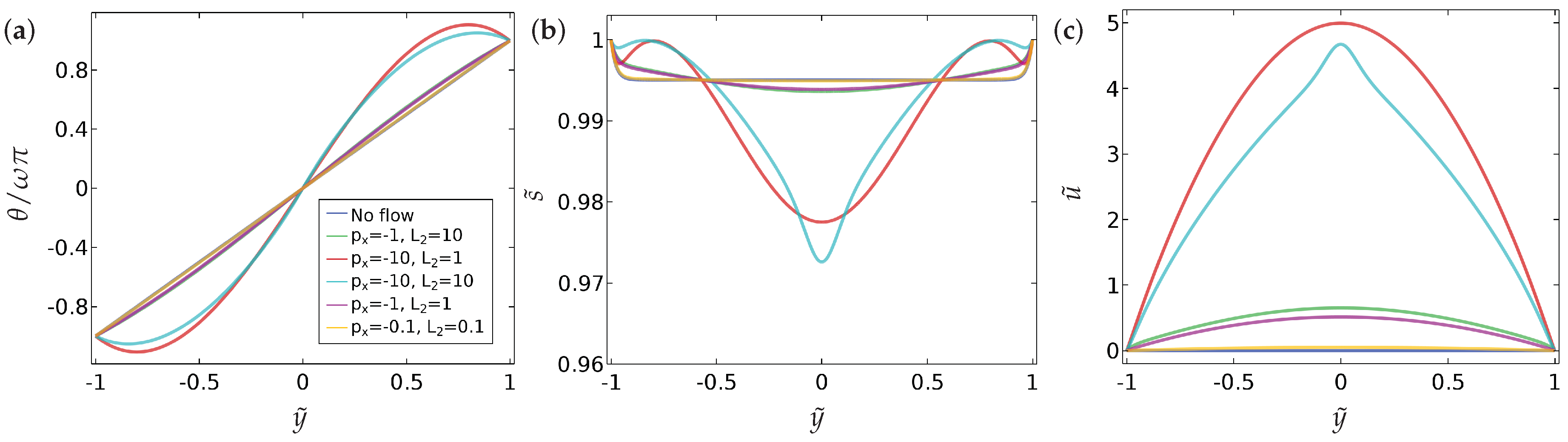
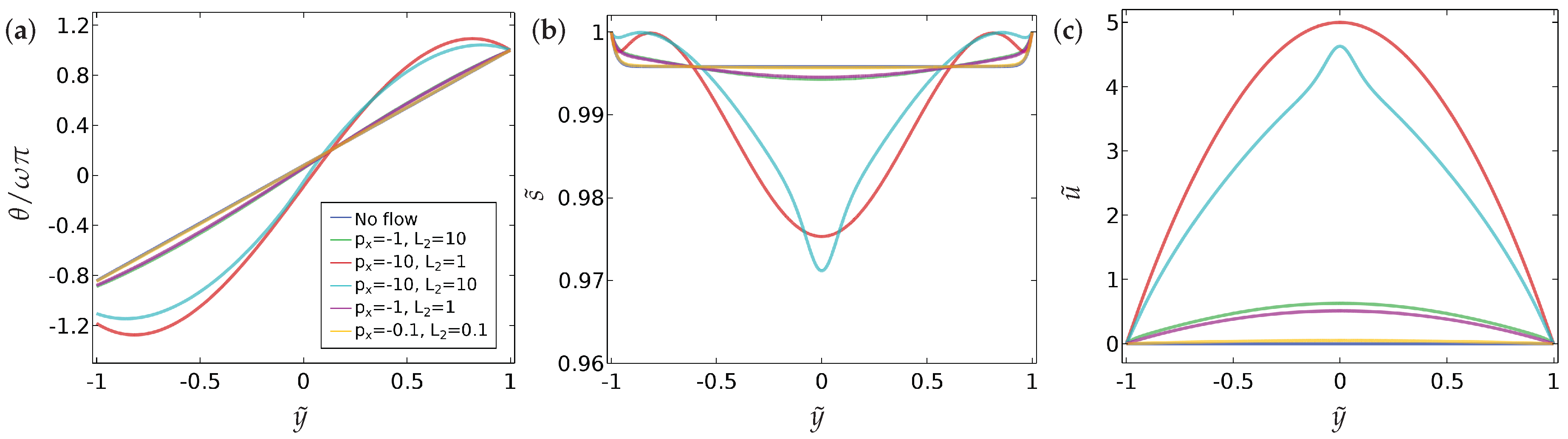
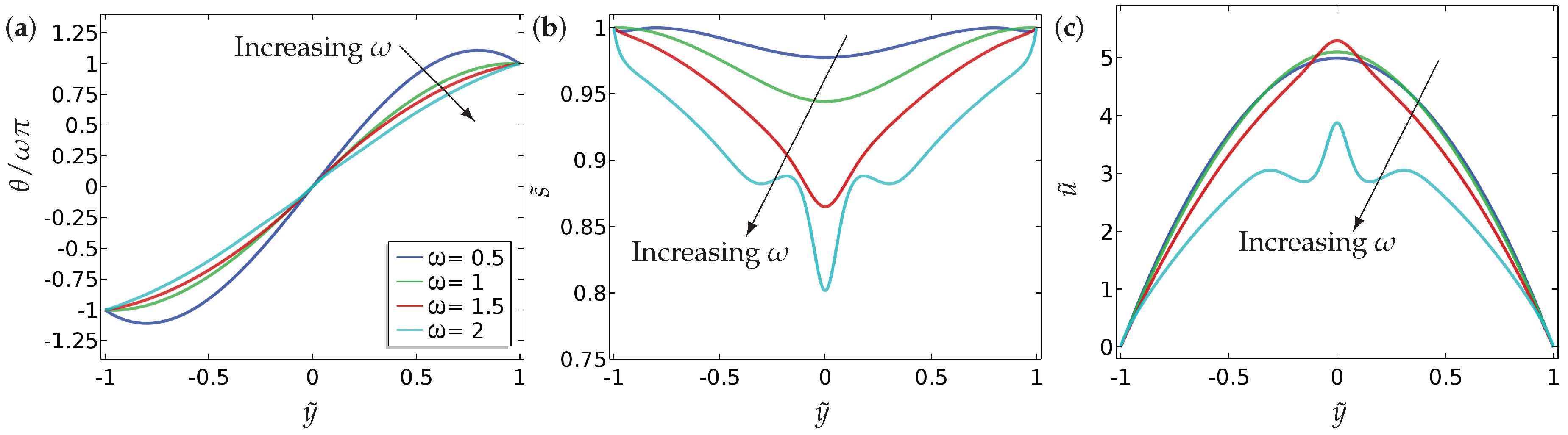
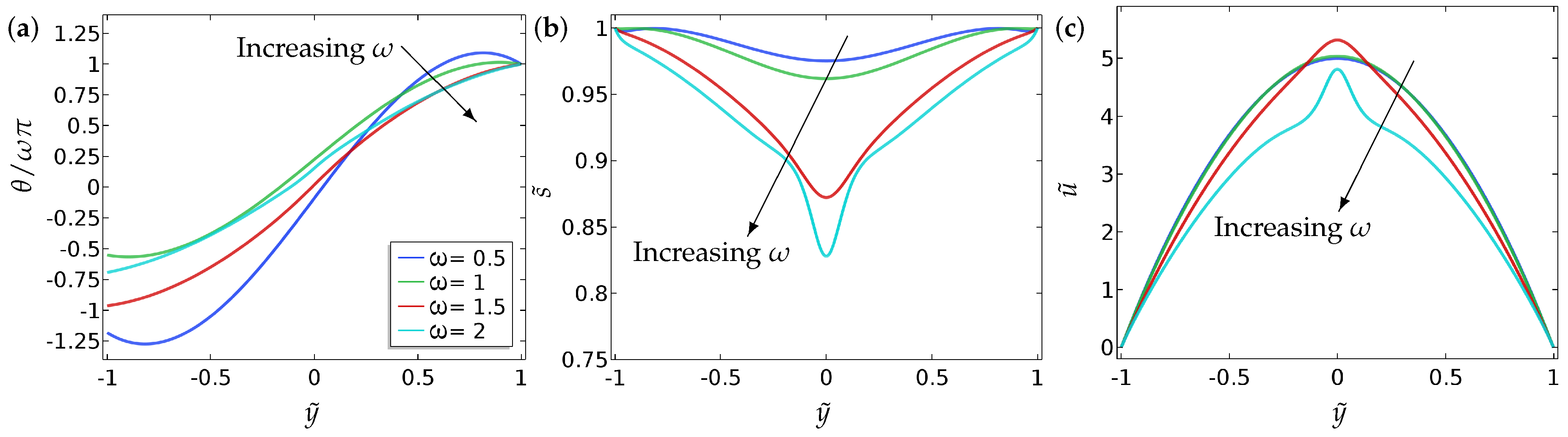
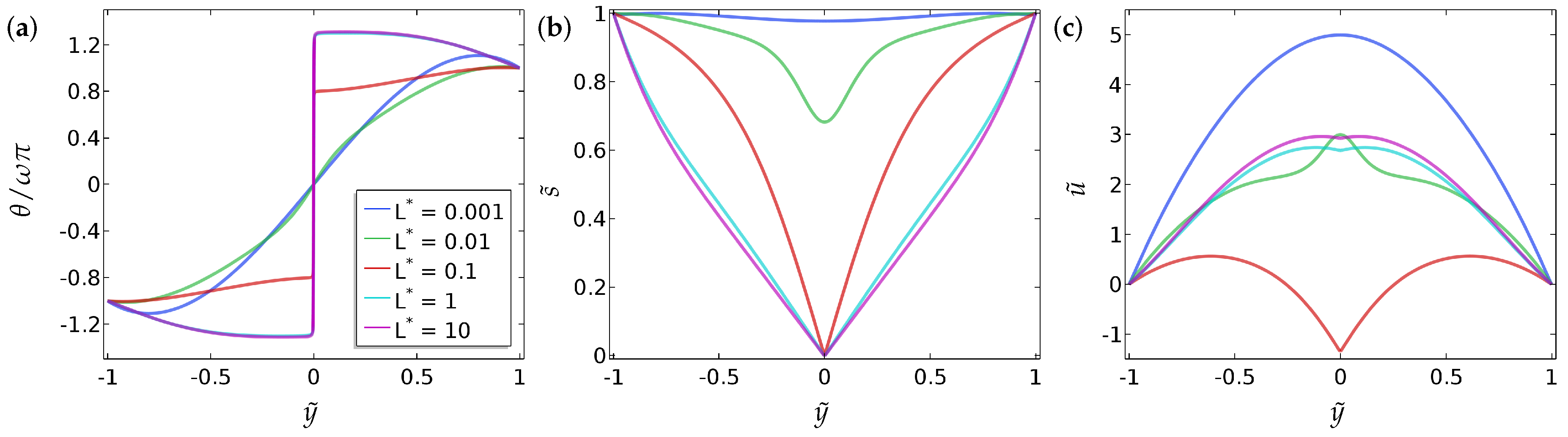
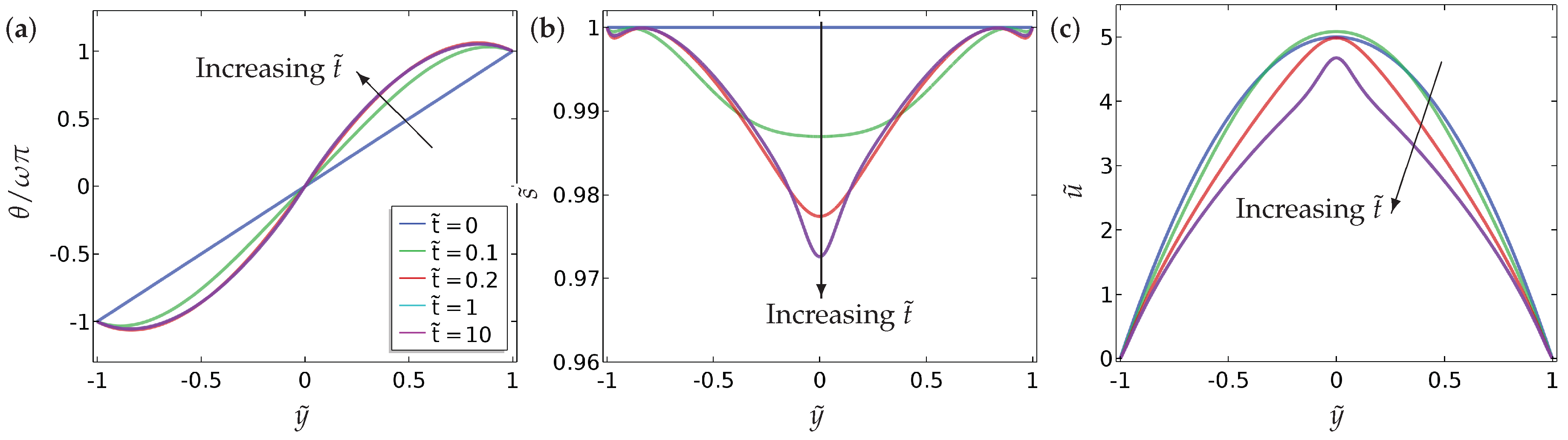
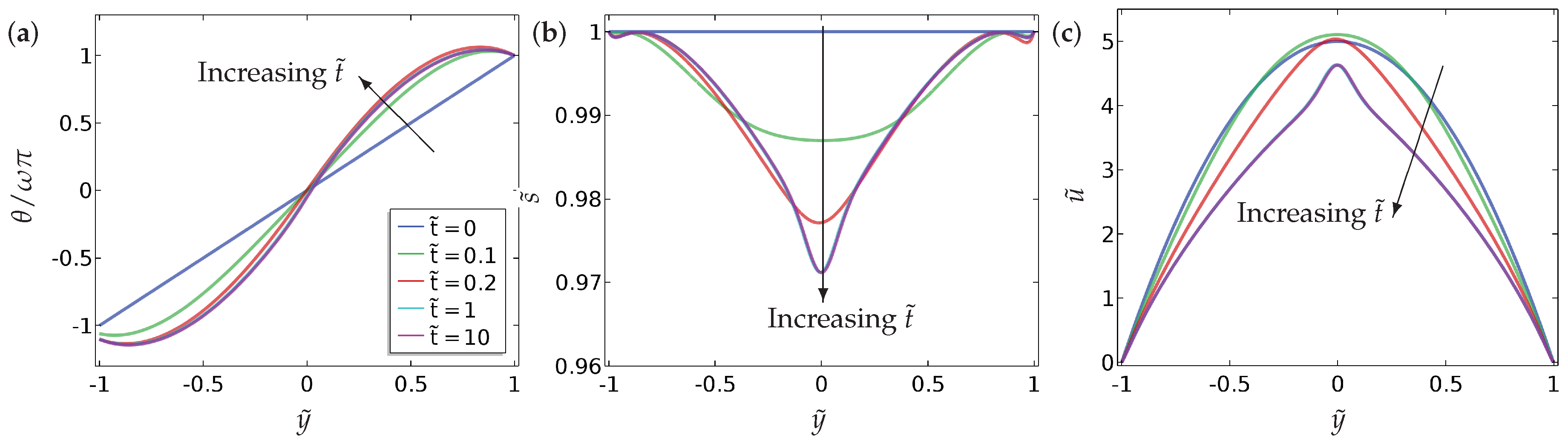
Our main findings can be summarised as follows.
- (a)
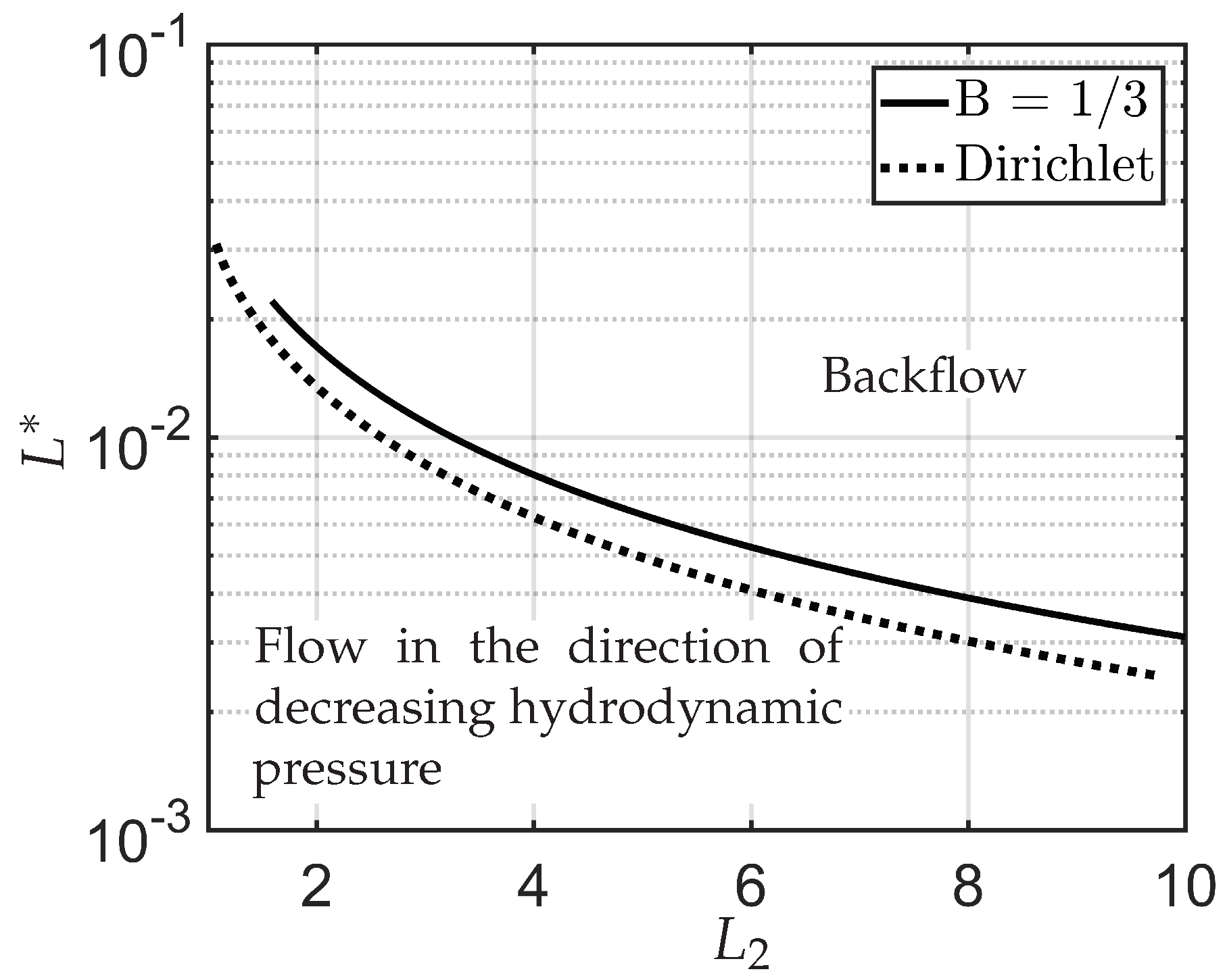
We compute a phase plane in terms of and , for a fixed , which demarcates regions of fluid flow in the direction of decreasing pressure from regions of fluid flow in the direction of increasing pressure and this flow reversal is a clear manifestation of backflow.
- (b)
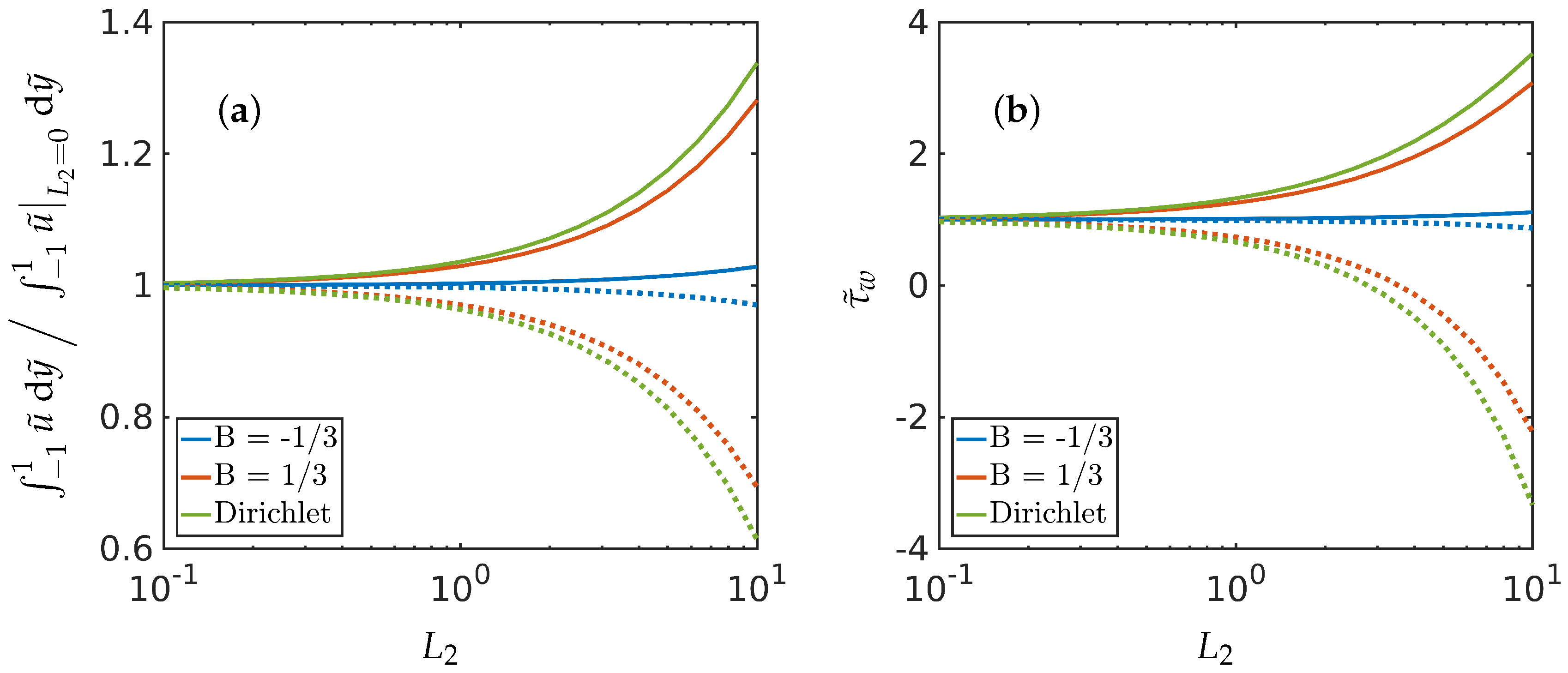
We compute the total flow rates in different parameter regimes. In particular, we show that backflow can be attained for a window of values of i.e., and these critical values depend on , the boundary conditions and other material parameters.
- (c)
We study two different kinds of boundary conditions for —Dirichlet and mixed boundary conditions. The mixed boundary conditions are phrased in terms of an anchoring coefficient B on the bottom surface and accompanied by a Dirichlet condition on the top surface. The mixed boundary conditions offer greater scope for tuning the solution landscape.
- (d)
We perform some investigations on how we can choose a suitable initial condition to attain the discontinuous solution for at long times, and this may be useful for studying multistability in such model settings.
The paper is organised as follows. In
Section 2, we present the governing equations, the boundary conditions and the initial conditions. In
Section 3, we present our results on the effects of
,
and
. In
Section 4, we perform the explicit analysis in the small
limit and in
Section 5, we give some conclusions.
2. Theory
We study spatio-temporal pattern formation in a long microfluidic channel
where
, filled with nematic liquid crystals under the action of a pressure gradient applied at the end
in the
x direction. This pressure gradient naturally induces a fluid flow and we assume a unidirectional channel flow in the
x-direction. There are two main macroscopic variables of interest: the flow field
, where
t is time, and the nematic order parameter, which is a measure of the nematic ordering. We work in a reduced two-dimensional Landau-de Gennes framework, similar to the setting in [
15,
16] for which the nematic order parameter
is a symmetric, traceless
matrix, with two degrees of freedom. Equivalently, we can write
where
is the 2D identity matrix, with
being the scalar order parameter and
being the two-dimensional director. The general Landau-de Gennes nematic order parameter,
, is a symmetric, traceless
matrix with five degrees of freedom but for severely confined systems, where the vertical
z-dimension is much smaller than the lateral dimensions; it is reasonable to assume that structural details are independent of the
z-coordinate and we can relate the reduced tensor,
in this paper to the full Landau-de Gennes
tensor as has been done in [
17]. A reduced approach, such as the one employed in this paper and others, is analytically and computationally more efficient and is a physically relevant approach for severely confined systems.
We work within the standard and powerful Beris–Edwards theoretical framework for nematodynamics [
24]. There are three governing equations: the incompressibility constraint, an evolution equation for the flow field, which is essentially the Navier–Stokes equation with an additional stress (
) due to the nematic ordering and an evolution equation for
, which has an additional stress induced by the fluid vorticity. The governing partial differential equations are given below.
where
is the material derivative,
and
are the density and viscosity of the fluid medium,
p is the hydrodynamic pressure,
is the fluid velocity, and prime
denotes the transpose. The nematic stress (
) is [
9,
24,
29]
where
is the scalar order parameter,
is the molecular field,
is the nematic elastic constant and
a and
c are parameters related to the temperature and material properties. We work with temperatures below the nematic–isotropic transition temperature and hence we take
. The evolution equation for the
tensor is given by [
11,
29]
where
is the rotational diffusion constant [
10,
21] and
is the anti-symmetric part of the velocity gradient tensor. We can also identify
with a two-dimensional vector:
where
We assume that all quantities of interest only depend on
y i.e., we work in a reduced one-dimensional setting, which is a physically relevant setting for very long channels with small height. Equations (
2) and (
4) can be recast in terms of the order parameter (
s) and the director angle (
) in one spatial dimension as
Using the following scalings,
Equations (
5)–(
7) can be non-dimensionalised as
where
and
L is the half-height of the channel. Physically,
is the scaled elastic constant. The parameter
where
is the Reynolds number and
is analogous to the Ericksen number (
) in terms of the rotational diffusion constant,
, rather than the viscosity
. It can also be interpreted as the ratio of the inertial to rotational forces. The parameter
is the product of ratio of the temperature and material constants and the ratio of the rotational to momentum diffusion.
The boundary conditions for
and
are
This simply means that we assume the nematic molecules are perfectly ordered at
and we impose the typical no-slip boundary conditions on
. For the nematic director, we look at two different cases: (i) symmetric Dirichlet conditions for
on
consistent with strong anchoring and in the spirit of [
8], (ii) a Neumann-type boundary condition modelling weak anchoring on
accompanied by a Dirichlet condition on
as shown below.
where
is the winding number and
B is a rescaled anchoring strength (see
Figure 1 for a sketch of these configurations). It is worth pointing out that positive
B models tangential or planar boundary conditions on the bottom substrate i.e., it originates from a surface energy of the form
that is minimised by either
or
, for a positive anchoring coefficient
A that measures the strength of the anchoring and we integrate over the surface
. The initial conditions for the system above Equations (
9)–(
11) are given by
where
is the root of the equation
for the asymmetric case.
We will often make comparisons between situations with no flow to situations with fluid flow. In the no-flow case, we simply set
in Equations (
9) and (
10) and analyse the resulting system
with the same boundary (Equations (
13), (
15) and (
16)) and initial conditions (Equations (
18) and (
19)).
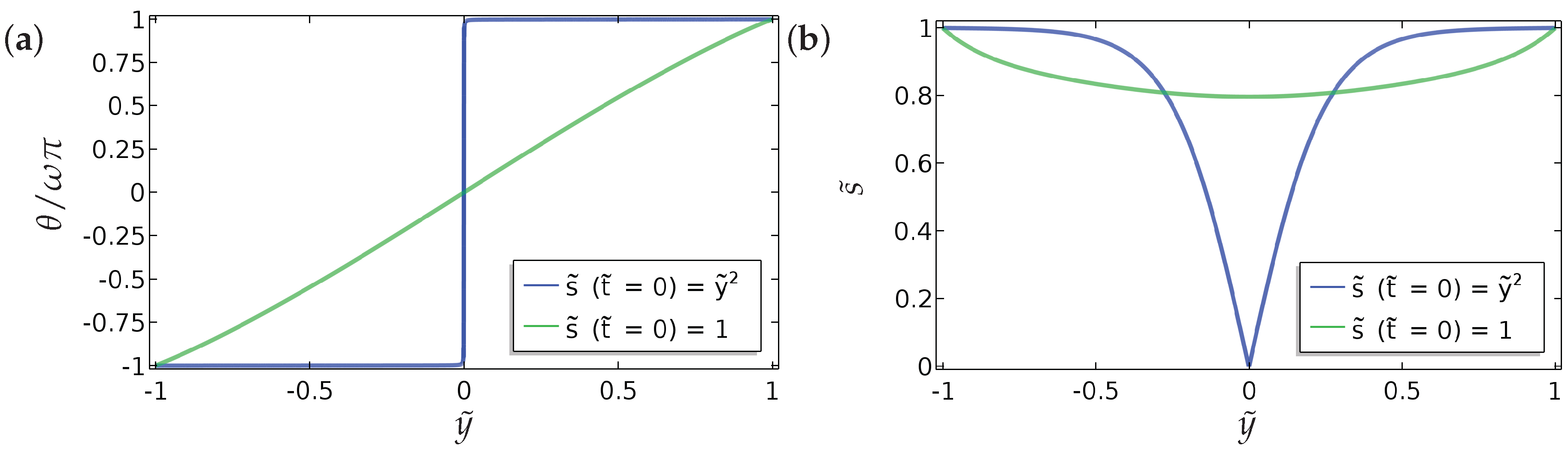
5. Conclusions
In this paper, we investigate the nematic order parameter (captured by the director orientation and the order parameter ) and flow profiles in a one-dimensional microfluidic channel, with Dirichlet boundary conditions and mixed boundary conditions for , as a function of the pressure gradient, the boundary conditions themselves (in terms of winding number and a measure of the anchoring strength B), the nematic elastic constant () and the scaled viscosities () in a reduced Beris–Edwards setting. For small , we can analyse the system and obtain at least semi-explicit solutions for the nematic order parameter and the flow profile, both with and without an applied pressure gradient. We consider continuous and discontinuous profiles for separately, again including the effect of the pressure gradient. In the discontinuous case, is effectively piecewise constant (without flow) for such solutions and discontinuities in are regularised by isotropic points with . We can analytically construct solutions with multiple discontinuities although we suspect that these solutions lose stability with respect to higher-dimensional perturbations. The analytical results set the scene for some interesting control problems on how to stabilise discontinuous solutions for small and these discontinuous solutions could offer interesting examples of domain walls with in three dimensions.
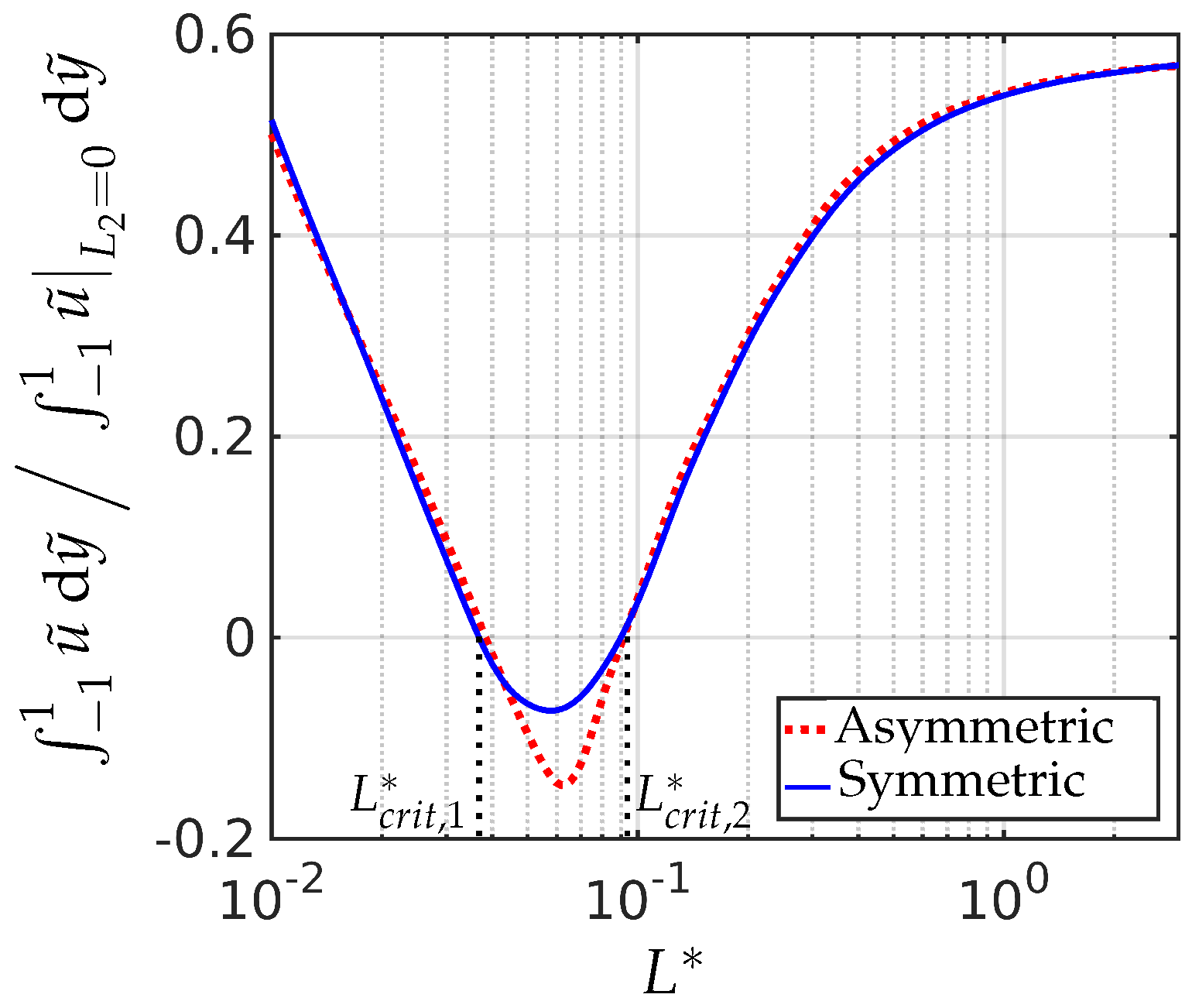
Our most interesting observations include the onset of flow reversal in these model microfluidic systems. We compute specific criteria for flow reversal (flow in the direction of the pressure gradient) as a function of
and
and in particular, based on the results in
Figure 10, we expect the curve in
Figure 5 to fold back on itself, so that for a given
large enough, flow reversal only occurs for a certain range of values
and not in the entire region above the dotted and solid curves in
Figure 5. The observed flow reversal is a distinct manifestation of backflow and only occurs for large enough
. We plan to investigate discontinuous order-reconstruction solutions in the presence of flow and backflow in microfluidic channels as a function of temperature (treating
a as a parameter or accounting for cases when
changes sign), geometrical dimensions and the anchoring coefficient
B in subsequent work.