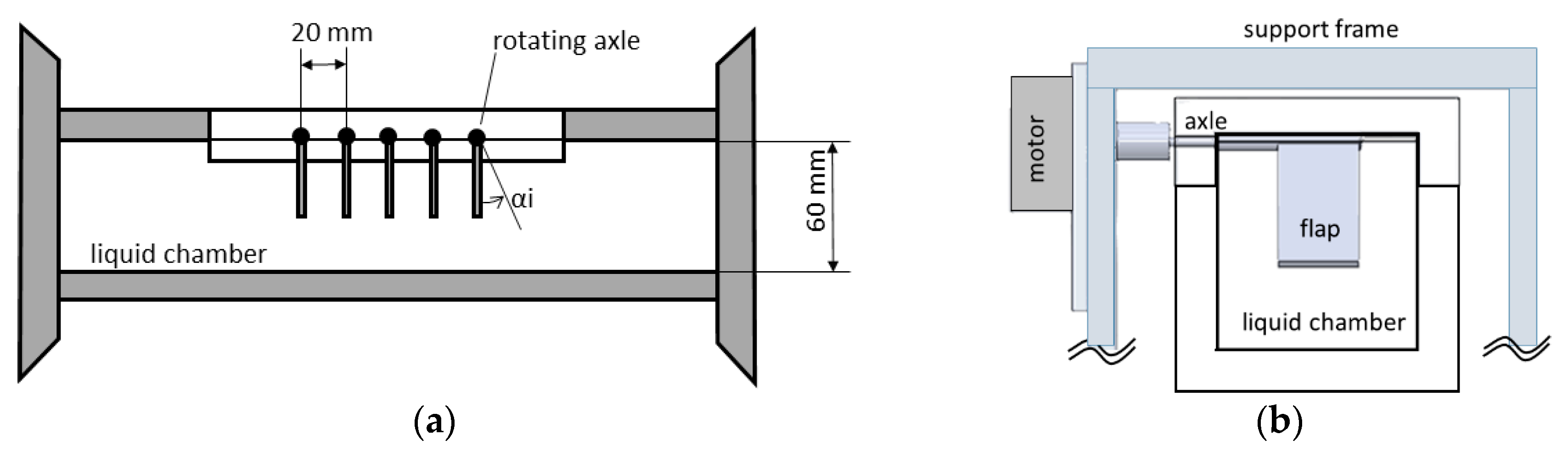
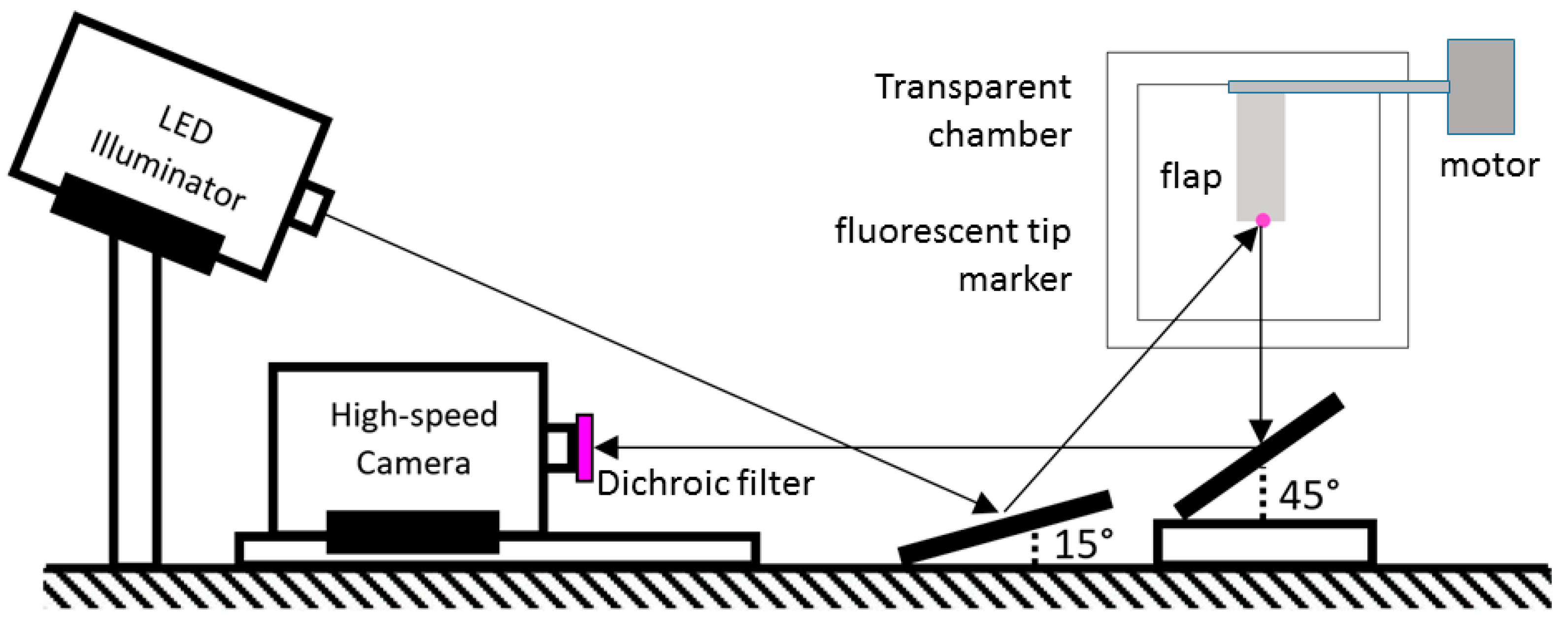
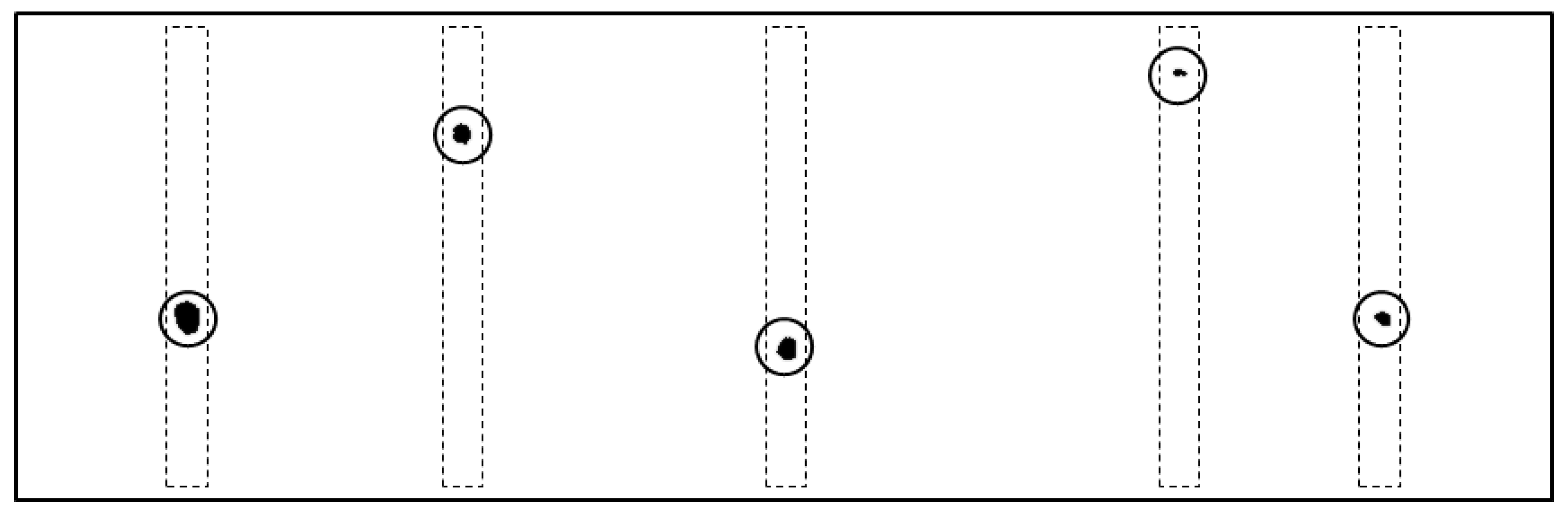
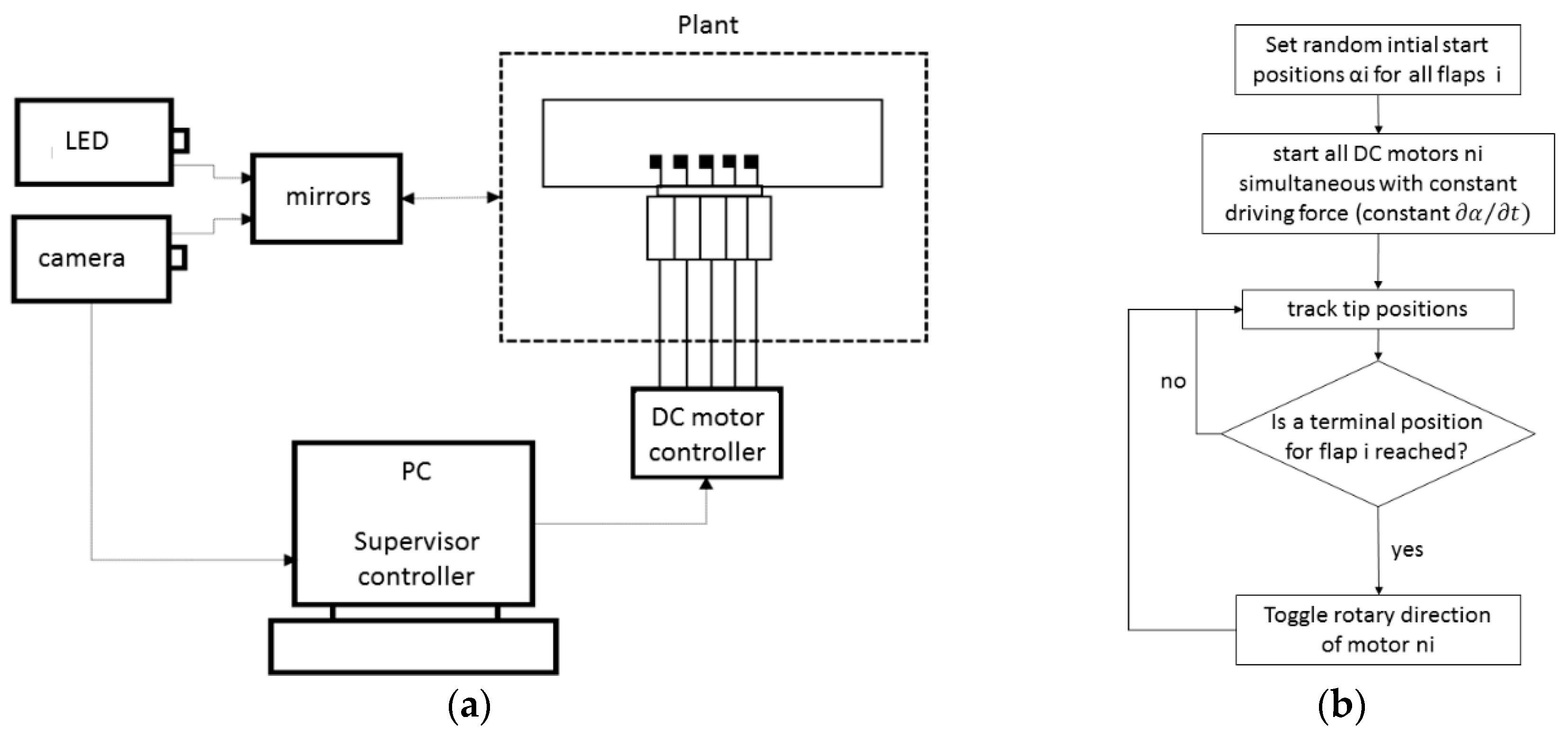
1. Introduction
A wide range of biological systems use synchronization in their movement patterns [
1,
2], ranging from small-scale unicellular organisms to larger scale sperms and microswimmers [
3,
4]. At low Reynolds numbers, this coordination is crucial for the propulsion of microswimmers or the generation of transport on ciliated walls. Motile cilia are found in many different tissues, from the brain [
5] to the lung and the oviduct, and in many organisms, from Chlamydomonas [
6] and Volvox [
7,
8] algae to Paramecium. It is the beat coordination of the invidiual cilia in the array that plays an essential role in the locomotion of sperm, the cleaning of breathing air, and the movement of oocytes in the fallopian tube [
9,
10,
11,
12]. Metachronal synchronization results when cilia beat with a certain constant phase shift between each other. Similar coordination was observed not only for natural cilia but also for artificial cilia and flagella in microswimmer propulsion [
12,
13,
14,
15]. Many studies have proposed ways to use the cilia propulsion mechanism in nanomechanics and microfluidic devices. Inspired by the progress made in the fabrication of small-scale flexible structures, the hydrodynamic interaction of artificial cilia has become again of interest to optimize such engineered systems. At low Reynolds numbers, the inertial terms in the Navier–Strokes equation can be neglected [
3], simplifying the momentum equation to the linear Stokes equation
with the pressure
p, the velocity
v and the dynamic viscosity
µ of the fluid. As the right-hand side in Equation (1) is time-independent, it suggests that for symmetric beating patterns it may not be possible to spontaneously come into a synchronized beating pattern [
16,
17]. However, the flexibility of the cilia adds another degree of freedom to the equation [
18,
19]. Typically, the beating pattern of natural cilia is non-symmetric in time; in the power stroke, the cilium is moved forward while stretched out straight, and in the return stroke it is retraced back near the wall. This was adopted by computer-simulation studies for 2D arrays of cilia [
20,
21], together with the “geometric clutch” hypothesis that was first introduced by Lindemann [
22,
23]. The results suggested that hydrodynamic interactions are sufficient to achieve spontaneous synchronization.
Synchronization of model flagella was studied for macroscopic rotating helices [
16] and colloidal spheres driven by optical traps [
24,
25]. However, up to now simple 2D symmetric flaps have not been tested on their possible self-synchronization, to the best of our knowledge. Often in such 2D systems, synchronization was just imposed by the control of the actuators to achieve maximum efficiency of the transport [
26]. Therefore, the process of spontaneous synchronization has not been studied in such experiments under well-defined boundary conditions so far. The aim of the present work is to introduce such an experiment and to test the conditions that lead to spontaneous synchronization. Therefore, we use silicon rubber flaps as artificial, macroscopic cilia that are driven by motor-controlled rotating axles in which the flaps are clamped in at one end and are forced to undergo a symmetric beating motion at a predefined frequency. The integration of the fluidic system inside a feedback control loop is done by vision-controlled implementation of the “geometric clutch” hypothesis. Bending deflections of the flaps’ tips are tracked while applying geometric thresholds for the toggling of the rotating direction of each individual motor separately. Hereby, we will experimentally prove that viscous coupling can force a row of individually beating flaps from random initial conditions into a synchronized beating pattern, forming a metachronal wave. The paper is structured as follows:
Section 2 describes the methods, and results are shown in
Section 3. Finally, discussion and conclusions are given in
Section 4.
3. Results
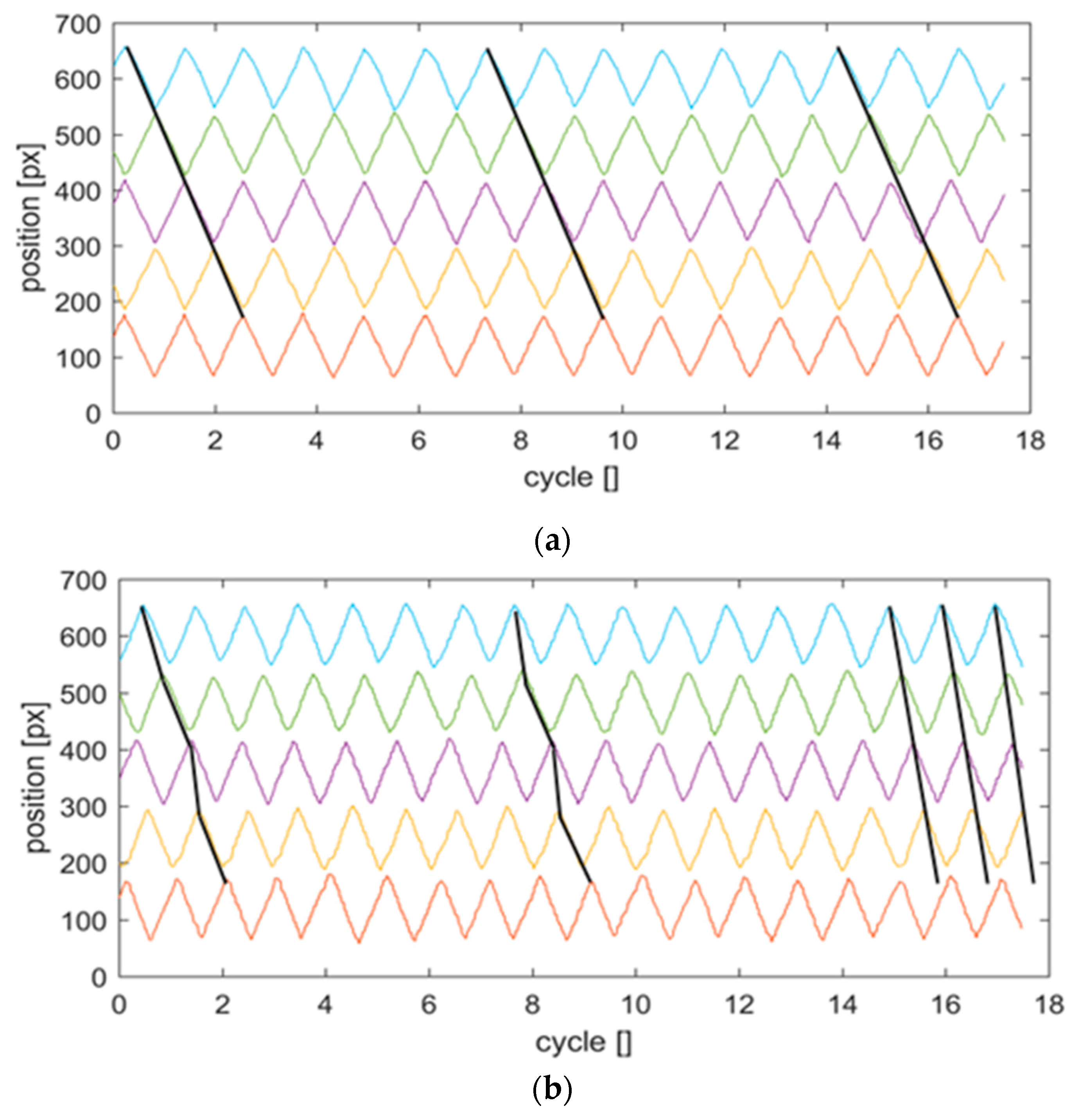
Figure 5 shows the recorded position trajectories for both situations: the control loop in reference situation and the control loop including strong viscous coupling.
Indeed, the results for the reference situation demonstrate that the phase relationship between the flaps in the row remains approximately constant over the number of recorded cycles. A small variation of flap
i = 3 is seen after 15 cycles, which is less than 10% phase drift. All flaps perform a zig-zag-type oscillatory motion while they remain in straight shape. In contrast, for the system with high viscous coupling, the phase differences are time-variant. The flexible flaps start bending as a reaction to the stronger fluid forces, which leads to a deviation of tip location relative to the position prescribed by the angle of the motor with the flap in straight shape. Maximum values of about 2 mm were observed, which corresponded to roughly 25% of the beat amplitude. The system comes after about 15 cycles into a coordinated synchronous motion when the phase lag among the tips remains approximately constant in space (between pairs) and in time. The straight black lines in
Figure 5 bottom show this observation clearly. The lines are passing through the instants where the individual beats reach their peak position. Only flap
i = 1 appears to be lagging behind the other tips. There are some possible explanations for this observation, which are discussed in the next section.
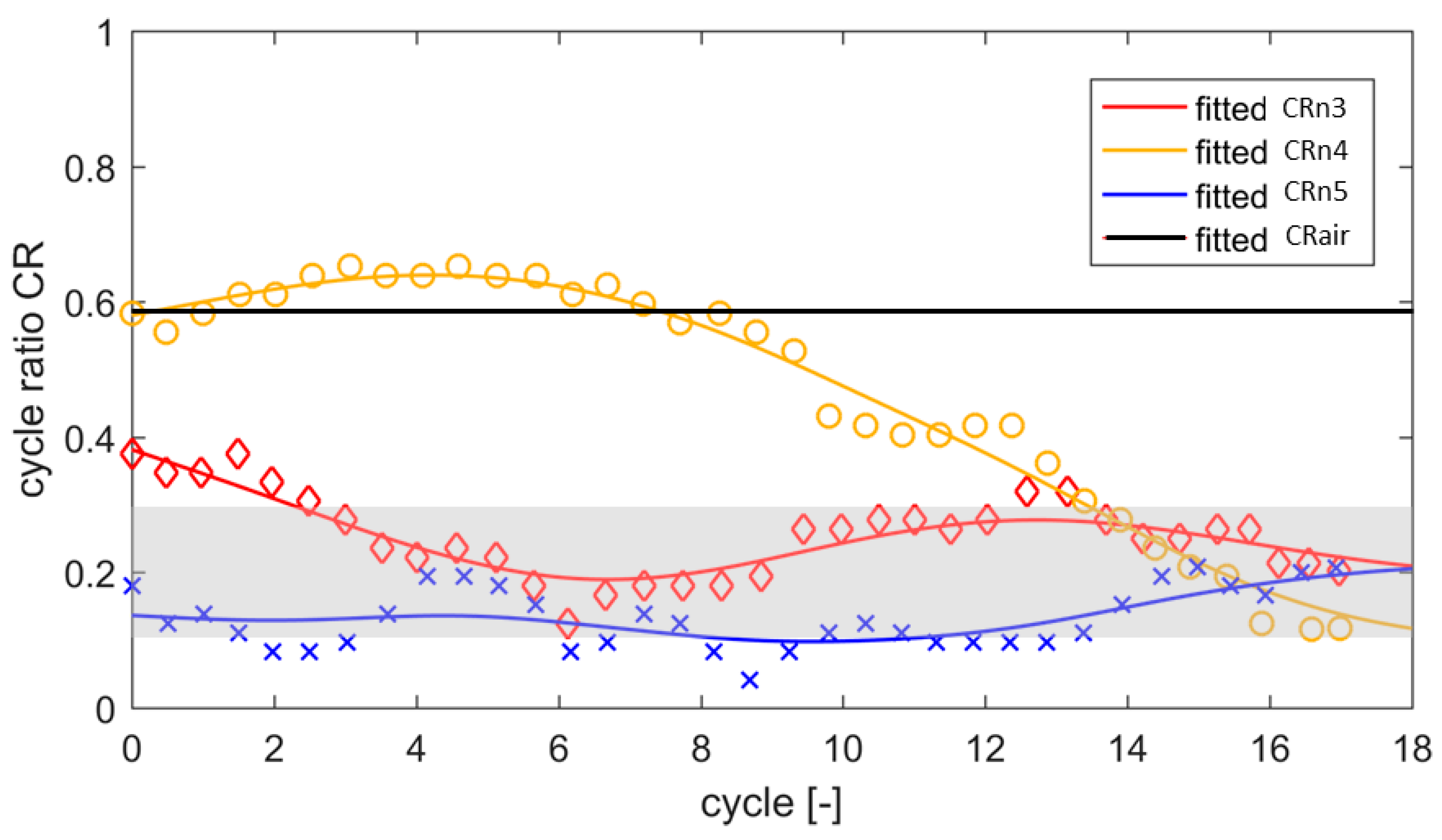
For further characterization of the metachronal coordination between neighboring beating flaps
ni and
ni−1, we define the cycle ratio
CR from the phase differences of reversal times
Tpeak in the corresponding beat cycles:
Figure 6 shows the temporal evolution of the phase differences between each couple of neighboring flap tips for flap
i = 2–5. The non-dimensional phase differences
CRn3–5 of the four synchronized flaps are found to converge to 15–25% of the cycle period between each neighboring couple. This is close to the phase lag observed in natural cilia to obtain optimum transport conditions [
3,
21]. For comparison, the black line shows the behavior of one pair of flaps
CRn4 for the reference case in air.
4. Discussion and Conclusions
Previous numerical models of the cilia beating patterns have simulated the spontaneous emergence of metachronal waves due to hydrodynamic interactions [
18,
21]. Included in these theoretical models is often the geometrical clutch hypothesis, which was introduced by Lindemann [
22,
23] to explain how the cilia motor is reversing the direction. It is assumed that once a cilium experiences certain bending, it retracts back following the beat stroke. Up to now, there has been no experimental proof of this spontaneous synchronization for rows of artificial 2D cilia under controlled conditions. In our study, we have verified the previous hypotheses in macroscopic experiments by documenting the spontaneous synchronization in a row of flaps due to their hydrodynamic interaction. This has been made possible by (i) introducing system flexibility through the use of silicon rubber flaps as artificial cilia, which start bending in the highly viscous environment at
Re = 0.12 and (ii) introducing online computer vision as the feedback methodology within the control loop that mimics the geometric clutch hypothesis. Since the silicon flaps bend as a reaction to the hydrodynamic coupling, it was important to optically track the flap tips for control of the beat reversal commands. This additional degree of freedom in the cilia tip motion relative to the imposed motor force allows coordination to take place. This load response has been measured and discussed for natural cilia and flagella in [
29,
30]. Our system is therefore equivalent to the key property of natural cilia required for synchronization, as they are able to change speed (or tip speed) in response to hydrodynamic load. Hydrodynamic coupling is herein the source driving the system to synchronization, as nothing else has changed between the two control experiments than the fluid. This agrees with the conclusions given in [
31].
The results show that a system of 5 individually beating flaps can form spontaneous synchronization after several cycles, while the same system in an inviscid environment remains fixed in its initial phase relationships. The observed convergence to phase differences of 15–25% of cycle duration agrees with the range found in natural cilia coordination for optimum flow transport [
3,
21]. This hints at a possible relaxation of the control system to a minimum of dissipation in the liquid [
21]. Additional flow measurements in our experiment are planned to gain details of the flow field during synchronization.
As seen from the results, the synchronization is not perfect, as the differences in phase do not converge to the exact same values. Flap number
i = 1 could not reach the phase relationship to the next as close as the others during the recording period of total number of 18 cycles. This could be related to the non-symmetric boundary effects for flap number
i = 1 and
i = 5. For both, the beating in direction away from the inner neighboring flaps is less influenced by viscous coupling than it is for the inner ones. As a result, the phase synchronization therefore may drift towards lock-on to either of the end flaps. A definite answer to the boundary effects can only be found by testing a chamber with a circular row of flaps, which eliminates these effects. However, variations in the phase shifts were also observed in the numerical simulations, even for imposed periodic boundary conditions [
21]. Real-time control is, in general, sensitive to time constrains and system internal delays, which may lead to aliasing effects [
32]. It takes 0.067 s from the detection of the terminal position to the action of the flap reversing the beat, given by the sampling frequency. At maximum tip speed, this delay equates to a possible variability of the amplitude of
. This uncertainty introduces a time variant parameter in the system synchronization. However, this random effect can be fairly neglected compared to the phase shift introduced by the bending of the flaps due to hydrodynamic interactions, as proven by comparison to the reference measurements in air, see also
Figure 6. In addition, during the calibration stage, the five motors were found to have slightly different speeds. Nevertheless, synchronization can even emerge in the presence of different intrinsic beat frequencies and oscillator noise as long as hydrodynamic coupling is strong enough. Fluctuations have been observed for natural systems, too, see ref. [
6].
A number of additional results is shown here to address several questions of importance regarding statistics and reproducibility of the results.
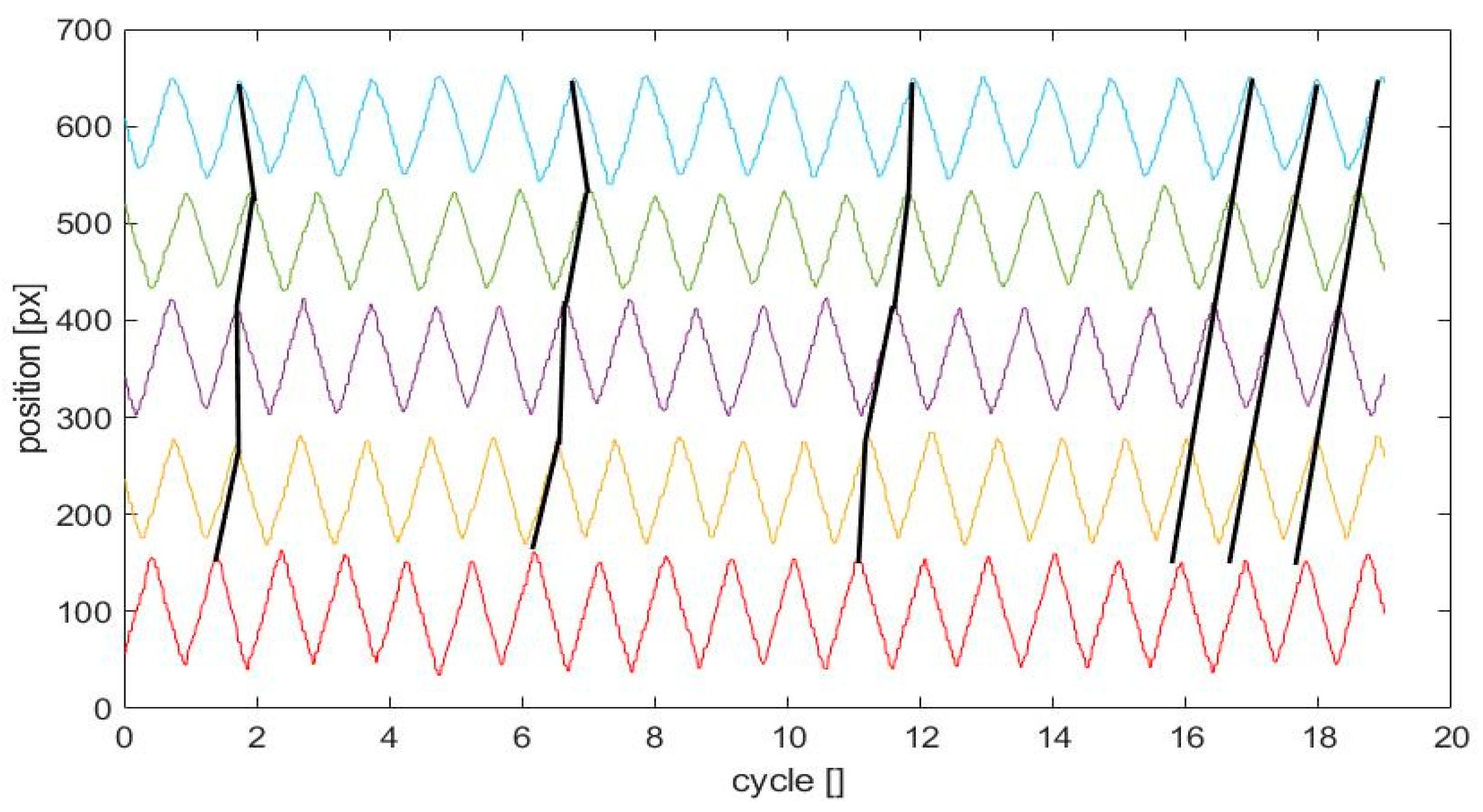
Figure 7 shows another experiment in the viscous liquid at random initial conditions.
The results prove that the system again gets into metachronal synchronization after about 15 cycles. Interestingly, while in
Figure 5 the metachronal wave runs from left to right (or from flap
i = 5 to
i = 1), it is the opposite for the other experiment shown in
Figure 7. As the beating profile of the cilia is in principal time-reversible and the cilia shape is symmetric, and all cilia are uniformly spaced, we assume that small deviations from symmetry in the motor response or in the shape of the flaps or the initial conditions play a role in selection of direction. Sometimes, we even could observe spontaneous symmetry breaking at times larger than 1 min. However, we could not judge these observations as physically relevant, as they only appeared at much later times, and possible accumulations and aliasing affects as discussed above may then play a role. The number of cycles to get into synchronization depends on the initial conditions, and we observed in several experiments a variation of this time-scale. Note, that we quantify this time of synchronization as the instant when all cilia pairs get into the phase relationship within the range marked as a gray-shaded box in
Figure 6. When the cilia start with a constant phase shift representing already a metachronal state, this time-scale is zero. On the other hand, all other experiments showed a maximum of equal or less than 15 cycles until synchronization was reached in the present system at the given properties of the liquid. We expect also a dependency on the Reynolds-number, which is left open for future studies with liquids of varying viscosity.
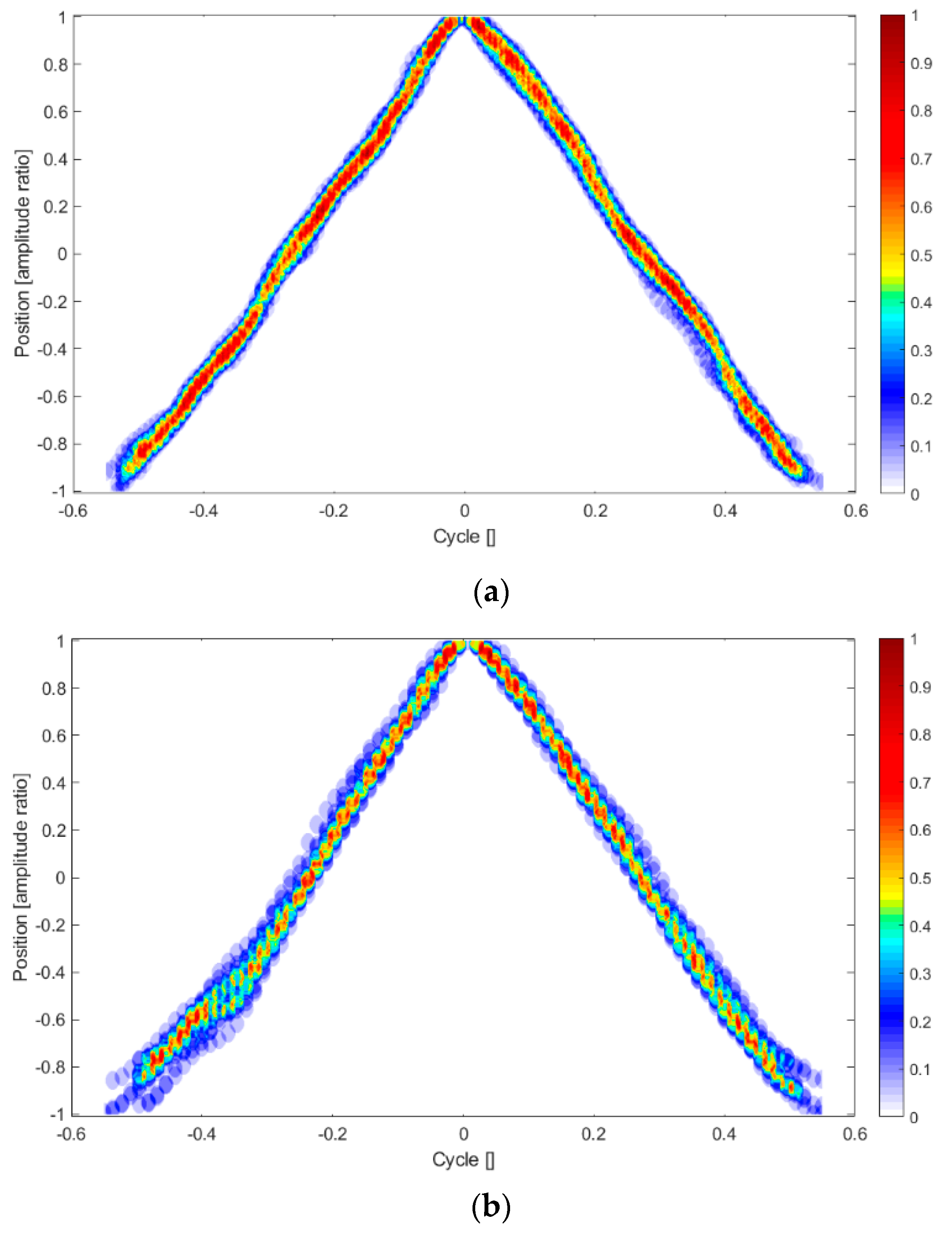
For further illustration of the variability in the motion pattern, we calculated the variance in the zig-zag type motion by superposition of the individual “teeth” in the zig-zag pattern. For reference, we fixed the tip of each tooth at the position of cycle time equal to 0. From the data superposed in this way, we calculated the probability function to be within a certain radial distance to the mean of the triangular shape using a box-counting method. The resulting distribution is shown as color plot in
Figure 8 for flap
i = 2. Dark red color means a probability of 1 that this position is reached in all successive cycles in a similar time relative to the tip of the teeth (defined by the search radius).
As demonstrated, the air experiment shows a rather sharp-edged triangle with small variations between individual beats. In comparison, the synchronization process in the viscous environment causes larger deviations, especially at the flap reversals, where neighboring flaps get closer to each other. Further evidence of this variability is demonstrated by comparing the normalized auto-correlation profiles of the flap motion as given in
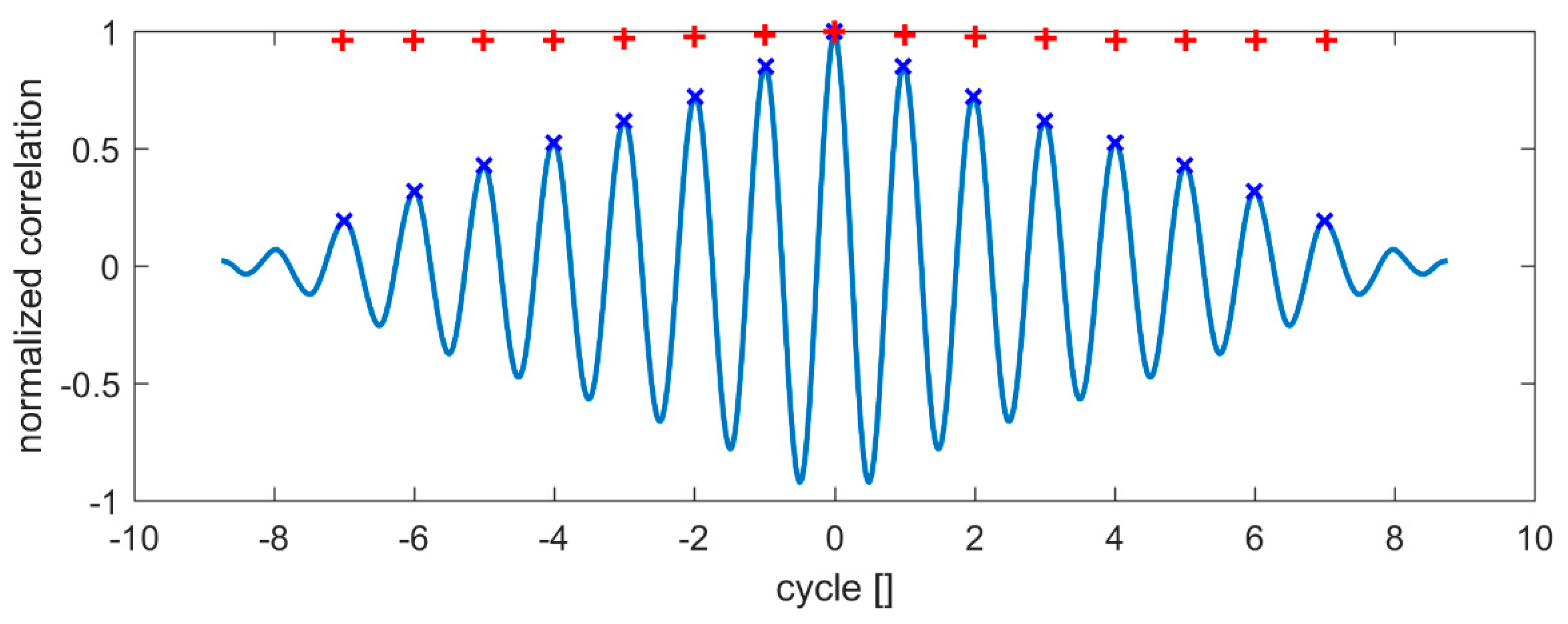
Figure 9. The normalized autocorrelation of a perfect zig-zag motion pattern would result in extrema of 1 and −1 at time-lags of even and odd multiples of half of the cycle ratio. For the air experiments, the positive peaks are all above a correlation value of 0.95, shown by the “+” type symbols in the plot. In comparison, in the viscous case successive cycles underlie the documented small variability during the synchronization process; therefore, the correlation peaks decrease with larger time-lags until correlation is fully lost after 8–9 cycles. Similar profiles can be shown also for other flaps in the row.
In the future, further improvements will be possible on the control loop timing to increase the sampling frequency and thus allow longer periods of study. This can be achieved by embedding the PC monitoring and control logic into the high-speed camera processor itself. It will allow or the extension of the studies to a wider range of Reynolds-numbers and parametric variations of the geometry of the cilia. One major difference between biological cilia and the flaps in our study is their 2D shape with rectangular cross-section. Nevertheless, we expect similar synchronization for cylinders as long as we are in the Stokes-flow regime where the shape of the body loses importance in viscous forces. Furthermore, the chamber offers optical access to capture the flow details using Particle Image Velocimetry simultaneously while the control loop is running. It might help to further investigate the above-claimed hypothesis of the relaxation of the control system towards a minimum of dissipation in the liquid.