3.1. Kinematic Parameters and Aerodynamic Coefficients of Wing Model
The wing model was tested at 5 flapping frequencies ranging from 20 Hz to 30 Hz. Videos were recorded by the Phantom camera system. Flapping frequency was measured by tracing ink markers 1 and 3 in
Figure 3. In such a way, the relationship between the input voltage of the motor and the flapping frequency has been established.
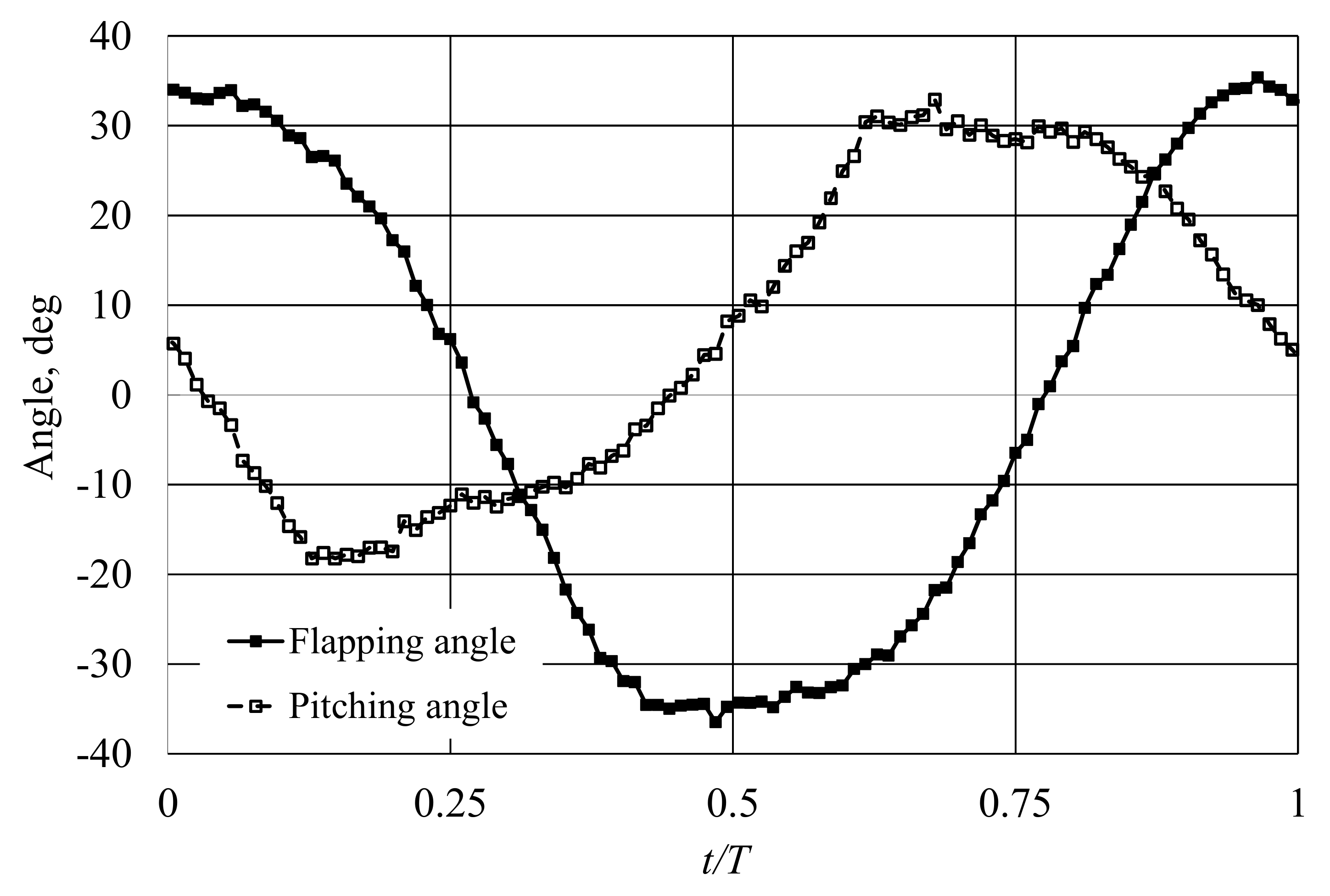
Next, the flapping and pitching angles in the flapper were examined at 20 Hz. Time variations of flapping and pitching angles in the middle section of the flapper are illustrated in
Figure 5. The peak-to-peak flapping angle amplitude of 70 degrees is about the same as in static measurements. It can be seen from the figure that the pitching angle leads the flapping angle by approximately 0.35
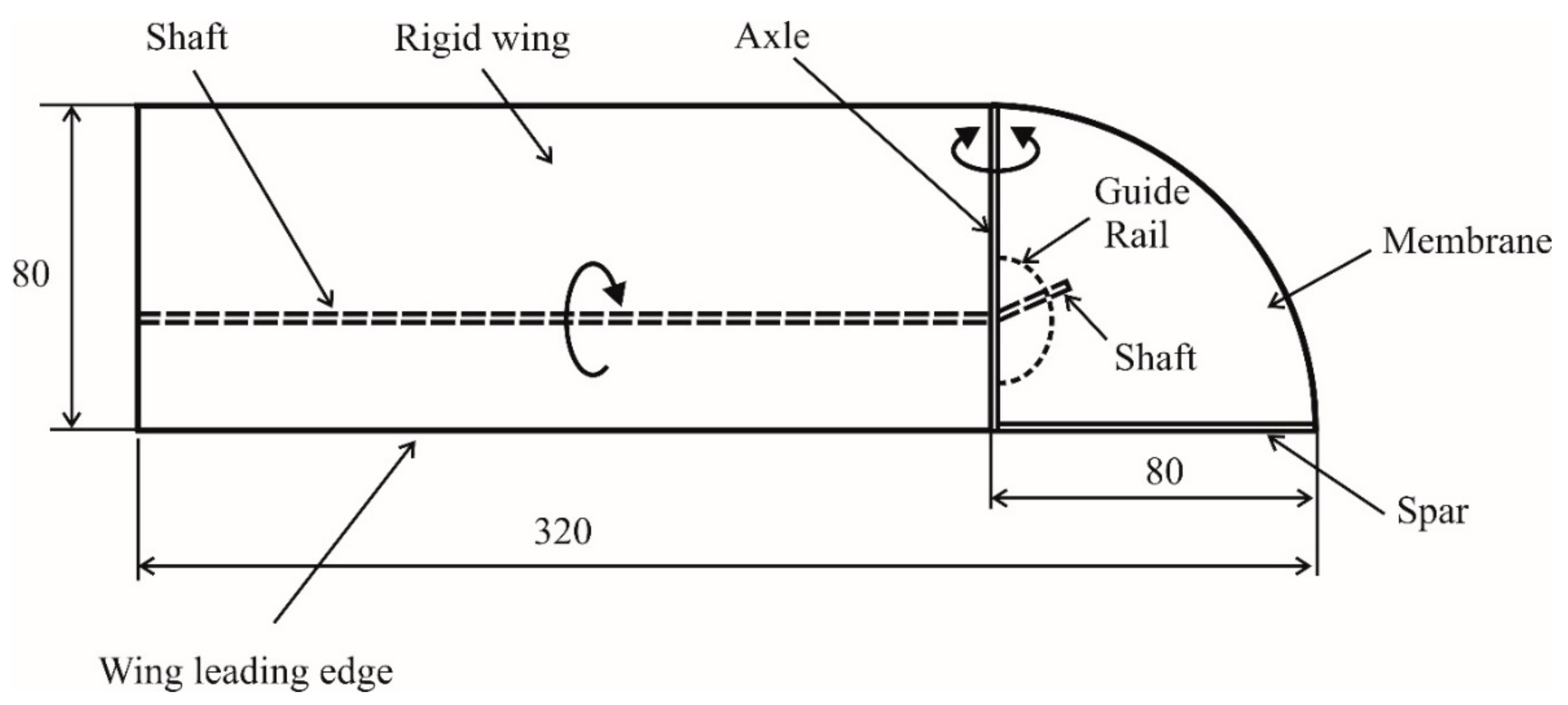
T. The time variation of the pitching angle is non-symmetrical, with a maximum of 33 degrees and minimum of −18 degrees. This asymmetry can be explained by the non-symmetric supporting structure of the flapper. Specifically, the mechanism of the guide rail is positioned underneath the membrane, as illustrated in
Figure 2. Therefore, the out-of-plane deformations of the membrane are constrained by the guide rail on the upstroke, but unconstrained on the downstroke.
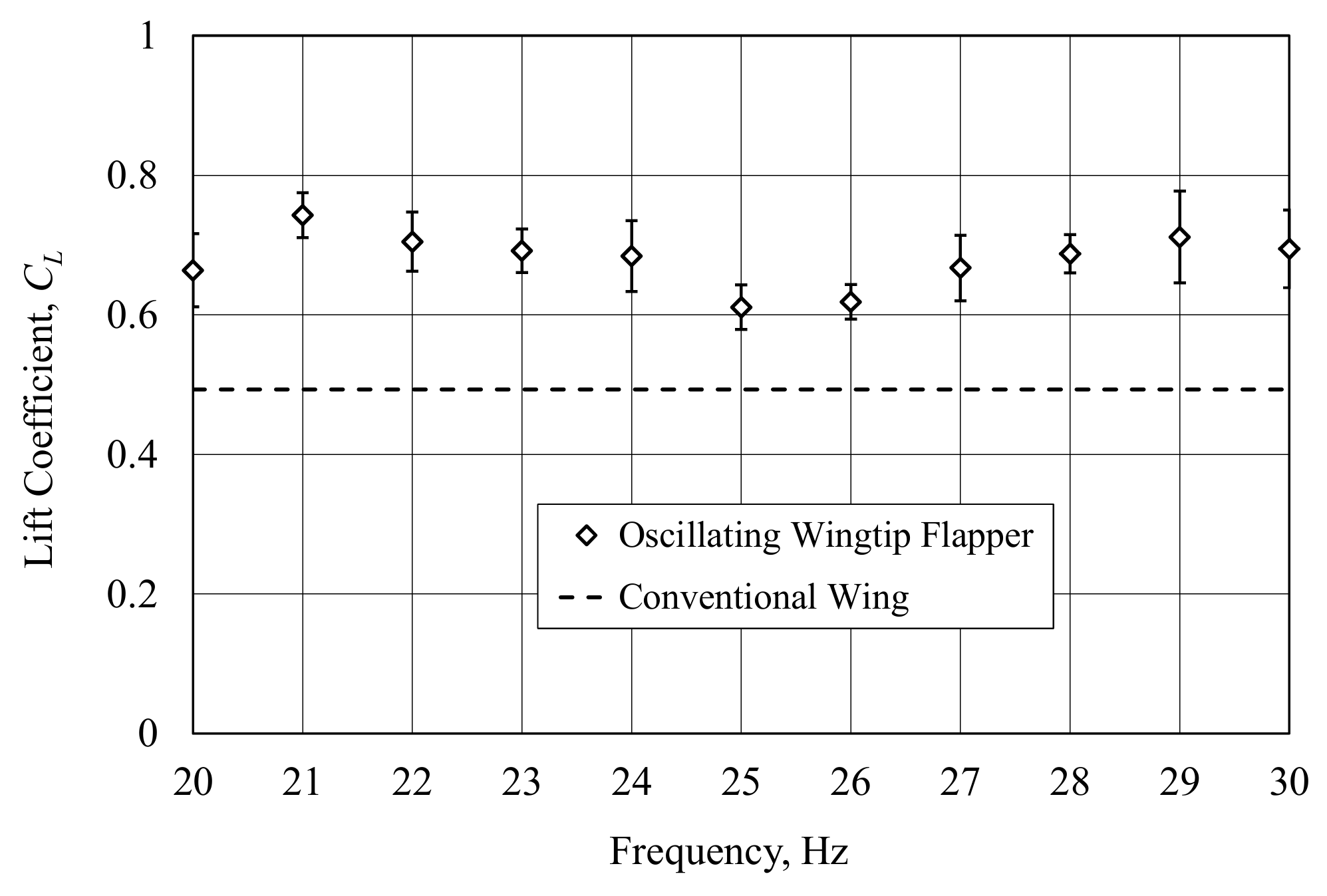
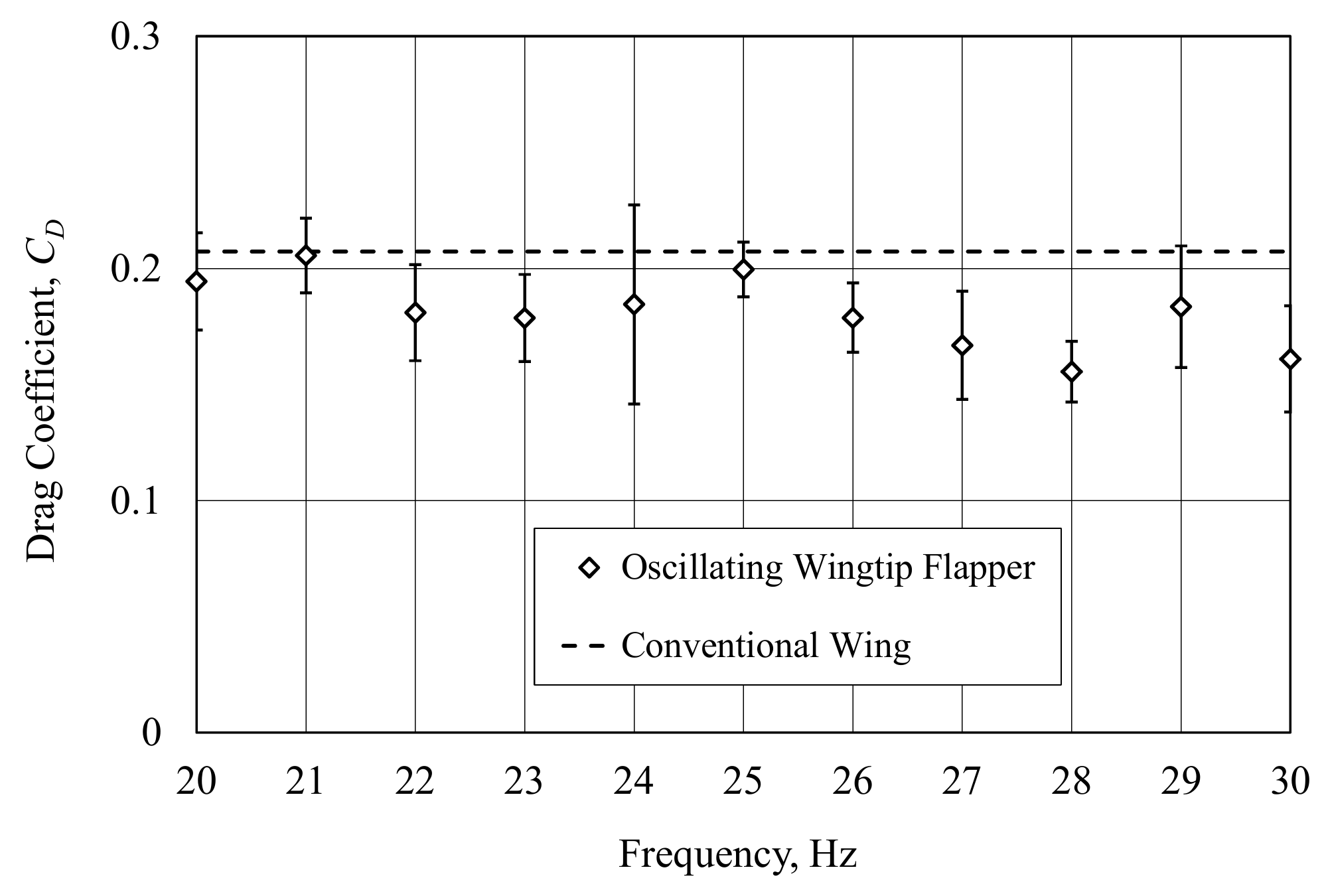
Stroke-averaged lift and drag forces, along with the wind tunnel speed, were recorded in wind tunnel experiments at the flapping frequency f = 20–30 Hz and corresponding reduced frequency k = 0.85–1.28. In addition, the experiment with the flapper fixed horizontally was conducted representing a conventional fixed wing and providing a basis for evaluation of the aerodynamic efficiency of the new wing design. The Reynolds number based on the wind tunnel velocity and the rigid wing chord is 24,390. At the flapping frequency of 20 Hz, the corresponding reduced frequency is 1.
Lift and drag coefficients were determined for each test, using as a reference the total wing area,
S, and the wind tunnel velocity,
V = 5 m/s. At each frequency, 10 tests were performed, providing the average and standard deviation values of the aerodynamic coefficients. Plots of the aerodynamic coefficients
CL and
CD are shown in
Figure 6 and
Figure 7, respectively. In order to illustrate variations in the aerodynamic coefficients, error bars were plotted in the figures based on standard deviation at each flapping frequency.
As can be seen in
Figure 6 and
Figure 7, the lift coefficients are higher and drag coefficients are lower for the wing with the wingtip flapper as compared to the conventional non-flapping wing. There is a 40% increase of the average lift coefficient. While there is no clear trend in the lift coefficient, a slight decrease of the drag coefficient with the frequency increase is observed. Note that an increase of the lift and a decrease of the drag on one-half of the wing is necessary for performing banked turns. Thus, differential oscillations in left and right wingtips can provide roll and yaw controls. The role of the flapping wingtip flappers in pitch controls will be addressed in future studies.
The lift-to-drag ratio,
CL/
CD, is an important performance measure, specifically, of a flight range of an aircraft. The results given in
Table 1 show that the lift-to-drag ratio increases with a flapping frequency increase. In the present work, a conventional wing case was obtained by fixing a flapper horizontally. The lift-to-drag ratio for the conventional wing is denoted in the table by the zero frequency case. The wing with the wingtip flapper surpasses the conventional wing on average by 60% or within a margin of 30–80% depending on frequency.
3.2. Smoke-Wire Flow Visualization
Experiments performed in the previous study [
18] with vertically and horizontally placed smoke-wires are discussed herein. Tests were conducted at the flapping frequency of 20 Hz.
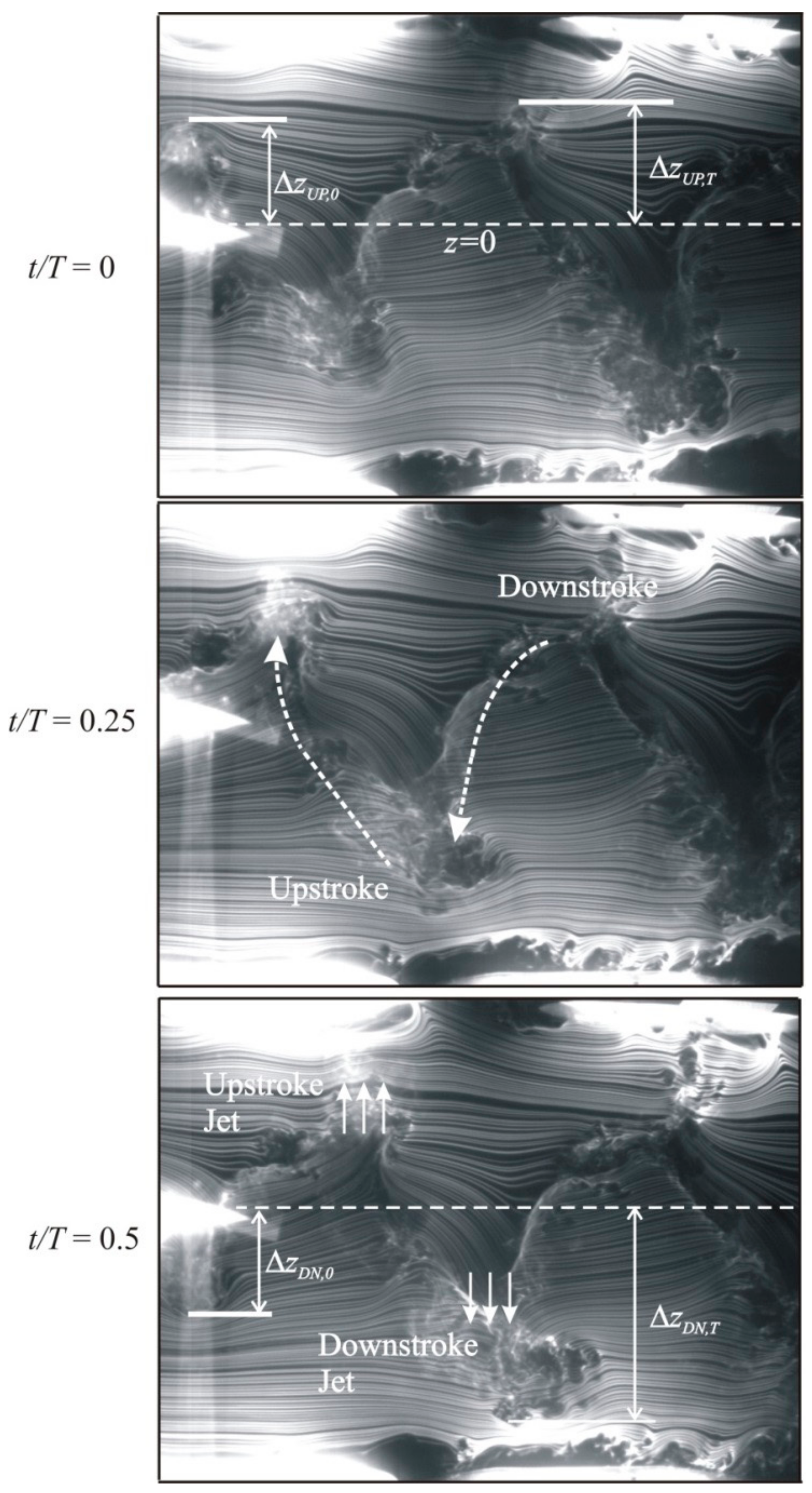
Flow streamlines on the vertical plane are shown in
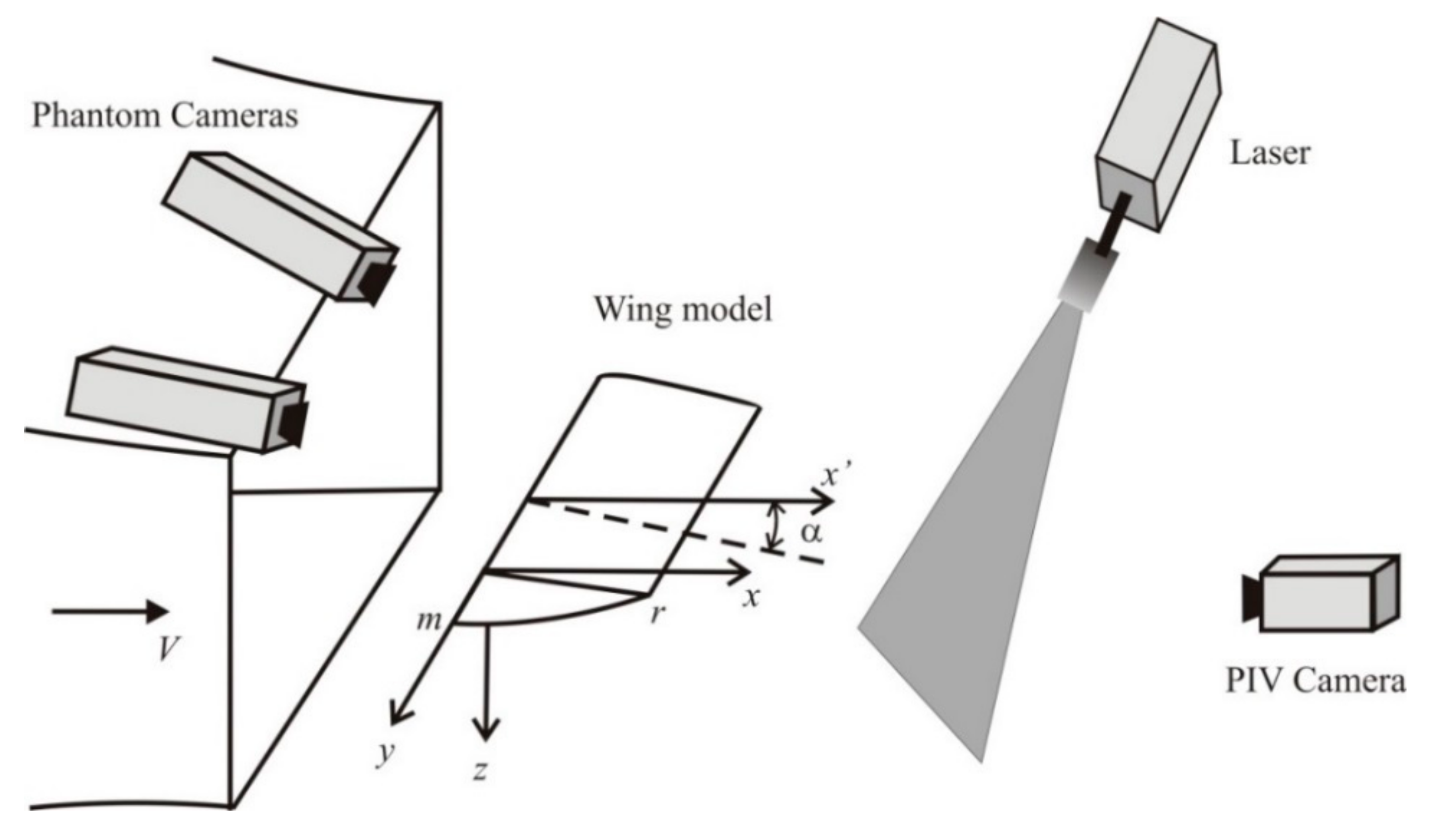
Figure 8 for three time instants. The free stream runs from the left to the right. The coordinates of the smoke-wire line, which was parallel to the
z-axis, were
x = −280 mm and
y = 60 mm (see
Figure 4). One concern in this test was the size of the oscillating wake relative to the area of the flow region in the test section. However, no substantial interfering of shear-layer vortices with the wake is observed within the first period of wake oscillations.
General observations were made about the wake dynamics shown in
Figure 8. Traces of the flapper are seen in the photographs. The wake oscillations follow the flapping motion. Streamlines are deformed and inclined near the plane
z = 0. The wake becomes turbulent at the top and bottom of the cycle.
The wavelength of the wake immediately behind the wing is 250 mm, which is approximately equal to the product of the flapping period and the wind speed. On the downstroke, the flow trailing the wing is rapidly deflected downward, forming a downward jet. On the upstroke, a smaller deflection of streamlines and a smaller upstroke jet are produced by the flapper (see
Figure 8).
Up and down amplitudes of wake oscillations just behind the wing trailing edge are about the same,
= 70 mm and they increase during the first period of the wake. Note that the maximal displacements of the flapper tip were found to be ±46 mm based on the flapping angle in
Figure 5. The peak-to-peak amplitude of wake oscillation in the
z-direction at the end of the period is 230 mm, which is much higher than the flapper wingtip amplitude of 92 mm. Also, a larger amount of air is pushed downward compared to the upward direction and
.
Flow streamlines on the horizontal plane
z = 0 are presented in
Figure 9 for three time instants. The free stream flows from the top down. Strong eddies are shed downstream from the corner point of the trailing edge, where a flapper is attached to the rigid wing. Eddies formed behind the rigid wing can also be seen in
Figure 9. Imprints of the flapper on the horizontal smoke plane on the up- and downstrokes are significantly different as seen in
Figure 9. There is a strong wingtip vortex generated on the downstroke.
3.3. Near-field PIV Measurements
Phase-locked PIV measurements were conducted for 27 flapping angles across a flapping cycle at each of 3 streamwise planes:
x/
c = 2, 3, and 5. The flapping frequency used in PIV measurements was set at 20 Hz. For a given flapping angle, 10 PIV picture pairs were recorded. A total of 810 image pairs were analyzed. The evolution of a system of vortices was investigated using vortex center and vortex core boundary identification methods described in [
19,
20].
Major vortex patterns were deduced from the observations of experimental data. They include the primary undulating vortex (FO), the secondary undulating vortex (FI), and the vortex ring (RO and RI).
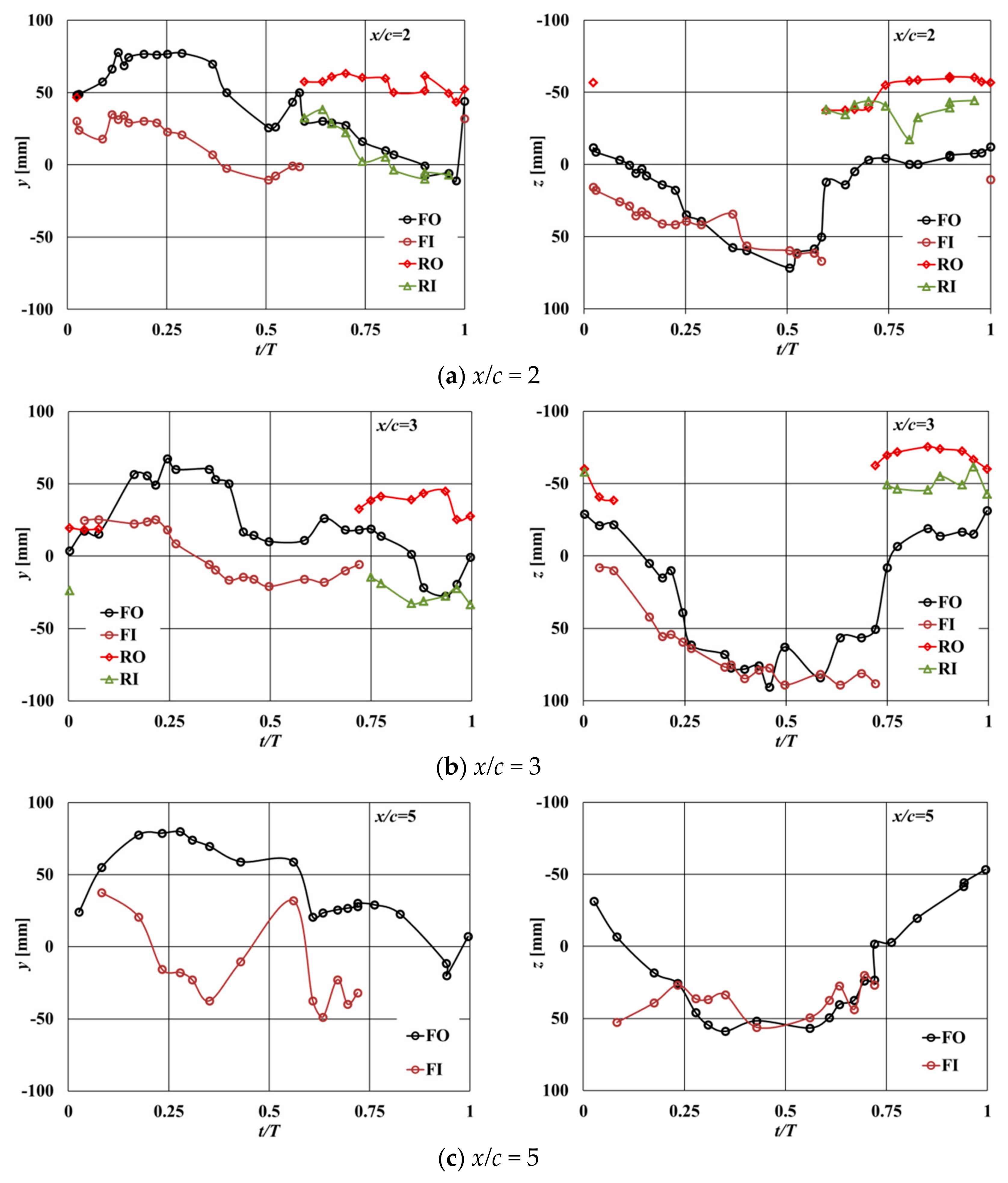
Figure 10 shows the trajectory of the FO vortex center in the
yz-planes. In this figure, the dashed line corresponds to the upstroke (UP), and the solid line is for the downstroke (DN). A position of the vortex center is related to the flapping angle of the leading edge spar,
=
(
t0), at the time
t0, when the vortex system left the flapper. Time histories of vortex center motion for all vortices are presented in
Figure 11.
There is a time delay (a phase lag) between the moment,
t0, when vortices shed from the flapper at
x/
c = 0 and the moment,
t, when they reached the PIV measurements plane
x/
c. In the present study, the value Δ
t =
t −
t0 is determined by using the PIV technique. Four small reflective markers were attached to the base and the tip of the flapper, and along the leading edge of the rigid part of the model. The markers located at
x/
c = 0 have been observed as bright spots on PIV images taken at a given station
x/
c. Tracking them and digitizing their positions allowed the determination of the time variation of the flapping angle of the leading edge spar,
(
t). The obtained function is similar to the one presented in
Figure 5. Simultaneously, the displacement of the center of the vortex FO in the vertical direction,
z(
t), was determined. For a given measurement plane, the time difference between time instants, corresponding to maxima of
z(
t) and of
(
t), was calculated, which is approximately equal to the time delay Δ
t. Then, the flapping angle of the leading edge spar can be found as
=
(
t0) =
(
t − Δ
t).
Figure 10 shows the primary vortex wandering in a counterclockwise direction. Its oscillations in both vertical,
z, and horizontal,
y, directions through the flapping cycle are illustrated in
Figure 11. On the contrary, the vortex core rotates in a clockwise direction (
Figure 12), which is the same sense of rotation as a wingtip vortex in a conventional fixed wing.
At
x/
c = 2, starting at
φ = −17° UP, the FO is shedding from the flapper near the tip of the rigid wing (point
r in
Figure 10). Between
φ = 36° UP and
φ = 44° UP, the FO vortex is rapidly shifting towards the flapper tip by about 55 mm. This change is also seen in
Figure 11a at
t/
T ~ 1. Through the downstroke, the FO is moving downward following the flapper tip.
The FI vortex starts shedding at
φ = 44° UP (
t/
T = 1) and continues shedding throughout the downstroke (
t/
T = 0–0.57). FO and FI have an opposite sense of rotation (
Figure 12a,b) moving approximately side-by-side (
Figure 11a–c). FI disappears on the
yz-plane
x/
c = 2 at
t/
T = 0.58 (
Figure 11a),
φ = −17° UP (
Figure 12d). Moreover, the distances between FO and FI in both
z and
y directions remain relatively small before this moment of time. These results are indicative of a cross-stream vortex closing FO and FI vortices.
Note from
Figure 11 that the amplitude of oscillations of the center of the vortex FO at
x/
c = 5 in the
z-direction is greater than that at
x/
c = 2 by approximately 40%. While the amplitude of the FI vortex center is decreased from
x/
c = 2 to 5 by almost two times.
The vortex ring includes the outer part, RO, and the inner part, RI (
Figure 12c,d). They shed from the trailing edge of the membrane during the second part of the upstroke and pronation (from
φ = −17° UP to
φ = 42° DN). The vortex ring is moving upward (in the negative
z-direction) from
x/
c = 2 to 3 and is out of the field of view at
x/
c = 5 (
Figure 11c).
A circulation and a core size were determined across a flapping cycle with the help of the vortex identification methods [
19,
20]. The minimum, maximum, and stroke-averaged values were calculated using these data. The results for the circulation and the core radius are presented in
Table 2 and
Table 3, respectively. In these tables,
max and
min refer to the maximum and minimum of the circulation strength and the sign denotes the direction of rotation. The stroke-averaged values,
ave, are also provided in tables.
Based on the circulation values, the FI vortex is much weaker than the FO. Similarly, the inner vortex RI is weaker than the outer vortex RO. For the FI, RO, and RI vortices, the maximum and average values decrease with the distance from the wing. For the FO vortex, however, a small increase of the circulation strengths of approximately 3% was found with the distance changing from x/c = 2 to 3. Circulation decreases significantly at the most distant station from the wing x/c = 5. For instance, the stroke-averaged circulation for the FO vortex decreases by almost 2 times.
As seen in
Table 3, the core size slightly increases from the station
x/
c = 2 to 3, except for the RI vortex. For the FO and FI vortices, the core size decreases significantly at
x/
c = 5, while the RO and RI disappear.
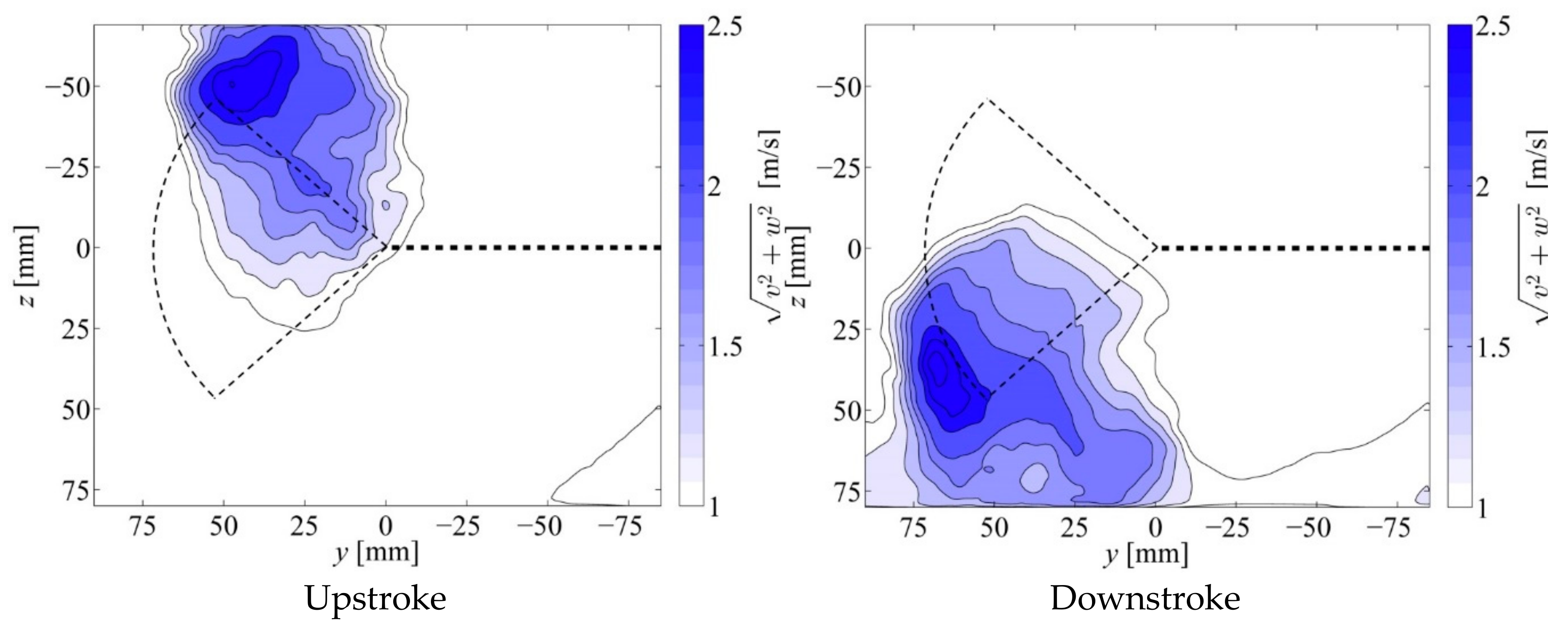
Smoke-wire observations of strong vertical jets seen in the
xz-plane in
Figure 8 are corroborated by velocity and vorticity fields in
Figure 12. The projections of these jets onto the
yz-plane are seen in
Figure 12 between vortex pairs FO–FI and RO–RI. Maps of the in-plane speed
averaged over the half-stroke are drawn in
Figure 13 to further illustrate jet flows. A color step of 0.2 m/s was used for the illustrations. As can be seen in
Figure 13, the airflow moves away from the flapper and downward or upward depending on the direction of flapping. The region of the maximum speed corresponds to approximately 2.5 m/s during both up- and downstroke.
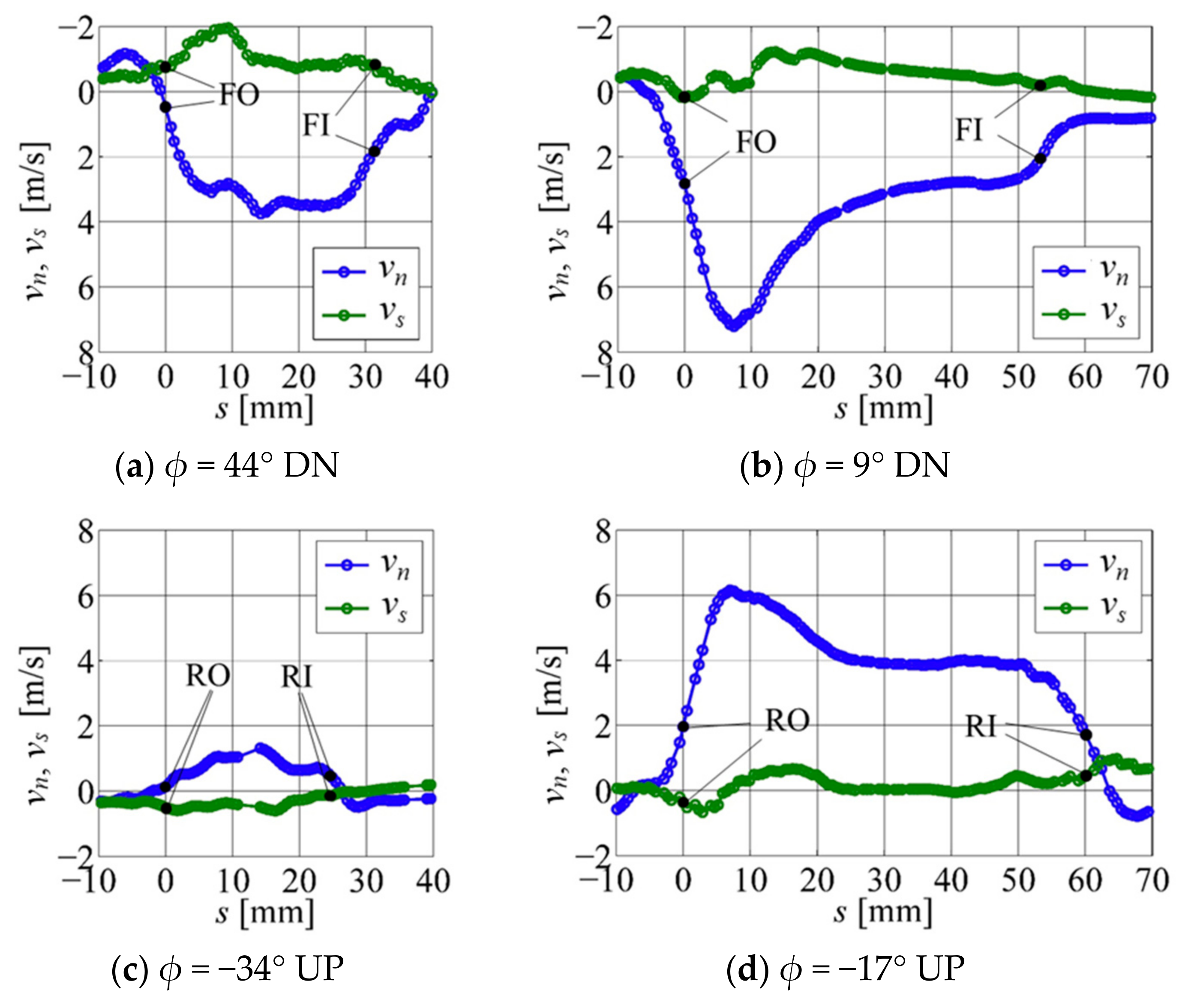
Velocity variations in jets are plotted in
Figure 14a–d for four values of the flapping angle presented in
Figure 12a–d, respectively. The
s-axis crosses the vortex centers of a given vortex pair, and the
n-axis is normal to
s-axis, as illustrated in
Figure 12. The velocity components along
n- and
s-axis are
vn and
vs, respectively. On the first half of the downstroke from
φ = 44° DN to 9° DN, the normal component,
vn, increases up to 7.2 m/s (
Figure 14a,b). The maximum of
vn reaches 6.1 m/s during the first half of the upstroke from
φ = −34° UP to −17° UP (
Figure 14c,d). In plots in
Figure 14b,d it is seen that
vn maxima are closer to FO and RO, respectively, where higher velocity magnitudes and gradients are observed. For all the four phases, the magnitude of
vs is much smaller than that of
vn, indicating the jet-like airflow.