1. Introduction
Liquid crystals belong to the broad class of soft matter, which appears in between crystalline solids and isotropic liquids. They are usually made of shape anisotropic organic molecules and exhibit a variety of phase transitions. A nematic is one of the simplest liquid crystals in which the constituent molecules have a preference to align with one another along one orientation in the system called the director and denoted by a dimensionless unit vector
. The nematic is apolar, i.e.,
and
are physically equivalent. In the nematic phase, two different types of topological defects or singularities are observed. These are either line defects, known as disclinations (showing the discontinuity in the inclination of molecules) or point defects (hedgehogs and boojums) where the director cannot be defined [
1,
2]. These defects cannot be eliminated by continuous deformation of the order parameter field; hence, they are topologically stable [
3]. They are characterized by strength or winding number ‘
s’, which is denoted by an integer or half-integer number. The strength ‘
s’ determines the number of times the director rotates around the singularity when one encircles the defect core [
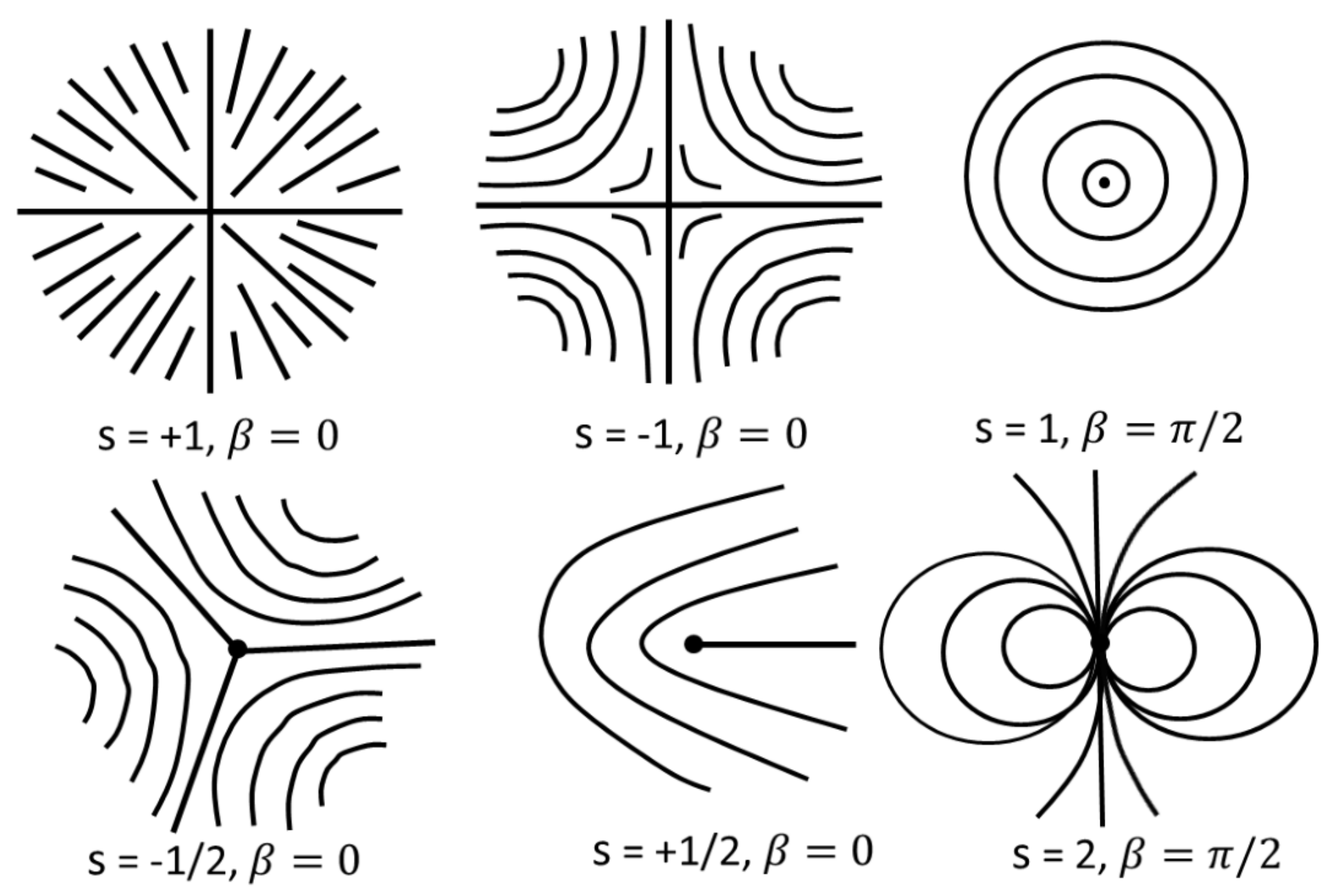
2]. Two oppositely-charged defects can annihilate one other. The orientation of the nematic director field (
) surrounding the defect can be expressed in terms of defect strength (
s) [
1]:
where
= tan
and
is a constant. Here, the defect strength
s depends on the symmetry of the medium. In the nematic phase,
s is the multiple of ±
, as the director has
≡
symmetry.
Figure 1 shows the schematic representation of the director structure of a few defects.
In the cholesteric phase (N
* ), the molecular chirality induces spontaneous twist, which leads to complicated, but stable networks of disclination lines in a planar cell, known as oily-streak defects [
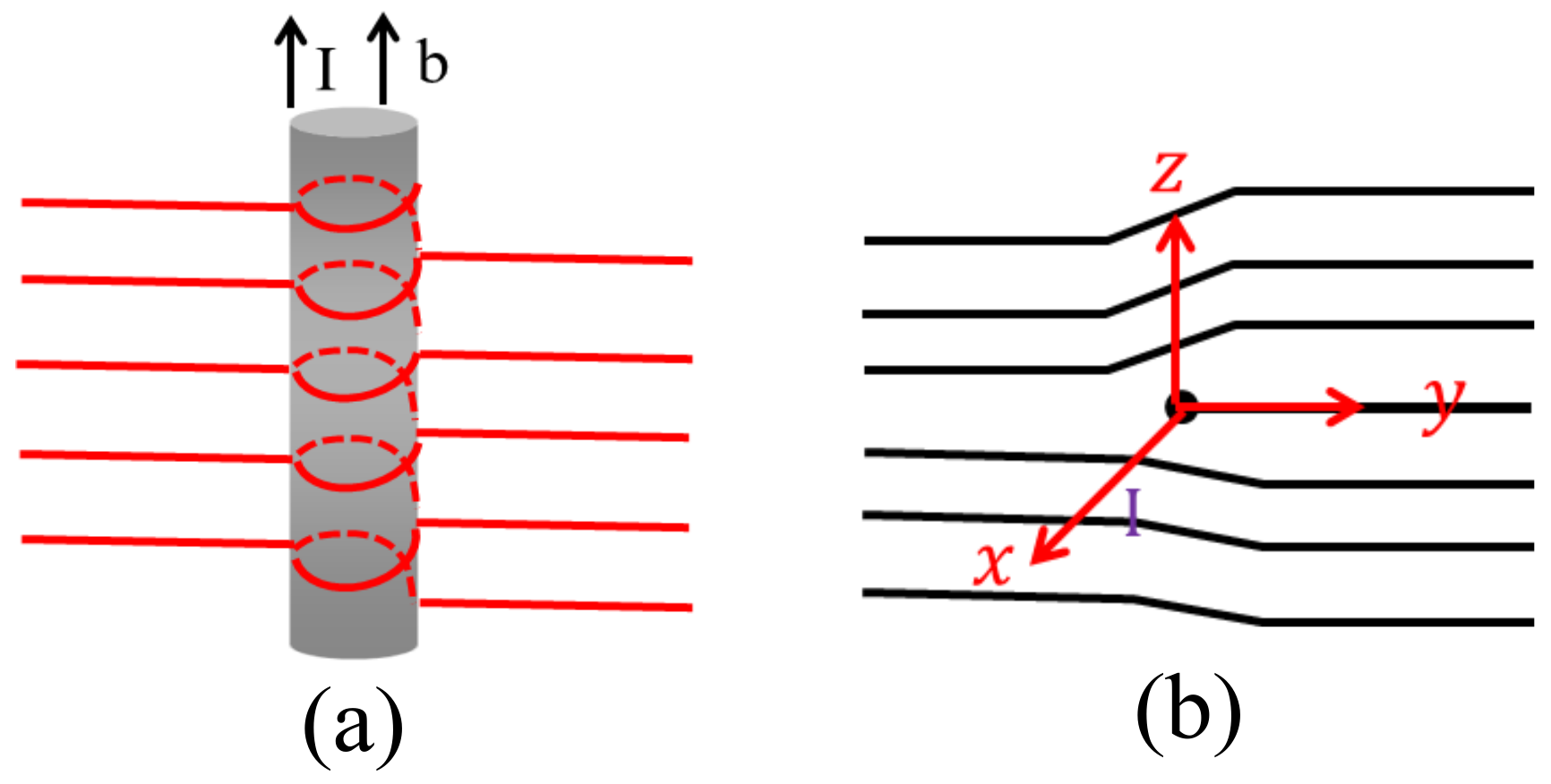
4]. These defects are easily observed under a polarizing optical microscope (POM). Smectic liquid crystals exhibit dislocations due to the layered structure. In this case, the distortion alters the smectic layer displacement field
u, which leads to the dislocations in the medium and is defined as [
3]:
where
signifies the direction of the lattice distortion,
d is the layer spacing and
is called Burger’s vector. Here, the nature of the defects depends on the relative orientations of
and the dislocation line. A schematic representation of dislocations in the SmA phase is shown in
Figure 2. If
is parallel to the dislocation line, it is called the “screw dislocations” (
Figure 2a). The smectic layers climb up or down by an integral number of
d upon going round the dislocation line, changing in a screw-like manner. On the other hand, if
is perpendicular to the dislocation line, it is called an “edge dislocation” (
Figure 2b). In this case, a few layers are either added or removed from one side of the dislocation line. The dislocation lines cannot be observed under POM. In addition to dislocations, smectic liquid crystals also show focal conic defects, and these defects can be observed under POM [
2].
1.1. Twist Grain Boundary Phase
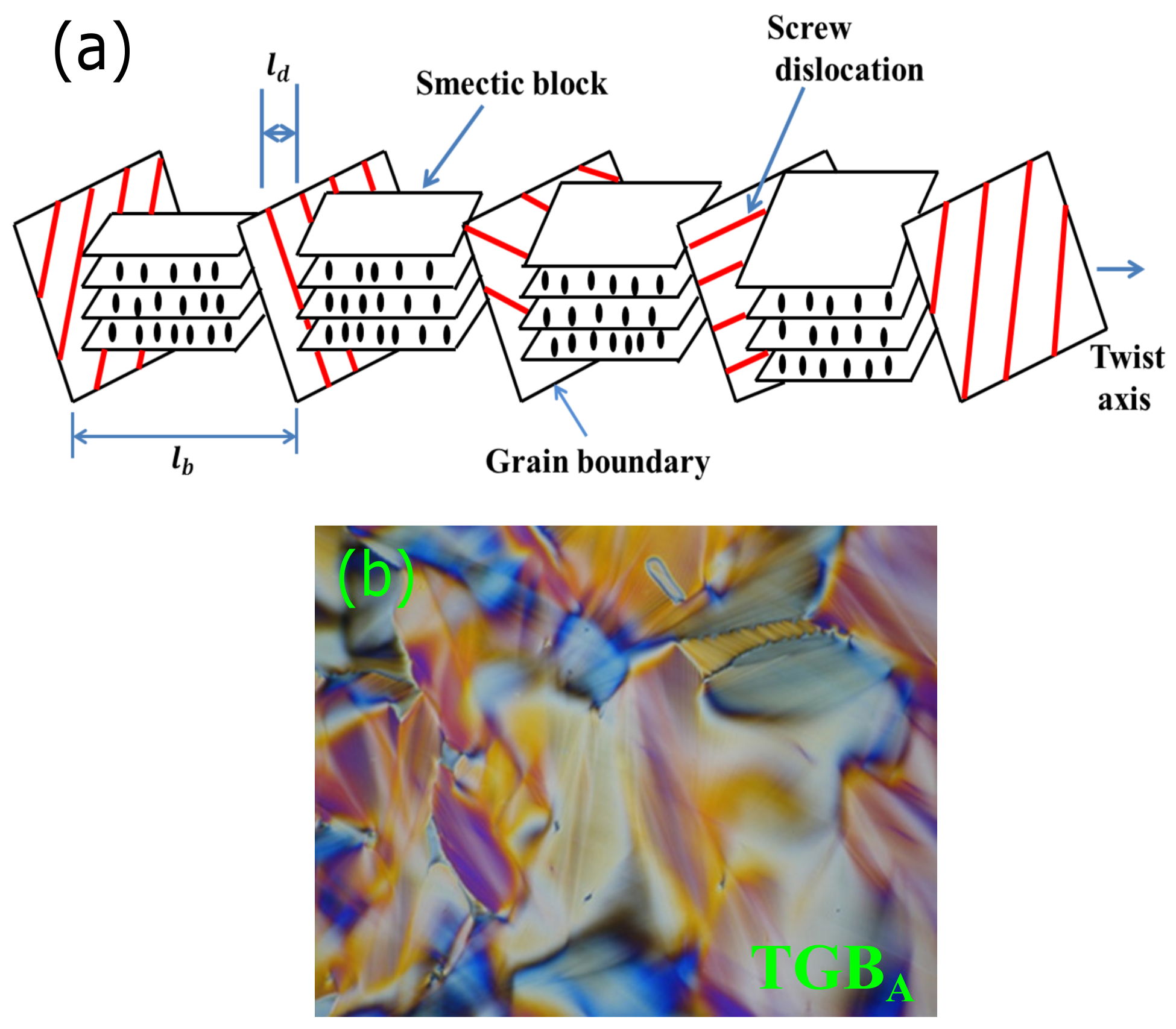
In highly chiral liquid crystals in between the cholesteric and SmA phase, occasionally, an intermediate phase with a relatively larger pitch is observed. In smectics, when molecular chirality increases, the competition between the twist formation and smectic layer formation leads to some frustrated structures, known as twist grain boundary phases [
5]. This is a thermodynamically-stable phase. Experimentally, it was first observed by Goodby et al. [
6]. The Twist Grain Boundary-A (TGB
A) phase has an analogy with the Abrikosov phase of Type-II superconductors in an external magnetic field, and it was first proposed by de Gennes [
1,
5]. Hence, they are also called Type-II smectic liquid crystals. In this analogy, the twist of a cholesteric phase penetrates into the SmA structure through a lattice of screw dislocations, which is similar to the magnetic flux lines penetrating a Type-II superconductor via a lattice of vortices. The detailed structure was theoretically calculated by Renn and Lubensky [
5]. A schematic representation of the arrangement of smectic-A blocks of the TGB
A phase is shown in
Figure 3. The parallel screw dislocations originate due to the rotation of successive smectic slabs relative to each other. The well-defined SmA blocks are separated by regularly-spaced planar arrays of parallel screw dislocations. The interaction between the dislocations forms grain boundaries, and the interaction among the grain boundaries stabilizes the TGB
A structure. The typical distance between two dislocations in a grain boundary is denoted as
, and the inter-grain boundary distance as
and usually
, and they are in the range of 20–30 nm [
7]. Later, several variants of the twist grain boundary phase were observed such as TGB
C [
8], TGB
C* [
9], UTGB
C* [
10,
11], etc. UTGB
C* has a three-dimensionally-modulated structure, and it was discovered in a binary mixture of a chiral and a nonchiral compounds.
1.2. Blue Phases
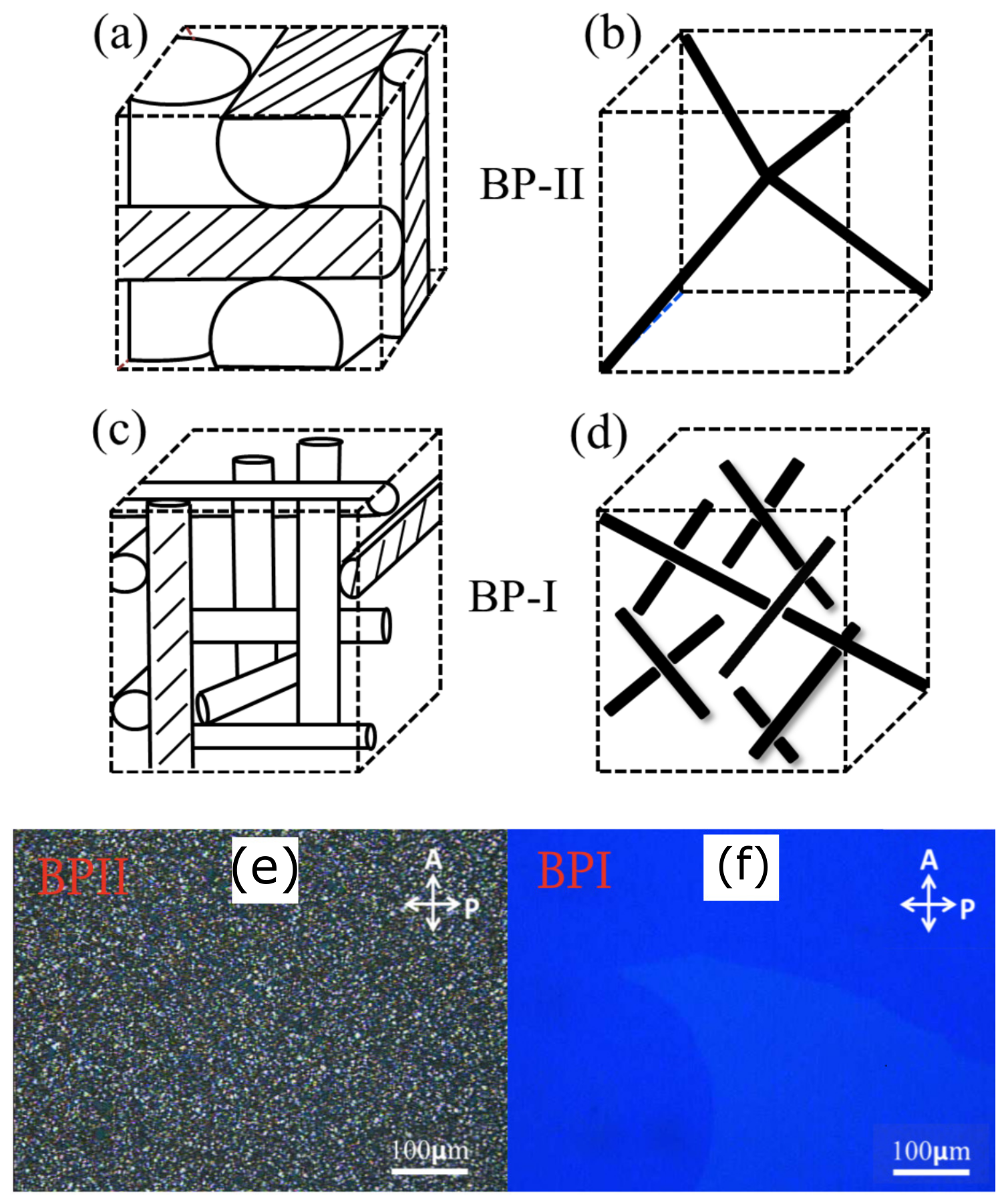
Blue phases are another type of frustrated phase observed in highly chiral liquid crystals. They appear between the Isotropic (I) and cholesteric (N
*) phase transition, and the temperature range in pure compounds is very narrow (∼1 K). In the early investigations, they appeared blue, hence being known as the blue phase. The defect-lattice structure and POM textures of BP-I and BP-II are shown in
Figure 4. In the cholesteric phase, the orientation of the local director can twist around two perpendicular axes, and the corresponding deformed structure is named as a “double-twist cylinder” [
1]. The double twist cylinders fill up the volume by stabilizing a lattice of defect-disclinations [
13,
14]. The defect lines arrange themselves forming different structures, and depending on their local arrangement, they are classified into Blue Phase (BP)-I, BP-II and BP-III. The BP-I, BP-II and BP-III have body-centered cubic, simple cubic and amorphous structure, respectively. The symmetry of BP-III is almost similar to the isotropic phase, hence it is very difficult to distinguish from the isotropic phase under POM. BP-I and BP-II can be identified under POM rather easily. The stability of BP-I increases with increasing chirality, whereas BP-II prevails up to a certain range of the temperature-chirality variation. There are a few methods known to increase the temperature range of BPs such as by dispersion of the polymer, nanoparticles and mixing of many liquid crystals and chiral dopant. Among them, polymer-stabilized BPs are very popular, and they were discovered by Kikuchi et al. [
15]. They showed that the range can be enhanced to more than 60 K and down to room temperature. This created immense interest in the field of liquid crystals, and consequently polymer-stabilized liquid crystal displays (LCDs) with superior display performance were reported [
16,
17,
18,
19]. There are many studies that have reported on the complex structure and optical properties of blue phases. Nevertheless, several fundamental aspects of these exotic phases are yet to be explored. For example, recently, several theoretical predictions were made on the defect dynamics and rheological properties of BP-II and BP-I [
20,
21,
22,
23,
24], which are yet to be explored experimentally.
3. Rheological Properties of the Twist Grain Boundary-A Phase
In pure compounds, the temperature range of the TGB
A phase is usually very short (1–2
C). Nevertheless, some attempts were made to characterize the rheological properties. Asnacios et al. studied the rheological properties of Cholesteryl Tetradecanoate (CT) and Cholesteryl Nonanoate (CN) and focused on the rheological properties near the N
*-SmA transition [
27]. From the temperature-dependent viscosity and shear rate-dependent shear stress, they found a short-range smectic-like behavior just above the SmA-N
* transition (T = T
N*-SmA + 1
C). They conjectured it to be a TGB-like phase. Later, Rajeswari et al. also studied the rheological properties of CN and its mixture with 4
-octyloxy-4-cyanobiphenyl (8OCB ) [
12]. They confirmed that indeed, a short-range smectic-like order in the cholesteric phase exists, and it was further enhanced by mixing a small amount of 8OCB compound.
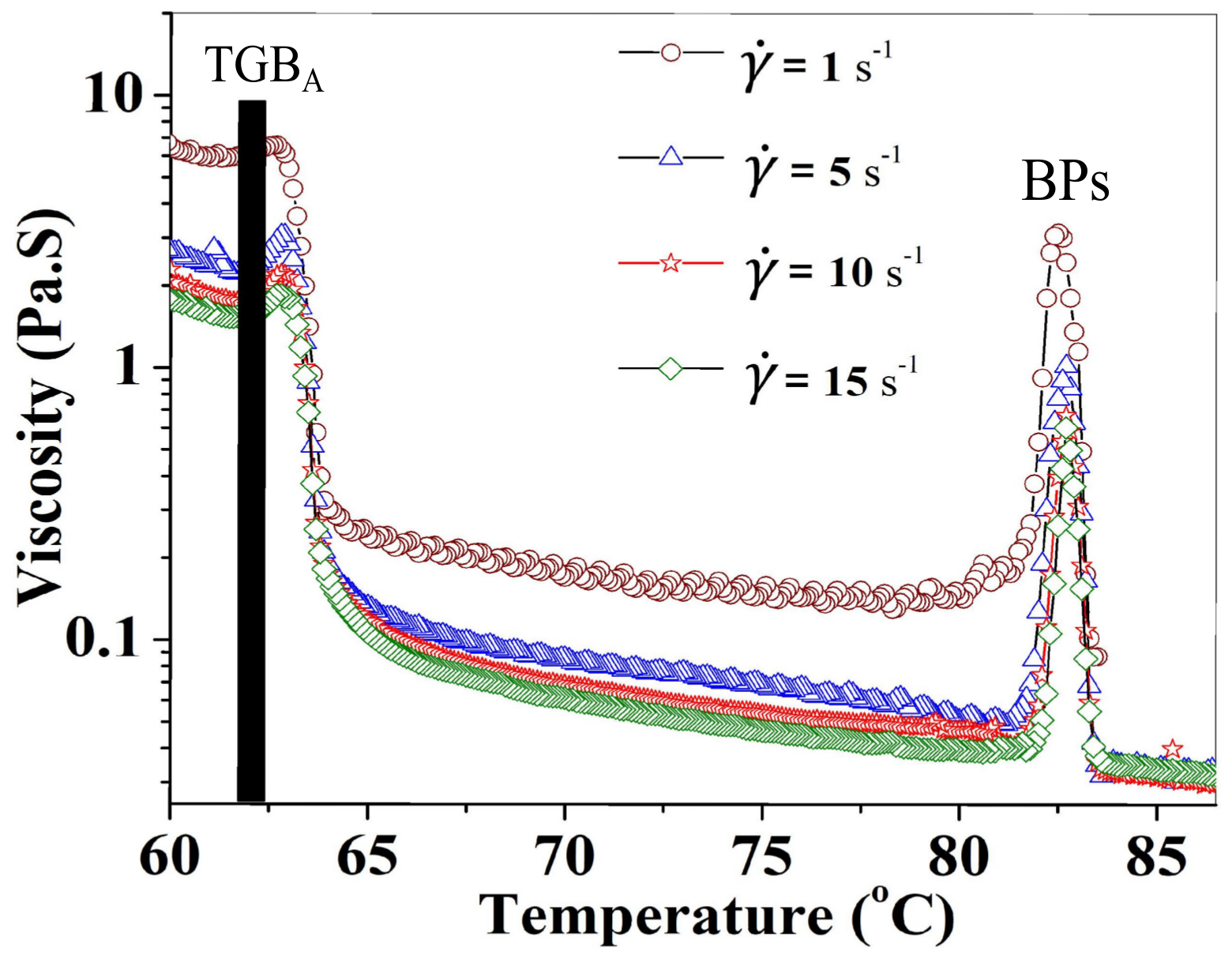
Figure 5 shows the temperature-dependent shear viscosity of the mixture with 20 wt % 8OCB. Apart from a sharp peak in the viscosity due to the blue phases, they observed another anomalous peak across the N
*-SmA transition. The latter one was attributed to the SmA to TGB
A phase transition. However, the narrow temperature range has always been a major problem to understand and correlate its physical properties with the structure.
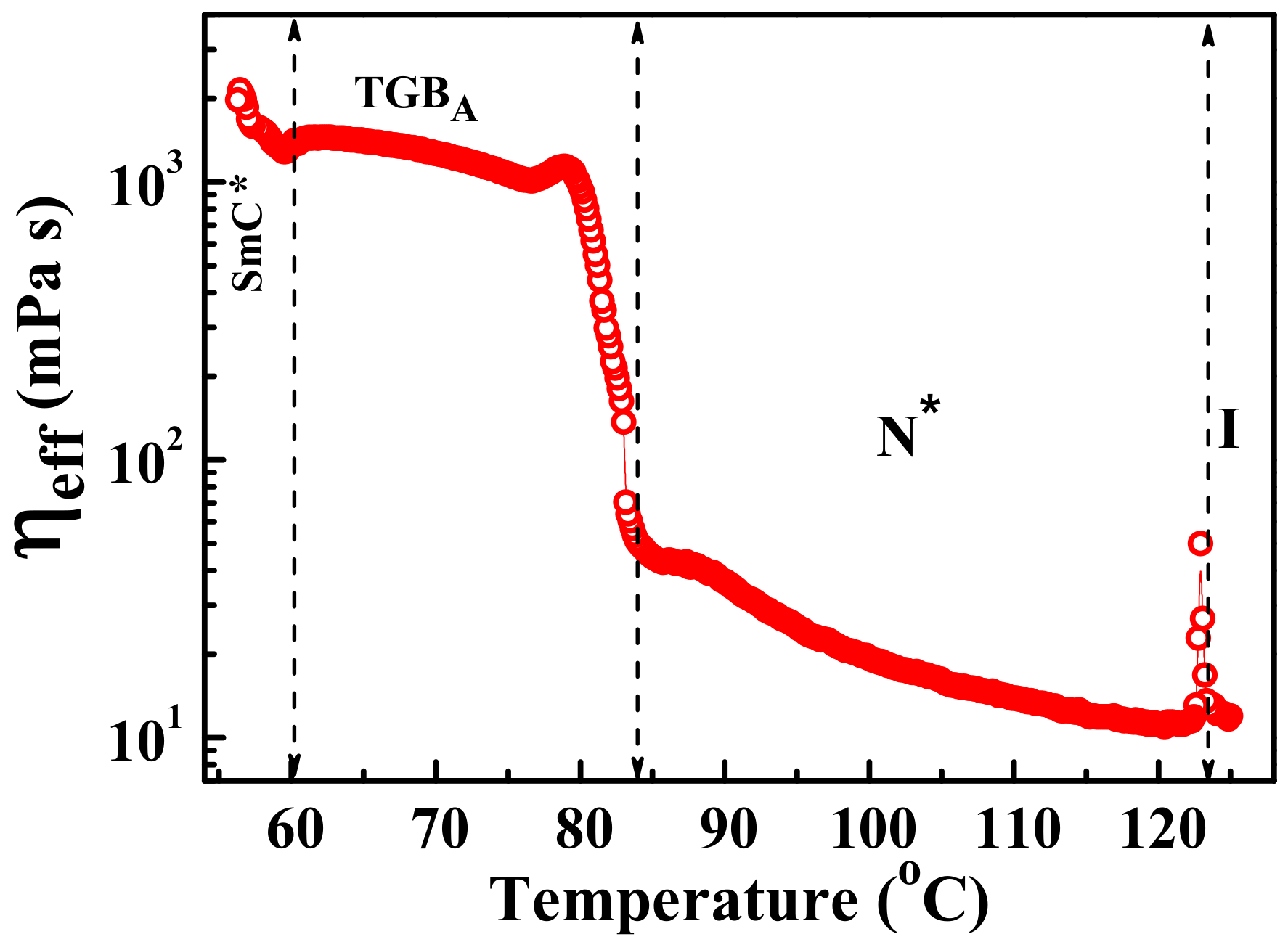
Recently, Rasmita et al. studied the rheological properties of a TGB
A phase with a wide temperature-range [
25]. It was discovered in a binary mixture of two compounds, namely 4-(2
-methyl butyl phenyl)4
-n-octylbiphenyl-4-carboxylate (CE8 ) and 2-cyano-4-heptyl-phenyl-4
- pentyl-4-biphenyl carboxylate (7(CN)5), where CE8 is a chiral and 7(CN)5 is a nonchiral compound, by Pramod et al. [
10,
11]. Sixty-three-point-six weight percent of CE8 and 36.4 wt % of 7(CN)5 in the mixture are known to show the following phase transitions: I 123
C N
* 83.5
C TGB
A 60.2
C SmC
*. Thus, the temperature range of the TGB
A phase is about 20
C. The phase transitions were identified from the temperature-dependent shear viscosity measurements (
Figure 6). The shear viscosity of the TGB
A phase is two orders of magnitude larger than that of the cholesteric phase.
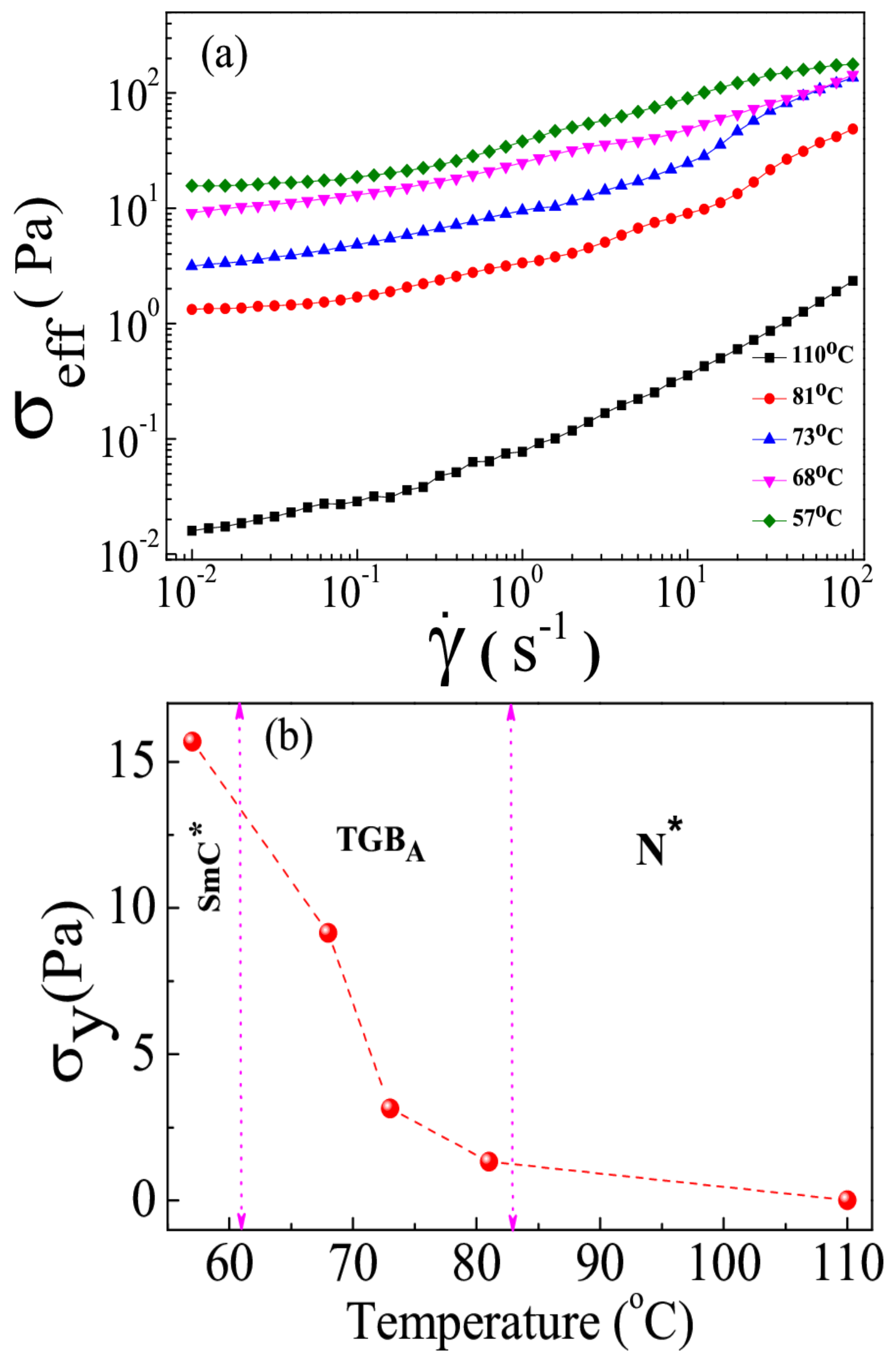
Figure 7a shows the shear rate-dependent shear stress of different phases of the mixture. At a low shear rate, where
, the shear stress tends to reach a constant value showing an apparent yield stress (
).
Figure 7b shows the variation of yield stress at different phases. In the N
* phase,
is negligibly small (
Pa). In the TGB
A phase,
≃ 10 Pa. Thus, the yield stress of TGB
A is three orders of magnitude larger than that of the N
* phase. However, the apparent yield stress of the TGB
A phase of the studied mixture is much larger than that known for low molecular weight smectic liquid crystals [
28,
29].
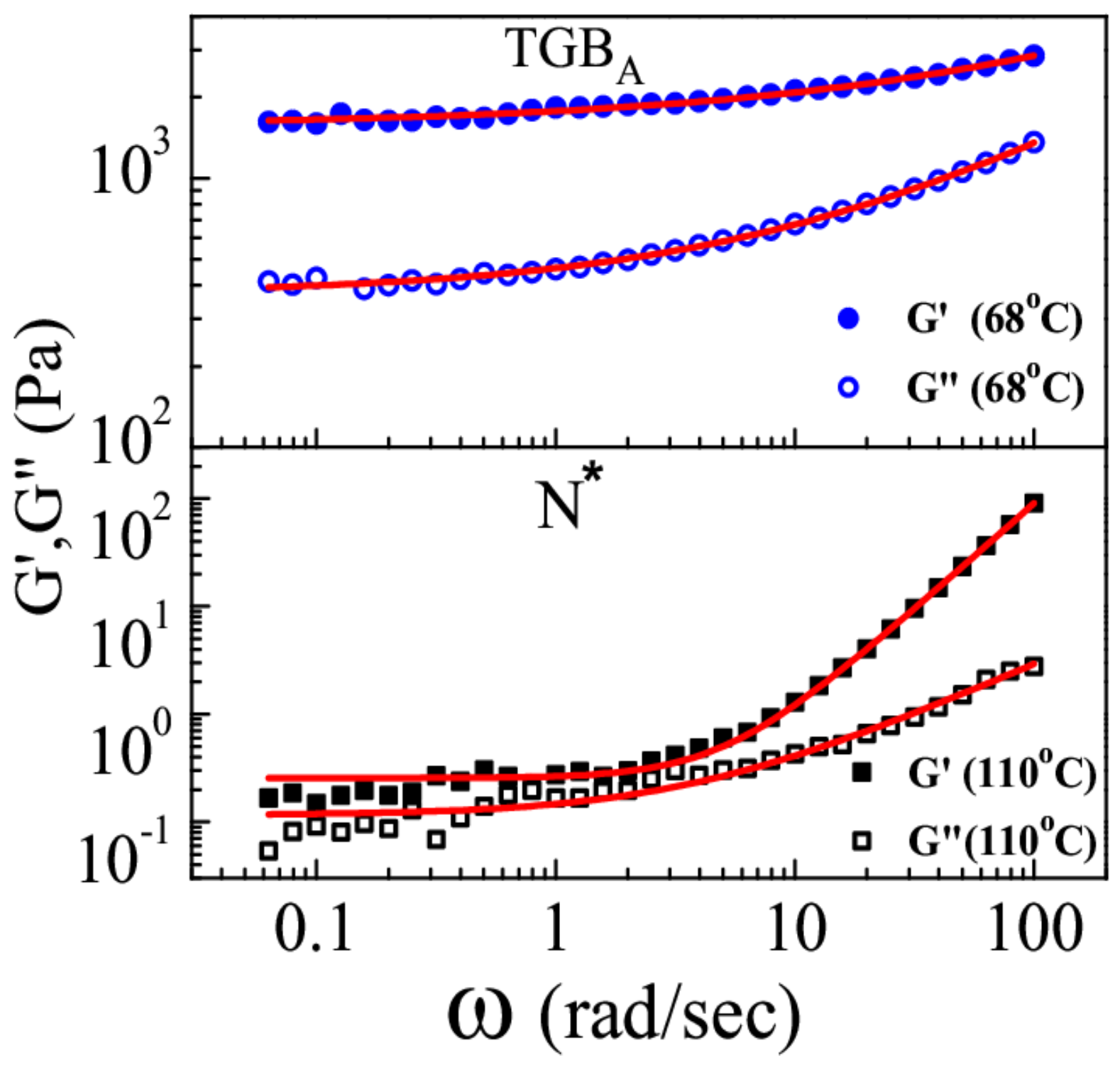
The frequency-dependent shear modulus (
and
) provides the dynamic response of the sample.
Figure 8 shows some representative frequency dependence of storage (
) and loss moduli (
) in the N
* and TGB
A phases. The role of defects and disorder on the viscoelastic properties of randomly-oriented Type-I smectic liquid crystals has been studied by many authors [
4,
30,
31,
32,
33,
34,
35,
36]. In the reported systems, the defects were either stabilized by quenched disorder or by dispersing colloidal particles in the liquid crystals. The storage modulus (
) of such a system shows a power-law behavior:
where
is the plateau modulus arising from the zero frequency shear modulus,
is the angular frequency,
is a constant and
is an exponent. The TGB
A is composed of rotating SmA blocks separated by grain boundaries made of parallel screw dislocations. These defects are inbuilt into the structure, and hence, cannot disappear due to the action of shear. The contribution of defects and disorder to the rheological properties of the TGB
A is analyzed by the same model.
obtained from the fitting of
(
) and
(
) at different temperatures is shown in
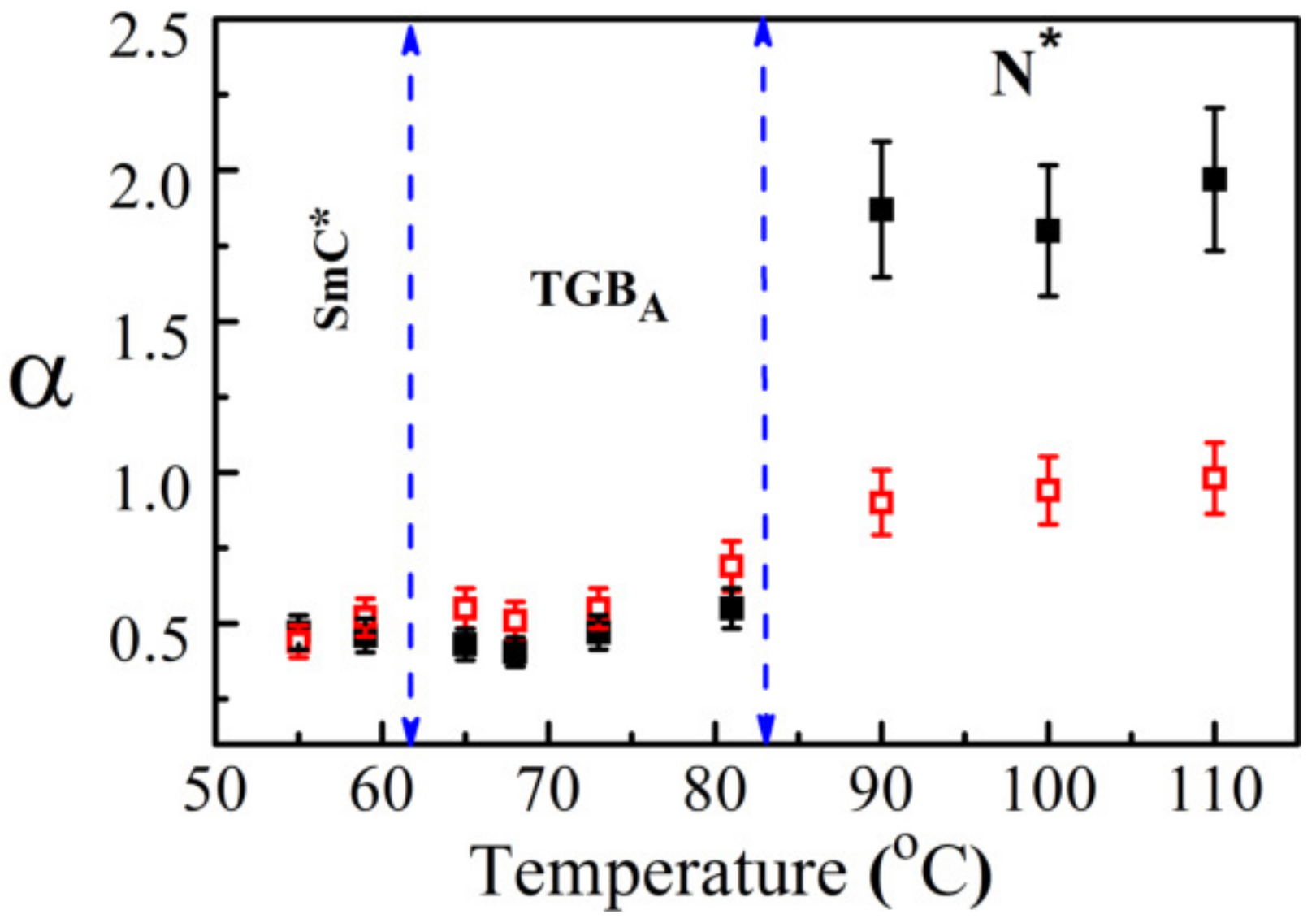
Figure 9. In the N
* phase,
obtained from the fitting of
and
is about two and one, respectively. The exponent
decreases in the TGB
A phase and is almost equal to
0.5. The solid-like behavior reflected by a plateau in
in the terminal zone has been studied and characterized theoretically in other mesophases, such as carbonaceous mesophases [
37]. The storage modulus of liquid crystalline systems with a defect network has been experimentally studied by Ramos et al. [
38]. They showed that the contributions from the disoriented part of the sample and regions of the sample where the layers are parallel to the shear direction are given by
and
respectively. Similarly the loss modulus has a contribution both from the disorientated parts (
) of the sample and a Maxwell fluid type contribution (
). In the TGB
A phase,
obtained from the fitting of
and
is equal and given by
. Hence, the storage and loss moduli have a major contribution from the disorientated layers of the TGB
A phase.
According to the soft glass rheology model, the glass transition is characterized by the power-law exponent, i.e.,
∼
. In this model, “
x” is an effective noise temperature that varies within 1
and is related to the exponent
by
[
39]. The system approaches the glass transition if
1, i.e.,
. In reference to
Figure 9, across the N
* to TGB
A phase transition,
x decreases from three to about 1.5, signifying that the rheological response of TGB
A is very close to many soft glassy materials.
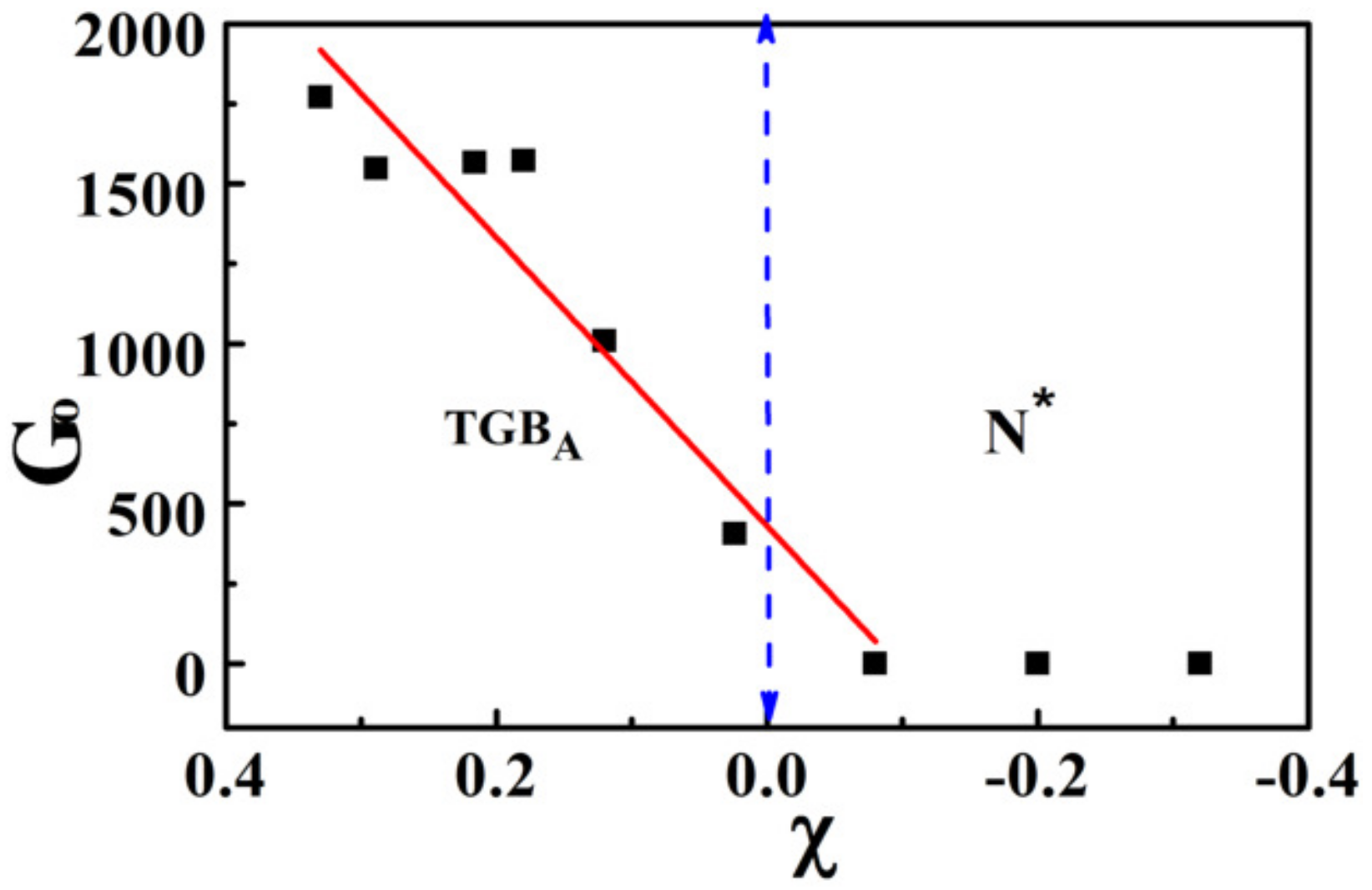
The temperature variation of
is directly related to the defects. The variation of
with reduced temperature
(T
N*-TGBA − T)/(T
N*-TGBA) is shown in
Figure 10. In the TGB
A phase,
is more than three orders of magnitude larger than the N
* phase (
Figure 10). In connection to the rubber elasticity, the elastic response of static defect network
varies as
≈
, where
is the line tension and
d is a typical average spacing between defects [
38]. The defect line tension
can be expressed as
, where
B is the layer compression modulus,
b =
is the Burger vector of integer strength
m and
is the defect core radius [
40]. There are many smectic liquid crystals in which
[
41] and
, where
is the smectic order parameter [
42]. Hence, the defect line tension (
) varies as
∼
. This implies that the elasticity of the static defect network varies as
with
≈ 0.9 [
42].
Figure 10 shows the variation of
with the least square fit parameter
. Assuming a medium value of Berger’s vector of integer strength
m = 2 [
43],
B ≈ 2 ×
Pa [
30,
41] and using the relation
, the calculated inter-defect spacing in the TGB
A phase is
26 nm. This calculated value is closely comparable with the experimentally-measured dislocation spacing in the TGB
A phase [
7].
4. Rheological Properties of Blue Phases
Recently, several theoretical predictions are made on the rheological properties of blue phases [
20,
21,
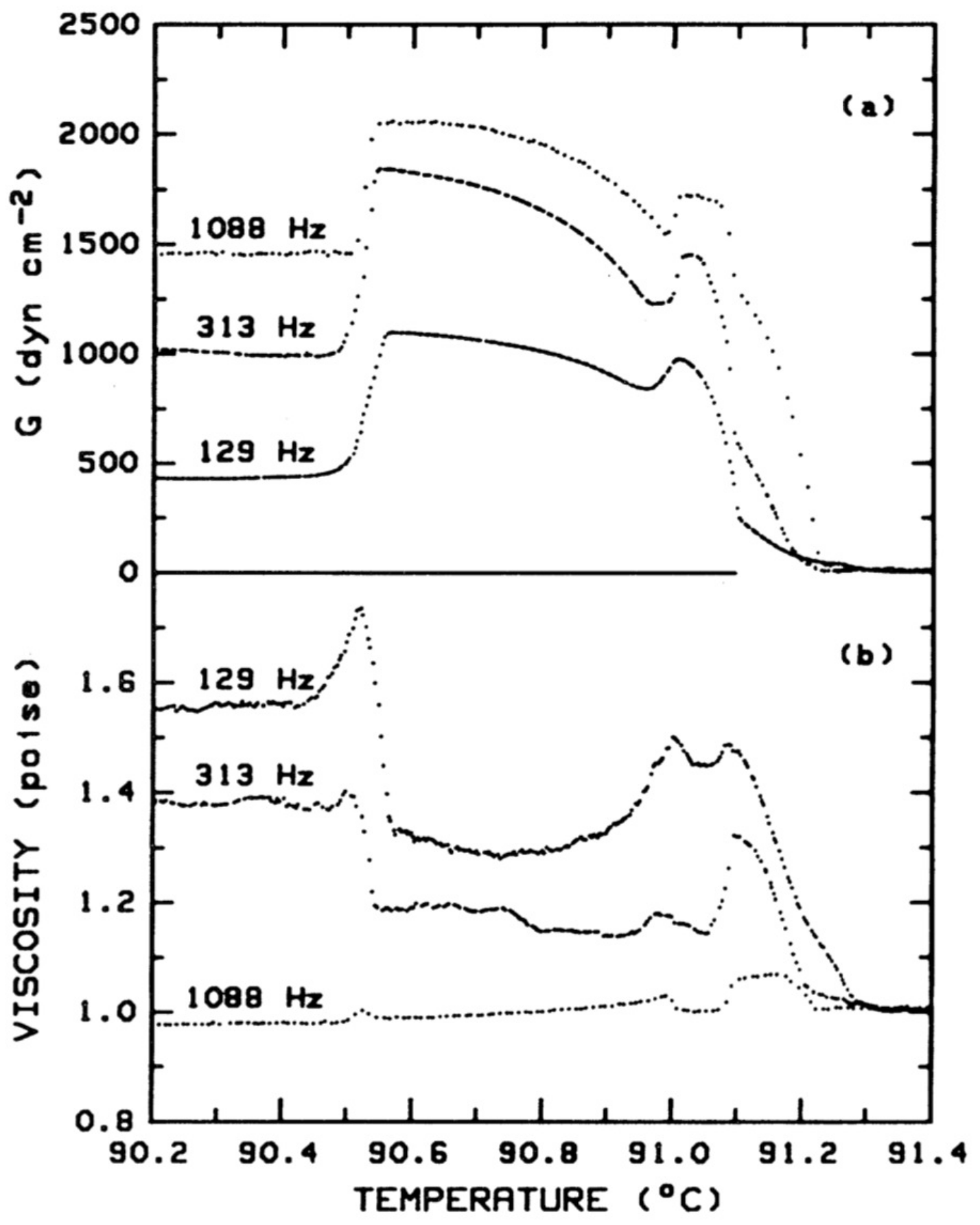
22]. However, experimentally, it is much less explored due to its narrow range of temperature. The rheological properties of BPs with a narrow range of temperature in CN were first reported by Kleiman et al. [
44]. It exhibits the following phase transitions: I 90.52
C BP-I 91.00
C BP-II 91.08
C BP-III 91.22
C N
*. It shows three blue phases, and the temperature ranges of BP-III, BP-II and BP-I are 14 mK, 8 mK and 48 mK, respectively.
Figure 11 shows the storage modulus and viscosity as a function of temperature. They showed that BP-I and BP-II are viscoelastic solids and that BP-III has cholesteric-like order.
Very recently, Rasmita et al. made detailed experimental studies on the rheology of BPs by taking a mixture of four fluorinated compounds and a highly chiral dopant [
26,
45]. It exhibits the following phase transitions: I 46.4
C, BP-II 41.4
C BP-I 36.6
C N
*. The temperature ranges of BP-I and BP-II are 4.8
C and 5
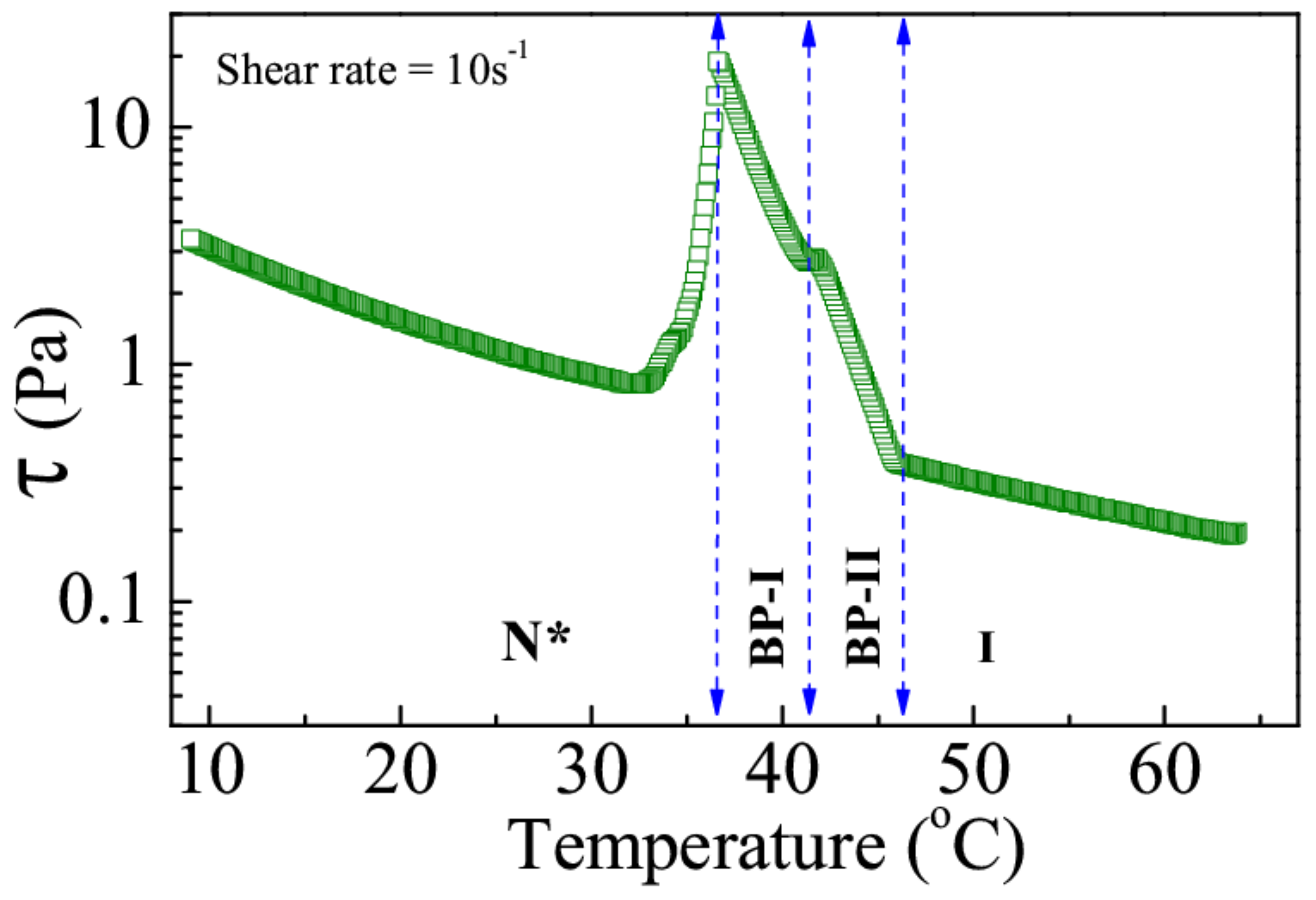
C, respectively, and much larger than the CN compound. The temperature-dependent shear stress at a fixed shear rate of the mixture is shown in
Figure 12. Distinct changes of stress (
) across the phase transitions are clearly observed. A small kink in the stress-curve marks the BP-II to BP-I phase transition. The shear stress of BP-I is larger than that of BP-II and N
* phase. This is consistent with the previous report, i.e., the elasticity of the BP-I is greater than that of BP-II.
Simultaneous optical rheomicroscopy measurements reveal the change in the textures across the phase transitions. For example, Grandjean–Cano lines are observed in the BP-II phase, and they are aligned perpendicular to the shear direction (
Figure 13a). The increase of shear stress as compared to the isotropic phase is due to the motion of the Grandjean–Cano lines. With decreasing temperature, some filamentary structures appear in the BP-I phase. This corresponds to the increase in shear stress in the BP-I phase as compared to the BP-II phase (
Figure 13b). These filamentary structures are continuously broken and reconnected under steady shear. The N
* phase (
Figure 13c,d) shows a typical texture of oily-streak defects. Dupuis et al. have studied the rheology of cholesteric blue phases by computer simulation [
22]. It was predicted that the shear forces can bend, twist and unlock the disclination lines. Under low shear, the defect network opposes the flow; hence, the apparent shear viscosity and shear stress become large. However, under high shear, they show shear thinning behavior signifying the disruption of the defect network.
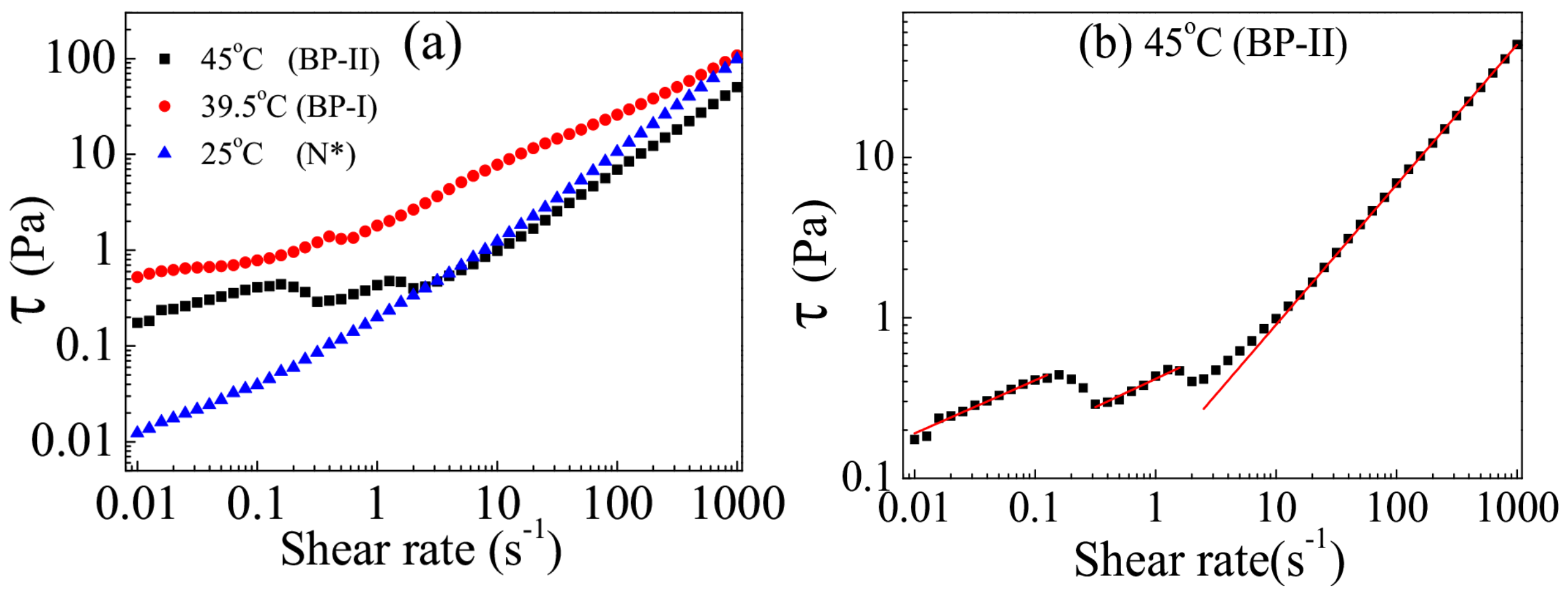
The flow behaviors of the BP-II, BP-I and N
* phases are shown in
Figure 14. The N
* phase exhibits a typical shear thinning behavior. The yield stresses of BP-II and BP-I are about one order of magnitude larger as compared to the N
* phase. BP-I and BP-II both exhibits multiple shear thinning behavior at a higher shear rate range. The shear stress of BP-II shows three distinct regimes, i.e., BP-II(1):
= 0.01–0.3 s
; BP-II(2):
= 0.3–2 s
and BP-II(3):
= 2–1000 s
.
Figure 14b shows a power-law fit;
=
a, which describes the data to a very good approximation. The fit parameters are:
a = 0.87 and
= 0.33 in BP-II(1);
a = 0.42 and
= 0.35 in BP-II(2);
a = 0.12 and
= 0.87 in BP-II(3).
Rheomicroscopy images at some representative shear rates are shown in
Figure 15. In a low shear rate regime (0.01–0.3 s
), in the BP-II phase, the Grandjean–Cano lines flow parallel to the shear direction (downward green arrows in BP-II). In the intermediate shear rate region (0.3–2 s
), these Grandjean–Cano lines are broken, and at a higher shear rate-range (2–1000 s
), the system shows a flow-aligned nematic-like state. The BP-I also shows multiple shear thinning regimes, but they are not clearly separable like BP-II. However, it is clear that multiple shear thinning is due to the breaking of texture at different shear rates as shown in
Figure 15 (see BP-I). The N
* phase shows uniform shear thinning behavior, and there are no notable changes observed in the textures up to the shear rate of 10 s
. Above this shear rate, probably the helix uncoils, and the sample flows like nematic, causing a decrease in the viscosity. Both BP-II and BP-I also exhibit the flow-induced nematic texture at a shear rate much higher than 200 s
.
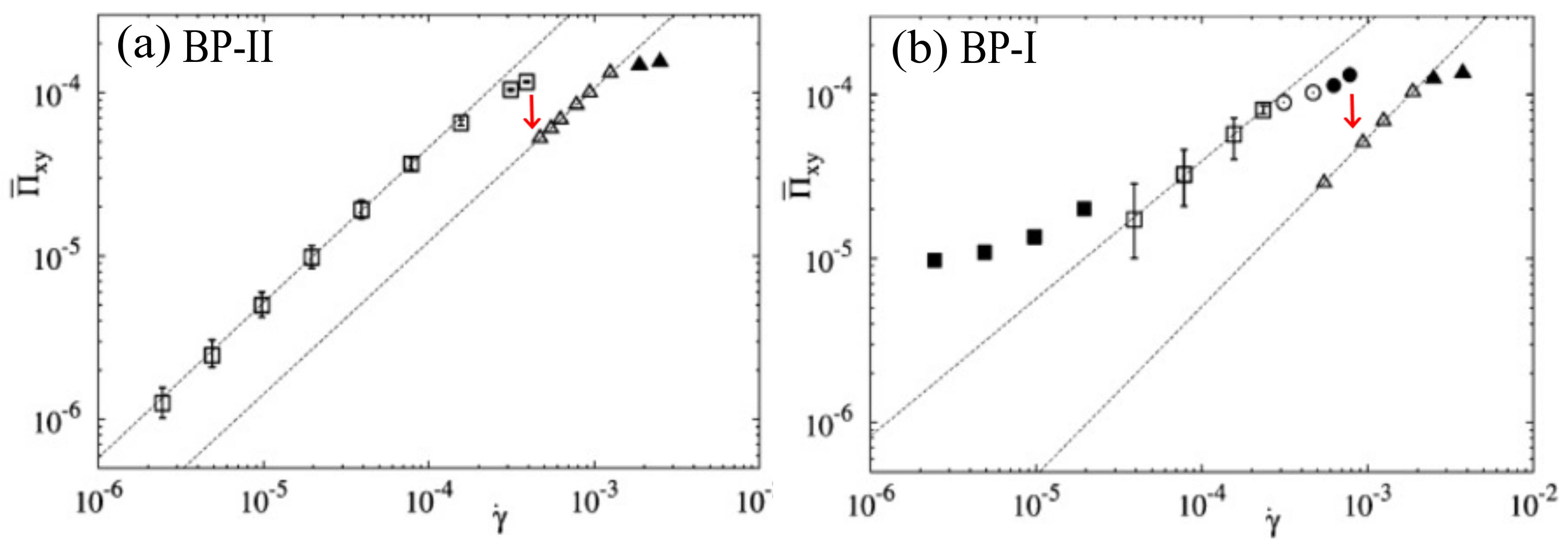
Recently, Henrich et al. studied the rheology of cubic blue phases by computer simulation [
20,
21,
23]. They have identified various flow regimes with increasing shear rate in both BP-I and BP-II. The typical flow curve in both phases is shown in
Figure 16. Experimental results of
Figure 14 qualitatively agree with the predictions of the simulation except that shear rate ranges are different.
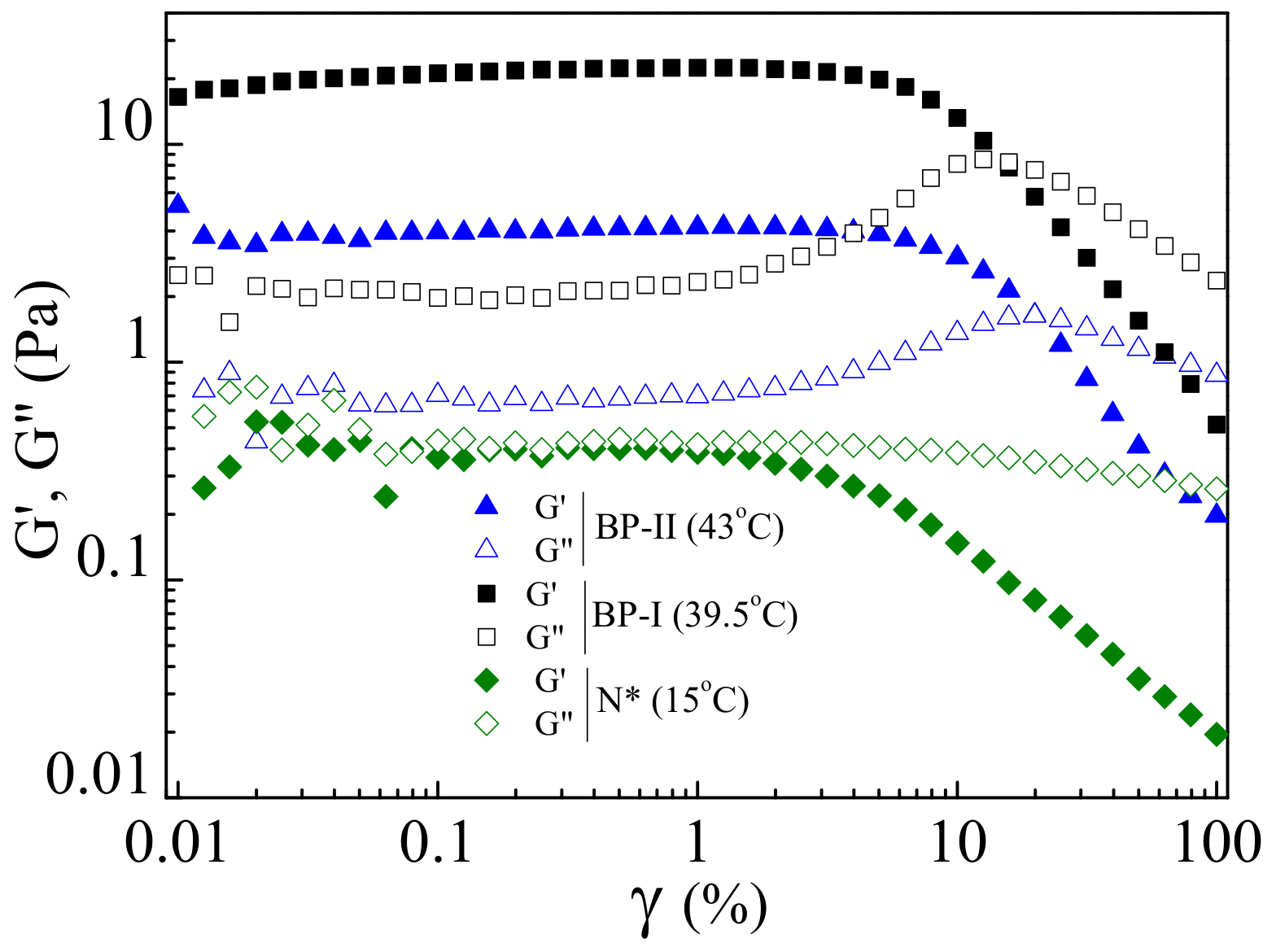
The deformation behavior of blue phases is further studied by the amplitude sweep. The results of amplitude sweep, i.e., the strain-dependent storage (
) and the loss (
) moduli at different temperatures representing different phases (BP-II, BP-I and N
*), are shown in
Figure 17. The N
* phase shows a typical fluid-like behavior. The shear moduli of both the blue phases (BP-II and BP-I) are higher than that of the N
* phase. The storage modulus (
) of BP-I is about five-times larger than that of BP-II. The Linear Visco-Elastic (LVE) ranges of both BP-II and BP-I are almost equal, i.e.,
= 4%. The strain-induced fluidization (the crossover of
and
), or the critical strain amplitude denoted by
, is 16% in the case of BP-I. However, in BP-II, it occurs at a slightly higher strain value (
= 20%) than that of BP-I. It was interpreted that in BP-II, the defect lines intersect with each other, which needs a larger strain amplitude to break.
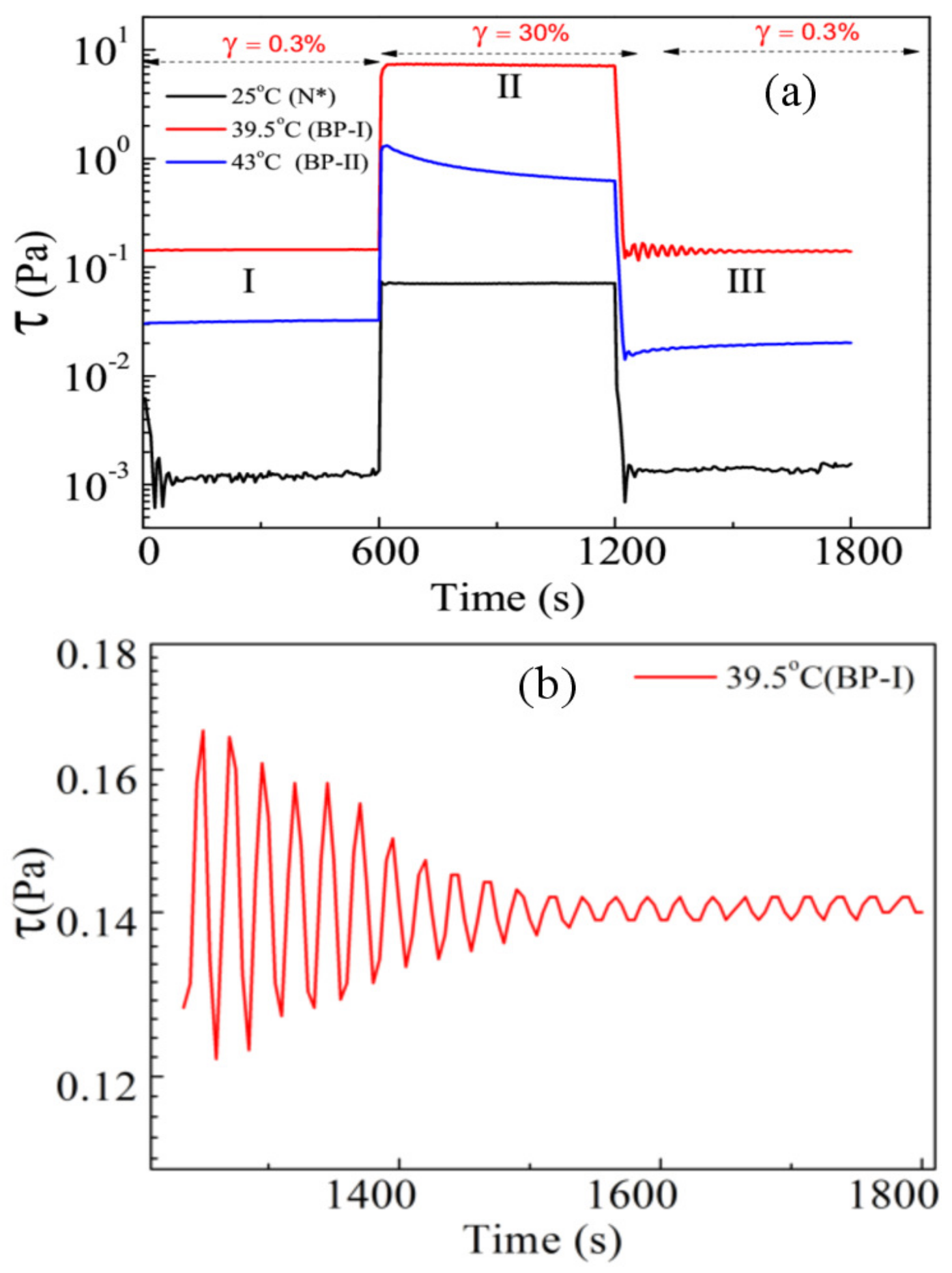
The dynamics of the defect networks are investigated by a step-strain measurement.
Figure 18a shows the shear stress response with time under the applied step strain. The applied strain is changed with time stepwise from 0.3–30% and then again back to 0.3%. Therefore, there are three regions with two steps in which 0.3% is within the LVE range and 30% is above the LVE range. The duration of each step is 600 s. The N
* phase shows a typical stress response under applied step strain in all the regions, as expected. Both BP-II and BP-I exhibit different responses in Region-II and Region-III than the cholesteric phase. In Region-II of BP-II, a gradual decrease of shear stress with time is observed. It could be due to the breaking of defect nodes under high strain followed by a continuous flow-aligned state. In Region-II of BP-I, a constant shear stress response is observed. BP-I shows sinusoidal oscillations of shear stress with time in Region-III that decays with time.
Figure 18b shows the periodic modulation of stress with time in Region-III of BP-I. Stress oscillation after cessation of shear in chiral liquid crystals has been simulated and characterized for cholesteric liquid crystals [
46]. The oscillation in shear stress of BP-I is attributed to the lattice distortion, i.e., displacement of defects from the equilibrium positions. The equilibrium structure tends to be restored upon removal of the strain, which gives rise to periodic stress oscillation, which decays with time [
25]. Hence, the step strain experiment reveals the different dynamical behavior of BP-I and BP-II due to their distinct defect structures.