Numerical Study of Natural Gas/Diesel Reactivity Controlled Compression Ignition Combustion with Large Eddy Simulation and Reynolds-Averaged Navier–Stokes Model
Abstract
:1. Introduction
2. Proposed Models and Validation
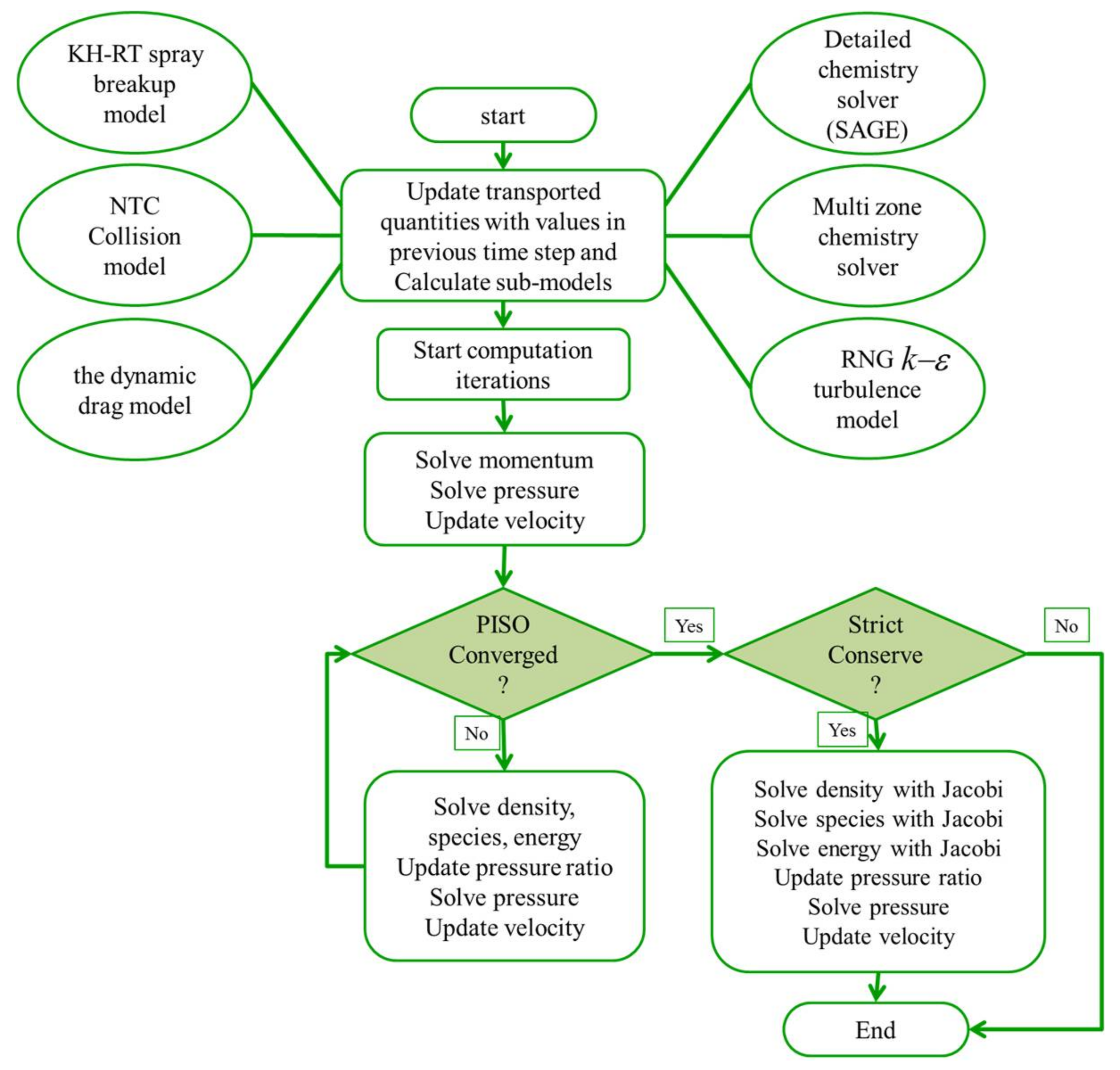
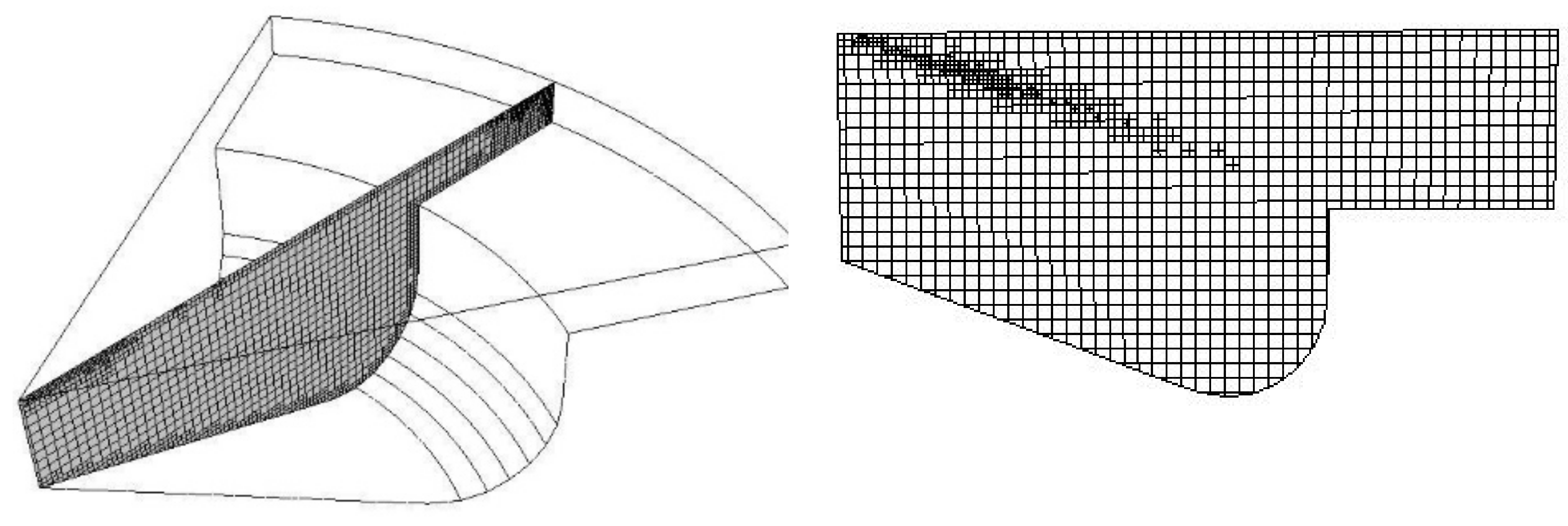
2.1. Computational Model
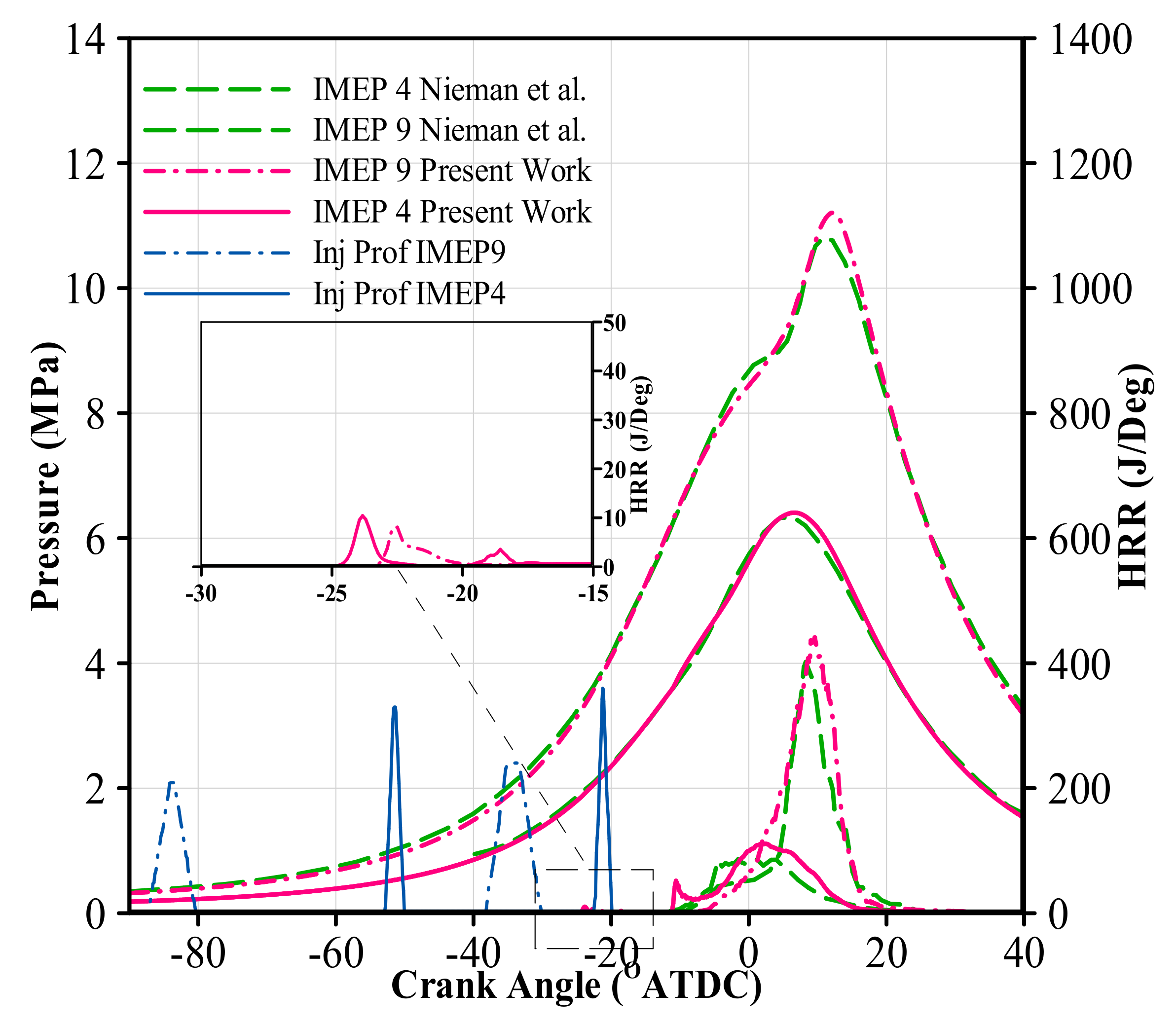
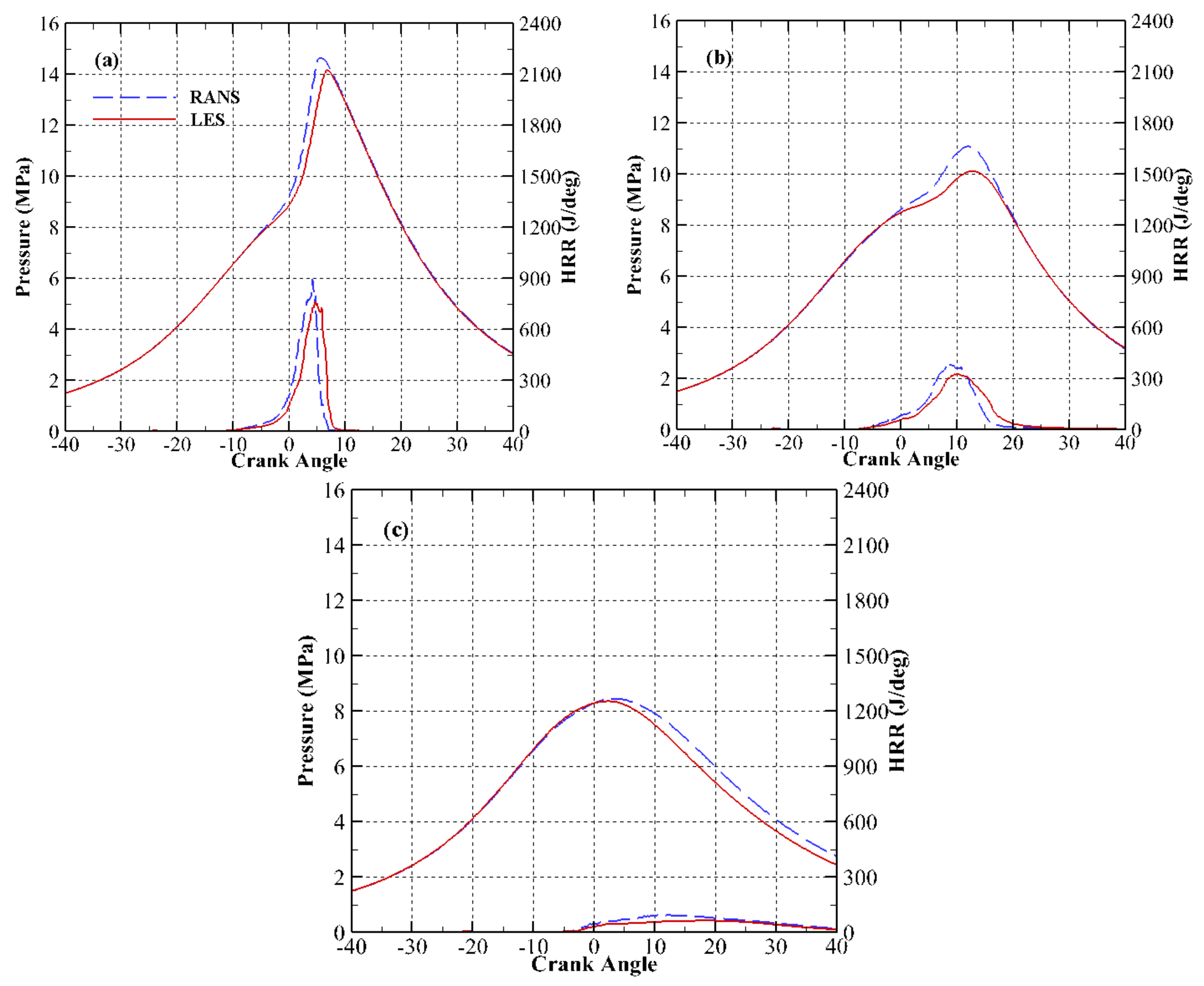
2.2. Validation of Model
2.3. LES Model Description
Dynamic Structure Model (One-Equation)
3. Results and Discussion
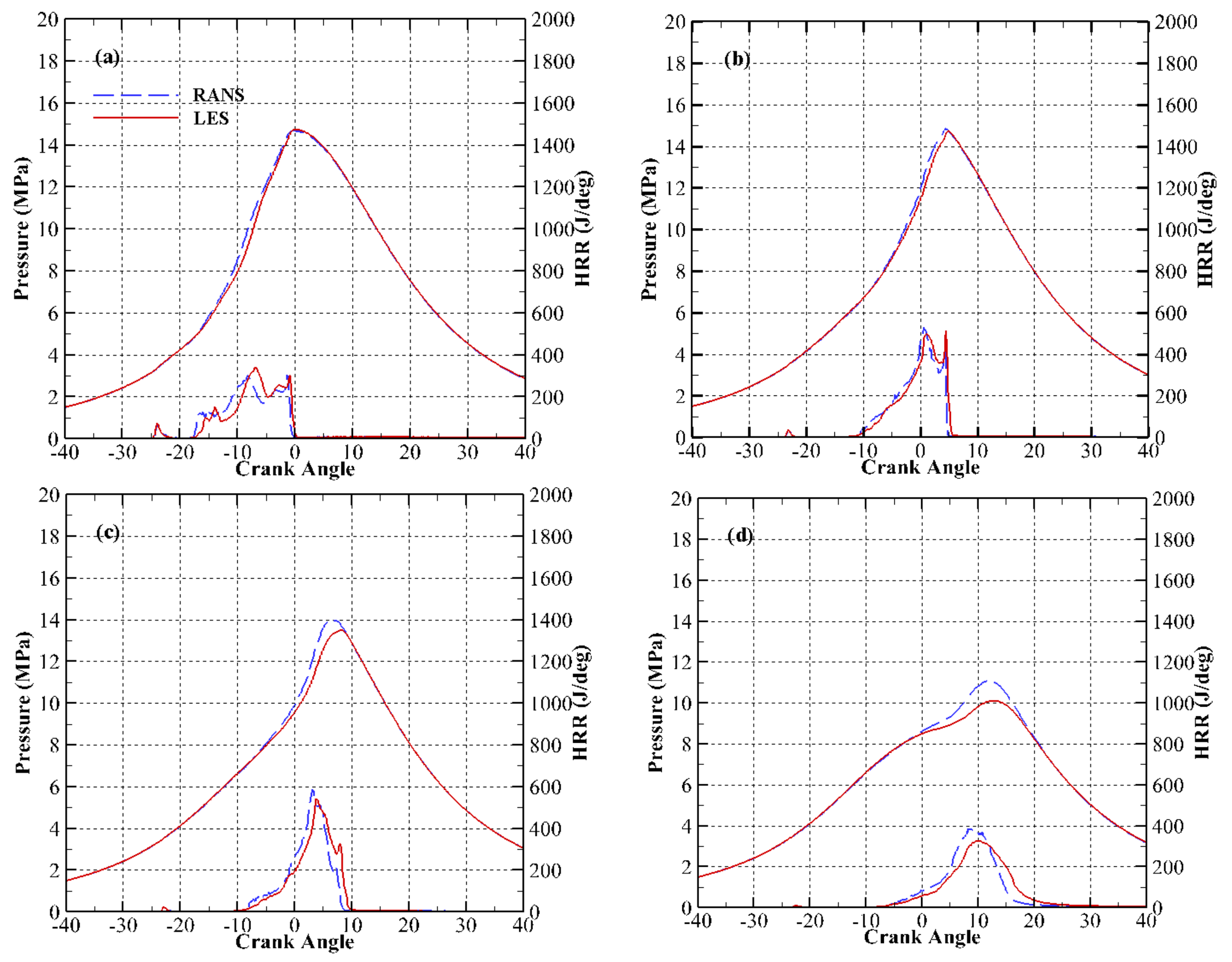
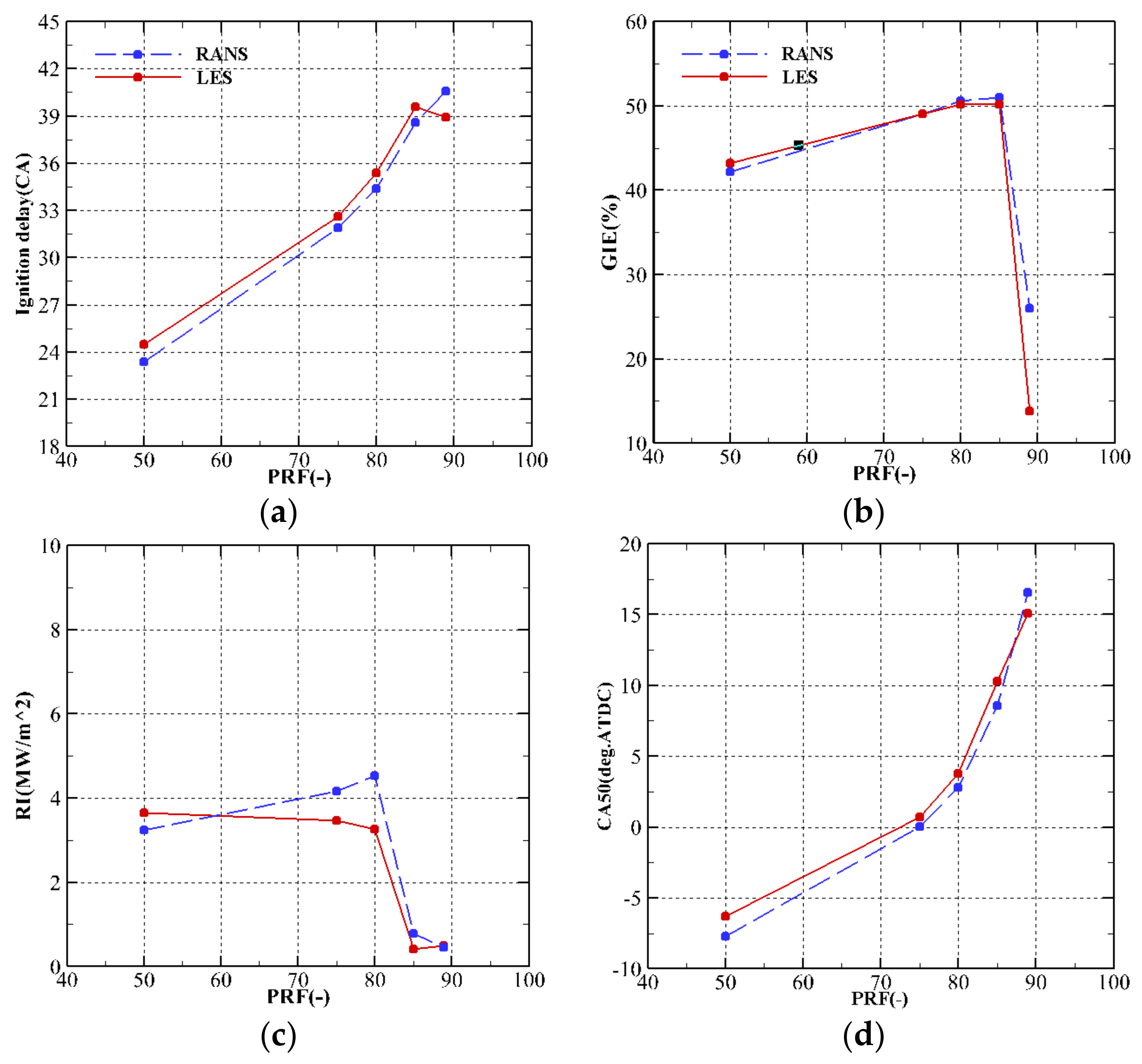
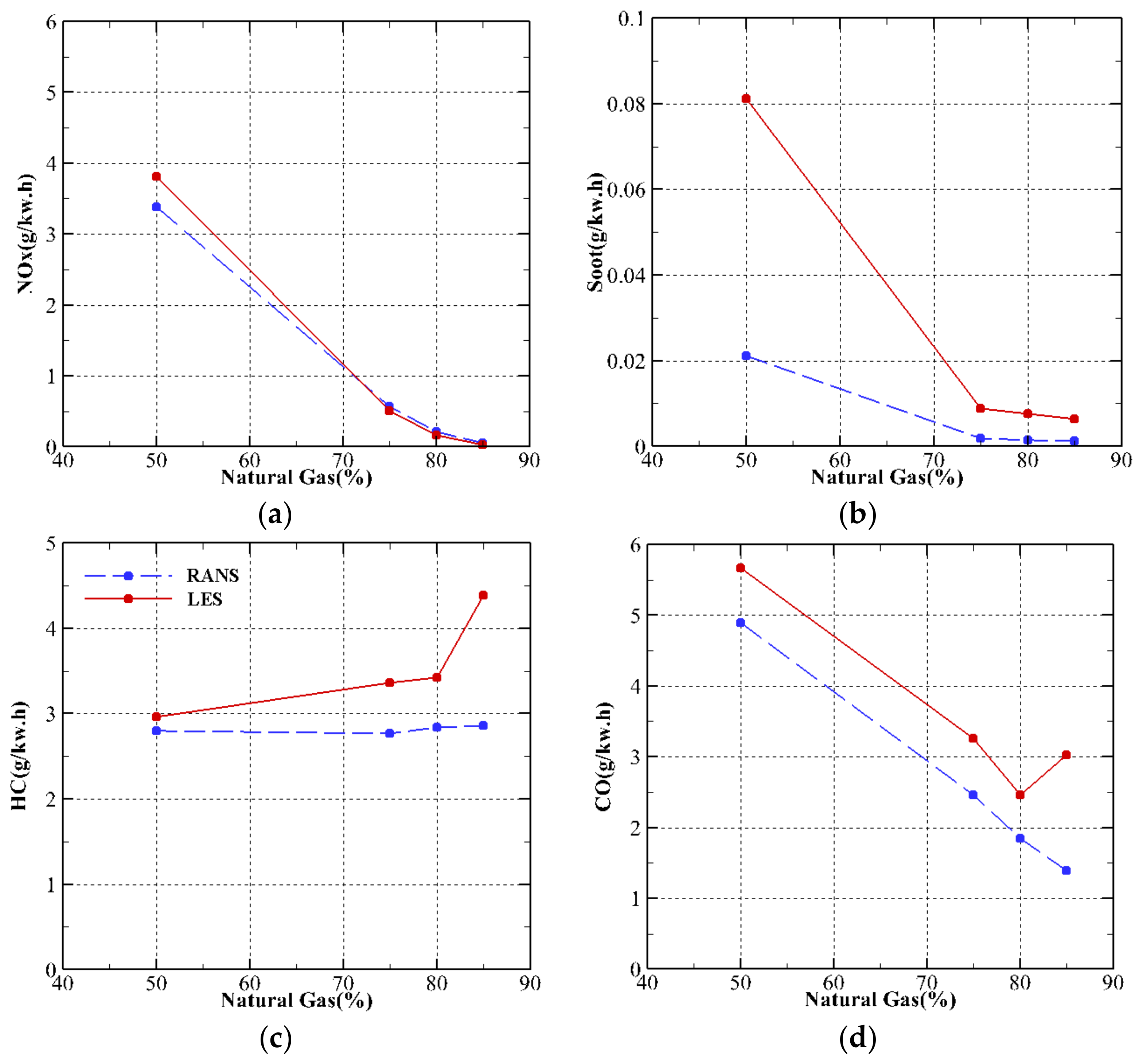
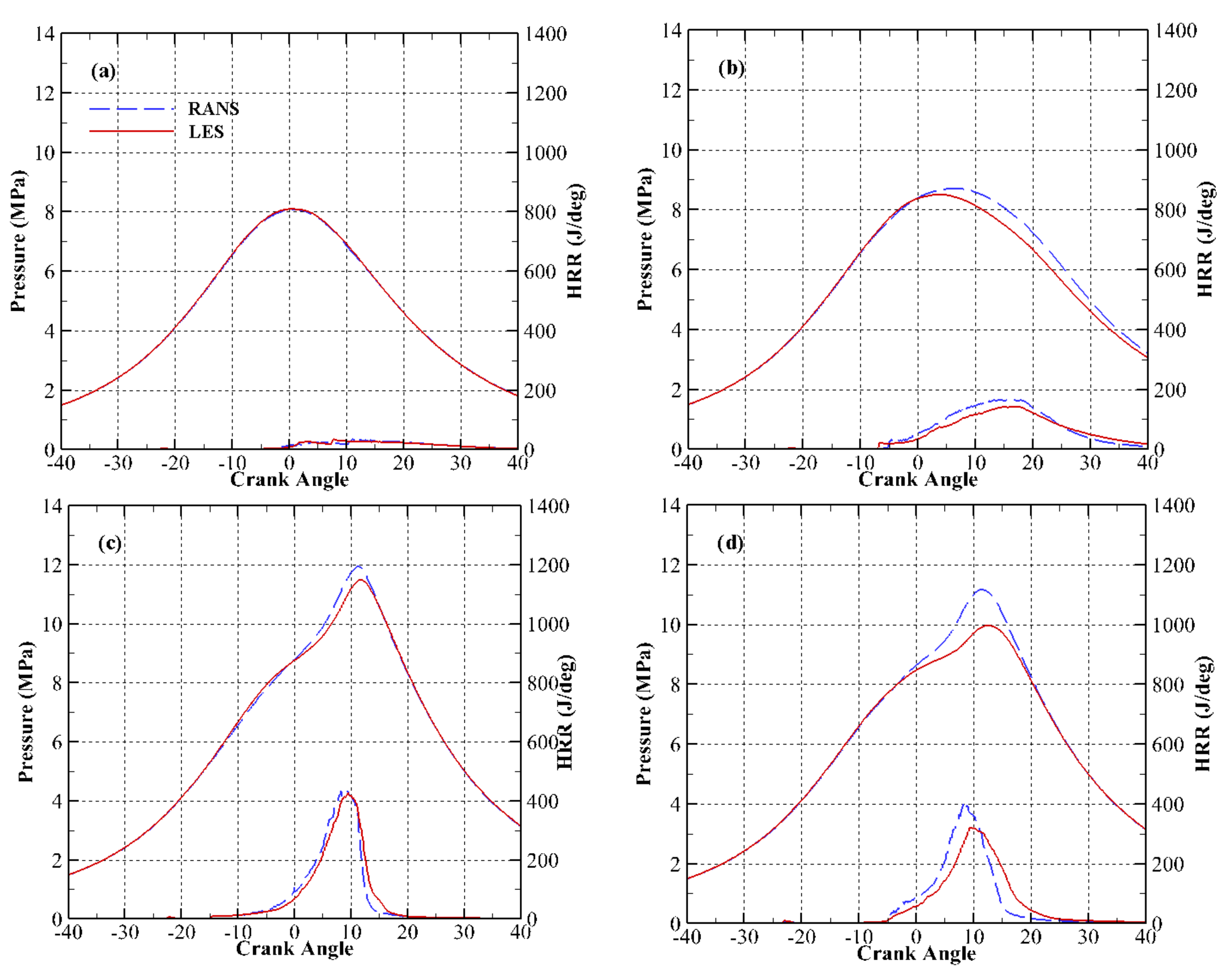
3.1. Effect of Natural Gas Mass Fraction
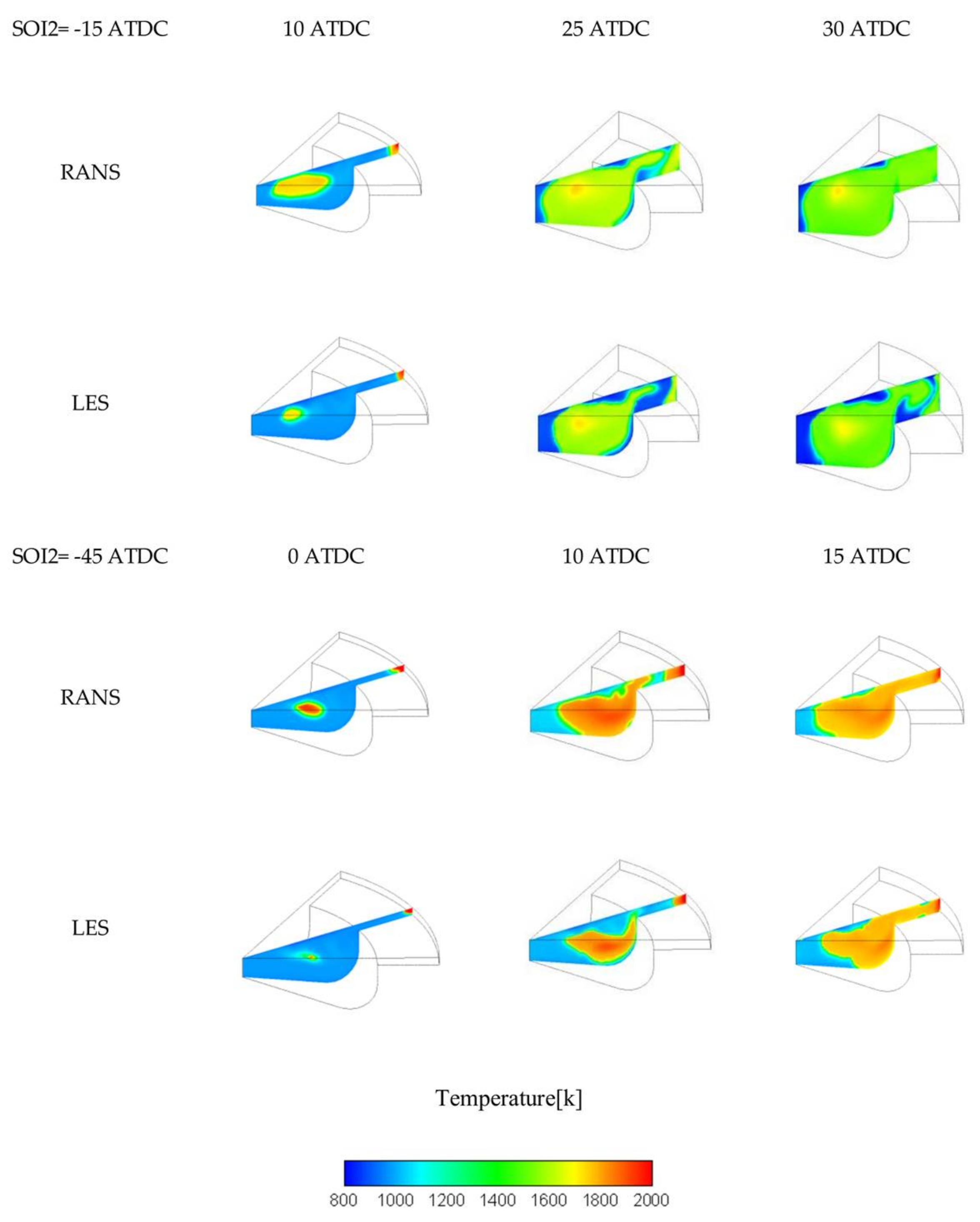
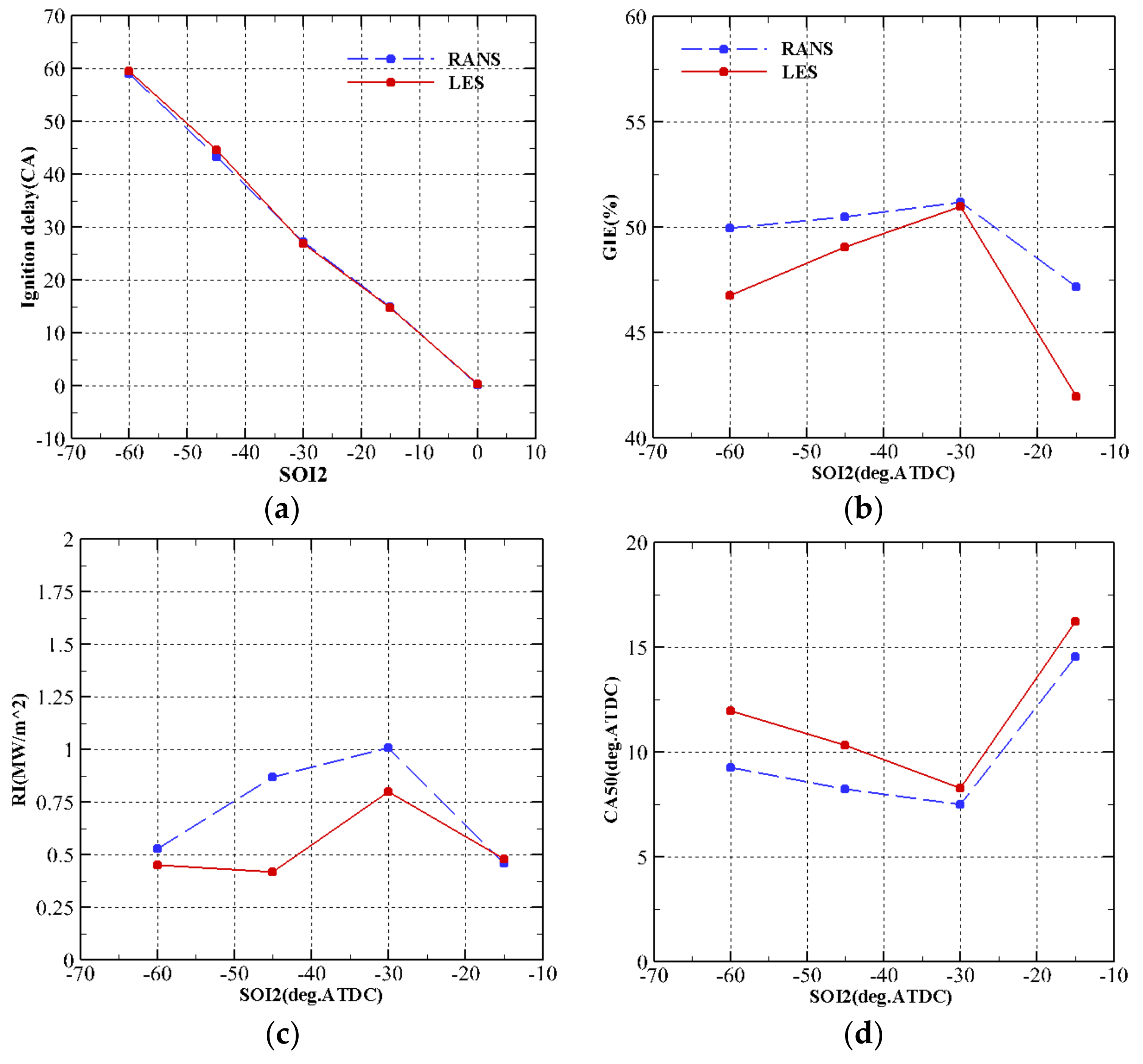
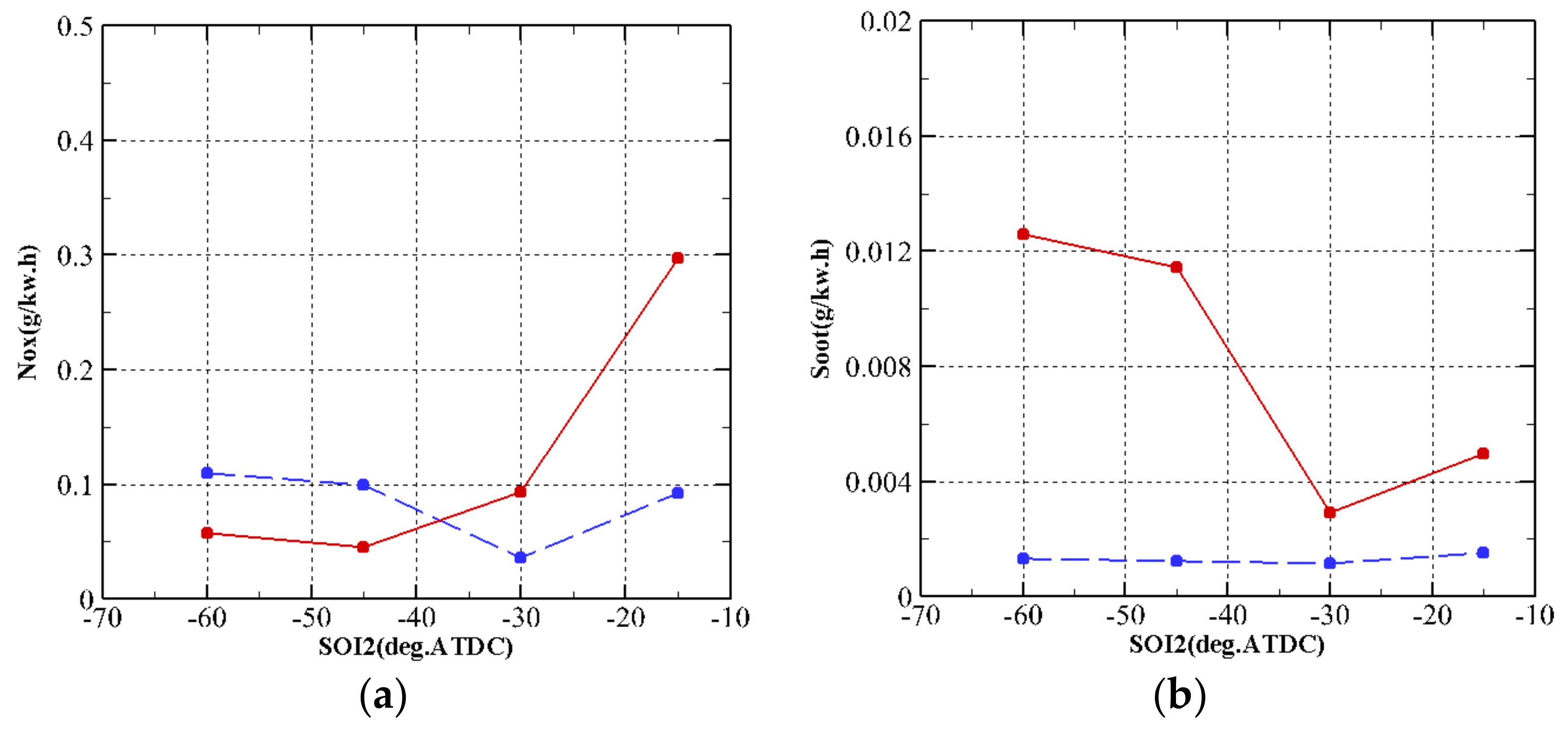
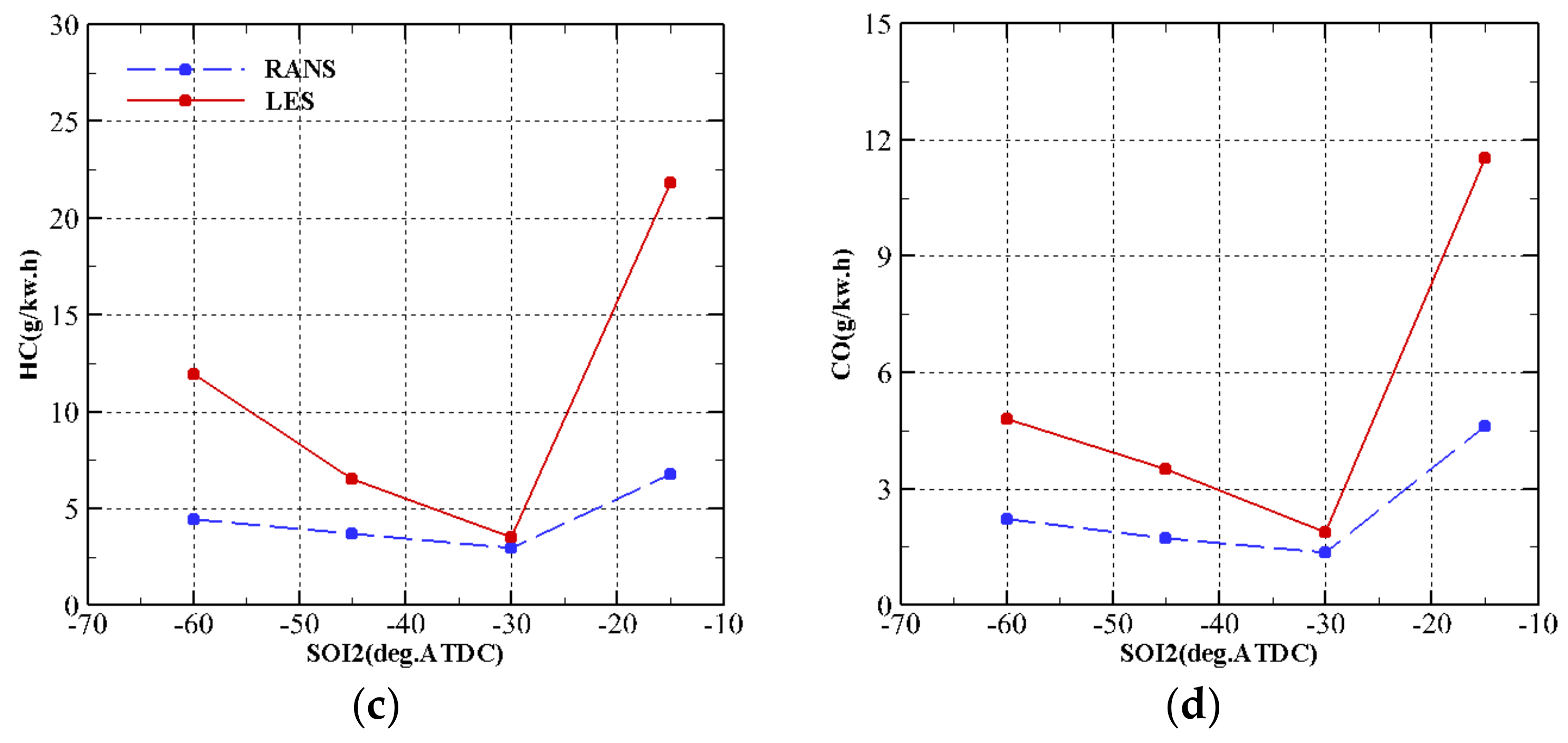
3.2. Effect of SOI2 Timing
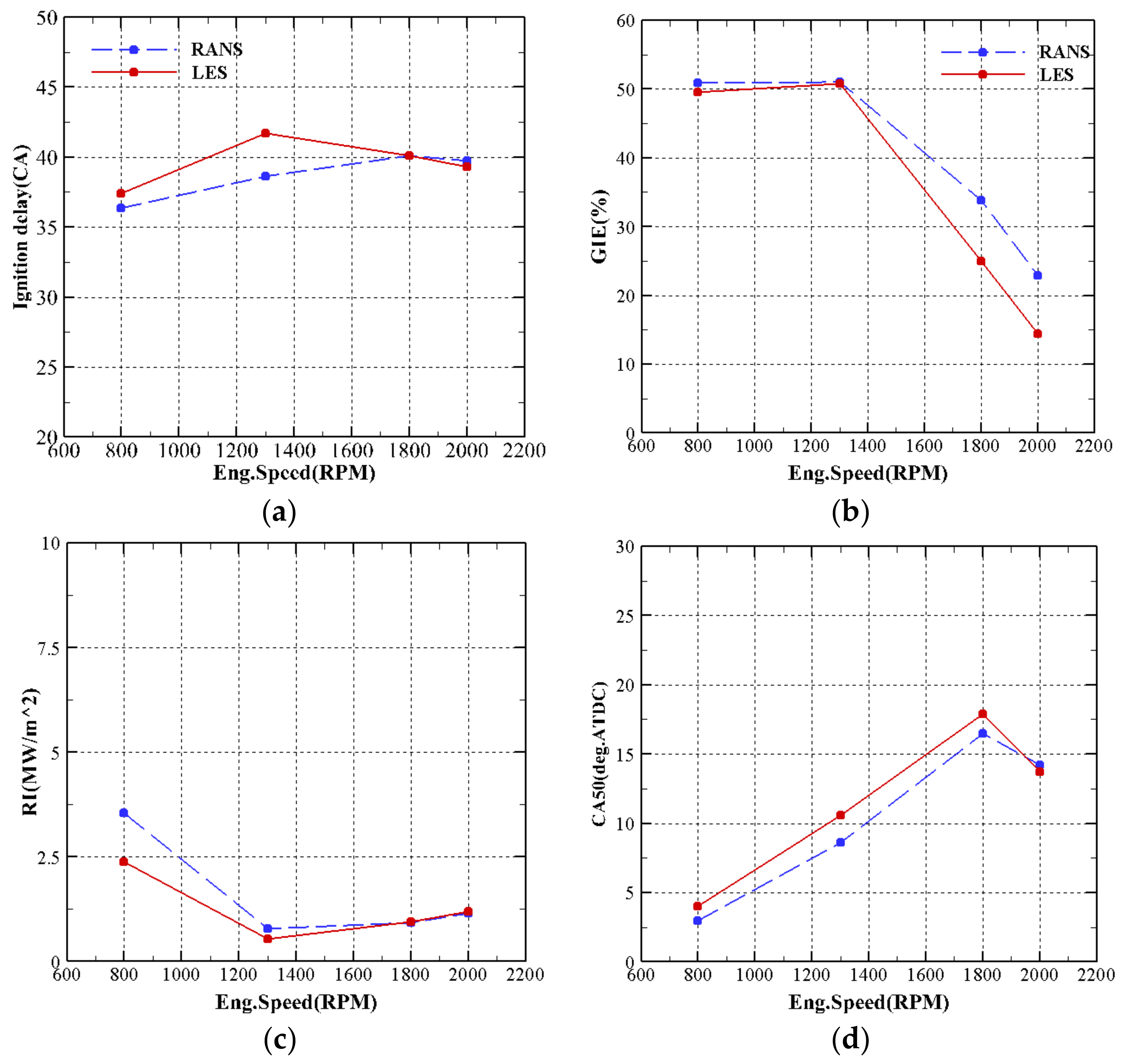
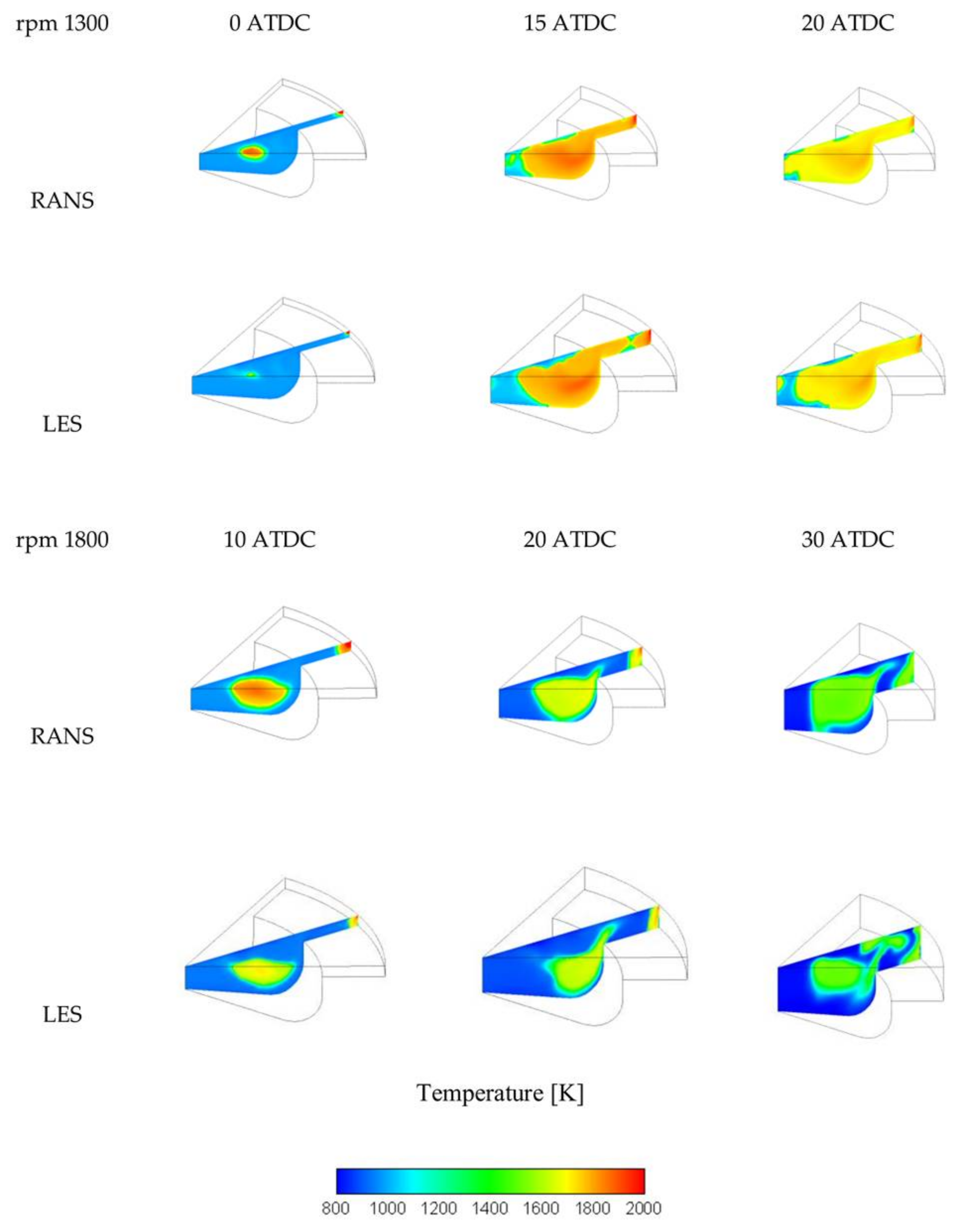
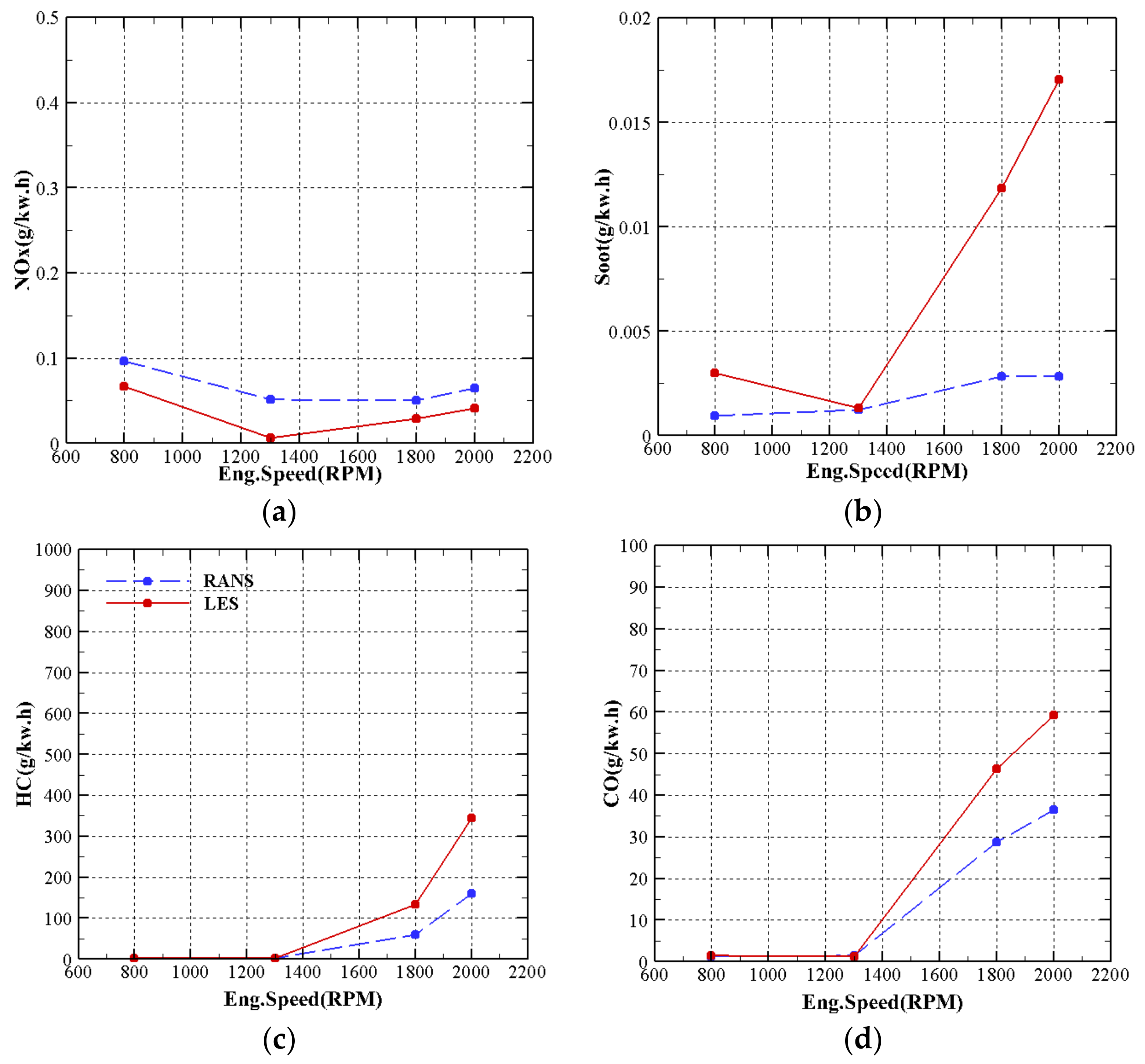
3.3. Effect of Engine Speed
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kokjohn, S.; Hanson, R.; Splitter, D.; Reitz, R. Fuel reactivity controlled compression ignition (RCCI): A pathway to controlled high-efficiency clean combustion. Int. J. Engine Res. 2011, 12, 209–226. [Google Scholar] [CrossRef]
- Kokjohn, S.L.; Hanson, R.M.; Splitter, D.A.; Reitz, R.D. Experiments and modeling of dual-fuel HCCI and PCCI combustion using in-cylinder fuel blending. SAE Int. J. Engines 2009, 2, 24–39. [Google Scholar] [CrossRef]
- Reitz, R.D. Directions in internal combustion engine research. Combust. Flame 2013, 1, 1–8. [Google Scholar] [CrossRef]
- Benajes, J.; Pastor, J.V.; García, A.; Monsalve-Serrano, J. An experimental investigation on the influence of piston bowl geometry on RCCI performance and emissions in a heavy-duty engine. Energy Convers. Manag. 2015, 103, 1019–1030. [Google Scholar] [CrossRef]
- Desantes, J.M.; Benajes, J.; García, A.; Monsalve-Serrano, J. The role of the in-cylinder gas temperature and oxygen concentration over low load reactivity controlled compression ignition combustion efficiency. Energy 2014, 78, 854–868. [Google Scholar] [CrossRef]
- Kakaee, A.; Rahnama, P.; Paykani, A. Numerical study of reactivity controlled compression ignition (RCCI) combustion in a heavy-duty diesel engine using 3D-CFD coupled with chemical kinetics. Int. J. Automot. Eng. 2014, 4, 792–804. [Google Scholar]
- Kakaee, A.-H.; Rahnama, P.; Paykani, A. Influence of fuel composition on combustion and emissions characteristics of natural gas/diesel RCCI engine. J. Nat. Gas Sci. Eng. 2015, 25, 58–65. [Google Scholar] [CrossRef]
- Kakaee, A.-H.; Nasiri-Toosi, A.; Partovi, B.; Paykani, A. Effects of piston bowl geometry on combustion and emissions characteristics of a natural gas/diesel RCCI engine. Appl. Therm. Eng. 2016, 102, 1462–1472. [Google Scholar] [CrossRef]
- Dempsey, A.B.; Walker, N.R.; Gingrich, E.; Reitz, R.D. Comparison of low temperature combustion strategies for advanced compression ignition engines with a focus on controllability. Combust. Sci. Technol. 2014, 186, 210–241. [Google Scholar] [CrossRef]
- Mahabadipour, H.; Srinivasan, K.K.; Krishnan, S.R. A second law-based framework to identify high efficiency pathways in dual fuel low temperature combustion. Appl. Energy 2017, 202, 199–212. [Google Scholar] [CrossRef]
- Reitz, R.D.; Duraisamy, G. Review of high efficiency and clean reactivity controlled compression ignition (RCCI) combustion in internal combustion engines. Prog. Energy Combust. Sci. 2015, 46, 12–71. [Google Scholar] [CrossRef]
- Paykani, A.; Kakaee, A.-H.; Rahnama, P.; Reitz, R.D. Progress and recent trends in reactivity-controlled compression ignition engines. Int. J. Engine Res. 2016, 17, 481–524. [Google Scholar] [CrossRef]
- Kakaee, A.-H.; Paykani, A.; Ghajar, M. The influence of fuel composition on the combustion and emission characteristics of natural gas fueled engines. Renew. Sustain. Energy Rev. 2014, 38, 64–78. [Google Scholar] [CrossRef]
- Paykani, A.; Kakaee, A.-H.; Rahnama, P.; Reitz, R.D. Effects of diesel injection strategy on natural gas/diesel reactivity controlled compression ignition combustion. Energy 2015, 90, 814–826. [Google Scholar] [CrossRef]
- Rahnama, P.; Paykani, A.; Reitz, R.D. A numerical study of the effects of using hydrogen, reformer gas and nitrogen on combustion, emissions and load limits of a heavy duty natural gas/diesel RCCI engine. Appl. Energy 2017, 193, 182–198. [Google Scholar] [CrossRef]
- Rahnama, P.; Paykani, A.; Bordbar, V.; Reitz, R.D. A numerical study of the effects of reformer gas composition on the combustion and emission characteristics of a natural gas/diesel RCCI engine enriched with reformer gas. Fuel 2017, 209, 742–753. [Google Scholar] [CrossRef]
- Nieman, D.E.; Dempsey, A.B.; Reitz, R.D. Heavy-duty RCCI operation using natural gas and diesel. SAE Int. J. Engines 2012, 5, 270–285. [Google Scholar] [CrossRef]
- Zoldak, P.; Sobiesiak, A.; Wickman, D.; Bergin, M. Combustion simulation of dual fuel CNG engine using direct injection of natural gas and diesel. SAE Int. J. Engines 2015, 8, 846–858. [Google Scholar] [CrossRef]
- Jia, Z.; Denbratt, I. Experimental investigation of natural gas-diesel dual-fuel RCCI in a heavy-duty engine. SAE Int. J. Engines 2015, 8, 797–807. [Google Scholar] [CrossRef]
- Kaario, O.; Pokela, H.; Kjäldman, L.; Tiainen, J.; Larmi, M. LES and RNG Turbulence Modeling in DI Diesel Engines; Society of Automotive Engineers: Warrendale, PA, USA, 2003. [Google Scholar]
- Naser, J.; Gosman, A. Prediction of compressible subsonic flow through an axisymmetric exhaust valve-port assembly. Proc. Inst. Mech. Eng. D J. Automob. Eng. 1995, 209, 289–295. [Google Scholar] [CrossRef]
- Naser, J.; Gosman, A. Flow Prediction in an Axisymmetric Inlet Valve/Port Assembly Using Variants of k-ε. Proc. Inst. Mech. Eng. D J. Automob. Eng. 1995, 209, 57–69. [Google Scholar] [CrossRef]
- Celik, I.; Yavuz, I.; Smirnov, A. Large eddy simulations of in-cylinder turbulence for internal combustion engines: A review. Int. J. Engine Res. 2001, 2, 119–148. [Google Scholar] [CrossRef]
- Rutland, C. Large-eddy simulations for internal combustion engines—A review. Int. J. Engine Res. 2011, 12, 421–451. [Google Scholar] [CrossRef]
- Yang, X.; Gupta, S.; Kuo, T.-W.; Gopalakrishnan, V. RANS and LES of IC Engine Flows–A Comparative Study. In Proceedings of the ASME 2013 Internal Combustion Engine Division Fall Technical Conference, Dearborn, MI, USA, 13–16 October 2013. [Google Scholar]
- Jhavar, R.; Rutland, C.J. Using Large Eddy Simulations to Study Mixing Effects in Early Injection Diesel Engine Combustion; Society of Automotive Engineers: Warrendale, PA, USA, 2006. [Google Scholar]
- Zhou, L.; Xie, M.-Z.; Jia, M.; Shi, J.-R. Large eddy simulation of fuel injection and mixing process in a diesel engine. Acta Mech. Sin. 2011, 27, 519–530. [Google Scholar] [CrossRef]
- Bottone, F.; Kronenburg, A.; Gosman, D.; Marquis, A. Large eddy simulation of diesel engine in-cylinder flow. Flow Turbul. Combust. 2012, 88, 233–253. [Google Scholar] [CrossRef]
- Banaeizadeh, A.; Afshari, A.; Schock, H.; Jaberi, F. Large-eddy simulations of turbulent flows in internal combustion engines. Int. J. Heat Mass Transf. 2013, 60, 781–796. [Google Scholar] [CrossRef]
- Toosi, A.N.; Farokhi, M.; Mashadi, B. Application of modified eddy dissipation concept with large eddy simulation for numerical investigation of internal combustion engines. Comput. Fluids 2015, 109, 85–99. [Google Scholar] [CrossRef]
- Xu, G.-L.; Yao, C.-D.; Rutland, C.J. Simulations of diesel–methanol dual-fuel engine combustion with large eddy simulation and Reynolds-averaged Navier–Stokes model. Int. J. Engine Res. 2014, 15, 751–769. [Google Scholar] [CrossRef]
- Richards, K.; Senecal, P.; Pomraning, E. CONVERGE (v2. 2.0); Theory Manual, Convergent Science: Madison, WI, USA, 2014. [Google Scholar]
- Reitz, R.D.; Diwakar, R. Structure of High-Pressure Fuel Sprays; Society of Automotive Engineers: Warrendale, PA, USA, 1987. [Google Scholar]
- Beale, J.C.; Reitz, R.D. Modeling spray atomization with the Kelvin-Helmholtz/Rayleigh-Taylor hybrid model. Atomization Sprays 1999, 9, 623–650. [Google Scholar]
- Schmidt, D.P.; Rutland, C. A new droplet collision algorithm. J. Comput. Phys. 2000, 164, 62–80. [Google Scholar] [CrossRef]
- Liu, A.B.; Mather, D.; Reitz, R.D. Modeling the Effects of Drop Drag and Breakup on Fuel Sprays; Wisconsin Univ-Madison Engine Research Center: Madison, WI, USA, 1993. [Google Scholar]
- Han, Z.; Reitz, R.D. Turbulence modeling of internal combustion engines using RNG κ-ε models. Combust. Sci. Technol. 1995, 106, 267–295. [Google Scholar] [CrossRef]
- Shahsavan, M.; Mack, J.H. Numerical study of a boosted HCCI engine fueled with n-butanol and isobutanol. Energy Convers. Manag. 2018, 157, 28–40. [Google Scholar]
- Raju, M.; Wang, M.; Dai, M.; Piggott, W.; Flowers, D. Acceleration of Detailed Chemical Kinetics Using Multi-Zone Modeling for CFD in Internal Combustion Engine Simulations; Society of Automotive Engineers: Warrendale, PA, USA, 2012. [Google Scholar]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C., Jr.; et al. GRI 3.0 Mechanism. Gas Research Institute, 1999. Available online: http://combustion.berkeley.edu/gri-mech/releases.html (accessed on 27 March 2018).
- Heywood, J.B. Internal Combustion Engine Fundamentals; Mcgraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Hiroyasu, H.; Kadota, T. Models for Combustion and Formation of Nitric Oxide and Soot in Direct Injection Diesel Engines. In Proceedings of the Automotive Engineering Congress and Exposition, Detroit, MI, USA, 23 February 1976. [Google Scholar]
- Namazian, M.; Heywood, J.B. Flow in the Piston-Cylinder-Ring Crevices of a Spark-Ignition Engine: Effect on Hydrocarbon Emissions, Efficiency and Power; Society of Automotive Engineers: Warrendale, PA, USA, 1982. [Google Scholar]
- Pomraning, E. Development of Large Eddy Simulation Turbulence Models; University of Wisconsin: Madison, WI, USA, 2000. [Google Scholar]
- Werner, H.; Wengle, H. Large-Eddy Simulation of Turbulent Flow over and around a cuBe in a Plate Channel; Turbulent Shear Flows 8; Springer: Berlin/Heidelberg, Germany, 1993; pp. 155–168. [Google Scholar]
- Amsden, A.A. KIVA-3V: A Block-Structured KIVA Program for Engines with Vertical or Canted Valves; Los Alamos National Lab.: Los Alamos, NM, USA, 1997. [Google Scholar]
- Nobakht, A.Y.; Saray, R.K.; Rahimi, A. A parametric study on natural gas fueled HCCI combustion engine using a multi-zone combustion model. Fuel 2011, 90, 1508–1514. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Displacement | 2.44 L |
| Bore × Stroke (cm) | 13.72 × 16.51 |
| Connecting rod size (cm) | 26.16 |
| Rate of compression | 16.1:1 |
| Swirl rate | 0.7 |
| Type of bowl | Mexican Hat |
| Valves No. | 4 |
| Intake valve closing | −143 ATDC |
| Exhaust valve opening | 130 ATDC |
| Common Rail Diesel Fuel Injector | |
| Holes No. | 6 |
| Diameter of hole (μm) | 250 |
| Included spray degree (degree) | 145 |
| Parameter | IMEP 4 Bar | IMEP 9 Bar |
|---|---|---|
| Intake Pressure (bar) | 1.0 | 1.75 |
| Intake Temperature (°C) | 60 | 60 |
| Engine Speed (rpm) | 800 | 1300 |
| Total Fuel Mass (mg) | 40 | 89 |
| Methane (% by mass) | 73 | 85 |
| Diesel SOI1 (°ATDC) | −52.9 | −87.3 |
| Diesel SOI2 (°ATDC) | −22.5 | −38.3 |
| Diesel in 1st Inj. (%) | 52 | 40 |
| EGR (%) | 5% | 0 |
| Case | GIE (%) | RI (MW/m2) | NOx (g/kW·h) | Soot (g/kW·h) | UHC (g/kW·h) | CO (g/kW·h) |
|---|---|---|---|---|---|---|
| Nieman et al. [17], IMEP 9 bar | 50.4 | 1.2 | 0.02 | 0.003 | 2.5 | 1.8 |
| Present Work IMEP 9 bar | 50.7 | 0.9 | 0.016 | 0.0012 | 2.72 | 1.22 |
| Absolute errors | 0.3 | 0.3 | 0.004 | 0.0018 | 0.22 | 0.58 |
| Nieman et al. [17], IMEP 4 bar | 45.1 | 0.2 | 0.24 | 0.004 | 10.8 | 10.5 |
| Present Work IMEP 4 bar | 47.1 | 0.19 | 0.158 | 0.0032 | 12.6 | 4.2 |
| Absolute errors | 2.0 | 0.01 | 0.082 | 0.0008 | 1.8 | 6.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakaee, A.-H.; Jafari, P.; Paykani, A. Numerical Study of Natural Gas/Diesel Reactivity Controlled Compression Ignition Combustion with Large Eddy Simulation and Reynolds-Averaged Navier–Stokes Model. Fluids 2018, 3, 24. https://doi.org/10.3390/fluids3020024
Kakaee A-H, Jafari P, Paykani A. Numerical Study of Natural Gas/Diesel Reactivity Controlled Compression Ignition Combustion with Large Eddy Simulation and Reynolds-Averaged Navier–Stokes Model. Fluids. 2018; 3(2):24. https://doi.org/10.3390/fluids3020024
Chicago/Turabian StyleKakaee, Amir-Hasan, Parvaneh Jafari, and Amin Paykani. 2018. "Numerical Study of Natural Gas/Diesel Reactivity Controlled Compression Ignition Combustion with Large Eddy Simulation and Reynolds-Averaged Navier–Stokes Model" Fluids 3, no. 2: 24. https://doi.org/10.3390/fluids3020024





