The Hydrodynamic Nonlinear Schrödinger Equation: Space and Time
Abstract
:1. Introduction
2. Analysis
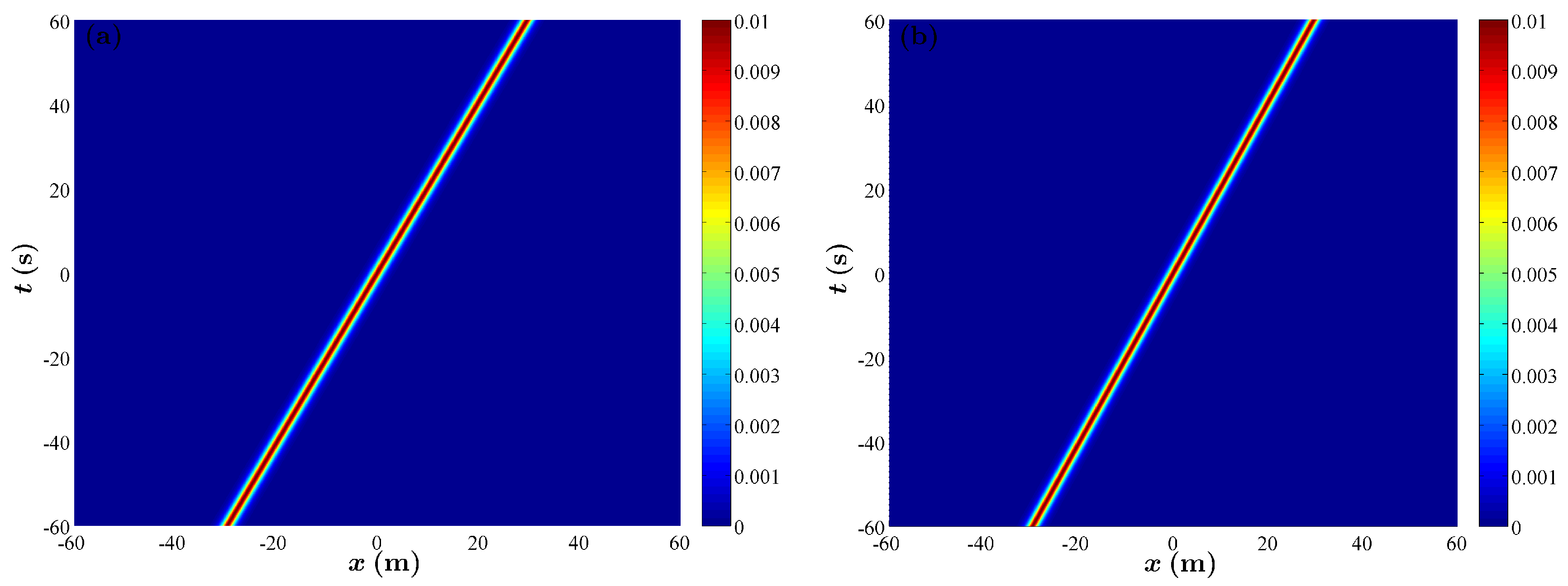
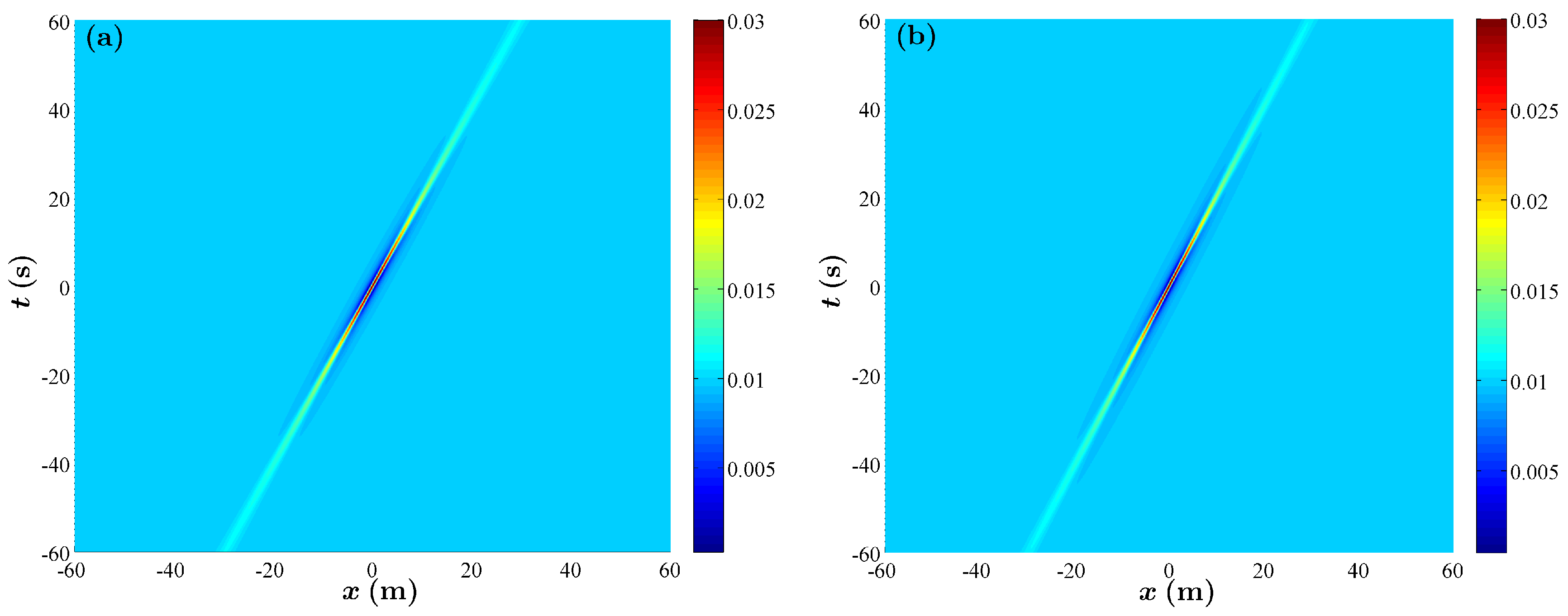
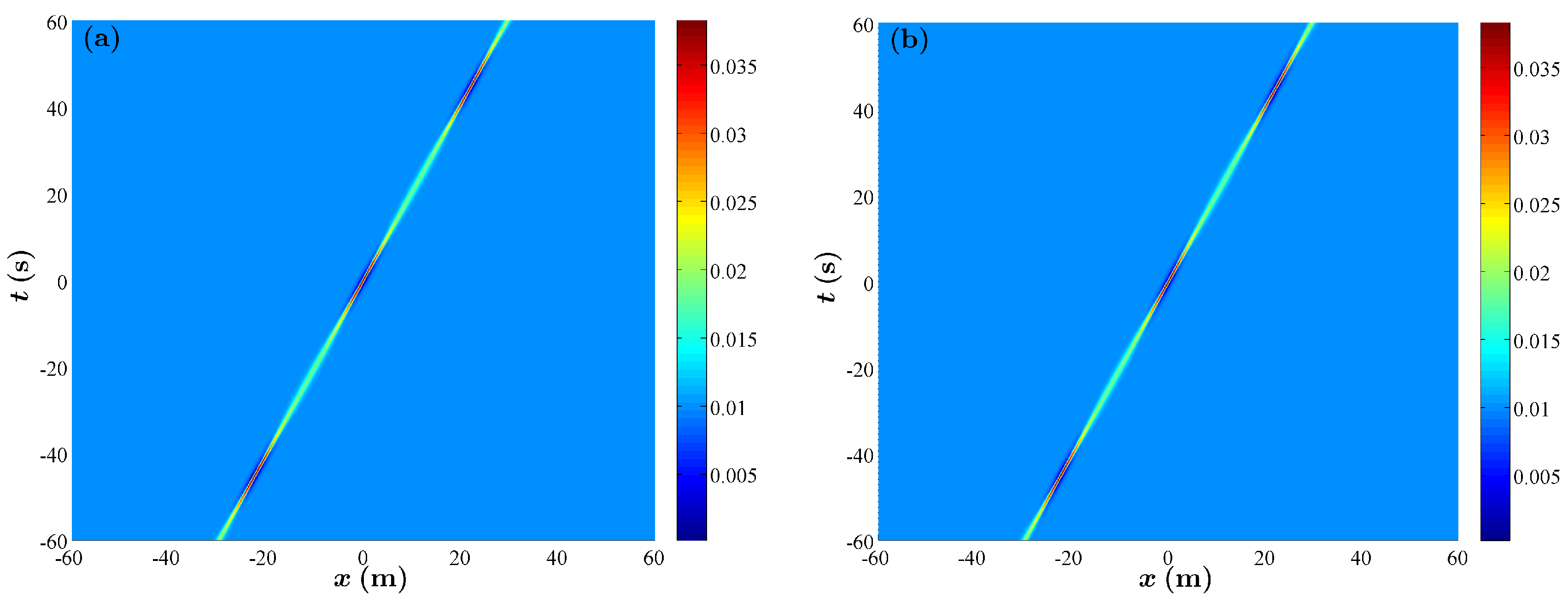
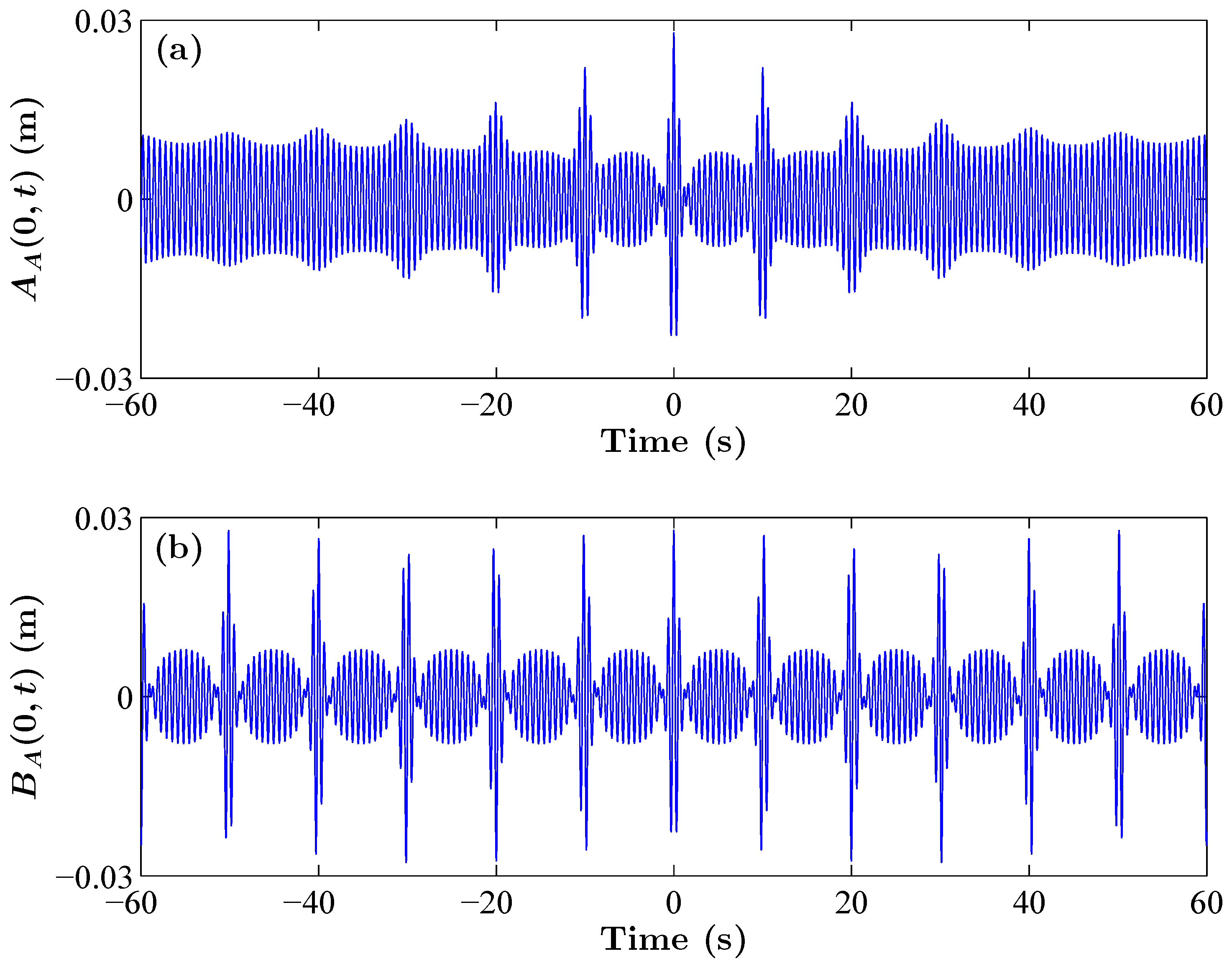
2.1. The Propagation of Wave Packets in Time and Space
2.2. The Evolution of Specific NLS Solutions
3. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| NLS | Nonlinear Schrödinger equation |
| MI | Modulation instability |
| AB | Akhmediev breather |
References
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: Berlin, Germany, 2009. [Google Scholar]
- Osborne, A. Nonlinear Ocean Waves & the Inverse Scattering Transform; Academic Press: Amsterdam, The Netherlands, 2010; Volume 97. [Google Scholar]
- Babanin, A. Breaking and Dissipation of Ocean Surface Waves; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Yuen, H.C.; Lake, B.M. Nonlinear deep water waves: Theory and experiment. Phys. Fluids (1958–1988) 1975, 18, 956–960. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Toffoli, A.; Waseda, T.; Houtani, H.; Kinoshita, T.; Collins, K.; Proment, D.; Onorato, M. Excitation of rogue waves in a variable medium: An experimental study on the interaction of water waves and currents. Phys. Rev. E 2013, 87, 051201. [Google Scholar] [CrossRef] [PubMed]
- Slunyaev, A.; Clauss, G.F.; Klein, M.; Onorato, M. Simulations and experiments of short intense envelope solitons of surface water waves. Phys. Fluids (1994–present) 2013, 25, 067105. [Google Scholar] [CrossRef]
- Chabchoub, A.; Onorato, M.; Akhmediev, N. Hydrodynamic solitons and breathers. In Rogue and Shock Waves; Onorato, M., Residori, S., Baronio, F., Eds.; Lecture Notes in Physics; Springer: Berlin, Germany, 2016. [Google Scholar]
- Chabchoub, A.; Kibler, B.; Finot, C.; Millot, G.; Onorato, M.; Dudley, J.M.; Babanin, A.V. The nonlinear Schrödinger equation and the propagation of weakly nonlinear waves in optical fibers and on the water surface. Ann. Phys. 2015, 361, 490–500. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Dias, F.; Kibler, B.; Akhmediev, N. Modulation instability, akhmediev breathers and continuous wave supercontinuum generation. Opt. Express 2009, 17, 21497–21508. [Google Scholar] [CrossRef] [PubMed]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F.T. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Tlidi, M.; Gandica, Y.; Sonnino, G.; Averlant, E.; Panajotov, K. Self-Replicating spots in the brusselator model and extreme events in the one-dimensional case with delay. Entropy 2016, 18, 64. [Google Scholar] [CrossRef]
- Dysthe, K.B.; Trulsen, K. Note on breather type solutions of the NLS as models for freak-waves. Phys. Scr. 1999, T82, 48–52. [Google Scholar] [CrossRef]
- Shrira, V.I.; Geogjaev, V.V. What makes the Peregrine soliton so special as a prototype of freak waves? J. Eng. Math. 2010, 67, 11–22. [Google Scholar] [CrossRef]
- Grimshaw, R.; Tovbis, A. Rogue waves: Analytical predictions. Proc. R. Soc. A 2013, 469, 20130094. [Google Scholar] [CrossRef]
- Akhmediev, N.; Eleonskii, V.M.; Kulagin, N.E. Generation of periodic trains of picosecond pulses in an optical fiber: Exact solutions. Sov. Phys. JETP 1985, 62, 894–899. [Google Scholar]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. Series B. Appl. Math. 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Feir, J. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Stokes, G.G. On the theory of oscillatory waves. Trans. Camb. Philos. Soc. 1847, 8, 441–473. [Google Scholar]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Techn. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Shabat, A.; Zakharov, V. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62. [Google Scholar]
- Kuznetsov, E. Solitons in a parametrically unstable plasma. Akademiia Nauk SSSR Doklady 1977, 236, 575–577. [Google Scholar]
- Ma, Y.C. The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud. Appl. Math. 1979, 60, 43–58. [Google Scholar] [CrossRef]
- Akhmediev, N.; Eleonskii, V.M.; Kulagin, N.E. Exact solutions of the first order of nonlinear Schrödinger equation. Theor. Math. Phys. (USSR) 1987, 72, 809–818. [Google Scholar] [CrossRef]
- Andonwati; Karjanto, N.; Van Groesen, E. Extreme wave phenomena in down-stream running modulated waves. Appl. Math. Model. 2007, 31, 1425–1443. [Google Scholar]
- Chabchoub, A.; Kibler, B.; Dudley, J.; Akhmediev, N. Hydrodynamics of periodic breathers. Philos. Trans. A Math. Phys. Eng. Sci. 2014, 372, 20140005. [Google Scholar] [CrossRef] [PubMed]
- Karjanto, N.; Van Groesen, E. Qualitative comparisons of experimental results on deterministic freak wave generation based on modulational instability. J. Hydro-Environ. Res. 2010, 3, 186–192. [Google Scholar] [CrossRef]
- Chabchoub, A.; Waseda, T. Hydrodynamic breathers modeling rogue waves. Proc. Violent Flows 2016, in press. [Google Scholar]
- Tulin, M.P.; Waseda, T. Laboratory observations of wave group evolution, including breaking effects. J. Fluid Mech. 1999, 378, 197–232. [Google Scholar] [CrossRef]
- Onorato, M.; Proment, D.; Clauss, G.; Klein, M. Rogue waves: From nonlinear Schrödinger breather solutions to sea-keeping test. PLoS ONE 2013, 8, e54629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alberello, A.; Chabchoub, A.; Babanin, A.V.; Monty, J.M.; Elsnab, J.; Lee, J.H.; Bitner-Gregersen, E.M.; Toffoli, A. The veolicty field underneath linear and nonlinear breaking waves. In Proceedings of the ASME 2016 30th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; p. 54481.
- Trulsen, K.; Dysthe, K.B. A modified nonlinear Schrödinger equation for broader bandwidth gravity waves on deep water. Wave Motion 1996, 24, 281–289. [Google Scholar] [CrossRef]
- Slunyaev, A.V.; Shrira, V.I. On the highest non-breaking wave in a group: Fully nonlinear water wave breathers versus weakly nonlinear theory. J. Fluid Mech. 2013, 735, 203–248. [Google Scholar] [CrossRef]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1979, 369, 105–114. [Google Scholar] [CrossRef]
- Trulsen, K.; Stansberg, C.T. Spatial evolution of water surface waves: Numerical simulation and experiment of bichromatic waves. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2001. [Google Scholar]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Genty, G.; Dudley, J.M.; Akhmediev, N. Hydrodynamic supercontinuum. Phys. Rev. Lett. 2013, 111, 054104. [Google Scholar] [CrossRef] [PubMed]
- Slunyaev, A. A high-order nonlinear envelope equation for gravity waves in finite-depth water. J. Exp. Theor. Phys. 2005, 101, 926–941. [Google Scholar] [CrossRef]
- Gramstad, O.; Trulsen, K. Hamiltonian form of the modified nonlinear Schrödinger equation for gravity waves on arbitrary depth. J. Fluid Mech. 2011, 670, 404–426. [Google Scholar] [CrossRef]
- Craig, W.; Guyenne, P.; Sulem, C. A Hamiltonian approach to nonlinear modulation of surface water waves. Wave Motion 2010, 47, 552–563. [Google Scholar] [CrossRef]
- Fermi, E.; Pasta, J.; Ulam, S. Studies of the Nonlinear Problems; Los Alamos Report LA-1940; Los Alamos Laboratory of the University of California: Los Alamos, NM, USA, 1955. [Google Scholar]
- Onorato, M.; Vozella, L.; Proment, D.; Lvov, Y.V. Route to thermalization in the α-Fermi–Pasta–Ulam system. Proc. Natl. Acad. Sci. USA 2015, 112, 4208–4213. [Google Scholar] [CrossRef] [PubMed]
- Kimmoun, O.; Hsu, H.C.; Branger, B.; Li, M.S.; Chen, Y.Y.; Kharif, C.; Onorato, M.; Kelleher, E.J.R.; Kibler, B.; Akhmediev, N.; et al. Modulation instability and phase-shifted Fermi-Pasta-Ulam recurrence. 2016; arXiv:1602.01604 [nlin.PS]. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chabchoub, A.; Grimshaw, R.H.J. The Hydrodynamic Nonlinear Schrödinger Equation: Space and Time. Fluids 2016, 1, 23. https://doi.org/10.3390/fluids1030023
Chabchoub A, Grimshaw RHJ. The Hydrodynamic Nonlinear Schrödinger Equation: Space and Time. Fluids. 2016; 1(3):23. https://doi.org/10.3390/fluids1030023
Chicago/Turabian StyleChabchoub, Amin, and Roger H. J. Grimshaw. 2016. "The Hydrodynamic Nonlinear Schrödinger Equation: Space and Time" Fluids 1, no. 3: 23. https://doi.org/10.3390/fluids1030023





