Electrodiffusion-Mediated Swelling of a Two-Phase Gel Model of Gastric Mucus
Abstract
:1. Introduction
2. Mathematical Model
2.1. Gel Evolution
2.2. Dissolved Ion Evolution
2.3. Bound Ion Evolution
2.4. Driving Potentials
3. Results
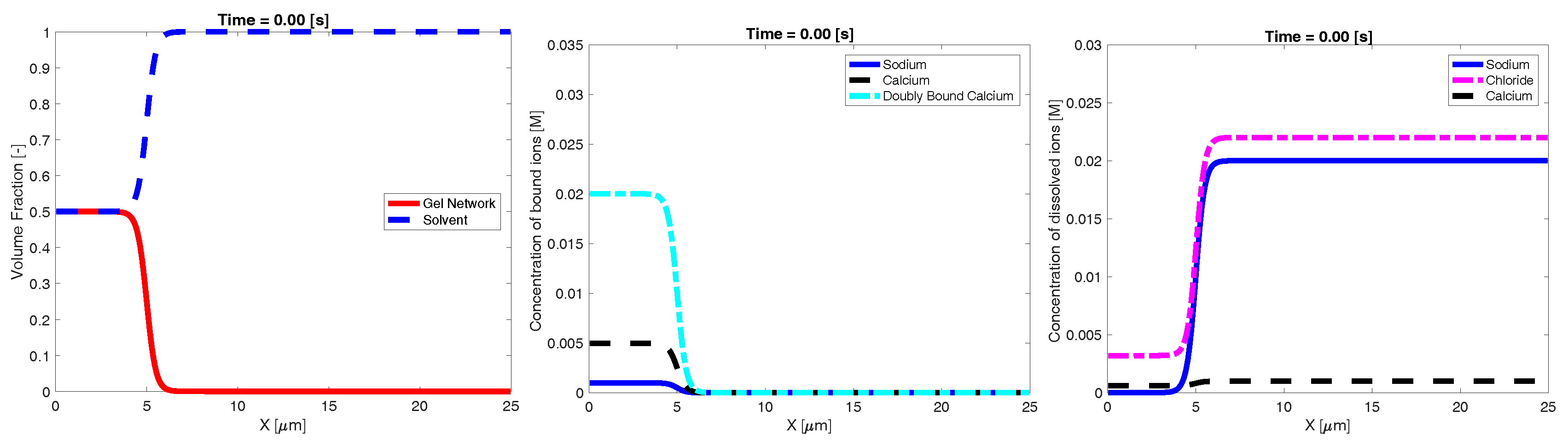
3.1. Numerical Experiments and Initial Conditions
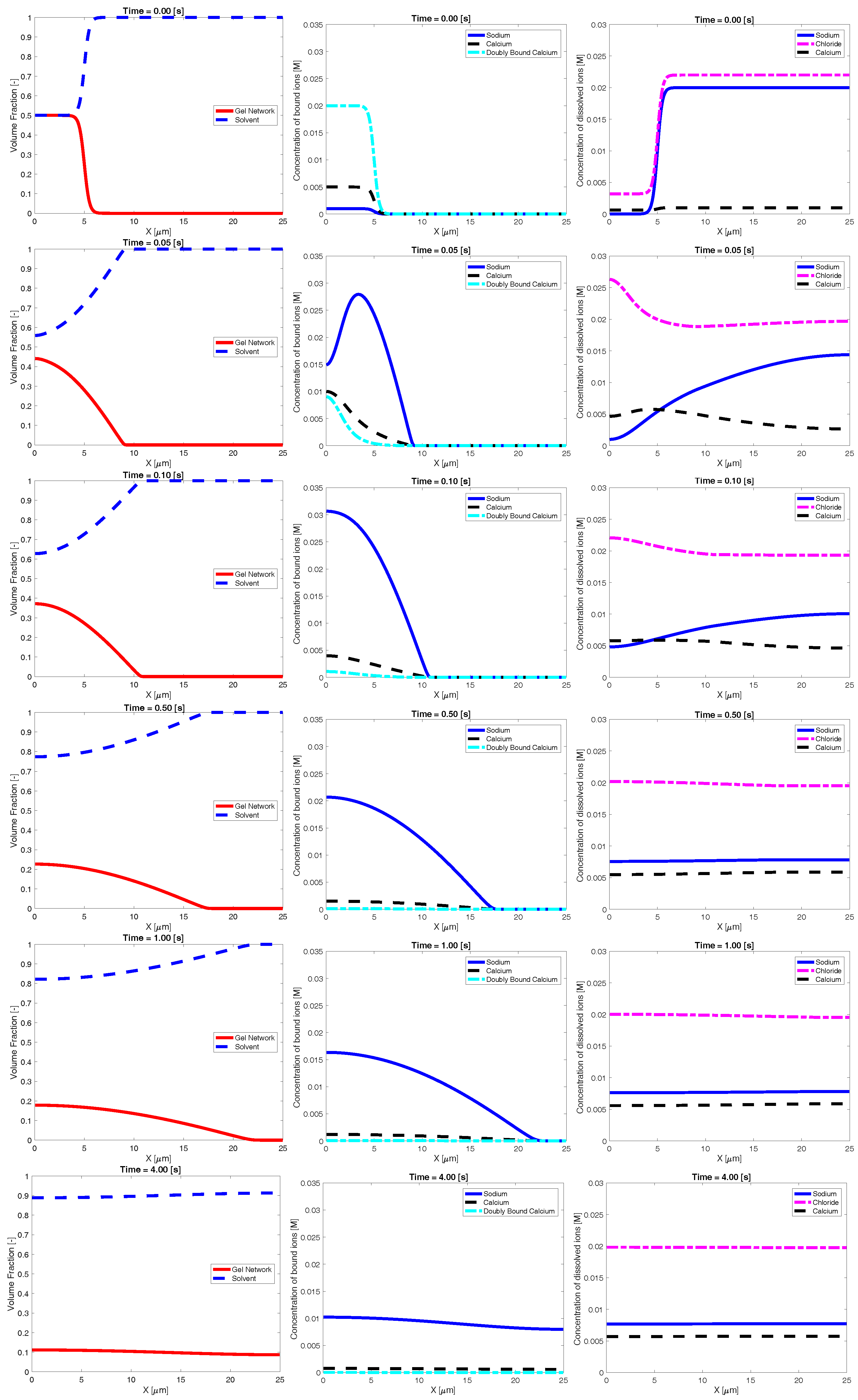
3.2. Gel Swelling Experiments
3.3. Front Propagation
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Numerical Scheme
- Given ionic concentrations ( and ), electric potential gradient (), and both volume fractions (), evaluate the potential gradients which act on the solvent and network phase ().
- Given the potential gradients on each phase (), solve the momentum equations to determine the network and solvent velocities ().
- Given their respective velocity fields, update the solvent and network volume fraction ().
- Given the two transport velocities and volume fractions ( and ), evolve the ionic concentrations while simultaneously solving for a new electric potential gradient (, and ).
Appendix A.1.1. Momentum Solve
Appendix A.1.2. Volume Fraction Advection
Appendix A.1.3. Ion Update
References
- Allen, A.; Flemström, G. Gastroduodenal Mucus Bicarbonate Barrier: Protection Against Acid and Pepsin. Am. J. Physiol. Cell Physiol. 2005, 288, C1–C19. [Google Scholar] [CrossRef] [PubMed]
- Perez-Vilar, J. Mucin granule intraluminal organization. Am. J. Respir. Cell Mol. Biol. 2007, 36, 183–190. [Google Scholar] [CrossRef] [PubMed]
- Verdugo, P. Polymer Biophysics of Mucus in Cystic Fibrosis. In Cilia, Mucus, and Mucociliary Interactions; Marcel Dekker: New York, NY, USA, 1998; pp. 167–190. [Google Scholar]
- Espinosa, M.; Noé, G.; Troncoso, C.; Ho, S.B.; Villalón, M. Acidic pH and Increasing [Ca(2+)] Reduce the Swelling of Mucins in Primary Cultures of Human Cervical Cells. Hum. Reprod. 2002, 17, 1964–1972. [Google Scholar] [CrossRef] [PubMed]
- Verdugo, P.; Deyrup-Olsen, I.; Martin, A.W.; Luchtel, D.L. Polymer Gel Phase Transition: The Molecular Mechanism of Product Release in Mucin Secretion. In Mechanics of Swelling; Springer: Berlin/Heidelberg, Germany, 1992; pp. 671–681. [Google Scholar]
- Cohen, J.; Macromolecules, Z.P. Viscosity of dilute polyelectrolyte solutions: Concentration dependence on sodium chloride, magnesium sulfate and lanthanum nitrate. Macromolecules 1989, 5, 2356–2358. [Google Scholar] [CrossRef]
- Horkay, F.; Basser, P.J.; Hecht, A.-M.; Geissler, E. Chondroitin Sulfate in Solution: Effects of Mono- and Divalent Salts. Macromolecules 2012, 45, 2882–2890. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horkay, F.; Basser, P.J.; Londono, D.J.; Hecht, A.-M.; Geissler, E. Ions in hyaluronic acid solutions. J. Chem. Phys. 2009, 131, 184902. [Google Scholar] [CrossRef] [PubMed]
- Yin, D.-W.; Horkay, F.; Douglas, J.F.; de Pablo, J.J. Molecular simulation of the swelling of polyelectrolyte gels by monovalent and divalent counterions. J. Chem. Phys. 2008, 129, 154902. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Douglas, J.F.; Ermi, B.D.; Amis, E.J. Influence of counterion valency on the scattering properties of highly charged polyelectrolyte solutions. J. Chem. Phys. 2001, 114, 3299–3313. [Google Scholar] [CrossRef]
- Quesada-Pérez, M.; Maroto-Centeno, J.A.; Forcada, J.; Hidalgo-Alvarez, R. Gel swelling theories: The classical formalism and recent approaches. Soft Matter 2011, 7, 10536–10547. [Google Scholar] [CrossRef]
- Sircar, S.; Keener, J.P.; Fogelson, A.L. The Effect of Divalent vs. Monovalent Ions on the Swelling of Mucin-Like Polyelectrolyte Gels: Governing Equations and Equilibrium Analysis. J. Chem. Phys. 2013, 138, 014901. [Google Scholar] [CrossRef] [PubMed]
- Sircar, S.; Roberts, A. Ion mediated crosslink driven mucous swelling kinetics. Discret. Contin. Dyn. Syst. Ser. B 2016, 21, 1937–1951. [Google Scholar] [CrossRef]
- Alt, W.; Dembo, M. Cytoplasm dynamics and cell motion: Two-phase flow models. Math. Biosci. 1999, 156, 207–228. [Google Scholar] [CrossRef]
- Cogan, N.G.; Keener, J.P. The Role of the Biofilm Matrix in Structural Development. Math. Med. Biol. J. IMA 2004, 21, 147–166. [Google Scholar] [CrossRef]
- Dembo, M. Mechanics and Control of the Cytoskeleton in Amoeba proteus. Biophys. J. 1989, 55, 1053–1080. [Google Scholar] [CrossRef]
- Du, J.; Fogelson, A.L. A Two-phase mixture model of platelet aggregation. Math. Med. Biol. J. IMA 2017, 35, 225–256. [Google Scholar] [CrossRef] [PubMed]
- Raynal, B.D.E.; Hardingham, T.E.; Sheehan, J.K.; Thornton, D.J. Calcium-dependent protein interactions in MUC5B provide reversible cross-links in salivary mucus. J. Biol. Chem. 2003, 278, 28703–28710. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, S.S.; Scheid, P.P. Gastric Mucus of the Guinea Pig: Proton Carrier and Diffusion Barrier. Am. J. Physiol. 1997, 272 Pt 1, G63–G70. [Google Scholar] [CrossRef]
- Crowther, R.S.; Marriott, C. Counter-ion binding to mucus glycoproteins. J. Pharm. Pharmacol. 1983, 36, 21–26. [Google Scholar] [CrossRef]
- Celli, J.; Gregor, B.; Turner, B.; Afdhal, N.H.; Bansil, R.; Erramilli, S. Viscoelastic Properties and Dynamics of Porcine Gastric Mucin. Biomacromolecules 2005, 6, 1329–1333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Celli, J.P.; Turner, B.S.; Afdhal, N.H.; Ewoldt, R.H.; McKinley, G.H.; Bansil, R.; Erramilli, S. Rheology of Gastric Mucin Exhibits a pH-Dependent Sol-Gel Transition. Biomacromolecules 2007, 8, 1580–1586. [Google Scholar] [CrossRef] [PubMed]
- Lai, S.K.; Wang, Y.-Y.; Wirtz, D.; Hanes, J. Micro- and Macrorheology of Mucus. Adv. Drug Deliv. Rev. 2009, 61, 86–100. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Hollinger, M.; Lachowicz-Scroggins, M.E.; Kerr, S.C.; Dunican, E.M.; Daniel, B.M.; Ghosh, S.; Erzurum, S.C.; Willard, B.; Hazen, S.L.; et al. Oxidation increases mucin polymer cross-links to stiffen airway mucus gels. Sci. Trans. Med. 2015, 7, 276ra27. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Guy, R.D.; Fogelson, A.L.; Wright, G.B.; Keener, J.P. An Interface-Capturing Regularization Method for Solving the Equations for Two-Fluid Mixtures. Commun. Comput. Phys. 2013, 14, 1322–1346. [Google Scholar] [CrossRef] [Green Version]
- Leveque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Lewis, O.L.; Keener, J.P.; Fogelson, A.L. A physics-based model for maintenance of the pH gradient in the gastric mucus layer. Am. J. Physiol. Gastrointest. Liver Physiol. 2017, 313, G599–G612. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Value |
|---|---|
| −45 | |
| 25 | |
| −0.5 | |
| 0 | |
| N | 6 |
| inner | 0.5 |
| bath | |
| Total bath Ca | 1 mM |
| Total bath Na | 0.2–200 mM |
| Total bath Cl | 0.2–202 mM |
| cm/s | |
| cm/s | |
| cm/s |
| Parameter | , | , | , | , |
|---|---|---|---|---|
| Dense Binding | Sparse Binding | Dense Binding | Sparse Binding | |
| Total inner Ca | 250 mM | mM | 250 mM | mM |
| Total inner Na | 5 mM | 1 mM | 5 mM | 1 mM |
| Total inner Cl | 5 mM | mM | 5 mM | mM |
| Ms | Ms | Ms | Ms | |
| s | s | s | s | |
| Ms | Ms | Ms | Ms | |
| s | s | s | s | |
| 1 M | 0.1 M | 1 M | 0.1 M |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewis, O.L.; Keener, J.P.; Fogelson, A.L. Electrodiffusion-Mediated Swelling of a Two-Phase Gel Model of Gastric Mucus. Gels 2018, 4, 76. https://doi.org/10.3390/gels4030076
Lewis OL, Keener JP, Fogelson AL. Electrodiffusion-Mediated Swelling of a Two-Phase Gel Model of Gastric Mucus. Gels. 2018; 4(3):76. https://doi.org/10.3390/gels4030076
Chicago/Turabian StyleLewis, Owen L., James P. Keener, and Aaron L. Fogelson. 2018. "Electrodiffusion-Mediated Swelling of a Two-Phase Gel Model of Gastric Mucus" Gels 4, no. 3: 76. https://doi.org/10.3390/gels4030076





