Spatial Estimation of Snow Water Equivalent for Glaciers and Seasonal Snow in Iceland Using Remote Sensing Snow Cover and Albedo
Abstract
:1. Introduction
2. Study Area
3. Data and Methods
3.1. Meteorological In Situ Data
3.2. Glacier Surface Mass Balance Data
3.3. Snow Cover and Albedo Data
3.4. Seasonal Snow Data
3.5. Model Forcing
3.6. SWE Reconstruction Model
3.7. Cold Content
4. Evaluation
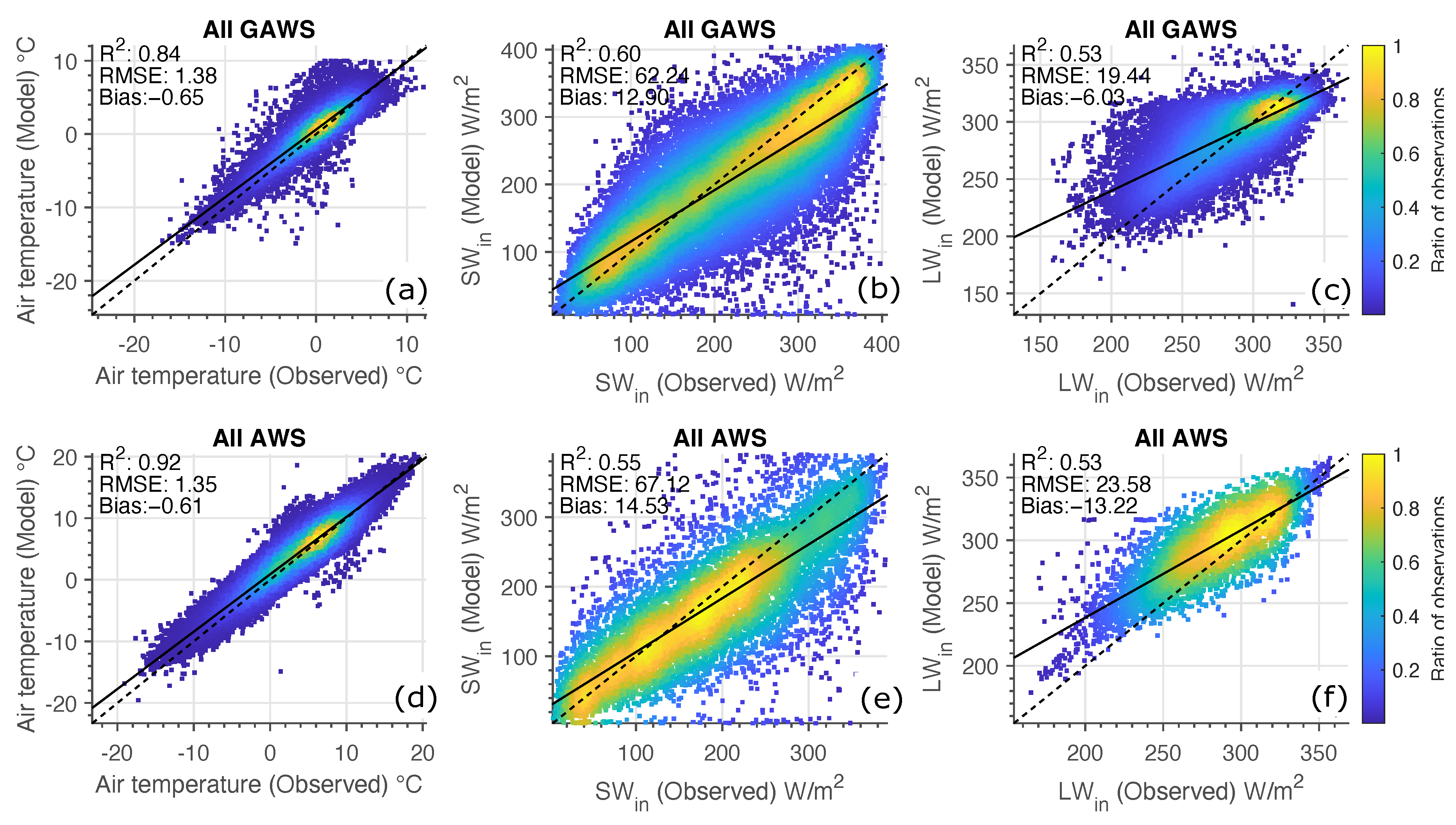
4.1. Energy Balance Components
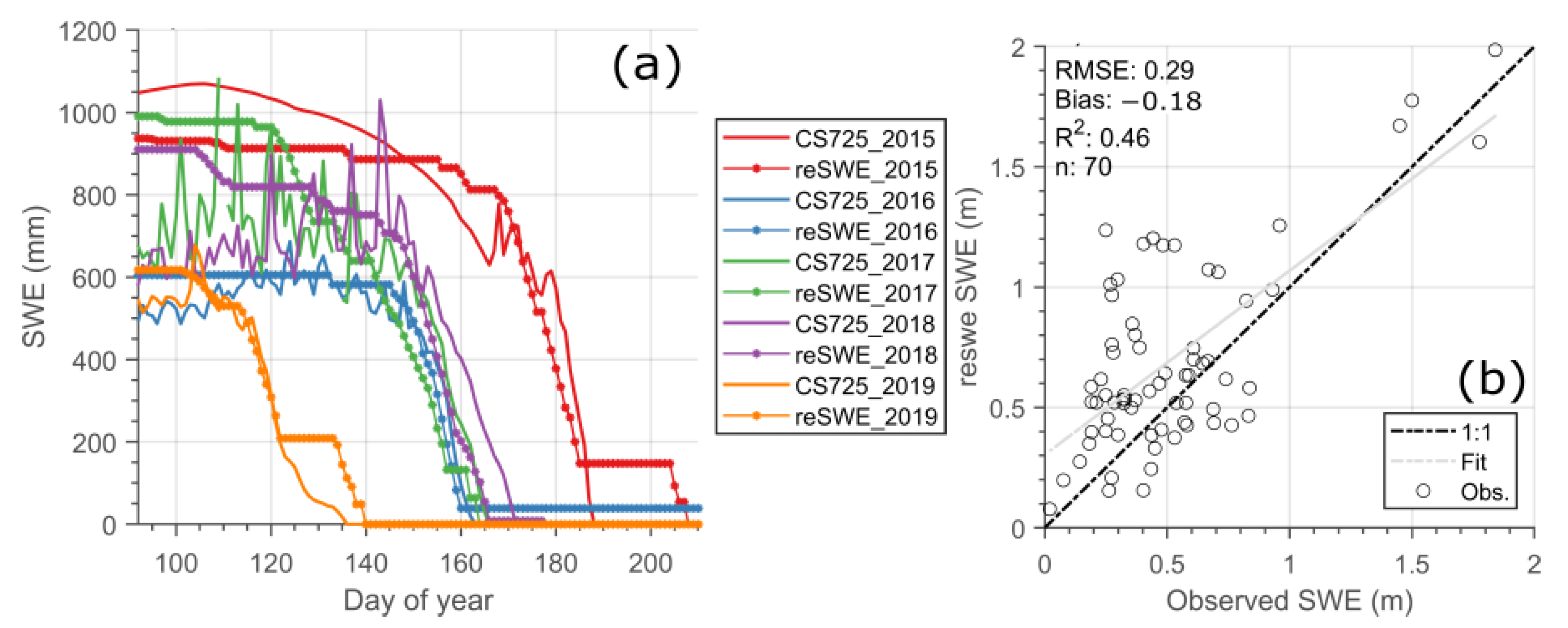
4.2. Summer Mass Balance for Glaciers
4.3. Seasonal Snow
5. Results
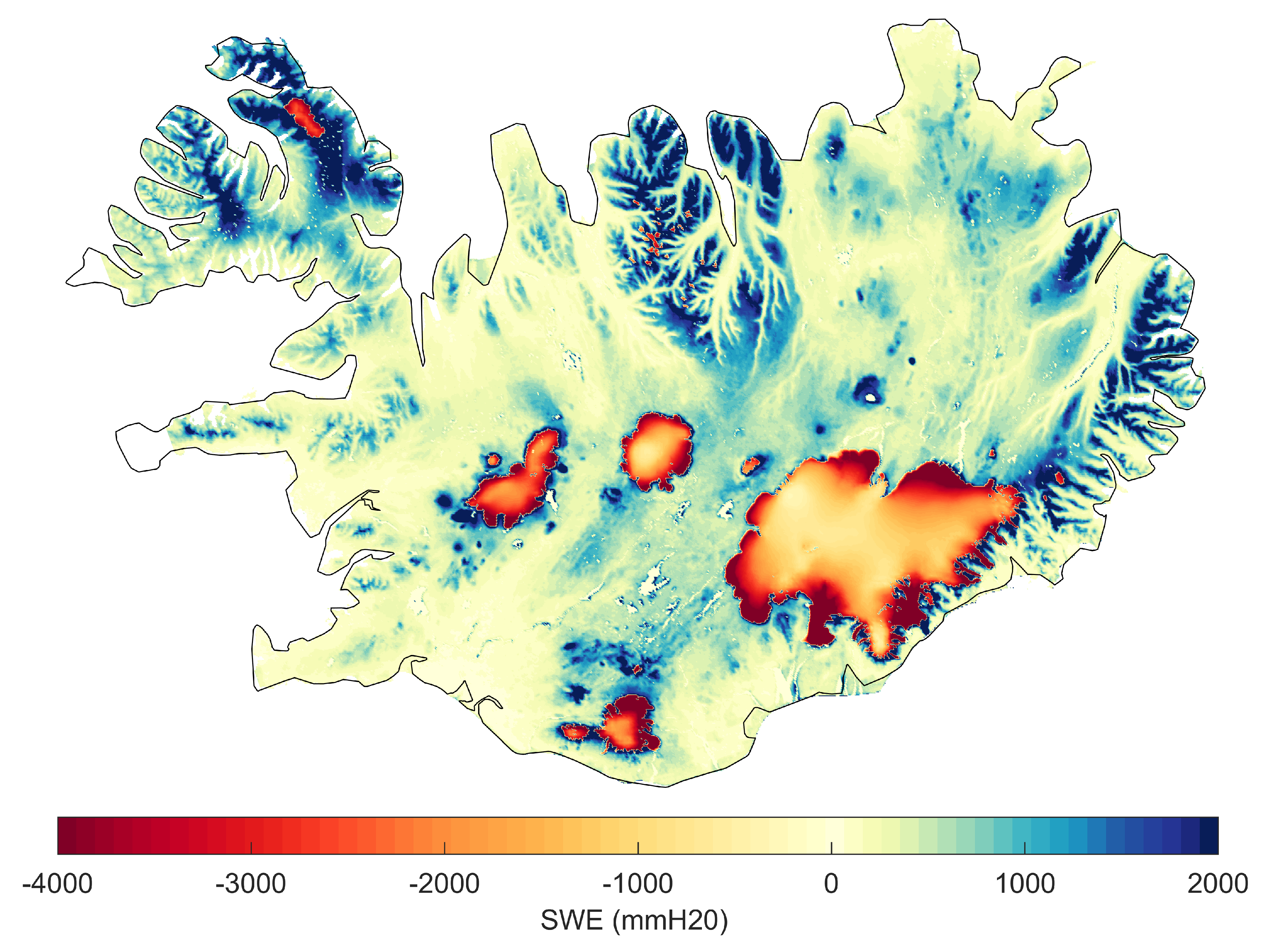
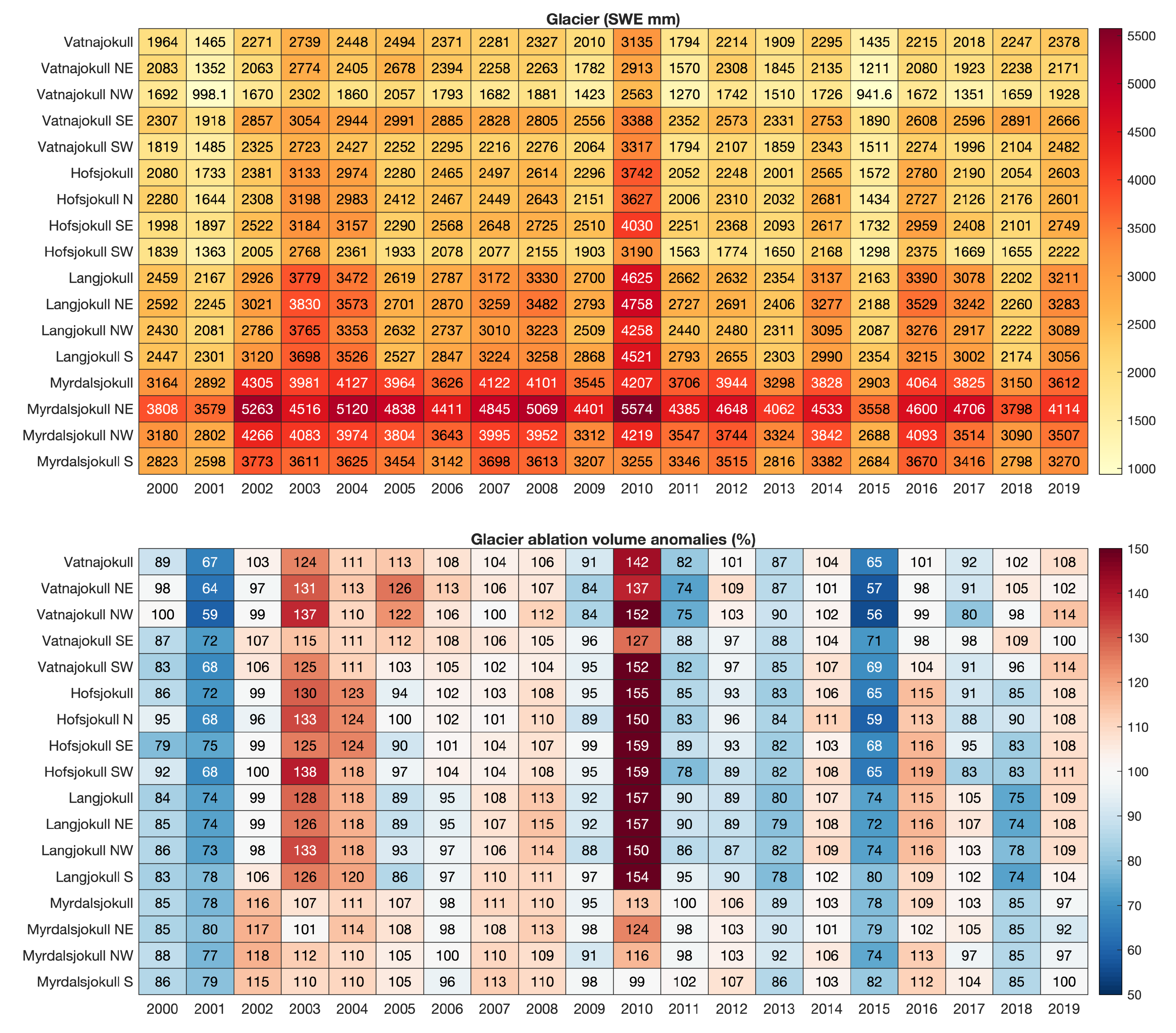
5.1. General Spatio-Temporal Characteristics of SWE
5.2. Inter-Annual Variability of SWE
5.3. Melt Trends
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Automatic Weather Station Statistics
| Lat. | Lon. | Ele. | Site Name | ID | N. T obs. | N. SW obs. | N. LW obs. |
|---|---|---|---|---|---|---|---|
| 63.979 | 21.6556 | 530 | Bláfjöll úrk. | L | 3313 | ||
| 63.969 | 21.666 | 530 | Bláfjöll | L | 3617 | ||
| 63.983 | 21.649 | 530 | Bláfjallaskáli | L | 3359 | ||
| 64.033 | 21.366 | 380 | Hellisskarð | L | 3412 | ||
| 64.055 | 21.253 | 360 | Ölkelduháls | L | 3434 | ||
| 64.056 | 21.346 | 597 | Skarðsmýrarfjall | L | 2451 | ||
| 64.240 | 21.463 | 771 | Skálafell | L | 3286 | ||
| 64.490 | 21.762 | 480 | Skarðsheiði Miðf. | L | 1734 | ||
| 64.452 | 21.403 | 500.5 | Botnsheiði | L | 3264 | ||
| 65.604 | 23.990 | 350 | Patreksfjörður | L | 861 | ||
| 65.552 | 21.825 | 377 | Arnkatla | L | 1072 | ||
| 65.578 | 21.322 | 282 | Ennishöfði | L | 704 | ||
| 65.656 | 23.002 | 510 | Þingmannaheiði | L | 236 | ||
| 66.044 | 23.307 | 753 | Þverfjall | L | 3571 | ||
| 66.075 | 23.198 | 550 | Seljalandsdalur | L | 3410 | ||
| 66.068 | 23.210 | 283 | Seljalandsdalur | L | 2611 | ||
| 65.123 | 20.696 | 383 | Austurárdalsháls | L | 1558 | ||
| 65.062 | 18.838 | 785 | Sáta | L | 3476 | ||
| 65.222 | 20.056 | 509 | Grímstunguheiði | L | 1203 | ||
| 65.313 | 19.847 | 490 | Auðkúluheiði Fri. | L | 420 | ||
| 65.230 | 19.717 | 506 | Kolka | L | 3557 | 944 | 944 |
| 65.341 | 17.243 | 405 | Svartárkot | L | 2939 | ||
| 65.748 | 18.001 | 580 | Vaðlaheiði | L | 3593 | ||
| 65.787 | 17.003 | 390 | Gæsafjöll | L | 1624 | ||
| 65.891 | 17.228 | 350 | Sóleyjarflatamelar | L | 1640 | ||
| 65.856 | 17.201 | 390 | Rauðhálsar | L | 721 | ||
| 65.060 | 16.210 | 563 | Upptyppingar | L | 3447 | ||
| 65.265 | 14.032 | 400 | Seyðisfjörður Kb. | L | 2280 | ||
| 65.223 | 14.258 | 949 | Gagnheiði | L | 3461 | ||
| 65.619 | 16.976 | 282 | Mývatn | L | 3615 | 2171 | 0 |
| 65.629 | 16.837 | 347 | Bjarnarflag | L | 1503 | ||
| 65.642 | 16.128 | 390 | Grímsstaðir á Fjöllum | L | 1268 | ||
| 65.710 | 16.878 | 560 | Reykjahlíðarheiði | L | 376 | ||
| 65.694 | 16.774 | 455 | Krafla | L | 1436 | ||
| 65.911 | 16.976 | 311 | Þeistareykir | L | 2535 | ||
| 65.375 | 15.883 | 450 | Möðrudalur | L | 2786 | ||
| 64.828 | 16.089 | 748 | Brúaröræfi | L | 2339 | ||
| 64.816 | 15.322 | 750 | Innri Sauðá | L | 726 | 554 | 554 |
| 64.798 | 14.789 | 590 | Líkárvatn | L | 1285 | ||
| 64.728 | 16.111 | 845 | Brúarjökull B10 | L | 2365 | 2392 | 2392 |
| 64.928 | 15.777 | 639 | Kárahnjúkar | L | 3617 | 527 | 527 |
| 65.108 | 15.529 | 373 | Brú á Jökuldal | L | 3615 | ||
| 64.815 | 15.423 | 655 | Eyjabakkar | L | 3617 | ||
| 65.079 | 14.674 | 573 | Hallormsstaðaháls | L | 3617 | ||
| 65.036 | 14.571 | 300 | Þórudalur | L | 336 | ||
| 64.995 | 14.510 | 300 | Brúðardalur | L | 2024 | ||
| 65.000 | 14.462 | 500 | Þórdalsheiði | L | 2360 | ||
| 65.018 | 14.453 | 640 | Hallsteinsdalsvarp | L | 2111 | ||
| 65.043 | 14.162 | 281 | Ljósá í Reyðarfirði | L | 734 | ||
| 65.161 | 13.688 | 559 | Neskaupstaður | L | 2666 | ||
| 63.775 | 19.677 | 870 | Tindfjöll | L | 2199 | ||
| 64.098 | 18.614 | 675 | Lónakvísl | L | 3474 | ||
| 64.025 | 18.119 | 555 | Laufbali | L | 3310 | ||
| 64.199 | 19.030 | 555 | Vatnsfell I | L | 454 | ||
| 64.195 | 19.046 | 539 | Vatnsfell | L | 2666 | ||
| 64.395 | 18.504 | 647 | Veiðivatnahraun | L | 3608 | 0 | 0 |
| 64.317 | 18.217 | 726 | Jökulheimar | L | 3601 | 2528 | 888 |
| 64.680 | 19.282 | 925 | Kerlingarfjöll | L | 336 | ||
| 64.604 | 19.018 | 693 | Setur | L | 3602 | 512 | 512 |
| 64.581 | 18.598 | 620 | Þúfuver | L | 3617 | ||
| 64.571 | 18.111 | 819 | Hágöngur | L | 2773 | ||
| 64.866 | 19.562 | 641 | Hveravellir | L | 3193 | ||
| 64.933 | 17.983 | 820 | Sandbúðir | L | 3579 | ||
| 64.133 | 19.725 | 279 | Haf við Ísakot | L | 422 | ||
| 66.063 | 18.630 | 450 | Ólafsfjörður | L | 2211 | ||
| 66.168 | 23.268 | 500 | Bolungarvík | L | 2327 | ||
| 66.152 | 18.936 | 546 | Fífladalir | L | 497 | ||
| 66.153 | 18.937 | 600 | Fífladalir | L | 38 | ||
| 66.153 | 18.935 | 550 | Siglufjörður | L | 2126 | ||
| 64.503 | 17.234 | 1689 | Dyngjujökull | G | 484 | ||
| 64.538 | 15.597 | 1141 | Hoff | G | 1688 | 1774 | |
| 64.514 | 20.450 | 588 | L01 | G | 2246 | 2254 | 2254 |
| 64.302 | 17.153 | 1207 | Ske02 | G | 37 | 39 | 39 |
| 64.728 | 16.111 | 779 | B10 | G | 3224 | 3296 | 3215 |
| 64.575 | 16.328 | 1216 | B13 | G | 2043 | 2725 | 2338 |
| 64.402 | 16.681 | 1526 | B16 | G | 2575 | 2730 | 2569 |
| 64.417 | 17.319 | 1405 | Grímsvötn | G | 2687 | 791 | |
| 64.182 | 16.335 | 528 | Br04 | G | 597 | 600 | |
| 64.368 | 16.282 | 1242 | Br07 | G | 395 | 397 | |
| 64.325 | 18.117 | 771 | T01 | G | 483 | 567 | 567 |
| 64.336 | 17.976 | 1068 | T03 | G | 1943 | 2586 | 2094 |
| 64.404 | 17.608 | 1466 | T06 | G | 2538 | 2632 | 1691 |
| 64.639 | 17.522 | 1945 | Bard | G | 1509 | 898 | |
| 64.406 | 17.267 | 1724 | Grímsfjall | G | 2495 | 1324 | |
| 63.611 | 19.158 | 1345 | MyrA | G | 385 | 413 | |
| 64.594 | 20.374 | 1095 | L05 | G | 2536 | 2544 | 2544 |
| 64.770 | 18.543 | 840 | HNA09 | G | 292 | 307 | 307 |
| 64.813 | 18.648 | 1235 | HNA13 | G | 294 | 307 | 307 |
| 64.677 | 15.581 | 766 | E01 | G | 106 | 121 | 121 |
| 64.611 | 15.615 | 1190 | E03 | G | 115 | 122 | 122 |
References
- Rittger, K.; Bair, E.H.; Kahl, A.; Dozier, J. Spatial estimates of snow water equivalent from reconstruction. Adv. Water Resour. 2016, 94, 345–363. [Google Scholar] [CrossRef]
- Sandoval-Solis, S. Water Resources Management in California; Springer International Publishing: Cham, Switzerland, 2020; pp. 35–44. [Google Scholar] [CrossRef]
- Elder, K.; Dozier, J.; Michaelsen, J. Snow accumulation and distribution in an Alpine Watershed. Water Resour. Res. 1991, 27, 1541–1552. [Google Scholar] [CrossRef]
- Elder, K.; Rosenthal, W.; Davis, R.E. Estimating the spatial distribution of snow water equivalence in a montane watershed. Hydrol. Process. 1998, 12, 1793–1808. [Google Scholar] [CrossRef]
- Einarsson, M.A. Climates of the Oceans, H. Van Loon (Ed.). Vol. 15 of World Survey of Climatology, Editor-in-Chief H. E. Landsberg. J. Climatol. 1984, 5, 673–697. [Google Scholar] [CrossRef]
- Perkins, H.; Hopkins, T.S.; Malmberg, S.A.; Poulain, P.M.; Warn-Varnas, A. Oceanographic conditions east of Iceland. J. Geophys. Res. Ocean. 1998, 103, 21531–21542. [Google Scholar] [CrossRef]
- Crochet, P.; Jóhannesson, T.; Jónsson, T.; Sigurðsson, O.; Björnsson, H.; Pálsson, F.; Barstad, I. Estimating the Spatial Distribution of Precipitation in Iceland Using a Linear Model of Orographic Precipitation. J. Hydrometeorol. 2007, 8, 1285–1306. [Google Scholar] [CrossRef]
- Hannesdóttir, H.; Sigurðsson, O.; Þrastarson, R.H.; Guðmundsson, S.; Belart, J.M.; Pálsson, F.; Magnússon, E.; Víkingsson, S.; Kaldal, I.; Jóhannesson, T. A national glacier inventory and variations in glacier extent in Iceland from the Little Ice Age maximum to 2019. Jökull 2020, 12, 1–34. [Google Scholar] [CrossRef]
- Hjaltason, S.; Guðmundsdóttir, M.; Haukdal, J.Á.; Guðmundsson, J.R. Energy Statistics in Iceland 2019; Technical Report; Orkustofnun: Reykjavík, Iceland, 2020. [Google Scholar]
- Jóhannesson, T.; Aðalgeirsdóttir, G.; Björnsson, H.; Crochet, P.; Elíasson, E.B.; Guðmundsson, S.; Jónsdóttir, J.; Ólafsson, H.; Pálsson, F.; Rögnvaldsson, Ó.; et al. Effect of Climate Change on Hydrology and Hydro-Resources in Iceland; Orkustofnun: Reykjavík, Iceland, 2007. [Google Scholar]
- Pálsson, F.; Gunnarsson, A.; Jónsson, G.; Pálsson, H.S.; Steinþórsson, S. Vatnajökull: Mass Balance, Meltwater Drainage and Surface Velocity of the Glacial Year 2018–2019; LV-2020-016; Landsvirkjun: Reykjavík, Iceland, 2020; pp. 1–56. [Google Scholar]
- Björnsson, H.; Sigurðsson, B.D.; Davíðsdóttir, B.; Ólafsson, J.S.; Ástþórsson, Ó.S.; Ólafsdóttir, S.; Baldursson, T.; Jónsson, T. Loftslagsbreytingar og áhrif þeirra á Íslandi: Skýrsla Vísindanefndar um Loftslagsbreytingar 2018; Veðurstofa Íslands: Reykjavík, Iceland, 2018; pp. 1–238. [Google Scholar]
- Schmidt, L.S.; Ađalgeirsdóttir, G.; Pálsson, F.; Langen, P.L.; Guđmundsson, S.; Björnsson, H. Dynamic simulations of Vatnajökull ice cap from 1980 to 2300. J. Glaciol. 2020, 66, 97–112. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573. [Google Scholar] [CrossRef]
- Björnsson, H.; Thorsteinsson, T. Climate Change and Energy Systems: Impacts, Risks and Adaptation in the Nordic and Baltic Countries; TemaNord, Nordic Council of Ministers: Copenhagen, Denmark, 2012. [Google Scholar] [CrossRef]
- Sveinsson, Ó. Energy in Iceland: Adaptation to Climate Change; UNU-FLORES Policy Briefs, United Nations University Institute for Integrated Management of Material Fluxes and of Resources (UNU-FLORES): Dresden, Germany, 2016. [Google Scholar]
- Ágústsson, H.; Hannesdóttir, H.; Thorsteinsson, T.; Pálsson, F.; Oddsson, B. Mass balance of Mýrdalsjökull ice cap accumulation area and comparison of observed winter balance with simulated precipitation. Jökull 2013, 63, 91–104. [Google Scholar] [CrossRef]
- Þorsteinsson, Þ.; Jóhannesson, T.; Sigurðsson, O.; Einarsson, B. Afkomumælingar á Hofsjökli 1988–2017; 2017-016; Veðurstofa Íslands: Reykjavík, Iceland, 2017; pp. 1–82. [Google Scholar]
- Pálsson, F.; Gunnarsson, A.; Pálsson, H.S.; Steinþórsson, S. Vatnajökull: Mass Balance, Meltwater Drainage and Surface Velocity of the Glacial Year 2020–2021; LV-2022-09; Landsvirkjun: Reykjavík, Iceland, 2022; pp. 1–62. [Google Scholar]
- Pálsson, F.; Gunnarsson, A.; Pálsson, H.S.; Steinþórsson, S. Afkomu- og Hraðamælingar á Langjökli Jökulárið 2018–2019; LV-2020-017; Landsvirkjun: Reykjavík, Iceland, 2020. [Google Scholar]
- Jónsson, T. Langtímasveiflur I, Snjóhula og Snjókoma; Greinargerð 02035; Veðurstofa Íslands: Reykjavík, Iceland, 2002; pp. 1–25. [Google Scholar]
- Jónsson, T.; Jónasson, K. Fimmtíu ára Snjódýpt á Íslandi; Greinargerð VÍ-G97025-ÚR20; Veðurstofa Íslands: Reykjavík, Iceland, 1997; pp. 1–25. [Google Scholar]
- Jóhannesson, T.; Sigurðsson, O. Samantekt um Snjómælingar á Hálendi Íslands; 2014-01; Veðurstofa Íslands: Reykjavík, Iceland, 2014; pp. 1–21. [Google Scholar]
- Sigurðsson, F.H.; Pálsdóttir, T.; Antonsson, T.K. Veðurstöð og Veðurfar á Hveravöllum á Kili; Rit Veðurstofu Íslands 20; Veðurstofa Íslands: Reykjavík, Iceland, 2003. [Google Scholar]
- Rist, S. Snjómæling Inni á Hálendinu Úrkomumælingar; Skilagrein 164; Vatnamælingar, Raforkumálastjóri: Reykjavík, Iceland, 1958; pp. 1–9. [Google Scholar]
- Rist, S. Snjómælingar vetur 1965/1966; Skilagrein 292; Vatnamælingar, Raforkumálastjóri: Reykjavík, Iceland, 1966; p. 1. [Google Scholar]
- Rist, S. Afstæð Snjódýptarmæling á Hálendinu; SR-81/03; Orkustofnun: Reykjavík, Iceland, 1981; pp. 1–4. [Google Scholar]
- Sigurðsson, O. Fyrirkomulag Snjómælinga á Hálendi Íslands; Greinargerð OSig-2002/03; Orkustofnun: Reykjavík, Iceland, 2002; pp. 1–3. [Google Scholar]
- Martinec, J.; Rango, A. Areal distribution of snow water equivalent evaluated by snow cover monitoring. Water Resour. Res. 1981, 17, 1480–1488. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Lundquist, J.D. Comparing and combining SWE estimates from the SNOW-17 model using PRISM and SWE reconstruction. Water Resour. Res. 2012, 48, W01506. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- Bair, E.H.; Abreu Calfa, A.; Rittger, K.; Dozier, J. Using machine learning for real-time estimates of snow water equivalent in the watersheds of Afghanistan. Cryosphere 2018, 12, 1579–1594. [Google Scholar] [CrossRef]
- Adam, J.C.; Lettenmaier, D.P. Adjustment of global gridded precipitation for systematic bias. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Adam, J.C.; Clark, E.A.; Lettenmaier, D.P.; Wood, E.F. Correction of Global Precipitation Products for Orographic Effects. J. Clim. 2006, 19, 15–38. [Google Scholar] [CrossRef]
- Cline, D.W.; Bales, R.C.; Dozier, J. Estimating the spatial distribution of snow in mountain basins using remote sensing and energy balance modeling. Water Resour. Res. 1998, 34, 1275–1285. [Google Scholar] [CrossRef]
- Molotch, N.P.; Painter, T.H.; Bales, R.C.; Dozier, J. Incorporating remotely-sensed snow albedo into a spatially-distributed snowmelt model. Geophys. Res. Lett. 2004, 31, L03501. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of subpixel snow covered area, grain size, and albedo from MODIS. Remote Sens. Environ. 2009, 113, 868–879. [Google Scholar] [CrossRef]
- Schneider, D.; Molotch, N.P. Real-time estimation of snow water equivalent in the Upper Colorado River Basin using MODIS-based SWE Reconstructions and SNOTEL data. Water Resour. Res. 2016, 52, 7892–7910. [Google Scholar] [CrossRef]
- Magnússon, E.; Belart, J.M.; Pálsson, F.; Anderson, L.S.; Gunnlaugsson, Á.Þ.; Berthier, E.; Ágústsson, H.; Geirsdóttir, Á. The subglacial topography of Drangajökull ice cap, NW-Iceland, deduced from dense RES-profiling. Jökull 2016, 66, 1–26. [Google Scholar] [CrossRef]
- Björnsson, H. Hydrology of Ice Caps in Volcanic Regions; Reykjavík Vísindafélag Íslendinga: Reykjavík, Iceland, 1988. [Google Scholar]
- Björnsson, H.; Pálsson, F.; Guðmundsson, M.T. Surface and bedrock topography of the Mýrdalsjökull ice cap, Iceland: The Katla caldera, eruption sites and routes of jökulhlaups. Jökull 2000, 49, 29–46. [Google Scholar] [CrossRef]
- Pálsson, F.; Guðmundsson, S.; Björnsson, H. Afkomu- Og Hraðamælingar á Langjökli Jökulárið 2011–2012; Technical Report LV-2015-076; Institute Earth Science, Univeristy Iceland and Landsvirkjun: Reykjavík, Iceland, 2013. [Google Scholar]
- Pálsson, F.; Gunnarsson, A.; Jónsson, G.; Pálsson, H.S.; Steinþórsson, S. Vatnajökull: Mass Balance, Meltwater Drainage and Surface Velocity of the Glacial Year 2014–2015; LV-2016-031; Landsvirkjun: Reykjavík, Iceland, 2016; pp. 1–64. [Google Scholar]
- Gunnarsson, A.; Gardarsson, S.M.; Pálsson, F.; Jóhannesson, T.; Sveinsson, O.G.B. Annual and inter-annual variability and trends of albedo of Icelandic glaciers. Cryosphere 2021, 15, 547–570. [Google Scholar] [CrossRef]
- Van den Broeke, M.; Reijmer, C.H.; Van De Wal, R.S. A study of the surface mass balance in Dronning Maud Land, Antarctica, using automatic weather stations. J. Glaciol. 2004, 50, 565–582. [Google Scholar] [CrossRef]
- Van den Broeke, M.; van As, D.; Reijmer, C.; Wal, R. Assessing and Improving the Quality of Unattended Radiation Observations in Antarctica. J. Atmos. Ocean. Technol. 2004, 21. [Google Scholar] [CrossRef]
- Gunnarsson, A.; Pálsson, F.; Aðalgeirsdóttir, G.; Björnsson, H.; Guðmundsson, S. Monitoring Energy Balance of Icelandic Glaciers for 25 years. In Proceedings of the 27th IUGG General Assembly, Montréal, QC, Canada, 8–18 July 2019. IUGG19-3435. [Google Scholar]
- Wang, L.; Qu, J.J.; Xiong, X.; Hao, X.; Xie, Y.; Che, N. A new method for retrieving band 6 of aqua MODIS. IEEE Geosci. Remote Sens. Lett. 2006, 3, 267–270. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.; Poli, P.; Brugge, R.; Fielding, M.; Fuentes, M.; Kållberg, P.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim Archive Version 2.0; ECMWF: Reading, UK, 2011; Volume 23. [Google Scholar]
- Rögnvaldsson, Ó.A. RÁVII: Tæknileg útfærsla á Niðurkvörðun á Íslandsveðri; Technical Repor; Belgingur-Reiknistofa í Veðurfræði: Reukjavik, Iceland, 2016. [Google Scholar]
- Crochet, P.; Jóhannesson, T. A data set of gridded daily temperature in Iceland, 1949–2010. Jökull 2011, 61, 1–17. [Google Scholar] [CrossRef]
- Nawri, N.; Björnsson, H.; Petersen, G.N.; Jónasson, K. Empirical Terrain Models for Surface Wind and Air Temperature over Iceland, VÍ, 2012-009; Veðurstofa Íslands: Reykjavík, Iceland, 2012. [Google Scholar]
- Gardner, A.S.; Sharp, M.J.; Koerner, R.M.; Labine, C.; Boon, S.; Marshall, S.J.; Burgess, D.O.; Lewis, D. Near-Surface Temperature Lapse Rates over Arctic Glaciers and Their Implications for Temperature Downscaling. J. Clim. 2009, 22, 4281–4298. [Google Scholar] [CrossRef]
- Hodgkins, R.; Carr, S.; Pálsson, F.; Guðmundsson, S.; Björnsson, H. Modelling variable glacier lapse rates using ERA-Interim reanalysis climatology: An evaluation at Vestari- Hagafellsjökull, Langjökull, Iceland. Int. J. Climatol. 2013, 33, 410–421. [Google Scholar] [CrossRef]
- Plüss, C.; Ohmura, A. Longwave Radiation on Snow-Covered Mountainous Surfaces. J. Appl. Meteorol. 1997, 36, 818–824. [Google Scholar] [CrossRef]
- Ohmura, A. Physical Basis for the Temperature-Based Melt-Index Method. J. Appl. Meteorol. 2001, 40, 753–761. [Google Scholar] [CrossRef]
- Gunnarsson, A.; Gardarsson, S.M.; Pálsson, F. Modeling of surface energy balance for Icelandic glaciers using remote sensing albedo. EGUsphere 2022, 2022, 1–43. [Google Scholar] [CrossRef]
- Brubaker, K.; Rango, A.; Kustas, W. Incorporating radiation inputs into the snowmelt runoff model. Hydrol. Process. 1996, 10, 1329–1343. [Google Scholar] [CrossRef]
- Dozier, J.; Warren, S.G. Effect of viewing angle on the infrared brightness temperature of snow. Water Resour. Res. 1982, 18, 1424–1434. [Google Scholar] [CrossRef]
- Jepsen, S.M.; Molotch, N.P.; Williams, M.W.; Rittger, K.E.; Sickman, J.O. Interannual variability of snowmelt in the Sierra Nevada and Rocky Mountains, United States: Examples from two alpine watersheds. Water Resour. Res. 2012, 48, W02529. [Google Scholar] [CrossRef]
- Guan, B.; Molotch, N.P.; Waliser, D.E.; Jepsen, S.M.; Painter, T.H.; Dozier, J. Snow water equivalent in the Sierra Nevada: Blending snow sensor observations with snowmelt model simulations. Water Resour. Res. 2013, 49, 5029–5046. [Google Scholar] [CrossRef]
- Bair, E.H.; Rittger, K.; Davis, R.E.; Painter, T.H.; Dozier, J. Validating reconstruction of snow water equivalent in California’s Sierra Nevada using measurements from the NASA Airborne Snow Observatory. Water Resour. Res. 2016, 52, 8437–8460. [Google Scholar] [CrossRef]
- Huai, B.; van den Broeke, M.R.; Reijmer, C.H. Long-term surface energy balance of the western Greenland Ice Sheet and the role of large-scale circulation variability. Cryosphere 2020, 14, 4181–4199. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Landry, C.C.; Hayashi, M.; Quinton, W.L.; Lundquist, J.D. Approximating snow surface temperature from standard temperature and humidity data: New possibilities for snow model and remote sensing evaluation. Water Resour. Res. 2013, 49, 8053–8069. [Google Scholar] [CrossRef]
- Cogley, J.; Arendt, A.; Bauder, A.; Braithwaite, R.; Hock, R.; Jansson, P.; Kaser, G.; Moller, M.; Nicholson, L.; Rasmussen, L.; et al. Glossary of Glacier Mass Balance and Related Terms; Vol. 86, IHP-VII Technical Documents in Hydrology; International Hydrological Programme: Paris, France, 2010. [Google Scholar]
- Jennings, K.S.; Kittel, T.G.F.; Molotch, N.P. Observations and simulations of the seasonal evolution of snowpack cold content and its relation to snowmelt and the snowpack energy budget. Cryosphere 2018, 12, 1595–1614. [Google Scholar] [CrossRef]
- Schmidt, L.S.; Aðalgeirsdóttir, G.; Guðmundsson, S.; Langen, P.L.; Pálsson, F.; Mottram, R.; Gascoin, S.; Björnsson, H. The importance of accurate glacier albedo for estimates of surface mass balance on Vatnajökull: Evaluating the surface energy budget in a regional climate model with automatic weather station observations. Cryosphere 2017, 11, 1665–1684. [Google Scholar] [CrossRef]
- Dragosics, M.; Meinander, O.; Jónsdóttír, T.; Dürig, T.; De Leeuw, G.; Pálsson, F.; Dagsson-Waldhauserová, P.; Thorsteinsson, T. Insulation effects of Icelandic dust and volcanic ash on snow and ice. Arab. J. Geosci. 2016, 9, 126. [Google Scholar] [CrossRef]
- Schmidt, L.S.; Langen, P.L.; Aðalgeirsdóttir, G.; Pálsson, F.; Guðmundsson, S.; Gunnarsson, A. Sensitivity of Glacier Runoff to Winter Snow Thickness Investigated for Vatnajökull Ice Cap, Iceland, Using Numerical Models and Observations. Atmosphere 2018, 9, 450. [Google Scholar] [CrossRef]





| Land | Glacier | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | ID | Name | Area | Area | Ratio | ||||||
| km | m a.s.l. | km | m a.s.l. | - | |||||||
| NE | AF | Austfirðir | 4115 | 438 | 1180 | 0 | 20 | 1073 | 1208 | 925 | <1% |
| NE | LA | Lagarfljótsós | 6569 | 532 | 1532 | 0 | 1658 | 1236 | 1791 | 629 | 25% |
| NE | JF | Jökulsá á Fjöllum | 6690 | 571 | 1822 | 0 | 1626 | 1366 | 1988 | 674 | 24% |
| NE | SF | Skjálfandafljót | 4422 | 668 | 1690 | 0 | 106 | 1472 | 1969 | 1041 | 2% |
| N | TR | Tröllaskagi | 3404 | 560 | 1432 | 0 | 83 | 1070 | 1394 | 812 | 2% |
| N | VH | Vestari Héraðsvötn | 3793 | 651 | 1321 | 0 | 250 | 1280 | 1789 | 830 | 6% |
| N | BL | Blanda | 2533 | 570 | 1136 | 0 | 237 | 1353 | 1789 | 837 | 9% |
| W | ST | Strandir | 3541 | 328 | 827 | 0 | 161 | 658 | 914 | 213 | 4% |
| W | VF | Vestfirðir | 5029 | 365 | 957 | 0 | - | - | - | - | - |
| SW | HB | Hvítá í Borgarfirði | 3844 | 399 | 1431 | 0 | 325 | 1169 | 1664 | 701 | 8% |
| SW | OA | Ölfusá | 6357 | 397 | 1375 | 0 | 691 | 1081 | 1715 | 419 | 10% |
| SW | ÞT | Þjórsá | 7830 | 591 | 1518 | 0 | 1041 | 1261 | 1994 | 624 | 13% |
| SW | MF | Markarfljót | 1228 | 524 | 1474 | 0 | 209 | 1078 | 1551 | 294 | 17% |
| SE | KF | Kúðafljót | 1279 | 244 | 1169 | 0 | 218 | 898 | 1387 | 223 | 17% |
| SE | SK | Skaftá | 2323 | 401 | 1084 | 0 | 490 | 1222 | 1758 | 636 | 21% |
| SE | NV | Núpsvötn | 1150 | 424 | 1384 | 0 | 680 | 1123 | 1724 | 93 | 60% |
| SE | GK | Gigjukvisl | 1854 | 121 | 1072 | 0 | 1502 | 1196 | 1724 | 61 | 81% |
| ID | Name | Area | Ratio | |||
|---|---|---|---|---|---|---|
| km2 | m a.s.l. | - | ||||
| Vatnajökull | 8995 | 1223 | 2030 | 0 | - | |
| VNE | NE | 1949 | 1229 | 1888 | 629 | 21% |
| VNW | NW | 1457 | 1406 | 1988 | 729 | 16% |
| VSE | SE | 2273 | 1066 | 2030 | 0 | 24% |
| VSW | SW | 3528 | 1225 | 1994 | 61 | 39% |
| Hofsjökull | 970 | 1252 | 1789 | 624 | - | |
| HN | N | 322 | 1289 | 1789 | 830 | 34% |
| HSE | SE | 453 | 1200 | 1789 | 637 | 47% |
| HSW | SW | 180 | 1346 | 1789 | 735 | 19% |
| Langjökull | 1003 | 1102 | 1435 | 419 | - | |
| LNE | NE | 364 | 1090 | 1435 | 419 | 33% |
| LNW | NW | 368 | 1137 | 1435 | 620 | 35% |
| S | 342 | 1020 | 1400 | 444 | 32% | |
| Mýrdalsjökull | 622 | 1000 | 1485 | 118 | - | |
| MNE | NE | 179 | 893 | 1377 | 223 | 28% |
| MNW | NW | 177 | 1051 | 1455 | 414 | 27% |
| MS | S | 300 | 997 | 1485 | 118 | 45% |
| Drangajökull | 162 | 658 | 914 | 213 | - | |
| DE | E | 62 | 653 | 872 | 297 | 37% |
| DW | W | 104 | 655 | 914 | 186 | 63% |
| Eyj | Eyjafjallajökull | 79 | 1156 | 1564 | 294 | - |
| (°C) | SW (W m) | LW (W m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Period | ID | No. Sites | RMSE | R | Bias | RMSE | R | Bias | RMSE | R | Bias |
| AMJJASO | L | 70 | 1.07 | 0.94 | −0.55 | 49.23 | 0.64 | 11.35 | 16.12 | 0.67 | −14.55 |
| AMJJASO | G | 20 | 1.10 | 0.84 | −0.65 | 55.74 | 0.63 | 14.80 | 13.40 | 0.63 | −6.30 |
| Apr | L | 69 | 1.11 | 0.91 | −1.06 | 33.73 | 0.56 | −3.61 | 9.45 | 0.76 | −16.89 |
| Apr | G | 1 | 1.19 | 0.92 | −0.57 | 45.08 | 0.39 | 6.58 | 18.19 | 0.39 | −31.94 |
| May | L | 69 | 1.14 | 0.88 | −0.99 | 45.77 | 0.56 | 12.26 | 9.19 | 0.79 | −14.75 |
| May | G | 18 | 1.25 | 0.83 | −1.04 | 56.81 | 0.41 | 19.68 | 13.88 | 0.61 | −13.53 |
| Jun | L | 69 | 1.12 | 0.83 | −0.42 | 55.93 | 0.57 | 26.09 | 9.49 | 0.69 | −14.46 |
| Jun | G | 20 | 0.90 | 0.74 | −0.71 | 61.32 | 0.45 | 23.42 | 12.80 | 0.63 | −6.74 |
| Jul | L | 69 | 0.96 | 0.85 | −0.13 | 54.42 | 0.53 | 23.13 | 8.79 | 0.70 | −12.82 |
| Jul | G | 20 | 0.94 | 0.56 | −0.53 | 57.92 | 0.50 | 25.50 | 12.57 | 0.61 | −2.85 |
| Aug | L | 70 | 0.84 | 0.86 | −0.33 | 55.96 | 0.49 | 9.44 | 26.39 | 0.56 | −17.83 |
| Aug | G | 19 | 1.03 | 0.60 | −0.65 | 47.18 | 0.55 | 9.74 | 12.48 | 0.61 | −3.17 |
| Sep | L | 70 | 0.78 | 0.93 | −0.50 | 25.64 | 0.61 | 1.30 | 9.89 | 0.71 | −11.02 |
| Sep | G | 17 | 1.11 | 0.82 | −0.58 | 34.44 | 0.50 | −4.88 | 13.32 | 0.55 | −4.57 |
| Oct | L | 63 | 0.76 | 0.94 | −0.70 | 9.63 | 0.78 | −8.77 | 8.64 | 0.68 | −11.92 |
| Oct | G | 12 | 0.77 | 0.94 | −0.45 | 27.81 | 0.41 | −6.52 | 11.31 | 0.55 | −4.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunnarsson, A.; Gardarsson, S.M. Spatial Estimation of Snow Water Equivalent for Glaciers and Seasonal Snow in Iceland Using Remote Sensing Snow Cover and Albedo. Hydrology 2024, 11, 3. https://doi.org/10.3390/hydrology11010003
Gunnarsson A, Gardarsson SM. Spatial Estimation of Snow Water Equivalent for Glaciers and Seasonal Snow in Iceland Using Remote Sensing Snow Cover and Albedo. Hydrology. 2024; 11(1):3. https://doi.org/10.3390/hydrology11010003
Chicago/Turabian StyleGunnarsson, Andri, and Sigurdur M. Gardarsson. 2024. "Spatial Estimation of Snow Water Equivalent for Glaciers and Seasonal Snow in Iceland Using Remote Sensing Snow Cover and Albedo" Hydrology 11, no. 1: 3. https://doi.org/10.3390/hydrology11010003






