Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
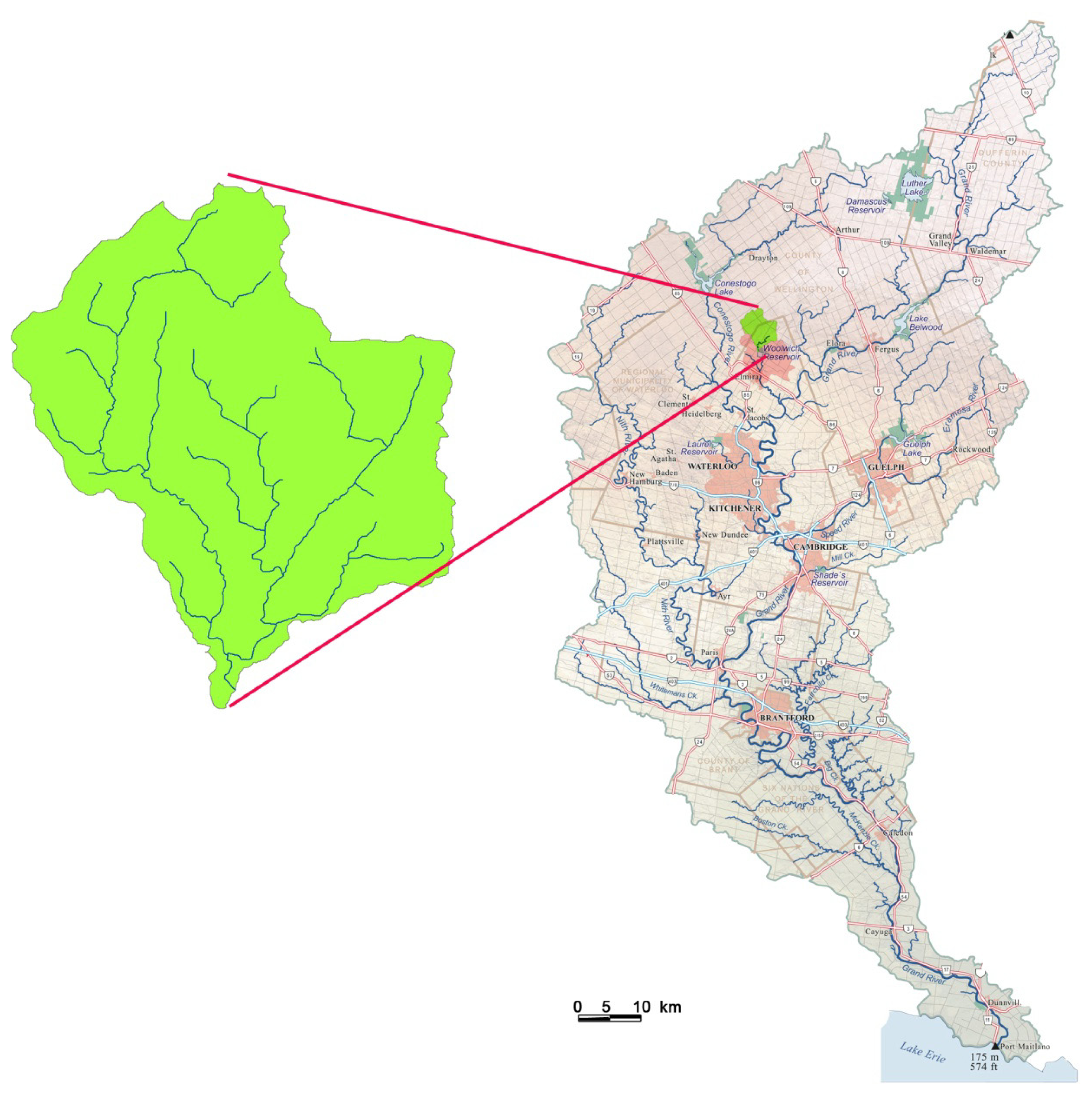

2.2. SWAT Model
2.3. APEX
2.4. MIKE SHE
2.5. Model Performance Evaluation
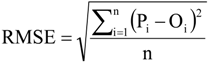
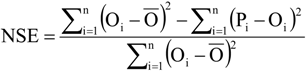
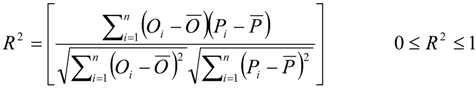
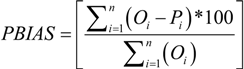
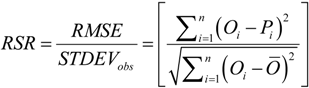
2.6. Model Calibration and Validation
| Description | Default Values | Calibrated Value |
|---|---|---|
| SWAT | ||
| Surface runoff/infiltration approach | curve number | |
| Evapotranspiration approach | Penman–Monteith | |
| Soil evaporation compensation factor | 0.01–1.00 | 1.00 |
| Initial soil water storage expressed as a fraction of field capacity water content | 0.01–1.00 | 0.95 |
| Snowfall temperature (°C) | 1.00 | −2.00 |
| Melt factor for sow on June 21 (mm H2O/°C-day) | 4.5 | 6.90 |
| Melt factor for snow on December 21(mm H2O/°C-day) | 4.5 | 1.40 |
| Snow pack temperature lag factor | 1.0 | 0.20 |
| Minimum snow water content that corresponds to 100% snow cover | 1.00 | 10.00 |
| Snowmelt base temperature (°C) | 0.5 | 0.00 |
| Surface runoff lag coefficient (d) | 0.00–4.00 | 0.20 |
| Curve number coefficient | 0.00–2.00 | 1.5 |
| Manning’s “n” value for overland flow | 0.014 | 0.15, 0.30 or 0.5 |
| Manning’s “n” value for main channel | 0.014 | 0.014 |
| MIKE SHE | ||
| Surface runoff/infiltration approach | diffusive wave approximation of the Saint Venant equations/simplified overland flow routing | |
| Evapotranspiration approach | Kristensen and Jensen methods | |
| Degree-day factor (mm snow/day/°C) | 2.0 | 3.5 |
| Threshold melting temperature (°C) | 0 | 0 |
| Manning’s M | ||
| Urban area | 90.9 | 109.1 |
| Agricultural crops | 5.9 | 7.1 |
| Hay/Pasture | 4.2 | 5.0 |
| Fallow land | 20 | 24 |
| Water | 25 | 30 |
| woodlot | 1.25 | 1.5 |
| APEX | ||
| Surface runoff/infiltration approach | curve number/Green and Ampt | |
| Evapotranspiration approach | Penman–Monteith | |
| Soil evaporation coefficient | 1.50–2.00 | 1.50 |
| Soil evaporation-plant cover factor | 0.01–0.50 | 0.10 |
| Runoff curve number initial abstraction | 0.05–0.40 | 0.20 |
| Groundwater storage threshold | 0.001–0.10 | 0.01 |
| SCS curve number index coefficient | 0.20–2.50 | 2.50 |
| Peak runoff rate-rainfall energy adjustment factor | 0.00–1.00 | 1.00 |
3. Results and Discussion
| Indicator | Calibration Period | Validation Period | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Hydrologic Year | 1994–95 | 1995–96 | 1996–97 | 1997–98 | 1990–91 | 1991–92 | 1992–93 | 1993–94 | |
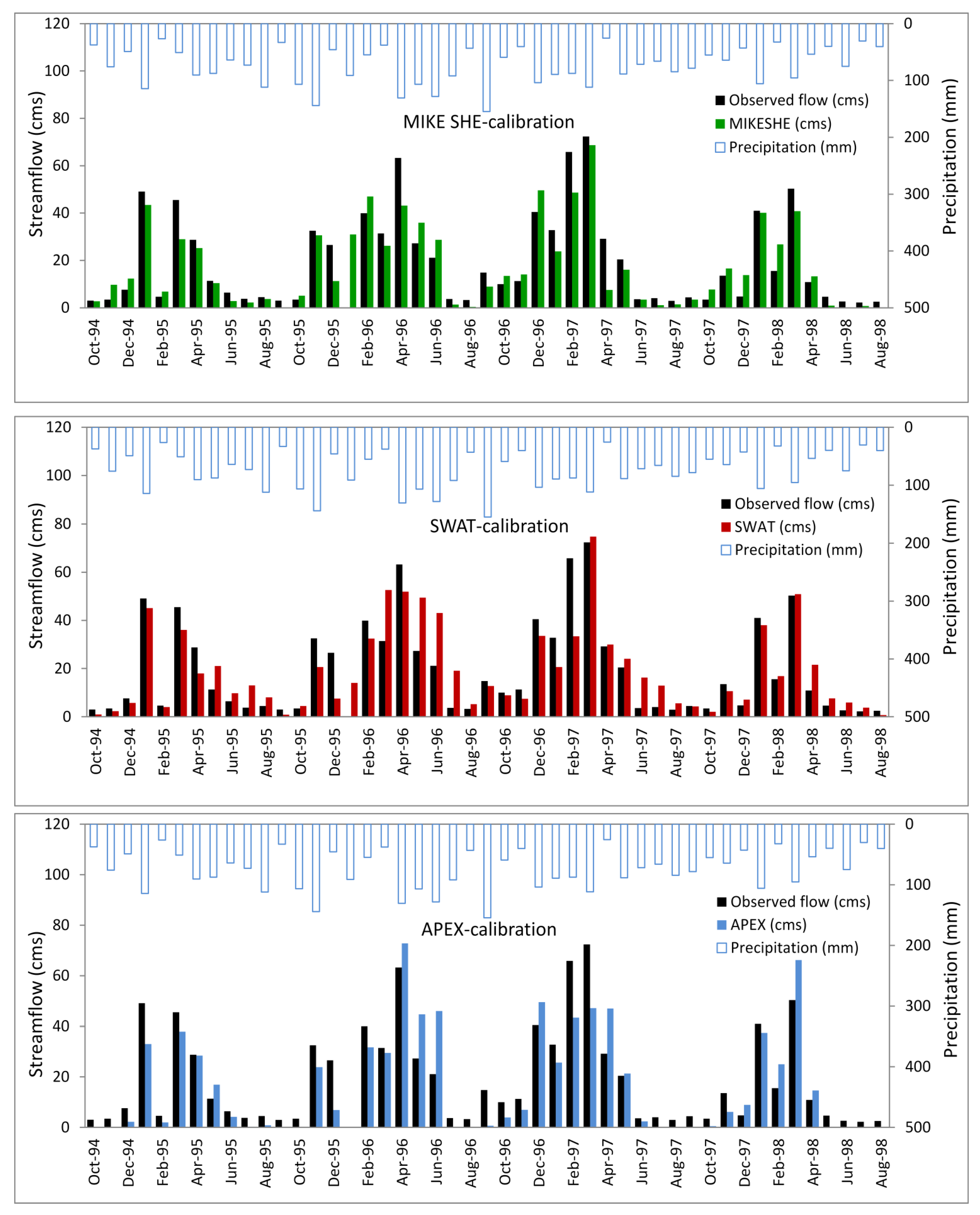
| Measured | Precipitation (mm) | 814 | 1136 | 906 | 677 | 1032 | 932 | 925 | 835 |
| Flowobs (mm) | 281 | 440 | 489 | 254 | 474 | 311 | 323 | 300 | |
| Surface runoff (mm) | 169 | 264 | 294 | 152 | 284 | 187 | 194 | 180 | |
| MIKE SHE | ET (mm) | 618 | 560 | 545 | 599 | 620 | 580 | 559 | 593 |
| Flowsim (mm) | 244 | 378 | 413 | 265 | 244 | 378 | 413 | 265 | |
| Surface runoff sim(mm) | 146 | 227 | 248 | 159 | 146 | 227 | 248 | 159 | |
| APEX | ET (mm) | 632 | 614 | 589 | 476 | 655 | 656 | 605 | 601 |
| Flowsim (mm) | 202 | 404 | 319 | 146 | 513 | 160 | 450 | 330 | |
| Surface runoff sim (mm) | 121 | 243 | 192 | 88 | 308 | 96 | 270 | 198 | |
| SWAT | ET (mm) | 563 | 500 | 506 | 459 | 566 | 520 | 519 | 454 |
| Flowsim (mm) | 272 | 514 | 448 | 273 | 506 | 325 | 482 | 365 | |
| Surface runoff sim (mm) | 163 | 308 | 269 | 164 | 304 | 195 | 289 | 219 | |
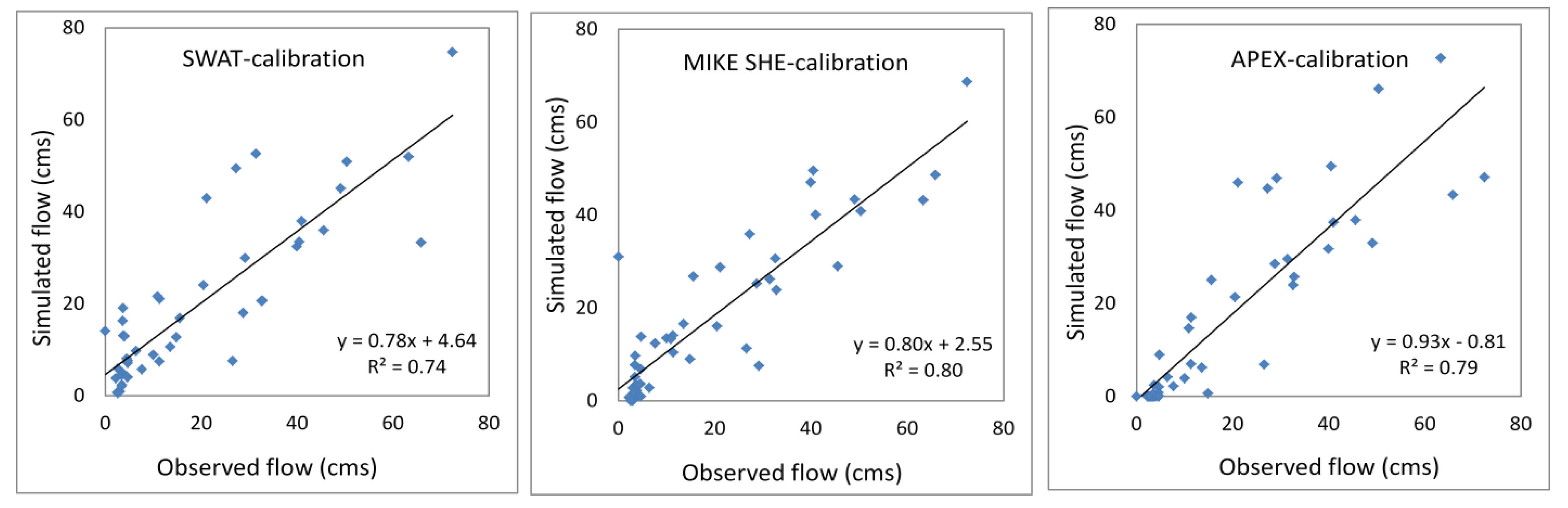


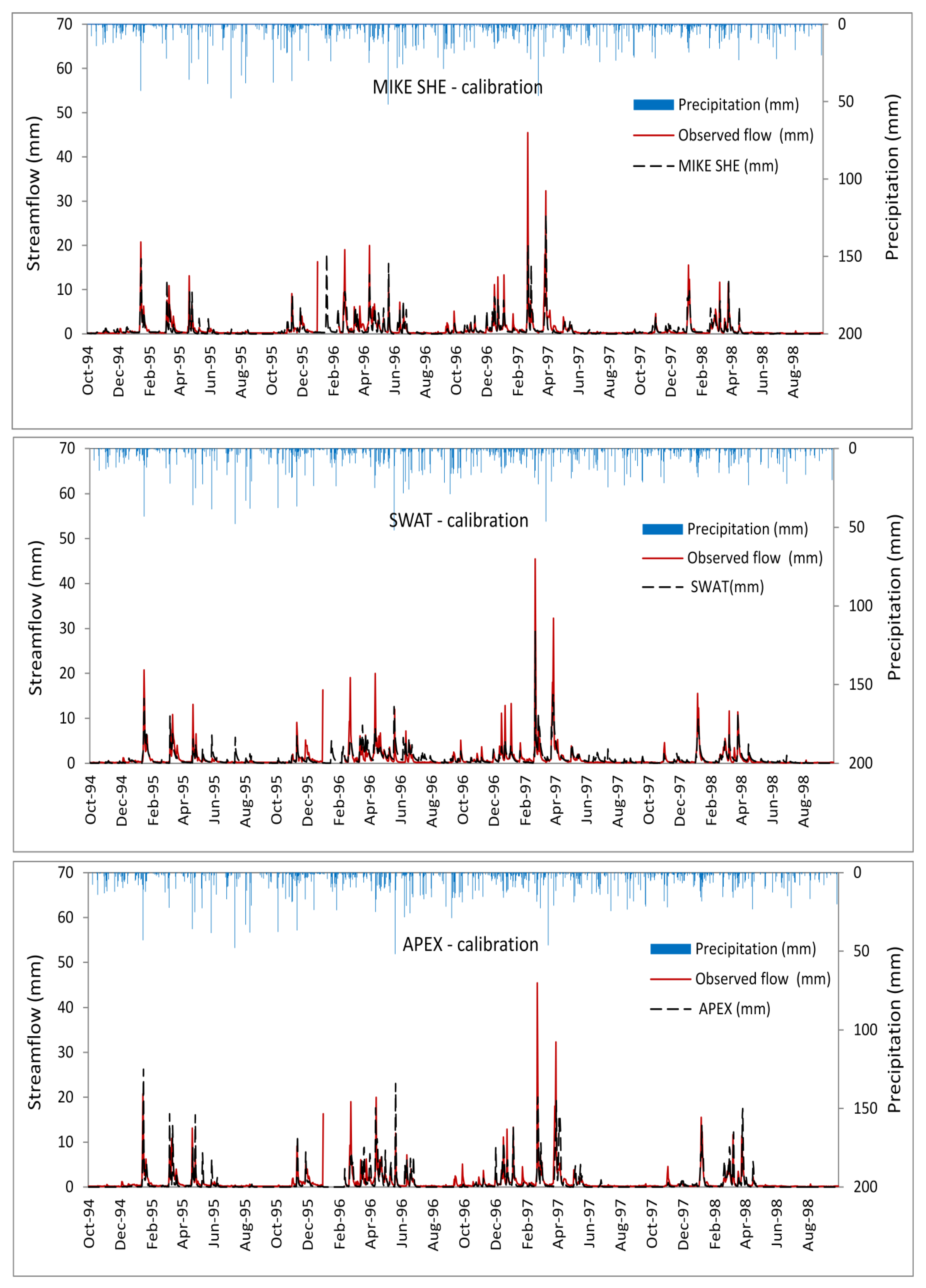
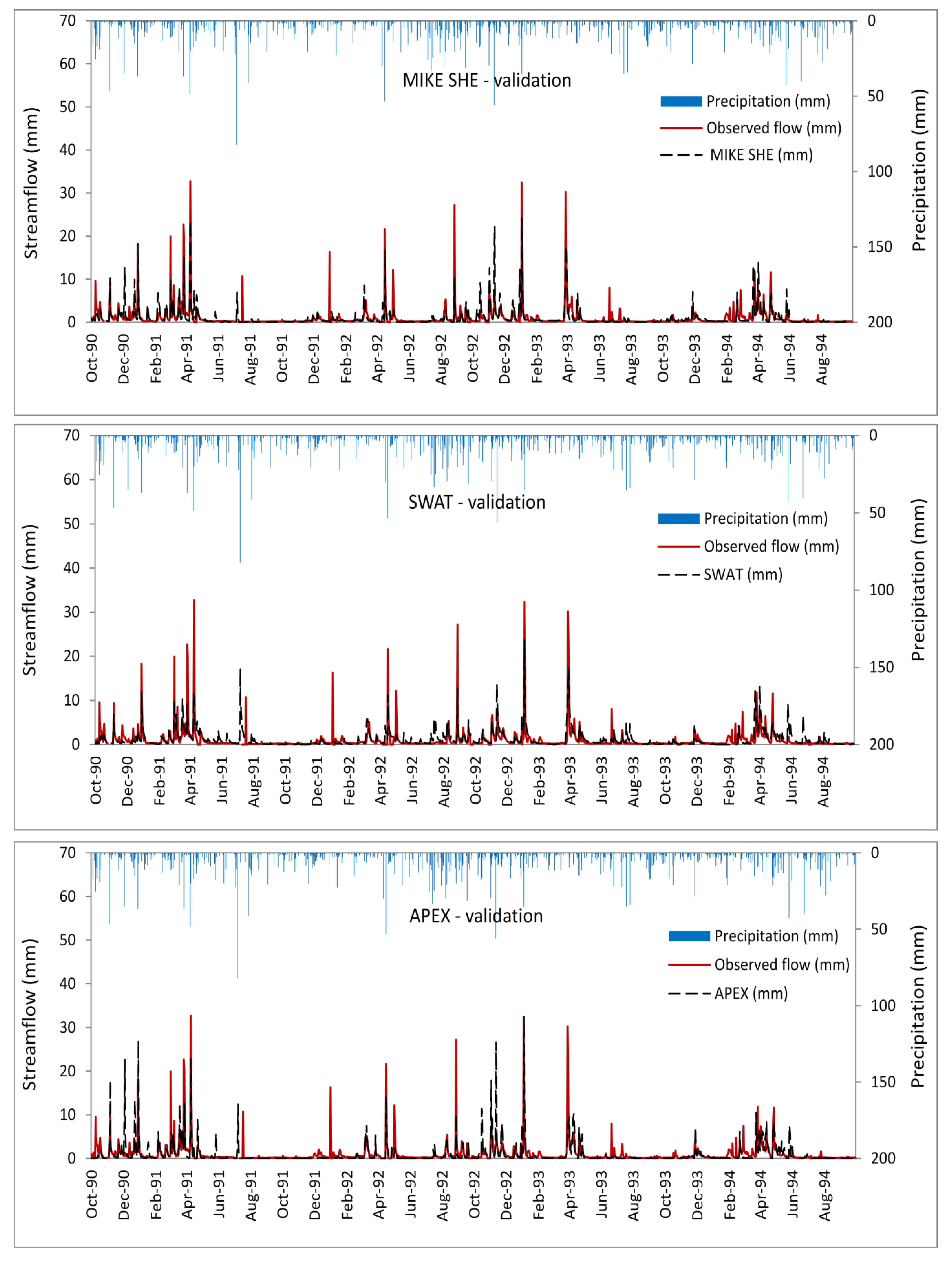
| Statistical Index | SWAT | MIKE SHE | APEX | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | Calibration | Validation | ||||
| R2 | 0.74 | 0.64 | 0.80 | 0.64 | 0.81 | 0.65 | |||
| RMSE | 9.89 | 12.04 | 8.70 | 11.42 | 9.43 | 14.75 | |||
| RSR | 0.27 | 0.34 | 0.21 | 0.29 | 0.32 | 0.44 | |||
| NSE | 0.73 | 0.73 | 0.79 | 0.71 | 0.76 | 0.70 | |||
| PBIAS | −3.14 | −12.50 | 6.67 | 3.57 | 11.71 | 13.07 | |||
| Statistical Index | SWAT | MIKE SHE | APEX | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | Calibration | Validation | ||||
| R2 | 0.57 | 0.41 | 0.59 | 0.44 | 0.51 | 0.31 | |||
| RMSE | 1.03 | 2.00 | 0.95 | 2.00 | 1.26 | 2.19 | |||
| RSR | 0.47 | 0.61 | 0.40 | 0.60 | 0.60 | 0.72 | |||
| NSE | 0.53 | 0.39 | 0.59 | 0.40 | 0.30 | 0.31 | |||
| PBIAS | −1.52 | −7.8 | 10.29 | 8.30 | 10.69 | 27.20 | |||
4. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References and Notes
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois River Watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Arabi, M.; Meals, D.W.; Hoag, D. Lessons Learned from the NIFA-CEAP: Simulation Modeling for the Watershed-Scale Assessment of Conservation Practices; North Carolina State University: Raleigh, NC, USA, 2012. [Google Scholar]
- Shi, P.; Chen, C.; Srinivasan, R.; Zhang, X.S.; Cai, T.; Fang, X.Q.; Qu, S.M.; Chen, X.; Li, Q.F. Evaluating the SWAT model for hydrological modeling in Xixian watershed and comparison with the XAJ model. J. Am. Water Resour. Manag. 2011, 25, 2595–2612. [Google Scholar] [CrossRef]
- Abu El-Nasr, A.; Arnold, J.G.; Feyen, J.; Berlamont, J. Modeling the hydrology of a catchment using a distributed and a semi distributed model. Hydrol. Process. 2005, 19, 573–587. [Google Scholar]
- Beven, K. A discussion of distributed hydrological modelling. In Distributed Hydrological Modelling; Abbott, M.B., Refsgaard, J.C., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 1996; pp. 255–278. [Google Scholar]
- Refsgaard, J.C.; Storm, B. MIKE SHE. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Williams, J.R. The EPIC Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 909–1000. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases. Trans. ASAE 2003, 46, 1553–1566. [Google Scholar] [CrossRef]
- Borah, D.K.; Arnold, J.G.; Bera, M.; Krug, E.C.; Liang, X.Z. Storm event and continuous hydrologic modeling for comprehensive and efficient watershed simulations. J. Hydrol. Eng. 2007, 12, 605–616. [Google Scholar] [CrossRef]
- Im, S.; Brannan, K.; Mostaghimi, S.; Cho, J. A comparison of SWAT and HSPF models for simulating hydrologic and water quality responses from an urbanizing watershed. In Proceedings of 2003 ASAE Annual Meeting, Las Vegas, NV, USA, 27–30 July 2003.
- Refsgaard, J.C.; Knudsen, J. Operational validation and intercomparison of different types of hydrological models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Nielsen, S.A.; Hansen, E. Numerical simulation of the rainfall runoff process on a daily basis. Nord. Hydrol. 1973, 4, 171–190. [Google Scholar]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connel, P.E.; Rasmussen, J. An introduction to the European Hydrological Systems–Systeme Hydrologique Europeen, “SHE”. 2. Structure of a physically based distributed modelling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connel, P.E.; Rasmussen, J. An introduction to the European Hydrological Systems–Systeme Hydrologique Europeen, “SHE”. 1. History and philosophy of a physically based distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Knudsen, J.; Thomsen, A.; Refsgaard, J.C. WATBAL: A semi-distributed, physically based hydrological modelling system. Nord. Hydrol. 1986, 17, 347–362. [Google Scholar]
- Presant, E.W.; Wicklund, R.E. Soils of Waterloo County; Report No. 44; Canada Department of Agriculture: Guelph, ON, Canada, 1971. [Google Scholar]
- Hoffman, D.W.; Matthews, B.C.; Wicklund, R.E. Soil Survey of Wellington County Ontario; Report No. 35; Ontario Soil Survey Canada, Department of Agriculture and Ontario Department of Agriculture: Guelph, ON, Canada, 1963. [Google Scholar]
- Carey, J.H.; Fox, M.E.; Brownlee, B.G.; Metcalfe, J.L.; Mason, P.D.; Yerex, W.H. The Fate and Effects of Contaminant in Canagagigue Creek 1. Stream Ecology and Identification of Major Contaminants; Scientific Series No.; Environment Canada: Burlington, ON, Canada, 1983. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool: Theoretical Documentation; Version 2000; Grassland, Soil and Water Research Laboratory, Agricultural Research Service: Temple, TX, USA, 2002. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool: User’s Manual; Version 2000; Grassland, Soil and Water Research Laboratory, Agricultural Research Service: Temple, TX, USA, 2002. [Google Scholar]
- Vazquez‐Amábile, G.; Engel, B.A. Use of SWAT to compute groundwater table depth and streamflow in Muscatatuck River Watershed. Trans. ASAE 2005, 48, 991–1003. [Google Scholar] [CrossRef]
- Williams, J.R.; Harman, W.L.; Magre, M.; Kizil, U.; Lindley, J.A; Padmanabhan, G.; Wang, E. APEX feedlot water quality simulation. Trans. ASAE 2006, 49, 61–73. [Google Scholar] [CrossRef]
- Williams, J.R.; Izaurralde, R.C. The APEX model. In Watershed Models; Singh, V.P., Frevert, D.K., Eds.; Taylor and Francis Group: Boca Raton, FL, USA, 2006; pp. 437–482. [Google Scholar]
- Williams, J.R.; Arnold, J.G.; Srinivasan, R. The APEX Model; Report No. 00-06; Blackland Research and Extension Center: Temple, TX, USA, 2000. [Google Scholar]
- Williams, J.R.; Izaurralde, R.C.; Steglich, E.M. Agricultural Policy/Environmental eXtender Model: Theoretical Documentation Version 0604; Report No. 2008-17; Blackland Research and Extension Center: Temple, TX, USA, 2008. [Google Scholar]
- DHI. MIKE SHE: An Integrated Hydrological Modeling System; Danish Hydraulic Institute: Hørsholm, Denmark, 2004. [Google Scholar]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrological and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Demissie, M. Hydrologic Modeling of the Iroquois River Watershed Using HSPF and SWAT; ISWS CR 2004–08. Illionois State Water Survey: Champaign, IL, USA, 2004. Available online: www.sws.uiuc.edu/pubdoc/CR/ISWSCR2004-08.pdf (accessed on 4 April 2014).
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the SWAT Model on a Large River Basin with Point and Nonpoint Sources. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Garbrecht, J.D. Hydrologic simulation on agricultural watersheds: Choosing between two models. Trans. ASAE 2003, 46, 1539–1551. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar]
- Oogathoo, S. Runoff Simulation in the Canagagigue Creek Watershed Using the MIKE SHE Model. Master’s Thesis, McGill University, Montreal, QC, Canada, 2006. [Google Scholar]
- Rong, H. Water Quality Evaluation under Climate Change Impacts for Canagagigue Creek watershed in southern Ontario. Master’s Thesis, University of Guelph, ON, Canada, 2009. [Google Scholar]
- Smedema, L.K.; Rycroft, D.W. Land Drainage—Planning and Design of Agricultural Drainage Systems; Cornell University Press: Ithaca, NY, USA, 1982. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivansan, R.; Williams, J.R. Soil and Water Assessment Tool:User’s Manual; Grassland, Soil and Water Research Laboratory, Agricultural Research Service: Temple, TX, USA, 2000. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20-39. https://doi.org/10.3390/hydrology1010020
Golmohammadi G, Prasher S, Madani A, Rudra R. Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT. Hydrology. 2014; 1(1):20-39. https://doi.org/10.3390/hydrology1010020
Chicago/Turabian StyleGolmohammadi, Golmar, Shiv Prasher, Ali Madani, and Ramesh Rudra. 2014. "Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT" Hydrology 1, no. 1: 20-39. https://doi.org/10.3390/hydrology1010020




