Direct Control of Spin Distribution and Anisotropy in Cu-Dithiolene Complex Anions by Light
Abstract
:1. Introduction
2. Results and Discussion
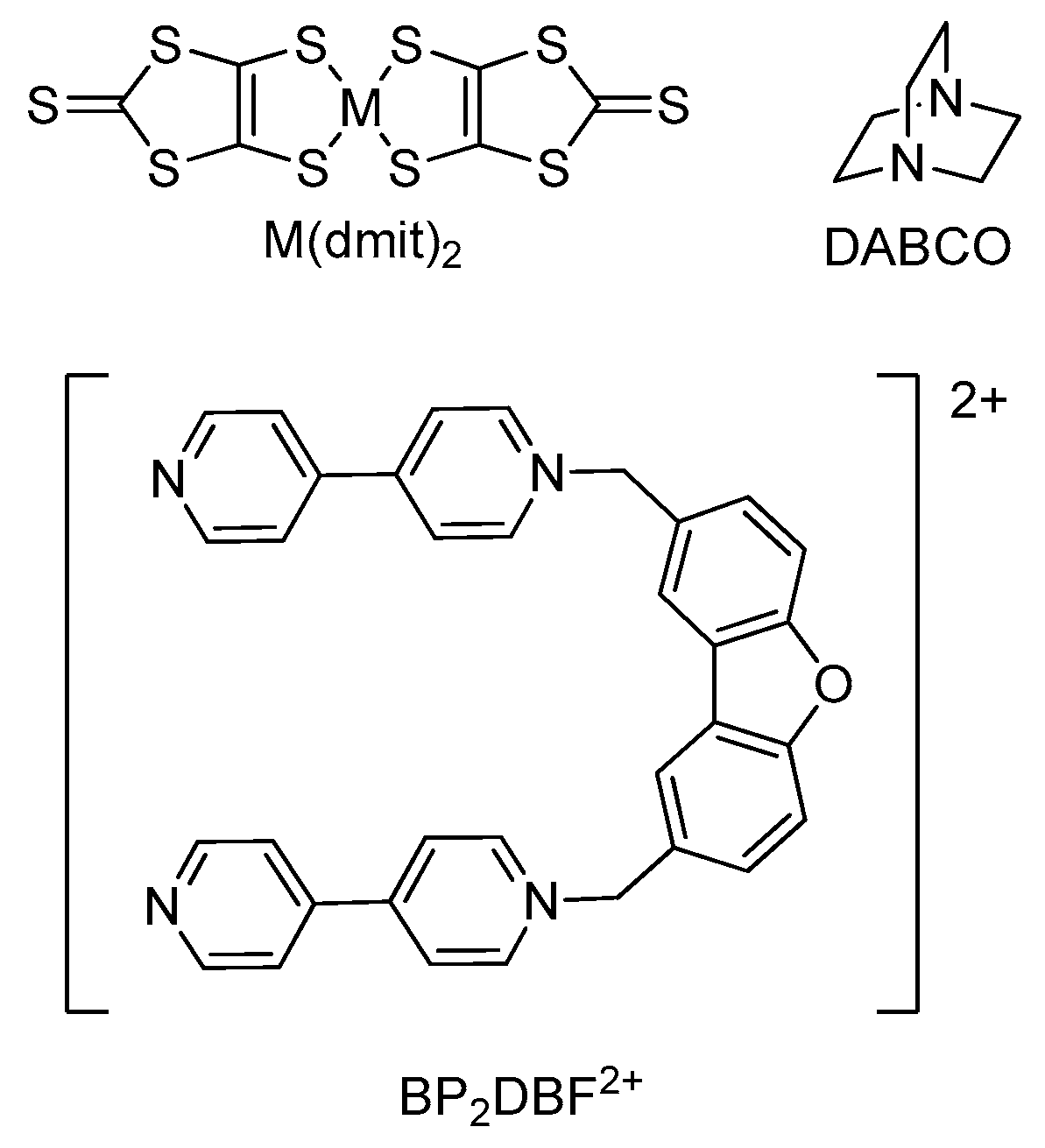
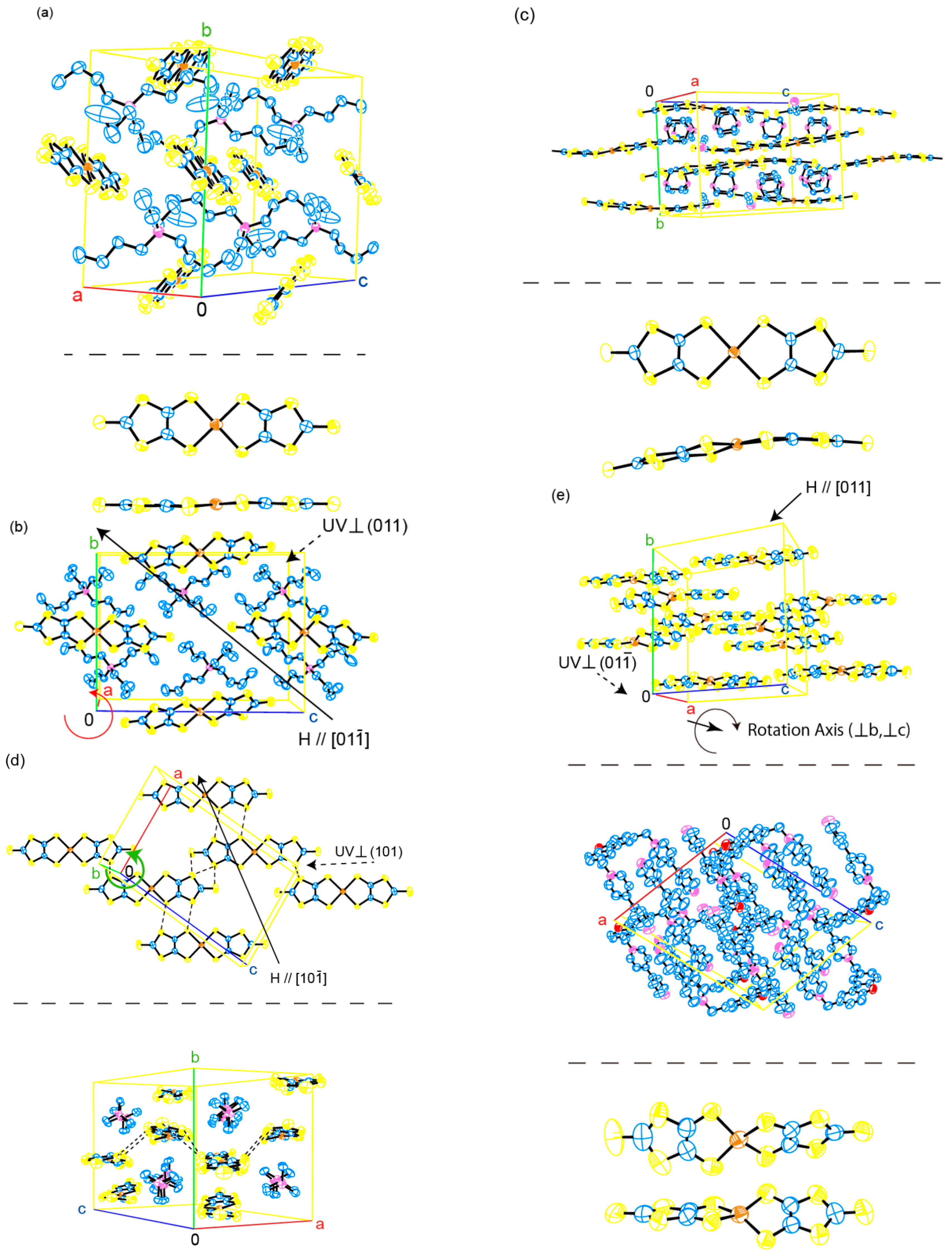
2.1. Crystal and Molecular Structures
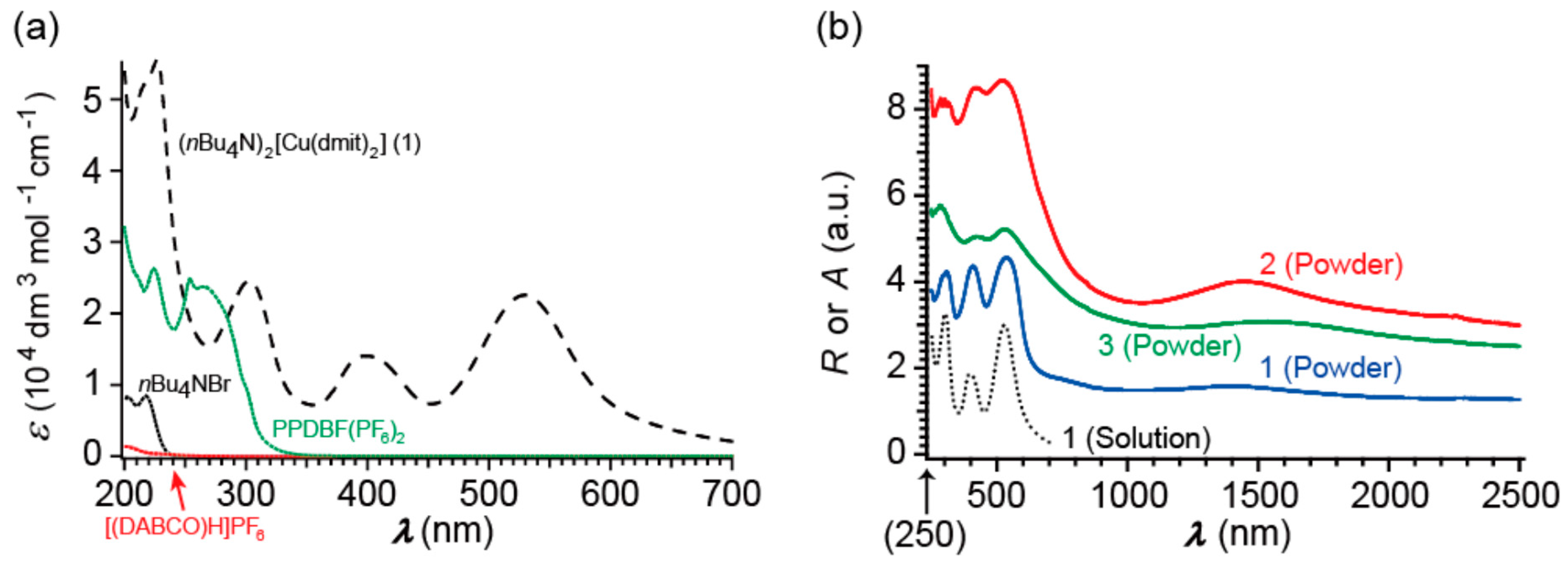
2.2. Molecular Structures and Spin Delocalization
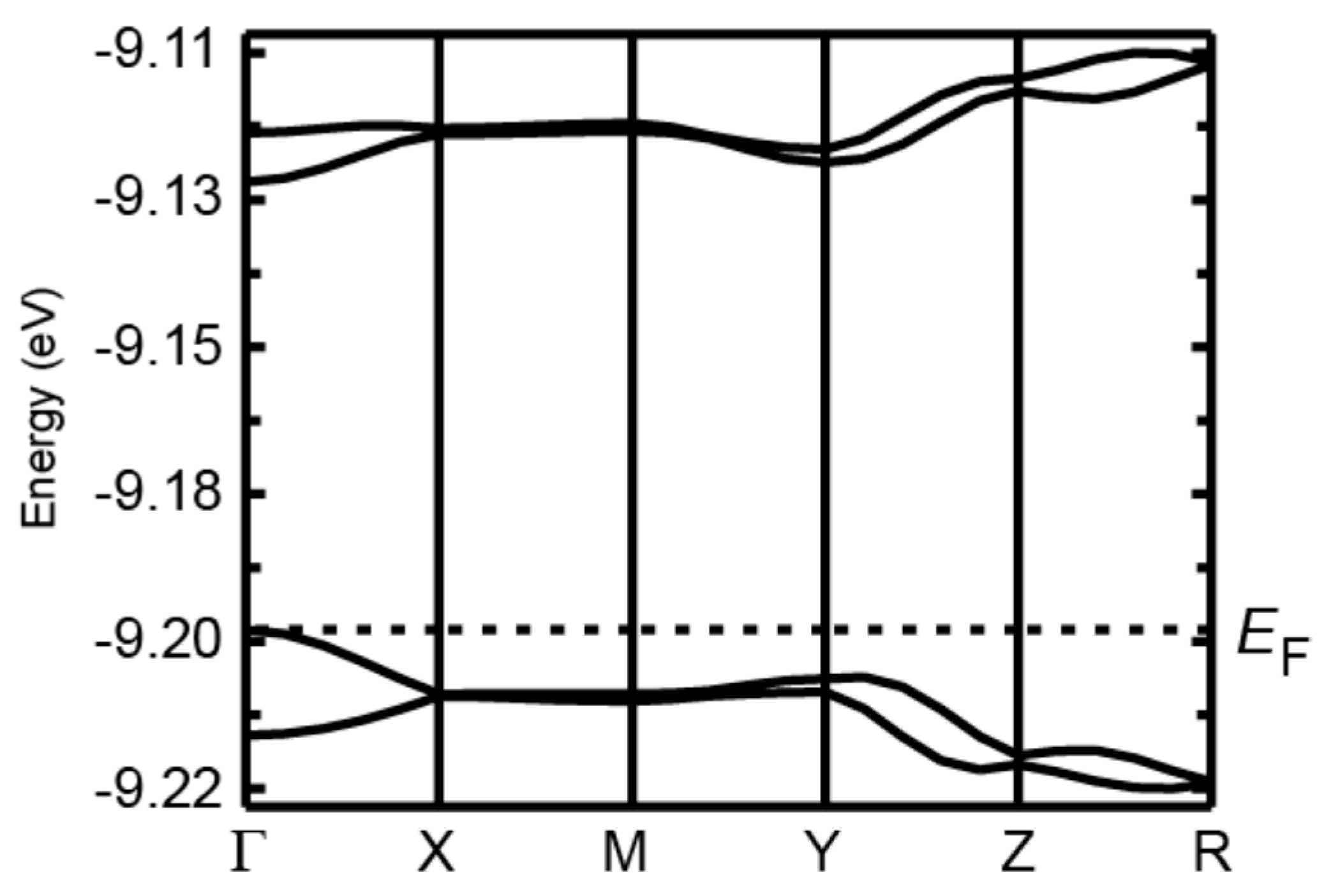
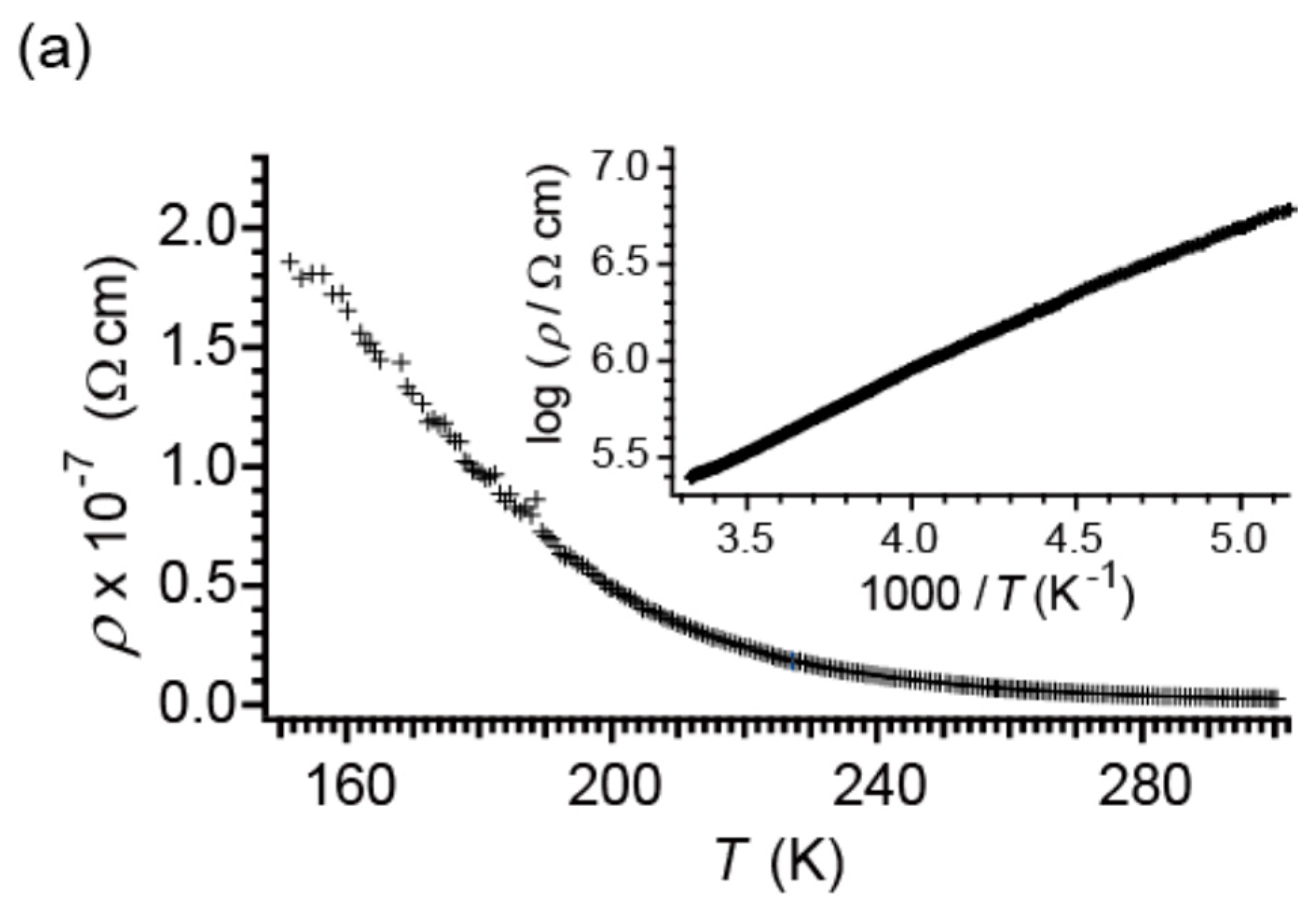
2.3. Electrical Properties under Dark Conditions
2.4. Electrical Properties under UV Irradiation
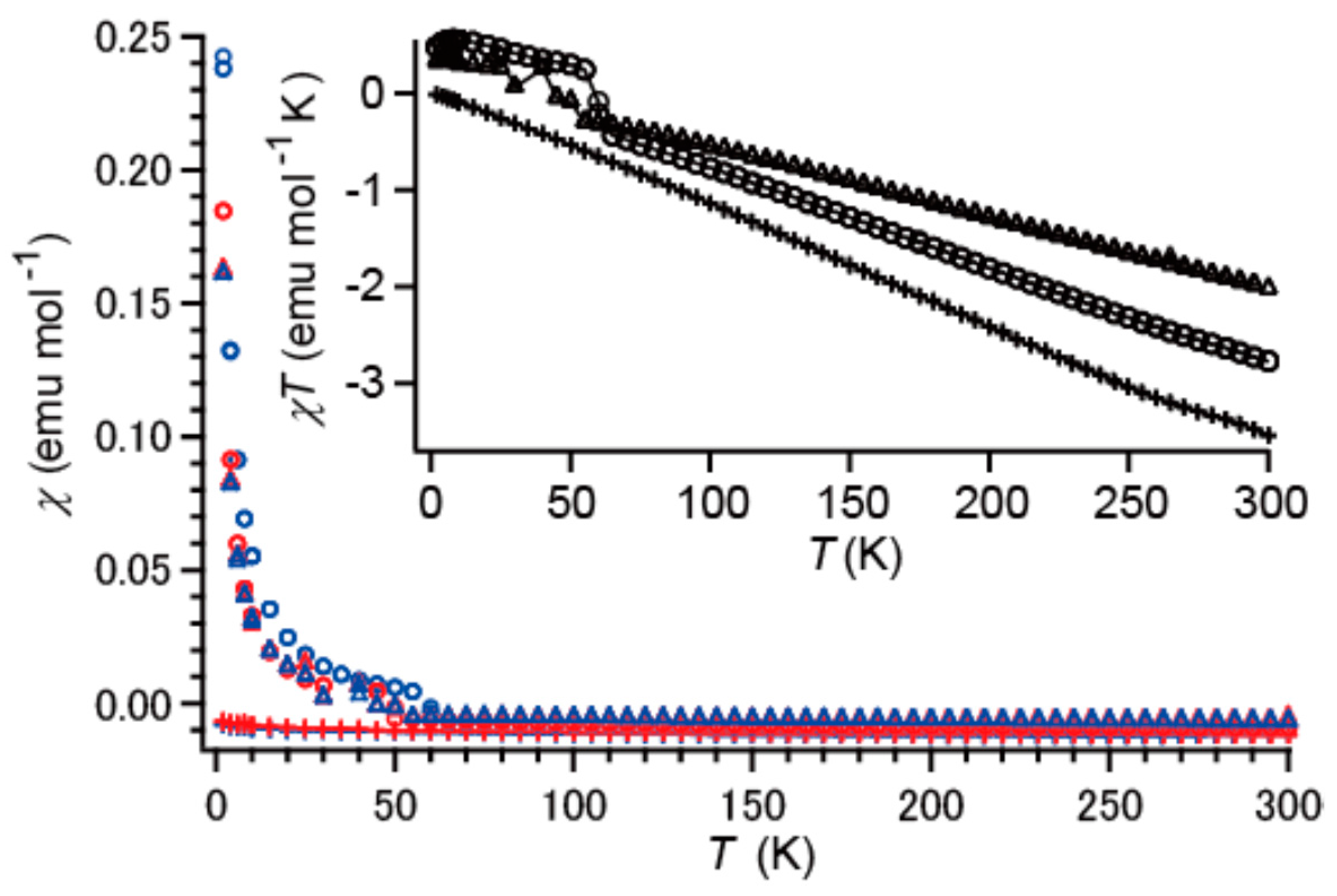
2.5. Magnetic Susceptibilities under Dark Conditions
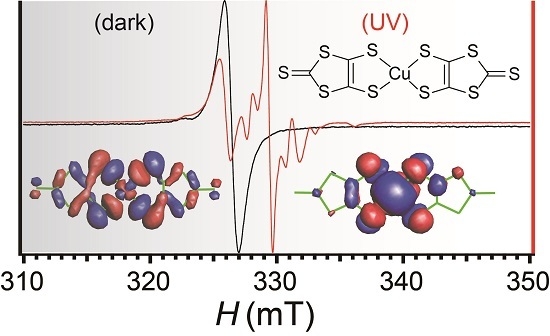
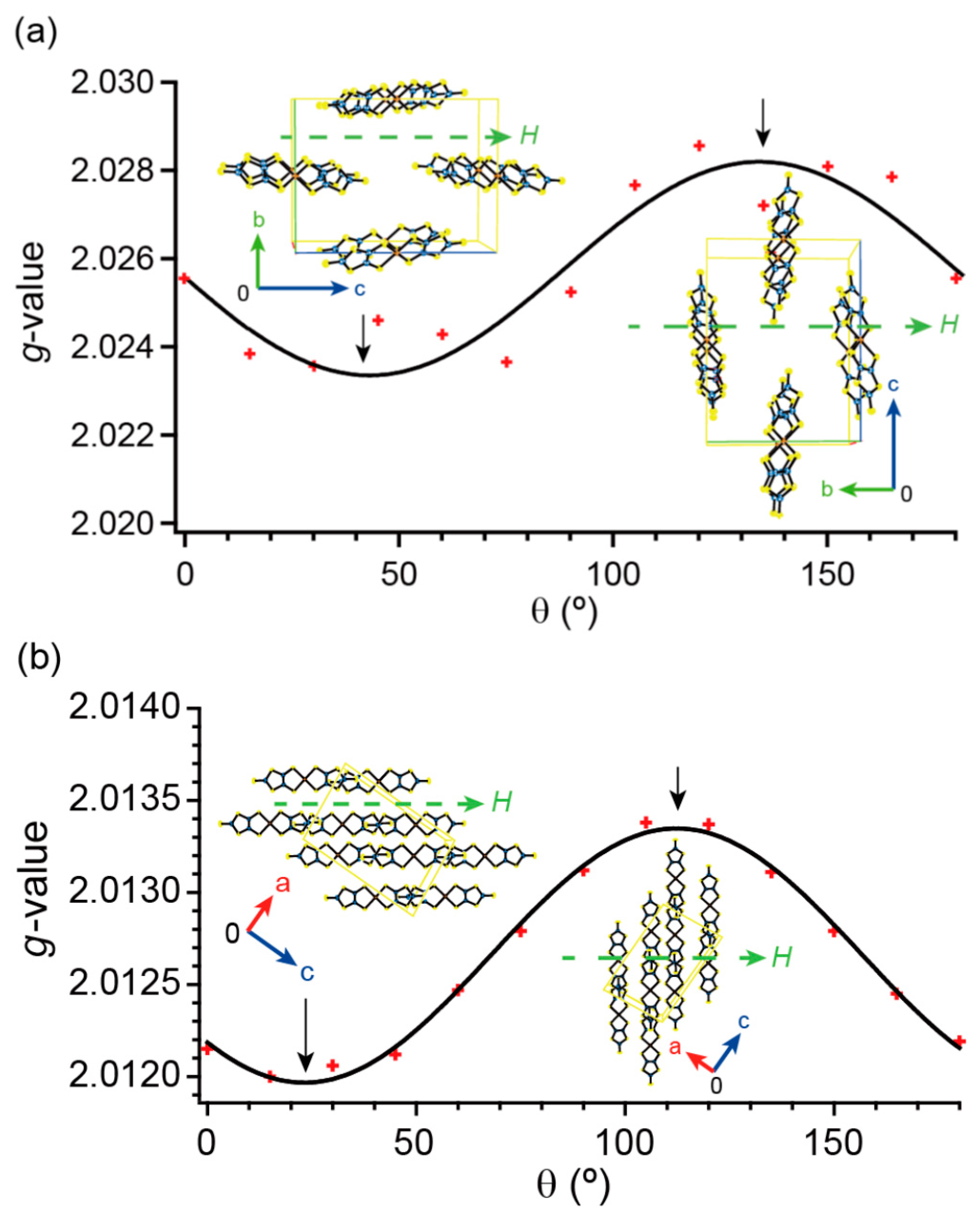
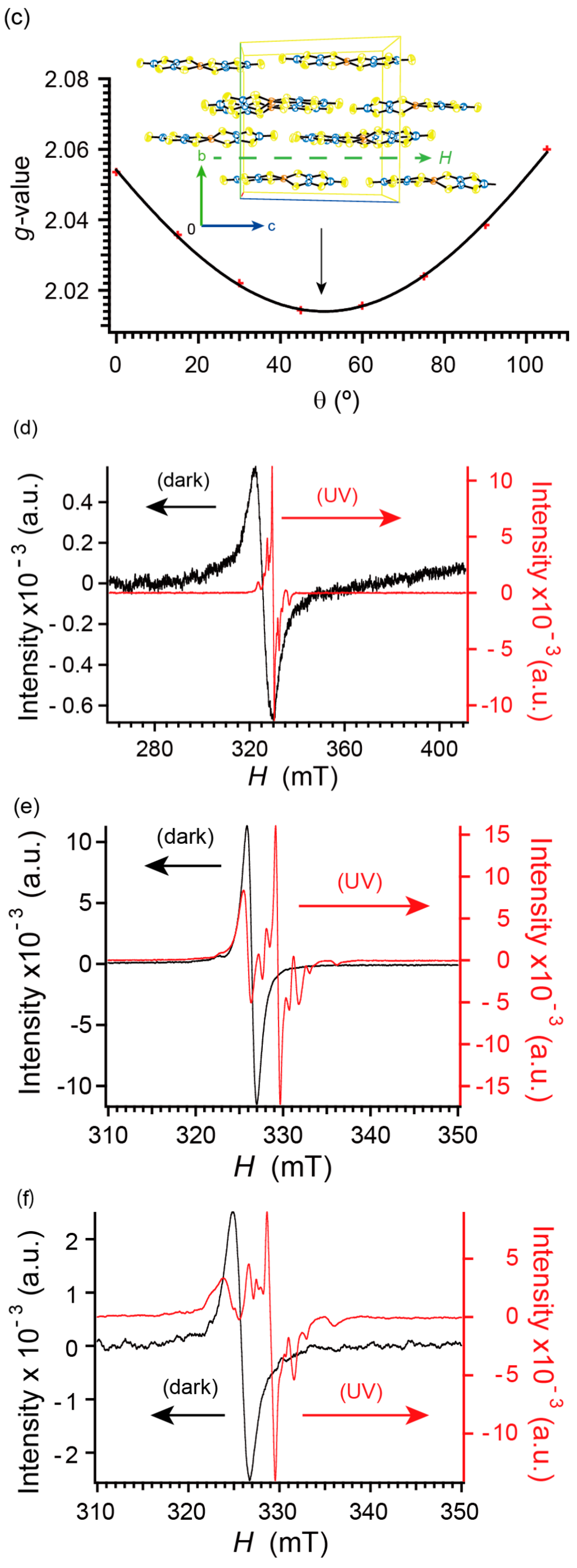
2.6. Electron Spin Resonance under Dark Conditions
2.7. Electron Spin Resonance under UV Irradiation
3. Experimental Section
3.1. Materials and Methods
3.2. UV Irradiation
3.3. Physical Property Measurements: General
3.4. Magnetic Susceptibility Measurements
3.5. Electrical Resistivity Measurements
3.6. Electron Spin Resonance
3.7. Calculations
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tissot, A. Photoswitchable spin crossover nanoparticles. New J. Chem. 2014, 38, 1840–1845. [Google Scholar] [CrossRef]
- Hatcher, L.E.; Lauren, E.; Raithby, P.R. Dynamic single-crystal diffraction studies using synchrotron radiation. Coord. Chem. Rev. 2014, 277–278, 69–79. [Google Scholar] [CrossRef]
- Gütlich, P.; Gasper, A.B.; Garcia, Y. Spin states switching in iron coordination compounds. Beilstein J. Org. Chem. 2013, 9, 342–391. [Google Scholar] [CrossRef] [PubMed]
- Letard, J.-F. Photomagnetism of iron(II) spin crossover complexes—The T(LIESST) approach. J. Mater. Chem. 2006, 16, 2550–2559. [Google Scholar] [CrossRef]
- Varret, F.; Boukheddaden, K.; Codjovi, E.; Enachescu, C.; Linares, J. On the competition between relaxation and photoexcitations in spin crossover solids under continuous irradiation. In Spin Crossover in Transition Metal Compounds II, Topics in Current Chemistry; Springer-Verlag Berlin: Berlin, Germany, 2004; Volume 234, pp. 199–229. [Google Scholar]
- Gütlich, P.; Garcia, Y.; Spering, H. Spin transition phenomena. In Magnetism: Molecules to Materials IV; Miller, J.S., Drillon, M., Eds.; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2003; pp. 271–344. [Google Scholar]
- Spiering, H.; Kohlhaas, T.; Romstedt, H.; Hauser, A.; Bruns-Yilmaz, C.; Kusz, J.; Gütlich, P. Correlations of the distribution of spin states in spin crossover compounds. Coord. Chem. Rev. 1999, 190–192, 629–647. [Google Scholar] [CrossRef]
- Hauser, A.; Jeftic, J.; Romstedt, H.; Hinek, R.; Spiering, H. Cooperative phenomena and light-induced bistability in iron(II) spin-crossover compounds. Coord. Chem. Rev. 1999, 190–192, 471–491. [Google Scholar] [CrossRef]
- Gütlich, P.; Ensling, J.; Tuczek, F. Metastable electronic states induced by nuclear decay and light. Hyperfine Interact. 1994, 84, 447–469. [Google Scholar] [CrossRef]
- Koshihara, S. Photo-induced phase transitions in organic and inorganic semiconductors. J. Lumin. 2000, 87–89, 77–81. [Google Scholar] [CrossRef]
- Först, M.; Hoffmann, M.C.; Dienst, A.; Kaiser, S.; Rini, M.; Tobey, R.I.; Gensch, M.; Manzoni, C.; Cavalleri, A. THz control in correlated electron solids: Sources and applications. In Terahertz Spectroscopy and Imaging; Peiponen, K.-E., Zeitler, A., Kuwata-Gonokami, M., Eds.; Springer Berlin Heidelberg: Berlin, Germany, 2013; pp. 611–631. [Google Scholar]
- Mori, T. Structural genealogy of BEDT-TTF-based organic conductors I. Parallel molecules: β and β″ phases. Bull. Chem. Soc. Jpn. 1998, 71, 2509–2526. [Google Scholar] [CrossRef]
- Mori, T.; Mori, H.; Tanaka, S. Structural genealogy of BEDT-TTF-based organic conductors II. Inclined molecules: θ, α and κ phases. Bull. Chem. Soc. Jpn. 1999, 72, 179–197. [Google Scholar] [CrossRef]
- Mori, T. Structural genealogy of BEDT-TTF-based organic conductors III. Twisted molecules: δ and α′ phases. Bull. Chem. Soc. Jpn. 1999, 72, 2011–2027. [Google Scholar] [CrossRef]
- West, A.R. Electrical properties. In Basic Solid State Chemistry; John Wiley & Sons: Chichester, UK, 1994; pp. 281–375. [Google Scholar]
- Cox, P.A. Electronic structure of solids. In Solid State Chemistry: Compounds; Cheetham, A.K., Day, P., Eds.; Clarendon Press: Oxford, UK, 1992; pp. 1–30. [Google Scholar]
- Ishikawa, T.; Hayes, S.A.; Keskin, S.; Corthey, G.; Hada, M.; Pichugin, K.; Marx, A.; Hirscht, J.; Shionuma, K.; Onda, K.; et al. Direct observation of collective modes coupled to molecular orbital-driven charge transfer. Science 2015, 350, 1501–1505. [Google Scholar] [CrossRef] [PubMed]
- Naito, T. (Ed.) Molecular Electronic and Related Materials: Control and Probe with Light; Transworld Research Network: Kerala, India, 2010; pp. 1–320.
- Naito, T.; Inabe, T.; Niimi, H.; Asakura, K. Light-induced transformation of molecular materials into devices. Adv. Mater. 2004, 16, 1786–1790. [Google Scholar] [CrossRef]
- Miyamoto, T.; Niimi, H.; Chun, W.-J.; Kitajima, Y.; Sugawara, H.; Inabe, T.; Naito, T.; Asakura, K. Chemical states of Ag in Ag(DMe-DCNQI)2 photoproducts and a proposal for its photoinduced conductivity change mechanism. Chem. Lett. 2007, 36, 1008–1009. [Google Scholar] [CrossRef]
- Naito, T.; Kakizaki, A.; Wakeshima, M.; Hinatsu, Y.; Inabe, T. Photochemical modification of magnetic properties in organic low-dimensional conductors. J. Solid State Chem. 2009, 182, 2733–2742. [Google Scholar] [CrossRef]
- Naito, T.; Kakizaki, A.; Inabe, T.; Sakai, R.; Nishibori, E.; Sawa, H. Growth of nanocrystals in a single crystal of different materials: A way of giving function to molecular crystals. Cryst. Growth Des. 2011, 11, 501–506. [Google Scholar] [CrossRef]
- Miyamoto, T.; Kitajima, Y.; Sugawara, H.; Naito, T.; Inabe, T.; Asakura, K. Origin of photochemical modification of resistivity of Ag(DMe-DCNQ)2 studied by X-Ray absorption fine structure. J. Phys. Chem. C 2009, 113, 20476–20480. [Google Scholar] [CrossRef]
- Miyamoto, T.; Niimi, H.; Kitajima, Y.; Naito, T.; Asakura, K. Ag L3-edge X-Ray absorption near-edge structure of 4d10 (Ag+) compounds: Origin of the edge peak and its chemical relevance. J. Phys. Chem. A 2010, 114, 4093–4098. [Google Scholar] [CrossRef] [PubMed]
- Naito, T.; Sugawara, H.; Inabe, T.; Kitajima, Y.; Miyamoto, T.; Niimi, H.; Asakura, K. UV-VIS induced vitrification of a molecular crystal. Adv. Funct. Mater. 2007, 17, 1663–1670. [Google Scholar] [CrossRef]
- Naito, T.; Sugawara, H.; Inabe, T. Mechanism of spatially resolved photochemical control of resistivity of a molecular crystalline solid. Nanotechnology 2007, 18, 424008. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tsutsumi, T.; Miyamoto, T.; Niimi, H.; Kitajima, Y.; Sakai, Y.; Kato, M.; Naito, T.; Asakura, K. Energy-filtered X-Ray photoemission electron microscopy and its applications to surface and organic materials. Solid State Electron. 2007, 51, 1360–1366. [Google Scholar] [CrossRef]
- Saiki, T.; Mori, S.; Ohara, K.; Naito, T. Capacitor-like behavior of molecular crystal β-DiCC[Ni(dmit)2]. Chem. Lett. 2014, 43, 1119–1121. [Google Scholar] [CrossRef]
- Burdett, J.K. Structural and compositional basis of high-temperature superconductivity: Properties of the magic electronic state. Inorg. Chem. 1993, 32, 3915–3922. [Google Scholar] [CrossRef]
- Yamamoto, H.M.; Ito, H.; Shigeto, K.; Tsukagoshi, K.; Kato, R. Direct formation of micro-/nanocrystalline 2,5-dimethyl-N,N′-dicyanoquinonediimine complexes on SiO2/Si substrates and multiprobe measurement of conduction properties. J. Am. Chem. Soc. 2006, 128, 700–701. [Google Scholar] [CrossRef] [PubMed]
- Naito, T.; Karasudani, T.; Mori, S.; Ohara, K.; Konishi, K.; Takano, T.; Takahashi, Y.; Inabe, T.; Nishihara, S.; Inoue, K. Molecular photoconductor with simultaneously photocontrollable localized spins. J. Am. Chem. Soc. 2012, 134, 18656–18666. [Google Scholar] [CrossRef] [PubMed]
- Naito, T.; Karasudani, T.; Ohara, K.; Takano, T.; Takahashi, Y.; Inabe, T.; Furukawa, K.; Nakamura, T. Simultaneous control of carriers and localized spins with light in organic materials. Adv. Mater. 2012, 24, 6153–6157. [Google Scholar] [CrossRef] [PubMed]
- Naito, T.; Karasudani, T.; Nagayama, N.; Ohara, K.; Konishi, K.; Mori, S.; Takano, T.; Takahashi, Y.; Inabe, T.; Kinose, S.; et al. Giant photoconductivity in NMQ[Ni(dmit)2]. Eur. J. Inorg. Chem. 2014, 2014, 4000–4009. [Google Scholar] [CrossRef]
- Alvarez, S.; Vicente, R.; Hoffmann, R. Dimerization and stacking in transition-metal bisdithiolenes and tetrathiolates. J. Am. Chem. Soc. 1985, 107, 6253–6277. [Google Scholar] [CrossRef]
- Cassoux, P.; Valade, L.; Kobayashi, H.; Kobayashi, A.; Clark, R.A.; Underhill, A.E. Molecular metals and superconductors derived from metal complexes of 1,3-dithiole-2-thione-4,5-dithiolate (dmit). Coord. Chem. Rev. 1991, 110, 115–160. [Google Scholar] [CrossRef]
- Williams, J.M.; Schultz, A.J.; Geiser, U.; Carlson, K.D.; Kini, A.M.; Wang, H.H.; Kwok, W.-K.; Whangbo, M.-H.; Schirber, J.E. Organic superconductors—New benchmarks. Science 1991, 252, 1501–1508. [Google Scholar] [CrossRef] [PubMed]
- Olk, R.-M.; Olk, B.; Dietzsch, W.; Kirmse, R.; Hoyer, E. The chemistry of 1,3-dithiole-2-thione-4,5-dithiolate (dmit). Coord. Chem. Rev. 1992, 117, 99–131. [Google Scholar] [CrossRef]
- Svenstrup, N.; Becher, J. The organic chemistry of 1,3-dithiole-2-thione-4,5-dithiolate (DMIT). Synthesis 1995, 3, 215–235. [Google Scholar] [CrossRef]
- Canadell, E. Electronic structure of two-band molecular conductors. New J. Chem. 1997, 21, 1147–1159. [Google Scholar]
- Kato, R.; Liu, Y.-L.; Hosokoshi, Y.; Aonuma, S.; Sawa, H. Se-substitution and cation effects on the high-pressure molecular superconductor, β-Me4N[Pd(dmit)2]2—A unique two-band system. Mol. Cryst. Liq. Cryst. 1997, 296, 217–244. [Google Scholar] [CrossRef]
- Rosa, A.; Ricciardi, G.; Baerends, E.J. Structural properties of M(dmit)2-based (M = Ni, Pd, Pt; dmit2− = 2-thioxo-1,3-dithiole-4,5-dithiolato) molecular metals. Insights from density functional calculations. Inorg. Chem. 1998, 37, 1368–1379. [Google Scholar] [CrossRef] [PubMed]
- Pullen, A.E.; Olk, R.-M. The coordination chemistry of 1,3-dithiole-2-thione-4,5-dithiolate (dmit) and isologs. Coord. Chem. Rev. 1999, 188, 211–262. [Google Scholar] [CrossRef]
- Kato, R. Conducting metal dithiolene complexes: Structural and electronic properties. Chem. Rev. 2004, 104, 5319–5346. [Google Scholar] [CrossRef] [PubMed]
- Mori, H. Materials viewpoint of organic superconductors. J. Phys. Soc. Jpn. 2006, 75, 051003. [Google Scholar] [CrossRef]
- Valade, L.; Tanaka, H. Molecular inorganic conductors and superconductors. In Molecular Materials; Bruce, D.W., O'Hare, D., Walton, R.I., Eds.; John Wiley & Sons Ltd: West Sussex, UK, 2010; pp. 211–280. [Google Scholar]
- Mercuri, M.L.; Deplano, P.; Pilia, L.; Serpe, A.; Artizzu, F. Interaction modes and physical properties in transition metal chalcogenolene-based molecular materials. Coord. Chem. Rev. 2010, 254, 1419–1433. [Google Scholar] [CrossRef]
- De Bonneval, B.G.; Ching, K.I.M.-C.; Alary, F.; Bui, T.-T.; Valade, L. Neutral d8 metal bis-dithiolene complexes: Synthesis, electronic properties and applications. Coord. Chem. Rev. 2010, 254, 1457–1467. [Google Scholar] [CrossRef]
- Papavassiliou, G.C.; Anyfantis, G.C.; Mousdis, G.A. Neutral metal 1,2-dithiolenes: Preparations, properties and possible applications of unsymmetrical in comparison to the symmetrical. Crystals 2012, 2, 762–811. [Google Scholar] [CrossRef]
- Tanaka, H.; Okano, Y.; Kobayashi, H.; Suzuki, W.; Kobayashi, A. A Three-dimensional synthetic metallic crystal composed of single-component molecules. Science 2001, 291, 285–287. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, A.; Tanaka, H.; Kobayashi, H. Molecular design and development of single-component molecular metals. J. Mater. Chem. 2001, 11, 2078–2088. [Google Scholar] [CrossRef]
- Kobayashi, A.; Fujiwara, E.; Kobayashi, H. Single-component molecular metals with extended-TTF dithiolate ligands. Chem. Rev. 2004, 104, 5243–5264. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.; Fujiwara, E.; Kobayashi, A.; Fujishiro, Y.; Nishibori, E.; Sakata, M.; Tanaka, M.; Tanaka, H.; Okano, Y.; Kobayashi, H. Single-component molecular conductor [Zn(tmdt)2] and related Zn complexes. Chem. Lett. 2005, 34, 1090–1091. [Google Scholar] [CrossRef]
- Kobayashi, A.; Okano, Y.; Kobayashi, H. Molecular design and physical properties of single-component molecular metals. J. Phys. Soc. Jpn. 2006, 75, 051002. [Google Scholar] [CrossRef]
- Zhou, B.; Shimamura, M.; Fujiwara, E.; Kobayashi, A.; Higashi, T.; Nishibori, E.; Sakata, M.; Cui, H.B.; Takahashi, K.; Kobayashi, H. Magnetic transitions of single-component molecular metal [Au(tmdt)2] and its alloy systems. J. Am. Chem. Soc. 2006, 128, 3872–3873. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Kobayashi, A.; Okano, Y.; Nakashima, T.; Aoyagi, S.; Nishibori, E.; Sakata, M.; Tokumoto, M.; Kobayashi, H. Single-component molecular conductor [Pt(tmdt)2] (tmdt = trimethylenetetrathiafulvalenedithiolate)—An advanced molecular metal exhibiting high metallicity. Adv. Mater. 2009, 21, 3596–3600. [Google Scholar] [CrossRef]
- Zhou, B.; Yajima, H.; Kobayashi, A.; Okano, Y.; Tanaka, H.; Kumashiro, T.; Nishibori, E.; Sawa, H.; Kobayashi, H. Single-component molecular conductor [Cu(tmdt)2] containing an antiferromagnetic heisenberg chain. Inorg. Chem. 2010, 49, 6740–6747. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Idobata, Y.; Kobayashi, A.; Cui, H.-B.; Kato, R.; Takagi, R.; Miyagawa, K.; Kanoda, K.; Kobayashi, H. Single-component molecular conductor [Cu(dmdt)2] with three-dimensionally arranged magnetic moments exhibiting a coupled electric and magnetic transition. J. Am. Chem. Soc. 2012, 134, 12724–12731. [Google Scholar] [CrossRef] [PubMed]
- Idobata, Y.; Zhou, B.; Kobayashi, A.; Kobayashi, H. Molecular alloy with diluted magnetic moments—Molecular kondo system. J. Am. Chem. Soc. 2012, 134, 871–874. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.B.; Kobayashi, H.; Ishibashi, S.; Sasa, M.; Iwase, F.; Kato, R.; Kobayashi, A. A single-component molecular superconductor. J. Am. Chem. Soc. 2014, 136, 7619–7622. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, S.; Yamamoto, T.; Nakazawa, Y.; Tamura, M.; Kato, R. Gapless spin liquid of an organic triangular compound evidenced by thermodynamic measurements. Nat. Commun. 2011, 2, 275. [Google Scholar] [CrossRef] [PubMed]
- Steimecke, G.; Kirmse, R.; Hoyer, E. Dimercaptoisotrithione. New, unsaturated 1,2-dithiolate ligand. Z. Chem. 1975, 15, 28–29. [Google Scholar] [CrossRef]
- Stach, J.; Kirmse, R.; Dietzsch, W.; Olk, R.M.; Hoyer, E. Single-crystal EPR spectra of tetra-n-butylammonium bis(isotrithione-3,4-dithiolato)cuprate(II) (copper-63). Inorg. Chem. 1984, 23, 4779–4780. [Google Scholar] [CrossRef]
- Matsubayashi, G.; Takahashi, K.; Tanaka, T. X-ray crystal structure of bis(N-ethylpyridinium) bis[4,5-dimercapto-1,3-dithiole-2-thionate(2-)]copper(II) and electrical properties of its oxidized salts. J. Chem. Soc. Dalton Trans. 1988, 967–972. [Google Scholar] [CrossRef]
- Guo, W.F.; Sun, X.B.; Sun, J.; Yu, W.T.; Wang, X.Q.; Zhang, G.H.; Xu, D. Preparation, single crystal growth and characterization of bis(tetrabutylammonium)bis(4,5-dithiolato-1,3-dithiole-2-thione)copper. Cryst. Res. Technol. 2007, 42, 349–335. [Google Scholar]
- Guo, W.F.; Sun, X.B.; Sun, J.; Yu, W.T.; Wang, X.Q.; Zhang, G.H.; Xu, D. Synthesis, crystal structure and third order nonlinear optical properties of bis(tetra-n-propylammonium) bis(2-thioxo-1,3-dithiole-4,5-dithiolato)cuprate(II). Cryst. Res. Technol. 2007, 42, 522–528. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Yu, W.-T.; Xu, D.; Wang, Y.-L.; Li, T.-B.; Zhang, G.-H.; Sun, X.-B.; Ren, Q. Bis(tetraethylammonium) bis(2-thioxo-1,3-dithiole-4,5-dithiolato)cuprate(II). Acta Crystallogr. E 2005, 61, m717–m719. [Google Scholar] [CrossRef]
- Li, T.; Hu, Y.; Ma, C.; He, G.; Zhao, R.; Li, J. Crystal structure and third-order nonlinear optical property study of a copper complex constructed by DMIT ligand. Mater. Chem. Phys. 2011, 130, 835–838. [Google Scholar] [CrossRef]
- Noma, H.; Ohara, K.; Naito, T. [Cu(dmit)2]2− Building block for molecular conductors and magnets with photocontrollable spin distribution. Chem. Lett. 2014, 43, 1230–1232. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Mott, N.F. Metal-Insulator Transitions, 2nd ed.; Taylor & Francis: London, UK, 1990; pp. 123–144. [Google Scholar]
- Jazwinski, J. Theoretical aspects of indirect spin-spin couplings. Nucl. Magn. Res. 2014, 43, 159–182. [Google Scholar]
- Kirmse, R.; Stach, J.; Dietzsch, W.; Steimecke, G.; Hoyer, E. Single-crystal EPR studies on nickel(III), palladium(III), and platinum(III) dithiolene chelates containing the ligands isotrithionedithiolate, o-xylenedithiolate, and maleonitriledithiolate. Inorg. Chem. 1980, 19, 2679–2685. [Google Scholar] [CrossRef]
- Teschmit, G.; Strauch, P.; Barthel, A.; Reinhold, J.; Kirmse, R. A single crystal EPR investigation on (n-Bu4N)2[Cu(dmit)2] in the antiferro-magnetically coupled host lattice (n-Bu4N)2[(dmit)Cu(tto)Cu(dmit)]: A contribution to the nature of the so-called “paramagnetic impurities”. Z. Naturforsch. B 1999, 54, 832–838. [Google Scholar] [CrossRef]
- Nakamura, T.; Takahashi, T.; Aonuma, S.; Kato, R. EPR investigation of the electronic states in β′-type [Pd(dmit)2]2 compounds (where dmit is 2-thioxo-1,3-dithiole-4,5-dithiolate). J. Mater. Chem. 2001, 11, 2159–2162. [Google Scholar] [CrossRef]
- Hoffmann, S.K.; Goslar, J.; Lijewski, S.; Zalewska, A. EPR and ESE of CuS4 complex in Cu(dmit)2: g-Factor and hyperfine splitting correlation in tetrahedral Cu–sulfur complexes. J. Magn. Reson. 2013, 236, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, S.K.; Goslar, J.; Lijewski, S.; Tadyszak, K.; Zalewska, A.; Jankowska, A.; Florczak, P.; Kowalak, S. EPR and UV-VIS study on solutions of Cu(II) dmit complexes and the complexes entrapped in zeolite A and ZIF-Cu(IM)2. Microporous Mesoporous Mater. 2014, 186, 57–64. [Google Scholar] [CrossRef]
- Schmitt, R.D.; Maki, A.H. Electronic ground state of bis(maleonitrile-dithiolene)nickel monoanion. Sulfur-33 hyperfine interaction. J. Am. Chem. Soc. 1968, 90, 2288–2292. [Google Scholar] [CrossRef]
- Kirmse, R.; Dietzsch, W. A single crystal EPR study of the palladium(III)-bis(maleonitriledithiolate)monoanion. J. Inorg. Nucl. Chem. 1976, 38, 255–257. [Google Scholar] [CrossRef]
- Kirmse, R.; Dietzsch, W.; Solovev, B.V. A single crystal EPR study of the platinum (III)-bis(maleonitriledithiolate)-monoanion. J. Inorg. Nucl. Chem. 1977, 39, 1157–1160. [Google Scholar] [CrossRef]
- Steimecke, G.; Sieler, H.-J.; Kirmse, R.; Hoyer, E. 1,3-dithiole-2-thione-4,5-dithiolate from carbon disulfide and alkali metal. Phosphorus Sulfur 1979, 7, 49–55. [Google Scholar] [CrossRef]
- Yordanov, N.D. Quantitative EPR spectrometry—“State of the art”. Appl. Magn. Reson. 1994, 6, 241–257. [Google Scholar] [CrossRef]
- Kai, A.; Miki, T. Electron spin resonance of sulfite radicals in irradiated calcite and aragonite. Radiat. Phys. Chem. 1992, 40, 469–476. [Google Scholar] [CrossRef]
- Inokuchi, H.; Kinoshita, M. The oxygen effect on electronic properties of α,α′-diphenyl-β-picrylhydrazyl. Bull. Chem. Soc. Jpn. 1960, 33, 1627–1629. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.; Millam, J. GaussView, Version 5; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noma, H.; Ohara, K.; Naito, T. Direct Control of Spin Distribution and Anisotropy in Cu-Dithiolene Complex Anions by Light. Inorganics 2016, 4, 7. https://doi.org/10.3390/inorganics4020007
Noma H, Ohara K, Naito T. Direct Control of Spin Distribution and Anisotropy in Cu-Dithiolene Complex Anions by Light. Inorganics. 2016; 4(2):7. https://doi.org/10.3390/inorganics4020007
Chicago/Turabian StyleNoma, Hiroki, Keishi Ohara, and Toshio Naito. 2016. "Direct Control of Spin Distribution and Anisotropy in Cu-Dithiolene Complex Anions by Light" Inorganics 4, no. 2: 7. https://doi.org/10.3390/inorganics4020007
APA StyleNoma, H., Ohara, K., & Naito, T. (2016). Direct Control of Spin Distribution and Anisotropy in Cu-Dithiolene Complex Anions by Light. Inorganics, 4(2), 7. https://doi.org/10.3390/inorganics4020007