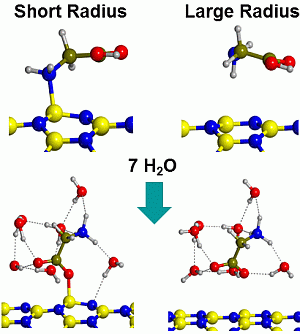
Gas-Phase and Microsolvated Glycine Interacting with Boron Nitride Nanotubes. A B3LYP-D2* Periodic Study
Abstract
:1. Introduction
2. Results and Discussion
2.1. Gas-Phase Interaction
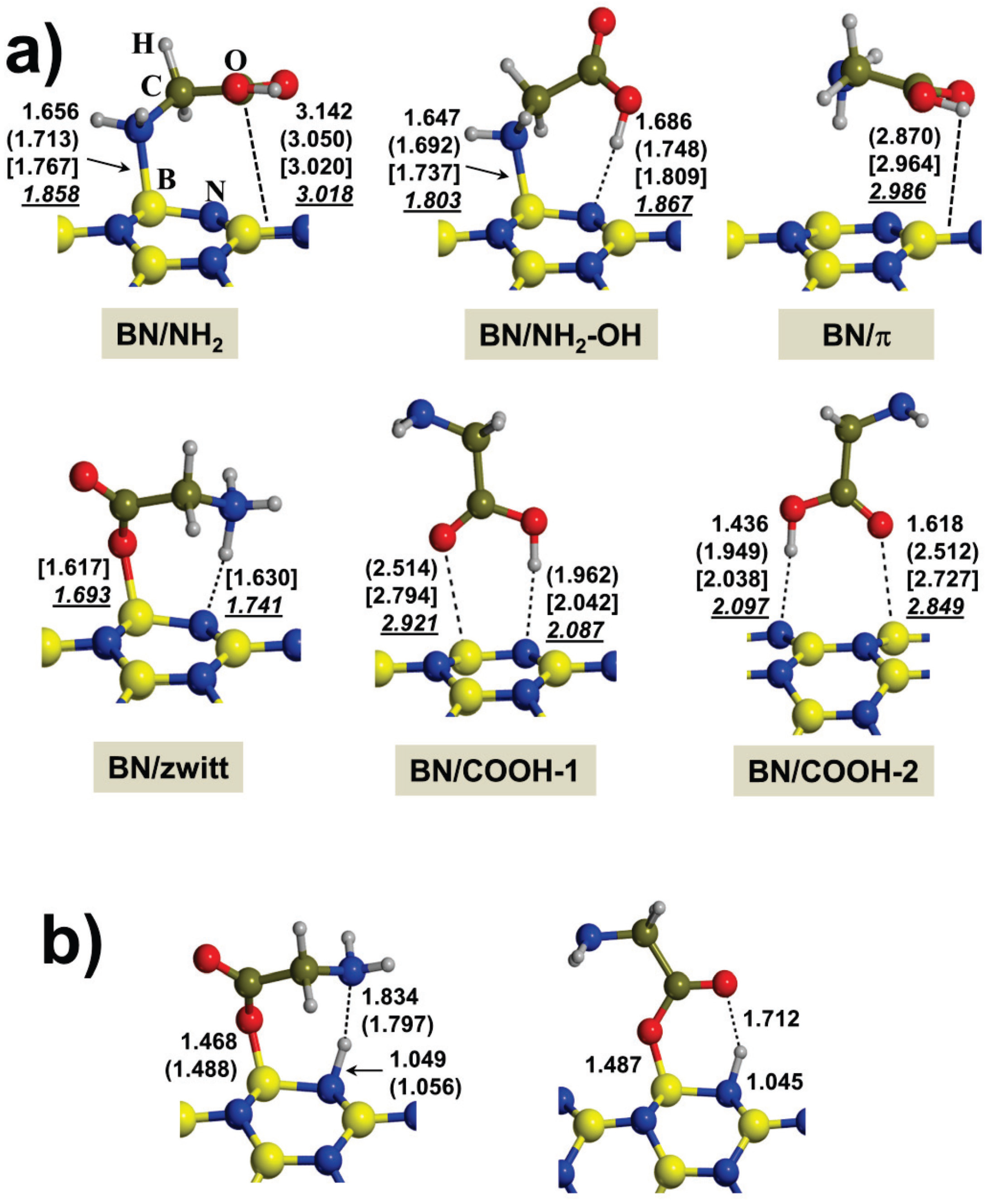
| System | Adduct | ∆Eel | ∆ED | ∆Eads | ∆Erel |
|---|---|---|---|---|---|
| Gly/BNNT(4,0) | BN/NH2 | −20.8 | −11.2 | −31.9 | 1.3 |
| BN/NH2-OH | −22.7 | −10.5 | −33.2 | 0.0 | |
| BN/π | - | - | - | - | |
| BN/zwitt | −20.7 | −10.4 | −31.2 | 2.0 | |
| BN/COOH-1 | −24.6 | −7.1 | −31.7 | 2.2 | |
| BN/COOH-2 | −9.8 | −7.8 | −17.6 | 15.6 | |
| Gly/BNNT(6,0) | BN/NH2 | −6.3 | −12.6 | −18.9 | 0.0 |
| BN/NH2–OH | −6.8 | −11.4 | −18.2 | 0.6 | |
| BN/π | +0.5 | −10.4 | −9.9 | 9.0 | |
| BN/zwitt | −1.8 | −11.7 | −13.5 | 5.4 | |
| BN/COOH-1 | −3.3 | −6.3 | −9.6 | 8.0 | |
| BN/COOH-2 | −3.3 | −6.2 | −9.5 | 8.1 | |
| Gly/BNNT(9,0) | BN/NH2 | +1.5 | −13.5 | −12.0 | 0.0 |
| BN/NH2–OH | +4.3 | −12.0 | −7.7 | 4.3 | |
| BN/π | +1.0 | −11.1 | −10.1 | 1.9 | |
| BN/zwitt | +14.0 | −12.5 | +1.5 | 13.5 | |
| BN/COOH-1 | −2.6 | −6.0 | −8.6 | 3.4 | |
| BN/COOH-2 | −2.2 | −6.1 | −8.3 | 3.7 | |
| Gly/BNNT(15,0) | BN/NH2 | +7.2 | −14.3 | −7.1 | 3.1 |
| BN/NH2–OH | +9.0 | −12.6 | −3.6 | 6.6 | |
| BN/π | +1.5 | −11.7 | −10.2 | 0.0 | |
| BN/zwitt | +20.7 | −13.1 | +7.6 | 17.8 | |
| BN/COOH-1 | −1.4 | −6.1 | −7.5 | 2.7 | |
| BN/COOH-2 | −1.4 | −6.2 | −7.6 | 2.6 |
| System | Adduct | Q (e) | Eg (eV) a |
|---|---|---|---|
| Gly/BNNT(4,0) | BN/NH2 | 0.30 | 3.68 |
| BN/NH2-OH | 0.22 | 3.69 | |
| Gly/BNNT(6,0) | BN/NH2 | 0.23 | 4.46 |
| BN/NH2-OH | 0.16 | 4.45 | |
| Gly/BNNT(9,0) | BN/NH2 | 0.19 | 5.29 |
| BN/π | −0.02 | 5.42 | |
| Gly/BNNT(15,0) | BN/π | −0.02 | 6.06 |
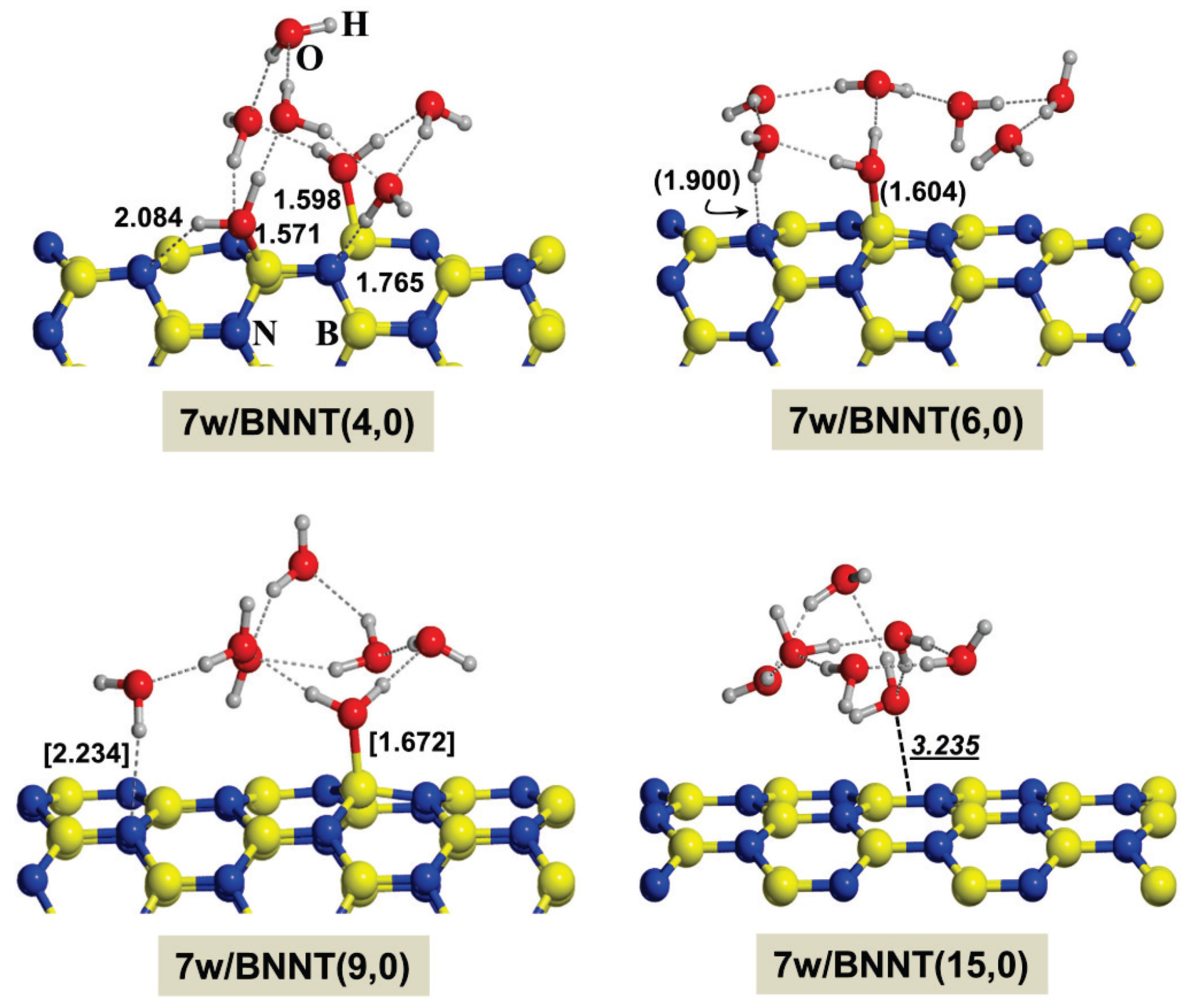
2.2. Microsolvated Interaction

| System | Adduct | ∆Erel | ∆ER1 | ∆ER2 | ∆ER3 |
|---|---|---|---|---|---|
| Gly/7w/BNNT(4,0) | BN/CONH | 5.4 | −28.9 | −11.5 | 11.9 |
| BN/CO-w/NH | 0.0 | −34.3 | −16.9 | 6.5 | |
| BN/NH-w/CO | 4.3 | −30.0 | −12.6 | 10.8 | |
| w/CONH | 2.6 | −31.7 | −14.3 | 9.1 | |
| Gly/7w/BNNT(6,0) | BN/CONH | 5.3 | −13.2 | −20.5 | 2.9 |
| BN/CO-w/NH | 2.9 | −15.7 | −23.0 | 0.4 | |
| BN/NH-w/CO | 4.2 | −14.4 | −21.7 | 1.7 | |
| w/CONH | 0.0 | −18.6 | −25.9 | −2.5 | |
| Gly/7w/BNNT(9,0) | BN/CONH | 12.4 | −5.1 | −20.7 | 2.7 |
| BN/CO-w/NH | 7.7 | −9.8 | −25.4 | −2.0 | |
| BN/NH-w/CO | 10.5 | −7.0 | −22.6 | 0.8 | |
| w/CONH | 0.0 | −17.5 | −33.1 | −9.7 | |
| Gly/7w/BNNT(15,0) | BN/CONH | - | - | - | - |
| BN/CO-w/NH | - | - | - | - | |
| BN/NH-w/CO | - | - | - | - | |
| w/CONH | 0.0 | −12.8 | −31.4 | −8.1 |
3. Computational Details
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kujawa, P.; Winnik, F.M. Innovation in Nanomedicine through Materials Nanoarchitectonics. Langmuir 2013, 29, 7354–7361. [Google Scholar] [CrossRef]
- Wong, S.S.; Joselevich, E.; Woolley, A.T.; Cheung, C.L.; Lieber, C.M. Covalently functionalized nanotubes as nanometre- sized probes in chemistry and biology. Nature 1998, 394, 52–55. [Google Scholar] [CrossRef]
- Aono, M.; Bando, Y.; Ariga, K. Nanoarchitectonics: Pioneering a New Paradigm for Nanotechnology in Materials Development. Adv. Mater. 2012, 24, 150–151. [Google Scholar] [CrossRef]
- Hong, R.; Fischer, N.O.; Verma, A.; Goodman, C.M.; Emrick, T.; Rotello, V.M. Control of Protein Structure and Function through Surface Recognition by Tailored Nanoparticle Scaffolds. J. Am. Chem. Soc. 2004, 126, 739–743. [Google Scholar] [CrossRef]
- You, C.-C.; Agasti, S.S.; De, M.; Knapp, M.J.; Rotello, V.M. Modulation of the Catalytic Behavior of α-Chymotrypsin at Monolayer-Protected Nanoparticle Surfaces. J. Am. Chem. Soc. 2006, 128, 14612–14618. [Google Scholar]
- Kang, Y.; Liu, Y.-C.; Wang, Q.; Shen, J.-W.; Wu, T.; Guan, W.-J. On the spontaneous encapsulation of proteins in carbon nanotubes. Biomaterials 2009, 30, 2807–2815. [Google Scholar]
- Gao, H.; Kong, Y. Simulation of DNA-nanotube interactions. Annu. Rev. Mater. Res. 2004, 34, 123–150. [Google Scholar] [CrossRef]
- Chen, X.; Kis, A.; Zettl, A.; Bertozzi, C.R. A cell nanoinjector based on carbon nanotubes. Proc. Natl. Acad. Sci. USA 2007, 104, 8218–8222. [Google Scholar] [CrossRef]
- Chen, R.J.; Bangsaruntip, S.; Drouvalakis, K.A.; Wong Shi Kam, N.; Shim, M.; Li, Y.; Kim, W.; Utz, P.J.; Dai, H. Noncovalent functionalization of carbon nanotubes for highly specific electronic biosensors. Proc. Natl. Acad. Sci.USA 2003, 100, 4984–4989. [Google Scholar] [CrossRef]
- Chen, R.J.; Zhang, Y.; Wang, D.; Dai, H. Noncovalent Sidewall Functionalization of Single-Walled Carbon Nanotubes for Protein Immobilization. J. Am. Chem. Soc. 2001, 123, 3838–3839. [Google Scholar] [CrossRef]
- Cui, Y.; Wei, Q.; Park, H.; Lieber, C.M. Nanowire Nanosensors for Highly Sensitive and Selective Detection of Biological and Chemical Species. Science 2001, 293, 1289–1292. [Google Scholar] [CrossRef]
- Staii, C.; Johnson, A.T.; Chen, M.; Gelperin, A. DNA-Decorated Carbon Nanotubes for Chemical Sensing. Nano Lett. 2005, 5, 1774–1778. [Google Scholar] [CrossRef]
- Heller, D.A.; Jeng, E.S.; Yeung, T.-K.; Martinez, B.M.; Moll, A.E.; Gastala, J.B.; Strano, M.S. Optical Detection of DNA Conformational Polymorphism on Single-Walled Carbon Nanotubes. Science 2006, 311, 508–511. [Google Scholar] [CrossRef]
- Pantarotto, D.; Partidos, C.D.; Graff, R.; Hoebeke, J.; Briand, J.-P.; Prato, M.; Bianco, A. Synthesis, Structural Characterization, and Immunological Properties of Carbon Nanotubes Functionalized with Peptides. J. Am. Chem. Soc. 2003, 125, 6160–6164. [Google Scholar] [CrossRef]
- Tu, X.; Manohar, S.; Jagota, A.; Zheng, M. DNA sequence motifs for structure-specific recognition and separation of carbon nanotubes. Nature 2009, 460, 250–253. [Google Scholar] [CrossRef]
- Golberg, D.; Bando, Y.; Huang, Y.; Terao, T.; Mitome, M.; Tang, C.; Zhi, C. Boron Nitride Nanotubes and Nanosheets. ACS Nano 2010, 4, 2979–2993. [Google Scholar] [CrossRef]
- Golberg, D.; Bando, Y.; Tang, C.C.; Zhi, C.Y. Boron Nitride Nanotubes. Adv. Mater. 2007, 19, 2413–2432. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M. Physisorption vs. chemisorption of probe molecules on boron nitride nanomaterials: The effect of surface curvature. Phys. Chem. Chem. Phys. 2013, 15, 13190–13198. [Google Scholar] [CrossRef]
- Magrez, A.; Kasas, S.; Salicio, V.; Pasquier, N.; Seo, J.W.; Celio, M.; Catsicas, S.; Schwaller, B.; Forró, L. Cellular Toxicity of Carbon-Based Nanomaterials. Nano Lett. 2006, 6, 1121–1125. [Google Scholar] [CrossRef]
- Chen, X.; Wu, P.; Rousseas, M.; Okawa, D.; Gartner, Z.; Zettl, A.; Bertozzi, C.R. Boron Nitride Nanotubes Are Noncytotoxic and Can Be Functionalized for Interaction with Proteins and Cells. J. Am. Chem. Soc. 2009, 131, 890–891. [Google Scholar]
- Yu, J.; Chen, Y.; Cheng, B.M. Dispersion of boron nitride nanotubes in aqueous solution with the help of ionic surfactants. Solid State Commun. 2009, 149, 763–766. [Google Scholar] [CrossRef]
- Zhi, C.; Bando, Y.; Tang, C.; Golberg, D. Immobilization of Proteins on Boron Nitride Nanotubes. J. Am. Chem. Soc. 2005, 127, 17144–17145. [Google Scholar] [CrossRef]
- Gao, Z.; Zhi, C.; Bando, Y.; Golberg, D.; Serizawa, T. Isolation of Individual Boron Nitride Nanotubes via Peptide Wrapping. J. Am. Chem. Soc. 2010, 132, 4976–4977. [Google Scholar] [CrossRef]
- Zhi, C.; Bando, Y.; Wang, W.; Tang, C.; Kuwahara, H.; Golberg, D. DNA-Mediated Assembly of Boron Nitride Nanotubes. Chem. Asian J. 2007, 2, 1581–1585. [Google Scholar] [CrossRef]
- Ciofani, G.; Raffa, V.; Menciassi, A.; Dario, P. Preparation of Boron Nitride Nanotubes Aqueous Dispersions for Biological Applications. J. Nanosci. Nanotechnol. 2008, 8, 6223–6231. [Google Scholar] [CrossRef]
- Ciofani, G.; Raffa, V.; Menciassi, A.; Cuschieri, A. Cytocompatibility, interactions, and uptake of polyethyleneimine-coated boron nitride nanotubes by living cells: Confirmation of their potential for biomedical applications. Biotechnol. Bioeng. 2008, 101, 850–858. [Google Scholar] [CrossRef]
- Ciofani, G.; Danti, S.; D’Alessandro, D.; Moscato, S.; Menciassi, A. Assessing cytotoxicity of boron nitride nanotubes: Interference with the MTT assay. Biochem. Biophys. Res. Commun. 2010, 394, 405–411. [Google Scholar] [CrossRef]
- Ciofani, G.; Danti, S.; D’Alessandro, D.; Ricotti, L.; Moscato, S.; Bertoni, G.; Falqui, A.; Berrettini, S.; Petrini, M.; Mattoli, V.; et al. Enhancement of Neurite Outgrowth in Neuronal-Like Cells following Boron Nitride Nanotube-Mediated Stimulation. ACS Nano 2010, 4, 6267–6277. [Google Scholar]
- Horváth, L.; Magrez, A.; Golberg, D.; Zhi, C.; Bando, Y.; Smajda, R.; Horváth, E.; Forró, L.; Schwaller, B. In Vitro Investigation of the Cellular Toxicity of Boron Nitride Nanotubes. ACS Nano 2011, 5, 3800–3810. [Google Scholar] [CrossRef]
- Akdim, B.; Kim, S.N.; Naik, R.R.; Maruyama, B.; Pender, M.J.; Pachter, R. Understanding effects of molecular adsorption at a single-wall boron nitride nanotube interface from density functional theory calculations. Nanotechnology 2009, 20, 355705. [Google Scholar] [CrossRef]
- Saikat, M.; Gowtham, S.; Ralph, H.S.; Ravindra, P.; Shashi, P.K. Theoretical study of physisorption of nucleobases on boron nitride nanotubes: A new class of hybrid nano-biomaterials. Nanotechnology 2010, 21, 165703. [Google Scholar] [CrossRef]
- Lin, Q.; Zou, X.; Zhou, G.; Liu, R.; Wu, J.; Li, J.; Duan, W. Adsorption of DNA/RNA nucleobases on hexagonal boron nitride sheet: An ab initio study. Phys. Chem. Chem. Phys. 2011, 13, 12225–12230. [Google Scholar] [CrossRef]
- Wu, X.; An, W.; Zeng, X.C. Chemical Functionalization of Boron−Nitride Nanotubes with NH3 and Amino Functional Groups. J. Am. Chem. Soc. 2006, 128, 12001–12006. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Scheicher, R.H.; Pandey, R.; Karna, S.P. Sensitivity of Boron Nitride Nanotubes toward Biomolecules of Different Polarities. J. Phys. Chem. Lett. 2011, 2, 2442–2447. [Google Scholar] [CrossRef]
- Yang, C.-K. Exploring the interaction between the boron nitride nanotube and biological molecules. Comput. Phys. Commun. 2011, 182, 39–42. [Google Scholar] [CrossRef]
- Noel, Y.; D’Arco, P.; Demichelis, R.; Zicovich-Wilson, C.M.; Dovesi, R. On the Use of Symmetry in the Ab Initio Quantum Mechanical Simulation of Nanotubes and Related Materials. J. Comput. Chem. 2010, 31, 855–862. [Google Scholar]
- Demichelis, R.; Noel, Y.; D’Arco, P.; Rerat, M.; Zicovich-Wilson, C.M.; Dovesi, R. Properties of Carbon Nanotubes: An ab Initio Study Using Large Gaussian Basis Sets and Various DFT Functionals. J. Phys. Chem. C 2011, 115, 8876–8885. [Google Scholar] [CrossRef]
- D’Arco, P.; Noel, Y.; Demichelis, R.; Dovesi, R. Single-layered chrysotile nanotubes: A quantum mechanical ab initio simulation. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef]
- Demichelis, R.; Noel, Y.; D’Arco, P.; Maschio, L.; Orlando, R.; Dovesi, R. Structure and energetics of imogolite: A quantum mechanical ab initio study with B3LYP hybrid functional. J. Mater. Chem. 2010, 20, 10417–10425. [Google Scholar] [CrossRef]
- Ferrari, A.M.; Szieberth, D.; Zicovich-Wilson, C.M.; Demichelis, R. Anatase(001) 3 ML Nanotubes, The First TiO2 Nanotube With Negative Strain Energies: A DFT Prediction. J. Phys. Chem. Lett. 2010, 1, 2854–2857. [Google Scholar] [CrossRef]
- Marx, D.; Hutter, J. Ab Initio Molcular Dynamics: Theory and Implementation. In Modern Methods and Algorithms of Quantum Chemistry; Grotendorst, J., Ed.; Forschungszentrum Jülich: Jülich, Germany, 2000. [Google Scholar]
- Rimola, A.; Civalleri, B.; Ugliengo, P. Neutral vs. Zwitterionic Glycine Forms at the Water/Silica Interface: Structure, Energies, and Vibrational Features from B3LYP Periodic Simulations. Langmuir 2008, 24, 14027–14034. [Google Scholar] [CrossRef]
- Rimola, A.; Corno, M.; Zicovich-Wilson, C.M.; Ugliengo, P. Ab initio modeling of protein/biomaterial interactions: Competitive adsorption between glycine and water onto hydroxyapatite surfaces. Phys. Chem. Chem. Phys. 2009, 11, 9005–9007. [Google Scholar] [CrossRef]
- Schwierz, N.; Horinek, D.; Liese, S.; Pirzer, T.; Balzer, B.N.; Hugel, T.; Netz, R.R. On the Relationship between Peptide Adsorption Resistance and Surface Contact Angle: A Combined Experimental and Simulation Single-Molecule Study. J. Am. Chem. Soc. 2012, 134, 19628–19638. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL09 User’s Manual; University of Torino: Torino, Italy, 2009; p. 307. [Google Scholar]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Civalleri, B.; Zicovich-Wilson, C.M.; Valenzano, L.; Ugliengo, P. B3LYP augmented with an empirical dispersion term (B3LYP-D*) as applied to molecular crystals. CrystEngComm 2008, 10, 405–410. [Google Scholar]
- Rimola, A.; Civalleri, B.; Ugliengo, P. Physisorption of aromatic organic contaminants at the surface of hydrophobic/hydrophilic silica geosorbents: A B3LYP-D modeling study. Phys. Chem. Chem. Phys. 2010, 12, 6357–6366. [Google Scholar] [CrossRef]
- Civalleri, B.; Maschio, L.; Ugliengo, P.; Zicovich-Wilson, C.M. Role of dispersive interactions in the CO adsorption on MgO (001): Periodic B3LYP calculations augmented with an empirical dispersion term. Phys. Chem. Chem. Phys. 2010, 12, 6382–6386. [Google Scholar] [CrossRef]
- Schafer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Doll, K.; Saunders, V.R.; Harrison, N.M. Analytical Hartree–Fock gradients for periodic systems. Int. J. Quantum Chem. 2001, 82, 1–13. [Google Scholar] [CrossRef]
- Doll, K. Implementation of analytical Hartree–Fock gradients for periodic systems. Comput. Phys. Commun. 2001, 137, 74–88. [Google Scholar] [CrossRef]
- Doll, K.; Dovesi, R.; Orlando, R. Analytical Hartree–Fock gradients with respect to the cell parameter for systems periodic in three dimensions. Theor. Chem. Acc. 2004, 112, 394–402. [Google Scholar] [CrossRef]
- Civalleri, B.; D’Arco, P.; Orlando, R.; Saunders, V.R.; Dovesi, R. Hartree-Fock geometry optimisation of periodic systems with the CRYSTAL code. Chem. Phys. Lett. 2001, 348, 131–138. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rimola, A.; Sodupe, M. Gas-Phase and Microsolvated Glycine Interacting with Boron Nitride Nanotubes. A B3LYP-D2* Periodic Study. Inorganics 2014, 2, 334-350. https://doi.org/10.3390/inorganics2020334
Rimola A, Sodupe M. Gas-Phase and Microsolvated Glycine Interacting with Boron Nitride Nanotubes. A B3LYP-D2* Periodic Study. Inorganics. 2014; 2(2):334-350. https://doi.org/10.3390/inorganics2020334
Chicago/Turabian StyleRimola, Albert, and Mariona Sodupe. 2014. "Gas-Phase and Microsolvated Glycine Interacting with Boron Nitride Nanotubes. A B3LYP-D2* Periodic Study" Inorganics 2, no. 2: 334-350. https://doi.org/10.3390/inorganics2020334