Linear Regression for Heavy Tails

Abstract

There exist several estimators of the regression line in the simple linear regression: Least Squares, Least Absolute Deviation, Right Median, Theil–Sen, Weighted Balance, and Least Trimmed Squares. Their performance for heavy tails is compared below on the basis of a quadratic loss function. The case where the explanatory variable is the inverse of a standard uniform variable and where the error has a Cauchy distribution plays a central role, but heavier and lighter tails are also considered. Tables list the empirical sd and bias for ten batches of one hundred thousand simulations when the explanatory variable has a Pareto distribution and the error has a symmetric Student distribution or a one-sided Pareto distribution for various tail indices. The results in the tables may be used as benchmarks. The sample size is n = 100 but results for n = ∞ are also presented. The error in the estimate of the slope need not be asymptotically normal. For symmetric errors, the symmetric generalized beta prime densities often give a good fit.

Contents
1 Introduction	2
2 Background	6
3 Three Simple Estimators: LS, LAD and RMP	12
4 Weighted Balance Estimators	21
4.1 Three Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	21
4.2 The Monotonicity Lemma . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	22
4.3 LAD as a Weighted Balance Estimator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	25
4.4 Variations on LAD: LADPC, LADGC, and LADHC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	26
5 Theil’s Estimator and Kendall’s $\mathit{\tau }$	27
6 Trimming	28
7 Tables	31
7.1 The Empirical sd and Bias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	32
7.2 Parameter Values . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	36
7.3 An Example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	38
8 Conclusions	40
A Tails	43
A.1 Tails of ${\widehat{a}}_{\mathrm{LAD}}$. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	43
A.2 Tails of ${\widehat{a}}_{\mathrm{RM}}$. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	44
A.3 Tails of ${\widehat{a}}_{\mathrm{WB}0}$. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	45
A.4 Tails of ${\widehat{a}}_{\mathrm{LADHC}}$ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	46
A.5 The Left Tail of $D_n$ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	49
B The Poisson Point Process Model	50
B.1 Distributions and Densities of Poisson Point Processes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	50
B.2 Equivalence of the Distributions ${\pi }_a$ for ξ > 1/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	52
B.3 Error Densities with Local Irregularities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	53
B.4 Two Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	54
B.5 Convergence for the LS Estimates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	57
B.6 Convergence for the RM Estimates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	59
C The EGBP Distributions	61
C.1 The Exponential Generalized Beta Prime Densities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	61
C.2 Basic Formulas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	63
C.3 The Closure of EGBP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	64
C.4 The Symmetric Generalized Beta Prime Distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	65
C.5 The Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	66
C.6 Fitting EGBP Distributions to Frequency Plots of log$|\widehat{a}|\left(E\right)$ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	66
C.7 Variations in the Error Density at the Origin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	69
References	71

1. Introduction

The paper treats the simple linear regression

$$Y_i=b+a{X}_i+Y_i^{*}i=1,\dots ,n$$

(1)

when the errors $Y_i^{*}$ are observations from a heavy tailed distribution, and the explanatory variables X_i too.

In linear regression, the explanatory variables are often assumed to be equidistant on an interval. If the values are random, they may be uniformly distributed over an interval or normal or have some other distribution. In this paper, the explanatory variables are random. The X_i are inverse powers of uniform variables U_i in (0,1): $X_i=1/U_i^{\xi }$. The variables X_i have a Pareto distribution with tail index ξ > 0. The tails become heavier as the index increases. For ξ ≥ 1, the expectation is infinite. We assume that the error variables $Y_i^{*}$ have heavy tails too, with tail index η > 0. The aim of this paper is twofold:

• The paper compares a number of estimators E for the regression line in the case of heavy tails. The distribution of the error is Student or Pareto. The errors are scaled to have InterQuartile Distance IQD = 1. The tail index ξ of the Pareto distribution of the explanatory variable varies between zero and three; the tail index η of the error varies between zero and four. The performance of an estimator E is measured by the loss function L(u) = u² applied to the difference between the slope a of the regression line and its estimate ${\widehat{a}}_E$. Our approach is unorthodox. For various values of the tail indices ξ and η, we compute the average loss for ten batches of a hundred thousand simulations of a sample of size one hundred. Theorems and proofs are replaced by tables and programs. If the error has a symmetric distribution, the square root of the average loss is the empirical sd (standard deviation). From the tables in Section 7, it may be seen that, for good estimators, this sd depends on the tail index of the explanatory variables rather than the tail index of the error. As a rule of thumb, the sd is of the order of

  1/10^{ξ + 1}  0 ≤ ξ ≤ 3,  0 ≤ η ≤ 4,  n = 100.

  (2)
  This crude approximation is also valid for errors with a Pareto distribution. It may be used to determine whether an estimator of the regression line performs well for heavy tails.
• The paper introduces a new class of non-linear estimators. A weighted balance estimator of the regression line is a bisector of the sample. For even sample size half the points lie below the bisector, half above. There are many bisectors. A weight sequence is used to select a bisector which yields a good estimate of the regression line. Weighted balance estimators for linear regression may be likened to the median for univariate samples. The LAD (Least Absolute Deviation) estimator is a weighted balance estimator. However, there exist weighted balance estimators which perform better when the explanatory variable has heavy tails.

The results of our paper are exemplary rather than analytical. They describe the outcomes of an initial exploration on estimators for linear regression with heavy tails. The numerical results in the tables in Section 7 may be regarded as benchmarks. They may be used to measure the performance of alternative estimators. Insight in the performance of estimators of the regression line for samples of size one hundred where the explanatory variable has a Pareto distribution and the error a Student or Pareto distribution may help to select a good estimator in the case of heavy tails.

The literature on the LAD(Least Absolute Deviation) estimator is extensive (see Dielman (2005)). The theory for the TS (Theil–Sen) estimator is less well developed, even though TS is widely used for data which may have heavy tails, as is apparent from a search on the Internet. A comparison of the performance of these two estimators is overdue.

When the tail indices ξ and η are positive, outliers occur naturally. Their effect on estimates has been studied in many papers. A major concern is whether an outlier should be accepted as a sample point. In simulations, contamination does not play a role. In this paper, outliers do not receive special attention. Robust statistics does not apply here. If a good fairy were to delete all outliers, that would incommode us. It is precisely the outliers which allow us to position the underlying distribution in the (ξ,η)-domain and select the appropriate estimator. Equation (2) makes no sense in robust regression. Our procedure for comparing estimators by computing the average loss over several batches of a large number of simulations relies on uncontaminated samples. This does not mean that we ignore the literature on robust regression. Robust regression estimates may serve as initial estimates. (This approach does not do justice to the special nature of robust regression, which aims at providing good estimates of the regression line when working with contaminated data.) In our paper, we have chosen a small number of geometric estimators of the regression line, whose performance is then compared for a symmetric and an asymmetric error distribution at various points in the ξ,η-domain, see Figure 1a. In robust regression, one distinguishes M-, R- and L-estimators. We treat the M-estimators LS and LAD. These minimize the ${\mathit{l}}^p$ distance of the residuals for p = 2 and p = 1, respectively. We have not looked at other values of p ∈ [1,∞). Tukey’s biweight and Huber’s Method are non-geometric M-estimators since the estimate depends on the scaling on the vertical axis. The R-estimators of Jaeckel and Jurečková are variations on the LAD estimator. They are less sensitive to the behaviour of the density at the median, as we show in Section 3. They are related to the weighted balance estimators WB40, and are discussed in Section 4. Least Trimmed Squares (LTS) was introduced in Rousseeuw (1984). It is a robust version of least squares. It is a geometric L estimator. Least Median Squares introduced in the same paper yields the central line of a closed strip containing fifty of the hundred sample points. It selects the strip with minimal vertical width. If the error has a symmetric unimodal density one may add the extra condition that there are twenty five sample points on either side of the strip. This estimator was investigated in a recent paper Postnikov and Sokolov (2015). Maximum Likelihood may be used if the error distribution is known. We are interested in estimators which do not depend on the error distribution, even though one has to specify a distribution for the error in order to measure the performance. Nolan and Ojeda-Revah (2013) uses Maximum Likelihood to estimate the regression line when the errors have a stable distribution and the explanatory variable (design matrix) is deterministic. The paper contains many references to applications. The authors write: “In these applications, outliers are not mistakes, but an essential part of the error distribution. We are interested in both estimating the regression coefficients and in fitting the error distribution.” These words also give a good description of the aim of our paper.

There is one recent paper which deserves special mention. It uses the same framework as our paper. In Samorodnitsky et al. (2007), the authors determined limit distributions for the difference ${\widehat{a}}_E-a$ for certain linear estimators for the linear regression $Y_i=a{X}_i+Y_i^{*}$. The error Y^* is assumed to have a symmetric distribution with power tails, and the absolute value of the explanatory variable also has a power tail. The tail indices are positive. The estimators are linear expressions in the error terms and functions of the absolute value of the explanatory variables (which in our paper are assumed to be positive):

$${\widehat{a}}_E-a=\sum |X_i{|}^{1/(\theta -1)}{Y}_i^{*}/\sum {\left|X_i\right|}^{\theta /(\theta -1)}.$$

The estimator E = E_θ depends on a parameter θ > 1 . The value θ = 2 yields LS. The paper distinguishes seven subregions in the positive (ξ,η)-quadrant with different rates of convergence. The paper is theoretical and focuses on the limit behaviour of the distribution of the estimator when the sample size tends to infinity. We look at the same range of values for the tail indices ξ and η, but our approach is empirical. We focus on estimators which perform well in terms of the quadratic loss function L(u) = u². Such estimators are non-linear. We allow non-symmetric error distributions, and our regression line may have a non-zero abscissa. We only consider two classes of dfs for the error term, Student and Pareto, and our explanatory variables have a Pareto distribution. We restrict attention to the rectangle, (ξ,η) ∈ [0,3] × [0,4]. In our approach, the horizontal line η = 1/2 and the vertical line ξ = 1/2 turn out to be critical, but for ξ,η ≥ 1/2 the performance of the estimators depends continuously on the tail indices. There are no sharply defined subregions where some estimator is optimal. Our treatment of the behaviour for n → ∞ is cursory. The two papers present complementary descriptions of linear regression for heavy tails.

Let us give a brief overview of the contents. The exposition in Section 2 gives some background and supplies the technical details for understanding the results announced above. The next four sections describe the estimators which are investigated in our paper. The first describes the three well-known estimators LS, LAD and RMP. Least Squares performs well for 0 ≤ η < 1/2 when the error has finite variance. Least Absolute Deviation performs well when ξ is small. The estimator RMP (RightMost Point) selects the bisector which passes through the rightmost sample point. Its performance is poor, but its structure is simple. The next section treats the Weighted Balance estimators. The third treats Theil’s estimator which selects the line such that Kendall’s tau vanishes for the residuals, rather than the covariance as for Least Squares. It also introduces a weighted version of the Theil–Sen estimator. The last of these four sections introduces four estimators based on trimming: the Weighted Least Trimmed Squares estimator, WLTS, a weighted version of the estimator introduced by Rousseeuw and described above, and three estimators which select a bisector for which a certain state function is minimal when the 25 furthest points above the bisector are trimmed and the furthest 25 below. For these three estimators, trimming is related to the procedure RANSAC proposed in Fischler and Bolles (1981) for image analysis.

The heart of our paper is the set of tables in Section 7 where for ξ = 0, 1/2, 1, 3/2, 2, 3 we compare the performance of different estimators. The errors have a Student or Pareto distribution. The tail index of these distributions varies over 0, 1/3, 1/2, 2/3, 1, 3/2, 2, 3, 4. To make the results for different values of the tail index η comparable, the errors are standardized so that their df F^* satisfies

F^*(−1/2) = 1/4  F^*(1/2) = 3/4.

(3)

This ensures that the InterQuartile Distance is IQD = 1. There are three sets of six tables corresponding to the six values of the tail index of the explanatory variable, ξ = 0, 1/2, 1, 3/2, 2, 3.

• The first set of tables lists the empirical sd for LS, LAD, Power Corrected LAD, the Theil–Sen estimator and three estimators based on trimming, all for errors with a Student distribution. The estimators do not depend on the tail index of the error.
• The second set of tables lists the empirical sd for the Hyperbolic Correction of LAD, the Right Median, RM, the Hyperbolic Balance estimators HB0 and HB40, Weighted Theil–Sen, and Weighted Least Trimmed Squares, WLTS, all for errors with a Student distribution. The estimators contain parameters which depend on the value of the tail indices, ξ and η. Thus, the Right Median, RM, depends on an odd positive integer which tells us how many of the rightmost points are used for the median. In WLTS, there are three parameters, the number of sample points which are trimmed, and two positive real valued parameters which determine a penalty for deleting sample points which lie far to the right.
• The third set of tables does the same as the second, but here the errors have a Pareto distribution. Both the empirical sd and bias of the estimates are listed.

The estimators yielding the tables are simple functions of the 2n real numbers which determine the sample. Apart from a choice of the parameters they do not depend on the form of the distribution of the error or the explanatory variable. The results show a continuous dependence of the empirical sd on the tail indices ξ and η both for Student and for Pareto errors. The sd and the value of the parameters are different in the third set of tables (Pareto errors) and the second (Student errors) but the similarity of the performance of the estimators for these two error distributions suggests that the empirical sds in these tables will apply to a wide range of error densities. The fourth table lists the optimal values of the parameters for various estimators. The example in Section 7.3 shows how the techniques of the paper should be applied to a sample of size n = 231 if neither the values of the tail indices ξ and η nor the distribution of the error are known.

The results in the three tables are for sample size n = 100. The explanatory variables are independent observations from a Pareto distribution on (1,∞), with tail index ξ > 0, arranged in decreasing order. One may replace these by the hundred largest points in a Poisson point process on (0,∞) with a Pareto mean measure with the same tail index. This is done in Appendix B. A scaling argument shows that the slope of the estimate of the regression line for the Poisson point process is larger by a factor approximately 100^ξ compared to the iid sample. For the Poisson point process the rule of thumb in Equation (2) for the sd of the slope for good estimators has to be replaced by

10^ξ−1  0 ≤ ξ ≤ 3,  0 ≤ η ≤ 4,  n = 100.

(4)

The performance decreases with ξ since the fluctuations in the rightmost point around the central value x = 1 increase and the remaining 99 sample points X_i, i > 1, with central value 1/i^ξ, tend to lie closer to the vertical axis as ξ increases and hence give less information about the slope of the regression line.

What happens if one uses more points of the point process in the estimate? For ξ ≤ 1/2, the full sequence of the points of the Pareto point process together with the independent sequence of errors $Y_n^{*}$ determines the true regression line almost surely. The full sequence always determines the distribution of the error variable, but for errors with a Student distribution and ξ > 1/2 it does not determine the slope of the regression line. For weighted balance estimators, the step from n = 100 to ∞ is a small one. If ξ is large, say ξ ≥ 3/4, the crude Equation (4) remains valid for sample size n > 100.

Conclusions are formulated in Section 8. The Appendix contains three sections: Appendix A treats tails and shows when tails of Weighted Balance estimators $\widehat{a}$ are comparable to those of the error Y^*, and when they have finite second moment; Appendix B gives a brief exposition of the alternative Poisson point process model; and Appendix C introduces EGBP distributions. These often give a surprisingly good fit to the distribution of the logarithm of the absolute value of ${\widehat{a}}_E$ for symmetric errors.

2. Background

In this paper, both the explanatory variables X_i and the errors $Y_i^{*}$ in the linear regression

$$Y_i=b+a{X}_i+Y_i^{*}i=1,\dots ,n$$

have heavy tails. The vectors(X₁, …, X_n) and $(Y_1^{*},\dots ,Y_n^{*})$ are independent; the $Y_i^{*}$ are iid; and the X_i are a sample from a Pareto distribution on (1,∞) arranged in decreasing order:

X_n < ⋯ < X₂ < X₁.

The Pareto explanatory variables may be generated from the order statistics U₁ < ⋯ < U_n of a sample of uniform variables on (0,1) by setting $X_i=1/U_i^{\xi }$. The parameter ξ > 0 is called the tail index of the Pareto distribution. Larger tail indices indicate heavier tails. The variables $Y_i^{*}$ have tail index η. They typically have a symmetric Student t distribution or a Pareto distribution. For the Student distribution, the tail index η is the inverse of the degrees of freedom. At the boundary, η = 0 and the Student distribution becomes Gaussian, the Pareto distribution exponential.

The problem addressed in this paper is simple: What are good estimators of the regression line for a given pair (ξ,η) of positive power indices?

For η < 1/2, the variable Y^* has finite variance and LS (Least Squares) is a good estimator. For ξ < 1/2, the Pareto variable X = 1/U^ξ has finite variance. In that case, the LAD (Least Absolute Deviation) often is a good estimator of the regression line. Asymptotically it has a (bivariate) normal distribution provided the density of Y^* is positive and continuous at the median, see Van de Geer (1988). What happens for (ξ,η) ∈ [1/2,∞)²? In the tables in Section 7, we compare the performance of several estimators at selected parameter values (ξ,η) for sample size n = 100. See Figure 1a. First, we give an impression of the geometric structure of the samples which are considered in this paper, and describe how such samples may arise in practice.

For large ξ, the distribution of the points X_i along the positive horizontal axis becomes very skewed. For ξ = 3 and a sample of a hundred $\mathbb{P}\{X_1>100X_2\}>1/5$. 1 Exclude the rightmost point. The remaining 99 explanatory variables then all lie in an interval which occupies less than one percent of the range. The point (X₁,Y₁) is a pivot. It yields excellent estimates of the slope if the absolute error is small. The estimator RMP (RightMost Point) may be expected to yield good results. This estimator selects the bisector which passes through (X₁,Y₁).

Definition 1.

A bisector of the sample is a line which divides the sample into two equal parts. For an even sample of size 2m, one may choose the line to pass through two sample points: m − 1 sample points then lie above the line and the same number below.

The estimator RMP will perform well most of the time but if Y^* has heavy tails RMP may be far off the mark occasionally, even when η < ξ. What is particularly frustrating are situations like Figure 1b where RMP so obviously is a poor estimate.

Figure 1a shows the part of (ξ,η)-space to which we restrict attention in the present paper. For practical purposes, the square 0 ≤ ξ, η ≤ 3/2 is of greatest interest. The results for other values of ξ and η may be regarded as the outcome of stress tests for the estimators.

Often, the variables $Y_i^{*}$ are interpreted as iid errors. It then is the task of the statistician to recover the linear relation between the vertical and horizontal coordinate from the blurred data for Y. The errors are then usually assumed to have a symmetric distribution, normal or stable.

There is a different point of view. For a bivariate normal vector (X,Y), there exists a line, the regression line y = b + ax, such that conditional on X = x the residual Y^* = Y − (ax + b) has a centred normal distribution independent of x. A good estimate of the regression line will help to obtain a good estimate of the distribution of (X,Y). This situation may also occur for heavy-tailed vectors.

Heffernan and Tawn (2004) studies the distribution of a vector conditional on the horizontal component being large. In this conditional extreme value model, the authors focus on the case where the conditional distribution of Y given X = x is asymptotically independent of x for x → ∞. The vector Z = (X,Y) conditioned to lie in a half plane H_t = {x > t} is a high risk scenario, denoted by Z^H_t. Properly normalized, the high risk scenarios Z^H_t may have a limit distribution for t → ∞. From univariate extreme value theory, we know that the horizontal coordinate of the limit vector has a Pareto or exponential distribution. In the Heffernan–Tawn model, the vertical coordinate of the limit vector is independent of the horizontal coordinate. Heffernan and Tawn in Heffernan and Tawn (2004) considered vectors with light tails. The results were extended to heavy tails by Heffernan and Resnick in Heffernan and Resnick (2007). See Balkema and Embrechts (2007) for a list of all limit distributions.

Given a sample of a few thousand observations from a heavy-tailed bivariate distribution, one will select a subsample of say the hundred points for which the horizontal coordinate is maximal. This yields a sequence x₁ > ⋯ > x₁₀₀. The choice of the horizontal axis determines the vertical coordinate in the points (x₁,y₁), …, (x₁₀₀,y₁₀₀). In the Heffernan–Tawn model, the vertical coordinate may be chosen to be asymptotically independent of x for x → ∞. To find this preferred vertical coordinate, one has to solve the linear regression Equation (1). The residuals, ${\widehat{y}}_i=y_i-(\widehat{b}+\widehat{a}{x}_i)$, allow one to estimate the distribution of the error $Y_i^{*}=Y_i-(b+a{X}_i)$ and the tail index η.

The model $(X_i,Y_i^{*})$, where X₁ > ⋯ > X_n are the extreme sample points and the vertical coordinates $Y_i^{*}$ are asymptotically iid and independent of the values X_i, yields a nice bivariate extension of univariate Extreme Value Theory. In our analysis of the Heffernan-Tawn model, it became clear that good estimates of the slope of the regression line for heavy tails are essential if one wants to apply the model. The interpretation of the data should not effect the statistical analysis. Our interest in the Heffernan–Tawn model accounts for the Pareto distribution of the explanatory variable and the assumption of heavy tails for the error term. It also accounts for our focus on estimates of the slope.

We restrict attention to geometric estimators of the regression line. Such estimators are called contravariant in Lehmann (1983). A transformation of the coordinates has no effect on the estimate of the regression line L. It is only the coordinates which are affected.

Definition 2.

The group $\mathcal{G}$ of affine transformations of the plane which preserve orientation and map right vertical half planes into right vertical half planes consists of the transformations

(x^′, y^′) = (px + q, ax + b + cy)  p > 0, c > 0.

(5)

An estimator of the regression line is geometric if the estimate is not affected by coordinate transformations in $\mathcal{G}$.

Simulations are used to compare the performance of different estimators. For geometric estimators, one may assume that the true regression line is the horizontal axis, that the Pareto distribution of the explanatory variables X_i is the standard Pareto distribution on (1,∞) with tail $\mathbb{P}\{X>x\}=1/x^{1/\xi }$, and that the errors are scaled to have IQD = 1. Scaling by the InterQuartile Distance IQD allows us to compare the performance of an estimator for different error distributions.

The aim of this paper is to compare various estimators of the regression line for heavy tails. The heart of the paper is the set of tables in Section 7. To measure the performance of an estimator E we use the loss function L(a) = a². We focus on the slope of the estimated regression line $y={\widehat{b}}_E+{\widehat{a}}_{E}x$. For given tail indices (ξ,η), we choose X = 1/U^ξ Pareto and errors Y^* with a Student or Pareto distribution with tail index η, scaled to have IQD = 1. We then compute the average loss L_r of the slope ${\widehat{a}}_E$ for r simulations of a sample of size n = 100 from this distribution. $L_r=\sum {({\widehat{a}}_E\left(i\right)-a)}^2/r$ where the sum is taken over the outcomes ${\widehat{a}}_E\left(i\right)$ for r simulations. We choose r = 10⁵. The square root $\gamma =\sqrt{L_r}$ is our measure of performance. It is known as RMSE (Root Mean Square Error). We do not use this term. It is ambiguous. The mean may indicate the average, but also the expected value. Moreover, in this paper, the error is the variable Y^* rather than the difference ${\widehat{a}}_E-a$. If the df F^* of Y^* is symmetric, the square root $\gamma =\sqrt{L_r}$ is the empirical sd of the sequence of r outcomes of ${\widehat{a}}_E$. The quantity γ is random. If one starts with a different seed, one obtains a different value γ. Since r is large. one may hope that the fluctuations in γ for different batches of r simulations is small. The fluctuations depend on the distribution of γ, and this distribution is determined by the tail of the random variable ${\widehat{a}}_E$. The average loss L_r is asymptotically normal if L has a finite second moment. For this, the estimate ${\widehat{a}}_E$ has to have a finite fourth moment. In Section 3, the distribution of γ is analyzed for ξ = η = i/10, i = 2, …, 7, for the estimator E = LS and Student errors. We show how the distribution of γ changes on passing the critical value η = 1/2.

The fluctuations in γ are perhaps even more important than the average value in determining the quality of an estimator. To quantify the fluctuations in γ we perform ten batches of 10⁵ simulations. This yields ten values γ_i for the empirical sd. Compute the average μ and the sd $\delta =\sqrt{{({\gamma }_1-\mu )}^2+\cdots +{({\gamma }_{10}-\mu )}^2}/3$. The two quantities μ and δ describe the performance of the estimator. Approximate δ by one of

…, 20, 10, 5, 2, 1, 0.5, 0.2, 0.1, 0.05, 0.02, 0.01, 0.005, 0.002, 0.001, 0.0005, 0.0002, 0.0001, 0.00005,…

Now, approximate the pair (μ,δ) by (m/10^k, d/10^k) with d ∈ {1, 2, 5} and m an integer. For the representation (m/10^k, d/10^k), it suffices to know the integers m,k and the digit d ∈ {1, 2, 5}. In our case, δ typically is small, 0 < δ < 1 for estimators with good performance. In that case, k is non-negative and one can reconstruct m and k from the decimal fraction m/10^k provided one writes out all k digits after the decimal point, including the zeros. That allows one to reconstruct the pair (m/10^k, d/10^k) from m/10^k[d]. This lean notation is also possible if one writes m/10^k as me − k, as in 17e + 6, the standard way to express seventeen million in R. In this paper, we often write m/10^k[d] except when this notation leads to confusion. Here are some examples: For (μ, δ) = (0.01297, 0.000282), (136.731 × 10⁻⁷, 1.437 × 10⁻⁷), (221.386, 3.768), (221.386, 37.68) and (334567.89, 734567.89) the recipe gives:

0.0130[2]  137e − 7[1]  221[5]  220[50]  0e + 6[1].

(6)

Actually, we still have to say how we reduce δ to d/10^k. Take d = 1; if 10^kδ lies in [0.7, 1.5], d = 2 for 1.5 ≤ 10^kδ < 3 and d = 5 for 3 ≤ 10^kδ < 7. Finally, define $m=round\left({10}^k\mu \right)$. In Equation (6), the reader sees at a glance the average of the outcomes γ_i of the ten batches, and the magnitude of the fluctuations.

Let us mention two striking results of the paper. The first concerns LAD (Least Absolute Deviation), a widely used estimator which is more robust than LS (Least Squares) since it minimizes the sum of the absolute deviations rather than their squares. This makes the estimator less sensitive to outliers of the error. The LAD estimate of the regression line is a bisector of the sample. For ξ > 1/2, the outliers of the explanatory variable affect the stability of the LAD estimate (see Rousseeuw (1991), p. 11).

Table 1. The empirical sd for ${\widehat{a}}_{\mathrm{LAD}}$.

$\mathit{\xi }\setminus \mathit{\eta }$	0	1/2	1	3/2	2	3	4
0	0.0969[2]	0.0951[2]	0.0917[5]	0.0869[2]	0.0810[5]	0.0681[5]	0.0560[5]
1/2	0.0641[2]	0.0690[2]	0.1[1]	3[5]	40[50]	1e+7[1]	2e+10[5]

lists some results from Section 7 for the empirical sd of the LAD-estimate.

The message from the table is clear. For errors with infinite second moment, η ≥ 1/2, use LAD, but not when ξ ≥ 1/2. Actually, the expected loss for ${\widehat{a}}_{\mathrm{LAD}}$ is infinite for η ≥ 1/2 for all ξ. In this respect LAD is no better than LS. If the upper tail of the error varies regularly with negative exponent, the quotient

$$Q\left(t\right):=\mathbb{P}\{Y^{*}>t\}/\mathbb{P}\{{\widehat{a}}_{\mathrm{LAD}}>t\}$$

is a bounded function on $\mathbb{R}$. See Theorem 2.

The discrepancy between the empirical sd, based on simulations, and the theoretical value is disturbing. Should a risk manager feel free to use LAD in a situation where the explanatory variable is positive with a tail which decreases exponentially and the errors have a symmetric unimodal density? Conversely, should she base her decision on the mathematical result in the theorem? The answer is clear: One hundred batches of a quintillion simulations of a sample of size n = 100 with X standard exponential and Y^* Cauchy may well give outcomes which are very different from 0.0917[5]. Such outcomes are of no practical interest. The empirical sds computed in this paper and listed in the tables in Section 7 may be used for risks of the order of one in ten thousand, but for risks of say one in ten million—risks related to catastrophic events—other techniques have to be developed.

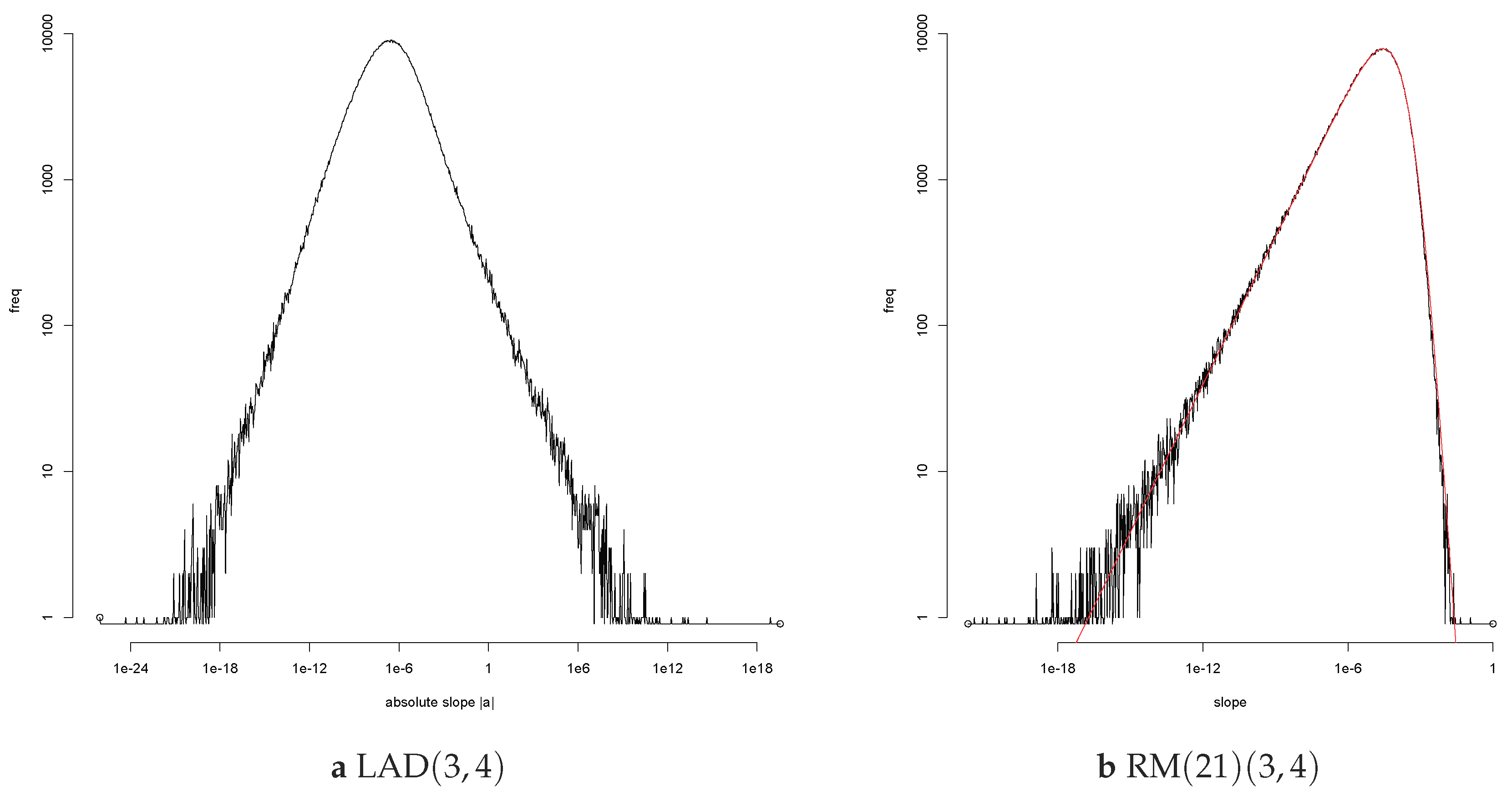
A million simulations allow one to make frequency plots which give an accurate impression of the density when a density exists. Such plots give more information then the empirical sd; they suggest a shape for the underlying distribution. We plot the log frequencies in order to have a better view of the tails. Log frequencies of Gaussian distributions yield concave parabolas. Figure 2 shows loglog frequency plots for two estimators of the regression line for errors with a symmetric Student distribution for (ξ,η) = (3,4). A loglog frequency plot of $|\widehat{a}|$ plots the log of the frequency of $log|\widehat{a}|$. It yields a plot with asymptotes with non-zero slopes if the df of $|\widehat{a}|$ has power tails at zero and infinity.

First, consider the loglog frequency plot of $|{\widehat{a}}_{\mathrm{LAD}}|$ on the left. The range of $|{\widehat{a}}_{\mathrm{LAD}}|$ in Figure 2a is impressive. The smallest value of |a| is of the order of 10⁻²⁴, the largest of the order of 10²⁰. A difference of more than forty orders of magnitude. Accurate values occur when X₁ is large and |Y^*| is small. The LAD estimate of the regression line is a bisector of the sample. In extreme cases it will pass through the rightmost point and agree with the RMP estimate. The value will then be of the order of 1/X₁. The minimum is determined by the minimal value of 10⁸ simulations of a standard uniform variable. For ξ = 3, this gives the rough value 10⁻²⁴ for the most accurate estimate. Large values of |a| are due to large values of |Y₁|. Because of the tail index η = 4, the largest value of |Y₁| will be of the order of 10²⁴. Then, |Y₁|/X₁ is of the order of 10¹⁸. For the tail index pair (ξ,η) = (3,4), the limits of computational accuracy for R are breached.

The asymptotes in the loglog frequency plots for $|\widehat{a}|$ correspond to power tails for $|\widehat{a}|$, at the origin and at infinity. The slope of the asymptote is the exponent of the tail. The plot on the right, Figure 2b, shows that it is possible to increase the absolute slope of the right tail and thus reduce the inaccurate estimates. The value 0e+16[1] for the sd of the LAD estimate of the slope is reduced to 0.00027[5] for RM(21). The Right Median estimate RM(21) with parameter 21 is a variation on the Rightmost Point estimate RMP. Colour the 21 rightmost sample points red and then choose the bisector of the sample which also is a bisector of the red points. This is a discrete version of the cake cutting problem: “Cut a cake into two equal halves, such that the icing is also divided fairly.” The RM estimate passes through a red and a black point. Below the line are 49 sample points, ten of which are red; above the line too. The tail index of $\widehat{a}={\widehat{a}}_{\mathrm{RM}\left(21\right)}$ is at most 2η/20 = 0.4 by Theorem A2. The estimate $\widehat{a}$ has finite sd even though the value 0.00027[5] shows that the fluctuations in the empirical sd for ten batches of a hundred thousand simulations are relatively large.

The smooth red curve in the right hand figure is the EGBP fit to the log frequency plot of $log|\widehat{a}|$, see Appendix C.

The tables in Section 7 compare the performance of various estimators. It is not the value of the empirical sds listed in these tables which are important, but rather the induced ordering of the estimators. For any pair (ξ,η) and any estimator E, the empirical sd and the value of the parameter will vary when the df F^* of the error Y^* is varied, but the relative order of the estimators is quite stable as one sees by comparing the results for Student and Pareto errors with the same tail indices.

The remaining part of this section treats the asymptotic behaviour of estimators when the sample size tends to ∞ via a Poisson point process approach. This part may be skipped on first reading.

Recall that our interest in the problem of linear regression for heavy tails was triggered by a model in extreme value theory. One is interested in the behaviour of a vector X when a certain linear functional $Z=\zeta \left(\mathbf{X}\right)$ is large. What happens to the distribution of the high risk scenario ${\mathbf{X}}^{H_t}$ for the half space H_t = {ζ ≥ t} for t → ∞? We consider the bivariate situation and choose coordinates such that ζ is the first coordinate. In the Heffernan–Tawn model, one can choose the second coordinate such that the two coordinates of the high risk scenario are asymptotically independent. More precisely there exist normalizations of the high risk scenarios, affine transformations mapping the vertical half plane H_t onto H₁ such that the normalized high risk scenarios converge in distribution. The limit scenario lives on H₁ = {x ≥ 1}. The first component of the limit scenario has a Pareto (or exponential) distribution and is independent of the second component. The normalizations which yield the limit scenario, applied to the samples, yield a limiting point process on {x > 0} (by the Extension Theorem, Theorem 14.12, in Balkema and Embrechts (2007).) If the limit scenario has density r(x)f^*(y) on H₁ with r(x) = λ/x^{λ + 1} on (1, ∞), the limit point process is a Poisson point process N₀ with intensity r(x)f^*(y) where r(x) = λ/x^{λ + 1} on (0, ∞). It is natural to use this point process N₀ to model the hundred points with the maximal x-values in a large sample from the vector X.

For high risk scenarios, estimators may be evaluated by looking at their performance on the hundred rightmost points of this Pareto point process. For geometric estimators the normalizations linking the sample to the limit point process do not affect the regression line since the normalizations belong to the group $\mathcal{G}$ used in the definition of geometric estimator above. The point process N₀ actually is a more realistic model than an iid sample.

For geometric estimators, there is a simple relation between the slope A_n of the regression line for the n rightmost points $({\tilde{X}}_i,Y_i^{*})$,i = 1, …, n, of the point process N₀ and the slope ${\widehat{a}}_n$ of the regression line for a sample of n independent observations $(X_i,Y_i^{*})$:

$$A_n=Z_n^{\xi }{\widehat{a}}_n\sqrt{\mathbb{E}{A}_n^2}={\zeta }_n\sqrt{\mathbb{E}{\widehat{a}}_n^2}{\zeta }_n=\sqrt{\mathbb{E}{Z}_n^{2\xi }}.$$

(7)

The first n points of the standard Poisson point process divided by the next point, Z_n, are the order statistics from the uniform distribution on (0,1) and independent of the Gamma(n + 1) variable Z_n with density xⁿe^−x/n! on (0,∞).) A simple calculation shows that ζ_n = n^ξ + c(ξ) + o(1) for n → ∞.

The point process N_a with points $({\tilde{X}}_i,Y_i)$, $Y_i=Y_i^{*}+a{X}_i$, has intensity r(x)f^*(y − ax). The step from n to n + 1 points in estimating the linear regression means that one reveals the n + 1 st point of the point process N_a. This point lies close to the vertical axis if n is large and very close if ξ > 0 is large too. The new point will give more accurate information about the abscissa b of the regression line than the previous points since the influence of the slope decreases. For the same reason, it will give little information on the value of the slope a. The point process approach allows us to step from sample size n = 100 to ∞ and ask the crucial question: Can one distinguish N_a and N₀ for a ≠ 0?

Almost every realization of N_a determines the probability distribution of the error but it need not determine the slope a of the regression line. Just as one cannot distinguish a sequence of standard normal variables W_n from the sequence of shifted variables W_n + 1/n with absolute certainty, one cannot distinguish the Poisson point process N_a from N₀ for ξ > 1/2 and errors with a Student distribution. The distributions of the two point processes N_a and N₀ are equivalent. See Appendix B for details.

The equivalence of the distributions of N_a and N₀ affects the asymptotic behaviour of the estimates A_n of the slope of the regression line for the Poisson point process. There exist no estimators for which A_n converges to the true slope. The limit, if it exists, is a random variable A_∞, and the loss (A_∞ − a)² is almost surely positive. Because of the simple scaling relation in Equation (7) between the estimate of the slope for iid samples and for N, the limit relation A_n ⇒ A_∞ implies $n^{\xi }{\widehat{a}}_n\Rightarrow A_{\infty }$.

For errors with finite second moment, the sd σ_n of the slope of the LS estimate A_n of the regression line y = ax + b based on the n rightmost points of the Poisson point process has a simple expression in terms of the positions of the explanatory variables x₁ > ⋯ > x_n, as does the sd ${\sigma }_n^0$ of the slope of the LS estimate of the regression ray y = ax (with abscissa b = 0). 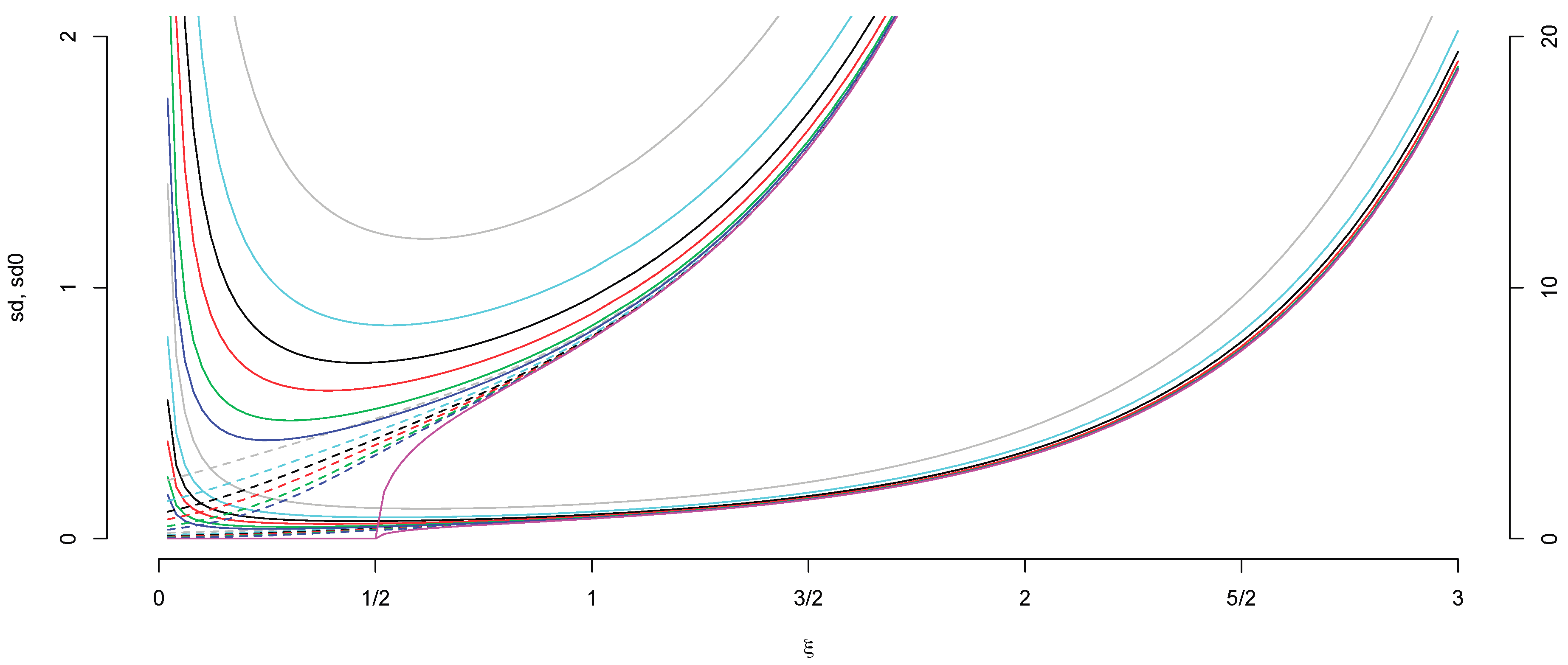We assume standard normal errors and let R calculate the value of σ_n = σ_n(ξ) and ${\sigma }_n^0={\sigma }_n^0\left(\xi \right)$ for various values of n and of ξ ∈ (0,3]. Since the explanatory variables are random, we use a million simulations to approximate these deterministic values. We also compute approximations to ${\sigma }_{\infty }^0={\sigma }_{\infty }=lim{\sigma }_n$ (see Appendix B.5). The plots in Figure 3 will answer questions such as the following:

• How does σ_∞ depend on ξ ∈ (0,3]?
• How much does the sd σ_n decrease if we reveal the next n points of the point process N₀?
• What is the effect of the unknown abscissa on the estimates? For what n will σ_n equal ${\sigma }_{20}^0$?

Figure A2 in Appendix B.4 shows the plots on a logarithmic scale and similar plots for the empirical sd of the Right Median estimates for Cauchy errors.

3. Three Simple Estimators: LS, LAD and RMP

Least Squares (LS) and Least Absolute Deviation (LAD) are classic estimators which perform well if the tail index η of the error is small (LS), or when the tail index ξ of the explanatory variable is small (LAD). For ξ,η ≥ 1/2, one may use the bisector of the sample passing through the RightMost Point (RMP) as a simple but crude estimate of the regression line.

At the critical value η = 1/2, the second moment of the error becomes infinite and the least squares estimator breaks down. Samples change gradually when ξ and η cross the critical value of 1/2. We investigate the break down of the LS estimator by looking at its behaviour for ξ = η = i/10, i = 2, …, 7, for errors with a Student distribution. It is shown that the notation in Equation (6) nicely expresses the decrease in the performance of the estimator on passing the critical exponent. We also show that even for bounded errors there may exist estimators which perform better than Least Squares. The estimator LAD is more robust than Least Squares. Its performance declines for ξ > 1/2, but even for ξ = 0 (exponential distribution) or ξ = −1 (uniform distribution) its good performance is not lasting. The RightMost Point estimate is quite accurate most of the time but may be far off occasionally. That raises the question whether an estimator which is far off 1% of the time is acceptable.

Least squares (LS) is simple to implement and gives good results for η < 1/2. Given the two data vectors x and y, we look for the point ax + be in the two-dimensional linear subspace spanned by x and e = (1, …, 1) which gives the best approximation to y. Set z = x − me where m is the mean value of the coordinates of x. The vectors e and z are orthogonal. Choose a₀ and b₀ such that y − a₀z ⊥ z and y − b₀e ⊥ e. Explicitly:

a₀ = 〈y, z〉/〈z, z〉  b₀ = 〈y, e〉/〈e, e〉.

The point we are looking for is

a₀z + b₀e = a₀x + (b₀ − ma₀)e = ax + be.

(8)

This point minimizes the sum of the squared residuals, where the residuals are the components of the vector y − (ax + be). Note that m is the mean of the components of x and s² = 〈z, z〉 the sample variance. Conditional on X = x, the estimate of the slope is

$${\widehat{a}}_{\mathrm{LS}}=\sum {\zeta }_i{Y}_i^{*}{\zeta }_i=(x_i-m)/s.$$

(9)

There is a simple relation between the standard deviation of Y^* and of the estimate ${\widehat{a}}_{\mathrm{LS}}$ of the slope: (ζ_i) is a unit vector; hence conditional on the configuration x of X

$$sd\left({\widehat{a}}_{\mathrm{LS}}\right)=sd\left(Y^{*}\right)/s.$$

If the sd of Y^* is infinite then so is the sd of the estimator ${\widehat{a}}_{\mathrm{LS}}$. That by itself does not disqualify the LS estimator. What matters is that the expected loss is infinite.

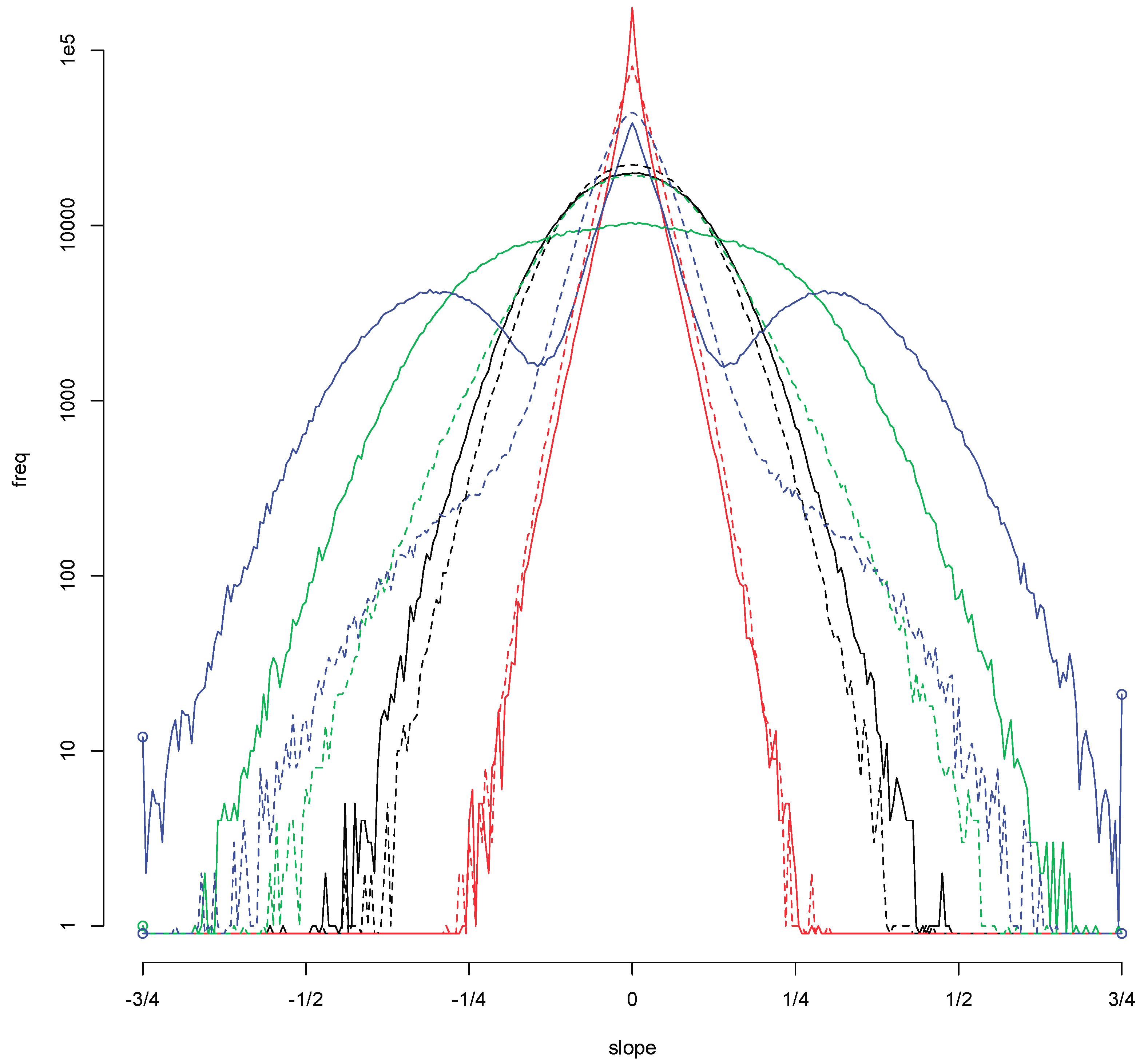
Let us see what happens to the average loss L_r when the number r of simulations is large for distributions with tail index ξ = η = τ as τ crosses the critical value 0.5 where the second moment of Y^* becomes infinite. Figure 4 shows the log frequency plots of ${\widehat{a}}_{\mathrm{LS}}$ for ξ = η = τ(i) = i/10 for i = 2, …, 7 based on ten batches of a hundred thousand simulations. The variable Y^* has a Student t distribution with 1/η degrees of freedom and is scaled to have interquartile distance one. The most striking feature is the change in shape. The parabolic form associated with the normal density goes over into a vertex at zero for τ = 0.5 suggesting a Laplace density, and a cusp for τ > 0.5. The cusp will turn into a singularity f(x) ∼ c/x^τ with τ = 1 − 1/η > 0 when Y^* has a Student distribution with tail index η > 1.

The change that really matters is not visible in Figure 4. It occurs in the tails.

The distribution of the average loss L_r depends on the tail behaviour of $L_1={\widehat{a}}_{LS}^2$. The Student variable Y^* with 1/η degrees of freedom has tails $\mathbb{P}\left\{\right|Y^{*}|>t\}\sim c/t^{1/\eta }$. This also holds for ${\widehat{a}}_{LS}$ which is a mixture of linear combinations of these variables by Equation (9). For η = i/10, i = 2, …, 7, the positive variable $L_1={\widehat{a}}_{\mathrm{LS}}^2$ has upper tail $\mathbb{P}\{L_1>t\}\sim c_i/t^{5/i}$. See Theorem 1.

First, consider the behaviour of the average Z_r(i) of r = 10⁶ independent copies of the variable Z(i) = 1/U^i/5 where U is standard uniform. The Pareto variable Z(i) has tail 1/z^5/i on (1, ∞). Its expectation is 2/3, 3/2, 4, ∞, ∞, ∞ for i = 2, 3, 4, 5, 6, 7. The average Z_r(i) has the form m_r(i) + s_r(i)W_r(i) where one may choose m_r(i) to be the mean of Z(i) if finite, and where W_r(i) converges in distribution to a centred normal variable for i = 2, and for i > 2 to a skew stable variable with index α = i/5 and β = 1. The asymptotic expression for Z_r is:

Z_r(i) = m_r(i) + s_r(i)W_r(i)  i = 2, 3, 4, 5, 6, 7

i = 2: $m_r\left(2\right)=2/3=\mathbb{E}Z\left(2\right)$, $s_r\left(2\right)=1/\sqrt{r}$, W_r(2) ⇒ c₂W₂;

i = 3: $m_r\left(3\right)=3/2=\mathbb{E}Z\left(3\right)$, s_r(3) = r^−2/5, W_r(3) ⇒ c₃W_5/3;

i = 4: $m_r\left(4\right)=4=\mathbb{E}Z\left(4\right)$, s_r(4) = r^−1/5, W_r(4) ⇒ c₄W_5/4;

i = 5: m_r(5) = logr, s_r(5) ≡ 1, W_r(5) ⇒ c₅W₁;

i = 6: m_r(6) = s_r(6) = r^1/5, W_r(6) ⇒ c₆W_5/6; and

i = 7: m_r(7) = s_r(7) = r^2/5, W_r(7) ⇒ c₇W_5/7.

For an appropriate constant C_i > 0, the variable $C_i{L}_1=C_i{\widehat{a}}_{LS}^2$ has tails asymptotic to 1/t^5/i, and hence the averages C_iL_r exhibit the asymptotic behaviour above. It is the relative size of the deterministic part m_r(i) of L_r compared to the size of the fluctuations s_r(i)W_r(i) of the random part which changes as i/10 passes the critical value 0.5. The quotients s_r(i)/m_r(i) do not change much if one replaces L_r by L_r, the batch sd. The theoretical results listed above are nicely reflected in the Hill estimate of the tail index, and the loss of precision in the empirical sds in

Table 2. Quantiles , empirical sd and slope.

$\mathit{\xi }=\mathit{\eta }$	1/5	3/10	2/5	1/2	3/5	7/10
0.999 quantile	1.28	0.999	1.09	1.33	1.95	2.87
emp sd	0.312[1]	0.196[1]	0.16[1]	0.19[5]	0.3[1]	1[1]
Hill est	0.15[1]	0.23[1]	0.35[2]	0.46[2]	0.59[5]	0.69[5]

.

For individual samples, it may be difficult to decide whether the parameters are ξ = η = 4/10 or 6/10. The pairs (4,4)/10 and (6,6)/10 belong to different domains in the classification in Samorodnitsky et al. (2007) but that classification is based on the behaviour for n → ∞. The relation between the estimates ${\widehat{a}}_{\mathrm{LS}}$ for (4,4)/10 and (6,6)/10 for samples of size n = 100 becomes apparent on looking at large ensembles of samples for parameter values (i,i)/10 when i varies from two to seven. The slide show was created in an attempt to understand how the change in the parameters affects the behaviour of the LS estimator. The estimate has a distribution which depends on the parameter. The dependence is clearly expressed in the tails of the distribution. The Hill estimates reflect nicely the tail index η of the error. A recent paper Mikosch and Vries (2013) gives similar results for samples with fixed size for LS in linear regression where the coefficient b in Equation (1) is random with heavy tails.

The simplicity of the LS estimator makes a detailed analysis of the behaviour of the average loss L_r possible for ${\widehat{a}}_{\mathrm{LS}}$. The critical value is η = 1/2. The relative size of the fluctuations rather than the absolute size of the sd signal the transition across the critical value. Note that the critical value η = 1/2 is not due to the “square” in Least Squares but to the exponent 2 in the loss function. There is a simple relation between the tails of the error distribution and of ${\widehat{a}}_{\mathrm{LS}}$. Appendix A.5 shows that $\mathbb{P}\{S<s\}/s^{[n/2]}$ is bounded. Lemma 3.4 in Mikosch and Vries (2013) then gives a very precise description of the tail behaviour of ${\widehat{a}}_{\mathrm{LS}}$ in terms of the tails of Y^*. We formulate this lemma as a Theorem below.

Theorem 1. (Mikosch and de Vries)

Let ${\widehat{a}}_{\mathrm{LS}}$ denote the slope of the LS estimate of the regression line in Equation (1) for a sample of size n ≥ 4 when the true regression line is the horizontal axis. Suppose Y^* has a continuous df and X a bounded density. Let $T\left(t\right)=\mathbb{P}\left\{\right|Y^{*}|>t\}/2$ vary regularly at infinity with exponent −λ < 0 and assume balance: there exists λ ∈ [−1,1] such that

$$\mathbb{P}\{\delta Y^{*}>t\}/T\left(t\right)\to 1+\delta \theta t\to \infty ,\delta =\pm 1.$$

Set M = (X₁ + ⋯ + X_n)/n and Z_i = X_i − M, $V=\sqrt{Z_1^2+\cdots +Z_n^2}$. Define

$$C_i=\mathbb{E}|Z_i{|}^{\lambda }/V^{2\lambda }{B}_i=\mathbb{E}sign\left(Z_i\right){\left|Z_i\right|}^{\lambda }/V^{2\lambda }i=1,\dots ,n.$$

(10)

If λ < [n/2], then

$$\mathbb{P}\{\delta {\widehat{a}}_{\mathrm{LS}}>t\}/T\left(t\right)\to \sum C_i+\delta \theta \sum B_{i}t\to \infty ,\delta =\pm 1.$$

Proof. 

Proposition A6 shows that there exists a constant A > 1 such that $\mathbb{P}\{V\le s\}<A{s}^{[n/2]}$ for s > 0. Set μ = ([n/2] + λ)/2. Then, ${\mathbb{E}\parallel \mathbf{U}\parallel }^{\mu }$ is finite for $\mathbf{U}=\mathbf{Z}/V^2$. Lemma 3.4 in Mikosch and Vries (2013) gives the desired result with $C_i=\mathbb{E}{\left|U_i\right|}^{\lambda }$ and $B_i=\mathbb{E}sign\left(U_i\right){\left|U_i\right|}^{\lambda }$. ☐

If one were to define the loss as the absolute value of the difference ${\widehat{a}}_{\mathrm{LS}}-a$ rather than the square, the expected loss would be finite for η < 1. In particular, the partial averages of ${\widehat{a}}_{\mathrm{LS}}$ for an iid sequence of samples of fixed size n converge almost surely to the true slope. In this respect, Least Squares is a good estimator for errors with tail index η < 1. For η = 1, a classic paper Smith (1973) shows that ${\widehat{a}}_{\mathrm{LS}}$ has a Cauchy distribution if the errors have a Cauchy distribution and the explanatory variable is deterministic.

Least Absolute Deviations (LAD) also known as Least Absolute Value and Least Absolute Error is regarded as a good estimator of the regression line for errors with heavy tails. The LAD estimator has not achieved the popularity of the LS estimator in linear regression. However, LAD has always been seen as a serious alternative to the simpler procedure LS. A century ago, the astronomer Eddington in his book Eddington (1914) discussed the problem of measuring the velocity of the planets and wrote: “This [LAD] is probably a preferable procedure, since squaring the velocities exaggerates the effect of a few exceptional velocities; just as in calculating the mean error of a series of observations it is preferable to use the simple mean residual irrespective of sign rather than the mean square residual”. 2 In a footnote he added: “This is contrary to the advice of most textbooks; but it can be shown to be true.” Forty years earlier, Edgeworth had propagated the use of LAD for astronomical observations in a series of papers in the Philosophical Magazine (see Koenker (2000)).

The LAD (Least Absolute Deviations) estimate of the regression line minimizes the sum of the absolute deviations rather than the sum of their squares. It was introduced (by Boscovitch) half a century before Gauss introduced Least Squares in 1806. Computationally, it is less tractable, but nowadays there exist fast programs for computing the LAD regression coefficients even if there are a hundred or more explanatory variables. Dielman (2005) gives a detailed oversight of the literature on LAD.

The names “least squares” and “least absolute deviations” suggest that one needs finite variance of the variables Y^* for LS and a finite first moment for LAD. That is not the case. Bassett and Koenker in their paper Bassett and Koenker (1978) on the asymptotic normality of the LAD estimate for deterministic explanatory variables observed: “The result implies that for any error distribution for which the median is superior to the mean as an estimator of location, the LAE [LAD] estimator is preferable to the least squares estimator in the general linear model, in the sense of having strictly smaller asymptotic confidence ellipsoids.” The median of a variable X is the value t which minimizes the expectation of |X − t|, but a finite first moment is not necessary for the existence of the median. The median of an odd number of points on a line is the middle point. It does not change if the positions of the points to the left and the right is altered continuously provided the points do not cross the median. Similarly, the LAD-regression line for an even number of points is a bisector which passes through two sample points. The estimate does not change if the vertical coordinatesof the points above and below are altered continuously provided the points do not cross the line. Proofs follow in the next section.

Under appropriate conditions, the distribution of ${\widehat{a}}_{LAD}$ is asymptotically normal. That is the case if the second moment of X is finite and the density of Y^* is positive and continuous at the median, see Van de Geer (1988). The LAD estimator of the regression line is not very sensitive to the tails of Y^* but it is sensitive to the behaviour of the distribution of Y^* at the median m₀. The sd of the normal approximation is inversely proportional to the density of Y^* at the median. LAD will do better if the density peaks at m₀ and worse if the density vanishes at m₀.

To illustrate this, we consider the case where X has a standard exponential distribution (ξ = 0) and Y^* has a density f^* which is concentrated on (−1,1) and symmetric. We consider four situations $f^{*}\left(y\right)=1/\left(4\sqrt{\left|y\right|}\right)$, f^* ≡ 1/2, f^*(y) = |y| and f^* ≡ 1 on the complement of [−1/2, 1/2]. Figure 5 shows the log frequencies of the estimator ${\widehat{a}}_{LAD}$ and ${\widehat{a}}_{LAD40}$. Here, LAD40 is a variation on LAD which depends on the behaviour of the distribution of Y^* at the 0.4 and 0.6 quantiles rather than the median. Ten batches of a hundred thousand simulations yield the log frequencies in Figure 5 and the given empirical sds.

The Gauss–Markov Theorem states that the least squares estimate ${\widehat{a}}_{LS}$ has the smallest sd among all estimates $\widehat{a}$ of the slope which are linear combinations of the y_i. It clearly does not apply to LAD or LAD40, see

Table 3. Three estimators.

${\mathit{y}}^{*}=$	$\mathit{O}\times {\mathit{U}}^2$	$\mathit{O}\times \mathit{U}$	$\mathit{O}\times \sqrt{\mathit{U}}$	$\mathit{O}\times (1+\mathit{U})/2$
LS	0.0467[1]	0.0603[2]	0.0739[2]	0.0798[2]
LAD	0.0308[1]	0.0982[2]	0.1774[5]	0.2132[5]
LAD40	0.0376[1]	0.0879[2]	0.1069[2]	0.0677[5].

. The incidental improvement of the performance by ten or thirty per cent is not sufficient to lure the reader away from LS. Our paper is not about optimal estimators. A glance at the first table in Section 7 shows that, for heavy tails, there exist estimators whose performance is abominable. The aim of our paper is to show that there also exist estimators which perform well.

Rightmost point (RMP or RM(1)) (similar to LAD, as we show below) is a weighted balance estimator. A balance estimate of the regression line is a bisector which passes through two of the hundred sample points. The regression line for RMP is the bisector which contains the rightmost sample point. The RMP estimate is accurate if X₁ is large, except in those cases where $|Y_1^{*}|$ is large too. In terms of the quadratic loss function employed in this paper, it is a poor estimator for η ≥ 1/2.

Table 4. The empirical sd of the estimate of the slope for LS, LAD and RMP. The breakdown of LS for $\eta >1/2$ is dramatic. Even the simple RMP performs better. For $\eta \ge 1/2$, Least Absolute Deviation is optimal.The sds decrease as ξ increases, as is to be expected, and the relative size of the fluctuations increases too.

	$\mathit{\xi }=0$	1/2	1	3/2	2	5/2	3
${\widehat{a}}_{\mathrm{LS}}$
$\eta =0$	0.0774[2]	0.0518[1]	0.00702[2]	0.00122[1]	0.000245[5]	0.000054[2]	0.0000131[5]
1/3	0.118[1]	0.0790[5]	0.0107[1]	0.00186[2]	0.00037[1]	0.000081[5]	0.000019[1]
1/2	0.23[1]	0.15[1]	0.020[1]	0.0034[2]	0.0007[1]	0.00015[5]	0.00004[1]
2/3	0[100]	30[50]	0[10]	1[1]	0.1[2]	0.01[2]	0.001[2]
1	0[100000]	20000[50000]	3000[5000]	0[1000]	0[100]	2[5]	0.1[1]
${\widehat{a}}_{\mathrm{LAD}}$
$\eta =0$	0.0971[2]	0.0641[2]	0.00859[2]	0.00149[1]	0.000295[5]	0.000066[2]	0.0000157[5]
1/3	0.0959[2]	0.0670[1]	0.00946[2]	0.00169[1]	0.000344[5]	0.0000764[5]	0.0000184[5]
1/2	0.0952[2]	0.0690[5]	0.0103[2]	0.00190[5]	0.00039[2]	0.000087[5]	0.000021[2]
2/3	0.0941[2]	0.072[1]	0.0120[2]	0.003[1]	0.00062[5]	0.00014[5]	0.00004[1]
1	0.0918[5]	0.11[5]	1[1]	0.0[1]	0.008[5]	0.00[1]	0.001[1]
${\widehat{a}}_{\mathrm{RMP}}$
$\eta =0$	0.1966[5]	0.0974[5]	0.0116[1]	0.00189[5]	0.00036[1]	0.000078[5]	0.000018[1]
1/3	0.290[5]	0.144[2]	0.0171[5]	0.0028[1]	0.00052[2]	0.000111[5]	0.000026[2]
1/2	0.6[1]	0.3[1]	0.04[1]	0.006[2]	0.0011[5]	0.0002[1]	0.00005[5]
2/3	4[5]	2[2]	0.3[5]	0.04[5]	0.01[1]	0.002[2]	0.0003[5]
1	300[500]	200[200]	20[50]	3[5]	1[1]	0.1[2]	0.02[5]

lists the empirical sd of the estimate $\widehat{a}$ of the slope for LS, LAD and RMP, based on ten batches of a hundred thousand simulations of a sample of size n = 100, for various values of the tail indices ξ and η. The explanatory variable X is Pareto with tail 1/x^1/ξ for ξ > 0 and standard exponential for ξ = 0; the dependent variable Y^* has a Student distribution with 1/η degrees of freedom for η > 0 and is normal for η = 0. The error is scaled to have InterQuartile Distance IQD = 1.

Rousseeuw in Rousseeuw (1984) observed: “Unfortunately, [LAD] is only robust with respect to vertical outliers, but it does not protect against bad leverage points.” This agrees with the deterioration of the LAD-estimate for η ≥ 1/2 when ξ increases. The good performance of the LAD estimates for ξ = 0 and the relatively small fluctuations reflect the robustness which is supported by the extensive literature on this estimator. It does not agree with the theoretical result below:

Theorem 2.

In the linear regression in Equation (1), let X have a non-degenerate distribution and let Y^*have an upper tail which varies regularly with non-positive exponent. Let the true regression line be the horizontal axis and let ${\widehat{a}}_n$ denote the slope of the LAD estimate of the regression line for a sample of size n. For each n > 1, the quotient

$$Q_n\left(t\right)=\mathbb{P}\{Y^{*}>t\}/\mathbb{P}\{{\widehat{a}}_n>t\}$$

(11)

is a bounded function on $\mathbb{R}$.

Proof. 

Let c₁ < c₂ be points of increase of the df of X. Choose δ₁ and δ₂ positive such that the intervals I₁ = (c₁ − δ₁, c₁ + δ₁) and I₂ = (c₂ − δ₂, c₂ + δ₂) are disjoint, and (c₁ − nδ₁, c₁ + nδ₁) and I₂ too. Let E denote the event that X₁ ∈ I₂ and the remaining n − 1 values X_i lie in I₁. The LAD regression line L passes through (X₁,Y₁). (If it does not, the line $L^{\prime }$ which passes through (X₁,Y₁) and intersects L in x = c₁ has a smaller sum of absolute deviations: Let δ denote the absolute difference in the slope of these two lines. The gain for X₁ is (c₂ − δ₂ − c₁)δ, and exceeds the possible loss (n − 1)δδ₁ for the the remaining n − 1 points.) It is known that the LAD estimate of the regression line is a bisector. We may choose the vertical coordinate so that y = 0 is a continuity point of F^* and 0 < F^*(0) < 1. A translation of Y^* does not affect the result. The event E₁ ⊂ E that Y₁ is positive and more than half the points (X_i,Y_i), i > 1, lie below the horizontal axis has probability $p\mathbb{P}E$ where p > 0 depends on F^*(0) and n. If E₁ occurs the regression line L will intersect the vertical line x = c₁ − δ₁ below the horizontal axis. For Y₁ = y > 0 the slope A of L then exceeds y/c where c = (c₂ + δ₂) − (c₁ + δ₁). Hence, $\mathbb{P}\{A>t\}\ge p\mathbb{P}E\mathbb{P}\{Y^{*}>ct\}$ for t > 0. Regular variation of the upper tail of Y^* implies that $\mathbb{P}\{Y^{*}>ct\}\ge (c^{\lambda }/2)\mathbb{P}\{Y^{*}>t\}$ for t ≥ t₀ where λ ≤ 0 is the exponent of regular variation of 1 − F^*. This yields the desired result for the quotient Q_n. ☐

How should one interpret this result? The expected loss (MSE) is infinite for η ≥ 1/2. In that respect, LAD is no better than LS. We introduce the notion of “light heavy” tails. Often heavy tails are obvious. If one mixes ten samples of ten observations each from a Cauchy distribution with ten samples of ten observations from a centred normal distribution, scaling each sample by the maximum of the ten absolute values to obtain point sets in the interval [−1,1], one will have no difficulty in selecting the ten samples which derive from the heavy-tailed Cauchy distribution, at least most of the time. In practice, one expects heavy tails to be visible in samples of a hundred points. However, heavy tails by definition describe the df far out. One can alter the density of a standard normal variable Z to have the form c/z² outside the interval (−12, 12) for an appropriate constant c. If one takes samples from the variable $Z^{\prime }$ with the new density the effect of the heavy tails will be visible, but only in very large samples. For a sample of a trillion independent copies of $Z^{\prime }$, the probability that one of the points lies outside the interval (−12, 12) is less than 0.000 000 000 000 01. Here, one may speak of “light heavy” tails. In the proof above, it is argued that under certain circumstances LAD will yield the same estimate of the regression line as RMP. The slope of the bisector passing through the rightmost point is comparable to Y₁ /X₁ and the upper tail of the df of this quotient is comparable to that of Y₁ . In our set-up a sufficient condition for LAD to agree with RMP is that X₁ > 100X₂. For a tail index ξ = 3, the probability of this event exceeds 0.2, as shown in Section 2. If X has a standard exponential distribution, the probability is less. The event {X₁ > 100X₂} = {U₁ < U₂/e¹⁰⁰} for X_i = −log(U_i) has probability e⁻¹⁰⁰.

Here are two questions raised by the disparity between theory and simulations:

(1) Suppose the error has heavy tails, η ≥ 1/2. Do there exist estimators E of the regression line for which the slope ${\widehat{a}}_E$ has finite second moment? In Section 4. it is shown that, for the balance estimators RM(m) (Right Median) and HB0(d) (Hyperbolic Balance at the median), one may choose the parameters m and d, dependent on the tail indices ξ and η, such that the estimate of the slope has finite second moment.

(2) Is it safe to use LAD for ξ < 1/2? Not really. For ξ < 1/2, the estimate ${\widehat{a}}_{\mathrm{LAD}}$ is asymptotically normal as the sample size goes to infinity provided the error has a positive continuous density at the median. This does not say anything about the loss for samples of size n = 100. The empirical sds for ξ = 0,1/2 and η = 0, 1/2, 1, 3/2, 2, 3, 4 are listed in Table 1. For ξ = 0, the performance of ${\widehat{a}}_{\mathrm{LAD}}$ is good; for ξ = 1/2 the performance for η ≥ 1 is bad, for η ≥ 3 atrocious. The empirical sd varies continuously with the tail indices. Thus, what should one expect for ξ = 1/4? Ten batches of a hundred thousand simulations yield the second row in

Table 5. Theempirical sd of ${\widehat{a}}_{\mathrm{LAD}}$ for Student errors with tail index $\eta$.

$\mathit{\xi }\setminus \mathit{\eta }$	0	1/3	1/2	2/3	1	3/2	2	3	4
0	0.0969[2]	0.0959[2]	0.0951[2]	0.0941[2]	0.0917[2]	0.0869[2]	0.0810[5]	0.0681[5]	0.0560[5]
1/4	0.2328[5]	0.2363[5]	0.238[1]	0.2389[5]	0.243[2]	0.26[2]	0.4[2]	10000[10000]	2e+6[5]
1/2	0.0641[2]	0.0670[2]	0.0690[2]	0.072[1]	0.1[1]	3[5]	40[50]	1e+7[2]	2e+10[5]
1	0.00861[5]	0.00943[5]	0.0104[5]	0.012[1]	1[1]	20[20]	10000[10000]	2e+6[2]	0e+15[2]

: For η ≥ 3, the performance is atrocious. The next sections describe estimators which perform better than LAD, sometimes even for ξ = 0. We construct an adapted version, LADGC, in which the effect of the large gap between X₁ and X₂ is mitigated by a gap correction (GC).

To obtain a continuous transition for ξ → 0, one should replace X = 1/U^ξ with U uniformly distributed on (0,1) by X = (U^ξ − 1)/ξ + ξ for ξ ∈ (0,1). In the table above, the entries for ξ = 1/4 and ξ = 1/2 then have to be divided by 4 and 2, respectively. The rule of thumb (in Equation (2)) is then valid for all ξ ∈ (0,1). Since the situation ξ ∈ (0,1/2) plays no role in this paper, we stick to the simple formula: X = 1/U^ξ for ξ > 0.

The words above might evoke the image of a regime switch in the far tails when LAD is contaminated by the pernicious influence of the RMP estimator due to configurations of the sample where the distribution of the horizontal coordinates exhibits large gaps. This image is supported by the loglog frequency plots. For small values of η, the plots suggest a smooth concave graph with asymptotic slope on the left (due to a df of $|{\widehat{\alpha }}_{\mathrm{LAD}}|$ asymptotic to cx for x → 0), and a steeper slope on the right suggesting a tail index <1 for the upper tail of $|{\widehat{a}}_{\mathrm{LAD}}|$. The two plots for ξ = 1/4 and η = 1,4 in Figure 6 have different shapes. The slope of the right leg of the right plot becomes less steep as one moves to the right. For two simulations, $|\widehat{a}|$ lies beyond the boundary value 10⁶. The maximal absolute value 5.3 × 10⁹. This single estimate makes a significant contribution to the average loss for η = 4. All this suggests that for η = 4 the tail of the df of $|{\widehat{a}}_{\mathrm{LAD}}|$ becomes heavier as one moves out further to the right.

4. Weighted Balance Estimators

Recall that a bisector is a line which divides the sample into two equal parts. It may be likened to the median of a one-dimensional sample. For odd sample size, bisectors contain a sample point, for even sample size, a bisector contains two sample points or none. The latter are called free bisectors. There are many bisectors, even if one restricts attention to bisectors through two points in a sample of size n = 100. The question is:

“How does one choose a bisector which is close to the regression line?”

For symmetrically distributed errors, balance is a good criterion for selecting a bisector. It is shown below how a decreasing sequence of non-negative weights allows one to define a bisector which is in balance. We give the intuitive background to the idea of a weighted balance estimator, some examples and the basic theory. The focus is on sample size n = 100. The extension to samples with an even number of observations is obvious. For a detailed exposition of the general theory and complete proofs, the reader is referred to the companion paper Balkema (2019).

The intuition behind the weighted balance estimators is simple. Assume the true regression line is the horizontal axis. Consider a sample of size n = 2m and a free bisector L. If the slope of the bisector is negative, the rightmost sample points will tend to lie above L; if the slope is positive, the rightmost points tend to lie below L. Now, introduce a decreasing sequence of weights, w₁ ≥ ⋯ ≥ w_n ≥ 0. The weight of the m points below the bisector will tend to increase as one increases the slope of the bisector. We prove that the increase in weight is indeed monotone. As the slope of the bisector L increases the weight of the m points below the bisector increases. At a certain moment the weight of the m points below L will surpass half the total weight. That determines the line of balance. This line L is the weighted balance estimate WB0 for the weight sequence w_i. For odd sample size, n = 2m + 1, the same argument works. We then consider bisectors which pass through one sample point to determine the WB0 estimate of the regression line for the given sample.

Strips may give more stable estimates. Consider a sample of size n = 100 and strips which contain twenty points such that of the remaining eighty points half lie above the strip and half below. Here, the weight w(B) of the set B of forty points below the strip will also increase if the slope of the strip increases and (by symmetry) the weight w(A) of the forty points above the strip will decrease. By monotonicity, as one increases the slope from −∞ to +∞, there is a moment when w(B) will surpass w(A). The centre line of that strip is the WB40 estimate of the regression line for the given weight sequence.

The monotonicity allows one to determine the slope of the estimates WB0 and WB40 by a series of bisections. The Weighted Balance estimator is fast. It is versatile. Both the RightMost Point estimator and Least Absolute Deviation are weighted balance estimators. RMP for the weight sequence 1,0, …, 0 and LAD for the random weight sequence w_i = X_i as we show below.

We now first give some examples. Then, we prove the monotonicity mentioned above. We then show that LAD is the weighted balance estimator for the weight sequence w_i = X_i. Appendix A contains an analysis of the tail behaviour of weighted balance estimators.

4.1. Three Examples

In this paper, we use three basic weight sequences. Two are deterministic.

(1) Let r = 2r₀ = 1 be a positive odd number less than n = 100. The weight sequence for RM(r) is (1, …, 1, 0, …, 0) with r ones. Colour the rightmost r sample points red and select a bisector L passing though two sample points, one black and one red. The bisector L₀ is in balance if there are r₀ red points below L₀ and r₀ red points above L₀. This bisector is the Right Median RM(r) estimate of the regression line. An infinitesimal anti-clock wise rotation of L₀ around the centre midway between the red and black point on L₀ yields a free bisector L; the fifty points below L weigh r₀ + 1 > r/2. The Right Median estimator is a variation on RMP. It takes account of the position of the r rightmost points and thus avoids the occasional erroneous choice of RMP. If r = 1, then RM(r) = RMP. For r = [n/2], RM(r) agrees with the estimator SBLR introduced in Nagya (2018).

(2a) The weight sequence 1, 1/2, …, 1/100 gives the rightmost point the largest weight. It is overruled by the next three points: w₂ + w₃ + w₄ > w₁. If Y₁ is very large, the bisector L through the rightmost point will have a large positive slope and the points z₂, …, z₉ will tend to lie below L. The weight of the 49 points below L, augmented with the left point on L, will then exceed half the total weight. For balance, the slope has to be decreased.

One can temper the influence of the rightmost point by choosing the weights to be the inverse of 2, …, 101 or 3, …, 102. In general, we define the hyperbolic weight sequence by

1/d, 1/(d + 1), 1/(d + 2), … , 1/(d − 1 + n).

(12)

The parameter d is positive. If it is large, the weights decrease slowly. Suppose the bisector L contains two points, z_L and z_R. The weight w_L of the left point is less than w_R, the weight of the right point. Let Ω denote the total weight and w(B) the weight of the points below L. If

w(B) + w_L < Ω/2 < w(B) + w_R

(13)

for the weight sequence in Equation (12), then L is the HB0(d) estimate of the regression line.

(2b) Instead of a bisector, one may consider a strip S which contains twenty points with forty points above S and forty below. Assume that S is closed and of minimal width. The boundary lines of S each contain one of the twenty points. For certain slopes, one of the boundary lines will contain two points and the strip will contain 21 points. Suppose the upper boundary contains two points, z_L to the left of z_R, and the set above S contains 39 points. Let w(B) be the weight of the forty points below S and w(A) the weight of the 39 points above S. If

w(A) + w_L < w(B) < w(A) + w_R

(14)

then the centre line of the strip is the Hyperbolic Weight HB40(d) estimate of the regression line.

(3) We shall see below that LAD is the weighted balance estimator for the random weight w_i = X_i. Since the X_i form an ordered sample from a continuous Pareto distribution, one cannot split the hundred sample points into two sets of fifty points with the same weight. It follows that there is a unique bisector L passing through two sample points such that the balance tilts according as one assigns the heavier point on L to the set above or below L.

4.2. The Monotonicity Lemma

In this section, X and Y^* are assumed to have continuous dfs. Almost all samples from (X,Y^*) then have the following properties:

• No vertical line contains two sample points.
• No two parallel lines contain four sample points.

In particular, no line contains more than two sample points. Configurations which satisfy the two conditions above are called unexceptional. For unexceptional configurations, there is a set of $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ lines which each contain exactly two sample points. The slopes γ of these lines are finite and distinct. They form a set $\Gamma \subset \mathbb{R}$ of size $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$.

Definition 3.

A weight w is a sequence w₁ ≥ ⋯ ≥ w_n ≥ 0 with w₁ > w_n.

Take an unexceptional sample of n points from (X,Y^*), a positive integer m < n and a line with slope $\gamma \in \mathbb{R}\setminus \Gamma$. As one translates the line upwards the number of sample points below the line increases by steps of one since γ does not lie in Γ, and hence the lines contain at most one sample point. There is an open interval such that for all β in this interval the line y = β + γx contains no sample point and exactly m sample points lie below the line. The total weight of these m sample points is denoted by w_m(γ). It depends only on m and γ. As long as the line L moves around without hitting a sample point, the set of m sample points below the line does not change and neither does its weight w_m(γ). What happens when γ increases?

Lemma 1.

For any positive integer m < n and any weight sequence w, the function γ ↦ w_m(γ) is well defined for $\gamma \in \mathbb{R}\setminus \Gamma$, increasing, and constant on the components of $\mathbb{R}\setminus \Gamma$.

Proof. 

Consider lines which contain no sample points. Let ${\gamma }_0\in \mathbb{R}\setminus \Gamma$ and let L₀ be a line with slope γ₀ which contains no sample points such that there are precisely m sample points below L₀. Let B denote the closed convex hull of these m sample points, and let A denote the closed convex hull of the n − m sample points above L₀. One can move the line around continuously in a neighbourhood of L₀ without hitting a sample point. For any such line between the convex sets A and B the weight of the m points below the line equals w_m(γ₀), the weight of B. If one tries to maximize the slope of this line then in the limit one obtains a line L with slope γ ∈ Γ. This line contains two sample points. The left point is a boundary point of B, the right one a boundary point of A. Consider lines which pass through the point z ∈ L midway between these two sample points. The line with slope γ − dγ < γ lies between the sets A and B and w_m(γ − dγ) = w_m(γ₀). For the line with slope γ + dγ > γ, there are m points below the line but the left point on L has been exchanged for the heavier right point. Hence, w_m(γ + dγ) ≥ w_m(γ − dγ) with equality holding only if the two points on L have the same weight. ☐

This simple lemma is the crux of the theory of weighted balance estimators. An example will show how it is applied.

Example 1.

Consider a sample of n = 100 points and take m = 40. Let w₁ ≥ ⋯ ≥ w₁₀₀ be a weight sequence. We are looking for a closed strip S in balance: There are forty points below the strip and forty points above the strip, and the weights of these two sets of forty sample points should be in balance. The weight w₄₀(γ) of the forty points below the strip depends on the slope γ. It increases as γ increases. The limit values for γ → ±∞ are

Ω₀ = w₄₀(−∞) = w₆₁ + ⋯ + w₁₀₀ Ω₁ = w₄₀(∞) = w₁ + ⋯ + w₄₀.

Similarly, the weight w₄₀(γ) of the forty points above the strip decreases from Ω₁ to Ω₀. Both functions are constant on the components of $\mathbb{R}\setminus \Gamma$. Weight sequences are not constant. Hence, Ω₀ < Ω₁. It follows from the monotonicity that here are points γ₀ ≤ γ₁ in Γ such that

$$\{w_{40}<w^{40}\}=(-\infty ,{\gamma }_0)\{w_{40}>w^{40}\}=({\gamma }_1,\infty )\mathrm{on}\mathbb{R}\setminus \Gamma .$$

(15)

If γ₀ = γ₁, there is a unique closed strip S of minimal height with slope γ₀ = γ₁ and we speak of strict balance. One of the boundary lines of S contains one sample point, the other two. This is the strip of balance. A slight change in the slope will cause one of the two points on the boundary line containing two points to fall outside the strip. Depending on which, the balance will tilt to one side or the other. Define the centre line of S to be the estimate of the regression line for the estimator WB40 for the given weight sequence. If γ₀ < γ₁ then for i = 0,1 let L_i with slope γ_i be the centre line of the corresponding strip S_i. Define the WB40 estimate as the line with slope (γ₀ + γ₁)/2 passing through the intersection of L₀ and L₀.

The example shows how to define for any sample size n and any non-constant weight w and any positive integer m < [n/2] for any unexceptional sample configuration a unique line, the WBm estimate of the regression line. Of particular interest is the case m = [n/2]. The strip then is a line and the estimator is denoted by WB0.

Definition 4.

For a sample of size n and m < [n/2], the Hyperbolic Balance estimator HBm(d) for d > 0 is the weighted balance estimator as in the example above (where m = 40) with the weight w_i = 1/(d − 1 + i) in Equation (12). If m = [n/2] we write HB0(d).

The WBm estimate of the slope of the regression line for unexceptional sample configurations is determined by the intersection of two graphs of piecewise constant functions, one increasing and the other decreasing, and so is the WB0 estimate. There either is a unique horizontal coordinate where the graphs cross and balance is strict, or the graphs agree on an interval I = (γ₀,γ₁). In the latter case, for γ ∈ (γ₀,γ₁) ∖ Γ, there exist closed strips whose boundaries both contain one sample point and which have the property that the m points below the strip and the m above have the same weight. We say that exact balance holds in γ. This yields the following result:

Proposition 1.

Let n be the sample size and m ≤ n/2 a positive integer, and let $\alpha \in \mathbb{R}\setminus \Gamma$. Let S be a closed strip of minimal height of slope α such that m sample points lie below S and m above. If n is even and m = n/2 then S is a line which contains no sample points, a free bisector; if n = 2m + 1 then S is a line which contains one sample point; if m < [n/2] both boundary lines of S contain one sample point. Let w₀ denote the weight of the m sample points below S and w⁰ the weight of the m points above S. Let $\widehat{\gamma }$ denote the slope of the WB estimate of the regression line.

• If w₀ < w⁰, then $\alpha <\widehat{\gamma }$,
• If w₀ > w⁰, then $\alpha >\widehat{\gamma }$,
• If w₀ = w⁰, exact balance holds at α.

In the case of exact balance, there is a maximal interval J = (γ₀,γ₁) with γ₀,γ₁ ∈ Γ such that w₀ = w⁰ for all strips S separating two sets of m sample points with slope γ ∈ J ∖ Γ. Both α and $\widehat{\gamma }$ lie in J.

Strict balance holds almost surely for LAD if the conditions of this section, that X and Y^* have continuous dfs, is satisfied. It also holds for RM0(r) if the sample size is even and r odd. We show below that, for sample size n = 100, it holds for HB0(d) for all integers d ≤ 370261 and for HB40(d) for all integers d ≤ 1000. In the case of strict balance, we need two values γ₂ <γ₃ such that w₀ < w⁰ in γ₂ and w₀ > w⁰ in γ₃. A series of bisections then allows us to approximate $\widehat{\gamma }$ at an exponential rate. If strict balance does not hold one needs to do more work. The programs on which the results in the tables in Section 7 are based determine for WB0 the indices of the two points on the bisector of balance, and for WB40 the indices of the two points on the one boundary and of the one point on the other boundary of the strip of balance. We then use the criteria in Equations (13) and (14) to check strict balance.

To show that exact balance does not occur for HB0 or HB40 for a particular value of the parameter d one has to solve a number theoretic puzzle: Can two finite disjoint sets of distinct inverse numbers 1/(d + i) have the same sum? We need R to obtain a solution.

Proposition 2.

For sample size n = 100 exact balance is not possible for HB0 with the hyperbolic weight sequences w_i = 1/(d − 1 + i) for parameter d ∈ {1, …, 370261} neither for HB40 for d ≤ 1000.

Proof. 

For HB0, the argument is simple. For d ≤ 370261, the set J_d = {d, …, d + 99} contains a prime power q = p^r, which may be chosen such that 2q > d + 99. For exact balance, there exist two disjoint subsets A and B of J_d containing fifty elements each such that the inverses have the same sum. That implies that 1/q = s where s is a signed sum $\sum {ϵ}_i/i$ over the remaining 99 elements i with ${ϵ}_i\in \{-1,1\}$. Write s as an irreducible fraction s = k/m and observe that m is not divisible by q since none of the 99 integers i in the sum is. However, 1/q = k/m implies k = 1 and m = q.

For HB40, one needs more ingenuity to show that exact balance does not occur. One has to show that J_d does not contain two disjoint subsets A and B of forty elements each such that the sums over the inverse elements of A and of B are equal. We show that there exist at least 21 elements in J_d which cannot belong to A ∪ B. Thus, for d = 1, the elements 23i, i = 1,2,3,4, cannot belong to A ∪ B since, for any non-empty subset of these four elements, the sum of the signed inverses is an irreducible fraction whose denominator is divisible by 23. This has to be checked! It does not hold in general. The sum of 1/i over all i ≤ 100 which are divisible by 25 is 1/12. The sum 1/19 + 1/38 + 1/57 − 1/76 equals (12 + 6 + 4 − 3)/12/19 = 1/12. Primes and prime powers in the denominators may disappear. One can ask R to check whether this happens. For d = 1, the set J_d contains 32 elements (23, 29, 31, 37, 41, 43, 46, 47, 49, 53, 58, 59, 61, 62, 64, 67, 69, 71, 73, 74, 79, 81, 82, 83, 86, 87, 89, 92, 93, 94, 97, and 98) which cannot lie in A ∪ B. For d = 2, …, 1000, the number varies but is never less than 32. ☐

Different weight sequence may yield the same estimates.

Proposition 3.

The weight sequences (w_i) and (cw_i + d) for c > 0 yield the same WB estimates.

Proof. 

The inequalities which define balance remain valid since there are m sample points on either side. ☐

The weight sequence (6, 1, …, 1) yields the RMP estimator, but so does any weight which is close to this weight, for instance (6, w₂, …, w₁₀₀) with 1 < w₁₀₀ ≤ w₂ ≤ 1.1. A weight sequence for which w₁ is large and the remaining weights cluster together will perform poorly if the error has heavy tails.

Proposition 4.

Let WB0 be the Weighted Balance estimator of the regression line for the weight sequence (w_i), i = 1, …, n = 2m. If

w₁ + w_{m + 2} + ⋯ + w_n > w₂ + ⋯ + w_{m + 1}

(16)

then WB0 = RMP.

Proof. 

Suppose z₁ does not lie on the line L of balance. Then, the weight of z₁ together with the m − 2 points on the same side of L and the lighter point on L is not greater than half the total weight. ☐

4.3. LAD as a Weighted Balance Estimator

We show that LAD = WB0 with weight w_i = X_i for even sample size. The proof for odd sample size is similar (see Balkema (2019)).

Theorem 3.

LAD = WB0 with weight w_i = X_i for sample size n = 2m.

Proof. 

First, consider lines which contain no sample points. Suppose k < m points lie below the line. If we translate the line upwards, the L¹ distance d = ∑|Y_i − (β + γX_i)|, decreases since for the majority of the points the difference Y_i − (β + γX_i) is positive. Thus, we may restrict attention to bisectors. Now, assume that the weight of the m points below the line is less than half the total weight: w_m < w^m. Move the line about without hitting a sample point. If we alter β, the distance d does not change since the change in the m positive terms in the sum is compensated by the change in the m negative terms. Now, increase the slope γ to γ + δ. The distance d decreases by δw^m due to the m positive terms of Y_i − (β + γX_i) and increases by δw_m due to the m negative terms. The assumption w_m < w^m implies a decrease in d. Thus, increase the slope as in the lemma above until we reach the line of balance. This line contains two sample points. For this line, the distance increases when it is rotated around the point midway between the sample points both clockwise and anti clockwise. ☐

The LAD estimate of the regression line for a sample of size n = 100 is (almost surely) a bisector containing two sample points. The estimate is defined in terms of the sum of the absolute vertical distance of the sample points to this line, but it exhibits an almost complete lack of sensitivity to the vertical coordinate. Consider an unexceptional configuration of a sample of a hundred points and let L denote the LAD estimate of the regression line. Now, move each of the sample points up or down the vertical line on which it lies, without crossing the bisector L. For the new configuration the line L still is the bisector in balance since the weights have not been altered. Hence, L is the LAD estimate of the regression line for the new configuration too. This observation is due to Bassett and Koenker (see Bassett and Koenker (1978)). For weighted balance estimators, its validity is obvious.

4.4. Variations on LAD: LADPC, LADGC, and LADHC

We introduce three “corrections” on the Least Absolute Deviation estimator which make it more resistant to outliers of the explanatory variable due to positive ξ: the Power Correction LADPC, the Gap Correction LADGC and the Hyperbolic Correction LADHC.

By treating LAD as a Weighted Balance estimator it becomes possible to replace the weight sequence X_i by a weight sequence in which very large values of X_i or large gaps between successive values X_i and X_i+1 are reduced so as to make the estimator more stable. We want the estimate to be responsive to the configuration of the explanatory variables, in particular the rightmost points, but to avoid situations where for instance x₃ has too loud a voice since x₃/x₄ is large. Even for ξ = 1/4, the gaps x₁/x₂ or x₂/x₃ may still be so large that they give rise to erroneous estimates, yielding poor performance for tail index η ≥ 3 as we saw in Section 3. The values of X_i with a low index tend to vary quite a bit. The values of X_i for i > n/2 are quite stable. For these values, one may replace the random weights by the deterministic weights of a hyperbolic weight sequence without any noticeable effect.

The power correction replaces the weight sequence $X_i=1/U_i^{\xi }$ by $w_i=1/\sqrt{U_i}$ or some other power $X_i^{\tau }$ where τ may depend on ξ. The weight sequence $X_i^{1/12}$ performs well for 1/2 ≤ ξ ≤ 3 and 0 ≤ η ≤ 4. We take that to be the standard power correction of LAD. If w₁/w₂ > 100, then the Weighted Balance estimator WB0 passes through (X₁,Y₁) and reduces to RMP. The Gap Correction ensures that the quotient w_i+1/w_i of successive weights is not too small, not smaller than the quotient for a hyperbolic weight sequence. We perform the power correction not on $X_i=1/U_i^{\xi }$ but on 1/U_i. (For ξ > 1, the gaps are so large that the rightmost terms of the power correction would agree with a hyperbolic sequence and fail to reflect the configuration of the x_i.) In the Hyperbolic Correction, the second half of the weight sequence of the Gap Correction is replaced by a deterministic hyperbolic weight sequence.

• LADPC (Power Correction) $w_i=X_i^{1/12}$ only for Pareto variables, ξ > 0.
• LADGC(d) (Gap Correction) has weights w_i that satisfy w₁ = 1 and

  $$w_{i+1}/w_i=X_{i+1}^{\tau }/X_i^{\tau }\vee (i+d-1)/(i+d)\tau =1\wedge 1/\xi .$$
• LADHC(d) (Hyperbolic Correction) has weights w_i that satisfy

  $${\omega }_i=\left\{\begin{array}{cc}{w}_i^{gc}/w_m^{gc}\hfill & i\le m\hfill \\ (m+d-1)/(i+d-1)\hfill & i>m\hfill \end{array}\right.m=[n/2]$$

  where $w_i^{gc}$ is the weight sequence of LADGC(d).

The tables in Section 7 show that these corrections improve the performance.

For deterministic weight sequences, the Weighted Balance estimators are geometric with respect to the group $\mathcal{G}$, and so is LAD. The adapted LAD-estimators, LADPC, LADGC and LADHC, are not. They are geometric with respect to the subgroup ${\mathcal{G}}_0$ of all transformations

(x, y) ↦ (cx + q, dy + ax + b)  c, d > 0, q = 0.

(17)

The transformations in ${\mathcal{G}}_0$ map the right half plane x ≥ 0 onto itself. Horizontal translations are taboo.

5. Theil’s Estimator and Kendall’s τ

Least squares chooses a regression line such that the residuals y_i − (ax_i + b) have zero mean and are uncorrelated with the n values x_i of the explanatory variable. The covariance vanishes. Theil in Theil (1950) showed that the median of the $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ lines passing through two sample points is an estimator of the regression line for which Kendall’s τ vanishes. The Theil–Sen estimator is widely used in papers on economy and climate change.

Kendall’s τ is a robust measure of the correlation or strength of association in a bivariate sample. It is non-parametric. It counts the number of inversions. An inversion holds for two indices i ≠ j if (y_j − y_i)/(x_j − x_i) is negative. The pair (i,j) is then called discordant. In a sample of n points, there are $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ pairs. If the number of inversions is $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ and the X_i are in decreasing order, then the y_i are in increasing order. If there are no inversions the two sequences have the same order. By definition:

$$\tau =2\frac{n_c-n_d}{n(n-1)}$$

(18)

where n_c is the number of concordant pairs and n_d the number of discordant pairs. For independent variables, τ is centred and asymptotically normal (for n → ∞) with variance 2(2n + 5)/(9n(n − 1)) (see Lehmann (1983)).

Let x and y be sequences of the same length with distinct values and define $\tau (y,x)$ as in Equation (18).

Proposition 5.

The function $a\mapsto \tau \left(a\right)=\tau (y+ax,x)$ is increasing.

Proof. 

It suffices to prove $\tau \left(a\right)>\tau \left(0\right)$ for $a>0$ (replace y by $y+a_{1}x$). Assume j < i. Set $c=y_j-y_i$ and $d=x_j-x_i>0$. Now, observe that (c + ad)/d lies between c/d and a and may be positive if c/d is negative but can not be negative if c is positive. ☐

It follows that one may determine $a=\widehat{a}$ such that $\tau \left(a\right)=0$ by finding a value $a_1$ where $\tau$ is negative and a value $a_2>a_1$ where $\tau$ is positive and then using successive bisections.

Theil in Theil (1950) proposed to use the median of the $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ quotients $(y_j-y_i)/(x_j-x_i)$ of the plane sample $(x,y)$ as an estimator of the slope of the regression line through the sample. He proved:

Theorem 4.

Let ${\widehat{a}}_T$ denote the Theil estimator of the slope. Then, $\tau \left({\widehat{a}}_T\right)=0$.

The estimator has a simple structure. It is called complete in Theil (1950) since it makes use of the complete set of quotients. Sen in Sen (1968) extended the estimator to the case where points may have the same x-coordinate. Siegel in Siegel (1982) introduced a variation where one first computes for each point the median of the quotients involving that point, and then takes the median of these medians. This is related to the $\mathrm{RM}(2k+1)$ estimator. The estimate ${\widehat{a}}_{\mathrm{RM}\left(m\right)}$ is the median of the slope of the lines through the $m=2k+1$ rightmost points dividing the sample into two equal parts.

Jaeckel in Jaeckel (1972) proposed a weighted version with weights $w_{ij}=x_j-x_i$, $j<i$. For deterministic explanatory variables $x_{i,n}$ under appropriate conditions, this weighted Theil–Sen estimate is asymptotically normal. (see Sievers (1978)). These conditions do not apply in our situation. For large values of ξ, the weights with $j=1$ will tend to dominate the sum. For the Weighted Balance estimator, replacing the weights X_i by the hyperbolic weights yielded good results. We therefore use the weights

$$w_{ij}\left(d\right)=\frac{1}{i+d}-\frac{1}{j+d}i<j$$

(19)

which promote pairs for which the smaller index is close to one and for which i and j are far apart. The parameter $d>0$ determines how strong this bias for the rightmost points is.

6. Trimming

Trimming is an excellent procedure for getting rid of the noisy outer observations in a sample from a heavy-tailed distribution. If one arranges the observations from a Student distribution with tail index η in decreasing order, $Y_1>Y_2>\cdots >Y_n$, the maximal term $Y_1$ has tail index η, the second largest term $Y_2$ has tail index η/2, the third largest tail index η/3, etc. For the very heavy tails (with index η = 4), deleting the eight largest and the eight most negative observations leaves us with variables $Y_9,\dots ,Y_{n-8}$ which have finite variance. Trimming reduces the sample size (and destroys independence), but this is compensated by the good behaviour of the remaining sample points. The number of sample points that have to be trimmed to get good performance depends on the tail index of the distribution.

Take samples of a hundred Student variables with tail index η ∈ {0, 1/3, 1/2, 2/3, 1, 3/2, 2, 3, 4} scaled by their IQD. Perform ten batches of a hundred thousand simulations, compute the average $\widehat{a}$ of the trimmed sample, the square root α of the average loss for each of the ten batches, and the average, $\overline{\alpha }$, and sd of these ten values of α. Do this for various values of m, where m is the number of observations which are deleted to the right and to the left. Thus, $\widehat{a}$ is the estimate of the centre of the distribution based on the 100 − 2m centre most observations. Figure 7a plots the values of $\overline{\alpha }$ for m = 0, …, 49 for the nine values of the tail index η. Note that—as a result of the scaling by the IQD—the nine plots fit in the same frame, the minimal values are comparable and for some unknown reason the plots all pass through approximately the same point. Note too that, even for η = 1/3, when Y has finite second moment, almost half the sample points are deleted to obtain the estimate ${\widehat{a}}_m\left(\eta \right)$ with the minimal loss. For η = 4, the optimal trimmed average is the median.

Rousseeuw (1984) suggests a trimming procedure for linear regression with heavy tails. Fix a positive integer m < n/2 − 1. For any slope $\gamma \in \mathbb{R}$, consider a closed strip S with slope γ such that there are m points above the strip and m points below. Compute the LS estimate $\widehat{b}\left(\gamma \right)+\widehat{a}\left(\gamma \right)x$ of the regression line based on the n − 2m points in the strip and the sum Q(γ) of the squared residuals. Define the Least Trimmed Squares estimate for this value of the trimming parameter m as the regression line L(γ) for which Q(γ) is minimal.

There are similarities with the theory of WB-estimators. The function Q is roughly V-shaped and the minimum is almost surely unique if X and Y have continuous dfs but Q is not decreasing to the left of its minimum or increasing to the right. The sum Q of the squared residuals in the strip S depends only on the way in which the strip S partitions the sample into three subsets of m, n − 2m and m points, but, to determine the minimum, one has to compute Q for all these different partitions. This makes LTS a computer intensive procedure. Note too that LTS uses the points inside the strip to estimate the regression line and WBm the points outside the strip.

In this paper, we only investigate Weighted Least Trimmed Squares (WLTS). By insisting on a minimal value of the squared residuals of the remaining points, the estimator does not pay special attention to the rightmost sample points. To compensate for this neglect, we introduce a reward. Divide Q by the product P of 1 + 1/i over the indices i of the n − 2m points in the strip. Since one wants to minimize Q, the reward for including the rightmost point is generous: Q is halved. One can introduce a positive parameter p to temper the reward, replacing 1 + 1/i by (1 + 1/i)^p. With the extra parameter p one can reduce the loss, but for certain values of the tail indices the loglog frequency plot of $|\widehat{a}(m,p)|$ for Pareto errors and for optimal m and p turns out to be bimodal, suggesting a dichotomy: choose γ to minimize Q or to include z₁ in the strip. See Figure 7b.

Therefore, a more complex reward function is used in this paper. It depends on two positive parameters p and r. We choose the strip S(γ) which minimizes the state function

$$T_{p,r}\left(\gamma \right)=logQ\left(\gamma \right)-p\sum _{{\mathbf{z}}_i\in S\left(\gamma \right)}\frac{1}{1+r(i-1)}.$$

(20)

The parameter r regulates how fast the reward decreases with the index i. The optimal values lie in (0,2). The parameter p determines the total effect on the state function. It may exceed 100. The distribution of $log|\widehat{a}|$ now has a good fit in the class of EGBP-distributions.

Given the trimming parameter m, one can compute for each γ a vector of T-values T_p,r with (p,r) ∈ Δ, and estimates ${\widehat{a}}_{p,r}$ for a finite set Δ ⊂ (0,∞)². By appropriate updating, one obtains a vector ${\widehat{a}}_{\mathrm{WLTS}(m,p,r)}$, (p,r) ∈ Δ. Now, compute the empirical sd for ten batches of 10⁵ simulations. The square root s = s(p,r) of the average loss over the million simulations is a function of (p,r). In Figure 8, Δ = {p₁, …, p₁₁} × {r₁, …, r₇} and we plot s(p,r) as a function of p for various values of r.

The performance of the resulting estimator WLTS is impressive.

The erratic dependence of p on the tail indices (ξ,η) suggests that it might be difficult to determine a good parameter triple (m, p, r) for a given sample of size n = 100 even if one has good estimates of the tail indices. The difference between the left and right plots in Figure 8 suggests that the parameters p and r may be sensitive to changes in the distribution of the error. For (ξ,η) = (1,1), the optimal trimming parameter m is the same for Student and Pareto errors, but the optimal values of the parameter p in the reward differ by a factor a thousand. In Figure 9, we plot in one figure the square root of the average loss in the estimate ${\widehat{a}}_{\mathrm{WLTS}}$ for Student and for Pareto errors for various values of r as a function of p. The minimal values for the two error distributions are not far apart but the difference in the optimal value of p and the difference in the structure of the graphs make it difficult to see how one should choose good parameter values if the distribution of the error is not known. These features place the WLTS(m, p, r) estimator hors concours.

We now turn to trimmed LAD. Let us first say a few words on terminology. Trimmed Least Squares as opposed to Least Trimmed Squares is investigated in Ruppert and Carroll (1980). In that paper, two procedures are compared. The trimming is based on a preliminary estimate of the slope of the regression line or on the Koenker–Bassett regression quantiles. The term Least Trimmed Squares introduced by Rousseeuw makes clear that one minimizes over all possible trimmings.

The LAD estimate is a bisector passing through two sample points. Hence, we consider trimming around a bisector. Given a positive integer m < n/2 − 1, for each bisector L of the sample, we consider the minimal closed strip S ⊃ L such that m sample points lie in the open half plane above S and m in the open half plane below. The boundary lines of S contain one sample point each. Define the state variable T = T_m as the sum of the absolute residuals of the n − 2m points in the strip with respect to the bisector L. Note that L is also a bisector of the sample restricted to the strip S. Define ${\widehat{a}}_m$ to be the slope of the bisector L for which the state variable T_m is minimal. The optimal value of the trimming parameter m is random. It minimizes the average loss over a million simulations. If the error has a symmetric Student distribution the optimal value of m is approximately 25. This holds for all values of the tail indices ξ and η. It also holds if we define the state function to be the sum of the squared residuals, or the difference between the maximal and minimal residual values. We therefore define the TB1, TB2 and TB∞ estimator of the regression line as the bisector L for which the corresponding state function T = T_m is minimal for m = 25. These three Trimmed Bisector estimators are based on trimming around a bisector. The difference between the three estimators is small.

It is not clear why the optimal value of m for trimming around bisectors should be m = 25. This value need not be optimal if the errors have a Pareto distribution.

7. Tables

There are three sets of six tables listing the empirical sd and bias for various estimators and error distributions for the six values ξ = 0, 1/2, 1, 3/2, 2, 3 of the tail exponent of the explanatory variable. These are followed by a set of twelve tables listing the parameter values.

Table 6. Empirical sd of the slope $\widehat{a}$ for estimators without a parameter for Student errors.

$\mathit{\eta }\setminus 0$	$\mathbf{LS}$	$\mathbf{LAD}$		$\mathbf{TS}$	$\mathbf{TB}1$	$\mathbf{TB}2$	$\mathbf{TB}\mathit{\infty }$
0	$0.0774\left[2\right]$	$0.0969\left[2\right]$		$0.0912\left[2\right]$	0.2578[5]	0.2371[5]	0.2227[5]
1/3	$0.1179\left[5\right]$	$0.0959\left[2\right]$		$0.1001\left[2\right]$	0.2094[5]	$0.1916\left[5\right]$	$0.1896\left[5\right]$
1/2	0.26[5]	$0.0951\left[2\right]$		$0.1041\left[5\right]$	$0.1888\left[5\right]$	$0.1726\left[5\right]$	$0.1770\left[5\right]$
2/3	1.6[5]	$0.0941\left[2\right]$		$0.1080\left[2\right]$	$0.1697\left[5\right]$	$0.1561\left[5\right]$	$0.1669\left[5\right]$
1	200[100]	$0.0917\left[2\right]$		$0.1147\left[2\right]$	$0.1390\left[5\right]$	$0.1302\left[5\right]$	$0.1516\left[5\right]$
3/2	1e+6[2e+6]	$0.0869\left[2\right]$		$0.1218\left[5\right]$	$0.1062\left[5\right]$	$0.1056\left[5\right]$	$0.1407\left[5\right]$
2	3e+9[5e+9]	$0.0810\left[5\right]$		$0.1257\left[5\right]$	$0.0838\left[5\right]$	$0.0936\left[5\right]$	$0.139\left[1\right]$
3	0[1e+17]	$0.0681\left[5\right]$		0.1242[5]	$0.0567\left[5\right]$	$0.095\left[1\right]$	0.153[1]
4	2e+24[5e+24]	$0.0560\left[5\right]$		0.1159[5]	$0.0417\left[5\right]$	0.124[5]	0.192[5]
$\eta \setminus 1/2$	LS	LAD	LADPC	TS	TB1	TB2	TB∞
0	$0.0518\left[1\right]$	$0.0641\left[2\right]$	$0.0711\left[2\right]$	$0.0822\left[2\right]$	0.258[1]	0.230[1]	0.2159[5]
1/3	$0.0788\left[5\right]$	$0.0670\left[2\right]$	$0.0720\left[2\right]$	$0.0913\left[2\right]$	0.2044[5]	0.1829[5]	0.1824[5]
1/2	0.17[2]	$0.0690\left[2\right]$	$0.0723\left[2\right]$	$0.0957\left[5\right]$	0.1827[5]	0.1640[5]	0.170[1]
2/3	1.0[5]	$0.072\left[1\right]$	$0.0726\left[2\right]$	$0.1001\left[2\right]$	0.163[1]	0.148[1]	0.1604[5]
1	120[50]	$0.1\left[1\right]$	$0.0727\left[2\right]$	$0.1083\left[5\right]$	$0.1331\left[5\right]$	$0.1236\left[5\right]$	$0.1452\left[5\right]$
3/2	0[1e+6]	3[5]	$0.0716\left[2\right]$	$0.1182\left[5\right]$	$0.1023\left[5\right]$	$0.1026\left[5\right]$	$0.135\left[1\right]$
2	1e+9[1e+9]	40[50]	$0.0695\left[5\right]$	$0.1253\left[5\right]$	$0.0835\left[5\right]$	$0.0960\left[5\right]$	$0.134\left[1\right]$
3	1e+16[1e+16]	1e+7[2e+7]	$0.0624\left[5\right]$	0.1298[5]	$0.0638\left[5\right]$	$0.113\left[2\right]$	0.153[2]
4	2e+23[5e+23]	2e+10[5e+10]	$0.055\left[1\right]$	0.1257[5]	$0.057\left[2\right]$	0.160[5]	0.21[1]
$\eta \setminus 1$	LS	LAD	LADPC	TS	TB1	TB2	TB∞
0	$0.00703\left[5\right]$	$0.00861\left[5\right]$	$0.01189\left[5\right]$	0.01660[5]	0.0647[2]	0.0558[2]	0.0514[2]
1/3	$0.0106\left[2\right]$	$0.00943\left[5\right]$	$0.01224\left[5\right]$	$0.0187\left[1\right]$	0.0491[2]	0.0424[2]	0.0424[2]
1/2	$0.022\left[5\right]$	$0.0104\left[5\right]$	$0.01239\left[5\right]$	$0.0197\left[1\right]$	0.0432[2]	0.0376[2]	0.0393[1]
2/3	0.1[1]	$0.012\left[1\right]$	$0.01259\left[5\right]$	$0.02084\left[5\right]$	0.0382[2]	0.0336[2]	0.0369[2]
1	10[10]	1[1]	$0.0130\left[1\right]$	$0.0230\left[1\right]$	0.0305[5]	0.0279[5]	0.0333[1]
3/2	30000[20000]	20[20]	$0.01328\left[5\right]$	$0.0260\left[1\right]$	$0.0234\left[2\right]$	$0.0238\left[5\right]$	0.0312[5]
2	1e+8[2e+8]	10000[10000]	$0.01339\left[5\right]$	0.0286[1]	$0.0197\left[2\right]$	$0.0237\left[2\right]$	0.0316[5]
3	0[1e+16]	2e+6[2e+6]	$0.0130\left[1\right]$	0.0314[2]	$0.0171\left[2\right]$	0.032[1]	0.038[1]
4	2e+23[5e+23]	0[2e+15]	$0.0123\left[5\right]$	0.0320[1]	$0.0182\left[5\right]$	0.049[1]	0.055[1]
$\eta \setminus 3/2$	LS	LAD	LADPC	TS	TB1	TB2	TB∞
0	$0.00122\left[1\right]$	$0.00149\left[1\right]$	0.00260[2]	0.00432[2]	0.0220[2]	0.0183[1]	0.0164[1]
1/3	$0.00184\left[5\right]$	$0.00167\left[2\right]$	$0.00271\left[2\right]$	0.00491[2]	0.0160[1]	0.0133[1]	0.0131[1]
1/2	$0.004\left[1\right]$	$0.00188\left[5\right]$	$0.00276\left[2\right]$	0.00521[2]	0.0137[1]	0.0116[1]	0.0120[1]
2/3	0.02[2]	$0.0028\left[5\right]$	$0.00282\left[2\right]$	$0.00556\left[2\right]$	0.0120[1]	0.0103[1]	0.0112[1]
1	3[5]	0.1[1]	$0.00296\left[2\right]$	0.00626[5]	0.0093[2]	0.0085[1]	0.0101[1]
3/2	5000[5000]	10[10]	$0.00313\left[2\right]$	0.00730[5]	0.0072[1]	0.0074[1]	0.0095[1]
2	2e+7[5e+7]	1e+6[2e+6]	$0.00328\left[2\right]$	0.00830[5]	$0.0063\left[1\right]$	0.0078[1]	0.0099[2]
3	1e+15[2e+15]	1e+8[2e+8]	$0.00344\left[5\right]$	0.00968[5]	$0.0062\left[2\right]$	0.0117[5]	0.0129[5]
4	0[1e+23]	3e+12[5e+12]	$0.00347\left[5\right]$	0.0104[1]	0.0074[2]	0.0187[5]	0.020[1]
$\eta \setminus 2$	LS	LAD	LADPC	TS	TB1	TB2	TB∞
0	$0.000243\left[5\right]$	$0.000296\left[5\right]$	0.000645[5]	0.00126[1]	0.0086[1]	0.00685[5]	0.00597[5]
1/3	$0.00036\left[1\right]$	$0.00034\left[1\right]$	$0.00068\left[1\right]$	0.00145[1]	0.00596[5]	0.00482[5]	0.00463[5]
1/2	$0.0008\left[5\right]$	$0.00041\left[5\right]$	$0.000693\left[5\right]$	0.00154[1]	0.00502[5]	0.00415[5]	0.00422[5]
2/3	0.004[5]	$0.001\left[1\right]$	$0.00071\left[1\right]$	0.00165[1]	0.00431[5]	0.00363[5]	0.00388[5]
1	1[1]	0.01[2]	$0.00075\left[1\right]$	0.00189[2]	0.0033[1]	0.00295[5]	0.00348[5]
3/2	1000[1000]	1[1]	$0.00082\left[1\right]$	0.00227[1]	0.00254[5]	0.00266[5]	0.00334[5]
2	0[1e+7]	0[100000]	$0.00089\left[1\right]$	0.00266[5]	0.00229[5]	0.00292[5]	0.0036[1]
3	1e+14[5e+14]	0[1e+7]	$0.00101\left[2\right]$	0.00328[2]	0.0025[1]	0.0047[2]	0.0050[2]
4	1e+22[2e+22]	1e+15[2e+15]	$0.00108\left[5\right]$	0.00372[5]	0.0032[2]	0.0079[2]	0.0081[5]
$\eta \setminus 3$	LS	LAD	LADPC	TS	TB1	TB2	TB∞
0	$0.0000129\left[5\right]$	$0.000016\left[1\right]$	0.000049[1]	0.000133[2]	0.00161[5]	0.00122[2]	0.00099[2]
1/3	$0.000019\left[2\right]$	$0.000018\left[1\right]$	0.000053[1]	0.000155[2]	0.00103[2]	0.00079[2]	0.00071[2]
1/2	$0.00004\left[2\right]$	$0.000022\left[1\right]$	0.000054[1]	0.000166[2]	0.00084[2]	0.00065[1]	0.00063[2]
2/3	0.0002[2]	$0.00005\left[5\right]$	$0.000055\left[2\right]$	0.000179[5]	0.00070[1]	0.00057[1]	0.00058[2]
1	0.02[5]	0.001[1]	$0.000060\left[2\right]$	0.000209[5]	0.00051[2]	0.00045[1]	0.00051[2]
3/2	30[50]	0.1[1]	$0.000068\left[2\right]$	0.000261[5]	0.00040[1]	0.00042[1]	0.00051[1]
2	100000[200000]	0[1000]	$0.000077\left[2\right]$	0.00032[1]	0.00038[2]	0.00051[5]	0.00057[5]
3	0[1e+13]	300000[500000]	$0.00010\left[1\right]$	0.00044[1]	0.00049[5]	0.0009[1]	0.0009[1]
4	1e+20[5e+20]	1e+13[2e+13]	$0.00012\left[1\right]$	0.00055[2]	0.0007[1]	0.0016[1]	0.0016[5]

shows the performance of six estimators which do not contain a parameter for Student errors. The succeeding tables show the performance of six estimators with a parameter, first for Student errors, then for Pareto errors.

The value of ξ can be estimated from the data. This determines the table which applies. In the first two sets the error has a symmetric Student distribution; in the third a Pareto distribution. The entries typically have the form m/10^k[d] where x_E = m/10^k is the mean of the ten quantities ${\gamma }_i=\sqrt{A_r}$ with $A_r=({\widehat{a}}_1^2+\cdots +{\widehat{a}}_r^2)/r$ the average loss for $\widehat{a}={\widehat{a}}_E$ over a batch of r = 10⁵ simulations of a sample of a hundred observations $(X_i,Y_i^{*})$. Here, $\widehat{a}={\widehat{a}}_E$ is the slope of the regression line estimated by E. The true regression line is the horizontal axis. The digit d ∈ {1, 2, 5} gives an indication of the size of the fluctuations in the ten observed values γ_i. See Equation (6) for the precise recipe.

The entries in the tables depend on the seed used in the simulations. We have used the seeds 2222 + 1, …, 2222 + 10⁶ for the ten batches of a hundred thousand simulations. A different sequence of seeds will give different outcomes. The size of the difference will be of the order of the quantity d/10^k above.

Colours are used to make the information in the tables more accessible. In each row, let y_∗ denote the minimum of the sums (m + 3d)/10^k over the six entries in the row corresponding to the different estimators, and x_∗ the corresponding value of x = m/10^k. (In

Table 7. Empirical sd of the slope $\widehat{a}$ for estimators with a parameter for Student errors.

$\mathit{\eta }\setminus 0$	$\mathbf{RM}\left[\mathit{r}\right]$	$\mathbf{HB}40\left[\mathit{d}\right]$	$\mathbf{HB}0\left[\mathit{d}\right]$	$\mathbf{LADHC}\left[\mathit{d}\right]$	$\mathbf{WTS}\left[\mathit{p}\right]$	$\mathbf{WLTS}[\mathit{m},\mathit{p},\mathit{r}]$
0	$0.1215\left[5\right]$	$0.0916\left[2\right]$	$0.0993\left[5\right]$	$0.0972\left[2\right]$	$0.0810\left[2\right]$	0.0706[2]
1/3	$0.1200\left[5\right]$	$0.0918\left[2\right]$	$0.0979\left[2\right]$	$0.0964\left[2\right]$	$0.0894\left[2\right]$	0.0722[2]
1/2	$0.1188\left[2\right]$	$0.0917\left[2\right]$	$0.0969\left[2\right]$	$0.0955\left[2\right]$	$0.0935\left[2\right]$	0.0726[2]
2/3	$0.1173\left[5\right]$	$0.0913\left[2\right]$	$0.0956\left[2\right]$	$0.0944\left[2\right]$	$0.0973\left[2\right]$	0.0727[2]
1	$0.1140\left[5\right]$	$0.0904\left[2\right]$	$0.0927\left[2\right]$	$0.0918\left[2\right]$	$0.1044\left[2\right]$	0.0717[1]
3/2	$0.1072\left[5\right]$	$0.0878\left[2\right]$	$0.0868\left[2\right]$	$0.0862\left[2\right]$	$0.1128\left[5\right]$	0.0680[2]
2	$0.0991\left[5\right]$	$0.0840\left[2\right]$	$0.0800\left[2\right]$	$0.0797\left[5\right]$	$0.1190\left[5\right]$	0.0626[2]
3	$0.0806\left[5\right]$	$0.0738\left[5\right]$	$0.0645\left[5\right]$	$0.0643\left[5\right]$	$0.125\left[1\right]$	0.0475[2]
4	$0.0633\left[5\right]$	$0.0626\left[2\right]$	$0.0498\left[2\right]$	$0.0497\left[2\right]$	0.129[1]	0.0331[2]
$\eta \setminus 1/2$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.0889\left[5\right]$	$0.0632\left[1\right]$	$0.0687\left[2\right]$	$0.0658\left[2\right]$	$0.0553\left[1\right]$	0.0398[1]
1/3	$0.0930\left[5\right]$	$0.0663\left[2\right]$	$0.0710\left[2\right]$	$0.0680\left[2\right]$	$0.0632\left[2\right]$	0.0421[1]
1/2	$0.0944\left[5\right]$	$0.0677\left[2\right]$	$0.0717\left[2\right]$	$0.0691\left[2\right]$	$0.0674\left[2\right]$	0.0428[1]
2/3	$0.0955\left[5\right]$	$0.0689\left[2\right]$	$0.0725\left[5\right]$	$0.0704\left[2\right]$	$0.0717\left[2\right]$	0.0430[1]
1	$0.0973\left[2\right]$	$0.0712\left[2\right]$	$0.0735\left[2\right]$	$0.0719\left[2\right]$	$0.0801\left[2\right]$	0.0424[1]
3/2	$0.0972\left[5\right]$	$0.0729\left[2\right]$	$0.0730\left[2\right]$	$0.0725\left[2\right]$	$0.0917\left[5\right]$	0.0396[1]
2	$0.0947\left[5\right]$	$0.0731\left[5\right]$	$0.0709\left[2\right]$	$0.0711\left[2\right]$	$0.1018\left[2\right]$	0.0356[1]
3	$0.0833\left[5\right]$	$0.0692\left[5\right]$	$0.0621\left[5\right]$	$0.0625\left[5\right]$	$0.117\left[1\right]$	0.0264[1]
4	$0.0706\left[5\right]$	$0.0624\left[5\right]$	$0.0512\left[5\right]$	$0.0512\left[2\right]$	0.129[1]	0.01825[5]
$\eta \setminus 1$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.0116\left[1\right]$	$0.00870\left[5\right]$	$0.00952\left[5\right]$	$0.00920\left[5\right]$	$0.00754\left[2\right]$	0.00706[5]
1/3	$0.0138\left[1\right]$	$0.00957\left[5\right]$	$0.01030\left[5\right]$	$0.00980\left[5\right]$	$0.00894\left[5\right]$	0.00860[5]
1/2	$0.0147\left[1\right]$	$0.01009\left[5\right]$	$0.01071\left[5\right]$	$0.01020\left[5\right]$	$0.00978\left[5\right]$	0.00936[5]
2/3	$0.0156\left[1\right]$	$0.01066\left[5\right]$	$0.01119\left[5\right]$	$0.01069\left[5\right]$	$0.01071\left[5\right]$	0.0100[1]
1	$0.01703\left[5\right]$	$0.01160\left[5\right]$	$0.01203\left[5\right]$	$0.01171\left[5\right]$	$0.0127\left[1\right]$	0.0109[1]
3/2	$0.0187\left[2\right]$	$0.0128\left[1\right]$	$0.0129\left[1\right]$	$0.01270\left[5\right]$	$0.0156\left[2\right]$	0.0110[1]
2	$0.0197\left[5\right]$	$0.01375\left[5\right]$	$0.01346\left[5\right]$	$0.01328\left[5\right]$	$0.0185\left[1\right]$	0.01040[5]
3	$0.0195\left[5\right]$	$0.0144\left[2\right]$	$0.0133\left[2\right]$	$0.0132\left[1\right]$	$0.0240\left[5\right]$	0.00839[5]
4	$0.0180\left[2\right]$	$0.0141\left[2\right]$	$0.0120\left[2\right]$	$0.0119\left[1\right]$	0.0288[5]	0.00617[5]
$\eta \setminus 3/2$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.00189\left[5\right]$	$0.00153\left[1\right]$	$0.00168\left[2\right]$	$0.00176\left[1\right]$	$0.00133\left[1\right]$	0.00123[1]
1/3	$0.00250\left[5\right]$	$0.00174\left[2\right]$	$0.00187\left[2\right]$	$0.00188\left[2\right]$	$0.00160\left[2\right]$	0.00159[2]
1/2	$0.00277\left[5\right]$	$0.00188\left[2\right]$	$0.00200\left[2\right]$	$0.00197\left[2\right]$	$0.00178\left[1\right]$	0.00183[2]
2/3	$0.00307\left[5\right]$	$0.00205\left[2\right]$	$0.00216\left[2\right]$	$0.00208\left[2\right]$	$0.00201\left[2\right]$	0.00204[2]
1	$0.00362\left[5\right]$	$0.00236\left[5\right]$	$0.00245\left[2\right]$	$0.00236\left[2\right]$	$0.00250\left[5\right]$	0.00236[2]
3/2	$0.0044\left[1\right]$	$0.00278\left[5\right]$	$0.00285\left[5\right]$	$0.00278\left[5\right]$	$0.00330\left[5\right]$	0.00261[5]
2	$0.0050\left[2\right]$	$0.00316\left[5\right]$	$0.00314\left[2\right]$	$0.00311\left[2\right]$	$0.00418\left[5\right]$	0.00269[5]
3	$0.0056\left[2\right]$	$0.0037\left[1\right]$	$0.0035\left[1\right]$	$0.00345\left[5\right]$	$0.0062\left[2\right]$	0.00243[5]
4	$0.0056\left[2\right]$	$0.00394\left[5\right]$	$0.00343\left[5\right]$	$0.00343\left[5\right]$	0.0082[5]	0.00200[5]
$\eta \setminus 2$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.00036\left[1\right]$	$0.000306\left[5\right]$	$0.00034\left[1\right]$	$0.000384\left[5\right]$	$0.000271\left[5\right]$	0.000245[5]
1/3	$0.00052\left[1\right]$	$0.00036\left[1\right]$	$0.00039\left[1\right]$	$0.00043\left[1\right]$	$0.000328\left[5\right]$	0.00033[1]
1/2	$0.00058\left[1\right]$	$0.00040\left[1\right]$	$0.000423\left[5\right]$	$0.000448\left[5\right]$	$0.000370\left[5\right]$	0.00038[1]
2/3	$0.00069\left[5\right]$	$0.00044\left[1\right]$	$0.00047\left[1\right]$	$0.000476\left[5\right]$	$0.000426\left[5\right]$	0.00044[1]
1	$0.00084\left[2\right]$	$0.00053\left[2\right]$	$0.00056\left[2\right]$	$0.00054\left[1\right]$	$0.00055\left[2\right]$	0.00054[2]
3/2	$0.0012\left[1\right]$	$0.00066\left[2\right]$	$0.00069\left[2\right]$	$0.00067\left[2\right]$	$0.00077\left[2\right]$	0.00065[2]
2	$0.00137\left[5\right]$	$0.00081\left[1\right]$	$0.00080\left[1\right]$	$0.00082\left[1\right]$	$0.00104\left[2\right]$	0.00070[2]
3	$0.0018\left[1\right]$	$0.00107\left[5\right]$	$0.00102\left[5\right]$	$0.00100\left[2\right]$	$0.0018\left[1\right]$	0.00072[2]
4	$0.00191\left[5\right]$	$0.00122\left[5\right]$	$0.00107\left[2\right]$	$0.00108\left[2\right]$	0.0025[1]	0.00066[1]
$\eta \setminus 3$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.000018\left[1\right]$	$0.000017\left[1\right]$	$0.000018\left[1\right]$	$0.000027\left[1\right]$	$0.0000150\left[5\right]$	0.0000130[5]
1/3	$0.000025\left[2\right]$	$0.000020\left[1\right]$	$0.000021\left[1\right]$	$0.000030\left[1\right]$	$0.000018\left[1\right]$	0.000018[1]
1/2	$0.000034\left[1\right]$	$0.000022\left[1\right]$	$0.000024\left[1\right]$	$0.000032\left[2\right]$	$0.0000210\left[5\right]$	0.000021[2]
2/3	$0.000040\left[5\right]$	$0.000026\left[1\right]$	$0.000029\left[2\right]$	$0.000033\left[2\right]$	$0.000025\left[1\right]$	0.000025[1]
1	$0.000054\left[2\right]$	$0.000032\left[2\right]$	$0.000035\left[2\right]$	$0.000038\left[2\right]$	$0.000033\left[1\right]$	0.000033[2]
3/2	$0.000086\left[5\right]$	$0.000046\left[5\right]$	$0.000050\left[5\right]$	$0.000049\left[2\right]$	$0.000054\left[5\right]$	0.000046[5]
2	$0.000122\left[5\right]$	$0.00006\left[1\right]$	$0.00007\left[1\right]$	$0.000065\left[2\right]$	$0.000077\left[5\right]$	0.000053[5]
3	$0.00020\left[2\right]$	$0.00011\left[2\right]$	$0.00010\left[1\right]$	$0.00010\left[1\right]$	$0.00017\left[5\right]$	0.000069[5]
4	$0.00024\left[1\right]$	$0.00013\left[1\right]$	$0.00012\left[1\right]$	$0.00012\left[1\right]$	$0.00025\left[5\right]$	0.000073[5]

,

Table 8. Empirical sd and bias of the slope $\widehat{a}$ for estimators with a parameter for Pareto errors.

$\mathit{\eta }\setminus 0$	$\mathbf{RM}\left[\mathit{r}\right]$	$\mathbf{HB}40\left[\mathit{d}\right]$	$\mathbf{HB}0\left[\mathit{d}\right]$	$\mathbf{LADHC}\left[\mathit{d}\right]$	$\mathbf{WTS}\left[\mathit{p}\right]$	$\mathbf{WLTS}[\mathit{m},\mathit{p},\mathit{r}]$
0	$0.1194\left[5\right]$	$0.0877\left[2\right]$	$0.0969\left[2\right]$	$0.0949\left[2\right]$	$0.0712\left[1\right]$	0.0778[2]
	0.0096[5]	0.0086[5]	0.0079[5]	0.0088[2]	0.0089[2]	−0.0280[5]
1/3	$0.1165\left[5\right]$	$0.0844\left[2\right]$	$0.0942\left[2\right]$	$0.0927\left[2\right]$	$0.0679\left[1\right]$	0.0823[2]
	0.0122[5]	0.0096[5]	0.0100[5]	0.0112[2]	0.0099[2]	−0.0462[5]
1/2	$0.1149\left[5\right]$	$0.0826\left[2\right]$	$0.0926\left[2\right]$	$0.0910\left[1\right]$	$0.0640\left[1\right]$	0.0823[2]
	0.0134[5]	0.0097[5]	0.0109[5]	0.0118[2]	0.0093[2]	−0.0561[2]
2/3	$0.1128\left[2\right]$	$0.0806\left[2\right]$	$0.0906\left[2\right]$	$0.0893\left[5\right]$	$0.0604\left[2\right]$	0.0812[2]
	0.0129[5]	0.0104[5]	0.0110[2]	0.0120[1]	0.0088[2]	−0.0650[2]
1	0.1085[5]	$0.0761\left[5\right]$	$0.0865\left[2\right]$	$0.0854\left[5\right]$	$0.0517\left[2\right]$	0.0702[5]
	0.0145[5]	0.0104[2]	0.0118[2]	0.0124[2]	0.0068[2]	−0.0890[2]
3/2	0.1006[5]	$0.0685\left[2\right]$	$0.0793\left[2\right]$	$0.0786\left[2\right]$	$0.0422\left[2\right]$	0.072[5]
	0.0137[2]	0.0096[2]	0.0125[2]	0.0133[1]	0.0055[1]	−0.0762[2]
2	0.0917[5]	$0.0601\left[2\right]$	0.0715[5]	0.0708[5]	$0.0333\left[2\right]$	0.055[1]
	0.0128[2]	0.0087[2]	0.0123[2]	0.0126[2]	0.0039[1]	−0.0657[1]
3	0.0733[5]	0.0434[2]	0.0556[5]	0.0553[2]	$0.0196\left[1\right]$	0.0376[5]
	0.0108[2]	0.0062[1]	0.0110[2]	0.0103[2]	0.00149[5]	−0.0417[1]
4	0.0571[5]	0.0296[2]	0.0412[5]	0.0408[2]	$0.0115\left[1\right]$	0.0236[2]
	0.0071[2]	0.0040[1]	0.0082[1]	0.0078[2]	0.00054[2]	−0.02674[5]
$\eta \setminus 1/2$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.0918\left[2\right]$	$0.0626\left[2\right]$	$0.0690\left[2\right]$	$0.0658\left[2\right]$	$0.0498\left[1\right]$	0.0517[2]
	0.0134[5]	0.0101[2]	0.0105[2]	0.0098[2]	0.0077[2]	−0.0131[2]
1/3	$0.0947\left[2\right]$	$0.0636\left[2\right]$	$0.0704\left[2\right]$	$0.0671\left[2\right]$	$0.0518\left[2\right]$	0.0534[2]
	0.0165[5]	0.0117[2]	0.0129[2]	0.0128[2]	0.0099[2]	−0.0218[2]
1/2	$0.0956\left[5\right]$	$0.0639\left[2\right]$	$0.0710\left[5\right]$	$0.0675\left[2\right]$	$0.0529\left[2\right]$	0.0533[2]
	0.0172[5]	0.0124[2]	0.0143[2]	0.0140[2]	0.0108[2]	−0.0263[1]
2/3	$0.0964\left[5\right]$	$0.0639\left[5\right]$	$0.0710\left[5\right]$	$0.0682\left[5\right]$	$0.0524\left[5\right]$	0.0535[5]
	0.0179[5]	0.0134[2]	0.0149[2]	0.0154[1]	0.0110[2]	−0.0284[1]
1	$0.0969\left[5\right]$	$0.0632\left[5\right]$	$0.0709\left[5\right]$	$0.0689\left[5\right]$	$0.0470\left[5\right]$	0.0517[2]
	0.0196[5]	0.0138[2]	0.0163[2]	0.0171[2]	0.0095[2]	−0.0328[2]
3/2	0.0951[5]	$0.0609\left[5\right]$	$0.0693\left[5\right]$	$0.0669\left[5\right]$	$0.0374\left[2\right]$	0.0463[2]
	0.0199[5]	0.0137[2]	0.0175[2]	0.0175[2]	0.0064[1]	−0.0351[1]
2	0.091[1]	$0.0569\left[5\right]$	0.0662[5]	0.0639[5]	$0.0309\left[2\right]$	0.0423[5]
	0.0203[5]	0.0128[2]	0.0178[2]	0.0165[2]	0.0048[1]	−0.0290[1]
3	0.079[1]	0.0453[5]	0.0560[5]	0.0549[5]	$0.0197\left[2\right]$	0.0299[2]
	0.0174[2]	0.0098[2]	0.0156[2]	0.0146[2]	0.00217[5]	−0.0183[1]
4	0.064[1]	0.0325[5]	0.0444[5]	0.0434[2]	$0.0122\left[1\right]$	0.0195[2]
	0.0127[2]	0.0066[1]	0.0122[2]	0.0115[2]	0.00102[5]	−0.01029[5]
$\eta \setminus 1$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.0134\left[1\right]$	$0.00907\left[5\right]$	$0.00995\left[5\right]$	$0.00944\left[5\right]$	$0.00692\left[5\right]$	0.00733[5]
	0.00236[5]	0.00158[2]	0.00165[2]	0.00148[2]	0.00096[2]	−0.00080[2]
1/3	0.0155[1]	$0.00987\left[5\right]$	$0.0108\left[1\right]$	$0.0102\left[1\right]$	$0.00748\left[5\right]$	0.00770[5]
	0.00306[5]	0.00205[2]	0.00216[5]	0.00203[5]	0.00130[2]	−0.00161[2]
1/2	0.0162[1]	$0.0102\left[1\right]$	$0.0113\left[1\right]$	$0.01053\left[5\right]$	$0.0078\left[1\right]$	0.00786[5]
	0.00329[5]	0.00223[2]	0.00244[5]	0.00229[5]	0.00145[2]	−0.00178[2]
2/3	0.0170[2]	$0.0105\left[1\right]$	$0.0116\left[1\right]$	$0.0111\left[1\right]$	$0.0081\left[1\right]$	0.00788[5]
	0.00353[5]	0.00241[5]	0.00263[5]	0.00258[5]	0.00159[2]	−0.00209[2]
1	$0.0183\left[2\right]$	$0.0111\left[1\right]$	$0.0123\left[1\right]$	$0.0121\left[1\right]$	$0.0089\left[2\right]$	0.0078[1]
	0.00408[5]	0.00272[5]	0.00303[5]	0.00309[5]	0.00183[2]	−0.00257[5]
3/2	$0.0196\left[2\right]$	$0.0115\left[1\right]$	$0.0131\left[2\right]$	$0.0134\left[2\right]$	$0.0100\left[5\right]$	0.00729[5]
	0.00462[5]	0.00298[5]	0.00348[5]	0.00366[5]	0.00200[5]	−0.00329[2]
2	0.0203[2]	$0.0115\left[1\right]$	$0.0135\left[2\right]$	$0.0130\left[2\right]$	$0.0086\left[5\right]$	0.00670[5]
	0.0048[1]	0.00309[5]	0.00373[5]	0.00367[5]	0.00164[2]	−0.00300[2]
3	0.0194[5]	0.0104[2]	0.0128[2]	0.0123[2]	$0.0048\left[1\right]$	0.0052[1]
	0.0048[1]	0.00279[5]	0.00366[5]	0.00358[5]	0.00078[2]	−0.00233[2]
4	0.0172[5]	0.0083[2]	0.0111[2]	0.0107[1]	$0.0030\left[1\right]$	0.00361[5]
	0.00389[5]	0.00210[5]	0.00315[5]	0.00309[5]	0.00038[1]	−0.00184[1]

and

Table 9. Empirical sd and bias of the slope $\widehat{a}$ for estimators with a parameter for Pareto errors.

$\mathit{\eta }\setminus 3/2$	$\mathbf{RM}\left[\mathit{r}\right]$	$\mathbf{HB}40\left[\mathit{d}\right]$	$\mathbf{HB}0\left[\mathit{d}\right]$	$\mathbf{LADHC}\left[\mathit{d}\right]$	$\mathbf{WTS}\left[\mathit{p}\right]$	$\mathbf{WLTS}[\mathit{m},\mathit{p},\mathit{r}]$
0	$0.00236\left[5\right]$	$0.00165\left[2\right]$	$0.00182\left[2\right]$	$0.00182\left[2\right]$	$0.00125\left[1\right]$	0.00133[1]
	0.000368[5]	0.000247[5]	0.000269[5]	0.000237[5]	0.000146[5]	−0.000073[5]
1/3	0.00301[5]	$0.00189\left[2\right]$	$0.00209\left[2\right]$	$0.00198\left[2\right]$	$0.00139\left[2\right]$	0.00142[1]
	0.00052[1]	0.000342[5]	0.000373[5]	0.000329[5]	0.000203[5]	−0.000132[5]
1/2	0.00333[5]	$0.00201\left[2\right]$	$0.00221\left[5\right]$	$0.00206\left[1\right]$	$0.00148\left[2\right]$	0.00147[2]
	0.00060[1]	0.000385[5]	0.000417[5]	0.00037[1]	0.000232[5]	−0.000167[5]
2/3	0.0037[1]	$0.00215\left[5\right]$	$0.00239\left[5\right]$	$0.00219\left[2\right]$	$0.00158\left[5\right]$	0.00152[2]
	0.00069[1]	0.000434[5]	0.000475[5]	0.00043[1]	0.000259[5]	−0.000159[5]
1	0.0042[1]	$0.00238\left[5\right]$	$0.00267\left[5\right]$	$0.00249\left[2\right]$	$0.00180\left[5\right]$	0.00150[5]
	0.00085[2]	0.000518[5]	0.000569[5]	0.000530[5]	0.000311[5]	−0.000239[5]
3/2	$0.0049\left[1\right]$	$0.00271\left[5\right]$	$0.00302\left[5\right]$	$0.0030\left[1\right]$	$0.0023\left[2\right]$	0.00154[5]
	0.00106[1]	0.00063[1]	0.00069[1]	0.00068[1]	0.000381[5]	−0.000302[5]
2	$0.0056\left[2\right]$	$0.00291\left[5\right]$	$0.0033\left[1\right]$	$0.0033\left[1\right]$	$0.0028\left[2\right]$	0.00142[2]
	0.00122[2]	0.00071[1]	0.00080[1]	0.00078[1]	0.00041[1]	−0.000429[5]
3	$0.0059\left[2\right]$	$0.0030\left[1\right]$	$0.0035\left[1\right]$	$0.00342\left[5\right]$	$0.003\left[1\right]$	0.00113[1]
	0.00139[2]	0.00075[1]	0.00089[1]	0.00087[1]	0.000312[5]	−0.000380[5]
4	0.0058[2]	0.0026[1]	0.0034[1]	0.00329[5]	$0.00100\left[5\right]$	0.00082[2]
	0.00132[2]	0.00067[1]	0.00086[1]	0.00086[1]	0.000138[5]	−0.000297[2]
$\eta \setminus 2$	RM[r]	HB40[d]	HB40[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.00046\left[2\right]$	$0.000340\left[5\right]$	$0.000374\left[5\right]$	$0.000416\left[5\right]$	$0.000260\left[5\right]$	0.000272[5]
	0.000054[1]	0.000041[1]	0.000044[1]	0.000042[2]	0.0000244[5]	−44e-7[5e-7]
1/3	$0.00064\left[2\right]$	$0.00041\left[1\right]$	$0.00044\left[1\right]$	$0.000452\left[5\right]$	$0.00030\left[1\right]$	0.000296[5]
	0.000089[2]	0.000059[1]	0.000063[1]	0.000059[1]	0.000035[1]	−0.000017[1]
1/2	0.00076[2]	$0.00044\left[2\right]$	$0.00049\left[1\right]$	$0.000471\left[5\right]$	$0.00032\left[1\right]$	0.000306[5]
	0.000113[2]	0.000069[1]	0.000074[1]	0.000068[2]	0.000040[1]	−0.000016[1]
2/3	0.00084[2]	$0.00049\left[2\right]$	$0.00053\left[2\right]$	$0.00051\left[1\right]$	$0.00034\left[1\right]$	0.000314[5]
	0.000130[2]	0.000079[1]	0.000084[1]	0.000079[2]	0.000046[1]	−0.000025[1]
1	0.00107[5]	$0.00057\left[2\right]$	$0.00061\left[2\right]$	$0.00059\left[2\right]$	$0.00041\left[2\right]$	0.000324[5]
	0.000186[5]	0.000099[1]	0.000107[2]	0.000099[1]	0.000057[1]	−0.000040[1]
3/2	$0.00133\left[5\right]$	$0.00069\left[2\right]$	$0.00076\left[2\right]$	$0.00073\left[2\right]$	$0.00055\left[5\right]$	0.00033[2]
	0.000249[5]	0.000129[2]	0.000140[2]	0.000132[2]	0.000073[1]	−0.000036[1]
2	$0.0016\left[1\right]$	$0.00079\left[5\right]$	$0.00088\left[5\right]$	$0.00089\left[5\right]$	$0.0007\left[1\right]$	0.00033[2]
	0.000304[5]	0.000157[2]	0.000174[2]	0.000164[5]	0.000084[2]	−0.000049[1]
3	$0.0020\left[2\right]$	$0.00090\left[5\right]$	$0.00106\left[5\right]$	$0.00104\left[5\right]$	$0.0009\left[5\right]$	0.000282[5]
	0.00039[1]	0.000191[5]	0.000215[5]	0.000207[5]	0.000077[2]	−0.000067[1]
4	0.0021[2]	$0.00089\left[5\right]$	0.00111[5]	0.00107[5]	$0.00035\left[5\right]$	0.000217[5]
	0.00043[1]	0.000193[5]	0.000235[5]	0.000227[2]	0.000043[1]	−0.000052[1]
$\eta \setminus 3$	RM[r]	HB40[d]	HB0[d]	LADHC[d]	WTS[p]	$\mathrm{WLTS}[m,p,r]$
0	$0.000024\left[2\right]$	$0.000019\left[1\right]$	$0.000021\left[1\right]$	$0.000030\left[1\right]$	$0.000015\left[1\right]$	0.000015[1]
	16e-7[1e-7]	135e-8[5e-8]	144e-8[5e-8]	18e-7[1e-7]	86e-8[5e-8]	6e-8[5e-8]
1/3	$0.00004\left[1\right]$	$0.000024\left[2\right]$	$0.000026\left[2\right]$	$0.000032\left[1\right]$	$0.000018\left[2\right]$	0.000017[1]
	28e-7[2e-7]	207e-8[5e-8]	219e-8[5e-8]	25e-7[1e-7]	126e-8[5e-8]	−14e-8[5e-8]
1/2	$0.000044\left[5\right]$	$0.000027\left[2\right]$	$0.000029\left[2\right]$	$0.000033\left[1\right]$	$0.000019\left[2\right]$	0.000017[1]
	39e-7[1e-7]	25e-7[1e-7]	26e-7[1e-7]	28e-7[1e-7]	148e-8[5e-8]	−26e-8[5e-8]
2/3	$0.000053\left[5\right]$	$0.000030\left[5\right]$	$0.000034\left[5\right]$	$0.000036\left[5\right]$	$0.000021\left[5\right]$	0.000018[1]
	47e-7[1e-7]	30e-7[1e-7]	31e-7[1e-7]	33e-7[1e-7]	172e-8[5e-8]	−32e-8[5e-8]
1	$0.00008\left[1\right]$	$0.00004\left[1\right]$	$0.00004\left[1\right]$	$0.000044\left[5\right]$	$0.000027\left[5\right]$	0.000019[1]
	74e-7[2e-7]	39e-7[1e-7]	42e-7[1e-7]	43e-7[1e-7]	223e-8[5e-8]	−43e-8[5e-8]
3/2	$0.00012\left[1\right]$	$0.000053\left[5\right]$	$0.00006\left[1\right]$	$0.000052\left[5\right]$	$0.00004\left[1\right]$	0.000020[1]
	0.0000159[2]	57e-7[2e-7]	61e-7[2e-7]	59e-7[2e-7]	31e-7[1e-7]	−74e-8[5e-8]
2	$0.00015\left[2\right]$	$0.00007\left[1\right]$	$0.00008\left[1\right]$	$0.000069\left[5\right]$	$0.00006\left[2\right]$	0.000021[2]
	0.0000191[5]	75e-7[2e-7]	82e-7[2e-7]	78e-7[2e-7]	40e-7[2e-7]	−112e-8[5e-8]
3	$0.00025\left[5\right]$	$0.00010\left[2\right]$	$0.00011\left[2\right]$	$0.00012\left[1\right]$	$0.00013\left[5\right]$	0.000020[1]
	0.000027[1]	0.0000109[5]	0.0000126[5]	0.0000120[5]	59e-7[5e-7]	−159e-8[5e-8]
4	0.0006[5]	$0.00012\left[2\right]$	$0.00014\left[2\right]$	$0.00014\left[1\right]$	$0.0003\left[2\right]$	0.000018[1]
	0.000034[2]	0.0000131[5]	0.0000158[5]	0.0000149[2]	7e-6[1e-6]	−22e-7[1e-7]

Weighted Least Trimmed Squares, WLTS, is excluded in determining the minimum.) The colour scheme is:

• red: 0 < x_E ≤ x_∗ (minimum);
• green: 0 < x_E ≤ y_∗ (indistinguishable from the minimum);
• blue: 0 < x_E ≤ 5y_∗/4 (excellent); and
• purple: 0 < x_E ≤ 2y_∗ (good).

A colourful table indicates that there are quite a few estimators which perform well.

The estimators are geometric. The estimated regression line does not change if one changes the coordinates, although the coordinates of the line do (see Equation (5)). The estimates of LADPC and LADHC are aberrant, they are not invariant under translations of the horizontal axis. They are geometric for the smaller group ${\mathcal{G}}_0$ (see Equation (17)).

In the second and third set of tables, the estimator depends on a parameter. The parameter may vary with the values of the tail indices ξ and η. It is chosen to minimize the average loss. The value of this optimal parameter is given in

Table 10. Parameter r = 2r₀ + 1 for Right Median, RM(r), with Student (left) and Pareto (right) errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3		$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	21	5	1	1	1	1		0	11	4	1	0	0	0
1/3	21	7	3	3	1	1		1/3	11	5	2	1	1	0
1/2	23	9	5	3	3	3		1/2	11	6	3	2	2	1
2/3	25	11	7	5	3	3		2/3	13	7	4	2	2	1
1	27	13	9	7	5	5		1	13	8	5	4	4	2
3/2	29	17	13	11	7	7		3/2	16	11	7	5	5	5
2	31	21	15	13	11	11		2	18	12	11	6	6	5
3	35	29	23	19	17	15		3	20	16	13	11	9	6
4	41	39	33	27	23	21		4	23	20	18	14	13	6

,

Table 11. Parameter d > 0 for Hyperbolic Balance 40, HB40(d), with Student (left) and Pareto (right) errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3		$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	12	3	1.5	1	0.8	0.8		0	15	3	1.5	1	1	0.8
1/3	15	4	2	1.2	1	1		1/3	15	4	2	1.2	1.2	1
1/2	15	4	2	1.5	1.2	1		1/2	15	4	2	1.5	1.2	1
2/3	15	5	2.5	1.5	1.2	1		2/3	20	5	2.5	1.5	1.5	1
1	20	6	3	2	1.5	1.2		1	25	6	3	2	2	1.2
3/2	25	8	4	2.5	2	1.5		3/2	30	8	4	3	2.5	1.5
2	30	10	5	4	3	2		2	40	10	5	4	4	2
3	40	20	10	6	6	4		3	50	20	10	8	6	4
4	60	30	15	12	12	6		4	100	40	20	15	12	6

,

Table 12. Parameter d > 0 for Hyperbolic Balance 50, HB0(d), with Student (left) and Pareto (right) errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3		$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	15	3	1.5	1.2	1	1		0	10	3	1.5	1.2	1	1
1/3	15	4	2	1.5	1.2	1		1/3	15	5	2	1.5	1.2	1.2
1/2	20	4	2	1.5	1.2	1.2		1/2	20	6	2.5	2	1.5	1.2
2/3	20	5	2	1.5	1.5	1.5		2/3	20	6	3	2	1.5	1.5
1	20	6	3	2	2	1.5		1	30	10	4	3	2	1.5
3/2	25	8	4	3	2.5	2		3/2	60	20	8	4	3	2
2	30	10	5	4	3	2.5		2	100	40	12	6	5	2.5
3	40	20	10	8	6	4		3	300	150	40	15	10	4
4	60	40	20	15	12	8		4	1000	500	120	40	20	6

,

Table 13. Parameter d > 0 for LAD with Hyperbolic Correction, LADHC(d), with Student (left) and Pareto (right) errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3		$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	12	3	1.5	1	0.8	0.8		0	15	3	1.5	1	1	0.8
1/3	15	4	2	1.2	1	1		1/3	15	4	2	1.2	1.2	1
1/2	15	4	2	1.5	1.2	1		1/2	15	4	2	1.5	1.2	1
2/3	15	5	2.5	1.5	1.2	1		2/3	20	5	2.5	1.5	1.5	1
1	20	6	3	2	1.5	1.2		1	25	6	3	2	2	1.2
3/2	25	8	4	2.5	2	1.5		3/2	30	8	4	3	2.5	1.5
2	30	10	5	4	3	2		2	40	10	5	4	4	2
3	40	20	10	6	6	4		3	50	20	10	8	6	4
4	60	30	15	12	12	6		4	100	40	20	15	12	6

,

Table 14. Parameter p > 0 for Weighted Theil–Sen, WTS(p), with Student (left) and Pareto (right) errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3		$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	15	2.5	1	1	1	1		0	2.5	1	1	1	1	1
1/3	15	3	1.2	1	1	1		1/3	3	1	1	1	1	1
1/2	15	4	1.5	1	1	1		1/2	4	1	1	1	1	1
2/3	20	5	2	1.2	1	1		2/3	5	1.2	1	1	1	1
1	25	6	3	2	1.5	1		1	10	2.5	1	1	1	1
3/2	25	8	5	4	3	1		3/2	15	8	1.2	1	1	1
2	30	12	8	6	5	4		2	25	15	2.5	1.2	1.2	1
3	50	30	15	8	6	5		3	100	60	15	3	2.5	1.2
4	80	50	25	12	10	8		4	400	150	50	20	12	1.5

,

Table 15. Parameters (m, p, r) for Weighted Least Trimmed Squares, WLTS(m, p, r), with Student errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	(5,0,0)	(6, 0, 0)	(1, 0. 04, 0.25)	(1, 0.4, 2.5)	(1, 0.25, 1.5)	(1, 0.3, 1.5)
1/3	(12, 0.008, 0.01)	(12, 0.005, 0.1)	(5, 0. 1,2)	(3, 0.12, 2.5)	(4, 0.2, 0.8)	(4, 0.2, 1.2)
1/2	(14, 0.008, 0.06)	(16, 0.02, 0.3)	(9, 0.12, 1.5)	(8, 0.15, 0.8)	(6, 0.25, 0.6)	(5, 0.3, 1.25)
2/3	(16, 0.012, 0.05)	(19, 0.04, 0.8)	(12, 0.15, 1)	(10, 0.15, 0.8)	(11, 0.3, 0.6)	(10, 0.3, 1)
1	(22, 0.04, 0.08)	(26, 0.08, 0.3)	(16, 0.2, 0.5)	(15, 0.4, 0.4)	(14, 0.3, 0.6)	(16, 0.8, 1.5)
3/2	(25, 0.1, 0.06)	(33, 0.25, 0.4)	(24, 0.5, 0.4)	(24, 0.8, 0.4)	(18, 0.6, 0.3)	(20, 3, 2.5)
2	(28, 0.15, 0.05)	(38, 0.5, 0.4)	(30, 0.8, 0.3)	(28, 1, 0.25)	(26, 1, 0.3)	(24, 3, 2.5)
3	(34, 0.5, 0.015)	(42, 1, 0.3)	(35, 1.2, 0.2)	(32, 1.5, 0.25)	(30, 1.5, 0.25)	(26, 8, 5)
4	(39, 0.8, 0.03)	(45, 1.5, 0.25)	(38, 1.5, 0.15)	(34, 1.5, 0.15)	(32, 1.5, 0.2)	(28, 10, 5)

and

Table 16. Parameters (m, p, r) for Weighted Least Trimmed Squares, WLTS(m, p, r), with Pareto errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	(4,25,0.04)	(5, 100, 0.06)	(5, 80, 0.12)	(6, 100, 0.2)	(4, 100, 0.15)	(3, 80, 0.25)
1/3	(7, 1.2, 0.08)	(9, 300, 0.15)	(9, 8, 0.2)	(8, 12, 0.25)	(8, 12, 0.25)	(5, 50, 0.2)
1/2	(9, 1, 0.1)	(11, 6, 0.15)	(10, 20, 0.25)	(9, 5, 0.25)	(10, 40, 0.4)	(9, 60, 0.4)
2/3	(11, 1.2, 0.12)	(13, 80, 0.25)	(12, 25, 0.3)	(10, 30, 0.4)	(12, 30, 0.4)	(9, 20, 0.4)
1	(25, 6, 0.3)	(17, 8, 0.3)	(16, 100, 0.4)	(15, 50, 0.5)	(15, 200, 0.4)	(15, 100, 0.6)
3/2	(34, 20, 0.4)	(25, 12, 0.4)	(22, 20, 0.4)	(23, 10, 0.6)	(18, 150, 0.6)	(16, 80, 0.6)
2	(38, 10, 0.3)	(33, 15, 0.5)	(25, 10, 0.5)	(27, 25, 0.5)	(25, 30, 0.6)	(21, 15, 0.6)
3	(42, 8, 0.25)	(39, 6, 0.4)	(32, 25, 0.6)	(31, 12, 0.5)	(29, 100, 0.5)	(25, 30, 0.6)
4	(43, 6, 0.2)	(42, 6, 0.4)	(36, 5, 0.4)	(33, 25, 0.5)	(31, 12, 0.5)	(28, 20, 0.5)

.

7.1. The Empirical sd and Bias

There are three tables:

• Estimators without parameters for Student errors:
  LS, Least Squares, and LAD, Least Absolute Deviation, are treated in Section 3. LAD is a Weighted Balance estimator with weight X_i; LADPC, power corrected LAD uses the weight $X_i^{1/12}$. It is introduced in Section 4.4. It is only defined for ξ > 0. TS, Theil–Sen, is a robust estimator which chooses the regression line for which Kendall’s tau vanishes, rather than the covariance as in LS. The slope is the median of the slopes of the 4950 line segments connecting two sample points (see Section 5). The three estimators TB1, TB2, TB∞ are based on samples for which 25 points above and 25 points below the bisector have been trimmed. The estimator chooses the bisector for which a certain state function T of the residuals is minimal. For TB1, T is the sum of the absolute values of the fifty remaining points; for TB2, T is the sum of the squares; and, for TB∞, T is the width, the difference between the largest and smallest residual (see Section 6).
  LS is optimal if and only if the error has a Gaussian distribution. LAD is good when η is small and the power correction LADPC is good when η is large. TS and TB1 are good, but not as good as LADPC. For the three estimators trimmed around the bisector, TB∞ is best for small values of η, TB1 for large values of η and TB2 for values in between.
• Estimators with a parameter and Student errors:
  The Hyperbolic balance estimators HB40(d) and HB0(d) are comparable. They use the weight sequence $1/d,1/(d+1),\dots ,1/(d-1+n)$ (see Equation (12)). The parameter d depends on the value of the tail indices. The estimator HB0 performs slightly better than HB40 when η is large. This may be due to the fact that for large η the Student density at the 0.4 and 0.6 quantiles is much smaller than at the median. The Right Median estimator RM(r) chooses the bisector which divides the r = 2r₀ + 1 rightmost (red) points equally into two sets of r₀ with one red point, the median, on the bisector (see Section 4). It is intuitive but its performance is not as good as that of the Hyperbolic Balance estimators. LADHC, the Hyperbolic Correction of LAD is indistinguishable from the Gap Correction, LADGC (see Equation (A4)). It performs well when η is large. Apart from these four weighted balance estimators, we consider the weighted Theil–Sen estimator WTS(p) introduced in Section 5. It performs well for small values of η. Weighted Least Trimmed Squares, WLTS(m, p, r), yields the smallest empirical sds but is hors concours since it is not clear how its parameters should be chosen when the error distribution is not known, see Section 6.
• Estimators with a parameter and Pareto errors:
  The estimators are the same as for Table 7 but now applied to Pareto errors. Weighted Theil–Sen is the best choice here. The empirical sd of WTS for Pareto errors often is much smaller than for Student errors. In 51 of the 54 rows, WTS yields the minimal square root of the average loss. The estimator WLTS is hors concours. The bias of WLTS is negative. For the other five estimators, the bias is positive, roughly one tenth of the sd.

7.2. Parameter Values

The parameter values, similar to the empirical sd and the bias in the tables above, depend on the seeds used for the simulations. Since the dependence of the average loss on the parameter is often locally quadratic the values of the parameter are imprecise. The dependence on the tail indices is monotonic. The values for ξ = 0 are aberrant since here the $1/\sqrt{n}$ asymptotic normality will apply. We have not been able to establish a simple functional relationship between the parameter and the tail indices even if the values at ξ = 0,1/2 are omitted. The parameter values for Pareto and Student errors differ. The difference may be large.

7.3. An Example

An example may help to explain how the parameter in the estimator functions for samples of size n ≠ 100. Consider a sample of size 231. The error distribution is not symmetric: the upper tail decreases as c/y, and the lower tail as $c^{\prime }/y^2$. The explanatory variables have a Pareto distribution with tail index ξ = 1. We want to apply the HB100(d) estimator: The estimate is the central line of a strip with a hundred points above the strip and a hundred points below. These two subsets of a hundred points are in balance with respect to the hyperbolic weight $w_i=1/(d-1+i)$. This estimator, similar to HB40 for sample size n = 100, is not very sensitive to the behaviour of the error density at the median.

If the error distribution is known, one determines the optimal value of the parameter d by a series of simulations for batches of a hundred thousand simulations. Throughout this paper we choose d to have the form d₀ × 10^k with d₀ ∈ {1, 1.2, 1.5, 2, 2.5, 3, 4, 5, 6, 8}. For the optimal value, we have computed the empirical sd and bias of ${\widehat{a}}_{\mathrm{HB}100\left(d\right)}$ over ten batches of a hundred thousand simulations:

d = 3  emp sd = 0.00403[2];  bias = 0.00021[1].

(21)

Here is the error density f^*: Start with a unimodal symmetric Pareto distribution with tail 1/(2 + 2y), replace observations $Y_i^{*}<-1$ by $-\sqrt{|Y_i^{*}|}$, and scale by the IQD = 2. This yields the error density $f^{*}\left(y\right)=1/{(1+2|y\left|\right)}^2$ on (−1, ∞) and $4\left|y\right|/{(1+4y^2)}^2$ on (−∞,−1).

If one knows the 231 sample points (X_i,Y_i), but the tail indices and error distribution are unknown, then one has to estimate the tail indices and determine the lack of symmetry in the error distribution. Use the Hill estimator $\widehat{\xi }$ for the tail index of the horizontal coordinate, see for instance De Haan and Ferreira (2006).Apply LADPC or one of the other estimators in Table 6 which do not contain a parameter to obtain a preliminary estimate ${\widehat{a}}_0$ of the slope of the regression line. Use the residuals $z_i=y_i-{\widehat{a}}_0{x}_i$ to determine an estimate $\widehat{\eta }$ of the tail index of the error and to determine the lack symmetry of the error distribution. Our program deletes the twenty rightmost points (since, for these points, the effect of an error in the estimate ${\widehat{a}}_0$ on the value of z_i may be large). The remaining 211 values z_i are shifted to make the median the origin and arranged in increasing order. Now, delete the middle points, retaining the 58 largest and the 58 smallest values. Compute the standardized Wilcoxon rank statistic T for these 116 values. For |T| ≤ 2, we assume that the distribution is symmetric and apply the Hill estimator to the 116 absolute values to determine $\widehat{\eta }$; for T ≥ 6 we assume extreme asymmetry and apply the Hill estimator to the 58 positive values; for 2 < T < 6 we augment these 58 values with the largest of the remaining absolute values, the number depending linearly on T, to estimate η. For T < −2, we do the same with signs changed. Now, determine the optimal value d_S of the parameter d for a sample of 231 observations from a Student distribution with tail index $\widehat{\eta }$ and d_P for a sample of 231 points from a Pareto distribution. Finally, apply the HB100(d) estimator to the sample where d is d_S or d_P or a geometric average of d_S and d_P depending on the value of |T|.

What is the performance of this two step estimator? For the initial LADPC estimate, ten batches of 10⁵ simulations give an empirical sd of 0.00470[2]and bias 0.00017[1]. Construct tables with the optimal value of the parameter d for various values of the tail indices for samples of size n = 231 for Student errors and Pareto errors as in the tables above to obtain

Table 17. The optimal parameter d for Hyperbolic Balance, HB100(d). Sample size n = 231 with Student (left) and Pareto (right) errors.

$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3		$\mathit{\eta }\setminus \mathit{\xi }$	0	1/2	1	3/2	2	3
0	30	3	1.5	1	0.8	0.6		0	30	4	1.5	1.2	1	0.8
1/3	30	4	2	1.5	1	0.6		1/3	40	6	2.5	1.5	1.2	1
1/2	30	5	2	1.5	1.2	0.8		1/2	40	8	3	2	1.5	1.2
2/3	30	5	2	1.5	1.5	1.2		2/3	40	8	3	2	1.5	1.2
1	30	6	3	2	2	1.5		1	50	8	4	2.5	2	1.5
3/2	40	8	4	3	2	2		3/2	60	15	5	3	2.5	2
2	50	10	5	4	3	2.5		2	60	20	8	5	3	2
3	60	20	8	6	5	3		3	120	40	15	10	5	4
4	80	30	15	10	10	5		4	200	60	25	12	10	8

.

These two tables may be used to determine the optimal value of the parameter d for any pair (ξ,η) in the rectangle [0,3] × [0,4] by interpolation. We calculated for S and P for the six values ξ = 0, 1/2, 1, 3/2, 2, 3 a linear approximation to $logd$ as a function of η and used these linear approximations for the interpolation. Of the million simulations, 269,024 were given the predicate “symmetric”, and 16,114 “extremely asymmetric”. Our estimates of (ξ, η) vary around a mean value (1.00,1.3) with sds (0.066,0.17) and correlation −2/10³. For the log of the parameter d, we found a mean value of 0.95 and sd 0.03. The empirical sd and bias for ten batches of 10⁵ simulations are

emp sd = 0.00405[2];  bias = 0.00023[1].

These are indistinguishable from the values in Equation (21). Knowledge of the tail indices ξ and η and of the distribution of the error need not improve the estimate! That is remarkable but perhaps not unreasonable. In the two-step estimate the parameter adapts to the configuration of the sample.

8. Conclusions

There are several estimators that perform well for linear regression with heavy tails.

The conclusions may be found in the tables in Section 7. The performance of Least Squares is atrocious if the error has heavy tails. This is also the case for Least Absolute Deviation if the explanatory variable has infinite second moment. The Theil–Sen estimator performs well and the Power Corrected LAD slightly better. Estimators with a parameter show an even better performance but one has to do some extra work to determine a good value of the parameter, as shown in the example in Section 7.3.

The tables contain an overwhelming amount of information. The performance varies with the tail indices ξ and η, and is different for symmetric and one-sided errors. The gaudy plot in Figure 1a in Section 2 is an indication of the complexity of the situation. This figure describes the optimal estimator for errors with a Student distribution. Least Squares is optimal when the errors have a normal distribution but, for Student distributions with two or three degrees of freedom, there exist estimators which outperform Least Squares. Of the dozen estimators which are investigated in this paper, eight are optimal for at least one point of the grid of the 54 values of tail indices (ξ,η) in Figure 1a. The tables in Section 7 give a more detailed picture of the performance, with colours indicating good performance. Section 7.1 compares the performance of various estimators.

In first instance, the tables are meant as a guide to practicing statisticians confronted with data for which the values of the explanatory variable show signs of an underlying distribution with a heavy tail. If the statistician is wont to work with Least Absolute Deviation, she might consider using the Power Correction LADPC or the Hyperbolic Correction LADHC to determine the the regression line in her sample. This would involve a closer look at the theory of Weighted Balance estimators presented in Section 4. If she is wont to work with the Theil–Sen estimator, she might consider using the Weighted Theil–Sen estimator WTS, perhaps with a different weight sequence. If her weight sequence outperforms our benchmark, we would be happy to receive an e-mail with details. If the sample is large, she might decide to use a faster robust estimator such as the Right Median. A glance at Figure A2 might be helpful to see the effect of a change in sample size.

In the Introduction, we made a number of ad hoc assumptions, assumptions on the distribution of the variables X and Y, on the sample size and the number of simulations, on the values of the tail indices, and on the loss function. We can now evaluate these assumptions in the light of the results obtained in our simulations.

(1) The explanatory variable is Pareto

The Generalized Pareto Distributions give a canonical description of tail behaviour in Extreme Value Theory. The Pareto distribution for tail index ξ > 0 goes over into the exponential distribution for ξ → 0. For us, the merit of the Pareto distribution is the chance to switch from iid observations $(X_i,Y_i^{*})$ to a Poisson point process on the right half plane. A sample of n observations corresponds to the n rightmost points of the Poisson point process.

(2) The error distribution is Student or Pareto

The assumption that the error has a symmetric distribution need not hold in applications. Hence, the estimators are also tested on errors with a one-sided distribution. (Alternative symmetric distributions are evaluated in Appendix C.7.) The difference between the empirical sd for Student and for Pareto errors is large for HB40 and WTS if η is large; the difference between the parameters may be large too, for instance in WTS with η = 4 or ξ = 0. In such cases, there will be uncertainty about the optimal value of the parameter if the distribution of the error is not known. For Weighted Least Trimmed Squares, there are three parameters, and in particular the behaviour of the second parameter, p, is erratic (see Table 7, Table 8 and Table 9 and Figure 9). For samples for which the error has an unknown distribution, it is not clear how the parameters for WLTS should be selected. That is the reason for placing WLTS hors concours.

(3) The tail index ξ of X assumes six values in [0,3] and η nine values in [0,4].

The empirical sds listed in the tables suggest a continuous dependence on the pair (ξ,η). The rule of thumb in Equation (2) that the empirical sd is of the order of $1/{10}^{\xi +1}$ applies for the entries in the tables in Section 7. The optimal parameter values listed in Section 7.2 are increasing in η and decreasing in ξ (if we exclude the two extra parameters in Weighted Least Trimmed Squares). For applications, one may restrict attention to tail indices $(\xi ,\eta )\in {[0,3/2]}^2$ since variables with infinite absolute first moment hardly occur in practice. It is reassuring that the regular behaviour of the estimators and parameters extends far beyond this square.

(4) Performance is measured on the basis of ten batches of 10⁵ simulations.

The bounds on the rectangle $(\xi ,\eta )\in [0,3]\times [0,4]$ are dictated by the software R version 3.2.1, and the sample size and the number of simulations by the hardware, the operating system OSX 10.6.8, the 3.06 GHz Intel Core 2 Duo processor and the 4 GB 1067 MHz DD3 memory on the iMac used for obtaining the results of this paper.

(5) The sample size is n = 100.

Statisticians are not interested in the asymptotic behaviour of an estimator ${\widehat{a}}_n$ for sample size n → ∞. They are confronted with a sample of fixed size, and do not have much control over the size n in general. If there is a universal limit distribution for n → ∞ the statistician may use this distribution to approximate the distribution of ${\widehat{a}}_n$. In our case, there is no universal limit law for ξ > 1/2 (see Samorodnitsky et al. (2007) and Appendix B), and there are advantages to using the distribution of ${\widehat{a}}_n$ for say n = 100 for a given error distribution as benchmark.

(6) The loss function is $L\left(u\right)=u^2$.

This is the standard loss function, but one may wonder whether it is suited to measure performance in a setting of heavy tails. The expected loss often is infinite. In our set up, it is the average loss which determines the optimal parameter and the performance of the estimator. There is a discrepancy between the empirical sd and the true sd. Thus, for (ξ,η) = (0,4) and Student errors, the empirical sd of ${\widehat{a}}_{\mathrm{LAD}}$ for ten batches of a hundred thousand observations is 0.0560[5]. The fluctuation in the sds of the ten batches is small, 1% of the average. The true sd is infinite since the tails of ${\widehat{a}}_{\mathrm{LAD}}$ vanish $1/x^{1/4}$. See the discussion at the end of Section 3.

What happens if one uses a different loss function? In Section 3, we observe that the Mikosch–de Vries Theorem, Theorem 1, shows that the Least Squares estimate has finite first moment for errors with tail index $\eta <1$. Does this mean that one may use LS for errors with tail index $\eta <1$, (and hence for practical purposes for all error distributions)? The answer may be found by looking at the distribution of the absolute value of the estimate $|{\widehat{a}}_{\mathrm{LS}}|$, rather than at particular moments of the estimate. A glance at the loglog frequency plots in Figure A5, comparing the first and the fourth, will convince the reader that the answer is “No”.

There are three questions which continually draw our attention like the powerful gravity fields of three bright stars. In the Appendix, each of these questions will receive proper attention in a section of its own. In each, there is a link to a simple mathematical structure.

• What is the relation between the empirical sds listed in the table and the true sd of the estimators ${\widehat{a}}_E$? Standard deviation is a basic concept in probability theory. How appropriate is this concept in describing the performance of estimators in linear regression for heavy tails? One might hope that, in a large sample of independent observations of ${\widehat{a}}_E$, in our case a million simulations, the empirical sd will give a good indication of the value of the true sd, $\sqrt{var{\widehat{a}}_E}$. This need not be the case, as we saw in Section 3. Appendix A shows that the Weighted Balance estimators RM, HB0 and LADHC may have finite second moment even for η = 4.
• There is an alternative model in which the iid Pareto variables $X=1/U^{\xi }$ are replaced by a Poisson point process M on (0, ∞) with points $X_1>X_2>\dots$ and mean measure $\mu (x,\infty )=1/x^{1/\xi }$. One may extend M to a Poisson point process M_a on $(0,\infty )\times \mathbb{R}$ with points $(X_i,Y_i)$ where $Y_i=a{X}_i+Y_i^{*}$ for an iid sequence of errors $Y_i^{*}$ independent of M. The importance of this point process was pointed out in Samorodnitsky et al. (2007). If the error Y^* has a positive $C^1$ density which satisfies simple regularity conditions at ±∞, then for ξ > 1/2 the probability distributions of the point processes N_a, $a\in \mathbb{R}$, are mutually absolutely continuous as shown in Appendix B. If the precise position of all points of N_a is known, this determines the df of Y^* almost surely, but not the slope a of the regression line.
• There are a dozen loglog density plots of $|{\widehat{a}}_E|$ for Student errors scattered throughout the paper. They all look the same. Apart from the usual small random fluctuations, we see a smooth concave curve with asymptotes which have non-zero slope. EGBP is a four-dimensional family of logconcave densities $f=e^{-\phi }$ on $\mathbb{R}$ which often give a good fit for these loglog frequency plots. The family EGBP of Exponential Generalized Beta Prime distributions is described in Appendix C, where we encounter several classic dfs: normal, symmetric and skew Laplace, Gumbel, beta, gamma, logistic, hyperbolic secant, Student and Snedecor’s F-distributions. We measure how good the fit is and compare the second moment of the associated Symmetric Generalized Beta Prime distribution to the empirical sd of the estimate $\widehat{a}$. A theoretical justification of the good fit does not exist and would be welcome.

In the heading of the paper, two authors are mentioned. The name of the main contributor is lacking. The programming language R, or rather the men and women who have contributed to make R into a versatile and efficient tool, should receive special mention here. What a telescope is to the astronomer, R is to the statistician.

This paper takes an exemplary approach. Instead of formulating conditions which the error distribution should satisfy in order that the distribution of the estimator should exhibit a certain asymptotic behaviour for sample size n → ∞, we consider two particular error distributions, Student and Pareto, and compute the empirical sd and bias for a large number of simulations for sample size n = 100. One reason for this approach is that there is no universal limit law when the tail index of the explanatory variable exceeds a half. Our approach is clumsy, as is evident from the many pages of tables in Section 7. In the more conventional theoretical approach, one would formulate conditions which the error distribution has to satisfy and then prove that the estimate exhibits a certain desired behaviour. Flexible conditions ensure wide applicability. However, the difference between the exemplary and the analytic approach is not as great as it seems. In both cases, one has to keep one’s fingers crossed on encountering a concrete sample.

The tables and figures give only a vague impression of the power of R. Here are two examples which show how the statistician and the program R interact:

• Weighted balance estimators work well since they are blind to the tails of the distribution. They only see the error distribution around the median. This suggests that the bias in the estimate of the slope for Pareto errors might be due not to the difference between the right and left tail, but to the lack of symmetry in the density at the median. There is a simple way to settle this question. Take a Pareto distribution with tail index η = 1 and normalize it to satisfy G(−1/2) = 1/4 and G(1/2) = 3/4 (the InterQuartile Distance then is IQD = 1). Now, flip the sign of the $Y_i^{*}$ which fall in the interval (−1/2,1/2) and compute the empirical sd and bias of HB0 for this altered error distribution (and ξ = 1). It turns out that roughly one third of the bias of $\widehat{a}$ is due to the lack of symmetry on the interval (−1/2,1/2).
• The estimators studied in this paper are general purpose estimators. How good is their performance compared to a specific estimator such as MLE for Cauchy errors? This will also tell us whether the performance of an estimator such as HB0 is only good compared to the other estimators, or whether it is good in an absolute sense. We compute the empirical sd of MLE for errors with a Cauchy distribution and ξ = 1. This involves an optimization procedure which needs an initial point. If one chooses the origin the MLE estimate is slightly better than HB0(3). However, the likelihood has many local maxima and the initial value (0,0) favours local maxima close to the origin which yield regression lines with small slopes. In a more extensive search of the optimum, where one also uses initial points further out, the empirical sd increases and HB0(3) outperforms MLE.

The observation that the paper is little more than a collection of examples and a tabulation of rote results obtained by varying the parameters in a small set of simple programs is not unjustified. Linear regression for heavy tails is a vast terrain. Many theoretical questions remain unanswered. We publish the paper in the hope that it may be helpful to statisticians who encounter heavy tailed variables in their linear regression.