1. Introduction
This article considers how the price for insurance and the number of people insured varies when the risk and other characteristics of the population change. We study these relationships, known as comparative statics, for insurance markets that suffer from either adverse or advantageous selection, and then consider the specific case of medical insurance markets.
The comparative statics of medical insurance markets is of interest, as these markets leave millions of Americans uninsured against medical risk. Eighty percent of the private medical insurance in the US is employer-provided
1, and employers are not allowed to discriminate according to relevant demographic and medical information when they price insurance provided to their employees.
2 Policies, such as the income-tax deductability of health insurance, or a “Cadillac tax” on expensive health plans, should induce changes in prices and quantity. I demonstrate that increases in the cost of insurance, such as the “Cadillac tax”, may actually increase the amount of insurance, rather than decrease it. The actual price and quantity effects of policies designed to shift either the supply or demand curves in insurance markets may have counter-intuitive effects. For example, many aspects of the Affordable Care Act (ACA), such as the Cadillac tax or ACA plan subsidies, that are designed to decrease or increase the amount of insurance, respectively, may have opposite effects.
In these models, the amount of risk left uninsured due to selection depends upon the distribution of risks—for example, what is the ratio of high-cost to low-cost individuals, and how different in average costs are high- and low-cost individuals. We use repeated cross-sections of medical expenditure data to infer such ratios, and use them in a model of insurance markets with asymmetric information. I also find that changes to the distribution of medical risk faced by consumers in recent years should have lead to more expensive medical insurance. It should also have lead to more people with medical insurance.
The price of employer-provided medical insurance to cover a single employee has grown five percent a year from 1996 to 2005. The price of family coverage has grown 5.7 percent per year over the same period.
3 At the same time, more Americans have gone without medical insurance. Among the non-poor and non-elderly, the percentage of individuals without private insurance rose 22 percent (18 percent to 22) from 1996 to 2004.
4One explanation for higher insurance prices is the well-documented growth in average medical spending (Swartz [
1]; Freudenheim [
2]). As medical costs grow, the supply curve for medical insurance shifts up, and induces movement along the demand curve. This new equilibrium price is higher, while equilibrium quantity is lower. However, changes in the distribution of medical expenditures (e.g., mean, median, variance, etc.) are the result of changes in the distribution of medical risk. In this case, the demand curve also shifts up. The new equilibrium price is larger, but whether the new equilibrium quantity is larger or smaller is unclear.
This article attempts to disentangle these changes. This study complements the findings of Gruber and Levy [
3], which documented similar (though differently measured) changes to the distribution of medical risk. We use changes in the distribution of medical expenditures in the US to infer changes in the distribution of medical risk. We then take these measured differences in the distribution of medical risk into a quantitative model of insurance choice with asymmetric information. We find that measured changes in the distribution of medical risk should have made insurance more expensive and more prevalent. While the former trend is consistent with the data, the latter is not.
This work can help shed light on recent research that considers alternative risk-adjustment factors; that is, what kinds of information could be used to price insurance that would limit the amount of market failure due to adverse selection. Both [
4,
5] find evidence that age-based health insurance prices may drive some of those age-specific markets to collapse. Here, we identify some of the characteristics of risk pools that make them sustainable.
The lessons from this exercise go beyond the sectoral concerns of medical insurance. If the source of uninsurance in other markets is asymmetric information, then this reminds us that distributions matter. If there is an across-the-board increase in risk, then insurance markets likely would provide more insurance, instead of less, as the demand curve shifts out further than the supply curve because of risk aversion. Furthermore, it introduces the notion that comparative statics do not depend upon the nature of the selection (adverse vs. advantageous). Instead, the comparative statics depend upon the stability of the equilibrium. For example, if wage volatility goes up, it matters whose wage volatility goes up.
This also relates to the market failure as discussed in recent work on insurance against aggregate, catastrophic risk [
6,
7,
8]. When a natural disaster strikes, it may test the solvency of the risk pool, leading to partial insurance. The risks under study here have idiosyncratic realizations, as opposed to the widespread loss of property due to an earthquake or hurricane. For example, we do not consider how insurance markets might deal with a flu pandemic. Likewise, the tax subsidy of health insurance should mitigate adverse selection, and the indirect nature of the contract (typically via employers, instead of directly to consumers) may also influence the extent of adverse selection.
2. A General Framework with Initial Results
Suppose there is a unit measure of risk-averse agents, heterogenous in their financial risk,
. Each agent’s risk is characterized by
, with conditional expectation
. Risk types are distributed according to a second distribution,
. Agents with wealth
w and preferences
5 have a willingness to pay for insurance,
, which is the dollar amount that makes the agent indifferent between paying
for insurance, or facing the risk without insurance:
Risk aversion means that willingness to pay for insurance is greater than expected outcome. An agent purchases insurance if his or her willingness to pay for insurance is larger than its price, —that is, if , and not otherwise. An inverse demand function, , provides the risk type(s) associated with a particular level of demand at price ϖ.
The demand curve for insurance is simply the ordering of the individual demands:
The demand curve is downward sloping by construction.
We assume that insurance firms provide insurance via price competition. These firms cannot provide risk-type contingent contracts because of asymmetric information. The sources of this asymmetric information may either be based in the microfoundations of the model, or due to legal constraints imposed upon insurers. In the case of the US medical insurance market, the latter case is certainly true—firms that offer their workers medical insurance are not allowed to discriminate the premiums paid for that insurance according to individual criteria such as age, gender, and health status. Given that employer-provided insurance is the dominant source of insurance, it is a reasonable assumption for this question.
Thus, firms offer a full insurance at price
ϖ, and agents select into the contract according to their demand. The firm’s per-contract profit is:
Free entry drives the expected profits of insurance firms to zero. Thus, the supply curve is the average cost of supplying insurance to the first agents who select into it. The shape of supply curve is determined by the mechanics of marginal selection at every price. The supply curve may or may not be monotonic, depending upon the expected cost of the each agent, relative to the average cost of the agents up to that agent.
An equilibrium is a price of insurance,
ϖ, and set of agents,
, who select, or pool, into that insurance contract, that are consistent with price equals average cost. Five equilibria types are possible:
The first equilibrium exhibits local favorable selection, as in Jovanovic [
9]. This could be due to heterogeneneity in risk preferences that was negatively correlated with expected cost. Alternatively, the final four equilibria exhibit local adverse selection. This typology of equilibria is necessary because different types of equilibria have different comparative statics. For the balance of the article, the tangency equilibria will be ignored, as they are not robust to changes in the supply and demand curves—either the equilibrium vanishes (supply and demand no longer cross), or two equilibria emerge from the changes (they further overlap).
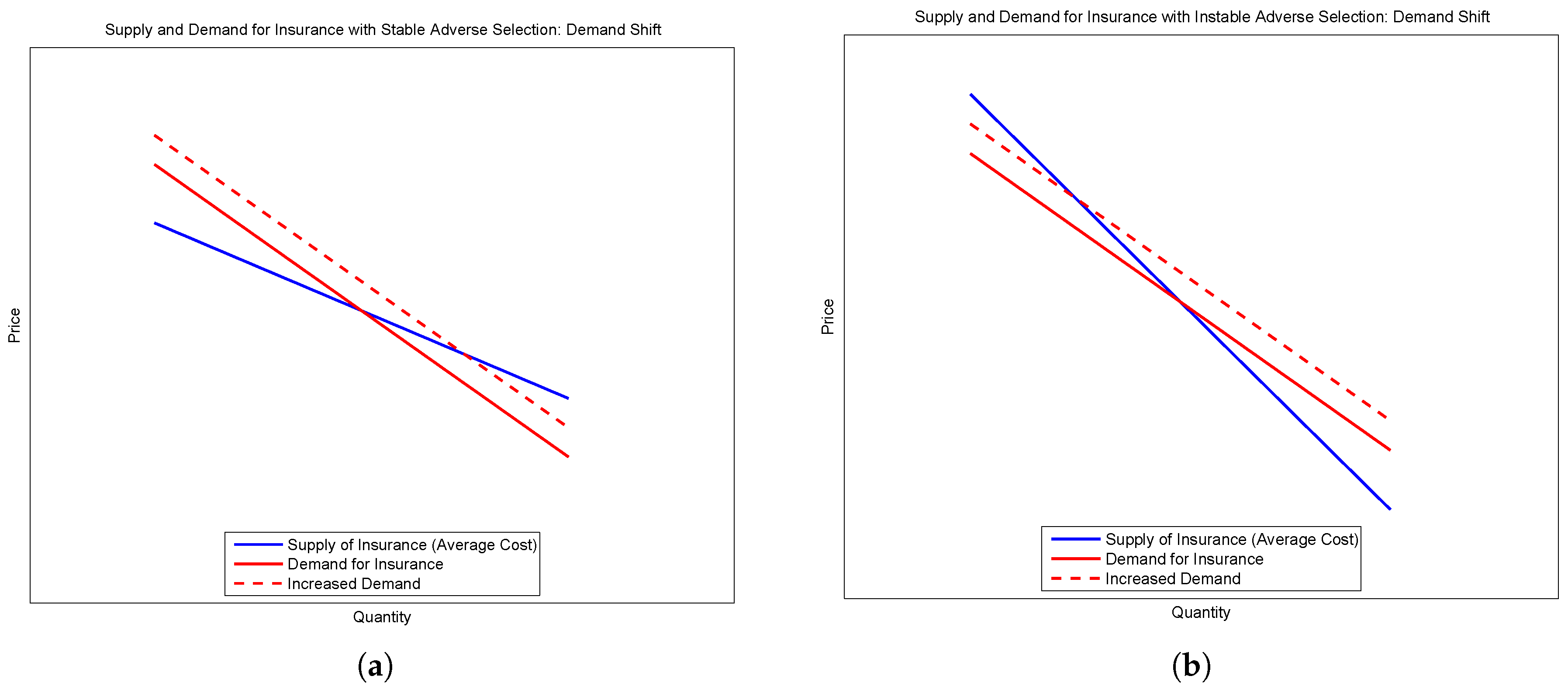
Consider the second and third types. Suppose there is an outward shift of demand without a shift in supply—for example, if agents become more risk averse. When demand starts above supply, the new equilibrium supports more insurance at a lower price. The price falls because the selection is locally adverse. However, when supply begins above demand, the shift in the demand curve leads to less insurance at a higher price. These two cases are demonstrated in the sub-figures of
Figure 1.
The response to a change in preferences can be characterized according to an equilibrium’s stability.
Definition 1. An equilibrium characterized by its marginal agent is locally stable, if, for all local and The stability refinement is similar to the trembling-hand refinement of Selten [
10], and the stability refinement of Kohlberg and Mertens [
11]. This refinement is intuitive—the equilibria in this model are pooling equilibria. The first and second equilibria are stable, while the third is not.
Changes in preferences are generally difficult to identify, whereas it may be more feasible to identify changes to the distribution of risk, Γ. Changes to the distribution of risk can be classified as symmetric or asymmetric. First, consider asymmetric changes. Such changes have consequences for the average cost (supply) curve, with relatively modest effects on the marginal benefit (demand) curve.
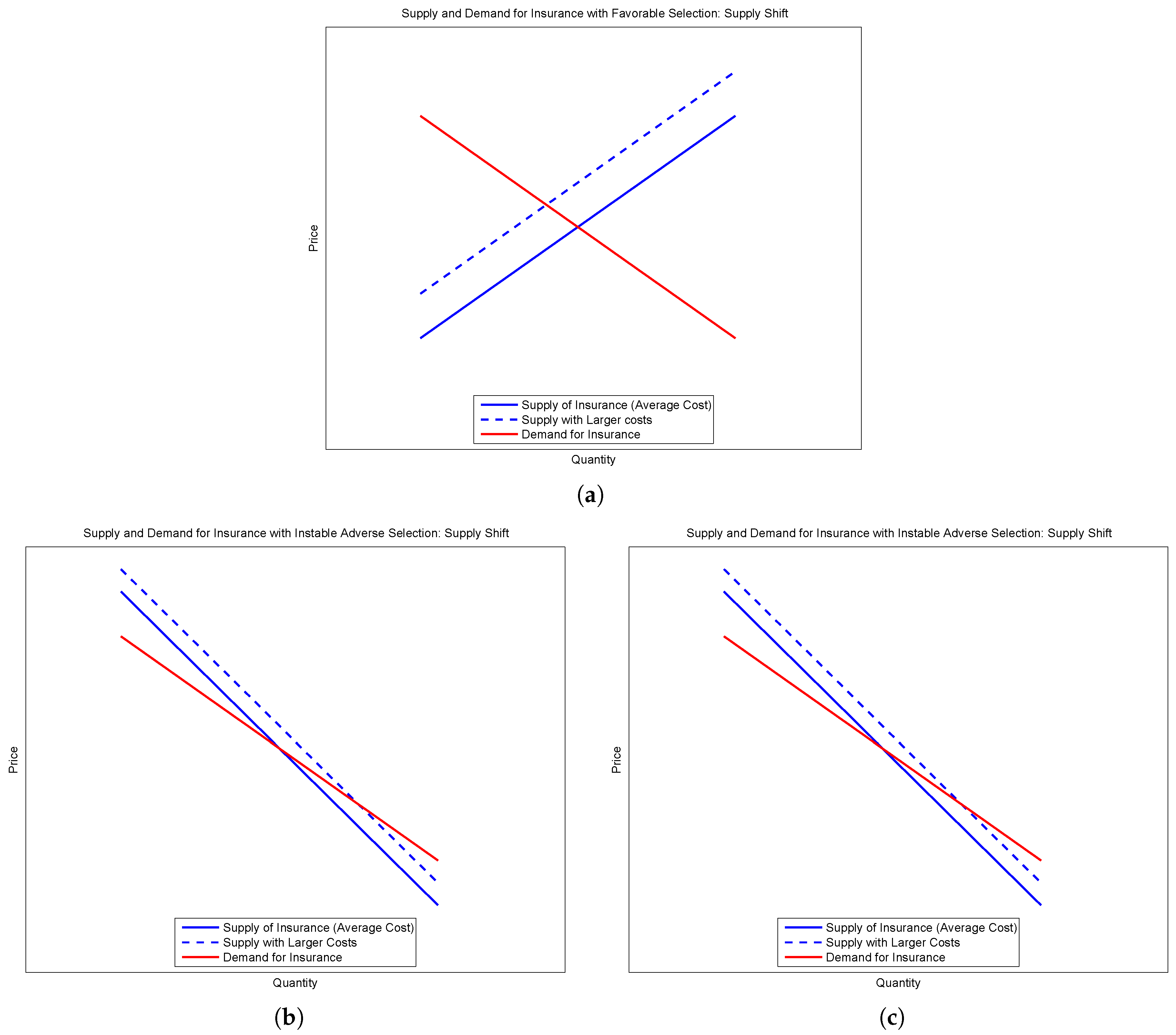
Figure 2 presents the three cases of interest—a (stable) equilibrium with favorable selection, and two equilibria exhibiting adverse selection, one stable and the other unstable.
The comparative statics depend upon the stability of the equilibrium. A shift up in the supply curve without a commensurate shift in the demand curve will lead to less insurance (a smaller pool) if we consider a stable equilibria. However, if we consider unstable equilibria, the opposite is true—a shift up in the supply curve will lead to an increase in the amount of insurance provided in spite of asymmetric information.
The number and stability of equilibria depend upon the micro-foundations of the model—preferences, and risk types and distributions, for example. In order to more clearly understand the relationship between risk and insurance in spite of asymmetric information, more assumptions are required.
3. A Series of Instructive Numerical Examples
Consider an economy with two types of agents who face a Bernoulli risk—they may catch an illness and have to go to the doctor. The cost of a visit,
L, is the same for both types, though the healthy differ from the sick in that they face a smaller probability of going to the doctor,
. Fraction
s of the population is sick, while the rest are healthy. The specific values for these parameters and calculations for each example can be found in
Table 1. If preferences for risk can be characterized by CARA, with degree of risk aversion
r, each agent’s willingness to pay for full insurance is:
Note that is an increasing function in each of its arguments. Sicker agents are willing to pay more for insurance, , and all agents are willing to pay more for full insurance as the cost of a visit grows, . It will also be useful to think of each agent’s certainty equivalent, —the amount an agent is willing to pay for insurance above and beyond a fair price.
The average medical cost in the economy is . Note that this value can increase because of increasing cost, L, or increasing probability of illness, . Suppose that the population is half sick and half healthy (. Furthermore, let , and set the probabilities of illness to and . The average medical cost is now 360, which would be the price of insurance if all agents chose full insurance bought in competitive markets with asymmetric information—the insurers do not provide type-based insurance. However, the healthy may not choose to buy such insurance, as their willingness to pay for insurance is less than its unfair price. This is the case here, using a calibration, —a healthy agent is only willing to pay 316 for insurance. The healthy go uninsured in such a market, while the sick sort into fairly-priced insurance.
Suppose that the price of a doctor’s visit rises to —a symmetric change in risk. Average medical costs rise to 450. Now note, though, that the healthy agents are willing to pay for unfairly-priced full insurance provided by a competitive market. That is, . As the cost of a visit grows, the certainty equivalent of the healthy agent grows faster than the price of insurance. More full insurance was provided because these changes were symmetric—both the healthy and the sick face larger risks.
Now suppose an asymmetric change, , keeping the price of a doctors visit at 1500. Average medical costs rise to 675. The healthy are not willing to pay this much for full insurance, as their willingness to pay for insurance does not change. Here, there is a decrease in insurance because the change was asymmetric.
This specification for risk is clearly not useful when considering the U.S. medical insurance market, as it is very coarse and does not allow for much heterogeneity. That said, it does suggest the general principle at work in the following section: following the average medical cost is not enough to determine whether an insurance market with incomplete information will allow for more insurance or less. The change in the distribution of risk that induced the change in the average medical cost is what determines the amount of insurance provided under asymmetric information. We will now apply that general principle to the preferred specification for medical risk.
4. A More General Setting
The model economy has a unit measure of risk-averse agents with utility function
. Each agent faces medical expenditures risk,
, and its risk is private information. The risks faced by agents are heterogeneous and are distributed according to Γ. This model was previously used in [
12], which contains the details of preference parameter estimation. The private information assumption means that insurers are not able to sort, so all agents face a common price of insurance,
ϖ. The purchase of insurance is subsidized at a rate
s, which is paid for using lump-sum taxes,
τ. Insurance is subsidized at a rate here as it is in the U.S. federal income tax code—here it is a positive subsidy, relative to wage income. The two are equivalent with constant absolute risk aversion. Depending upon type, each agent has a willingness to pay for insurance,
, which makes them indifferent between facing the risk associated with with their type,
, and paying for insurance. The decision to purchase insurance,
, is a discrete choice:
If (i.e., ), then the agent purchases insurance, and does not otherwise. Because of asymmetric information, agents do not get access to fairly-priced insurance. The distribution of is the demand curve for full insurance.
The market to provide full insurance is competitive, so that the price of insurance is equal to the average realized risk of the insured. Thus, we define an equilibrium to be:
the insurance choice,
, is the optimal solution to Equation (
1);
insurance price, ϖ, is equal to the average realized risk of the insured; and,
tax level, τ, is equal to the total cost of the subsidy of medical insurance.
The specification of preferences and risk heterogeneity is chosen to mirror several empirical facts, while also aiding in the computation of equilibria. The cross-sectional distribution of medical expenditures has three main features: a large number of zeros, a monotonically-decreasing partial density, and a fat, Pareto-like tail.
In order to match the three main features of the distribution of medical expenditures, we will use the following specification of individual risk and heterogeneity:
individual i faces risk according to the exponential distribution, parameterized by ; and,
these types are distributed according to the Gamma distribution, with parameters α and β.
These two assumptions lead to a cross-sectional (i.e., unconditional) Pareto-type distribution of realized medical risk, with all three characteristics. This specification of uncertainty was originally proposed by Harris [
13], though in a different context. Preferences against this risk are assumed to exhibit CARA.
CARA preferences are tractable, especially in this context. The willingness to pay for insurance, given type
, parameter of risk aversion
r, and upper bound of risk
κ can be written as:
Note that willingness to pay for insurance with CARA preferences is independent of wages or wealth.
It can be shown that this willingness to pay is monotonically decreasing in
. Because of this, equilibria can be characterized by their marginal agent type,
, whose willingness to pay for insurance is equal to its price. The price of medical insurance is equal to the average realized risk of the insured:
where
is the incomplete gamma function.
These specifications also mitigate the problem of multiple equilibria.
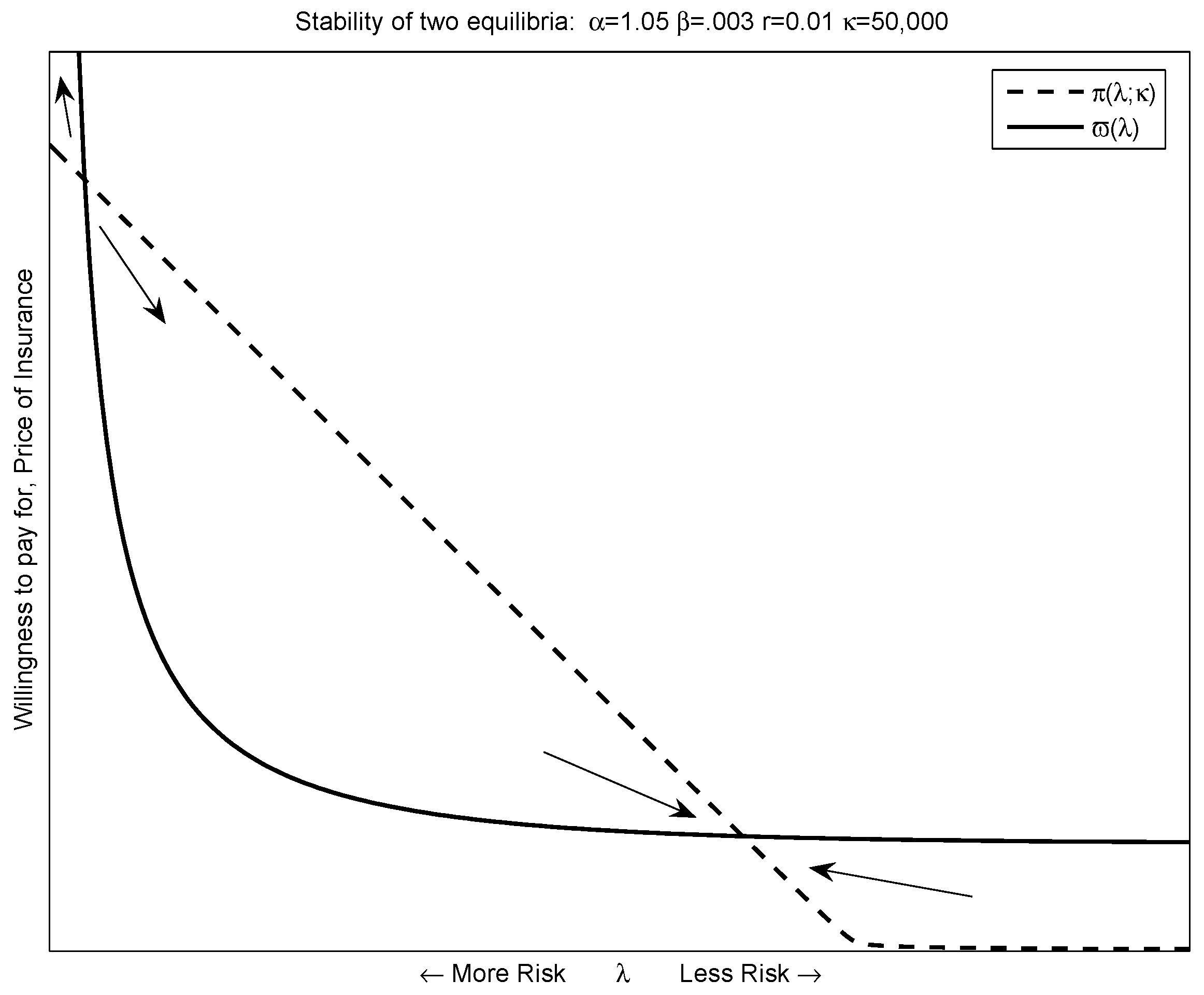
Figure 3 plots out the supply and demand curves for a set of candidate parameters—the degree of risk aversion,
r, upper bound of risk faced by an agent,
κ, and the distribution of medical risk,
α and
β. Preferences and adverse selection (due to asymmetric information) lead to a downward-sloping supply curve. In this case, there are two potential equilibria. Other parameterizations could lead to one equilibrium (the supply and demand curve are just tangent), or no equilibria—the case where no risk sharing is possible.
Because the movements in insurance rates and prices are steady, it is unlikely that the equilibria we observe is unstable.
Figure 3 demonstrates that the equilibrium with more insurance is the stable of the two. Parameter values that lead to a single equilibrium lead to unstable equilibria.
Medical insurance in the U.S. is primarily provided in the context of firms. Thus, the ideal data set would consider risk sharing across individuals within a firm. Unfortunately, such data is not publicly available. Instead, we use data from a nationally representative data set. To the extent that risks faced by workers within a firm look like the general population, this will be a useful examination. If workers could act on the distribution of medical risks within a firm, or firms could fire workers for being poor medical risks, this would be an unreasonable approximation. However, in both cases, such behavior might very well be either infeasible or illegal. Part of the medical risk under consideration here is latent—factors such as family history can impact future expectations—and information about it would thus be difficult to gather reliably. Even for evident medical conditions, it may be against the law for supervisors or co-workers to be informed about the health status of others, let alone act upon it.
Alternatively, one might worry that workers do not have an opportunity to take-up insurance within a firm. Decreases in the overall insurance rate may be due to fewer firms offering insurance, instead of fewer workers taking it up. This model does not account for these sorts of changes. Evidence suggests that these kinds of changes are not important. Stanton [
14] finds that the number of workers employed by firms that offered medical insurance rose from 1996 to 2002. The decrease in employer-provided insurance over this period is instead tied to decreases in take-up by employees, and, to a lesser extent, fewer employees being eligible for medical insurance.
Here, we use the Medical Expenditure Panel Survey (MEPS). The MEPS is a series of overlapping two-year panels, with information on annual medical expenditures, charges, and insurance status. The panel aspect of the data is beyond the focus of this article—we use the series of cross sections in the MEPS, starting in 1996, going to 2004, in order to infer each year’s distribution of medical risk—each year’s Gamma distribution, its pair. We will later use these values to infer the amount of private insurance possible in the asymmetric-information model.
We restrict the sample to the non-elderly and the non-poor in order to avoid complications due to Medicare and Medicaid. Veterans are also removed, due to access to VA care. In all three cases, publicly-provided insurance can crowd out private insurance. This restriction also avoids potential confusion about private insurance among the elderly (over 65).
Unfortunately, the data do not present a perfect candidate for the insurable (i.e., covered by insurance) realizations of medical risk. One potential measure is the total charges for an individual over a year. Because medical insurance contracts typically have co-payments or deductibles, this is an imprecise measure of the realized insurable medical risk.
This specification of risk has an internally-coherent and tractable way to back out the insurable fraction of total risk. If a fraction of an exponential risk is insurable, parameterized by λ, then this fraction of a risk is also an exponential risk. This new risk is parameterized by . If this fraction ρ is common across agents, then all of the exponential risks are scaled by ρ. A common ρ might come from the fact that these co-insurance rates are used to solve a hidden-action problem, and type privacy does not allow for discrimination. Finally, since β is a scale parameter for the Gamma distribution, the new distribution of insurable risk is also a Gamma distribution, with parameters α and .
The distribution of insurable risk can also be inferred from the distribution of medical expenditures paid by private insurance companies for the privately insured. The first moment of the conditional distribution, the average realized risk of the insured, can be found by integrating the expected realized risk over the types who choose insurance; i.e.,
The average square of realized risk of the insured (i.e., the second non-central conditional moment) is found similarly:
These are two unique moments that identify the two parameters of the risk distribution, .
That said, the amount paid for treatment by a private insurance company is unlikely to be the amount billed to the uninsured. Insurance companies buy a large volume of medical goods and services throughout a year, and frequently bargain with with medical providers over the cost of treatment. This bargaining power is not available to the individual uninsured patient. The resolution here is the same as for charges—assume a common proportional mark-up from the expenditures paid for by private medical insurance companies. This new marked-up distribution of risk is also a Gamma distribution, with parameters α and . The balance of this article will use both methods—marking up from private medical expenditures, and marking down from total charges. Both series tell the same story.
It may be useful to characterize changes in α and β. As the discussions of mark-up and mark-down above suggest, changes in β are easier to interpret. Since β is a scale parameter, a decrease in β scales up the medical risk faced by every agent an equal amount.
The parameter
α is best characterized by a distribution’s kurtosis. A distribution’s kurtosis is the ratio of its fourth moment to the square of its second moment (variance). As discussed in Balanda and MacGillivray [
15], kurtosis is synonymous with “peakedness” and “tail weight.” Two distributions may have the same variance, but kurtosis measures whether that variance is due to a large amount of moderate dispersion or a moderate amount of large dispersion. Flatter distributions have lower kurtosis.
Changes in kurtosis are central to the ability of insurance markets to spread risk across types. The variance of risk types may increase. If this increase is because many types became a little more different, then it is unlikely that many will newly refuse to buy the same insurance. However, if a few of the agents became very different from the rest, then cross-type risk sharing becomes less likely.
The kurtosis for a gamma distribution is . Thus, as α decreases, the risk types are becoming more and more disparate, and market failure becomes more pervasive. The sickest members of the population are becoming relatively more sick than the rest of the population. We will refer to this effect as the kurtosis effect—as α increases, risk types become more similar, and insurance becomes more widespread. When κ is large, the kurtosis effect dominates.
However, the calibrated value of
κ is only $5600. This reflects the many ways in which uninsured individuals can seek and receive free or uncompensated care. Hospitals reported providing an average of $20 billion per year in uncompensated and charity care (American Hospital Association [
16]). The charity portion of care reflects the not-for-profit and humanitarian missions of many hospitals. Uncompensated care is typically provided in emergency rooms, where hospitals are required to provide care independent of insurance status or ability to pay. In either case, this provides an upper bound risk faced by an uninsured individual, and it has consequences for an agent’s willingness to pay for insurance (i.e., in distribution, the demand curve for insurance). The calibrated value for CARA risk aversion,
, is in the range of risk preferences estimated by Cohen and Einav [
17].
The subsidy rate, s, has important implications for the calibration. Because ninety percent of the privately insured get medical insurance from their employer, and the cost of that insurance is not taxed as wage income would be, the subsidy rate is the marginal tax rate faced by the individual. Marginal tax rates are important, because they provide extra incentive to have insurance, and increase the insurance rate. This model corresponds to a competitive labor market where workers are compensated with their productivity, and only their compensation can come in the form of taxed wages or untaxed medical insurance.
Saez [
18] provides the average marginal tax rates for the US. These calculations stop at the year 2000. The marginal tax rate for the year 2001 and later will be the average value for the years 1996 to 2000.
When α decreases, the marginal agent faces a larger risk, and her willingness to pay for insurance increases. However, when that agent faces only a fraction of the realized risk (i.e., κ is small), the marginal agent’s willingness to pay for insurance does not increase more than the increase in the price of insurance. Here, the price of insurance is increasing because everyone who has insurance is also becoming more expensive. The kurtosis effect is dominated by the price effect of decreasing α.
Recall the claim in Swartz [
1] that increases in the average cost of care led to the increased price of insurance, and therefore fewer people had medical insurance. If the increase in average medical expenditure is due to a common increase in medical risk (
β goes down), then the insurance rate may increase. As everyone’s medical risk grows, so does their certainty equivalent—how much above and beyond a fair price each agent is willing to pay for insurance. Larger certainty equivalents allow for more risk sharing across types. If the increase in medical expenditure is the result of a change in the shape of the distribution of medical risk, then the outcome is ambiguous—either the price effect or the kurtosis effect may dominate.
As described in
Table 2, the changes inferred from 1996 to 2004 are a mixture of the two. Over this period, we might derive these changes as coming from two sources: an increasing price of medical goods and services (falling
β); and an increasing incidence of costly medical conditions (falling
α). This latter trend is consistent with the aging American population and the increased incidence of obesity, each associated with costly medical conditions.
The mark-up rate for a given year is exactly identified as the ratio of the price of insurance and the average medical expenditure paid for insurance on behalf of the insured, both from the data. The mark-down rate from total charges for a particular year is found by matching the model’s price of insurance to that found in the data. These estimates are presented in
Table 2. The price of insurance used here is the average price of single-coverage employer-provided medical (hospital and doctor) insurance in the US, as reported in the MEPS. Since the risk is reported on the individual level, the price of the corresponding coverage is considered as well. As mentioned in the introduction, the price of single-coverage and family-coverage employer-provided insurance grew at similar rates. Over this period, family coverage (covering two or more individuals) was steadily two-and-a-half times as expensive as single coverage. The implicit assumption is that there are constant returns to scale when it comes to family insurance plans versus single coverage, and there is no differential selection across them.
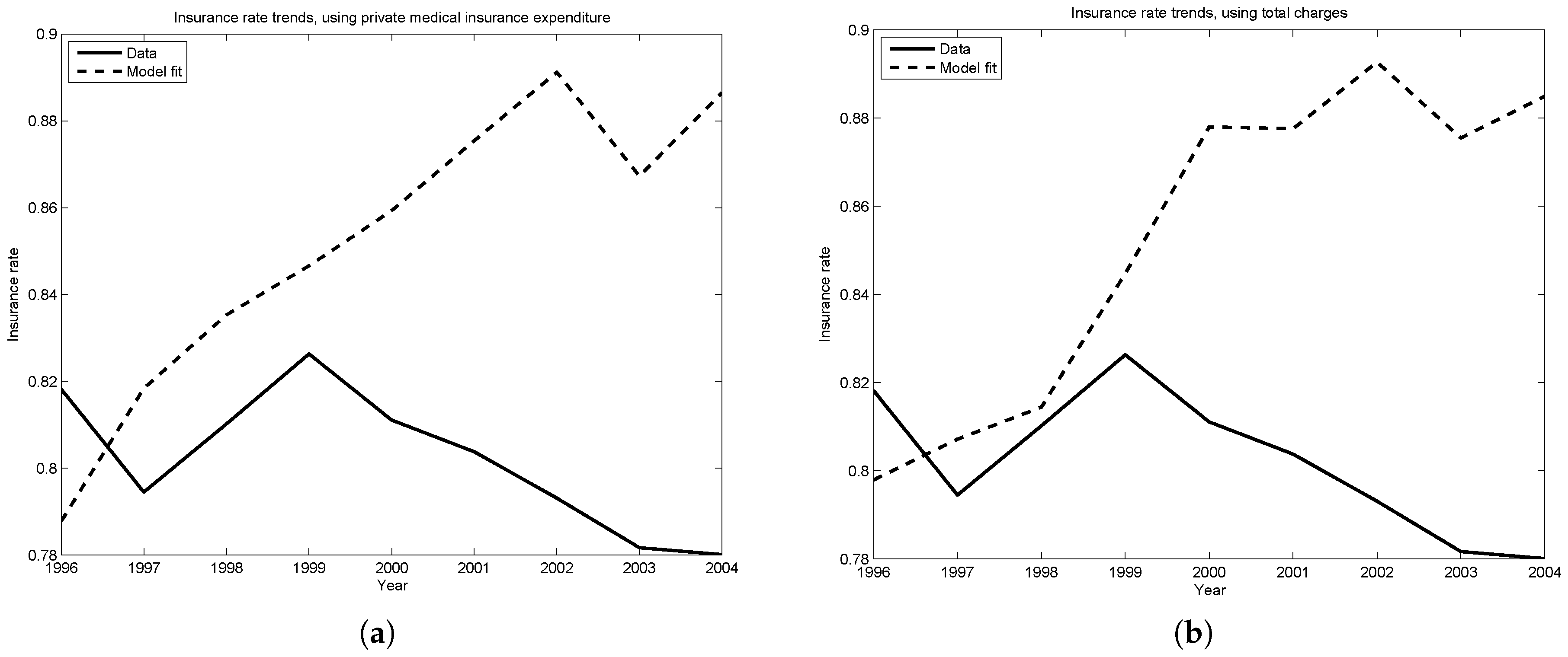
Figure 4a,b plot the insurance rate predicted by the model against the rate observed in the data. The two trends are within four percentage points of one another until 2001, the year of significant tax reform legislation. Since this tax reform decreased the marginal tax rates faced by households, this may explain why the model predicts increasing insurance rates, while the data finds insurance rates dropping slightly since 2000.
Figure 5a,b assess the relative importance of changes in the level of risk (
β) and the shape of risk (
α). They each plot two counterfactual insurance rates—the first, if the shape of the distribution of risk stayed the same, but the level of risk changed as described in
Table 2 (i.e.,
for all years,
for all
t); the second, if the level of risk did not change, but the shape of the distribution of risk changed as described in the same table (i.e.,
for all years,
for all
t).
Changes common to the medical risk of all agents are driving the insurance rate trends predicted by the model. Inferred changes in the shape in the distribution of medical risk (i.e., changes in α) play a very small roll in the predicted trends. Thus, in this period, changes due to the shifting age distribution or obesity have very little explanatory power. Instead, the model suggests a focus on changes common to all agents, such as moving prices for medical goods and services.