1. Introduction
We study the problem of optimal insurance design. This is a risk sharing problem between an insured financial agent and an insurer who typically holds a whole portfolio of similar insured risks. There is a vast literature on this optimal insurance design problem, see for instance Arrow [
1,
2], Raviv [
3], Gollier [
4] and Gollier-Schlesinger [
5]. Classical literature assumes that the preferences of both the insured and the insurer are modeled by the expected utility framework. Using this expected utility setting the Pareto optimal insurance design is determined. Usually, this results in choosing a deductible and co-insurance above this deductible. Raviv [
3] investigates necessary and sufficient conditions leading to deductibles and co-insurance, and the cost of insurance is identified to be the driving force behind deductibles.
As described in Yaari [
6] and Bernard
et al. [
7], this framework fails to explain various phenomena that are observed in practice, for instance, that financial agents prefer to purchase extended insurance cover for relatively small claims over buying protection against disastrous large claims. Bernard
et al. [
7] modify the original framework by introducing a probability distortion which tries to describe human behavior more appropriately. In particular, these probability distortions reflect that small and large claims are over-weighted by individuals which results in insurance covers different from deductibles.
In the present paper we choose a different approach for the modeling of the preferences of the insurer. In insurance practice, solvency of an insurance company is determined through a regulatory risk measure. This regulatory risk measure is the equity the insurance company needs to hold in order to run its business from a supervisory point of view. This risk measure is directly related to the insurance policies the company is selling and, henceforth, should directly reflect the quality of the insurance portfolio. The insurance company’s and the shareholders’ preferences, respectively, are then satisfied if the expected return on this regulatory risk measure, i.e., risk bearing equity, is sufficiently large.
In the present paper we model the regulatory risk measure with the expected shortfall risk measure (also called Tail-Value-at-Risk) as it is used in the Swiss Solvency Test [
8]. Assuming that this risk measure reflects the necessary equity that needs to be provided by shareholders, the premium risk loading is model by a cost-of-capital approach which is equivalent to the expected return on this shareholders’ equity. In this spirit we obtain a risk-adjusted premium calculation principle which is the essential difference to the constant risk premium case considered in the literature, see formula (3’) in Raviv [
3] or formula (2) in Bernard
et al. [
7]. As a result, the price of insurance will directly be related to the regulatory requirements and it will reflect the diversification within the insurance portfolio. The crucial result will be that insurance for small claims is comparatively cheap because it only marginally triggers the expected shortfall risk measure. This exactly explains that individuals purchase more insurance for small claims whereas insurance for large claims seems rather expensive in their judgment.
Organization of the paper. In the next section we introduce the insurance claim model which is based on a common risk factor that affects all claims simultaneously and idiosyncratic components that only influence individual claims. Based on this model we formulate the optimal insurance design problem from the viewpoint of the insured. In
Section 3 we introduce the regulatory risk measure and we describe the related risk-adjusted premium calculation principle. The crucial point will be that idiosyncratic risk is diversifiable which substantially simplifies the regulatory risk measure and the related risk-adjusted premium calculation. Based on this risk-adjusted premium we determine the optimal insurance design in
Section 4 and we conclude this section with various properties and examples of the optimal insurance design. All results and statements are proved in the appendix.
A. Proofs
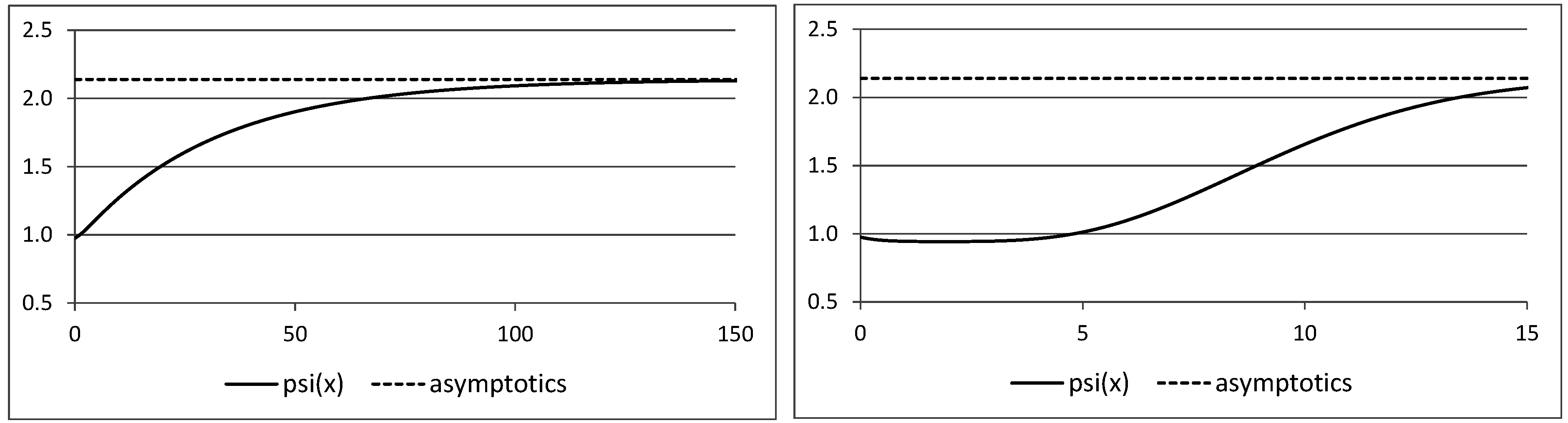
Proof of Lemma 1. The function
is strictly increasing for all
. Since
is a non-decreasing function, also the function
is non-decreasing for all
. But then independence between
and Θ implies that also
is non-decreasing. Assume there exist
such that
Inequality
,
-a.s., and identity (25) then imply that we must have
,
-a.s. Because the support of
is
we must have that
I is constant on
, and from
we see that this constant is equal to zero. Therefore, Equation (25) cannot occur unless
. This proves the strict increasing property.
Next we prove Lipschitz continuity of
. From
non-decreasing it follows that for all
and for all
we obtain (
I is also non-decreasing)
This implies that for any
and, moreover, using independence between Θ and
and integrability of
,
Thus, the function
is Lipschitz continuous and strictly increasing. As a consequence the remaining properties follow from Proposition A.3 in McNeil
et al. [
11]. This proves Lemma 1. ☐
Proof of Theorem 1. The first two premium identities follow from Equation (6). Choose a measurable function
. We obtain
We calculate the last term, using the tower property for conditional expectations in the first step,
basically, this is simply the application of Bayes’ theorem. This implies that
and proves the last identity for the choice
.
Next we prove the premium inequality. Choose
. Observe that the function
is component-wise non-decreasing. Moreover, the function
is also non-decreasing. Since
and Θ are independent, the FKG inequality implies, see Fortuin
et al. [
13],
where in the second last step we have used that
φ is a density and, thus, normalized. This closes the proof of Theorem 1. ☐
Proof of Theorem 2. For given
we recall Equation (7) which allows to rewrite
ψ as follows, set
,
Differentiability of
ψ follows from Leibniz’ integral rule. Moreover, we have
We define the new probability measure
by
This allows to rewrite
as follows: for
Observe that
and
are non-decreasing. FKG inequality [
13] then implies that
, which proves the claim. ☐
Proof of Lemma 2. The proof follows from Kamien-Schwartz [
14]. Note that the optimal control problem in Kamien-Schwartz [
14] is formulated on a finite interval
for
x. This can be achieved by a change of variables
in Equations (11)–(14) and then one checks that all the conditions are fulfilled. ☐
Proof of Lemma 3. Note that we need to distinguish the two cases
and
for the domain of
u. In the latter case we need
, due to
(Inada conditions). This implies that we need to have
and, thus,
Therefore, the initial wealth
should at least be able to finance the full insurance cover premium
if
u has support
. If the support of
u is
the wealth
is also allowed to become negative, and therefore no constraint is needed.
Proof of (i). Consider
given in Equation (16). Note that
is continuous and non-increasing in
λ. Therefore, we would like to consider the limits
and
of
. Note that
. This implies for
that
and, hence, for
we have
This means that for
we have
because we buy full insurance cover. On the other hand we have for any
i.e., we have point-wise (in
x) convergence to 0. Using that
provides an integrable upper bound, we can apply Lebesgue’s dominated convergence theorem to obtain
This immediately implies that there is
such that
. Moreover, for
the function
is non-increasing in
λ and on a set of positive Lebesgue measure it is strictly increasing, therefore
is strictly increasing in
λ and hence, there is a unique
with
. This proves (i).
Proof of (ii). We consider
The function
is non-decreasing in
x (note that we replace
by
if
u has support
). This implies that
is non-increasing in
x and, hence, the claim follows.
Proof of (iii). This is an immediate consequence of the increasing property of .
Proof of (iv). This is an immediate consequence of the boundedness of and the Inada condition at the left endpoint of u.
Proof of (v). From Equation (16) we get premium identity, see also Equation (21),
Note that the bracket
is decreasing in
. Therefore,
needs to be increasing for the premium identity to be fulfilled. Since this increasing property needs to be strict on a set of positive Lebesgue measure for
,
is strictly decreasing in
.
Observe from the premium identity
Therefore, lower bound
and upper bound
are strictly decreasing in
P. This implies that the term
needs to be increasing for the premium identity to be fulfilled. Since this increasing property needs to be strict on a set of positive Lebesgue measure we obtain that
is strictly decreasing in
P. ☐
Proof of Theorem 3. We start by calculating the derivative w.r.t.
P in Equation (21). Observe that the derivatives at the boundaries vanish and we obtain
From this we immediately conclude that
We now calculate the derivative of
U from Equation (20). This provides
Using Equation (27) for the middle term on the right-hand side of the above identity provides the claimed derivative of
U. The second derivative of
U is then given by (observe that the derivatives at the boundaries vanish)
Both
and
are decreasing which immediately implies that
and we have concavity. ☐
Proof of Theorem 4. Consider the function
The first derivative w.r.t.
P is given by
From Lemma 3 we know that
is decreasing in
P, this implies that
and, henceforth, insurance cover
are non-decreasing in
P for all
x.
Proof of (i). Full insurance cover means that
. Therefore, we need to have point-wise convergence
because otherwise we would get the following contradiction
This point-wise convergence requires for all
which implies
The latter implies that
as
. We prove this by contradiction: assume that
is bounded by
. Choose
. Continuity and strict monotonicity of all involved functions implies that there exists
P sufficiently close to
such that for all
This implies that
, which is a contradiction. Moreover, this also implies that
for all
P sufficiently large. Theorem 3 then reads as
Note that for any
we have
which implies that
for all
P sufficiently close to
. Therefore, full insurance cover is never optimal.
Proof of (ii). If
we need to have
which immediately provides the claim. Therefore, we can concentrate on
. No insurance means that
. In that case we need to have
as
. We prove this by contradiction. Assume that
. In that case we have
But this immediately implies that we buy insurance for all
x sufficiently large, and hence
P is bounded from below by a strictly positive constant. This contradicts
. Therefore, we have
This implies that for any
P sufficiently small we have
This implies that for all
P sufficiently small we have
. In view of Theorem 3 this implies that
for all
P sufficiently small because the first integral in Theorem 3 is equal to zero. Therefore, no insurance is never optimal. ☐
Proof of Proposition 1. (i) From Theorem 4 we know that we cannot have full insurance cover if is optimal. This implies that . Therefore, it is sufficient to consider . Condition (22) then implies that is non-decreasing in any x and for all . Therefore, for all , which implies that is of Type I.
(ii) Condition (23) implies that is strictly decreasing in 0, and henceforth, we have for all sufficiently close to 0. If then we have and for all x sufficiently close to 0, therefore . If then for all x sufficiently close to 0 and henceforth which implies that is of Type II if . ☐