Quadratic Unconstrained Binary Optimization Approach for Incorporating Solvency Capital into Portfolio Optimization
Abstract
1. Introduction
1.1. Our Contribution
1.2. Multi-Objective Portfolio Optimization
1.3. Extension of Portfolio Optimization by Solvency Capital Requirement
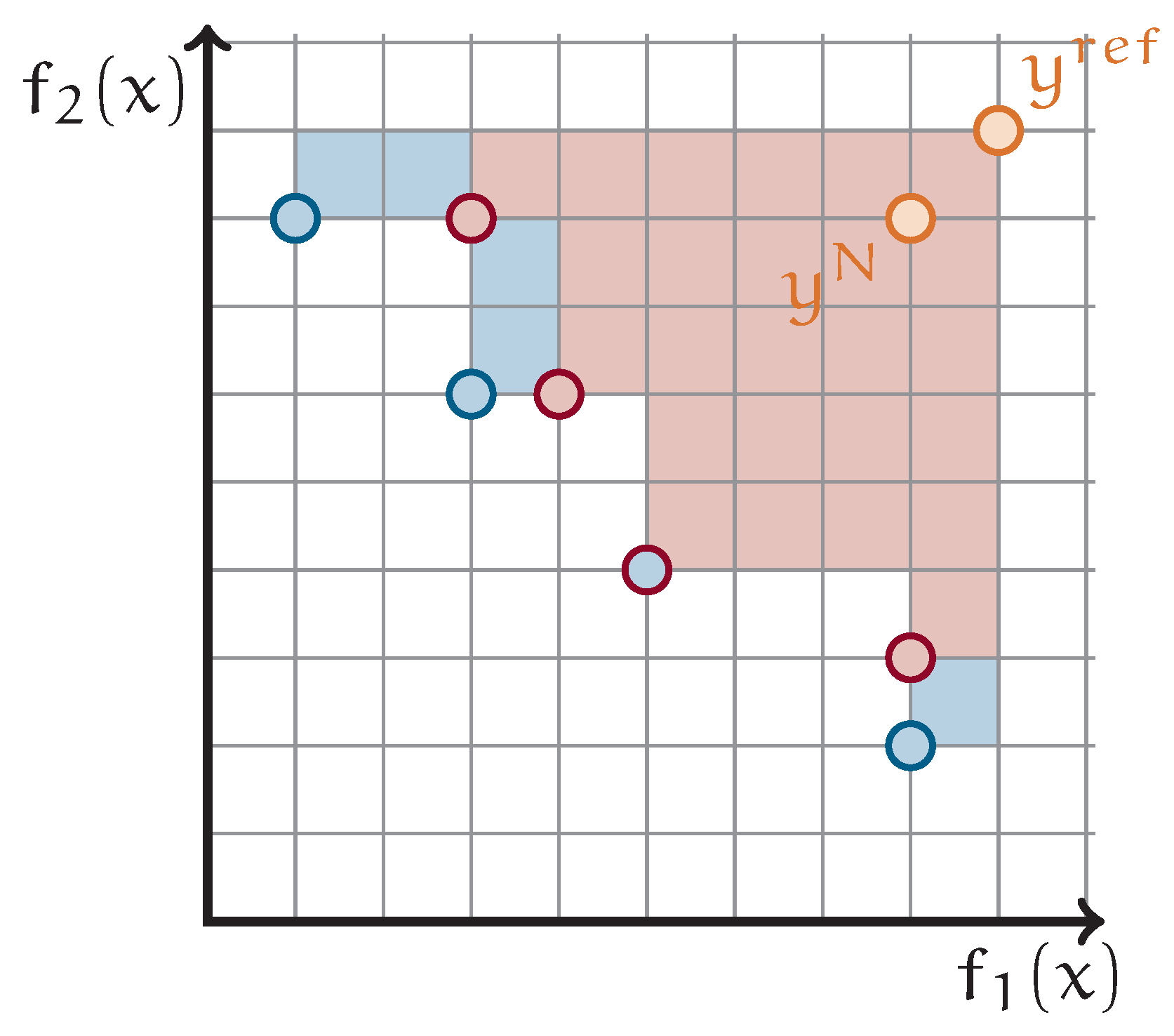
1.4. Finding Pareto-Optimal Points by Solving QUBOs
2. The QUBO Formulation
2.1. Finding a Quadratic Approximation for SCR
2.2. Discretization of Continuous Variables
2.3. Constraints
3. Experimental Results
3.1. Results on the Quadratic Approximation of SCR
3.2. Results on Solving the Multi-Objective Problem
4. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Artzner, Philippe, Freddy Delbaen, Eber Jean-Marc, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Bauer, Daniel, Andreas Reuss, and Daniela Singer. 2012. On the calculation of the solvency capital requirement based on nested simulations. ASTIN Bulletin 42: 453–99. [Google Scholar] [CrossRef]
- Blank, Julian, and Kalyanmoy Deb. 2020. pymoo: Multi-objective optimization in python. IEEE Access 8: 89497–509. [Google Scholar] [CrossRef]
- Braun, Markus, Thomas Decker, Marcelin Gallezot, Niklas Hegemann, Sven Kerstan, and Yuanheng Zhou. 2023. pygrnd. Available online: https://github.com/JoSQUANTUM/pygrnd (accessed on 29 November 2023).
- Dächert, Kerstin, Ria Grindel, Elisabeth Leoff, Jonas Mahnkopp, Florian Schirra, and Jörg Wenzel. 2022. Multicriteria asset allocation in practice. OR Spectrum 44: 349–73. [Google Scholar] [CrossRef]
- Ehrgott, Matthias. 2005. Multicriteria Optimization. Berlin: Springer Science & Business Media, vol. 491. [Google Scholar]
- Elsokkary, Nada, Faisal Shah Khan, Davide La Torre, Travis S. Humble, and Joel Gottlieb. 2017. Financial portfolio management using adiabatic quantum optimization: The case of abu dhabi securities exchange. Paper presented at 2017 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, September 12–14; pp. 1–4. [Google Scholar]
- European Commission. 2015. Commission Delegated Regulation (eu) 2015/35. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32015R0035&rid=1 (accessed on 29 November 2023).
- European Parliament and European Council. 2009. Directive 2009/138/ec. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2009:335:0001:0155:en:PDF (accessed on 29 November 2023).
- Halffmann, Pascal, Luca E. Schäfer, Kerstin Dächert, Kathrin Klamroth, and Stefan Ruzika. 2022. Exact algorithms for multiobjective linear optimization problems with integer variables: A state of the art survey. Journal of Multi-Criteria Decision Analysis 29: 341–63. [Google Scholar] [CrossRef]
- IBM. 2023. Available online: https://newsroom.ibm.com/2023-12-04-IBM-Debuts-Next-Generation-Quantum-Processor-IBM-Quantum-System-Two,-Extends-Roadmap-to-Advance-Era-of-Quantum-Utility (accessed on 25 January 2024).
- Jonen, Christian, Tamino Meyhöfer, and Zoran Nikolić. 2023. Neural networks meet least squares monte carlo at internal model data. European Actuarial Journal 13: 399–425. [Google Scholar] [CrossRef]
- Krah, Anne-Sophie, Zoran Nikolić, and Ralf Korn. 2020. Least-squares monte carlo for proxy modeling in life insurance: Neural networks. Risks 8: 116. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- Nelder, John Ashworth, and Robert W. M. Wedderburn. 1972. Generalized linear models. Journal of the Royal Statistical Society Series A: Statistics in Society 135: 370–84. [Google Scholar] [CrossRef]
- Paszke, Adam, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, and et al. 2019. Pytorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems 32. Red Hook: Curran Associates, Inc., pp. 8024–35. [Google Scholar]
- Rosenberg, Gili, Poya Haghnegahdar, Phil Goddard, Peter Carr, Kesheng Wu, and Marcos López De Prado. 2015. Solving the optimal trading trajectory problem using a quantum annealer. Paper presented at 8th Workshop on High Performance Computational Finance, Austin, TX, USA, November 15; pp. 1–7. [Google Scholar]
- Seelbach Benkner, Marcel, Maximilian Krahn, Edith Tretschk, Zorah Lähner, Michael Moeller, and Vladislav Golyanik. 2023. QuAnt: Quantum Annealing with Learnt Couplings. Paper presented at International Conference on Learning Representations (ICLR), Kigali, Rwanda, May 1–5. [Google Scholar]
- Shalev-Shwartz, Shai, and Shai Ben-David. 2014. Understanding Machine Learning. Cambridge: Cambridge University Press. [Google Scholar]
- Somma, Rolando D., Daniel Nagaj, and Mária Kieferová. 2012. Quantum speedup by quantum annealing. Physical Review Letters 109: 050501. [Google Scholar] [CrossRef] [PubMed]
- Venturelli, Davide, and Alexei Kondratyev. 2019. Reverse quantum annealing approach to portfolio optimization problems. Quantum Machine Intelligence 1: 17–30. [Google Scholar] [CrossRef]
- Virtanen, Pauli, Ralf Gommers, Travis E. Oliphant, Matt Haberland, Tyler Reddy, David Cournapeau, Evgeni Burovski, Pearu Peterson, Warren Weckesser, Jonathan Bright, and et al. 2020. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods 17: 261–72. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Leo, Sheng-Tao Wang, Soonwon Choi, Hannes Pichler, and Mikhail D Lukin. 2020. Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices. Physical Review X 10: 021067. [Google Scholar] [CrossRef]
- Zitzler, Eckart, and Lothar Thiele. 1998. Multiobjective optimization using evolutionary algorithms—A comparative case study. In Parallel Problem Solving from Nature—PPSN V. Edited by Agoston E. Eiben, Thomas Bäck, Marc Schoenauer and Hans-Paul Schwefel. Berlin/Heidelberg: Springer, pp. 292–301. [Google Scholar]


| Asset Class i | Asset Class i | ||||
|---|---|---|---|---|---|
| 1 | 14 | ||||
| 2 | 15 | ||||
| 3 | 16 | ||||
| 4 | 17 | ||||
| 5 | 18 | ||||
| 6 | 19 | ||||
| 7 | 20 | ||||
| 8 | 21 | ||||
| 9 | 22 | ||||
| 10 | 23 | ||||
| 11 | 24 | ||||
| 12 | 25 | ||||
| 13 | 26 |
| Epoch | 1 | 2 | 10 | 100 |
|---|---|---|---|---|
| Training Error | ||||
| Validation Error |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turkalj, I.; Assadsolimani, M.; Braun, M.; Halffmann, P.; Hegemann, N.; Kerstan, S.; Maciejewski, J.; Sharma, S.; Zhou, Y. Quadratic Unconstrained Binary Optimization Approach for Incorporating Solvency Capital into Portfolio Optimization. Risks 2024, 12, 23. https://doi.org/10.3390/risks12020023
Turkalj I, Assadsolimani M, Braun M, Halffmann P, Hegemann N, Kerstan S, Maciejewski J, Sharma S, Zhou Y. Quadratic Unconstrained Binary Optimization Approach for Incorporating Solvency Capital into Portfolio Optimization. Risks. 2024; 12(2):23. https://doi.org/10.3390/risks12020023
Chicago/Turabian StyleTurkalj, Ivica, Mohammad Assadsolimani, Markus Braun, Pascal Halffmann, Niklas Hegemann, Sven Kerstan, Janik Maciejewski, Shivam Sharma, and Yuanheng Zhou. 2024. "Quadratic Unconstrained Binary Optimization Approach for Incorporating Solvency Capital into Portfolio Optimization" Risks 12, no. 2: 23. https://doi.org/10.3390/risks12020023
APA StyleTurkalj, I., Assadsolimani, M., Braun, M., Halffmann, P., Hegemann, N., Kerstan, S., Maciejewski, J., Sharma, S., & Zhou, Y. (2024). Quadratic Unconstrained Binary Optimization Approach for Incorporating Solvency Capital into Portfolio Optimization. Risks, 12(2), 23. https://doi.org/10.3390/risks12020023







