Gaussian and Affine Approximation of Stochastic Diffusion Models for Interest and Mortality Rates
Abstract
:1. Introduction
2. Basic Life Insurance Framework
- is a stochastic process with continuous paths,
- is a stochastic process with continuous paths,
- is the natural filtration generated by the joint process, .
3. Gaussian Diffusion Approximation
- (a)
- the column vector is a d-dimensional standard Wiener process, ,
- (b)
- the mapping, , which is composed of the bounded and measurable mappings and , is jointly measurable on ,
- (c)
- the mapping is jointly measurable on ,
- (d)
- there exists a constant , such thatfor all , , where is the Euclidean norm.
4. Affine Diffusion Approximation
5. Approximation Error When Valuating Insurance Claims
6. Numeric Illustration

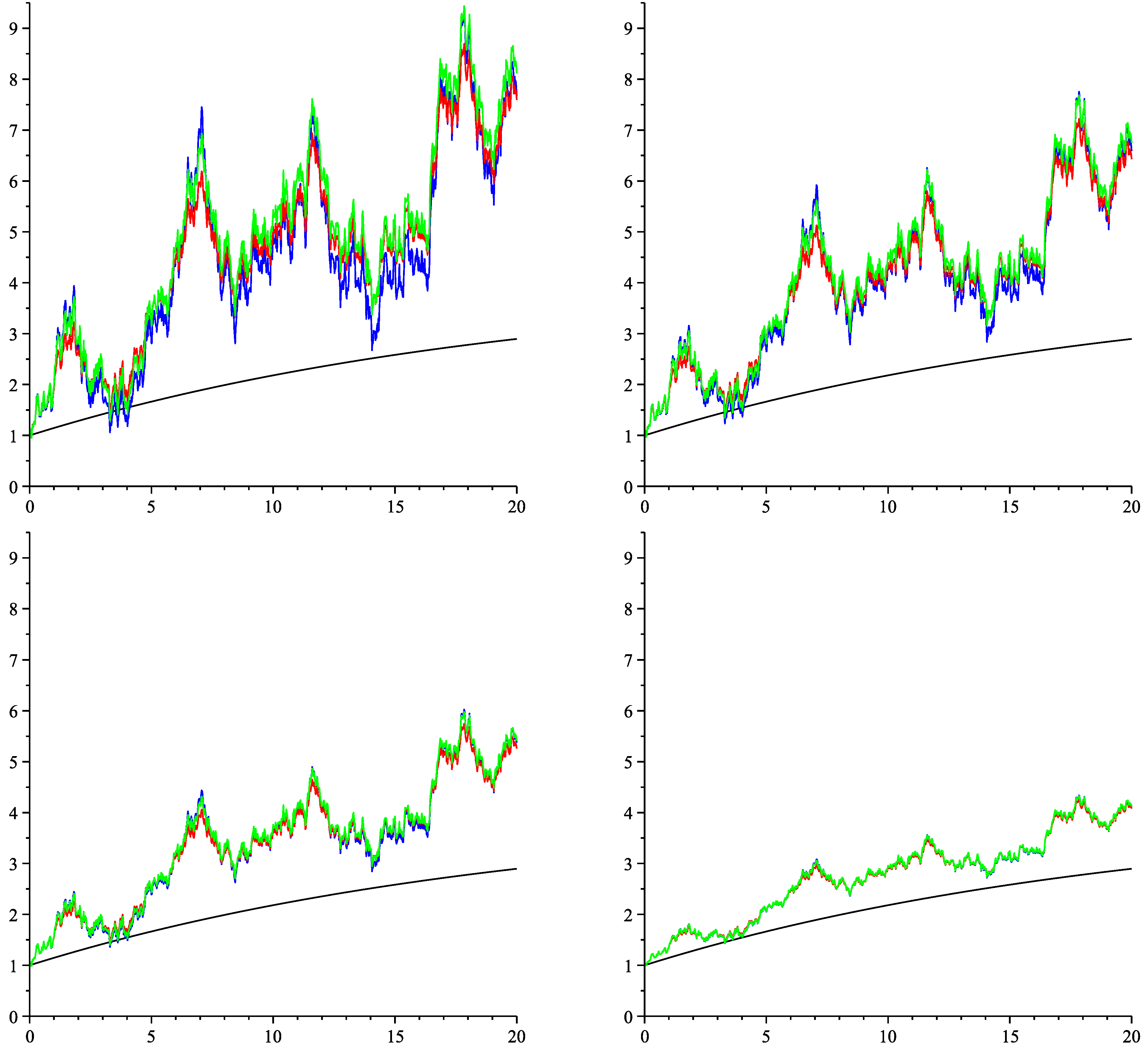

| Valuation w.r.t. the Single Simulated Path | ||||
|---|---|---|---|---|
| true value | 0.37988 | 0.43749 | 0.50274 | 0.57575 |
| expectation approximation | 0.65644 | 0.65644 | 0.65644 | 0.65644 |
| (relative error) | 0.72804 | 0.50046 | 0.30573 | 0.14016 |
| Gaussian approximation | 0.39773 | 0.44968 | 0.50926 | 0.57768 |
| (relative error) | 0.04700 | 0.02785 | 0.01296 | 0.00336 |
| affine approximation | 0.41127 | 0.45185 | 0.50731 | 0.57635 |
| (relative error) | 0.08264 | 0.03283 | 0.00910 | 0.00105 |
| Valuation w.r.t. 10,000 Simulations | ||||
|---|---|---|---|---|
| true value | 0.68733 | 0.67571 | 0.66712 | 0.65827 |
| expectation approximation | 0.65644 | 0.65644 | 0.65644 | 0.65644 |
| (mean absolute deviation) | 0.16151 | 0.13076 | 0.09186 | 0.04839 |
| Gaussian approximation | 0.70483 | 0.68155 | 0.66873 | 0.65835 |
| (mean absolute deviation) | 0.10065 | 0.05486 | 0.02272 | 0.00500 |
| linear noise approximation | 0.70280 | 0.68152 | 0.66875 | 0.65839 |
| (mean absolute deviation) | 0.04802 | 0.02486 | 0.00863 | 0.00113 |
7. Proofs
- we have and for all ,
- the continuous function, α, has a finite bound, , on ,
- the mapping, , is Lipschitz-continuous in x with Lipschitz constant K,
- for all s,
- for all s,
- the continuous function has a finite bound on ,
8. Conclusions
Acknowledgments
Conflicts of Interest
References
- T. Björk. Arbitrage Theory in Continuous Time, 2nd ed. New York, NY, USA: Oxford University Press, 2004. [Google Scholar]
- O. Vasicek. “An equilibrium characterization of the term structure.” J. Financ. Econ. 5 (1977): 177–188. [Google Scholar] [CrossRef]
- J.C. Cox, J.E. Ingersoll, and S.A. Ross. “A theory of the term structure of interest rates.” Econometrica 53 (1985): 385–407. [Google Scholar] [CrossRef]
- D. Heath, R. Jarrow, and A. Morton. “Bond pricing and the term structure of interest rates: A new methodology for contingent claims valuation.” Econometrica 60 (1992): 77–105. [Google Scholar] [CrossRef]
- J.A. Beekman, and C.P. Fuelling. “Interest and mortality randomness in some annuities.” Insur. Math. Econ. 9 (1990): 185–196. [Google Scholar] [CrossRef]
- J.A. Beekman, and C.P. Fuelling. “Extra randomness in certain annuity models.” Insur. Math. Econ. 10 (1991): 275–287. [Google Scholar] [CrossRef]
- D. Dufresne. “The distribution of a perpetuity, with application to risk theory and pension funding.” Scand. Actuar. J. 1 (1990): 39–79. [Google Scholar] [CrossRef]
- A. De Schepper, F. de Vijlder, M.J. Goovaerts, and R. Kaas. “Interest randomness in annuities certain.” Insur. Math. Econ. 11 (1992): 271–281. [Google Scholar] [CrossRef]
- G. Parker. “Two stochastic approaches for discounting actuarial functions.” ASTIN Bull. 24 (1994): 167–181. [Google Scholar] [CrossRef]
- R. Norberg, and C.M. Møller. “Thieles differential equation with stochastic interest of diffusion type.” Scand. Actuar. J. 1 (1996): 37–49. [Google Scholar] [CrossRef]
- S.-A. Persson. “Stochastic interest rate in life insurance: The principle of equivalence revisited.” Scand. Actuar. J. 2 (1998): 97–112. [Google Scholar] [CrossRef]
- M.A. Milevsky, and S.D. Promislow. “Mortality derivatives and the option to annuitise.” Insur. Math. Econ. 29 (2001): 299–318. [Google Scholar] [CrossRef]
- M.H. Dahl. “Stochastic mortality in life insurance: market reserves and mortality-linked insurance contracts.” Insur. Math. Econ. 35 (2004): 113–136. [Google Scholar] [CrossRef]
- E. Biffis. “Affine processes for dynamic mortality and actuarial valuations.” Insur. Math. Econ. 37 (2005): 443–468. [Google Scholar] [CrossRef]
- L. Ballotta, and S. Haberman. “The fair valuation problem of guaranteed annuity options: The stochastic mortality environment case.” Insur. Math. Econ. 38 (2006): 195–214. [Google Scholar] [CrossRef]
- A.J. Cairns, D. Blake, and K. Dowd. “Pricing death: Frameworks for the valuation and securitization of mortality risk.” Astin Bull. 36 (2006): 79–120. [Google Scholar] [CrossRef]
- M. Dahl, and T. Møller. “Valuation and hedging of life insurance liabilities with systematic mortality risk.” Insur. Math. Econ. 39 (2006): 193–217. [Google Scholar] [CrossRef]
- D.F. Schrager. “Affine stochastic mortality.” Insur. Math. Econ. 38 (2006): 81–97. [Google Scholar] [CrossRef]
- D. Bauer, M. Börger, J. Ruß, and H.J. Zwiesler. “The volatility of mortality.” Asia-Pac. J. Risk Insur. 3 (2008): 184–211. [Google Scholar] [CrossRef]
- V.R. Young. “Pricing life insurance under stochastic mortality via the instantaneous Sharpe ratio.” Insur. Math. Econ. 42 (2008): 691–703. [Google Scholar] [CrossRef]
- Z. Shang, M. Goovaerts, and J. Dhaene. “A recursive approach to mortality-linked derivative pricing.” Insur. Math. Econ. 49 (2011): 240–248. [Google Scholar] [CrossRef]
- H. Huang, M.A. Milevsky, and T.S. Salisbury. “Optimal retirement consumption with a stochastic force of mortality.” Insur. Math. Econ. 51 (2012): 282–291. [Google Scholar] [CrossRef]
- S. Tappe, and S. Weber. “Stochastic mortality models: An infinite-dimensional approach.” Finance and Stochastics. (in press). [CrossRef]
- M.C. Christiansen, and A. Niemeyer. “On the forward rate concept in multi-state life insurance.” Ulm, Germany: Preprint Series of the Faculty of Economics and Mathematics at the University of Ulm, 2013. [Google Scholar]
- K.R. Miltersen, and S.A. Persson. “Is mortality dead? Stochastic forward force of mortality rate determined by no arbitrage.” In Working paper. Norway: University of Bergen, 2005. [Google Scholar]
- P.E. Kloeden, and E. Platen. Numerical Solution of Stochastic Differential Equations. Berlin, Germany: Springer, 1992. [Google Scholar]
© 2013 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Christiansen, M.C. Gaussian and Affine Approximation of Stochastic Diffusion Models for Interest and Mortality Rates. Risks 2013, 1, 81-100. https://doi.org/10.3390/risks1030081
Christiansen MC. Gaussian and Affine Approximation of Stochastic Diffusion Models for Interest and Mortality Rates. Risks. 2013; 1(3):81-100. https://doi.org/10.3390/risks1030081
Chicago/Turabian StyleChristiansen, Marcus C. 2013. "Gaussian and Affine Approximation of Stochastic Diffusion Models for Interest and Mortality Rates" Risks 1, no. 3: 81-100. https://doi.org/10.3390/risks1030081




