1. Introduction
The sustainability of the pension fund relies on the strict observance of accounting equations. The objective of the fund normally is not to search for the best return at each time, but to find the appropriate balance between risk and gain so as to be able to pay the retirement benefits over the long period of liability [
1]. However, managers of the fund are tempted to promise more than normally due from fair actuarial calculations, because the measures recommended against risk often contradict “the search for the optimal compromise between risk and return” [
2] (p. 139). The French legislators have become aware of the danger, as it is reflected in the warrant of the 29 of November 2006 (
Décret no 2006-1499) specifying the conditions of the reorganization of certain funds out of equilibrium.
For example, this warrant was invoked in the agreement of the 23rd of April 2007 establishing the contributions to the French pension fund for bailiffs (CARCO). An additional contribution of 4.1% was imposed to subscribers without benefits to be paid in the future, just for the sake of rescuing the fund.
1 In fact, even from 2004 onwards, a contribution for solidarity of 2% was required for the same purpose of filling the gap between the so-called “special technical provision” and the so-called “mathematical technical provision”, that is to say, to save the fund from insolvency. It was scheduled to cease after the gap was filled, but the additional contribution was instead increased to 4.1% in 2007. Moreover, this agreement contains an item whereby this additional contribution is allowed to be adjusted if the sum to be gained, namely 8,232,000 euros, is not attained.
A second example is the French pension fund for private hospitals (
Caisse de retraite desétablissements de soins privés (CRESP)).
2 The fund declared a gap of 27.6 million euros in 2009 and of 41.4 million euros in 2010 between the theoretical and the recorded reserves. The ratio of the net present value of contributors to liabilities for beneficiaries (the “coverage ratio”) was estimated at 86%, then far from the value of 100% where it should be. The impossibility to pay benefits with the current parameters was explicitly acknowledged in 2003.
3 The situation was explicitly assigned to the bad performance on the stock exchange.
4The French system works as a hybrid system. This is not exactly the same as a system with defined contributions [
3]: at the moment of retirement, the capital acquired in the account of the employee is transformed into benefits. The employee acquires points, and the point has a value that can vary until the age of retirement where it is fixed by contract. The employee is promised a certain number of points. What is unknown is the value of the point at the moment of the settlement. In the normal working of a pension fund, each contributor assesses a certain amount of money to the fund on a regular basis, usually monthly. During his activity in the firm affiliated to the fund, the contributor is not allowed to withdraw his contribution. At retirement, the fund is committed to pay for a benefit by contract, which is due until death and can no longer be changed. The computation of the benefit is done from the capital invested by the contributor all along his period of contribution, augmented by the interest rate and by the mortality rate of other contributors dead in activity. It also takes into account the expected interest rate until the death of the contributor, and the expected mortality of other contributors (this is the principle of mutualization). By construction, sustainability of the fund is obtained through investment in predictable assets-which should involve little risk-through an acute forecasting of forthcoming mortality, and through respect of accounting rules. The difficulty comes from the fact that the fund must balance present contributions with forthcoming pension benefits, and not, as in pay-as-you-go pensions, with benefits of the present pensioners.
Especially when the stock exchange is on the rise, the financier, the person in charge of yield profits from the capital of the fund, is tempted to bet on risky assets so as to maximize profit. But this is an error, because the financier, contrary to the pension fund, has no commitment to pay benefits on due date. The point is that the probability to reach the objective of benefit payments on due date is higher with long duration assets than with risky assets; it is that the logic of sure yields should supersede the logic of profit maximization, although the latter looks attractive. Similarly, longevity forecasts can under-estimate the actual improvement of survival, due to the rapid increase of hygiene and medicine, so that no annuity provider should determine the annuity rate solely on the basis of these forecasts. Finally, the manager, willing to attract more customers, should not be mistaken by current high rates of return on the stock market to promise more than the actuarial value of retirement benefits.
At the beginning of the fund, the scarcity of beneficiaries compared with contributors causes an important money flow into the fund.
The temptation arises to increase the commitment for pensions beyond their due actuarial values in order to attract more contributors. This can be due to an inadequate culture of pay-as-yougo pensions, which favors short-sighted arbitrage, or to a hope of too optimistic returns from investments on the financial market through too risky assets.
The fund fixes the value of the retirement benefits from the computation of the actuary done with a riskless long-term interest rate, but entrusts the management of the fund to a financier, who is not an insurer and invests in risky assets on the stock market. This can be due to a misunderstanding of the actuarial work and an inadequate trust in risk management [
4,
5].
Errors can also come from too conservative a forecast of life expectancy. For example, as Cohen [
6] pointed out, “the planners of the Social Security system in the United States during the 1930s failed to anticipate the remarkable improvement in the survival of older Americans.” In July 2011, the French government lengthened the work duration of three months, because the national institute of statistical studies (INSEE) measured that life expectancy was increasing faster than expected. This is the third possible error that shall be addressed.
The active population can also experience a drastic downsizing, which can have deleterious consequences if the fund, already out of equilibrium, is led to mutualize the contributions of different generations, that is to say, to use the funds affected to one generation to pay for another generation [
7].
My overall objective is first to measure how a deviation is multiplied over time, because of the long run liability of the fund over the future, and second, to develop a warning aid through the differential equation giving the velocity (hence the rate) at which the current assets decrease. Ponds [
8] was also concerned with solvency of the fund, but in a context of generational accounting related to defined-benefit schemes, which is less frequent than contribution-defined schemes, and he neither evaluated the rate of decline nor decomposed this rate among the types of error.
In theory, only bonds should be used, but in the practical case that I present, managers have largely introduced risky assets into their capital. Solvency II norms provide a supplementary safety, but whatever the protections, fatal deviations are likely to remain. The argument of Solvency II amounts to have investments in stocks cost very high, but what will happen if firm bonds are no longer paid? Solvency II will not save everything, it will save only what is known, it is just a repair device of the deviations made so far.
5If the reorganization plan is taken, either by the managers of the fund who realize the coming insolvency or by a control authority, it usually relies on an increase of contributions of active contributors-sponsoring firm and active members of the plan-and on reduced retirement benefits of the contributors retiring after the date of the reorganization plan. For the two French pension funds I have mentioned, the duration of the re-organization plans were explicitly fixed to 20 years. The return to equilibrium is a function of controls and of the inherited liabilities at the date of the reorganization plan. One may wonder why does the government not control the pension funds, having in mind that such control would be beneficial? In France, pension funds have escaped the supervision of the control commission until now, but the government has recently indulged in extending the competence of this commission to organizations practicing insurance, through the mentioned warrant of 29 November 2006. However, pension funds in the industry are too numerous to be controlled in time. This explains why the person in charge of controlling the actors-contributors, financier, actuary, government-is the manager of the fund. He/she is then the person in charge of the solvency of the fund, unless an insurance company takes his/her place-in this case, the solvency of the fund is under control.
My contribution is firstly to enrich the general description done by [
9] to the specific French case of pension funds and in focusing on the practical recent situation of French pension funds, secondly to suggest a warning device through the splitting up into its components of the slope with which deficits grow. This enables the minimal extra performance on the stock market to absorb the extra bonus and the possible error on mortality estimation. As soon as this warning signal is negative, measures are to be taken without waiting for the situation to worsen. My topic is again the practical case; it concerns neither participating contracts with with-profit bonuses, which do not concern France, nor adjustments of contributions or premiums, because contributions in France result from (long) negotiations between employees and employers and do not change easily, nor variable benefit accrual, which does not apply to French pension funds. From the analytical formula that I shall give, I shall evaluate the constructed early warning signal numerically, so as to present a practical indicator. I shall estimate the respective weights of the errors made on the interest rate, the extra bonus, and the mortality forecast.
2. Model
2.1. Sustainable Working of Pension Funding
For the sake of simplicity, I assume that assets associated with beneficiaries are invested at the same interest rate than those associated with still active contributors. The interest rate covers both a stochastic interest rate and stochastic stock returns, for I do not have to go in the detail of the portfolio.
At time
t, cohort
τ =
t −
a of age a has contributed amount of:
where
pg(
t −
a,
s) is the total number of contributors aged
s and born at time
t −
a,
mg(
t −
a,
s) is their instantaneous contributions per head into the fund at age
s, usually taken as a fixed percent of wages,
![Risks 01 00001 i034]()
(
u) is the actual interest rate at time
u of assets bought for still active people. I shall use the index
g to specify that the first argument of the associated function corresponds to the number of the cohort.
The capital gathered by cohort
t −a at age
ω of retirement (assumed constant in time) is then returned to beneficiaries through retirement benefits
cg(
t −
a,
s) for one euro at age
s until maximal age
ω† of life, so that the capital left by cohort
t −
a at age
a =
ω, ··· ,
ω† is:
which is the continuous version of classical actuarial calculus and where
lg(
t −
a,
b) is the expected cohort probability of surviving from age
ω to age
b ∈ [
ω,
ω†]:
with
µ(
t,
x) the usual continuous-time force of mortality at time
t and age
x. I denote
![Risks 01 00001 i035]()
(
t −
a,
b) as the actual survival probability and
lg(
t −
a,
b) as the expected one.
The accounting balance of the fund giving the value
cg(
τ,
b) for generation
τ of the pension for one euro for cohort
τ and age
b is obtained when the entire capital gathered by cohort
τ has been entirely paid back to beneficiaries of cohort
τ , after the percentages taken by the fund (at entry, on the interest rate, or at sale) which do not appear in the equations for the sake of clarity:
For
cg(
τ,
b) =
cg(
τ) constant with age,
which is the continuous-time version of the classical actuarial calculus of retirement benefits.
The annual discrete-time version of Equation (5) is:
where
r(
u) denotes the mean interest rate for year
u.
2.2. Deviation from Actuarial Equilibrium
The percentages received by the fund at sale of the contract are incentives for promising more attractive pensions, especially if the fund benefits from a favorable ratio of active/beneficiaries and if the financial market lets people hope for high returns. In certain funds, the contribution is used to buy points. The price of a point can vary over time. The total number of points acquired at retirement time is changed into pension benefits. The error consists in allowing bonus points to contributors, hence a commitment for higher retirement benefits for one euro. In other funds without points, the mechanism of allowing bonus is similar. For one euro at the beginning of the contract (at retirement), a constant cg(τ)(1 + δ) is promised instead of the constant cg(τ) at equilibrium of Equation (5).
Because the fund is bound by contract to pay for the beneficiaries until their deaths, through Equation (4) or Equation (5), any temporary deviation from this accounting balance engages the fund for decades and for its corresponding deficit. The error then runs from the beginning to the point of the reorganization plan (as observed in practice, benefits and points allocations change only slowly because they are decided after negotiations between employees and employers). The entire capital gathered by cohort τ is entirely paid back to beneficiaries of cohort τ . Although the environment is uncertain, the pension fund makes sure “fair” promises to the cohort at retirement. This assumption explains why, even small, an extra bonus leads to insolvency.
The fund can be in permanent sustainable regime when the deviation occurs. However, practically, bonus points are allowed shortly after the creation of the fund, at t0, so, because of the disproportionate length of liability compared with the period of working of the fund, it is more realistic to consider that the deviation is made from the very beginning of the fund.
Depending on the contract, the capital paid to the fund by an individual who dies before retiring is either paid back to the spouse, paid as a lump sum, or, by far the most frequent case, it remains in the fund and is used in the mutualization system to increase retirement benefits paid to survivors. I focus on this latter case to study the consequences of an extra bonus in the account of the fund. Moreover, mortality in most developed countries where pension funding can exist is sufficiently low before usual age of retirement to discard the first option.
Three deviations can accumulate: the fund is committed by contract to pay more than
cg, say (1 +
δ)
cg in order to capture subscribers; the interest rate has been forecast as
r(
t) but its realization is
![Risks 01 00001 i034]()
(
t); the survival has been forecast as
lg but its realization is
![Risks 01 00001 i035]()
. The payment
cg is stipulated in a contract, then it cannot be adjusted dynamically. To change
cg, the trade unions and the management of the firm must agree on a new contract, which is hard to obtain. This happens when the plan is reorganized.
The solvency of the fund depends on three accounts, corresponding to three groups of people:
The current assets for one euro and for a beneficiary of generation
t −
a <
t −
ω† (then dead at
t) is:
which is null if
δ = 0,
![Risks 01 00001 i035]()
= lg, and
![Risks 01 00001 i034]()
=
r. If
δ > 0, it can also be non-negative if also
![Risks 01 00001 i034]()
>
r, which is exactly the bet made by financiers in a context of rising stock exchange.
Late cohorts
t0−
ω†, ··· ,t −
ω†, where
t0is the starting date of the fund, have left a deficit at time
t of:
The current assets remaining for one euro and for a beneficiary of age
a ∈ [
ω,
ω†] at time
t is:
At time
t, present beneficiaries have a capital of:
The capital brought by contributors in activity is:
Expected liabilities for one euro and for these future beneficiaries are (1 +
δ)
cg(
t −
a).
The current assets of the fund are:
Time elapsed since the beginning of the fund appears only in xD(t): for δ > 0, the accumulation of losses is linear in time, after the initial phase of the arrival of beneficiaries to be paid by the fund, causing the coefficient of linearity to decrease to its permanent regime, depending only on contributions, interest rate, and survival. The term independent of duration xP (t) + xA(t) starts from 0 at the beginning of the fund to increase to its level of permanent regime.
The dynamic of debt left by the dead is:
with
From Equation (10), second expression, the dynamic of the capital related to the pensioners is:
Summing Equation (13) and (15) yields:
where the first term
![Risks 01 00001 i034]()
(
t)
xP (
t) is the interest over the debt, the second term
Kg(
t −
ω,
ω) is the capital entering the current assets for the old and the dead, and the third term multiplied by dt represents the payment of benefits between
t and
t + dt.
Equation (16) yields the growth rate of the sum of the deficit left by late cohorts and the current assets for pensioners. When this growth rate is negative, this is an early warning signal sent to the manager of the fund.
I suggest now to examine simplified versions of this key Equation (16), in order to assess the relative importance of the error on the interest rate, the error on payment of benefits, and the error on mortality forecasting.
2.3. The Relative Importance of Each Error
At
cg and
Kg constant,
where
resembles the expression of the actual life expectancy at age
ω, except that survival functions are taken by generation, and generations vary.
6For
δ = 0,
![Risks 01 00001 i034]()
(
t) =
r(
t),
![Risks 01 00001 i033]()
(
t,
a) =
µ(
t,
a), actuarial equations imply:
with
which is a sort of life expectancy at age
ω, but again with both generation and time varying.
Define Δ
r(
t) as:
and Δ
µ(
t,
u) as:
where
![Risks 01 00001 i033]()
is the actual mortality rate. In the past, the variations of mortality have concerned all ages. There has not been such a thing as a mortality intensity changing at a given age and unchanged at other ages. This allows me to assume that the error on mortality forecast is approximately the same at all ages over
ω:
Subsequently,
From the French life tables
7 2004-6, 2005-7, 2006-8, 2007-9, and 2008-10, I estimated
µ(
t + 1,
a) −
µ(
t,
a) at each age and successively at 2005, 2006, 2007, 2008, and 2009 from
a = 65 to
a = 95 years of age, as a proxy for Δ
µ(
t,
a), which turns out to be approximately independent of age a (Δ
µ(
t,
a) ≈ Δ
µ(
t)): the error Δ
µ(
t) made in forecasting should be of the same order of magnitude than the yearly actual variation, notably if mortality is forecast at year
t + 1 as the value taken at year
t. On these data, I found that (
µ(
t + 1,
b) −
µ(
t,
b))(
b −
ω), for
ω = 65 and
b = 65, ··· , 95, is equal to −0.0149 (SD = 0.0151) on average for men and to −0.0163 (SD = 0.013) for women. These low values allow the assumption | Δ
µ(
b −
ω) |≪ 1, for
b = 65, ··· , 95, which leads to the first-order approximation of the “life expectancy” at
t:
For Δ
r(
t) ≪
r(
t) and
δ ≪ cg, using Equation (19) and taking
![Risks 01 00001 i037]()
and
xP (
t) at
![Risks 01 00001 i034]()
=
r and
δ = 0, the variation of the amount of current assets is:
which is a differential system with state variables
xD(
t),
xP (
t), and y(
τ +
ω,
t) (defined in the third equation of System (26)),
τ =
t0, ··· ,
t and linear controls Δ
r(
t),
δ, and Δ
µ(
t), except that
δ is fixed by contract and cannot be changed dynamically and except that Δ
r(
t) and Δ
µ(
t) are exogenous.
At the first-order, the term
![Risks 01 00001 i038]()
Δ
r(
t) vanishes, and Equation (26) boils down to:
where, consistently, the extra bonus (
δ> 0) adds a negative term, as do an under-estimation of mortality (Δ
µ(
t) < 0) and a bad performance Δ
r(
t) < 0 on stocks (the coefficients of Δ
r and of
δµ are positive by construction). Equation (27) is an original result: it completes the display of information on the economic health of the fund. It adds the detail of the components of the velocity
![Risks 01 00001 i039]()
the state
xD(
t) +
xP (
t) of the current assets; it states how the stock exchange should extra-perform the actuarial rate at each date to rescue the situation endangered by the allowance of the extra bonus or by an unexpected improvement of mortality at old ages. It tells which component is responsible for the variations of
xD(
t) +
xP (
t); it allows the manager to assess his/her chances to rescue the situation in the case of a declining amount of current assets.
The variable
![Risks 01 00001 i040]()
behaves as an early warning signal that the pension fund has made errors that compromise its solvency in the future. The simple fact that
xD +
xP is decreasing is already enough to warn the manager that something is going wrong;
ξ(
t) specifies the importance of each error. As we shall see below, we can even estimate the values of each error Δ
r(
t),
δ, and Δ
µ from the follow-up of
ξ(
t) over four time units, a piece of information that the sole knowledge of
xD(
t) +
xP (
t) does not allow.
In the noteworthy case of a perfect forecasting of mortality, it is not enough that Δ
r(
t) > 0, but, from Equation (27), the manager should have
![Risks 01 00001 i041]()
, or:
In case of too high retirement benefits
cg, the denominator is negative and, as the numerator is positive, Δ
r(
t) should be positive. Equation (28) gives a clear rule of how the return on the stock exchange must extra-perform to counterbalance the extra bonus. Actuaries advise
δ = 0, Δ
r(
t) = 0, and Δ
µ(
t) = 0, but financiers allowing the extra bonus
δ bet that Δ
r(
t) will be high enough to ensure that
![Risks 01 00001 i042]()
, having no knowledge really on
![Risks 01 00001 i043]()
. Extra bonuses are allowed for commercial purposes, without measuring the long-term consequences on the solvency of the fund, trusting the stock exchange to fill the gap. Equation (27) or Equation (28) allow the computation of the necessary extra asset return Δ
r(
t): if it is unrealistic, the manager had better re-organize the fund without waiting for
x(
t) to be low enough. The problem is that Δ
r(
t) can be less than the threshold given by Equation (27) or Equation (28), even negative for a long period of time, as what happened during the financial crisis of 2008-2009. Then Equation (27) clearly indicates the weight of each error Δ
r(
t),
δ, and Δ
µ(
t) in the short term. An estimate of the time to insolvency when the current assets are
x(
t) at time
t is
![Risks 01 00001 i044]()
, where A is the right hand side of Equation (27).
2.4. The Early Warning Signal in Practice
Discrete-time Expression One annual discrete-time approximation of Equation (27) is:
This formula can be used for practical computation.
Numerical values I simulated 200 time series of interest rates
r(
t) and life tables
µ(
t,
u),
u = 0, 99,
t = 1, ··· , 50. The life tables were generated from Ledermann model life tables [
10]. For each time series, I simulated
δ drawn at random in [0, 0.3], Δ
e0 : = ě0 −
e0 in [−6, 6] years, the error made on the forecast of the life expectancy at birth
e0, itself drawn at random between 75 and 90 years. Δ
µ, the
![Risks 01 00001 i035]()
, and the
lg are deduced from Δ
e0. The standard deviation σr of the interest rate was drawn at random from [0%, 5%], so that
![Risks 01 00001 i034]()
(
t) was taken from a Gaussian distribution N (
![Risks 01 00001 i050]()
,
σr), with
![Risks 01 00001 i050]()
drawn at random from [−3%, 3%]. The error on the interest rate Δ
r(
t) = Δ
r was drawn at random in [−3%, 3%],
Time to Insolvency On the 128 simulated time-series for which
xD(
t) +
xP (
t) decreased until becoming negative, I found a significant positive correlation, as expected, between
ξ(
t) and the first time
tmin when
xD(
t) +
xP (
t) < 0 for the first time. The regression over the 128 trials of the mean value
![Risks 01 00001 i045]()
of
ξ(
t) over time on
tmin yields:
where the star indicates statistical significance at the 5% level and standard deviations are put in parentheses below their coefficients. Equation (30) shows that the more negative
E(
ξ), the sooner the moment when
xD +
xP < 0. Moreover, for the 128 simulated time series for which
xD +
xP < 0 before the time horizon of the simulation, on average,
E(
ξ) =
![Risks 01 00001 i046]()
, which shows that
E(
ξ) is significantly negative when the pension fund is doomed to insolvency (net the effect of the capital brought by contributors in activity).
Numerical Evaluation of the Early Warning Signal ¿From these 128 simulated time series, I estimated the coefficients associated with each of the three errors in Equation (27) (or Equation (29)) as:
The three respective coefficients of Δ
r(
t),
δ, and Δ
µ(
t) can be computed by the fund manager, because they are built from forecast interest rates and mortality, not from the actual values of these variables. The manager can also compute
ξ(
t) directly from the knowledge of
xD(
t) +
xP (
t) followed up over four successive time units. Then, by solving a linear system of three equations identifying (
xD(
t + 1) +
xP (
t + 1)) − (
xD(
t) +
xP (
t)) to a linear combination of Δ
r(
t),
δ, and Δ
µ(
t), for
t taking four successive values and the coefficients estimated as in Equation (31), the manager can estimate the three errors Δ
r(
t),
δ, and Δ
µ(
t). The manager reiterates the procedure at each time unit to estimate how the errors vary in time. I tested it numerically and the estimation works very well to find again the input values of Δ
r(
t),
δ, and Δ
µ(
t).
Moreover, on the 128 simulated time series leading to
xD(
t) +
xP (
t) < 0, I find the weights of each error appearing in Equation (27) (as means of the coefficients expressed in Equation (31)), with standard deviations in parentheses below mean values, as:
which shows the prior importance of a good prediction of mortality. Mortality intervenes in the computation of retirement benefits for one euro and in deficits. The manager should under-estimate mortality from the start, but technological progress is so unpredictable that mortality can decline faster than expected. The second message of Equation (32) is that the weight of Δ
r is high enough that, definitely, the manager should not invest in risky assets where errors are more likely to occur than with riskless assets. Finally, the coefficient of
δ, the error made on retirement benefits for one euro, is the lowest one. However, there is no biological intuition as for Δ
µ or economic guess as for Δr to prevent the manager from offering a high
δ. Even with a low weight in Equation (32), a high
δ can prove as deleterious for the pension solvency as the other errors weighted by higher coefficients.
3. Conclusions
I have examined the consequences of deviations on the sustainability of the fund. I have highlighted how errors, either on investment or in payment of benefits, are multiplied by the liability structure and its long-term kinematics. Developing on actuarial equations, I showed notably that even a small extra bonus (δ) of retirement benefits is enough to carry the fund away into deficits, which grow linearly with time. I expressed the current assets analytically, and wrote the differential equation (27) expressing the velocity with which this amount of current assets varies. I deduced the minimal excess return on stocks (Equation (28)) necessary to counter-balance the extra bonus and the error on mortality forecasting if any. I deduced an estimate at each time t of the time to insolvency.
Population size and age structure in a pension fund should play no role, because each contributed euro corresponds to a benefit. However, the necessity to pay for the deficits left by dead cohorts leads the fund to mutualize the contributions, giving a role to the liability structure and hence to population stocks. However, the mutualization does not rescue the fund in the mean term. Equation (27) helps knowing if the entry of new capital
![Risks 01 00001 i047]()
is enough to counter-balance deficits and push x’(
t) to positive values, the manager having the responsibility to lower the benefit to attain
δ = 0 with the new entrants. Otherwise, an insufficient Δ
r(
t) runs off the fund to insolvency, and a reorganization plan (consisting of fixing a
δ< 0 temporarily) is mandatory, for fear of insolvency.
The policy recommendation is that the French State asks the commission for auditing; the very basis of the Marini [
11] report and of the warrant of 29 November 2006 is to control liabilities and assets together. My contribution is to recapitulate the process leading a pension fund to insolvency, to write down Equation (27) that clarifies the weight of each component in the decline of the current assets, and finally to pose the constraint that the early warning signal defined by Equation (27) must be non-negative (
ξ(
t) ≥ 0). This warning signal helps assess the chances to rescue the fund through the stock exchange, and in case that this issue is unlikely, to accelerate the decision to re-organize the plan before the amount of current assets has fallen down to low values.
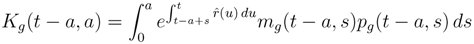
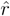 (u) is the actual interest rate at time u of assets bought for still active people. I shall use the index g to specify that the first argument of the associated function corresponds to the number of the cohort.
(u) is the actual interest rate at time u of assets bought for still active people. I shall use the index g to specify that the first argument of the associated function corresponds to the number of the cohort. 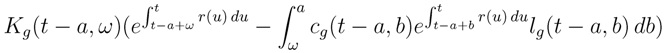
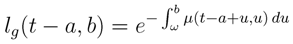
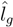 (t − a, b) as the actual survival probability and lg(t − a, b) as the expected one.
(t − a, b) as the actual survival probability and lg(t − a, b) as the expected one. 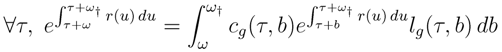
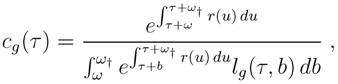
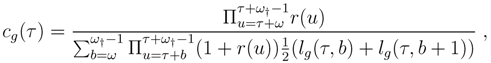
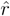 (t); the survival has been forecast as lg but its realization is
(t); the survival has been forecast as lg but its realization is 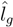 . The payment cg is stipulated in a contract, then it cannot be adjusted dynamically. To change cg, the trade unions and the management of the firm must agree on a new contract, which is hard to obtain. This happens when the plan is reorganized.
. The payment cg is stipulated in a contract, then it cannot be adjusted dynamically. To change cg, the trade unions and the management of the firm must agree on a new contract, which is hard to obtain. This happens when the plan is reorganized. = lg, and
= r. If δ > 0, it can also be non-negative if also
> r, which is exactly the bet made by financiers in a context of rising stock exchange.
Late cohorts t0− ω†, ··· ,t − ω†, where t0is the starting date of the fund, have left a deficit at time t of: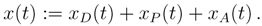
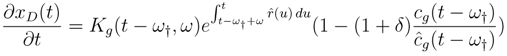
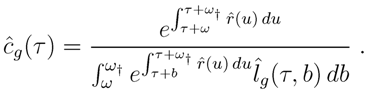
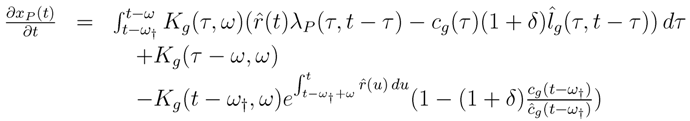
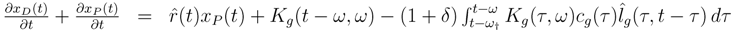
 (t)xP (t) is the interest over the debt, the second term Kg(t − ω, ω) is the capital entering the current assets for the old and the dead, and the third term multiplied by dt represents the payment of benefits between t and t + dt.
(t)xP (t) is the interest over the debt, the second term Kg(t − ω, ω) is the capital entering the current assets for the old and the dead, and the third term multiplied by dt represents the payment of benefits between t and t + dt. 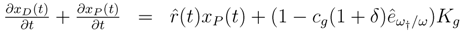

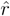 (t) = r(t),
(t) = r(t), 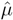 (t, a) = µ(t, a), actuarial equations imply:
(t, a) = µ(t, a), actuarial equations imply:
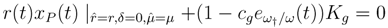
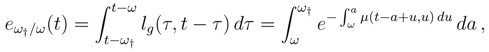
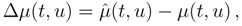
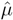 is the actual mortality rate. In the past, the variations of mortality have concerned all ages. There has not been such a thing as a mortality intensity changing at a given age and unchanged at other ages. This allows me to assume that the error on mortality forecast is approximately the same at all ages over ω:
is the actual mortality rate. In the past, the variations of mortality have concerned all ages. There has not been such a thing as a mortality intensity changing at a given age and unchanged at other ages. This allows me to assume that the error on mortality forecast is approximately the same at all ages over ω:
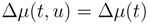
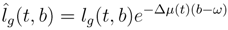
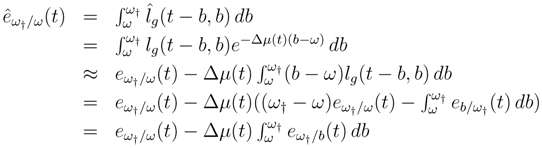
 and xP (t) at
and xP (t) at  = r and δ = 0, the variation of the amount of current assets is:
= r and δ = 0, the variation of the amount of current assets is:
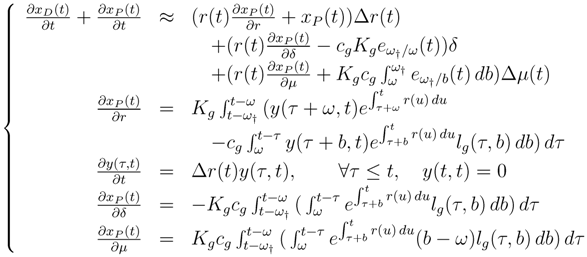
 Δr(t) vanishes, and Equation (26) boils down to:
Δr(t) vanishes, and Equation (26) boils down to:
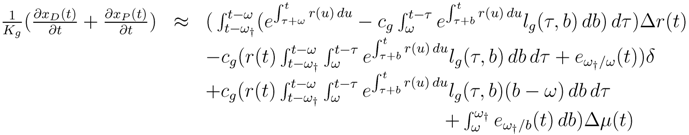
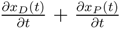 the state xD(t) + xP (t) of the current assets; it states how the stock exchange should extra-perform the actuarial rate at each date to rescue the situation endangered by the allowance of the extra bonus or by an unexpected improvement of mortality at old ages. It tells which component is responsible for the variations of xD(t) + xP (t); it allows the manager to assess his/her chances to rescue the situation in the case of a declining amount of current assets.
the state xD(t) + xP (t) of the current assets; it states how the stock exchange should extra-perform the actuarial rate at each date to rescue the situation endangered by the allowance of the extra bonus or by an unexpected improvement of mortality at old ages. It tells which component is responsible for the variations of xD(t) + xP (t); it allows the manager to assess his/her chances to rescue the situation in the case of a declining amount of current assets. behaves as an early warning signal that the pension fund has made errors that compromise its solvency in the future. The simple fact that xD + xP is decreasing is already enough to warn the manager that something is going wrong; ξ(t) specifies the importance of each error. As we shall see below, we can even estimate the values of each error Δr(t), δ, and Δµ from the follow-up of ξ(t) over four time units, a piece of information that the sole knowledge of xD(t) + xP (t) does not allow.
behaves as an early warning signal that the pension fund has made errors that compromise its solvency in the future. The simple fact that xD + xP is decreasing is already enough to warn the manager that something is going wrong; ξ(t) specifies the importance of each error. As we shall see below, we can even estimate the values of each error Δr(t), δ, and Δµ from the follow-up of ξ(t) over four time units, a piece of information that the sole knowledge of xD(t) + xP (t) does not allow.  , or:
, or:
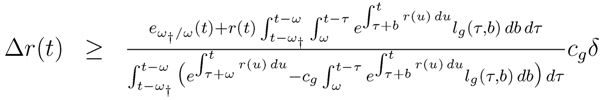
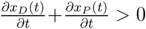 , having no knowledge really on
, having no knowledge really on 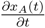 . Extra bonuses are allowed for commercial purposes, without measuring the long-term consequences on the solvency of the fund, trusting the stock exchange to fill the gap. Equation (27) or Equation (28) allow the computation of the necessary extra asset return Δr(t): if it is unrealistic, the manager had better re-organize the fund without waiting for x(t) to be low enough. The problem is that Δr(t) can be less than the threshold given by Equation (27) or Equation (28), even negative for a long period of time, as what happened during the financial crisis of 2008-2009. Then Equation (27) clearly indicates the weight of each error Δr(t), δ, and Δµ(t) in the short term. An estimate of the time to insolvency when the current assets are x(t) at time t is
. Extra bonuses are allowed for commercial purposes, without measuring the long-term consequences on the solvency of the fund, trusting the stock exchange to fill the gap. Equation (27) or Equation (28) allow the computation of the necessary extra asset return Δr(t): if it is unrealistic, the manager had better re-organize the fund without waiting for x(t) to be low enough. The problem is that Δr(t) can be less than the threshold given by Equation (27) or Equation (28), even negative for a long period of time, as what happened during the financial crisis of 2008-2009. Then Equation (27) clearly indicates the weight of each error Δr(t), δ, and Δµ(t) in the short term. An estimate of the time to insolvency when the current assets are x(t) at time t is 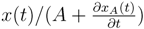 , where A is the right hand side of Equation (27).
, where A is the right hand side of Equation (27). 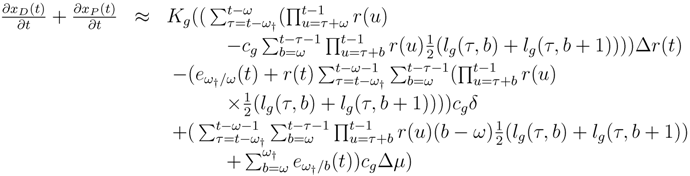
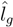 , and the lg are deduced from Δe0. The standard deviation σr of the interest rate was drawn at random from [0%, 5%], so that
, and the lg are deduced from Δe0. The standard deviation σr of the interest rate was drawn at random from [0%, 5%], so that 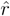 (t) was taken from a Gaussian distribution N (
(t) was taken from a Gaussian distribution N (  , σr), with
, σr), with  drawn at random from [−3%, 3%]. The error on the interest rate Δr(t) = Δr was drawn at random in [−3%, 3%],
drawn at random from [−3%, 3%]. The error on the interest rate Δr(t) = Δr was drawn at random in [−3%, 3%],  of ξ(t) over time on tmin yields:
of ξ(t) over time on tmin yields:
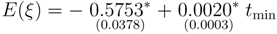
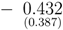 , which shows that E(ξ) is significantly negative when the pension fund is doomed to insolvency (net the effect of the capital brought by contributors in activity).
, which shows that E(ξ) is significantly negative when the pension fund is doomed to insolvency (net the effect of the capital brought by contributors in activity).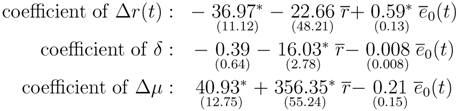
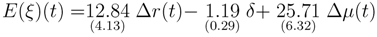
 is enough to counter-balance deficits and push x’(t) to positive values, the manager having the responsibility to lower the benefit to attain δ = 0 with the new entrants. Otherwise, an insufficient Δr(t) runs off the fund to insolvency, and a reorganization plan (consisting of fixing a δ< 0 temporarily) is mandatory, for fear of insolvency.
is enough to counter-balance deficits and push x’(t) to positive values, the manager having the responsibility to lower the benefit to attain δ = 0 with the new entrants. Otherwise, an insufficient Δr(t) runs off the fund to insolvency, and a reorganization plan (consisting of fixing a δ< 0 temporarily) is mandatory, for fear of insolvency. and the period life expectancy at time t is
.










