Abstract
In this paper, we study a three step iterative scheme to approximate fixed points of Suzuki’s generalized non-expansive mappings. We establish some weak and strong convergence results for such mappings in uniformly convex Banach spaces. Further, we show numerically that the considered iterative scheme converges faster than some other known iterations for Suzuki’s generalized non-expansive mappings. To support our claim, we give an illustrative numerical example and approximate fixed points of such mappings using Matlab program. Our results are new and generalize several relevant results in the literature.
Keywords:
Suzuki’s generalized non-expansive mappings; iterative schemes; fixed points; weak and strong convergence results; uniformly convex Banach space MSC:
47H09; 47H10; 54H25
1. Introduction
Throughout this paper, we assume that is the set of all positive integers. We consider that C is a nonempty subset of a Banach space X and , the set of all fixed points of the mapping T on C. A mapping is said to be non-expansive if , for all . It is called quasi non-expansive if and , for all and for all .
We know that is nonempty when X is uniformly convex, C is bounded closed convex subset of X and T is non-expansive mapping, (cf. [1]).
In 2008, Suzuki [2] introduced the concept of generalized non-expansive mappings which is also called condition and defined as:
A self mapping T on C is said to satisfy condition if,
Suzuki obtained existence of fixed points and convergence results for such mappings. Suzuki also showed that the notion of mappings satisfying condition is more general than the notion of non-expansive mappings.
The following example supports the above claim.
Example 1
([2]). Define a self mapping T on by
Here T satisfies Suzuki’s condition , but T is not a non-expansive mapping.
On the other hand, Banach contraction principle states that fixed point of contraction mappings can be approximated by Picard iterative scheme. In this scheme the sequence is defined as follows:
It is well known that Picard iterative scheme does not converge to a fixed point of non-expansive mappings.
Therefore, in 1953, Mann [3] introduced a new iterative scheme to approximate the fixed points of non-expansive mappings. In this iterative scheme the sequence is defined in the following manner:
where is a sequence in , satisfying appropriate conditions. It is also known that Mann iterative scheme fails to converge to fixed points of pseudo-contractive mappings.
So in 1974, Ishikawa [4] introduced a two step Mann iterative scheme to approximate fixed points of pseudo-contractive mappings, where the sequence is defined by
where and are sequences in , satisfying appropriate conditions.
Rhoades [5] made a remark on the rate of convergence of Mann and Ishikawa iterative schemes: Mann iterative scheme for decreasing functions converges faster than Ishikawa scheme. For increasing functions Ishikawa iterative scheme is better than Mann iterative scheme, also Mann iterative scheme appears to be independent of the initial guess (see also [6]).
In 2000, Noor [7] introduced the following iterative scheme for general variational inequalities. In this scheme is defined by
where , and are sequences in . He also studied the convergence criteria of this scheme. After that, in 2007, Agrawal et al. [8] introduced the following two step iterative scheme for nearly asymptotically non-expansive mappings. In this scheme is defined as follows:
where and are sequences in . They claimed that newly defined iterative scheme converges to a fixed point of contraction mappings same rate of convergence as Picard scheme but converges faster than Mann iterative scheme.
In 2014, Abbas and Nazir [9] introduced a new iterative scheme to approximate fixed points of non-expansive mappings in uniformly convex Banach space. In this scheme the sequence starting at initial guess is defined as:
where , and are sequences in . Authors showed numerically that this scheme converges to a fixed point of contraction mapping, faster than all of Picard, Mann and Agarwal iterative schemes.
In 2014, Thakur et al. [10] introduced the following iterative scheme for non-expansive mappings. In this scheme the sequence is defined as follows:
where , and are sequences in . Authors proved that this process converges to a fixed point of contraction mapping, faster than all of Picard, Mann, Ishikawa, Noor, Agarwal and Abbas and Nazir iterative schemes in the sense of Berinde [11].
Recently, Sahu et al. [12] and Thakur et al. [13] introduced the following same iterative scheme for non-expansive mappings in uniformly convex Banach space:
where , and are sequences in . Authors proved that this scheme converges to a fixed point of contraction mapping, faster than all the known iterative schemes. Also, the authors provided an example to support their claim.
In 2011, Phuengrattana [14] proved convergence results for Suzuki’s generalized non-expansive mappings by using Ishikawa iterative scheme in uniformly convex Banach spaces. Recently, fixed point theorems for Suzuki’s generalized non-expansive mappings and nonlinear mappings have been studied by a large number of researchers, e.g., see [15,16,17,18,19,20].
Motivated by the above, we prove some weak and strong convergence results using iterative scheme (8) for Suzuki’s generalized non-expansive mappings in uniformly convex Banach spaces. Our results generalize and extend the corresponding results of Sahu et al. [12], Thakur et al. [13] and many others in the literature.
2. Preliminaries
In this section, we recall following definitions, propositions and lemmas which will be used in our main results.
Definition 1.
Let C be a nonempty, closed and convex subset of a Banach space X. A mapping is called demiclosed with respect to , if for each sequence in C and each , converges weakly at x and converges strongly at y imply that .
Definition 2.
A Banach space X is said to satisfy Opial’s condition [21] if for each weakly convergent sequence to ,
holds, for all , with .
Definition 3.
Let be a bounded sequence in a Banach space X. For , we set
The asymptotic radius of relative to C is defined by
The asymptotic center of relative to C is the set
It is well known that, consists exactly one point, in the case when X is uniformly convex Banach space.
Proposition 1
([2]). Let T be a self mapping on a nonempty subset C of a Banach space X.
- (i)
- If T is non-expansive then T satisfies the condition .
- (ii)
- Every mapping satisfying condition with a fixed point is quasi non-expansive.
- (iii)
- If T satisfies condition , then
Lemma 1
([2]). Let T be a self mapping on a subset C of a Banach space X with the Opial’s property. Assume that T satisfies condition . If converges weakly to z and , then . That is, is demiclosed at zero.
Lemma 2
([2]). Let T be a self map on a weakly compact convex subset C of a uniformly convex Banach space X. Assume that T satisfies condition , then T has a fixed point.
Lemma 3
([22]). Suppose X is uniformly convex Banach space and for all . Let and be two sequences in X such that , and holds, for some . Then .
3. Main Results
In this section, we prove some weak and strong convergence theorems using iterative scheme (8) for Suzuki’s generalized non-expansive mappings in uniformly convex Banach spaces. First, we obtain following useful lemmas to be use in next theorems.
Lemma 4.
Let C be a nonempty, closed and convex subset of a uniformly convex Banach space X and let be a Suzuki’s generalized non-expansive mapping with . Let be a sequence defined by iterative scheme (8), then exists for all .
Proof.
Let and . Since T satisfies condition , therefore by Proposition 1, T is quasi non-expansive mapping. That is,
Now from iterative scheme (8), we get
And
This shows that the sequence is non-increasing and bounded below for all . Hence, exists. □
Lemma 5.
Let C be a nonempty, closed and convex subset of a uniformly convex Banach space X and let be a Suzuki’s generalized non-expansive mapping. Let be a sequence defined by iterative scheme (8). Then if and only if is bounded and .
Proof.
By Lemma 4, exists and is bounded. Put
Since T satisfies condition , we have
Similarly,
Again,
Now,
Taking the lim inf on both sides, we get
Thus,
Conversely, assume that is bounded and . Let , by Proposition 1, we have
⇒. Since X is uniformly convex, is singleton, hence we have . □
Theorem 1.
Let C be a nonempty, closed and convex subset of a uniformly convex Banach space X and let be a Suzuki’s generalized non-expansive mapping. Let be a sequence defined by iterative scheme (8). Assume that X satisfies Opial’s condition, then converges weakly to a point of .
Proof.
Let , then exists by Lemma 4. Now we prove that has unique weak sub-sequential limit in . Let x and y be weak limits of the subsequences and of respectively. From Lemma 5, and is demiclosed at zero by Lemma 1. This implies that ⇒, similarly .
Next we show uniqueness. If , then by using Opial’s condition,
This is a contradiction, so . Consequently, converges weakly to a point of . □
Theorem 2.
Let C be a nonempty, closed and convex subset of a uniformly convex Banach space X and let be a Suzuki’s generalized non-expansive mapping. Let be a sequence defined by iterative scheme (8). Then converges to a point of if and only if or , where .
Proof.
Necessity is obvious.
Conversely, assume that . From Lemma 4, exists, for all therefore by assumption. We show that is a Cauchy sequence in C. As , for given , there exists such that for all ,
In particular, . Therefore there exists such that
Now for ,
This shows that is a Cauchy sequence in C. As C is closed subset of a Banach space X, so that there exists a point such that . Now gives that . □
Theorem 3.
Let C be a nonempty, compact and convex subset of a uniformly convex Banach space X, and let T and be as in Lemma 5, then the sequence converges strongly to a fixed point of T.
Proof.
By Lemma 2, , so by Lemma 5, we have . Since C is compact, there exists a subsequence of such that strongly for some . By Proposition 1, we have
Letting , we get that . This implies that i.e., . Also, exists by Lemma 4. Thus p is the strong limit of the sequence itself. □
Senter and Dotson [23] introduced the notion of mapping satisfying condition (I) which is defined as follows.
Definition 4.
A self map T on C is said to satisfy condition , if there is a nondecreasing function with and , ∀ such that , for all , where .
Now we also prove a strong convergence result using condition .
Theorem 4.
Let C be a nonempty, closed and convex subset of a uniformly convex Banach space X and let be a Suzuki’s generalized non-expansive mapping satisfying condition . Then the sequence defined by iterative scheme (8) converges strongly to a fixed point of T.
Proof.
We proved in Lemma 5 that
From condition and (22), we get
Since is a nondecreasing function satisfying , hence we have
Now all the conditions of Theorem 2 are satisfied, therefore by its conclusion converges strongly to a fixed point of T. □
Remark 1.
All the results in this paper generalize the corresponding results of Sahu et al. [12], Thakur et al. [13] and many others because mappings here are generalized non-expansive and iterative scheme is more general than the others.
Now, we furnish the following example to support our results.
Example 2.
Define a self mapping T on by
Here T is a Suzuki’s generalized non-expansive mapping, but T is not a non-expansive.
Verification. Take and , then
And
Hence T is not a non-expansive mapping.
Now we verify that T is a Suzuki’s generalized non-expansive mapping.
Here following cases arise:
Case I. If either or . Then in both the cases T is non-expansive mapping and hence T is Suzuki’s generalized non-expansive mapping.
Case II. Let . Then . For , we must have ⇒ and hence . Now,
And
Hence ⇒.
Case III. Let . Then . For , we must have , which gives two possibilities:
(a) Let , then , i.e., ⇒ So
Hence ⇒.
(b) Let , then , i.e., ⇒ and , so . Since and ⇒. Since and is already included in Case I. Therefore consider, and . Then
And
Hence ⇒.
Thus T is Suzuki’s generalized non-expansive mapping.
With help of Matlab Program Software, we obtain the comparison Table 1 and Figure 1 for various iterative schemes with control sequences , , and initial guess .

Table 1.
A comparison table of iterative schemes.
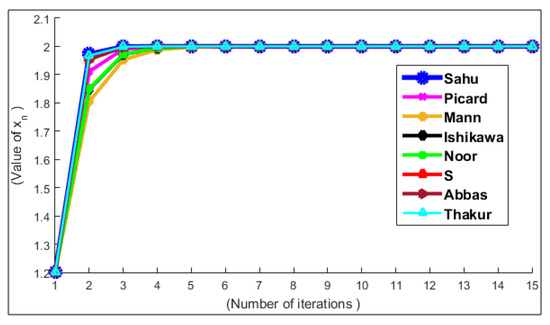
Figure 1.
Convergence behavior of Sahu iterative scheme with other iterative schemes.
Remark 2.
The iterative scheme (8) converges faster than the Picard, Mann, Ishikawa, Noor, Agarwal, Abbas and Thakur iterative schemes for Suzuki’s generalized non-expansive mappings as shown in the above table and figure. The class of Suzuki’s generalized non-expansive mappings is bigger than the class of non-expansive mappings as shown in the Example 2.
Author Contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to the anonymous referees for their valuable comments and suggestions which improve the paper. The second author is grateful to Council of Scientific and Industrial Research (CSIR), India, for providing the Senior Research Fellowship under the grant (09/112(0536)/2016-EMR-I).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Browder, F.E. Non-expansive nonlinear operators in a Banach space. Proc. Natl. Acad. Sci. USA 1965, 54, 1041–1044. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T. Fixed point theorems and convergence theorems for some generalized non-expansive mappings. J. Math. Anal. Appl. 2008, 340, 1088–1095. [Google Scholar] [CrossRef]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Ishikawa, S. Fixed points by a new iteration method. Proc. Am. Math. Soc. 1974, 44, 147–150. [Google Scholar] [CrossRef]
- Rhoades, B. Some fixed point iteration procedures. Int. J. Math. Math. Sci. 1991, 14, 1–16. [Google Scholar] [CrossRef]
- Rhoades, B. Fixed point iterations using infinite matrices, III. Constr. Comput. Method. Differ. Integral Equ. 1974, 430. [Google Scholar] [CrossRef]
- Noor, M.A. New approximation schemes for general variational inequalities. J. Math. Anal. Appl. 2000, 251, 217–229. [Google Scholar] [CrossRef]
- Agrawal, R.P.; O’Regan, D.; Sahu, D.R. Iterative construction of fixed points of nearly asymptotically non-expansive mappings. J. Nonlinear Convex Anal. 2007, 8, 61–79. [Google Scholar]
- Abbas, M.; Nazir, T. A new faster iteration process applied to constrained minimization and feasibility problems. Mater. Vesn. 2014, 66, 223–234. [Google Scholar]
- Thakur, D.; Thakur, B.S.; Postolache, M. New iteration scheme for numerical reckoning fixed points of non-expansive mappings. J. Inequal. Appl. 2014, 328. [Google Scholar] [CrossRef]
- Berinde, V. Picard iteration converges faster than Mann iteration for a class of quasi-contractive operators. Fixed Point Theory Appl. 2004, 2, 97–105. [Google Scholar] [CrossRef]
- Sahu, V.K.; Pathak, H.K.; Tiwari, R. Convergence theorems for new iteration scheme and comparison results. Aligarh Bull. Math. 2016, 35, 19–42. [Google Scholar]
- Thakur, B.S.; Thakur, D.; Postolache, M. New iteration scheme for approximating fixed point of non-expansive mappings. Filomat 2016, 30, 2711–2720. [Google Scholar] [CrossRef]
- Phuengrattana, W. Approximating fixed points of Suzuki’s generalized non-expansive mappings. Nonlinear Anal. Hybrid Syst. 2011, 5, 583–590. [Google Scholar] [CrossRef]
- Kassab, W.; Turcanu, T. Numerical reckoning fixed points of (ρE)-type mappings in modular vector spaces. Mathematics 2019, 7, 390. [Google Scholar] [CrossRef]
- Dhomphongsa, S.; Inthakon, W.; Kaewkhao, A. Edelstein’s method and fixed point theorems for some generalized non-expansive mappings. J. Math. Anal. Appl. 2009, 350, 12–17. [Google Scholar] [CrossRef]
- Garcia-Falset, J.; Llorens-Fuster, E.; Suzuki, T. Fixed point theory for a class of generalized non-expansive mappings. J. Math. Anal. Appl. 2011, 375, 185–195. [Google Scholar] [CrossRef]
- Uddin, I.; Imdad, M.; Ali, J. Convergence theorems for a hybrid pair of generalized non-expansive mappings in Banach spaces. Bull. Malay. Math. Sci. 2015, 38, 695–705. [Google Scholar] [CrossRef]
- De la Sen, M.; Abbas, M. On best proximity results for a generalized modified Ishikawa’s iterative scheme driven by perturbed 2-cyclic like-contractive self-maps in uniformly convex Banach spaces. J. Math. 2019, 2019, 1356918. [Google Scholar] [CrossRef]
- Thakur, B.S.; Thakur, D.; Postolache, M. A new iterative scheme for numerical reckoning fixed points of Suzuki’s generalized non-expansive mappings. Appl. Math. Comp. 2016, 275, 147–155. [Google Scholar] [CrossRef]
- Opial, Z. Weak convergence of the sequence of successive approximations for non-expansive mappings. Bull. Am. Math. Soc. 1967, 73, 595–597. [Google Scholar] [CrossRef]
- Schu, J. Weak and strong convergence to fixed points of asymptotically non-expansive mappings. Bull. Aust. Math. Soc. 1991, 43, 153–159. [Google Scholar] [CrossRef]
- Senter, H.F.; Dotson, W.G. Approximating fixed points of non-expansive mappings. Proc. Am. Math. Soc. 1974, 44, 375–380. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).