Bifurcation and Stability Analysis of a System of Fractional-Order Differential Equations for a Plant–Herbivore Model with Allee Effect

Abstract

This article concerns establishing a system of fractional-order differential equations (FDEs) to model a plant–herbivore interaction. Firstly, we show that the model has non-negative solutions, and then we study the existence and stability analysis of the constructed model. To investigate the case according to a low population density of the plant population, we incorporate the Allee function into the model. Considering the center manifold theorem and bifurcation theory, we show that the model shows flip bifurcation. Finally, the simulation results agree with the theoretical studies.

1. Introduction

Mathematical modeling for various biological problems is considered to be an exciting research area in the discipline of applied mathematics. In the literature, many biological phenomena were modeled and formulated mathematically [1,2,3,4,5,6]. For example, Liu and Xiao established a predator–prey system in discrete time to analyze the local stability and the bifurcation of solutions around the positive equilibrium point [4]. Kangalgil and Kartal analyzed the host–parasite model that led to a system of differential equations of piecewise constant arguments at specific time t, as well as the stability of all obtained equilibrium points; they showed the conditions of flip and Neimark–Sacker bifurcation [6]. Most of these studies are restricted to integer-order differential equations or differential equations with piecewise constant arguments. However, it was seen that many problems in biology, as well as in other fields such as engineering, finance, and economics, could be formulated successfully using fractional-order differential equations [1,5,7,8,9,10,11,12,13].

The nonlocal property of fractional-order models not only depends on the current state but also depends on its prior historical states [14]. The transformation of an integer-order model into a fractional-order model needs to be precise with respect to the order of differentiation $\alpha$. However, a small change in $\alpha$ may cause a big change in the behavior of the solutions [15].

Fractional-order differential equations can model complex biological phenomena with non-linear behavior and long-term memory, which cannot be represented mathematically by integer-order differential equations (IDEs) [16,17]. For example, Bozkurt established the glioblastoma multiforme (GBM)–immune system (IS) interaction using a fractional-order differential equation system to include the delay time (memory effect) [5].

In general, the origin of plant–herbivore interactions is derived from predator–prey systems [18,19], which is described in many studies using discrete and continuous time [6,20,21,22,23]. The usual discrete host–parasite models have the form

$$\{\begin{array}{c}{P}_{n+1}=\mu P_n·f\left(P_n,H_n\right)\\ H_{n+1}=c\mu P_n\left(1-f\left(P_n,H_n\right)\right),\end{array}$$

(1)

where $P$ and $H$ are the densities of the host (a plant) and the parasite (a herbivore), $\mu$ is the host’s inherent rate of increase $(\mu =e^r$ where $r$ is the intrinsic rate of increase) in the absence of the parasites, $c$ is the biomass conversion constant, and $f$ is the function defining the fractional survival of hosts from parasitism [21].

In Reference [23], the authors considered a system of differential equations of plant–herbivore interactions as follows:

$$\{\begin{array}{c}\frac{dx}{dt}=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\alpha x\left(t\right)y\left(t\right)\\ \frac{dy}{dt}=-sy\left(t\right)+\beta x\left(t\right)y\left(t\right).\end{array}$$

(2)

Kartal in Reference [20] generalized the system in Equation (2) by combining discrete and continuous time as follows:

$$\{\begin{array}{c}\frac{dx}{dt}=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\alpha x\left(t\right)y(⟦t⟧)\\ \frac{dy}{dt}=-sy\left(t\right)+\beta x(⟦t⟧)y\left(t\right),\end{array}$$

(3)

where $x\left(t\right)$ and $y\left(t\right)$ denote the populations of the plant and herbivore, respectively, $⟦t⟧$ is the integer part of $t\in [0,\infty )$ and the parameters belonging to $R^{+}$, $r$ is the growth rate, $K$ is the carrying capacity, and $\alpha$ is the predation rate of the plant species, while $s$ and $\beta$ represent the death rate and conversion factor of the herbivores, respectively.

In our study, we consider a model as a system of FDEs as follows:

$$\{\begin{array}{c}{D}^{\alpha }x\left(t\right)=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\gamma f\left(t\right)y\left(t\right)\\ D^{\alpha }y\left(t\right)=\beta f\left(t\right)y\left(t\right)-dy\left(t\right),\end{array}$$

(4)

where $f\left(t\right)$ represents the Holling type II function given by

$$f\left(t\right)=\frac{e·\sigma ·x\left(t\right)}{1+h·e·\sigma ·x\left(t\right)}.$$

(5)

In Equation (4), $r$ is the growth rate of the plant population, $K$ denotes the carrying capacity, $\gamma$ denotes the predation rate of the plant species, $\beta$ is the conversion of consumed plant biomass into new herbivore biomass, and $d$ is the per capita rate of death. In Equation (5), $e$ is the encounter rate, which depends on the movement velocity of the herbivore species. The parameter $\sigma$ $(0<\sigma \le 1)$ is the fraction of food items encountered that the herbivore ingests, while $h$ is the handling time for each prey item, which incorporates the time required for the digestive tract to handle the item.

Definition 1.

[24] Let $f:R^{+}\to R$ be a function, where the fractional integral of order$\alpha >0$is given by

$$I_0^{\alpha }f\left(x\right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{{\displaystyle \int }}_0^x{\left(x-t\right)}^{\alpha -1}f\left(t\right)dt,$$

(6)

provided the right side is pointwise defined on$R^{+}.$

Definition 2.

[24] Let $f:R^{+}\to R$ be a continuous function. The Caputo fractional derivative of order $\alpha \in \left(n-1, n\right)$ is given by

$$D^{\alpha }f\left(x\right)=I_0^{n-\alpha }f\left(x\right)D^{n}f\left(x\right), D=\frac{d}{dt}.$$

(7)

2. Stability Analysis

2.1. Equilibrium Points

Let us consider the system

$$\{\begin{array}{c}{D}^{\alpha }x\left(t\right)=f\left(x\left(t\right),y\left(t\right)\right)=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\gamma f\left(t\right)y\left(t\right)\\ D^{\alpha }y\left(t\right)=g\left(x\left(t\right),y\left(t\right)\right)=\beta f\left(t\right)y\left(t\right)-dy\left(t\right).\end{array}$$

(8)

We want to discuss the stability of the system in Equation (8). Let us perturb the equilibrium point by adding ${\epsilon }_1\left(t\right)>0$ and ${\epsilon }_2\left(t\right)>0$, that is

$$x\left(t\right)-\overline{x}={\epsilon }_1\left(t\right)\mathrm{and}y\left(t\right)-\overline{y}={\epsilon }_2\left(t\right).$$

(9)

Thus, we have

$$D^{\alpha }\left({\epsilon }_1\left(t\right)\right)\simeq f\left(\overline{x},\overline{y} \right)+\frac{\partial f\left(\overline{x},\overline{y} \right)}{\partial x}{\epsilon }_1\left(t\right)+\frac{\partial f\left(\overline{x},\overline{y} \right)}{\partial y}{\epsilon }_2\left(t\right),$$

(10)

and

$$D^{\alpha }\left({\epsilon }_2\left(t\right)\right)\simeq g\left(\overline{x},\overline{y} \right)+\frac{\partial g\left(\overline{x},\overline{y} \right)}{\partial x}{\epsilon }_1\left(t\right)+\frac{\partial g\left(\overline{x},\overline{y} \right)}{\partial P}{\epsilon }_2\left(t\right).$$

(11)

Using the fact $f\left(\overline{x},\overline{y} \right)=g\left(\overline{x},\overline{y} \right)=0,$ we obtain a linearized system about $\left(\overline{x},\overline{y}\right)$ such as

$${\mathrm{D}}^{\mathsf{\alpha }}\mathrm{Z}=\mathrm{JZ},$$

(12)

where $Z=\left({\epsilon }_1\left(t\right),{\epsilon }_2\left(t\right)\right)$, and J is the Jacobian matrix evaluated at the point $\left(\overline{x},\overline{y}\right)$,

$$J={\left(\begin{array}{cc}\frac{\partial f\left(\overline{x},\overline{y} \right)}{\partial x}& \frac{\partial f\left(\overline{x},\overline{y} \right)}{\partial y}\\ \frac{\partial g\left(\overline{x},\overline{y} \right)}{\partial x}& \frac{\partial g\left(\overline{x},\overline{y} \right)}{\partial y}\end{array}\right)|}_{\left(x\left(t\right),y\left(t\right)\right)=\left(\overline{x},\overline{y}\right)}.$$

(13)

We have $B^{-1}JB=C$, where C is a diagonal matrix of J given by

$$C=\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right],$$

(14)

where ${\lambda }_1$ and ${\lambda }_2$ are the eigenvalues and B represents the eigenvectors of J. Therefore, we get

$$\{\begin{array}{c}{D}_{*}^{\alpha }{\eta }_1={\lambda }_1{\eta }_1\\ D_{*}^{\alpha }{\eta }_2={\lambda }_2{\eta }_2\end{array},\mathrm{where}\eta =\left[\begin{array}{c}{\eta }_1\\ {\eta }_2\end{array}\right]\mathrm{and}\eta =B^{-1}Z,$$

(15)

whose solutions are given by the following Mittag–Leffler functions:

$${\eta }_1\left(t\right)={\displaystyle \sum }_{n=0}^{\infty }\frac{{\left({\lambda }_1\right)}^n{t}^{n\alpha }}{\mathsf{\Gamma }\left(n\alpha +1\right)}{\eta }_1\left(0\right)=E_{\alpha }\left({\lambda }_1{t}^{\alpha }\right){\eta }_1\left(0\right),$$

(16)

and

$${\eta }_2\left(t\right)={\displaystyle \sum }_{n=0}^{\infty }\frac{{\left({\lambda }_2\right)}^n{t}^{n\alpha }}{\mathsf{\Gamma }\left(n\alpha +1\right)}{\eta }_2\left(0\right)=E_{\alpha }\left({\lambda }_2{t}^{\alpha }\right){\eta }_2\left(0\right).$$

(17)

Using the result of Reference [25], if $\left|arg\left({\lambda }_1\right)\right|>\frac{\alpha \pi }{2}$ and $\left|arg\left({\lambda }_2\right)\right|>\frac{\alpha \pi }{2},$ then ${\eta }_1\left(t\right)$ and ${\eta }_2\left(t\right)$ are decreasing; consequently, ${\epsilon }_1\left(t\right)$ and ${\epsilon }_2\left(t\right)$ are decreasing. Let the solution $\left({\epsilon }_1\left(t\right),{\epsilon }_2\left(t\right)\right)$ of Equation (12) exist. If the solution of Equation (12) is increasing, then $\left(\overline{x},\overline{y}\right)$ is unstable; otherwise, if $\left({\epsilon }_1\left(t\right),{\epsilon }_2\left(t\right)\right)$ is decreasing, then $\left(\overline{x},\overline{y}\right)$ is locally asymptotically stable. The equilibrium points of the system in Equation (8) are

$${\mathsf{\Lambda }}_1=\left(0,0\right),{\mathsf{\Lambda }}_2=\left(K,0\right),\mathrm{and}{\mathsf{\Lambda }}_3=\left(\frac{d}{e·\sigma ·\left(\beta -hd\right)},\frac{r\beta \left(Ke\sigma \left(\beta -hd\right)-d\right)}{e^2{\sigma }^2\gamma K{\left(\beta -hd\right)}^2}\right),$$

where $\beta >hd$ and $K>\frac{d}{e\sigma \left(\beta -hd\right)}$.

2.2. Local Stability

The Jacobian matrix for the system in Equation (8) is given as

$$J\left(\overline{x},\overline{y}\right)=\left(\begin{array}{cc}r-\frac{2r\overline{x}}{K}-\frac{\gamma ·e·\sigma ·\overline{y}}{{\left(1+h·e·\sigma ·\overline{x}\right)}^2}& -\frac{\gamma ·e·\sigma ·\overline{x}}{1+h·e·\sigma ·\overline{x}}\\ \frac{\beta ·e·\sigma ·\overline{y}}{{\left(1+h·e·\sigma ·\overline{x}\right)}^2}& \frac{\beta ·e·\sigma ·\overline{x}}{1+h·e·\sigma ·\overline{x}}-d\end{array}\right).$$

(18)

For ${\mathsf{\Lambda }}_1=\left(0,0\right),$ we have the characteristic equation

$$\left(-{\lambda }_1-d\right)\left(r-{\lambda }_2\right)=0⟹{\lambda }_1=-d\mathrm{and}{\lambda }_2=r.$$

Theorem 1.

Let ${\Lambda }_1=\left(0,0\right)$ be the extinction point of the system in Equation (8). Then, the equilibrium point ${\Lambda }_1$ of the system in Equation (8) is a saddle point.

For the case where only the plant population exists, we consider the equilibrium point ${\mathsf{\Lambda }}_2=\left(\mathrm{K},0\right).$ The characteristic equation around ${\mathsf{\Lambda }}_2$ is as follows:

$$\left(-r-{\lambda }_1\right)·\left(\frac{\beta e\sigma K}{1+he\sigma K}-d-{\lambda }_2\right)=0.$$

(19)

Theorem 2.

Assume that ${\Lambda }_2=\left(K,0\right)$ is the equilibrium point of the system in Equation (8). Then, the following statements are true:

(i) 

For $r>0$, if $d>\frac{\beta e\sigma K}{1+he\sigma K}$, then ${\Lambda }_2$ is locally asymptotically stable;

(ii) 

For $r>0$, if $d<\frac{\beta e\sigma K}{1+he\sigma K},$ then ${\Lambda }_2$ is an unstable saddle point.

To discuss the local stability of ${\mathsf{\Lambda }}_3=\left(\frac{\mathrm{d}}{\mathrm{e}·\mathsf{\sigma }·\left(\mathsf{\beta }-\mathrm{hd}\right)},\frac{\mathrm{r}\mathsf{\beta }\left(\mathrm{Ke}\mathsf{\sigma }\left(\mathsf{\beta }-\mathrm{hd}\right)-\mathrm{d}\right)}{{\mathrm{e}}^2{\mathsf{\sigma }}^2\mathsf{\gamma }\mathrm{K}{\left(\mathsf{\beta }-\mathrm{hd}\right)}^2}\right),$ which means a plant–herbivore interaction exists, we consider the linearized system of the system in Equation (8) at ${\mathsf{\Lambda }}_3.$ From the Jacobian matrix $\mathrm{J}\left({\mathsf{\Lambda }}_3\right)$ of Equation (8),

$$J\left({\mathsf{\Lambda }}_3\right)=\left(\begin{array}{cc}r\left(1-\frac{2d}{e\sigma K\left(\beta -hd\right)}-\frac{Ke\sigma \left(\beta -hd\right)-d}{e\sigma K\beta }\right)& -\frac{\gamma d}{\beta }\\ \frac{r\left(Ke\sigma \left(\beta -hd\right)-d\right)}{e\sigma K\gamma }& 0\end{array}\right),$$

(20)

we obtain the characteristic equation

$${\lambda }^2+A_1\lambda +A_2=0,$$

(21)

where

$$A_1=r\left(\frac{2d}{e\sigma K\left(\beta -hd\right)}+\frac{Ke\sigma \left(\beta -hd\right)-d}{e\sigma K\beta }-1\right)\mathrm{and}{A}_2=\frac{rd\left(Ke\sigma \left(\beta -hd\right)-d\right)}{e\sigma K\beta }.$$

By considering Equation (21), we obtain the theorem below.

Theorem 3.

Let the system in Equation (8) have a positive equilibrium point${\Lambda }_3.$ Then, the following statements are true:

(i) 

Assume that $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)}$ and $d>\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$, where $hKe\sigma >1$. If

$$r>2\beta \left(\beta -hd\right)\left(\frac{2de\sigma K\beta +\left(Ke\sigma \left(\beta -hd\right)-d\right)\left(e\sigma K\left(\beta -hd\right)+2de\sigma K-2d\right)}{4d^2{\beta }^2+{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2{\left(\beta -hd\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}\right),$$

then we either attain real or complex conjugates roots with negative real parts, where $\left|arg\left(\lambda \right)\right|$ > $\frac{\alpha \pi }{2}$ is equivalent to the Routh–Hurwitz case. Thus, ${\Lambda }_3$ is locally asymptotically stable;

(ii) 

Assume that $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)}$ and $d<\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$, where $hKe\sigma >1$. If

$$r<2\beta \left(\beta -hd\right)\left(\frac{2de\sigma K\beta +\left(Ke\sigma \left(\beta -hd\right)-d\right)\left(e\sigma K\left(\beta -hd\right)+2de\sigma K\left(\beta -hd\right)-2d\right)}{4d^2{\beta }^2+{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2{\left(\beta -hd\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}\right),$$

then we attain complex conjugates with positive real parts and

$$\left|ta{n}^{-1}\left(\sqrt{\frac{4de\sigma K\beta \left(Ke\sigma \left(\beta -hd\right)-d\right){\left(\beta -hd\right)}^2}{r{\left(2d\beta -e\sigma K\beta \left(\beta -hd\right)+\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)\right)}^2}-1}\right)\right|>\frac{\alpha \pi }{2},$$

(22)

which implies that ${\Lambda }_3$ is locally asymptotically stable.

Proof. 

(i) 

Let us consider the case where $\mathsf{\Delta }={\left(A_1\right)}^2-4A_2>0$. From

$$\begin{array}{c}r\left(\frac{4d^2{\beta }^2+{\left(\beta -hd\right)}^2{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}{e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}\right)\hfill \\ +2\left(\frac{2d\left(Ke\sigma \left(\beta -hd\right)-d\right)-2de\sigma K\beta -e\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-2de\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)}{e^2{\sigma }^2{K}^2\beta \left(\beta -hd\right)}\right)\hfill \\ >0,\hfill \end{array}$$

we have

$$r>2\beta \left(\beta -hd\right)\left(\frac{2de\sigma K\beta +\left(Ke\sigma \left(\beta -hd\right)-d\right)\left(e\sigma K\left(\beta -hd\right)+2de\sigma K\left(\beta -hd\right)-2d\right)}{4d^2{\beta }^2+{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2{\left(\beta -hd\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}\right),$$

(23)

where $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)} .$ Furthermore, computations show that, for

$$2d\beta +\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-e\sigma K\left(\beta -hd\right)\beta >0,$$

(24)

we obtain $d>\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$, where $hKe\sigma >1$. In this case, we have $A_1>0$.

Since $K>\frac{d}{e\sigma \left(\beta -hd\right)}$, it is obvious that $A_2>0$. This completes the proof of (i).

(ii) 

Let us consider the case, where $\mathsf{\Delta }={\left(A_1\right)}^2-4A_2<0$. In this case, we have

$$r<2\beta \left(\beta -hd\right)·(\frac{2de\sigma K\beta +\left(Ke\sigma \left(\beta -hd\right)-d\right)\left(e\sigma K\left(\beta -hd\right)+2de\sigma K\left(\beta -hd\right)-2d\right)}{4d^2{\beta }^2+{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2{\left(\beta -hd\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2})$$

(25)

where $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)}.$

Furthermore, if

$$2d\beta +\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-e\sigma K\left(\beta -hd\right)\beta <0,$$

(26)

then $d<\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$ and $hKe\sigma >1$, which implies that $A_1<0$.

This completes the proof of the theorem. □

Example 1.

In this section, we analyze the stability conditions for the system in Equation (8) that shows a plant–herbivore model with fractional-order differential equations. The values of the parameters are $K=10, e\sigma =1.2, h=1, d=0.00175, \beta =1.5,$ and $\gamma =1$, where the order of the system is $\alpha =0.9$. In Figure 1, we obtain the bifurcation structure of the system in Equation (8) for the initial values $\left(x_0,y_0\right)=\left(0.6, 0.75\right)$, where the blue graph represents the plant population, and the red graph denotes the herbivore population. Obviously, an increase in the plant population allows the herbivore population to increase. After that, an interaction between both populations occurs. Figure 2 is the per capita for each population, which shows that, after a specific capacity of the habitat, the herbivore population will not be able to find enough food, and this may lead to death or migration.

3. Existence and Uniqueness

Considering the system in Equation (8) with initial conditions $x\left(0\right)>0$ and $y\left(0\right)>0$, the initial value problem can be written in the form

$$D^{\alpha }U\left(t\right)=AU\left(t\right)+x\left(t\right)BU\left(t\right)+y\left(t\right)CU\left(t\right), t\in (0,T].$$

(27)

$U\left(0\right)=U_0,$ where $U\left(t\right)=\left[\begin{array}{c}x\left(t\right)\\ y\left(t\right)\end{array}\right]$ and $U\left(0\right)=\left[\begin{array}{c}x\left(0\right)\\ y\left(0\right)\end{array}\right]$. Let us assume $x\left(0\right)\ge a$ and $y\left(0\right)>0$ when $t>\sigma \ge 0$. In this case, the initial value problem can be written as

$$D^{\alpha }U\left(t\right)=\left[\begin{array}{cc}r& 0\\ 0& -d\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ y\left(t\right)\end{array}\right]+x\left(t\right)\left[\begin{array}{cc}-\frac{r}{K}& 0\\ 0& \frac{\beta e\sigma }{1+he\sigma a}\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ y\left(t\right)\end{array}\right]+y\left(t\right)\left[\begin{array}{cc}-\frac{\gamma e\sigma }{1+he\sigma a}& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ y\left(t\right)\end{array}\right].$$

(28)

Definition 3.

Assume that $C^{*}\left[0, T\right]$ is the class of continuous column vector $U\left(t\right)$ whose components $x\left(t\right), y\left(t\right)\in C\left[0, T\right]$ are the class of continuous functions on $\left[0, T\right].$ The norm of $U\in C^{*}\left[0, T\right]$ is given by $\Vert U\Vert =\underset{t}{sup}\left|e^{-Nt}x\left(t\right)\right|+\underset{t}{sup}\left|e^{-Nt}y\left(t\right)\right|.$ When $t>\sigma \ge 0,$ we write $C_{\sigma }^{*}\left[0, T\right]$ and $C_{\sigma }\left[0, T\right]$.

Definition 4.

$U\in C^{*}\left[0, T\right]$ is a solution of the initial value problem in Equation (27) if (i) and (ii) hold.

(i) 

$\left(t, U\left(t\right)\right)\in D,$$t\in \left[0, T\right]$, where $D=\left[0,T\right]\times K, K=\left\{\left(x\left(t\right), y\left(t\right)\right):a<x\left(t\right)\le \overline{a} , \left| y\left(t\right)\right|\le b \right\};$

(ii) 

$U\left(t\right)$ satisfies Equation (27).

If Definition 4 holds, we obtain the theorem below.

Theorem 4.

Let $U\in C^{*}\left[0, T\right]$ be a solution of the initial value problem given in Equation (27). Then, $U$ is a unique solution for Equation (27).

Proof. 

Let us write

$$I^{1-\alpha }\frac{d}{dt}U\left(t\right)=AU\left(t\right)+x\left(t\right)BU\left(t\right)+y\left(t\right)CU\left(t\right).$$

(29)

Operating with $I^{\alpha }$, we obtain

$$U\left(t\right)=U\left(0\right)+I^{\alpha }\left(AU\left(t\right)+x\left(t\right)BU\left(t\right)+y\left(t\right)CU\left(t\right)\right).$$

(30)

Now, let $F:C^{*}\left[0,T\right]$ $\to C^{*}\left[0,T\right]$ be defined by

$$FU\left(t\right)=U\left(0\right)+I^{\alpha }\left(AU\left(t\right)+x\left(t\right)BU\left(t\right)+y\left(t\right)CU\left(t\right)\right).$$

(31)

Then,

$$\begin{array}{ll}{e}^{-Nt}\Vert FU-FV\Vert \hfill & =e^{-Nt}{I}^{\alpha }\left(A\left(U\left(t\right)-V\left(t\right)\right)+x\left(t\right)B\left(U\left(t\right)-V\left(t\right)\right)+y\left(t\right)C\left(U\left(t\right)-V\left(t\right)\right)\right)\hfill \\ & \le \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{{\displaystyle \int }}_0^t{\left(t-s\right)}^{\alpha -1}{e}^{-N\left(t-s\right)}\left(U\left(s\right)-V\left(s\right)\right)e^{-Ns}\left(A+\overline{a} B+bC\right)\hfill \\ & \le \frac{\left(A+\overline{a} B+bC\right)}{N^{\alpha }}\Vert U-V\Vert {{\displaystyle \int }}_0^t\frac{s^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}ds.\hfill \end{array}$$

This implies that $\Vert FU-FV\Vert \le \frac{\left(A+\overline{a} B+bC\right)}{N^{\alpha }}\Vert U-V\Vert .$ If we choose $N$ such that $N^{\alpha }>A+\overline{a} B+bC,$ then we obtain $\Vert FU-FV\Vert \le \Vert U-V\Vert$, and the operator $F$ given by Equation (31) has a unique fixed point.

Consequently, Equation (30) has a unique solution $U\in C^{*}\left[0, T\right].$ From (30), we have

$$\begin{array}{cc}U\left(t\right)\hfill & =U\left(0\right)+\left(\frac{t^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}\left(AU\left(0\right)+x\left(0\right)BU\left(0\right)+y\left(0\right)CU\left(0\right)\right)\right)\hfill \\ & +I^{\alpha +1}\left(A{U}^{\prime }\left(t\right)+x^{\prime }\left(t\right)BU\left(t\right)+x\left(t\right)B{U}^{\prime }\left(t\right)+y^{\prime }\left(t\right)CU\left(t\right)+y\left(t\right)CU’\left(t\right)\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\frac{U\left(t\right)}{dt}\hfill & =\frac{t^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}\left(AU\left(0\right)+x\left(0\right)BU\left(0\right)+y\left(0\right)CU\left(0\right)\right)\hfill \\ & +I^{\alpha }\left(A{U}^{\prime }\left(t\right)+x^{\prime }\left(t\right)BU\left(t\right)+x\left(t\right)B{U}^{\prime }\left(t\right)+y^{\prime }\left(t\right)CU\left(t\right)+y\left(t\right)CU’\left(t\right)\right)\hfill \\ & \Rightarrow e^{-Nt}\left(\frac{U\left(t\right)}{dt}\right)=e^{-Nt}(\frac{t^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}\left(AU\left(0\right)+x\left(0\right)BU\left(0\right)+y\left(0\right)CU\left(0\right)\right)\hfill \\ & +I^{\alpha }\left(A{U}^{\prime }\left(t\right)+x^{\prime }\left(t\right)BU\left(t\right)+x\left(t\right)B{U}^{\prime }\left(t\right)+y^{\prime }\left(t\right)CU\left(t\right)+y\left(t\right)CU’\left(t\right)\right)),\hfill \end{array}$$

from which we can deduce that $U^{\prime }\in C_{\sigma }^{*}\left[0, T\right].$ Thus, we have

$$\begin{array}{ll}\frac{dU\left(t\right)}{dt}\hfill & =\frac{d}{dt}{I}^{\alpha }\left(AU\left(t\right)+x\left(t\right)BU\left(t\right)+y\left(t\right)CU\left(t\right)\right)\hfill \\ & \Rightarrow I^{1-\alpha }\frac{dU\left(t\right)}{dt}=I^{1-\alpha }·\frac{d}{dt}{I}^{\alpha }\left(AU\left(t\right)+x\left(t\right)BU\left(t\right)+y\left(t\right)CU\left(t\right)\right),\hfill \\ & \Rightarrow D^{\alpha }U\left(t\right)=AU\left(t\right)+x\left(t\right)BU\left(t\right)+y\left(t\right)CU\left(t\right)\hfill \end{array}$$

and $U\left(0\right)=U_0+I^{\alpha }\left(AU\left(0\right)+x\left(0\right)BU\left(0\right)+y\left(0\right)CU\left(0\right)\right)=U_0$.

Therefore, this initial value problem is equivalent to the initial value problem in Equation (27). □

4. Analyzing the Plant–Herbivore Population at Low Density

Allee in 1931 established an important role in the dynamical behavior of populations. He showed that population dynamics with logistic equations in a low population size should be modified with the Allee function in order to represent a realistic phenomenon [26].

By considering the logistic equation, the density increases when the per capita growth rate decreases monotonically; however, it is shown that, in logistic population models with the Allee effect, the per capita growth rate increases to a maximum point at low population density and decreases when the density of the population increases [26]. Many theoretical and laboratory studies showed the essential need of the Allee effect in small populations. Based on the biological studies, the following assumptions are necessary for defining the Allee function:

(a)

If $N=0$, then $a\left(N\right)=0;$

(b)

$a^{\prime }\left(N\right)>0$ for $N\in \left(0, \infty \right)$;

(c)

$\underset{N\to \infty }{\lim }a\left(N\right)=1$ [26,27,28,29,30,31].

Considering the conditions above, we apply an Allee function at time $t$ to the system in Equation (8) as follows:

$$\{\begin{array}{c}{D}^{\alpha }x\left(t\right)=\left(rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\frac{\gamma e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma ·x\left(t\right)}\right)\left(\frac{x\left(t\right)}{E_0+x\left(t\right)}\right)\\ D^{\alpha }y\left(t\right)=\frac{\beta e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma ·x\left(t\right)}-dy\left(t\right),\end{array}$$

(32)

where $t>0$ and $\left(x\left(0\right), y\left(0\right)\right)=\left(x_0, y_0\right).$ Moreover, we define $E_0$ as the Allee coefficient of the plant population, and $a\left(x\right)=\frac{x\left(t\right)}{E_0+x\left(t\right)}$ is the Allee function. The herbivore population is dependent on the plant population. Thus, if

$$x\left(t\right)<\frac{d}{e\sigma \left(\beta -dh\right)},$$

(33)

then the plant population is not sufficient for the herbivore to exist.

For a low population size of the plant population, let us consider the stability conditions around ${\mathsf{\Lambda }}_3$. The Jacobian matrix at ${\mathsf{\Lambda }}_3$ is given by

$$J\left(\overline{x},\overline{y}\right)=\left(\begin{array}{cc}\frac{rd}{E_{0}e\sigma \left(\beta -hd\right)+d}\left(1-\frac{2d}{e\sigma K\left(\beta -hd\right)}-\frac{Ke\sigma \left(\beta -hd\right)-d}{e\sigma K\beta }\right)& -\frac{\gamma d^2}{\beta \left(E_{0}e\sigma \left(\beta -hd\right)+d\right)}\\ \frac{r\left(Ke\sigma \left(\beta -hd\right)-d\right)}{e\sigma \gamma K}& 0\end{array}\right).$$

(34)

Thus, we obtain the characteristic equation

$${\lambda }^2+B_1\lambda +B_2=0,$$

(35)

where $B_1=\frac{rd}{E_{0}e\sigma \left(\beta -hd\right)+d}\left(\frac{2d}{e\sigma K\left(\beta -hd\right)}+\frac{Ke\sigma \left(\beta -hd\right)-d}{e\sigma K\beta }-1\right)$ and $B_2=\frac{r{d}^2\left(Ke\sigma \left(\beta -hd\right)-d\right)}{e\sigma K\beta \left(E_{0}e\sigma \left(\beta -hd\right)+d\right)}.$

Theorem 5.

Let the system in Equation (32) have a positive equilibrium point ${\Lambda }_3.$ Then, the following statements are true:

(i) 

Assume that $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)}$ and $d>\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$, where $hKe\sigma >1$. If

$$r>2\beta \left(\beta -hd\right)\left(\frac{2de\sigma K\beta +\left(Ke\sigma \left(\beta -hd\right)-d\right)\left(e\sigma K\left(\beta -hd\right)+2de\sigma K-2d\right)}{4d^2{\beta }^2+{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2{\left(\beta -hd\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}\right),$$

(36)

then we either attain real roots or complex conjugates with negative real parts, where $\left|arg\left(\lambda \right)\right|$>$\frac{\alpha \pi }{2}$ is equivalent to the Routh–Hurwitz case, which means that ${\Lambda }_3$ is locally asymptotically stable;

(ii) 

Assume that $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)}$ and $d<\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$, where $hKe\sigma >1$. If

$$r<2\beta \left(\beta -hd\right)\left(\frac{2de\sigma K\beta +\left(Ke\sigma \left(\beta -hd\right)-d\right)\left(e\sigma K\left(\beta -hd\right)+2de\sigma K\left(\beta -hd\right)-2d\right)}{4d^2{\beta }^2+{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2{\left(\beta -hd\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}\right),$$

(37)

then both roots are complex conjugates with positive real parts and

$$\left|ta{n}^{-1}\left(\sqrt{\frac{4de\sigma K\beta \left(Ke\sigma \left(\beta -hd\right)-d\right){\left(\beta -hd\right)}^2}{r{\left(2d\beta -e\sigma K\beta \left(\beta -hd\right)+\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)\right)}^2}-1}\right)\right|>\frac{\alpha \pi }{2},$$

(38)

which implies that ${\Lambda }_3$ is locally asymptotically stable.

Proof. 

(i) 

Let us consider the case where $\mathsf{\Delta }={\left(A_1\right)}^2-4A_2>0$. Since

$$\frac{rd}{{\left(E_{0}e\sigma \left(\beta -hd\right)+d\right)}^2}\left(\frac{4d^2{\beta }^2+{\left(\beta -hd\right)}^2{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}{e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2}\right)+\frac{2}{E_{0}e\sigma \left(\beta -hd\right)+d}\left(\frac{2d\left(Ke\sigma \left(\beta -hd\right)-d\right)-2de\sigma K\beta -e\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-2de\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)}{e^2{\sigma }^2{K}^2\beta \left(\beta -hd\right)}\right)>0$$

we have

$$r>\frac{2\left(E_{0}e\sigma \left(\beta -hd\right)+d\right)\beta \left(\beta -hd\right)}{d}\frac{\left(2de\sigma K\beta +e\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)+2de\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-2d\left(Ke\sigma \left(\beta -hd\right)-d\right)\right)}{4d^2{\beta }^2+{\left(\beta -hd\right)}^2{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2},$$

(39)

where $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)}.$ Furthermore, from

$$2d\beta +\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-e\sigma K\left(\beta -hd\right)\beta >0,$$

(40)

we have $d>\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$, where $hKe\sigma >1$. Thus, $A_1>0$. Additionally, it is obvious that $A_2>0$. This completes the proof of (i).

(ii) 

Let us consider the case where $\mathsf{\Delta }={\left(A_1\right)}^2-4A_2<0$. In this case, we have

$$r<\frac{2\left(E_{0}e\sigma \left(\beta -hd\right)+d\right)\beta \left(\beta -hd\right)}{d}\frac{\left(2de\sigma K\beta +e\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)+2de\sigma K\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-2d\left(Ke\sigma \left(\beta -hd\right)-d\right)\right)}{4d^2{\beta }^2+{\left(\beta -hd\right)}^2{\left(Ke\sigma \left(\beta -hd\right)-d\right)}^2+e^2{\sigma }^2{K}^2{\left(\beta -hd\right)}^2{\beta }^2},$$

(41)

where $\beta >\frac{Ke\sigma hd\left(1+2d\right)+2d}{Ke\sigma \left(1+2d\right)}.$ If

$$2d\beta +\left(\beta -hd\right)\left(Ke\sigma \left(\beta -hd\right)-d\right)-e\sigma K\left(\beta -hd\right)\beta <0,$$

(42)

then $d<\frac{\beta \left(hKe\sigma -1\right)}{h\left(Ke\sigma +1\right)}$ and $hKe\sigma >1$, which implies that $A_1<0$. This completes the proof of the theorem. □

Theorem 6.

The system in Equation (32) has a unique solution in $W=\left\{\left(x, y\right)\in R_{+}^2:a<x\le \frac{d}{e\sigma \left(\beta -dh\right)} and \left|y\right|\le b\right\}$ if

$$\frac{e\sigma K\left(\beta -dh\right)\left(rd\left(1+he\sigma a\right)-\gamma e\sigma bd\right)+r{d}^2\left(1+he\sigma a\right)}{e^2{\sigma }^{2}K\left(1+he\sigma a\right){\left(\beta -dh\right)}^2\left(E_0+a\right)M^{\alpha }}<1,$$

(43)

and

$$\frac{\beta d+d\left(1+he\sigma a\right)\left(\beta -dh\right)}{\left(1+he\sigma a\right)\left(\beta -dh\right)N^{\alpha }}<1.$$

(44)

Proof. 

Let $H\in C^{*}\left[0, T\right]$ be a solution of the initial values problem in Equation (32), which holds $\left(t, H\left(t\right)\right)\in V,$ where $t\in \left[0, T\right]$ and $V=\left[0, T\right]\times W.$ The Equation (32) can be written as

$$\{\begin{array}{c}{I}^{1-\alpha }\frac{dx\left(t\right)}{dt}=\left(rx\left(t\right)·\left(1-\frac{x\left(t\right)}{K}\right)-\frac{\gamma e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma ·a}\right)\left(\frac{x\left(t\right)}{E_0+a}\right)\\ I^{1-\alpha }\frac{dy\left(t\right)}{dt}=\frac{\beta e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma a}-dy\left(t\right).\end{array}$$

(45)

By operating both sides with $I^{\alpha }$, we get

$$\{\begin{array}{c}x\left(t\right)-x\left(0\right)=I^{\alpha }\left\{\left(rx\left(t\right)·\left(1-\frac{x\left(t\right)}{K}\right)-\frac{\gamma e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma a}\right)\left(\frac{x\left(t\right)}{E_0+a}\right)\right\}\\ y\left(t\right)-y\left(0\right)=I^{\alpha }\left\{\frac{\beta e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma a}-dy\left(t\right)\right\}.\end{array}$$

(46)

Let us define the operator $F:C\left[0,T\right]\to C\left[0,T\right]$ by

$$\{\begin{array}{c}Fx\left(t\right)=x\left(0\right)+I^{\alpha }\left\{\left(rx\left(t\right)·\left(1-\frac{x\left(t\right)}{K}\right)-\frac{\gamma e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma a}\right)\left(\frac{x\left(t\right)}{E_0+a}\right)\right\}\\ Fy\left(t\right)=y\left(0\right)+I^{\alpha }\left\{\frac{\beta e\sigma x\left(t\right)y\left(t\right)}{1+he\sigma a}-dy\left(t\right)\right\}.\end{array}$$

(47)

From Equation (47), we can write

$$\begin{array}{ll}Fx\left(t\right)-F\tilde{x}\hfill & \left(t\right)=I^{\alpha }\left\{\left(\frac{1}{E_0+a}\right)\left(\left(r-\frac{\gamma e\sigma y\left(t\right)}{1+he\sigma a}\right)\left(x^2\left(t\right)-{\tilde{x}}^2\left(t\right)\right)-\frac{r\left(x^3\left(t\right)-{\tilde{x}}^3\left(t\right)\right)}{K}\right)\right\}\hfill \\ & =I^{\alpha }\left(x\left(t\right)-\tilde{x}\left(t\right)\right)\left\{\left(\frac{1}{E_0+a}\right)\left(\left(r-\frac{\gamma e\sigma y\left(t\right)}{1+he\sigma a}\right)\left(x\left(t\right)+\tilde{x}\left(t\right)\right)-\frac{r\left(x^2\left(t\right)+x\left(t\right)\tilde{x}\left(t\right)+{\tilde{x}}^2\left(t\right)\right)}{K}\right)\right\}. \hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}{e}^{-Mt}\left(Fx\left(t\right)-F\tilde{x}\left(t\right)\right)\hfill & \\ & \le \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left(\frac{1}{E_0+a}\right){{\displaystyle \int }}_0^t{\left(t-s\right)}^{\alpha -1}{e}^{-M\left(t-s\right)}(x\left(t\right)\hfill \\ & -\tilde{x}\left(t\right))e^{Ms}(\left(r-\frac{\gamma e\sigma y\left(t\right)}{1+he\sigma a}\right)\left(x\left(t\right)+\tilde{x}\left(t\right)\right)\hfill \\ & -\frac{r{\left(x\left(t\right)+\tilde{x}\left(t\right)\right)}^2}{K}-\frac{rx\left(t\right)\tilde{x}\left(t\right)}{K})ds,\hfill \end{array}$$

which gives

$$\Vert Fx\left(t\right)-F\tilde{x}\left(t\right)\le x\left(t\right)\Vert -\Vert \tilde{x}\left(t\right)\Vert \left(\frac{e\sigma K\left(\beta -dh\right)\left(rd\left(1+he\sigma a\right)-\gamma e\sigma bd\right)+r{d}^2\left(1+he\sigma a\right)}{e^2{\sigma }^{2}K\left(1+he\sigma a\right){\left(\beta -dh\right)}^2\left(E_0+a\right)}\right){{\displaystyle \int }}_0^t\frac{s^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}ds\le \Vert x\left(t\right)-\tilde{x}\left(t\right)\Vert \left(\frac{e\sigma K\left(\beta -dh\right)\left(rd\left(1+he\sigma a\right)-\gamma e\sigma bd\right)+r{d}^2\left(1+he\sigma a\right)}{e^2{\sigma }^{2}K\left(1+he\sigma a\right){\left(\beta -dh\right)}^2\left(E_0+a\right)M^{\alpha }}\right).$$

Thus, if we choose $\tilde{M}$ such that $\frac{e\sigma K\left(\beta -dh\right)\left(rd\left(1+he\sigma a\right)-\gamma e\sigma bd\right)+r{d}^2\left(1+he\sigma a\right)}{e^2{\sigma }^{2}K\left(1+he\sigma a\right){\left(\beta -dh\right)}^2\left(E_0+a\right)M^{\alpha }}<1,$ we obtain

$$\Vert Fx\left(t\right)-F\tilde{x}\left(t\right)\Vert \le \Vert x\left(t\right)-\tilde{x}\left(t\right)\Vert .$$

Moreover, we can obtain

$$\Vert Fy\left(t\right)-F\tilde{y}\left(t\right)\Vert \le y\left(t\right)-\tilde{y}\left(t\right)\Vert \left(\frac{\beta d+d\left(1+he\sigma a\right)\left(\beta -dh\right)}{\left(1+he\sigma a\right)\left(\beta -dh\right)N^{\alpha }}\right).$$

If we choose $\tilde{N}$ such that $\frac{\beta d+d\left(1+he\sigma a\right)\left(\beta -dh\right)}{\left(1+he\sigma a\right)\left(\beta -dh\right)N^{\alpha }}<1,$ then $\Vert Fy\left(t\right)-F\tilde{y}\left(t\right)\Vert \le \Vert y\left(t\right)-\tilde{y}\left(t\right)\Vert .$

Similarly, one can show that Equation (46) is equivalent to the initial value problem in Equation (32). This completes the proof. □

Example 2.

The values of the chosen parameters are similar to those in Example 1. The blue graph represents the plant population, while the red graph denotes the herbivore population. The Allee coefficient is given by $E_0=0.14$. Figure 3 shows the bifurcation structure of the system in Equation (32) under the initial values $\left(x_0,y_0\right)=\left(0.6, 0.75\right)$. Figure 4 shows the per capita for the plant–herbivore population. We realized that, for a low density of the plant population, the dearth or migration of the herbivore population will occur earlier than expected. The plant population can recover after the herbivore population disappears from that habitat.

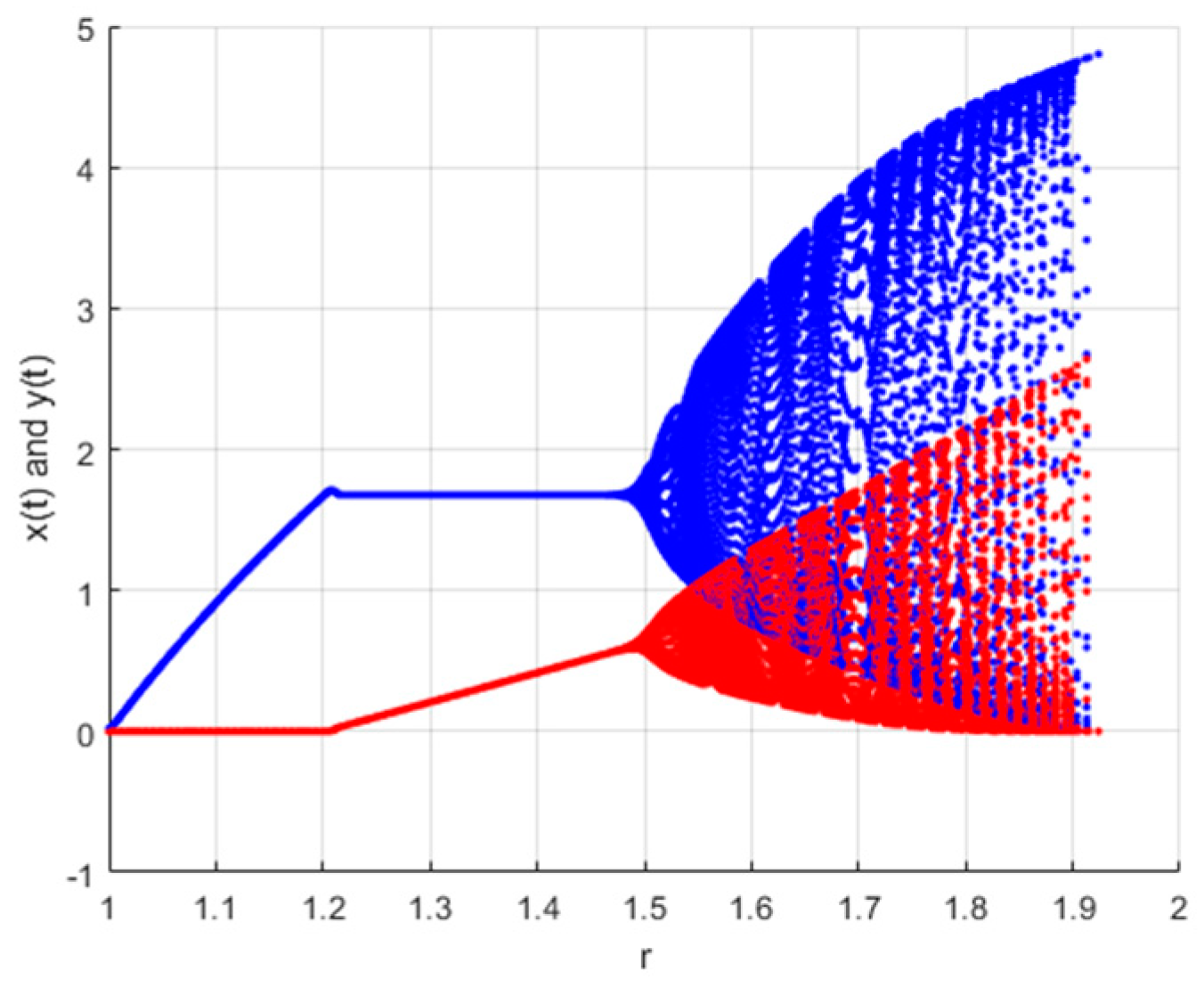
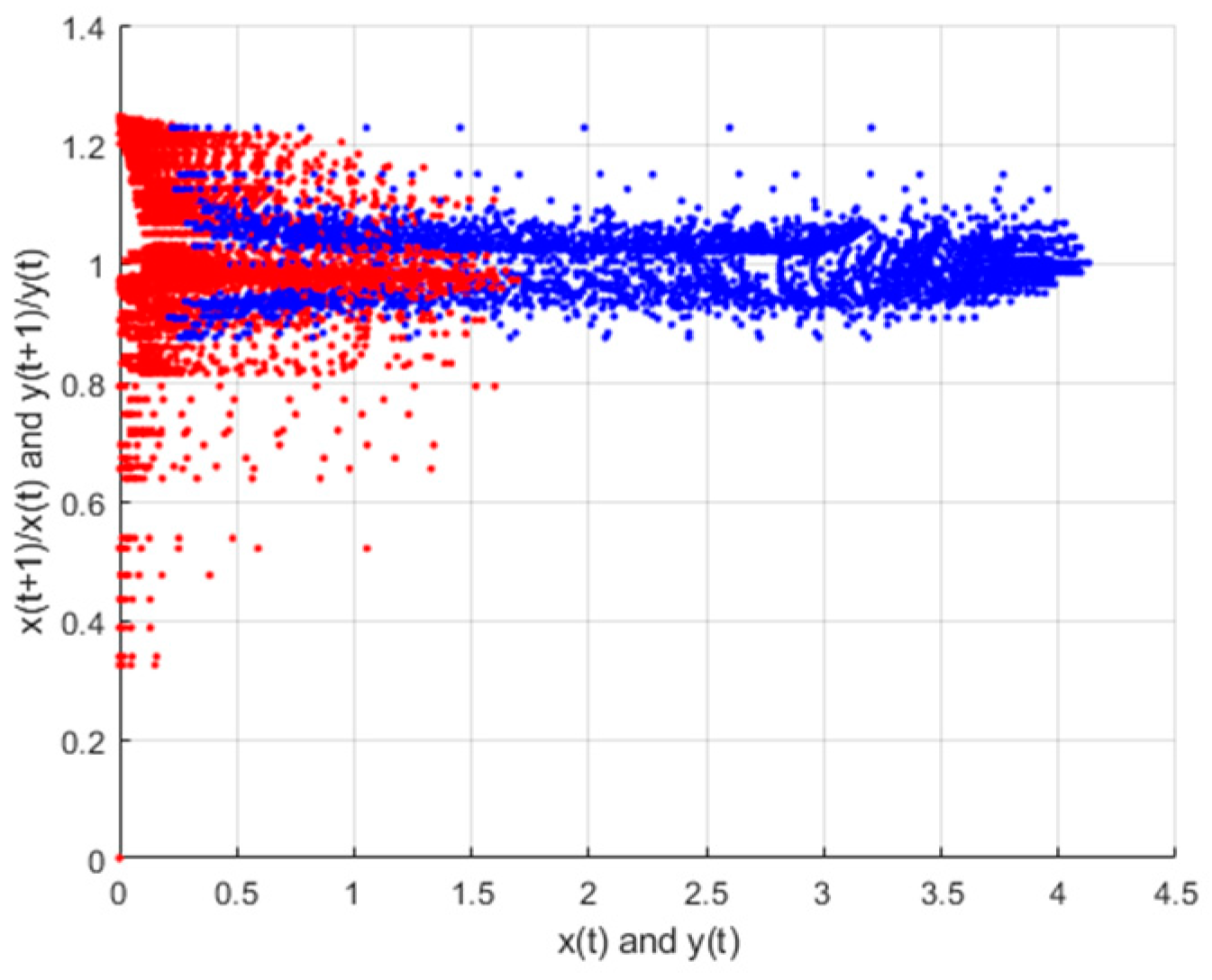
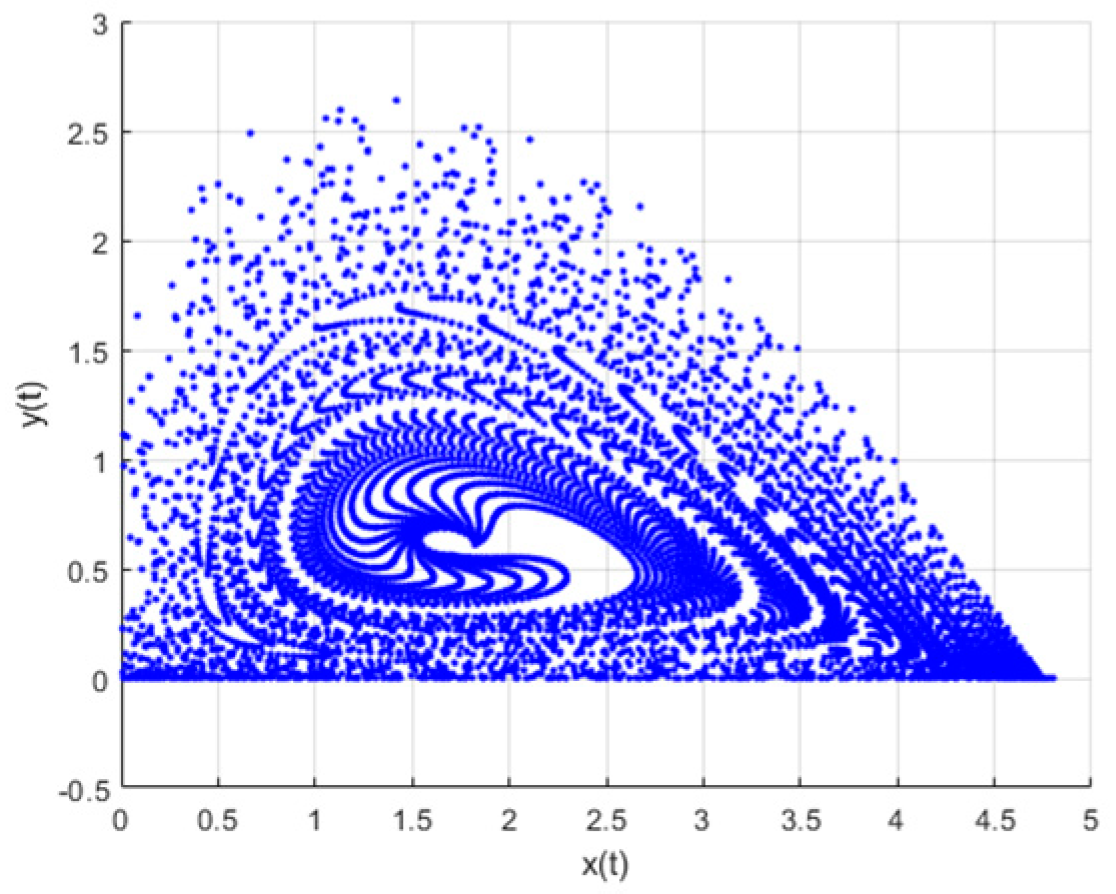
5. Flip Bifurcation with Discretization Process

In this section, we consider at first the discretization process and the analysis of flip bifurcation. This discretization is an approximation for the right-hand side of the fractional differential equation $D^{\alpha }x\left(t\right)=f\left(x\left(t\right)\right), t>0,$ where $\alpha \in \left(0, 1\right)$. We modify our system in Equation (8) in considering the discrete time effect on the model.

The discretization of Equation (8) is as follows:

$$\{\begin{array}{c}{D}^{\alpha }P\left(t\right)=rP\left(\left[\frac{t}{x}\right]x\right)\left(1-\frac{P\left(\left[\frac{t}{x}\right]x\right)}{K}\right)-\frac{\gamma e\sigma P\left(\left[\frac{t}{x}\right]x\right)H\left(\left[\frac{t}{x}\right]x\right)}{1+\overline{h}e\sigma P\left(\left[\frac{t}{x}\right]x\right)}\\ D^{\alpha }H\left(t\right)=\frac{\beta e\sigma P\left(\left[\frac{t}{x}\right]x\right)H\left(\left[\frac{t}{x}\right]x\right)}{1+\overline{h}e\sigma P\left(\left[\frac{t}{x}\right]x\right)}-dH\left(\left[\frac{t}{x}\right]x\right).\end{array}$$

(48)

For $t\in [0,h),\frac{t}{h}\in \left[0,1\right)$, we have

$$\{\begin{array}{c}{D}^{\alpha }P\left(t\right)=r{P}_0\left(1-\frac{P_0}{K}\right)-\frac{\gamma e\sigma P_0{H}_0}{1+\overline{h}e\sigma P_0}\\ D^{\alpha }H\left(t\right)=\frac{\beta e\sigma P_0{H}_0}{1+\overline{h}e\sigma P_0}-d{H}_0.\end{array}$$

(49)

The solution of Equation (49) reduces to

$$\{\begin{array}{c}{P}_1\left(t\right)=P_0+\frac{t^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{P}_0\left(r\left(1-\frac{P_0}{K}\right)-\frac{\gamma e\sigma H_0}{1+\overline{h}e\sigma P_0}\right)\\ H_1\left(t\right)=H_0+\frac{t^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{H}_0\left(\frac{\beta e\sigma P_0}{1+\overline{h}e\sigma P_0}-d\right).\end{array}$$

(50)

Let $t\in [h,2h),\frac{t}{h}\in \left[1,2\right)$, where we obtain

$$\{\begin{array}{c}{P}_2\left(t\right)=P_1+\frac{{\left(t-h\right)}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{P}_1\left(r\left(1-\frac{P_1}{K}\right)-\frac{\gamma e\sigma H_1}{1+\overline{h}e\sigma P_1}\right)\\ H_2\left(t\right)=H_1+\frac{{\left(t-h\right)}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{H}_1\left(\frac{\beta e\sigma P_1}{1+\overline{h}e\sigma P_1}-d\right).\end{array}$$

(51)

In repeating the discretization process n times, we get

$$\{\begin{array}{c}{P}_{n+1}\left(t\right)=P_n+\frac{{\left(t-nh\right)}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{P}_n\left(r\left(1-\frac{P_n}{K}\right)-\frac{\gamma e\sigma H_n}{1+\overline{h}e\sigma P_n}\right)\\ H_{n+1}\left(t\right)=H_n+\frac{{\left(t-nh\right)}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{H}_n\left(\frac{\beta e\sigma P_n}{1+\overline{h}e\sigma P_n}-d\right).\end{array}$$

(52)

For $t\in [nh,\left(n+1\right)·h)$, while $t\to \left(n+1\right)·h$ and $\alpha \to 1$, we have

$$\{\begin{array}{c}{P}_{n+1}\left(t\right)=P_n+\frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{P}_n\left(r\left(1-\frac{P_n}{K}\right)-\frac{\gamma e\sigma H_n}{1+\overline{h}e\sigma P_n}\right)\\ H_{n+1}\left(t\right)=H_n+\frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}{H}_n\left(\frac{\beta e\sigma P_n}{1+\overline{h}e\sigma P_n}-d\right).\end{array}$$

(53)

The Jacobian matrix $J$ of Equation (53) at the equilibrium points is

$$J\left({\mathsf{\Lambda }}_3\right)=\left(\begin{array}{cc}1+\frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}r\left(1-\frac{2d}{e\sigma K\left(\beta -\overline{h}d\right)}-\frac{Ke\sigma \left(\beta -\overline{h}d\right)-d}{e\sigma K\beta }\right)& -\frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}·\frac{\gamma d}{\beta }\\ \frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}\left(\frac{r\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{e\sigma \gamma K}\right)& 1\end{array}\right),$$

(54)

where ${\mathsf{\Lambda }}_3=\left(\frac{d}{e\sigma \left(\beta -\overline{h}d\right)},\frac{r\beta \left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{e^2{\sigma }^2\gamma K{\left(\beta -\overline{h}d\right)}^2}\right)$ is the positive equilibrium point of Equation (53).

Theorem 7.

Let ${\Lambda }_3$ be the equilibrium point of the system in Equation (53) and assume that $\Delta \ge 0,$ i.e.,

$$r\ge \frac{4\gamma de\sigma K\beta {\left(\beta -\overline{h}d\right)}^2\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{{\left(2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)\right)}^2}.$$

(55)

If

$$h<\sqrt[\alpha ]{\frac{2\mathsf{\Gamma }\left(\alpha +1\right)}{r}\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)},$$

(56)

where $\beta <\frac{\overline{h}d\left(Ke\sigma \overline{h}+1\right)}{Ke\sigma \overline{h}-1}$ and $Ke\sigma \overline{h}>1,$ then ${\mathsf{\Lambda }}_3$ is local asymptotically stable.

Proof. 

The characteristic equation of $J\left({\mathsf{\Lambda }}_3\right)$ is of the form

$${\lambda }^2-Tr\left(J\left({\mathsf{\Lambda }}_3\right)\right)+Det\left({\mathsf{\Lambda }}_3\right)=0,$$

(57)

where

$$Tr\left(J\left({\mathsf{\Lambda }}_3\right)\right)=2-\frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}r\left(\frac{2d}{e\sigma K\left(\beta -\overline{h}d\right)}+\frac{Ke\sigma \left(\beta -\overline{h}d\right)-d}{e\sigma K\beta }-1\right),$$

(58)

and

$$Det\left(J\left({\mathsf{\Lambda }}_3\right)\right)=1-\frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}r\left(\frac{2d}{e\sigma K\left(\beta -\overline{h}d\right)}+\frac{Ke\sigma \left(\beta -\overline{h}d\right)-d}{e\sigma K\beta }-1\right)+\frac{h^{2\alpha }}{{\left(\mathsf{\Gamma }\left(\alpha +1\right)\right)}^2}·\frac{r\gamma d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{\beta e\sigma \gamma K}.$$

(59)

From Equations (58) and (59), we have

$$\sqrt{\Delta }=\frac{h^{\alpha }r}{\mathsf{\Gamma }\left(\alpha +1\right)}\sqrt{{\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)}^2-\frac{4\gamma d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{r\beta e\sigma \gamma K}}.$$

Thus, the characteristic equation of $J\left({\mathsf{\Lambda }}_3\right)$ has two eigenvalues, which are

$$\begin{array}{c}{\lambda }_{1,2}\hfill \\ =1-\frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)\hfill \\ \pm \frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\sqrt{{\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma h+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)}^2-\frac{4\gamma d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{r\beta e\sigma \gamma K}}.\hfill \end{array}$$

If both $\left|{\lambda }_1\right|<1$ and $\left|{\lambda }_2\right|<1$, then the equilibrium point is locally asymptotically stable. From

$$\begin{array}{c}\left|{\lambda }_1\right|\hfill \\ =|1-\frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)\hfill \\ -\frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\sqrt{{\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)}^2-\frac{4\gamma d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{r\beta e\sigma \gamma K}}|<1,\hfill \end{array}$$

(60)

we obtain

$$\frac{h^{2\alpha }{r}^2}{4{\left(\mathsf{\Gamma }\left(\alpha +1\right)\right)}^2}\frac{4\gamma d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{r\beta e\sigma \gamma K}-\frac{4h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)+4>0,$$

(61)

where $\beta <\frac{\overline{h}d\left(Ke\sigma \overline{h}+1\right)}{Ke\sigma \overline{h}-1}$ and $Ke\sigma \overline{h}>1$. For $\frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}=\mu$, Equation (61) can be rewritten as follows:

$$\frac{4\gamma d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{r\beta e\sigma \gamma K}{\mu }^2-4\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)\mu +4>0,$$

(62)

where we obtain

$$h<\sqrt[\alpha ]{\frac{2\mathsf{\Gamma }\left(\alpha +1\right)}{r}\left(\frac{2\beta dr\gamma -r\gamma d\left(\beta -\overline{h}d\right)\left(Ke\sigma \overline{h}+1\right)}{2\gamma d\left(\beta -\overline{h}d\right)\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}+\sqrt{\frac{r^2{\left(2\beta -\left(\beta -\overline{h}d\right)\left(Ke\sigma \overline{h}+1\right)\right)}^2}{4{\left(\beta -\overline{h}d\right)}^2{\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}^2}-\frac{r\beta e\sigma K}{d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}}\right).}$$

(63)

From

$$\begin{array}{c}\left|{\lambda }_2\right|\hfill \\ =|1-\frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)\hfill \\ +\frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\sqrt{{\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)}^2-\frac{4\gamma d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}{r\beta e\sigma \gamma K}}|<1,\hfill \end{array}$$

(64)

we have

$$\begin{gathered} \frac{h^{\alpha }r}{2\mathsf{\Gamma }\left(\alpha +1\right)}\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)<2\Rightarrow h \\ <\sqrt[\alpha ]{\frac{4\mathsf{\Gamma }\left(\alpha +1\right)}{r}\left(\frac{e\sigma K\beta \left(\beta -\overline{h}d\right)}{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}\right)}. \end{gathered}$$

(65)

Considering Equations (63) and (65) together, we obtain

$$h<\sqrt[\alpha ]{\frac{2\mathsf{\Gamma }\left(\alpha +1\right)}{r}\left(\frac{2\beta d-\left(\beta -\overline{h}d\right)d\left(Ke\sigma \overline{h}+1\right)}{e\sigma K\beta \left(\beta -\overline{h}d\right)}\right)} .$$

This completes the proof. □

Consider $\mathsf{\Omega }=\left\{\left(r,K,\gamma ,e,\sigma ,\overline{h},\beta ,d\right):\Delta \ge 0,h=h_1\right\}$, where

$$h_1=\sqrt[\alpha ]{\frac{2\mathsf{\Gamma }\left(\alpha +1\right)}{r}\left(\frac{2\beta dr\gamma -r\gamma d\left(\beta -\overline{h}d\right)\left(Ke\sigma \overline{h}+1\right)}{2\gamma d\left(\beta -\overline{h}d\right)\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}+\sqrt{\frac{r^2{\left(2\beta -\left(\beta -\overline{h}d\right)\left(Ke\sigma \overline{h}+1\right)\right)}^2}{4{\left(\beta -\overline{h}d\right)}^2{\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}^2}-\frac{r\beta e\sigma K}{d\left(Ke\sigma \left(\beta -\overline{h}d\right)-d\right)}}\right)}.$$

(66)

The theorem below shows flip bifurcation of the equilibrium point ${\mathsf{\Lambda }}_3$ when the parameters $\left(r,K,\gamma , e, \sigma , \overline{h}, \beta , d \right)$ vary in the small neighborhood of $\mathsf{\Omega }$.

Theorem 8.

Let ${\Lambda }_3$ be the equilibrium point of the system in Equation (53). If $\chi ={\delta }_5+{\delta }_3{}^2\ne 0,$ the Equation (53) undergoes flip bifurcation. Furthermore, if ${\delta }_5+{\delta }_3{}^2>0$ then the bifurcation of the second period points is stable, while, for ${\delta }_5+{\delta }_3{}^2<0$, it shows an unstable behaviour.

Proof. 

In Theorem 7, we consider the analysis in a neighborhood given as $\mathsf{\Omega }$. Let $\mu =\frac{h^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}$ and ${\mu }^{*}$ be a perturbation of the parameter. The perturbed form of Equation (53) is as follows:

$$\{\begin{array}{c}{P}_{n+1}\left(t\right)=P_n+\left(\mu +{\mu }^{*}\right)P_n\left(r\left(1-\frac{P_n}{K}\right)-\frac{\gamma e\sigma H_n}{1+\overline{h}e\sigma P_n}\right)\\ H_{n+1}\left(t\right)=H_n+\left(\mu +{\mu }^{*}\right)H_n\left(\frac{\beta e\sigma P_n}{1+\overline{h}e\sigma P_n}-d\right).\end{array}$$

(67)

For $X_n=P_n-\frac{d}{e\sigma \left(\beta -hd\right)}$ and $Y_n=H_n-\frac{r\beta \left(Ke\sigma \left(\beta -hd\right)-d\right)}{e^2{\sigma }^2\gamma K{\left(\beta -hd\right)}^2}$, the system in Equation (67) can be formulated as

$$\left(\begin{array}{c}{X}_{n+1}\\ Y_{n+1}\end{array}\right)=\left(\begin{array}{c}{\psi }_{11}{X}_n+{\psi }_{12}{Y}_n+{\psi }_{13}{X}_n{Y}_n+{\mu }^{*}\left({\phi }_{11}{X}_n+{\phi }_{12}{Y}_n+{\phi }_{13}{X}_n{Y}_n\right)\\ {\psi }_{21}{X}_n+{\psi }_{22}{Y}_n+{\psi }_{23}{X}_n{Y}_n+{\mu }^{*}\left({\phi }_{21}{X}_n+{\phi }_{22}{Y}_n+{\phi }_{23}{X}_n{Y}_n\right)\end{array}\right),$$

(68)

where

$${\psi }_{11}=1+\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma },{\psi }_{12}=-\frac{d\mu \gamma }{\beta },{\psi }_{13}=-\frac{\gamma e\sigma \mu \left(\beta -hd\right)}{\beta },{\phi }_{11}=\frac{Kde\sigma r\left(\beta -1\right)-d}{e\sigma },{\phi }_{12}=-\frac{d\gamma }{\beta },{\phi }_{13}=-\frac{\gamma e\sigma \left(\beta -hd\right)}{\beta },{\psi }_{21}=\frac{r\beta \mu \left(Ke\sigma \left(\beta -hd\right)-d\right)}{e\sigma \gamma K\left(\beta -hd\right)}, {\psi }_{22}=1,{\psi }_{23}=\mu e\sigma \left(\beta -hd\right),{\phi }_{21}=\frac{r\beta \left(Ke\sigma \left(\beta -hd\right)-d\right)}{e\sigma \gamma K\left(\beta -hd\right)},{\phi }_{22}=0, {\phi }_{23}=e\sigma \left(\beta -hd\right).$$

For $\chi =\left(\begin{array}{cc}{\psi }_{11}& {\psi }_{12}\\ {\psi }_{21}& {\psi }_{22}\end{array}\right)$, the eigenvectors of $T$ that correspond to the eigenvalues ${\lambda }_1$ and ${\lambda }_2$ are

$$\left(\begin{array}{c}{Q}_1\\ Q_2\end{array}\right)=Q_2\left(\begin{array}{c}\frac{d\mu \gamma e\sigma }{2e\sigma \beta +\mu \beta \left(e\sigma hdr\left(\beta -1\right)-d\right)}\\ 1\end{array}\right)\mathrm{and} \left(\begin{array}{c}{Q}_3\\ Q_4\end{array}\right)=Q_4\left(\begin{array}{c}\frac{e\sigma d\mu \gamma {\beta }^{-1}}{e\sigma +\mu \left(e\sigma hdr\left(\beta -1\right)-d\right)-{\lambda }_2}\\ 1\end{array}\right),$$

(69)

where ${\lambda }_1=-1$ and $\left|{\lambda }_2\right|\ne 1$.

Here, we choose $Q_2=-\left(2+\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)$ and $Q_4=-\left(1+\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }-{\lambda }_2\right)$. Then, we have an invertible matrix

$$\overline{T}=\left(\begin{array}{cc}{Q}_1& Q_3\\ Q_2& Q_4\end{array}\right)=\left(\begin{array}{cc}-\frac{d\mu \gamma }{\beta }& -\frac{d\mu \gamma }{\beta }\\ -2-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }& {\lambda }_2-1-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\end{array}\right).$$

(70)

Let us consider the following transformation:

$$\left(\begin{array}{c}{X}_n\\ Y_n\end{array}\right)=\left(\begin{array}{cc}-\frac{d\mu \gamma }{\beta }& -\frac{d\mu \gamma }{\beta }\\ -2-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }& {\lambda }_2-1-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\end{array}\right)\left(\begin{array}{c}{u}_n\\ v_n\end{array}\right).$$

(71)

Taking ${\overline{T}}^{-1}$ on both sides of Equation (68), we have

$$\left(\begin{array}{c}{u}_{n+1}\\ v_{n+1}\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& {\lambda }_2\end{array}\right)\left(\begin{array}{c}{u}_n\\ v_n\end{array}\right)+\left(\begin{array}{c}{f}_1\left(X_n,Y_n,{\mu }^{*}\right)\\ f_2\left(X_n,Y_n,{\mu }^{*}\right)\end{array}\right),$$

(72)

where

$$\begin{array}{l}{X}_n=-\frac{d\mu \gamma }{\beta }\left(u_n+v_n\right),Y_n=-\left(2+\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)u_n+\left({\lambda }_2-1-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)v_n,\hfill \\ X_n{Y}_n=\frac{d\mu \gamma }{\beta }\left(2+\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)u_n^2-\frac{d\mu \gamma }{\beta }\left({\lambda }_2-3-2\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)u_n{v}_n-\frac{d\mu \gamma }{\beta }\left({\lambda }_2-1-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)v_n^2,\hfill \\ f_1\left(X_n,Y_n,{\mu }^{*}\right)=\frac{\left({\lambda }_2-1-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)}{-\frac{d\mu \gamma }{\beta }\left({\lambda }_2+1\right)}\left(-\frac{\gamma e\sigma \mu \left(\beta -hd\right)}{\beta }{X}_n{Y}_n+{\mu }^{*}\left(\frac{Kde\sigma r\left(\beta -1\right)-d}{e\sigma }\right)X_n-\frac{d\gamma }{\beta }{Y}_n-\frac{\gamma e\sigma \left(\beta -hd\right)}{\beta }{X}_n{Y}_n\right),\hfill \end{array}$$

and

$$\begin{array}{cc}{f}_2\left(X_n,Y_n,{\mu }^{*}\right)\hfill & =\frac{\left({\lambda }_2-1-\mu \frac{e\sigma hdr\left(\beta -1\right)-d}{e\sigma }\right)}{-\frac{d\mu \gamma }{\beta }\left({\lambda }_2+1\right)}(-\frac{\gamma e\sigma \mu \left(\beta -hd\right)}{\beta }{X}_n{Y}_n\hfill \\ & +{\mu }^{*}\left(\frac{Kde\sigma r\left(\beta -1\right)-d}{e\sigma }\right)X_n-\frac{d\gamma }{\beta }{Y}_n-\frac{\gamma e\sigma \left(\beta -hd\right)}{\beta }{X}_n{Y}_n)\hfill \\ & +\frac{1}{\left({\lambda }_2+1\right)}\left(\mu e\sigma \left(\beta -hd\right)X_n{Y}_n+{\mu }^{*}\left(\frac{r\beta \left(Ke\sigma \left(\beta -hd\right)-d\right)}{e\sigma \gamma K\left(\beta -hd\right)}\right)X_n+e\sigma \left(\beta -hd\right)X_n{Y}_n\right).\hfill \end{array}$$

Let us formulate the center manifold $W^c\left(0,0,0\right)=\left\{\left(u_n,v_n,{\mu }^{*}\right)\in {ℝ}^3:v_n=\kappa \left(u_n,{\mu }^{*}\right),\kappa \left(0,0\right)=0,D\kappa \left(0,0\right)=0 \right\}$ at the point $\left(0,0\right)$ in a neighbourhood of ${\mu }^{*}=0$. Let us have a center manifold such as $\kappa \left(u_n,{\mu }^{*}\right)={\varphi }_1{u}_n^2$ $+{\varphi }_2{\mu }^{*}{u}_n$ $+O\left({\left(\left|u_n\right|+\left|{\mu }^{*}\right|\right)}^3\right)$, where

$${\varphi }_1=\frac{-\gamma e\sigma \mu \left(\beta -hd\right){\left(2+\frac{\mu \left(e\sigma hdr\left(\beta -1\right)-d\right)}{e\sigma }\right)}^2-d{\mu }^2\gamma e\sigma \left(\beta -hd\right)\left(2+\frac{\mu \left(e\sigma hdr\left(\beta -1\right)-d\right)}{e\sigma }\right)}{\beta \left({\lambda }_2^2-1\right)},$$

and

$${\varphi }_2=\frac{K\left(\beta -hd\right){\left(2e\sigma +\mu \left(e\sigma hdr\left(\beta -1\right)-d\right)\right)}^2-\gamma K\left(\beta -hd\right)\left(Kde\sigma r\left(\beta -1\right)-d\right)\left(2e\sigma +\mu \left(e\sigma hdr\left(\beta -1\right)-d\right)\right)+rd{\mu }^{2}e\sigma \left(Ke\sigma \left(\beta -hd\right)-d\right)}{e^2{\sigma }^{2}K\mu \left(\beta -hd\right){\left({\lambda }_2+1\right)}^2},$$

which satisfy

$$M\left(\kappa \left(u_n,{\mu }^{*}\right)\right)=\kappa \left(-u_n+f_1\left(u_n,\kappa \left(u_n,{\mu }^{*}\right),{\mu }^{*}\right)-{\lambda }_2\kappa \left(u_n,{\mu }^{*}\right)-f_2\left(u_n,\kappa \left(u_n,{\mu }^{*}\right),{\mu }^{*}\right)\right)=0.$$

(73)

Thus, we have

$$f\left(u_n\right)=-u_n+{\delta }_1{u}_n{\mu }^{*}+{\delta }_2{u}_n{\left({\mu }^{*}\right)}^2+{\delta }_3{u}_n^2+{\delta }_4{u}_n^2{\mu }^{*}+{\delta }_5{u}_n^3+O\left({\left(\left|u_n\right|+\left|{\mu }^{*}\right|\right)}^5\right),$$

(74)

where

$$\begin{array}{l}{\delta }_1=\frac{1}{{\psi }_{12}\left({\lambda }_2+1\right)}\left\{{\psi }_{12}\left({\phi }_{11}\left({\lambda }_2-{\psi }_{11}\right)-{\psi }_{12}{\phi }_{21}\right)-{\psi }_{12}\left(1+{\psi }_{11}\right)\left({\lambda }_2-{\psi }_{11}\right)\right\},\hfill \\ {\delta }_2=\frac{a_2}{{\psi }_{12}\left({\lambda }_2+1\right)}\left\{{\psi }_{12}\left({\phi }_{11}\left({\lambda }_2-{\psi }_{11}\right)-{\psi }_{12}{\phi }_{21}\right)+{\psi }_{12}{\left({\lambda }_2-{\psi }_{11}\right)}^2\right\}\hfill \\ {\delta }_3=\frac{-1}{{\lambda }_2+1}\left({\psi }_{13}\left(1+{\psi }_{11}\right)\left({\lambda }_2-{\psi }_{11}\right)-{\psi }_{12}{\psi }_{23}\right),\hfill \\ {\delta }_4=\frac{1}{{\psi }_{12}\left({\lambda }_2+1\right)}\left\{a_2{\psi }_{12}\left({\lambda }_2+1\right)\left({\psi }_{13}\left({\lambda }_2-{\psi }_{11}\right)-{\psi }_{12}{\psi }_{23}\right)+a_1{\psi }_{12}\left({\phi }_{11}\left({\lambda }_2-{\psi }_{11}\right)-{\psi }_{12}{\phi }_{12}\right)+a_1{\phi }_{12}{\left({\lambda }_2-{\psi }_{11}\right)}^2-{\psi }_{12}\left(1+{\psi }_{11}\right)\left({\phi }_{13}\left({\lambda }_2-{\psi }_{11}\right)-{\psi }_{12}{\phi }_{23}\right)\right\},\hfill \end{array}$$

and

$${\delta }_5=\frac{a_1\left({\lambda }_2-2{\psi }_{11}-1\right)\left({\psi }_{13}\left({\lambda }_2-{\psi }_{11}\right)-{\psi }_{12}{\psi }_{23}\right)}{{\lambda }_2+1}.$$

According to the flip bifurcation conditions in References [1,32], we obtain that, if ${\delta }_5+{\delta }_3{}^2\ne 0,$ the system in Equation (53) undergoes flip bifurcation. Furthermore, if ${\delta }_5+{\delta }_3{}^2>0$, then the bifurcation of the second period points is stable, while, for ${\delta }_5+{\delta }_3{}^2<0$, it is unstable. □

Example 3.

By considering the same parameter values given in the previous examples, and according to the conditions of Theorem 8, we illustrate Example 3 by changing the carrying capacity of the plant population. Figure 5 and Figure 6 demonstrate the phase plane portraits of the system in Equation (8) for the carrying capacity values.

6. Conclusions

In this paper, the biological dynamics of fractional-order differential equations in a plant–herbivore model was discussed and analyzed. The local stability of the obtained equilibrium points and the existence and uniqueness of the solution in the system in Equation (27) were analyzed (see Example 1). An impressive result was considered in Section 4 where we found that, for a low size of the plant population, the herbivore population disappears. We noticed that the plant–herbivore model is mainly dependent on the plant population size and carrying capacity (see Example 2). On the other hand, we investigate possible bifurcation types, where we saw that the system exhibits a flip bifurcation structure (Section 5). Similar bifurcation studies were observed in many plant–herbivore models such as in References [4,17], where they obtained periodic or quasi-periodic solutions. Finally, we conclude that the environmental carrying capacity of the plant population has a strong effect on the system in Equation (27), while the density of the plant species shows an essential effect for the system in Equation (32). The numerical simulations were carried out using Matlab 2018.