A Note on the Equivalence of Fractional Relaxation Equations to Differential Equations with Varying Coefficients
Abstract
:1. Introduction
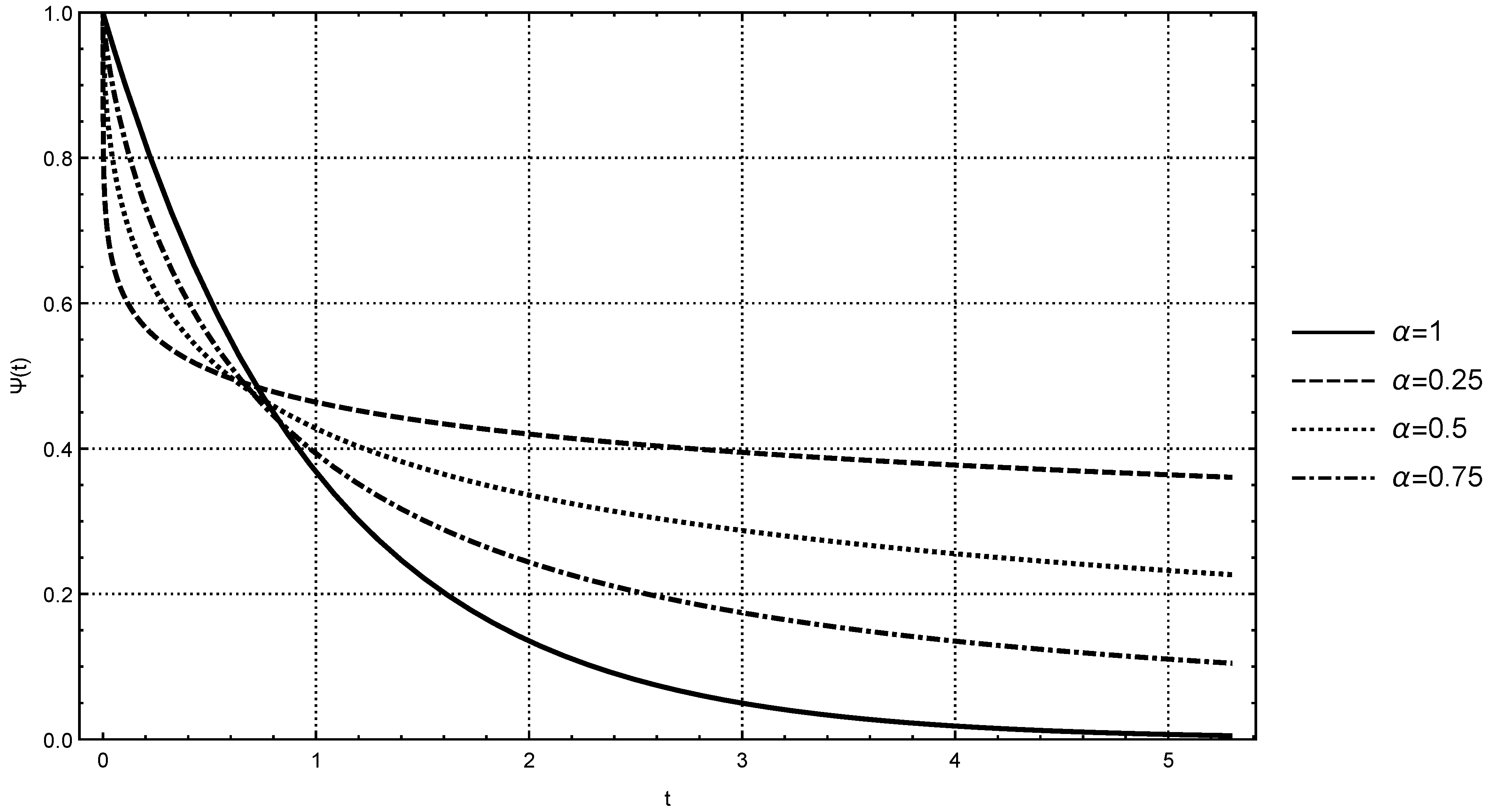
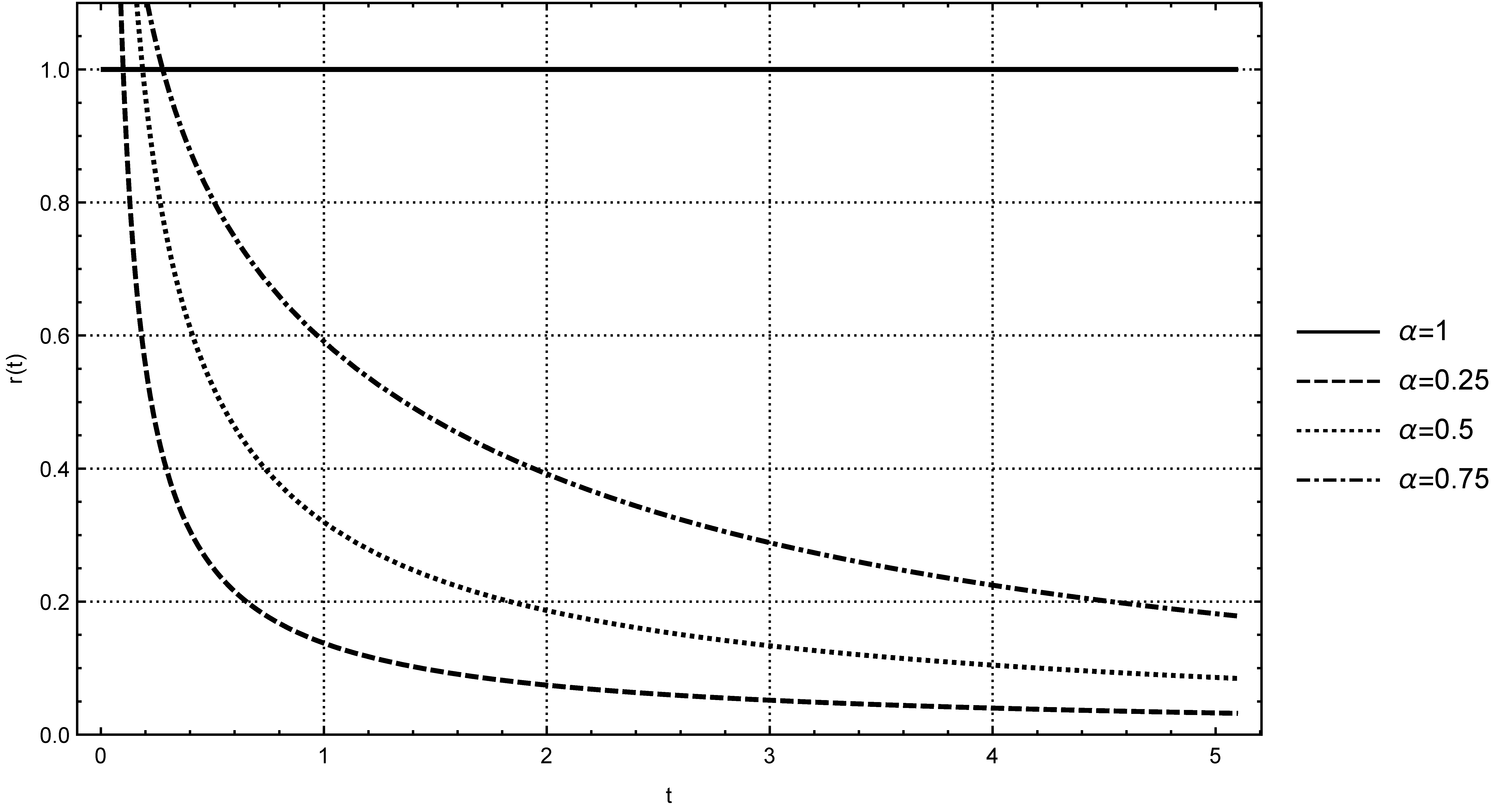
2. Mittag–Leffler Function as a Solution of the Fractional Relaxation Process
3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Mainardi, F.; Gorenflo, R. Time-fractional derivatives in relaxation processes: A tutorial survey. Fract. Calc. Appl. Anal. 2007, 10, 269–308. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. Mittag–Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Sandev, T.; Petreska, I.; Lenzi, E.K. Effective potential from the generalized time-dependent Schrödinger equation. Mathematics 2016, 4, 59. [Google Scholar] [CrossRef]

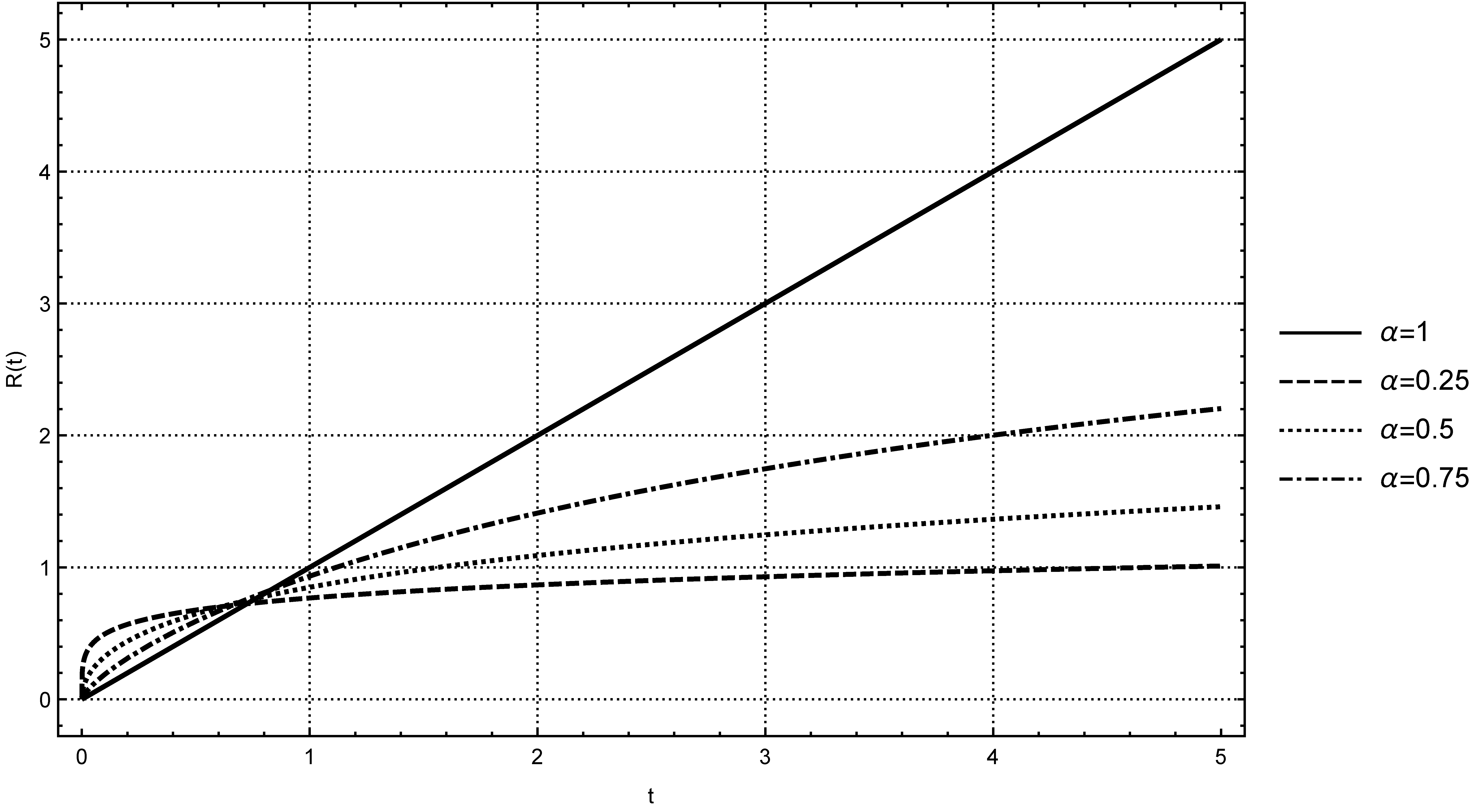
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mainardi, F. A Note on the Equivalence of Fractional Relaxation Equations to Differential Equations with Varying Coefficients. Mathematics 2018, 6, 8. https://doi.org/10.3390/math6010008
Mainardi F. A Note on the Equivalence of Fractional Relaxation Equations to Differential Equations with Varying Coefficients. Mathematics. 2018; 6(1):8. https://doi.org/10.3390/math6010008
Chicago/Turabian StyleMainardi, Francesco. 2018. "A Note on the Equivalence of Fractional Relaxation Equations to Differential Equations with Varying Coefficients" Mathematics 6, no. 1: 8. https://doi.org/10.3390/math6010008



