Application of Tempered-Stable Time Fractional-Derivative Model to Upscale Subdiffusion for Pollutant Transport in Field-Scale Discrete Fracture Networks
Abstract
:1. Introduction
2. Monte Carlo Simulations and the Fractional Advection–Dispersion Equation
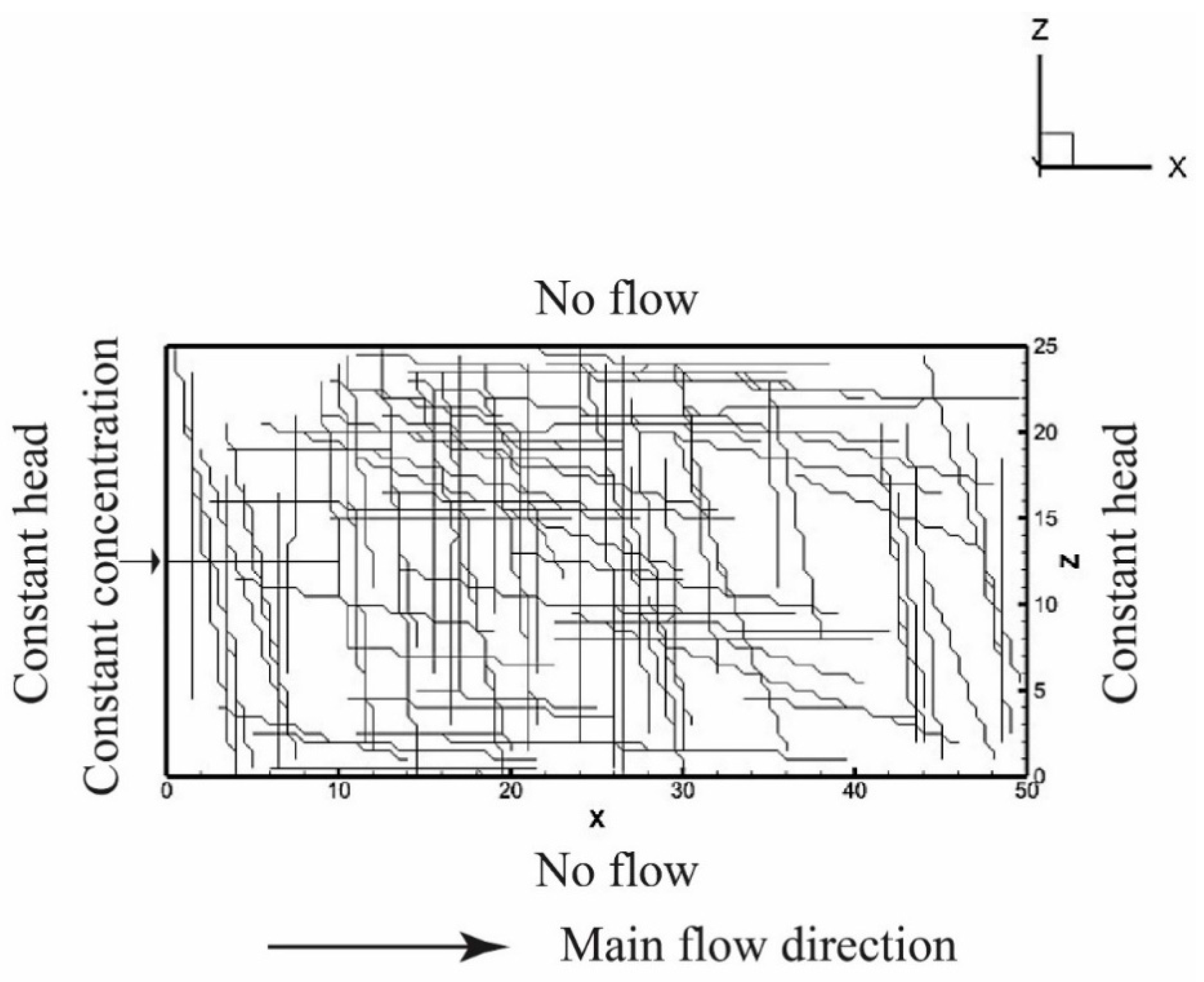
2.1. Generating the Random Discrete Fracture Networks
- (1)
- Fracture location: distributed randomly over the entire domain, with a random seed selected for each realization;
- (2)
- Fracture orientation: two fracture sets followed mixed Gaussian distributions (each Gaussian distribution is equally weighted and has its own mean and variance), with a mean and standard deviation of 0° ± 10° for the first set, and 90° ± 10° for the second set;
- (3)
- Fracture length: log-normal distribution, with 10 length bins—the mean of the smallest length bin is 2.5 m (which is 1/10 of the minimum length of the x and z domain sizes), and the mean of the largest length bin is 25 m (which is the minimum length of the x and z domain sizes);
- (4)
- Fracture aperture: exponential distribution, with 10 aperture bins—the mean of the smallest aperture bin is 0.001 m, and the mean of the largest aperture bin is 0.0015 m.
2.2. Modeling Groundwater Flow and Pollutant Transport through the Discrete Fracture Networks
2.3. Applying the Fractional Advection–Dispersion Equations to Quantify Transport
3. Results of Monte Carlo Simulations
4. Discussion
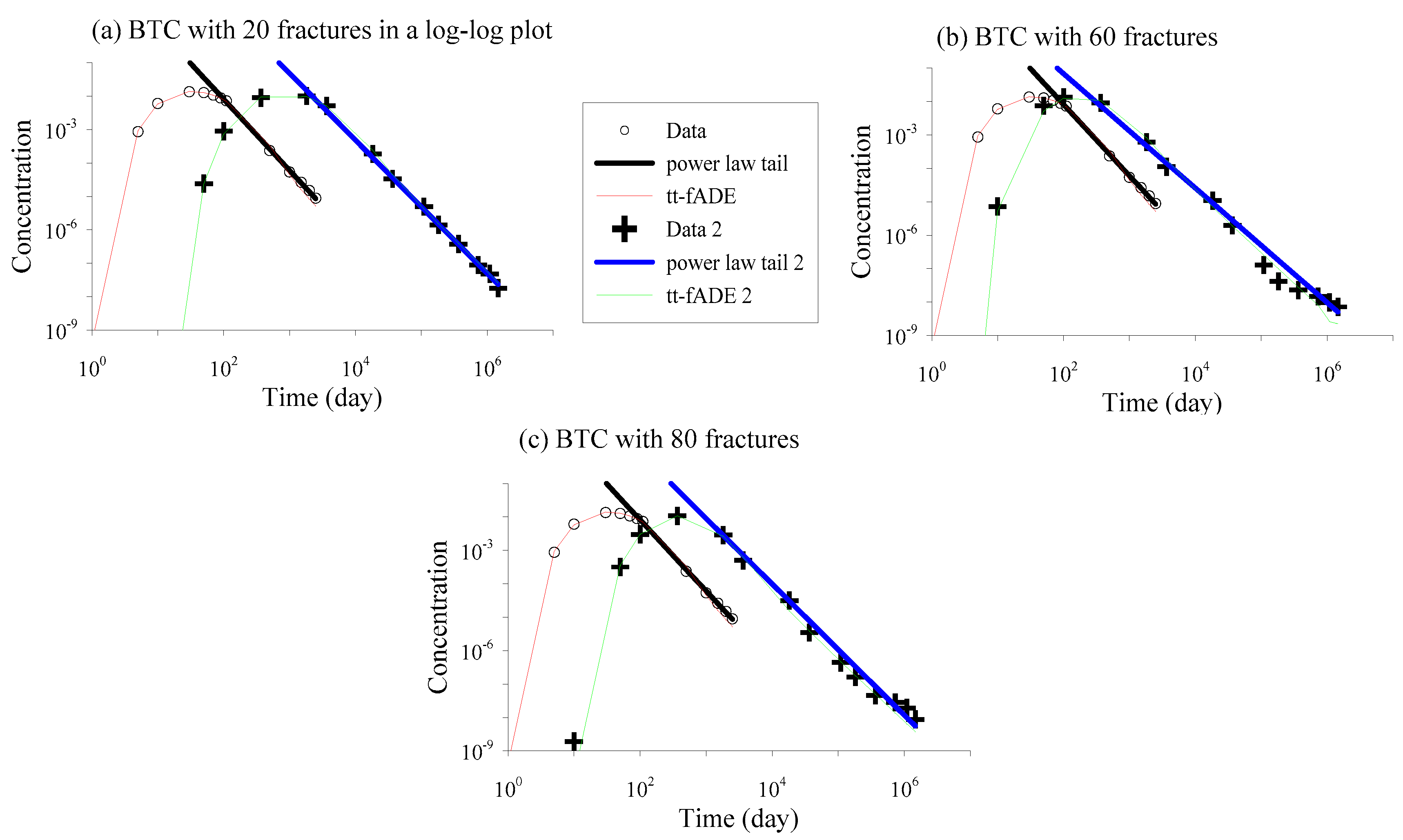
4.1. Impact of Fracture Density on Non-Fickian Transport
4.2. Impact of Fracture Orientation on Non-Fickian Transport
4.3. Impact of Matrix Permeability on Late-Time BTC
4.4. How to Approximate the Time Index γ Given the Limited Late-Time BTC
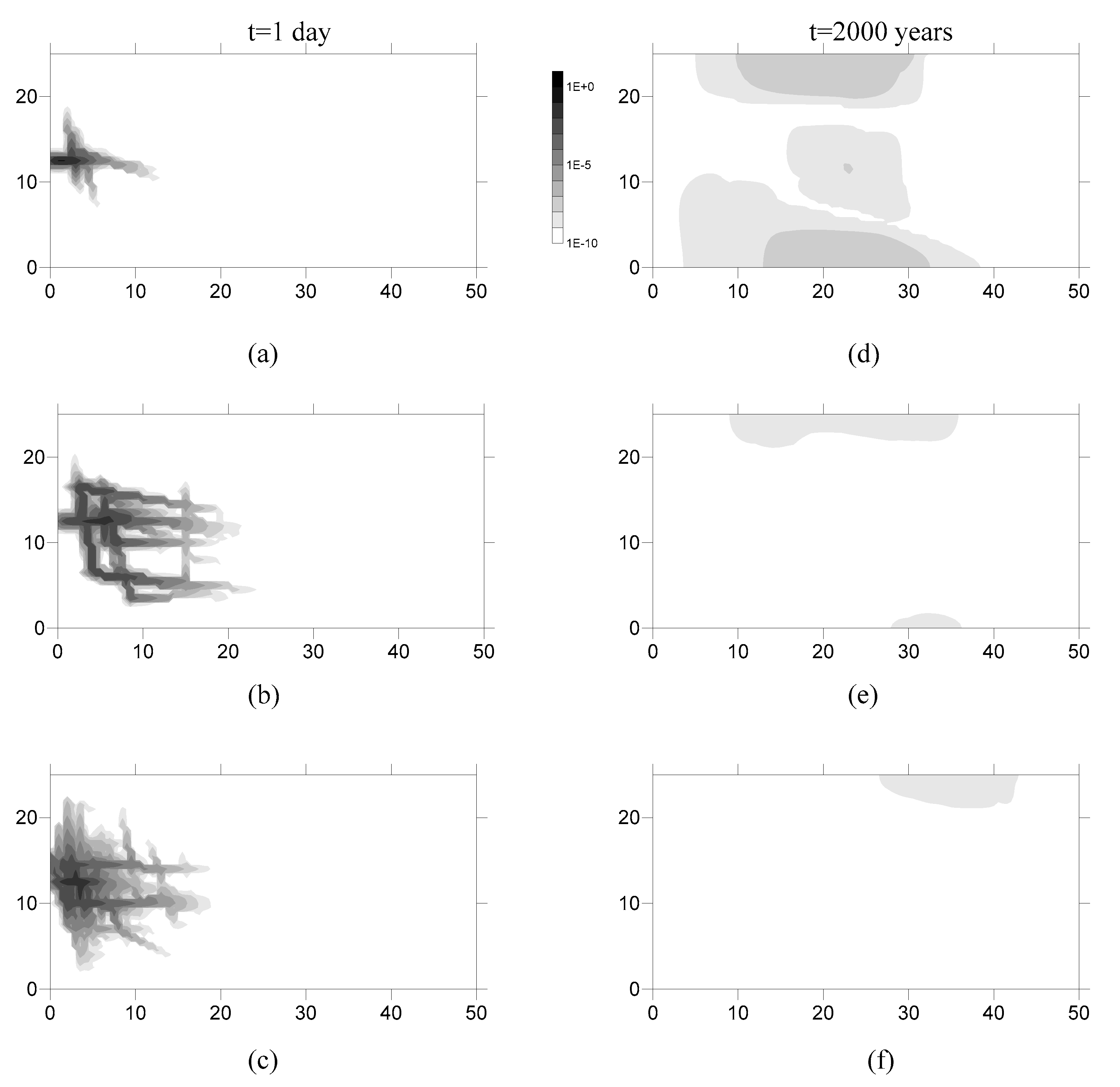
4.5. Subdiffusive Transport Shown by Plume Snapshots
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gorenflo, R.; Mainardi, F. Fractional Calculus. In Fractals and Fractional Calculus in Continuum Mechanics; Mainardi, F., Ed.; Springer: Vienna, Austria, 1997; pp. 223–276. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.G.; Stowell, H.H.; Zayernouri, M.; Hansen, S.E. A review of applications of fractional calculus in Earth system dynamics. Chaos Solitons Fractals 2017, 102, 29–46. [Google Scholar] [CrossRef]
- Fogg, G.E.; Zhang, Y. Debates—Stochastic subsurface hydrology from theory to practice: A geologic perspective. Water Resour. Res. 2016, 52, 9235–9245. [Google Scholar] [CrossRef]
- Coats, K.H.; Smith, B.D.; van Genuchten, M.T.; Wierenga, P.J. Dead-End Pore Volume and Dispersion in Porous Media. Soil Sci. Soc. Am. J. 1964, 4, 73–84. [Google Scholar] [CrossRef]
- Haggerty, R.; McKenna, S.; Meigs, L.C. On the late-time behaviour of tracer breakthrough curves. Water Resour. Res. 2000, 36, 3467–3479. [Google Scholar] [CrossRef]
- Klepikova, M.V.; Le Borgne, T.; Bour, O.; Dentz, M.; Hochreutener, R.; Lavenant, N. Heat as a tracer for understanding transport processes in fractured media: Theory and field assessment from multiscale thermal push-pull tracer tests. Water Resour. Res. 2016, 52, 5442–5457. [Google Scholar] [CrossRef] [Green Version]
- Becker, M.W.; Shapiro, A.M. Tracer transport in fractured crystalline rock: Evidence of nondiffusive breakthrough tailing. Water Resour. Res. 2000, 36, 1677–1686. [Google Scholar] [CrossRef]
- Kang, P.K.; Le Borgne, T.; Dentz, M.; Bour, O.; Juanes, R. Impact of velocity correlation and distribution on transport in fractured media: Field evidence and theoretical model. Water Resour. Res. 2015, 51, 940–959. [Google Scholar] [CrossRef] [Green Version]
- Becker, M.W.; Shapiro, A.M. Interpreting tracer breakthrough tailing from different forced-gradient tracer experiment configurations in fractured bedrock. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Chang, F.X.; Chen, J.; Huang, W. Anomalous diffusion and fractional advection-diffusion equation. Acta Phys. Sin. 2005, 54, 1113–1117. [Google Scholar]
- Huang, G.; Huang, Q.; Zhan, H. Evidence of one-dimensional scale-dependent fractional advection-dispersion. J. Contam. Hydrol. 2006, 85, 53–71. [Google Scholar] [CrossRef] [PubMed]
- Green, C.T.; Zhang, Y.; Jurgens, B.C.; Starn, J.J.; Landon, M.K. Accuracy of travel time distribution (TTD) models as affected by TTD complexity, observation errors, and model and tracer selection. Water Resour. Res. 2014, 50, 6191–6213. [Google Scholar] [CrossRef]
- Garrard, R.M.; Zhang, Y.; Wei, S.; Sun, H.; Qian, J. Can a Time Fractional-Derivative Model Capture Scale-Dependent Dispersion in Saturated Soils? Groundwater 2017, 55, 857–870. [Google Scholar] [CrossRef] [PubMed]
- Schumer, R.; Meerschaert, M.M.; Baeumer, B. Fractional advection-dispersion equations for modeling transport at the Earth surface. J. Geophys. Res. Earth Surf. 2009, 114, 1–15. [Google Scholar] [CrossRef]
- Drummond, J.D.; Aubeneau, A.F.; Packman, A.I. Stochastic modeling of fine particulate organic carbon dynamics in rivers. Water Resour. Res. 2014, 50, 4341–4356. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, D.; Zhang, Y.; Chen, L. Understanding partial bed-load transport: Experiments and stochastic model analysis. J. Hydrol. 2015, 521, 196–204. [Google Scholar] [CrossRef]
- Reeves, D.M.; Benson, D.A.; Meerschaert, M.M.; Scheffler, H.P. Transport of conservative solutes in simulated fracture networks: 2. Ensemble solute transport and the correspondence to operator-stable limit distributions. Water Resour. Res. 2008, 44, 1–20. [Google Scholar] [CrossRef]
- Zhang, Y.; Baeumer, B.; Reeves, D.M. A tempered multiscaling stable model to simulate transport in regional-scale fractured media. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Zhao, Z.; Rutqvist, J.; Leung, C.; Hokr, M.; Liu, Q.; Neretnieks, I.; Hoch, A.; Havlíček, J.; Wang, Y.; Wang, Z.; et al. Impact of stress on solute transport in a fracture network: A comparison study. J. Rock Mech. Geotech. Eng. 2013, 5, 110–123. [Google Scholar] [CrossRef]
- Zhao, Z.; Jing, L.; Neretnieks, I.; Moreno, L. Numerical modeling of stress effects on solute transport in fractured rocks. Comput. Geotech. 2011, 38, 113–126. [Google Scholar] [CrossRef]
- Selroos, J.; Walker, D.D.; Ström, A.; Gylling, B.; Follin, S. Comparison of alternative modelling approaches for groundwater flow in fractured rock. J. Hydrol. 2002, 257, 174–188. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Cushman, J.H. Monte Carlo Simulation of Contaminant Transport: II. Morphological Disorder in Fracture Connectivity. Transp. Porous Media 1998, 31, 183–211. [Google Scholar] [CrossRef]
- Outters, N. A Generic Study of Discrete Fracture Network Transport Properties Using FracMan/MAFIC; SKB-R-03-13; International Atomic Energy Agency (IAEA): Vienna, Austria, 2003. [Google Scholar]
- Gustafson, G.; Fransson, Å. The use of the Pareto distribution for fracture transmissivity assessment. Hydrogeol. J. 2006, 14, 15–20. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. A fractal model based on a new governing equation of fluid flow in fractures for characterizing hydraulic properties of rock fracture networks. Comput. Geotech. 2016, 75, 57–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Benson, D.A.; Meerschaert, M.M.; Labolle, E.M.; Scheffler, H.P. Random walk approximation of fractional-order multiscaling anomalous diffusion. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Cortis, A.; Birkholzer, J. Continuous time random walk analysis of solute transport in fractured porous media. Water Resour. Res. 2008, 44, 1–11. [Google Scholar] [CrossRef]
- McKenna, S.A.; Meigs, L.C.; Haggerty, R. Tracer tests in a fractured dolomite: 3. Double porosity, multiple-rate mass transfer processes in convergent flow tracer tests. Water Resour. Res. 2001, 37, 1143–1154. [Google Scholar] [CrossRef]
- Cook, P.G. A Guide to Regional Groundwater Flow in Fractured Rock Aquifers; CSIRO: Canberra, Australia, 2003; p. 107. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications: New York, NY, USA, 1972; ISBN 0-486-65675-6. [Google Scholar]
- Painter, S.; Cvetkovic, V. Upscaling discrete fracture network simulations: An alternative to continuum transport models. Water Resour. Res. 2005, 41, 1–10. [Google Scholar] [CrossRef]
- Lei, Q. Characterisation and Modelling of Natural Fracture Networks: Geometry, Geomechanics and Fluid Flow. Ph.D. Thesis, Imperial College London, London, UK, 2016. [Google Scholar]
- Bakshevskaia, V.A.; Pozdniakov, S.P. Simulation of Hydraulic Heterogeneity and Upscaling Permeability and Dispersivity in Sandy-Clay Formations. Math. Geosci. 2016, 48, 45–64. [Google Scholar] [CrossRef]
- Kang, P.K.; Dentz, M.; Le Borgne, T.; Juanes, R. Anomalous transport on regular fracture networks: Impact of conductivity heterogeneity and mixing at fracture intersections. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 92, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Benson, D.A.; Baeumer, B. Predicting the tails of breakthrough curves in regional-scale alluvial systems. Ground Water 2007, 45, 473–484. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Benson, D.A.; LaBolle, E.M.; Reeves, D.M. Spatiotemporal Memory and Conditioning on Local Aquifer Properties; DOE/NV/0000939-01, Publication #45244; Desert Research Institute: Las Vegas, NV, USA, 2009; p. 64. [Google Scholar]
- Kelly, J.F.; Bolster, D.; Meerschaert, M.M.; Drummond, J.D.; Packman, A.I. FracFit: A robust parameter estimation tool for fractional calculus models. Water Resour. Res. 2017, 53, 2559–2567. [Google Scholar] [CrossRef]
- Cacas, M.C.; Ledoux, E.; de Marsily, G.; Tillie, B.; Barbreau, A.; Durand, E.; Feuga, B.; Peaudecerf, P. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation: 1. The flow model. Water Resour. Res. 1990, 26, 479–489. [Google Scholar] [CrossRef]
- McClure, M.W.; Mark, W.; Horne, R.N. Discrete Fracture Network Modeling of Hydraulic Stimulation: Coupling Flow and Geomechanics; Springer: Berlin, Germany, 2013; ISBN 3319003836. [Google Scholar]
- Therrien, R.; McLaren, R.G.; Sudicky, E.; Panday, S.M. HydroGeoSphere a Three-dimensional Numerical Model Describing Fully-integrated Subsurface and Surface Flow and Solute Transport; Groundwater Simulations Group, University of Waterloo: Waterloo, ON, Canada, 2010; p. 429. [Google Scholar]
- Chakraborty, P.; Meerschaert, M.M.; Lim, C.Y. Parameter estimation for fractional transport: A particle-tracking approach. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Geiger, S.; Cortis, A.; Birkholzer, J.T. Upscaling solute transport in naturally fractured porous media with the continuous time random walk method. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for network of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef]
- Fiori, A.; Becker, M.W. Power law breakthrough curve tailing in a fracture: The role of advection. J. Hydrol. 2015, 525, 706–710. [Google Scholar] [CrossRef]
- Klimczak, C.; Schultz, R.A.; Parashar, R.; Reeves, D.M. Cubic law with aperture-length correlation: Implications for network scale fluid flow. Hydrogeol. J. 2010, 18, 851–862. [Google Scholar] [CrossRef]
- Keller, A.A.; Roberts, P.V.; Blunt, M.J. Effect of fracture aperture variations on the dispersion of contaminants. Water Resour. Res. 1999, 35, 55–63. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, B.; Jiang, Y. Effects of fracture surface roughness on macroscopic fluid flow and solute transport in fracture networks. Rock Mech. Rock Eng. 2014, 47, 2279. [Google Scholar] [CrossRef]
- Edery, Y.; Geiger, S.; Berkowitz, B. Structural controls on anomalous transport in fractured porous rock. Water Resour. Res. 2016, 52, 5634–5643. [Google Scholar] [CrossRef]
- Callahan, T.J.; Reimus, P.W.; Bowman, R.S.; Haga, M.J. Using multiple experimental methods to determine fracture/matrix interactions and dispersion of nonreactive solutes in saturated volcanic tuff. Water Resour. Res. 2000, 36, 3547–3558. [Google Scholar] [CrossRef]
- Therrien, R.; Sudicky, E. Three-dimensional analysis of variably-saturated flow and solute transport in discretely-fractured porous media. J. Contam. Hydrol. 1996, 23, 1–44. [Google Scholar] [CrossRef]
- Schumer, R.; Benson, D.A.; Meerschaert, M.; Baeumer, B. Fractal mobile/immobile solute transport. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Zhang, Y.; Baeumer, B. Tempered anomalous diffusion in heterogeneous systems. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Green, C.T.; Baeumer, B. Linking aquifer spatial properties and non-Fickian transport in mobile-immobile like alluvial settings. J. Hydrol. 2014, 512, 315–331. [Google Scholar] [CrossRef]
- Moreno, L.; Tsang, C.F. Multiple-Peak Response to Tracer Injection Tests in Single Fractures: A Numerical Study. Water Resour. Res. 1991, 27, 2143–2150. [Google Scholar] [CrossRef]
- Gerke, H.H. Preferential flow descriptions for structured soils. J. Plant Nutr. Soil Sci. 2006, 169, 382–400. [Google Scholar] [CrossRef]
- Reeves, D.M.; Parashar, R.; Pohll, G.; Carroll, R.; Badger, T.; Willoughby, K. Practical guidelines for horizontal hillslope drainage networks in fractured rock. Eng. Geol. 2013, 163, 132–143. [Google Scholar] [CrossRef]
- Neuman, S.P. Multiscale relationships between fracture length, aperture, density and permeability. Geophys. Res. Lett. 2008, 35, L22402. [Google Scholar] [CrossRef]
- Hirthe, E.M.; Graf, T. Fracture network optimization for simulating 2D variable-density flow and transport. Adv. Water Resour. 2015, 83, 364–375. [Google Scholar] [CrossRef]
- LaBolle, E.M.; Fogg, G.E. Role of Molecular Diffusion in Contaminant Migration and Recovery in an Alluvial Aquifer System. Transp. Porous Media 2001, 42, 155–179. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Matrix | - | - | - |
| Hydraulic conductivity | Kxx = Kyy = Kzz | 5 × 10−8, 10−7, 10−6 | m·s−1 |
| Specific storage | Ss | 10−3 | m−1 |
| Porosity | θs | 0.3 | - |
| Longitudinal dispersivity | αL | 0.01 | m |
| Transverse dispersivity | αT | 0.001 | m |
| Vertical_transverse dispersivity | αV | 0.001 | m |
| Tortuosity | τ | 1 | - |
| Fractures | - | - | - |
| Conductivity (computed) | Kf | (ρgωf2)/(12μ) a | m·s−1 |
| Specific storage (computed) | Ssf | ρgαω b = 4.3 × 10−6 | m−1 |
| Longitudinal dispersivity | αLf | 0.01 | m |
| Transverse dispersivity | αTf | 0.001 | m |
| Vertical_transverse dispersivity | αVf | 0.001 | m |
| Solute | - | - | - |
| Free-solution diffusion coefficient | Dfree | 10−9 | m2/s |
| Initial conditions | - | - | - |
| Concentration | Ct=0 | 0 | kg/m3 |
| Boundary conditions | - | - | - |
| Inflow concentration | Cx=0 | 1 | kg/m3 |
| Simulation Settings | - | - | - |
| Tracer pulse | Ttracer | 10 | s |
| a ωf stands for aperture; μ stands for fluid viscosity | - | - | |
| b αω stands for fluid compressibility | - | - | |
| Fracture Numbers | v [m/day] | D [m2/day] | β [dayγ−1] | γ [Dimensionless] | λ [day−1] | SBTC [Dimensionless] |
|---|---|---|---|---|---|---|
| 20 (0°~90°) | 0.46 | 9.40 | 2.17 | 0.885 | 3.29 × 10−10 | −2.088 |
| 60 (0°~90°) | 10.53 | 40.36 | 5.46 | 0.667 | 3.76 × 10−14 | −1.712 |
| 80 (0°~90°) | 12.11 | 93.84 | 27.66 | 0.827 | 1.75 × 10−8 | −1.965 |
| 60 (−45°~45°) | 20.72 | 29.37 | 14.75 | 0.673 | 3.24 × 10−8 | −1.689 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, B.; Zhang, Y.; Reeves, D.M.; Sun, H.; Zheng, C. Application of Tempered-Stable Time Fractional-Derivative Model to Upscale Subdiffusion for Pollutant Transport in Field-Scale Discrete Fracture Networks. Mathematics 2018, 6, 5. https://doi.org/10.3390/math6010005
Lu B, Zhang Y, Reeves DM, Sun H, Zheng C. Application of Tempered-Stable Time Fractional-Derivative Model to Upscale Subdiffusion for Pollutant Transport in Field-Scale Discrete Fracture Networks. Mathematics. 2018; 6(1):5. https://doi.org/10.3390/math6010005
Chicago/Turabian StyleLu, Bingqing, Yong Zhang, Donald M. Reeves, HongGuang Sun, and Chunmiao Zheng. 2018. "Application of Tempered-Stable Time Fractional-Derivative Model to Upscale Subdiffusion for Pollutant Transport in Field-Scale Discrete Fracture Networks" Mathematics 6, no. 1: 5. https://doi.org/10.3390/math6010005
APA StyleLu, B., Zhang, Y., Reeves, D. M., Sun, H., & Zheng, C. (2018). Application of Tempered-Stable Time Fractional-Derivative Model to Upscale Subdiffusion for Pollutant Transport in Field-Scale Discrete Fracture Networks. Mathematics, 6(1), 5. https://doi.org/10.3390/math6010005






