On Minimal Covolume Hyperbolic Lattices
Abstract
:1. Introduction
2. Hyperbolic Lattices with Parabolic Elements
2.1. Hyperbolic n-Space
2.2. Cusped Hyperbolic Orbifolds of Finite Volume
2.3. Hyperbolic Coxeter Polyhedra and Discrete Reflection Groups with Few Generators
2.4. Arithmetic Hyperbolic Coxeter Groups
2.5. The Euler Characteristic and the Covolume of a Hyperbolic Coxeter Group
2.6. The Computer Program CoxIter
3. Minimal Volume Cusped Hyperbolic Orbifolds
3.1. The Arithmetic Case
3.1.1. Even Dimensions
3.1.2. Odd Dimensions
- (1)
- If :
- (2)
- If :
- (3)
- If r is even:
- (1)
- When looking at realisations of orbifolds with volumes equal to the minimal values for , there remains a need to study the case and to look for a candidate in the commensurability class of PO that is conjugate to the fundamental group of the minimal volume hyperbolic orbifold of dimension 15.
- (2)
- It is an interesting but difficult question whether, and to what extent, non-arithmetic considerations can perturb the picture described in Section 3 in such a way that for some .
Acknowledgments
Conflicts of Interest
References
- Kellerhals, R. Hyperbolic orbifolds of minimal volume. Comput. Methods Funct. Theory 2014, 14, 465–481. [Google Scholar] [CrossRef]
- Belolipetsky, M. On volumes of arithmetic quotients of SO(1,n). Annali della Scuola Normale Superiore di Pisa Classe di Scienze 2004, 3, 749–770. [Google Scholar]
- Belolipetsky, M. Addendum to: “On volumes of arithmetic quotients of SO(1,n)”. Annali della Scuola Normale Superiore di Pisa Classe di Scienze 2007, 6, 263–268. [Google Scholar]
- Belolipetsky, M.; Emery, V. On volumes of arithmetic quotients of PO(n,1)∘, n odd. Proc. Lond. Math. Soc. 2012, 105, 541–570. [Google Scholar] [CrossRef]
- Emery, V. Du Volume des Quotients Arithmétiques de l’Espace Hyperbolique. Ph.D. Thesis, University of Fribourg, Fribourg, Switzerland, 2009. (In French). [Google Scholar]
- Borcherds, R. Automorphism groups of Lorentzian lattices. J. Algebra 1987, 111, 133–153. [Google Scholar] [CrossRef]
- Guglielmetti, R.; Jacquemet, M.; Kellerhals, R. On commensurable hyperbolic Coxeter groups. Geom. Dedicata 2016, 183, 143–167. [Google Scholar] [CrossRef]
- Guglielmetti, R. CoxIter—Computing invariants of hyperbolic Coxeter groups. LMS J. Comput. Math. 2015, 18, 754–773. [Google Scholar] [CrossRef]
- Emery, V. Even unimodular Lorentzian lattices and hyperbolic volume. J. Reine Angew. Math. 2014, 690, 173–177. [Google Scholar] [CrossRef]
- Tschantz, S.; Vanderbilt University. Private communication, 2017.
- Ratcliffe, J. Foundations of Hyperbolic Manifolds, 2nd ed.; Graduate Texts in Mathematics; Springer: New York, NY, USA, 2006; Volume 149. [Google Scholar]
- Kellerhals, R. Volumes of cusped hyperbolic manifolds. Topology 1998, 37, 719–734. [Google Scholar] [CrossRef]
- Hild, T. The cusped hyperbolic orbifolds of minimal volume in dimensions less than ten. J. Algebra 2007, 313, 208–222. [Google Scholar] [CrossRef]
- Hild, T. Cusped Hyperbolic Orbifolds of Minimal Volume in Dimensions Less than 11. Ph.D. Thesis, University of Fribourg, Fribourg, Swithzerland, 2007. [Google Scholar]
- Vinberg, È.B. Hyperbolic groups of reflections. Uspekhi Matematicheskikh Nauk 1985, 40, 29–66, 255. [Google Scholar] [CrossRef]
- Vinberg, È.B.; Shvartsman, O.V. Discrete Groups of Motions of Spaces of Constant Curvature. In Geometry, II; Encyclopaedia of Mathematical Sciences; Springer: Berlin, Germany, 1993; Volume 29, pp. 139–248. [Google Scholar]
- Felikson, A.; Tumarkin, P. Hyperbolic Coxeter Polytopes. Available online: http://www.maths.dur.ac.uk/users/anna.felikson/Polytopes/polytopes.html (accessed on 1 May 2017).
- Kaplinskaja, I.M.; Vinberg, E. On the groups O18,1() and O19,1(). Doklady Akademii Nauk SSSR 1978, 238, 1273–1275. [Google Scholar]
- Vinberg, E. The groups of units of certain quadratic forms. Matematicheskii Sbornik 1972, 87, 18–36. [Google Scholar]
- Maclachlan, C.; Reid, A. The Arithmetic of Hyperbolic 3-Manifolds; Graduate Texts in Mathematics; Springer: New York, NY, USA, 2003; Volume 219. [Google Scholar]
- Tumarkin, P. Hyperbolic Coxeter polytopes in with n + 2 hyperfacets. Matematicheskie Zametki 2004, 75, 909–916. [Google Scholar]
- Coxeter, H.S.M.; Moser, W. Generators and Relations for Discrete Groups, 4th ed.; Springer: Berlin, Germany; New York, NY, USA, 1980; Volume 14, p. ix+169. [Google Scholar]
- Steinberg, R. Endomorphisms of Linear Algebraic Groups; Memoirs of the American Mathematical Society, No. 80; American Mathematical Society: Providence, RI, USA, 1968; p. 108. [Google Scholar]
- Heckman, G.J. The volume of hyperbolic Coxeter polytopes of even dimension. Indag. Math. 1995, 6, 189–196. [Google Scholar] [CrossRef]
- Tumarkin, P.V. Hyperbolic n-dimensional Coxeter polytopes with n + 3 facets. Trudy Moskovskogo Matematicheskogo Obshchestva 2004, 65, 253–269. [Google Scholar]
- Vinberg, E.B. Non-arithmetic hyperbolic reflection groups in higher dimensions. Mosc. Math. J. 2015, 15, 593–602, 606. [Google Scholar]
- Ratcliffe, J.; Tschantz, S. Volumes of integral congruence hyperbolic manifolds. J. Reine Angew. Math. 1997, 488, 55–78. [Google Scholar]
- Hild, T.; Kellerhals, R. The FCC lattice and the cusped hyperbolic 4-orbifold of minimal volume. J. Lond. Math. Soc. 2007, 75, 677–689. [Google Scholar] [CrossRef]
- Conway, J.H.; Sloane, N.J.A. Sphere Packings, Lattices and Groups, 3rd ed.; Springer: New York, NY, USA, 1999; Volume 290, p. lxxiv+703. [Google Scholar]
- Viazovska, M. The sphere packing problem in dimension 8. ArXiv e-prints, 2016; arXiv:math.NT/1603.04246. [Google Scholar]
- Cohn, H. A conceptual breakthrough in sphere packing. Not. Am. Math. Soc. 2017, 64, 102–115. [Google Scholar]
- Jacquemet, M. New Contributions to Hyperbolic Polyhedra, Reflection Groups, and Their Commensurability. Ph.D. Thesis, University of Fribourg, Fribourg, Switzerland, 2015. [Google Scholar]
- Mcleod, J. Hyperbolic reflection groups associated to the quadratic forms . Geom. Dedicata 2011, 152, 1–16. [Google Scholar]
- Ratcliffe, J.G.; Tschantz, S.T. On volumes of hyperbolic Coxeter polytopes and quadratic forms. Geom. Dedicata 2013, 163, 285–299. [Google Scholar]




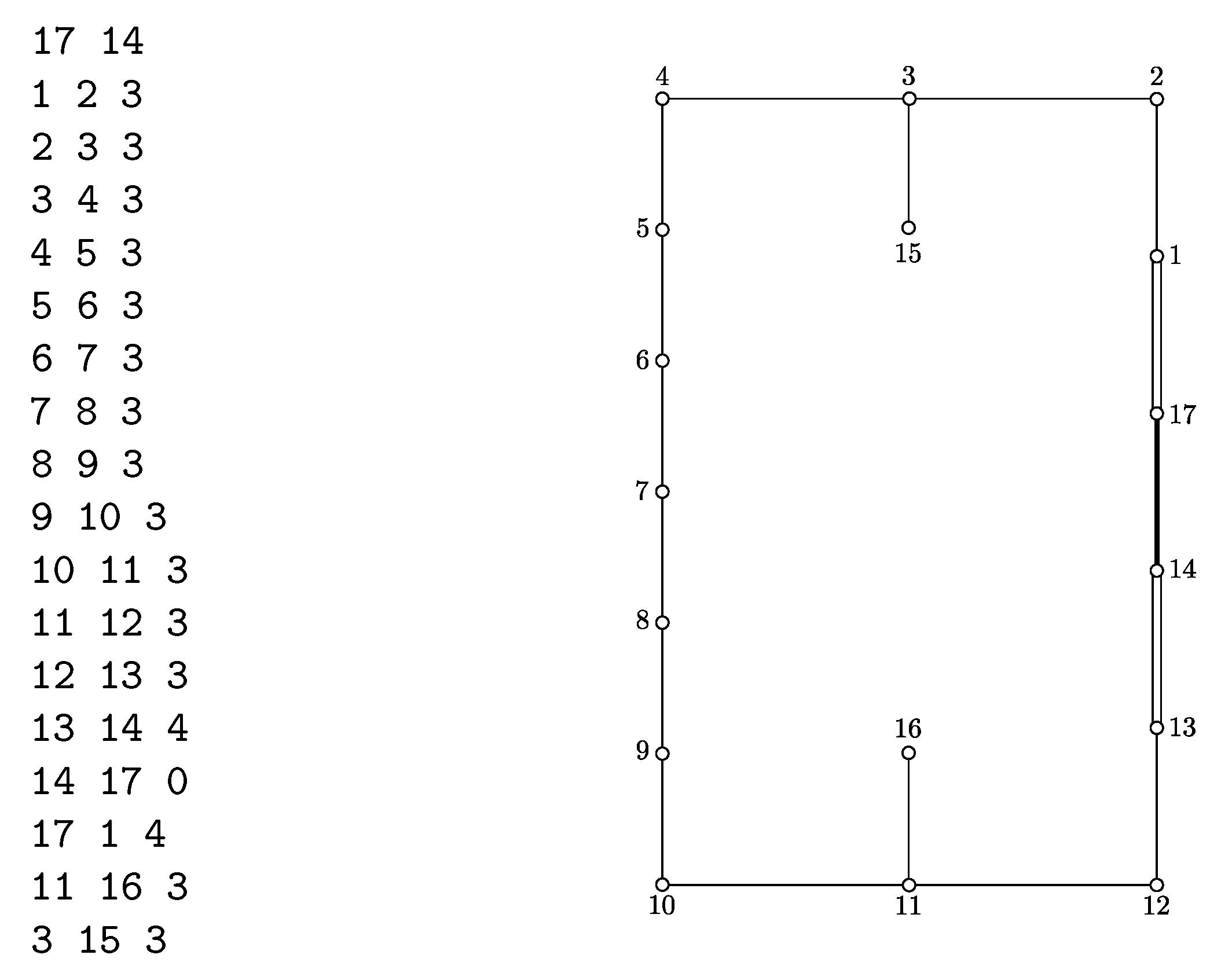
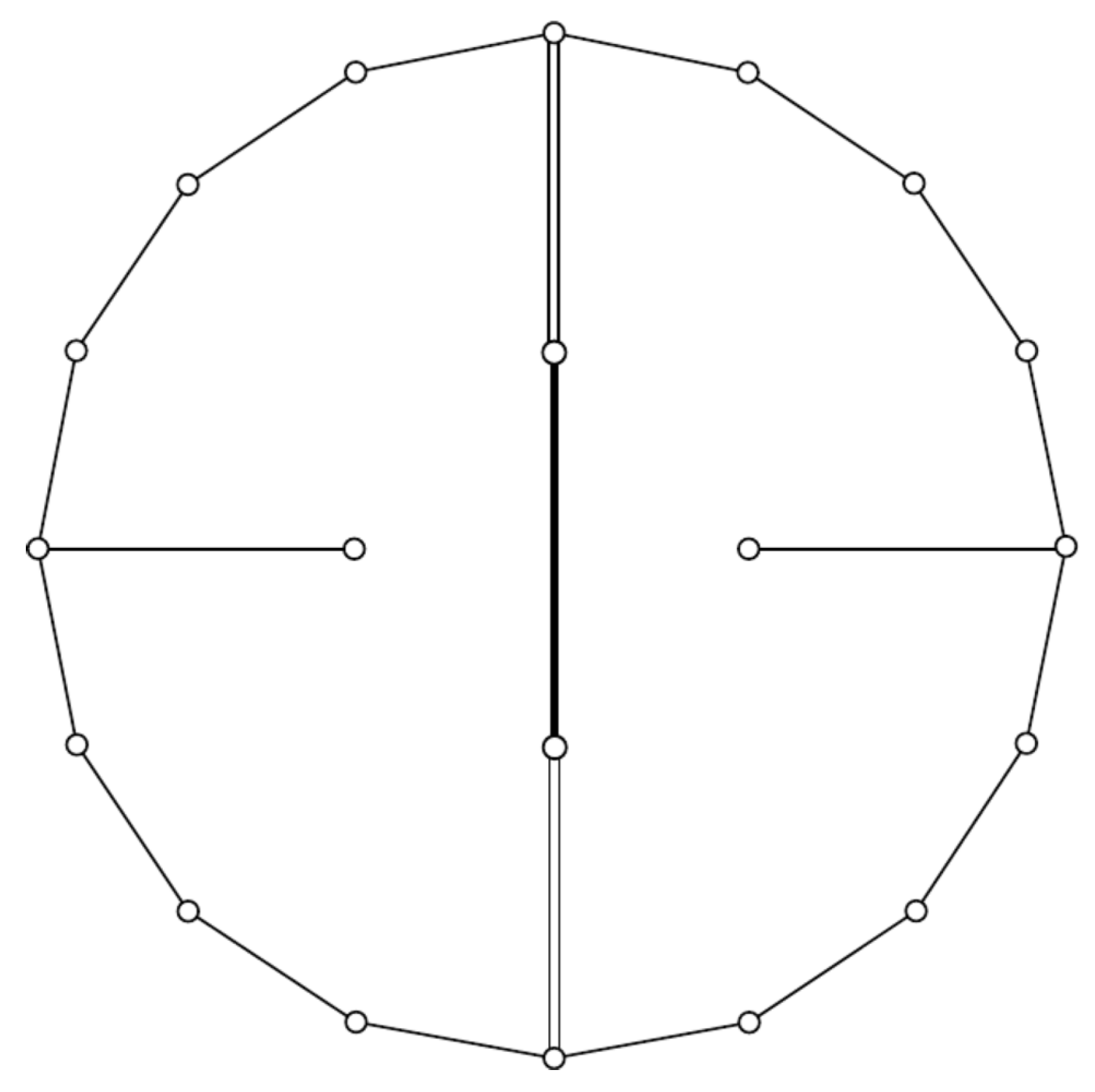
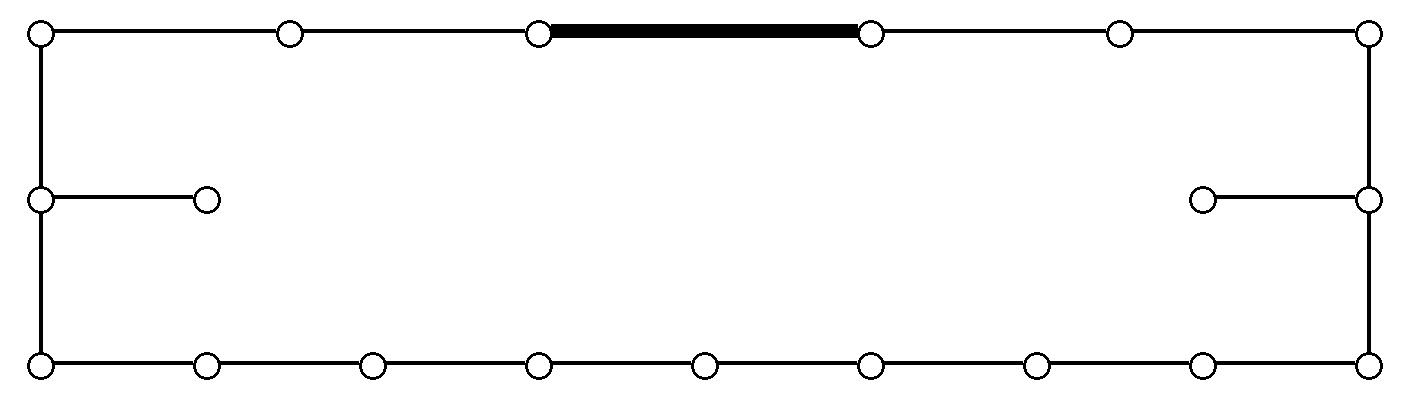
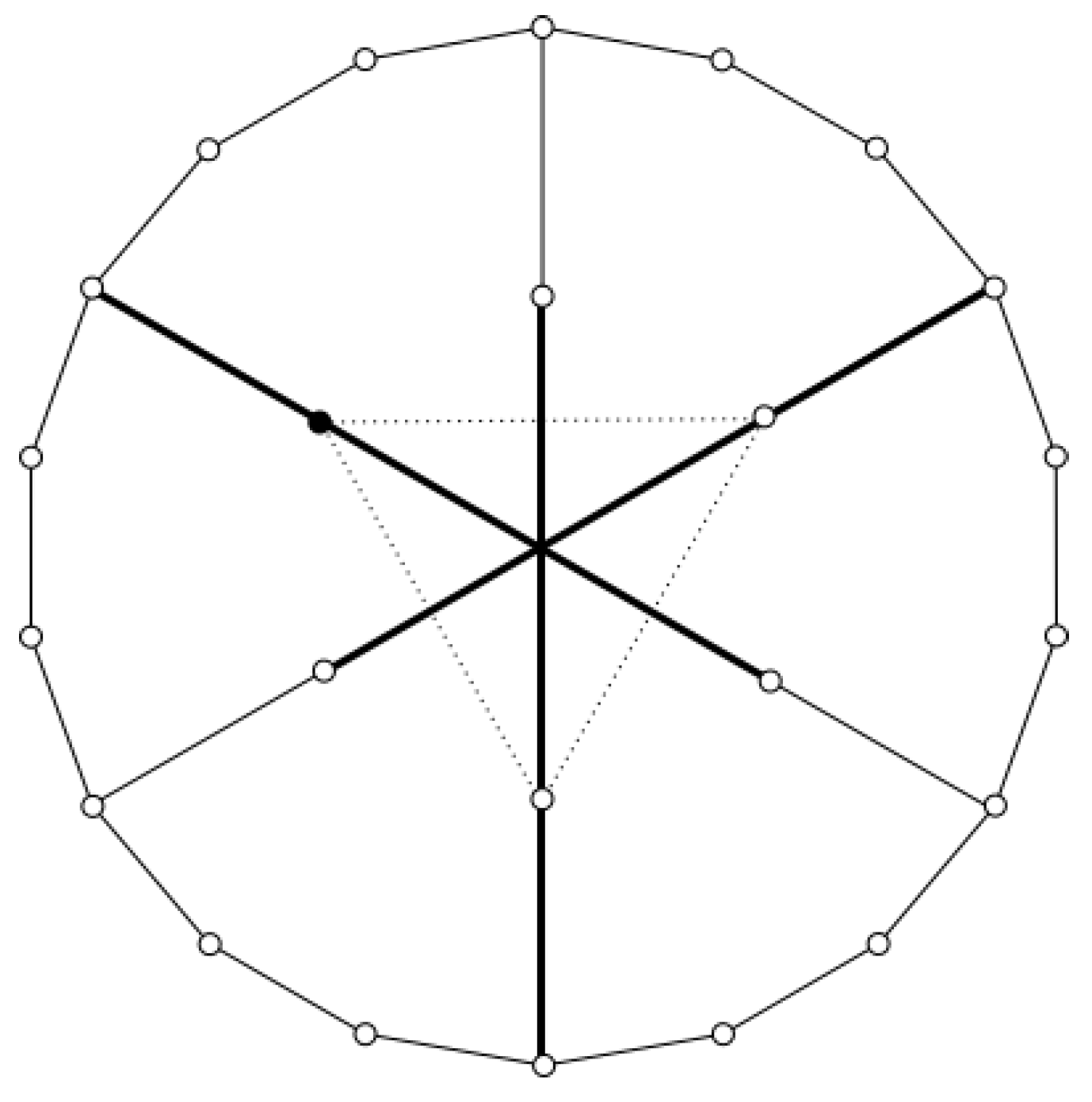

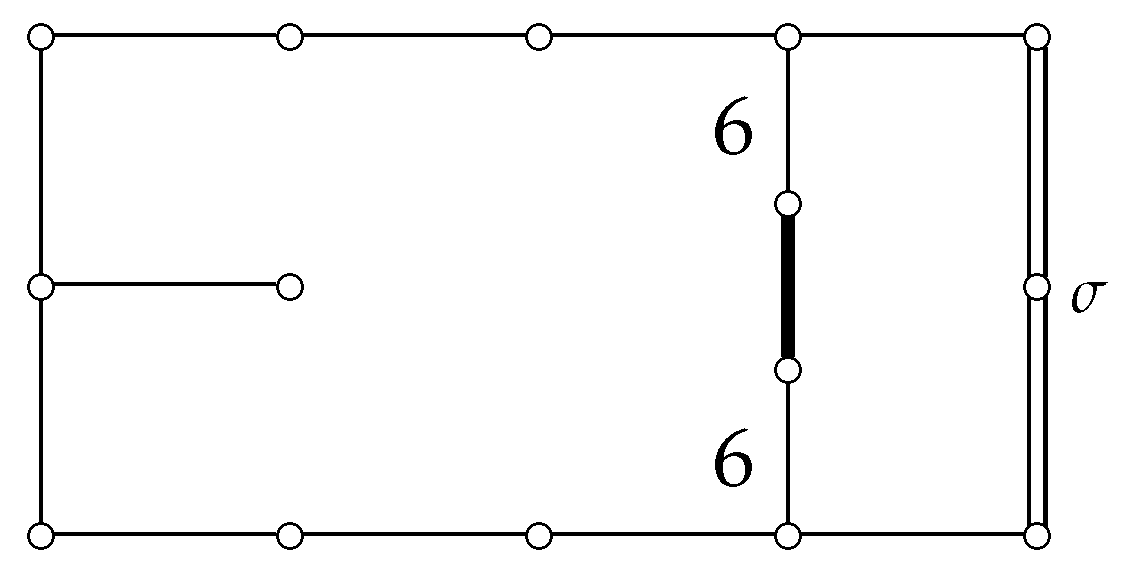

| dim n | |
|---|---|
| 2 |  |
| 3 |  |
| 4 | 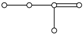 |
| 5 |  |
| 6 | 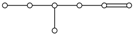 |
| 7 | 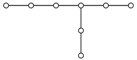 |
| 8 |  |
| 9 |  |
| Graph | Exponents | Growth polynomial |
|---|---|---|
| n | |
|---|---|
| 2 | 0.95493 |
| 3 | 0.85328 |
| 4 | 0.73046 |
| 5 | 0.60695 |
| 6 | 0.49339 |
| 7 | 0.39441 |
| 8 | 0.31114 |
| 9 | 0.24285 |
| 10 | 0.18789 |
| 25 | 0.00238 |
| 10 | 12 | 14 | 16 | 18 | |
|---|---|---|---|---|---|
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kellerhals, R. On Minimal Covolume Hyperbolic Lattices. Mathematics 2017, 5, 43. https://doi.org/10.3390/math5030043
Kellerhals R. On Minimal Covolume Hyperbolic Lattices. Mathematics. 2017; 5(3):43. https://doi.org/10.3390/math5030043
Chicago/Turabian StyleKellerhals, Ruth. 2017. "On Minimal Covolume Hyperbolic Lattices" Mathematics 5, no. 3: 43. https://doi.org/10.3390/math5030043
APA StyleKellerhals, R. (2017). On Minimal Covolume Hyperbolic Lattices. Mathematics, 5(3), 43. https://doi.org/10.3390/math5030043




