On the Duality of Regular and Local Functions
Abstract
:1. Introduction
2. Motivation
2.1. Generalized Functions
2.2. Symbolic Calculation
3. Idea
4. Preliminaries
5. Feasibilities
6. Definitions
7. Calculation Rules
8. A Regularization–Localization Duality
9. Four Subspaces
10. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
References
- Wei, G.W.; Gu, Y. Conjugate filter approach for solving Burgers’ equation. J. Comput. Appl. Math. 2002, 149, 439–456. [Google Scholar] [CrossRef]
- Hörmander, L. The Analysis of Linear Partial Differential Operators I; Die Grundlehren der mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Lighthill, M.J. An Introduction to Fourier Analysis and Generalised Functions; Cambridge University Press: Cambridge, NY, USA, 1958. [Google Scholar]
- Woodward, P.M. Probability and Information Theory, with Applications to Radar; Pergamon Press Ltd.: Oxford, UK, 1953. [Google Scholar]
- Benedetto, J.J. Harmonic Analysis and Applications; CRC Press Inc.: Boca Raton, FL, USA, 1996. [Google Scholar]
- Feichtinger, H.G.; Strohmer, T. Gabor Analysis and Algorithms: Theory and Applications; Birkhäuser: Boston, MA, USA, 1998. [Google Scholar]
- Gasquet, C.; Witomski, P. Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets; Springer: New York, NY, USA, 1999; Volume 30. [Google Scholar]
- Strichartz, R.S. A Guide to Distribution Theorie and Fourier Transforms; World Scientific Publishing Co. Pte Ltd.: Singapore, 2003. [Google Scholar]
- Brandwood, D. Fourier Transforms in Radar and Signal Processing; Artech House, Inc.: Norwood, MA, USA, 2003. [Google Scholar]
- Rahman, M. Applications of Fourier Transforms to Generalized Functions; WIT Press: Southampton, UK, 2011. [Google Scholar]
- Kammler, D.W. A first Course in Fourier Analysis; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Messiah, A. Quantum Mechanics—Two Volumes Bound as One; Dover Publications, Inc.: Mineola, NY, USA, 1999. [Google Scholar]
- Simon, B. Distributions and their Hermite expansions. J. Math. Phys. 1971, 12, 140–148. [Google Scholar] [CrossRef]
- Gracia-Bondía, J.M.; Varilly, J.C. Algebras of Distributions Suitable for Phase-Space Quantum Mechanics. I. J. Math. Phys. 1988, 29, 869–879. [Google Scholar] [CrossRef]
- Becnel, J.; Sengupta, A. The Schwartz Space: Tools for Quantum Mechanics and Infinite Dimensional Analysis. Mathematics 2015, 3, 527–562. [Google Scholar] [CrossRef]
- Fischer, J.V. On the duality of discrete and periodic functions. Mathematics 2015, 3, 299–318. [Google Scholar] [CrossRef]
- Wolfram Mathematica. Available online: http://reference.wolfram.com/language/tutorial/SymbolicCalculations.html (accessed on 7 August 2017).
- Python SymPy. Available online: https://en.wikipedia.org/wiki/SymPy (accessed on 7 August 2017).
- Fischer, J. Calculation Rules for Discrete Functions, Periodic Functions and Discrete Periodic Functions. ResearchGate 2017. Available online: https://www.researchgate.net/publication/316582622_Calculation_Rules_for_Discrete_Functions_Periodic_Functions_and_Discrete_Periodic_Functions (accessed on 7 August 2017). [CrossRef]
- Fischer, J. There is only one Fourier Transform. ResearchGate 2017. Available online: https://www.researchgate.net/publication/316855293_There_is_only_one_Fourier_Transform (accessed on 7 August 2017). [CrossRef]
- Fischer, J. A Formula Connecting Fourier Series and Fourier Transform. ResearchGate 2017. Available online: https://www.researchgate.net/publication/316659619_A_Formula_Connecting_Fourier_Series_and_Fourier_Transform (accessed on 7 August 2017). [CrossRef]
- Fischer, J. Fourier Transforms and Fourier Series and Their Interrelations. ResearchGate 2017. Available online: https://www.researchgate.net/publication/316140184_Fourier_Transforms_and_Fourier_Series_and_Their_Interrelations (accessed on 7 August 2017). [CrossRef]
- Fischer, J.; Molkenthin, T.; Chandra, M. SAR Image Formation as Wavelet Transform. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), VDE Verlag GmbH, Berlin, Germany, 18–26 May 2006. [Google Scholar]
- Schwartz, L. Théorie des Distributions, Tome II; Hermann: Paris, France, 1959. [Google Scholar]
- Zemanian, A. Distribution Theory and Transform Analysis—An Introduction to Generalized Functions, with Applications; McGraw-Hill Inc.: New York, NY, USA, 1965. [Google Scholar]
- Horváth, J. Topological Vector Spaces and Distributions; Addison-Wesley Publishing Company: Reading, MA, USA, 1966. [Google Scholar]
- Trèves, F. Topological Vector Spaces, Distributions and Kernels: Pure and Applied Mathematics; Academic Press Inc.: Mineola, NY, USA, 1967. [Google Scholar]
- Bracewell, R.N. Fourier Transform and its Applications; McGraw-Hill Book Company: New York, NY, USA, 1965. [Google Scholar]
- Grubb, G. Distributions and Operators; Springer Science+Business Media: New York, NY, USA, 2009; Volume 252. [Google Scholar]
- Dubois-Violette, M.; Kriegl, A.; Maeda, Y.; Michor, P.W. Smooth*-Algebras. Prog. Theor. Phys. Supp. 2002, 144, 54–78. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Unser, M.; Ward, J.P. Generalized Poisson Summation Formulas for Continuous Functions of Polynomial Growth. J. Fourier Anal. Appl. 2017, 23, 442–461. [Google Scholar] [CrossRef]
- Walter, W. Einführung in die Theorie der Distributionen; BI-Wissenschaftsverlag, Bibliographisches Institut & FA Brockhaus: Mannheim, Germany, 1994. [Google Scholar]
- Hunter, J.K.; Nachtergaele, B. Applied Analysis; World Scientific Publishing Company: Singapore, 2001. [Google Scholar]
- Beals, R. Advanced Mathematical Analysis: Periodic Functions and Distributions, Complex Analysis, Laplace Transform and Applications; Springer: New York, NY, USA, 1973; Volume 12. [Google Scholar]
- Wei, G. Wavelets generated by using discrete singular convolution kernels. J. Phys. A Math. Gen. 2000, 33, 8577. [Google Scholar] [CrossRef]
- Wei, G. Discrete singular convolution for the solution of the Fokker–Planck equation. J. Chem. Phys. 1999, 110, 8930–8942. [Google Scholar] [CrossRef]
- Estrada, R.; Kanwal, R.P. Regularization, pseudofunction, and Hadamard finite part. J. Math. Anal. Appl. 1989, 141, 195–207. [Google Scholar] [CrossRef]
- Wei, G. Quasi wavelets and quasi interpolating wavelets. Chem. Phys. Lett. 1998, 296, 215–222. [Google Scholar] [CrossRef]
- Wei, G.; Wang, H.; Kouri, D.J.; Papadakis, M.; Kakadiaris, I.A.; Hoffman, D.K. On the mathematical properties of distributed approximating functionals. J. Math. Chem. 2001, 30, 83–107. [Google Scholar] [CrossRef]
- Hoffman, D.K.; Kouri, D.J. Distributed approximating function theory for an arbitrary number of particles in a coordinate system-independent formalism. J. Phys. Chem. 1993, 97, 4984–4988. [Google Scholar] [CrossRef]
- Hoffman, D.K.; Kouri, D.J. Distributed approximating functionals: A new approach to approximating functions and their derivatives. In Proceedings of the Third International Conference on Mathematical and Numerical Aspects of Wave Propagation (SIAM), edited by Gary Cohen, Mandelieu-La Napoule, France, 24–28 April 1995; pp. 56–83. [Google Scholar]
- Hoffman, D.; Wei, G.; Zhang, D.; Kouri, D. Shannon—Gabor wavelet distributed approximating functional. Chem. Phys. Lett. 1998, 287, 119–124. [Google Scholar] [CrossRef]
- Bodmann, B.G.; Hoffman, D.K.; Kouri, D.J.; Papadakis, M. Hermite distributed approximating functionals as almost-ideal low-pass filters. Sampl. Theory Signal Image Process. 2008, 7, 15. [Google Scholar]
- Friedrichs, K.O. On the differentiability of the solutions of linear elliptic differential equations. Commun. Pure Appl. Math. 1953, 6, 299–326. [Google Scholar] [CrossRef]
- Schechter, M. Modern Methods in Partial Differential Equations: An Introduction; McGraw-Hill Inc.: New York, NY, USA, 1977. [Google Scholar]
- Yosida, K. Functional Analysis, Reprint of the Sixth (1980) Edition; Springer-Verlag: Berlin, Germany, 1995; Volume 11. [Google Scholar]
- Gaffney, M.P. A special Stokes’s theorem for complete Riemannian manifolds. Ann. Math. 1954, 60, 140–145. [Google Scholar] [CrossRef]
- Ni, L.; Markenscoff, X. The self-force and effective mass of a generally accelerating dislocation I: Screw dislocation. J. Mech. Phys. Solids 2008, 56, 1348–1379. [Google Scholar] [CrossRef]
- Ashino, R.; Desjardins, J.S.; Heil, C.; Nagase, M.; Vaillancourt, R. Pseudo-differential operators, microlocal analysis and image restoration. In Advances in Pseudo-Differential Operators; Birkhäuser Verlag: Basel, Switzerland, 2004; pp. 187–202. [Google Scholar]
- Boyd, J.P. Asymptotic Fourier Coefficients for a C∞ Bell (Smoothed-Top-Hat) and the Fourier Extension Problem. J. Sci. Comput. 2006, 29, 1–24. [Google Scholar] [CrossRef]
- Termonia, P.; Voitus, F.; Degrauwe, D.; Caluwaerts, S.; Hamdi, R. Application of Boyds periodization and relaxation method in a spectral atmospheric limited-area model. Part I: Implementation and reproducibility tests. Mon. Weather Rev. 2012, 140, 3137–3148. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1992; Volume 61. [Google Scholar]
- Cordero, E.; Tabacco, A. Localization operators via time-frequency analysis. In Advances in Pseudo-Differential Operators; Birkhäuser Verlag: Basel, Switzerland, 2004; pp. 131–147. [Google Scholar]
- Ashino, R.; Boggiatto, P.; Wong, M.W. Advances in Pseudo-Differential Operators; Birkhäuser Verlag: Basel, Switzerland, 2004; Volume 155. [Google Scholar]
- Daubechies, I. Time-frequency localization operators: A geometric phase space approach. IEEE Trans. Inf. Theory 1988, 34, 605–612. [Google Scholar] [CrossRef]
- Oberguggenberger, M.B. Multiplication of Distributions and Applications to Partial Differential Equations; Longman Scientific & Technical: Harlow, Essex, UK, 1992; Volume 259. [Google Scholar]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Triebel, H. A localization property for Bspq and Fspq spaces. Stud. Math. 1994, 109, 183–195. [Google Scholar]
- Feichtinger, H.G.; Gröchenig, K. Gabor frames and time-frequency analysis of distributions. J. Funct. Anal. 1997, 146, 464–495. [Google Scholar] [CrossRef]
- Skrzypczak, L. Heat and Harmonic Extensions for Function Spaces of Hardy–Sobolev–Besov Type on Symmetric Spaces and Lie Groups. J. Approx. Theory 1999, 96, 149–170. [Google Scholar] [CrossRef]
- Feichtinger, H.G. Modulation spaces: Looking back and ahead. Sampl. Theory Signal Image Process. 2006, 5, 109. [Google Scholar]
- Nguyen, H.Q.; Unser, M. A sampling theory for non-decaying signals. Appl. Comput. Harmon. Anal. 2017. [Google Scholar] [CrossRef]
- Feichtinger, H.G. Thoughts on Numerical and Conceptual Harmonic Analysis. In New Trends in Applied Harmonic Analysis; Birkhäuser: Cham, Switzerland, 2016; pp. 301–329. [Google Scholar]
- Daubechies, I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Gröchenig, K. Localization of frames, Banach frames, and the invertibility of the frame operator. J. Fourier Anal. Appl. 2004, 10, 105–132. [Google Scholar] [CrossRef]
- Wilczok, E. New uncertainty principles for the continuous Gabor transform and the continuous wavelet transform. Doc. Math. 2000, 5, 201–226. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press, Elsevier: Burlington, MA, USA, 1999. [Google Scholar]
- Higgins, J.R. Sampling Theory in Fourier and Signal Analysis: Foundations; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Gröchenig, K.; Zimmermann, G. Hardy’s theorem and the short-time Fourier transform of Schwartz functions. J. Lond. Math. Soc. 2001, 63, 205–214. [Google Scholar] [CrossRef]
- Schoenberg, I.J. On totally positive functions, Laplace integrals and entire functions of the Laguerre-Pólya-Schur type. Proc. Natl. Acad. Sci. USA 1947, 33, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Schoenberg, I. On variation-diminishing integral operators of the convolution type. Proc. Natl. Acad. Sci. USA 1948, 34, 164–169. [Google Scholar] [CrossRef] [PubMed]
- Boyd, J.P. Asymptotic coefficients of Hermite function series. J. Comput. Phys. 1984, 54, 382–410. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Dover Publications: Mineola, NY, USA, 2001. [Google Scholar]
- Janssen, A.; Strohmer, T. Hyperbolic secants yield Gabor frames. Appl. Comput. Harmon. Anal. 2002, 12, 259–267. [Google Scholar] [CrossRef]
- Fazio, E.; Renzi, F.; Rinaldi, R.; Bertolotti, M.; Chauvet, M.; Ramadan, W.; Petris, A.; Vlad, V. Screening-photovoltaic bright solitons in lithium niobate and associated single-mode waveguides. Appl. Phys. Lett. 2004, 85, 2193–2195. [Google Scholar] [CrossRef]
- Smith, J.O.; Serra, X. PARSHL: An Analysis/Synthesis Program for Non-Harmonic Sounds Based on a Sinusoidal Representation. Technical Report CCRMA STAN-M-43. Available online: https://ccrma.stanford.edu/STANM/stanms/stanm43/stanm43.pdf (accessed on 7 August 2017).
- Boggiatto, P. Localization operators with L p symbols on modulation spaces. In Advances in Pseudo-differential Operators; Birkhäuser Verlag: Basel, Switzerland, 2004; pp. 149–163. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech house, Inc.: Norwood, MA, USA, 2005. [Google Scholar]
- Yaroslavsky, L. Efficient algorithm for discrete sinc interpolation. Appl. Opt. 1997, 36, 460–463. [Google Scholar] [CrossRef] [PubMed]
- Guichard, F.; Malgouyres, F. Total variation based interpolation. In Proceedings of the 9th European Signal Processing Conference, Rhodes, Greece, 8–11 September 1998; pp. 1–4. [Google Scholar]
- Coleri, S.; Ergen, M.; Puri, A.; Bahai, A. Channel estimation techniques based on pilot arrangement in OFDM systems. IEEE Trans. Broadcast. 2002, 46, 223–229. [Google Scholar] [CrossRef]
- Serra, X.; Smith, J. Spectral modeling synthesis: A sound analysis/synthesis system based on a deterministic plus stochastic decomposition. Comput. Music J. 1990, 14, 12–24. [Google Scholar] [CrossRef]
- Muquet, B.; Wang, Z.; Giannakis, G.B.; De Courville, M.; Duhamel, P. Cyclic prefixing or zero padding for wireless multicarrier transmissions? IEEE Trans. Commun. 2002, 50, 2136–2148. [Google Scholar] [CrossRef]



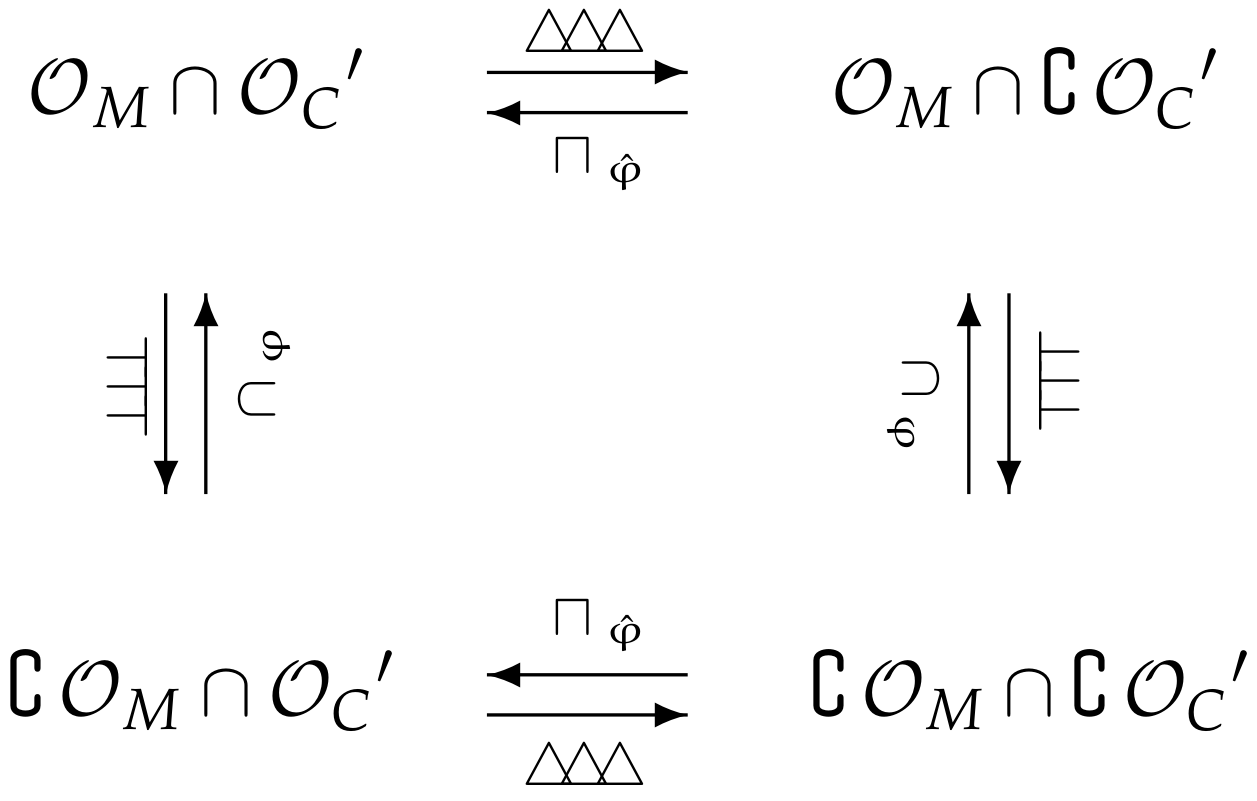

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, J.V. On the Duality of Regular and Local Functions. Mathematics 2017, 5, 41. https://doi.org/10.3390/math5030041
Fischer JV. On the Duality of Regular and Local Functions. Mathematics. 2017; 5(3):41. https://doi.org/10.3390/math5030041
Chicago/Turabian StyleFischer, Jens V. 2017. "On the Duality of Regular and Local Functions" Mathematics 5, no. 3: 41. https://doi.org/10.3390/math5030041
APA StyleFischer, J. V. (2017). On the Duality of Regular and Local Functions. Mathematics, 5(3), 41. https://doi.org/10.3390/math5030041





