On Autonomy Imposition in Zero Interval Limit Perturbation Expansion for the Spectral Entities of Hilbert–Schmidt Integral Operators †
Abstract
:1. Introduction
2. Integral Operators and Their Spectral Properties
3. Perturbation Scheme at the Zero Interval Limit
4. Constraints on the Kernel and the Construction of the Perturbation Series
5. Error Analysis
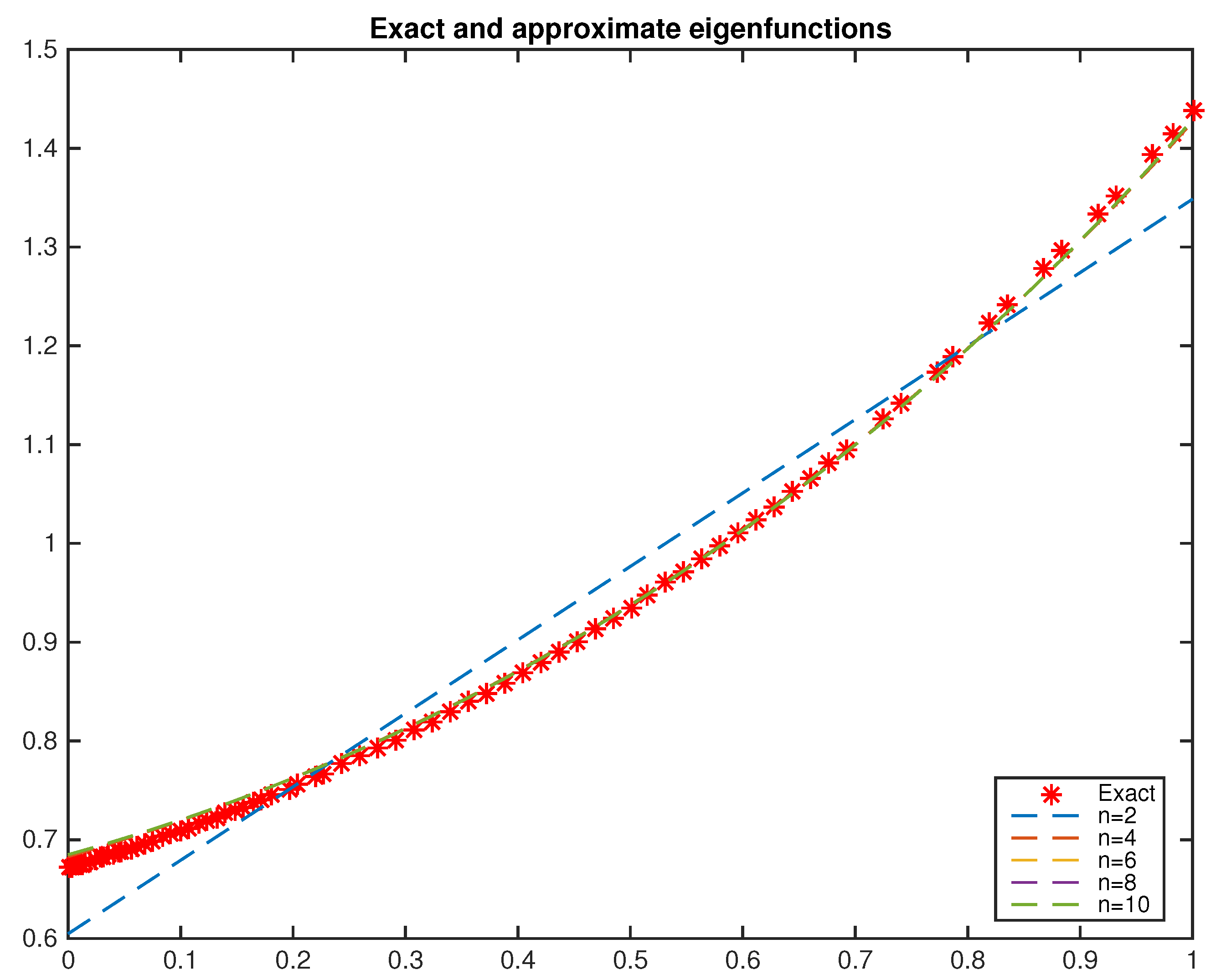
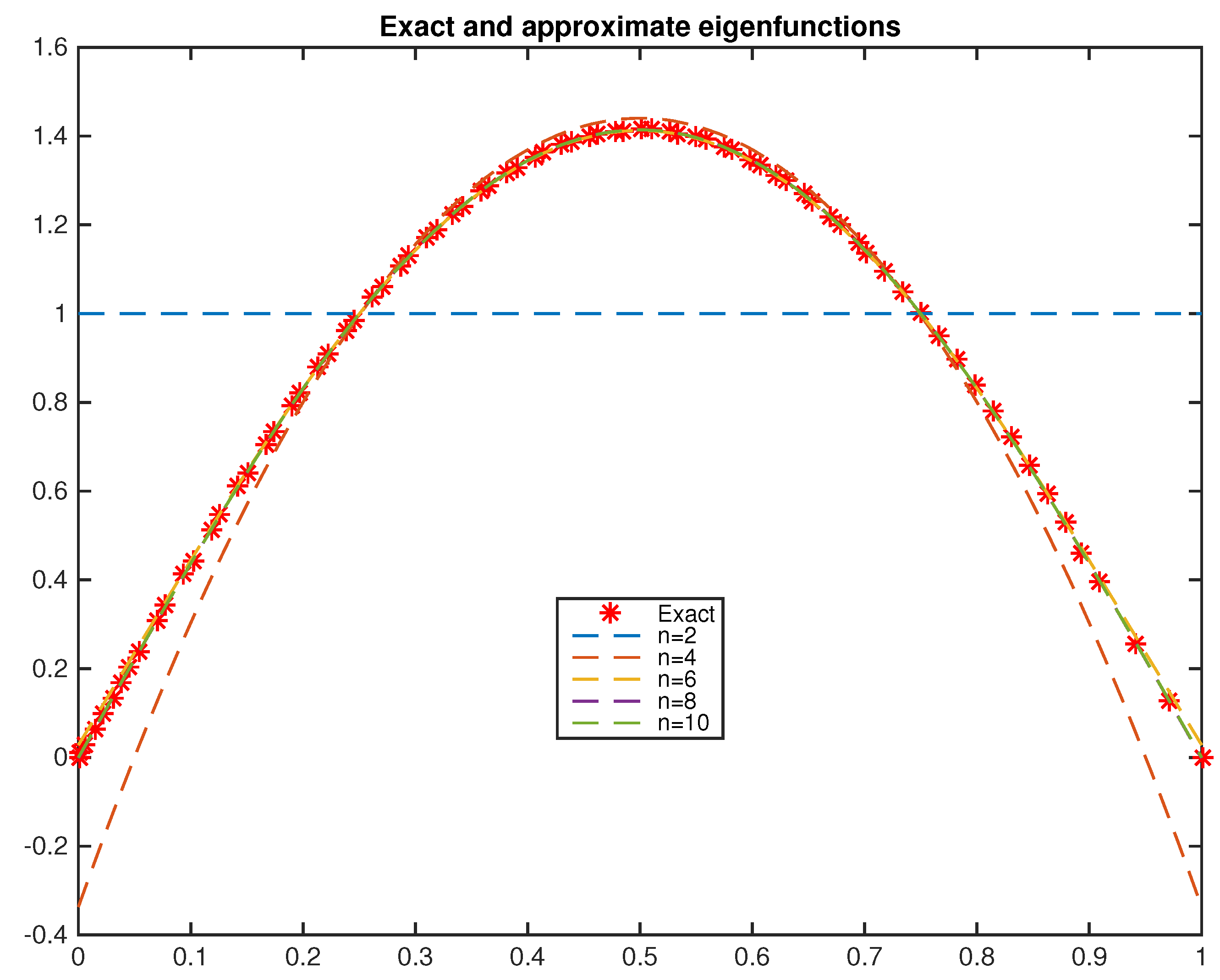
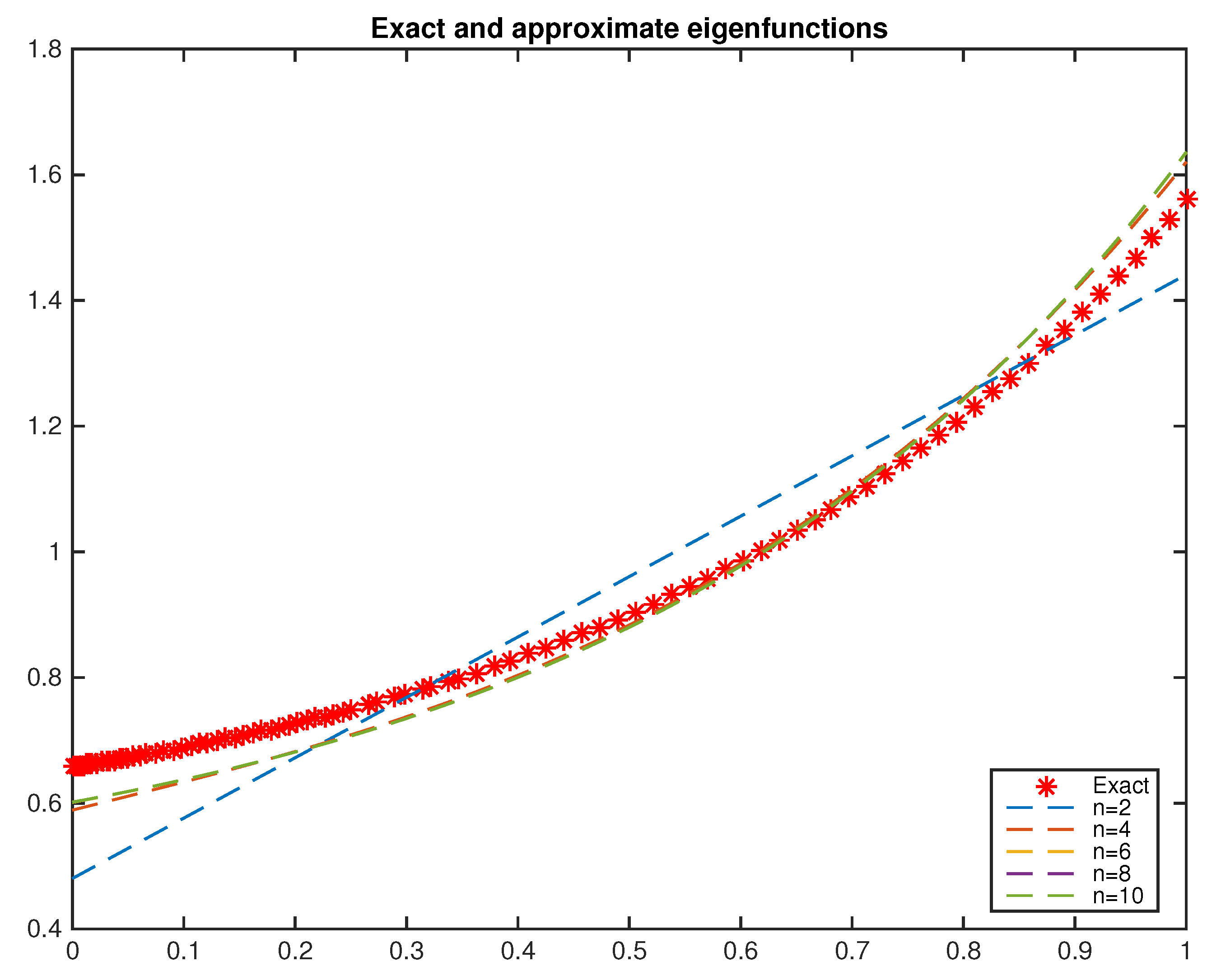
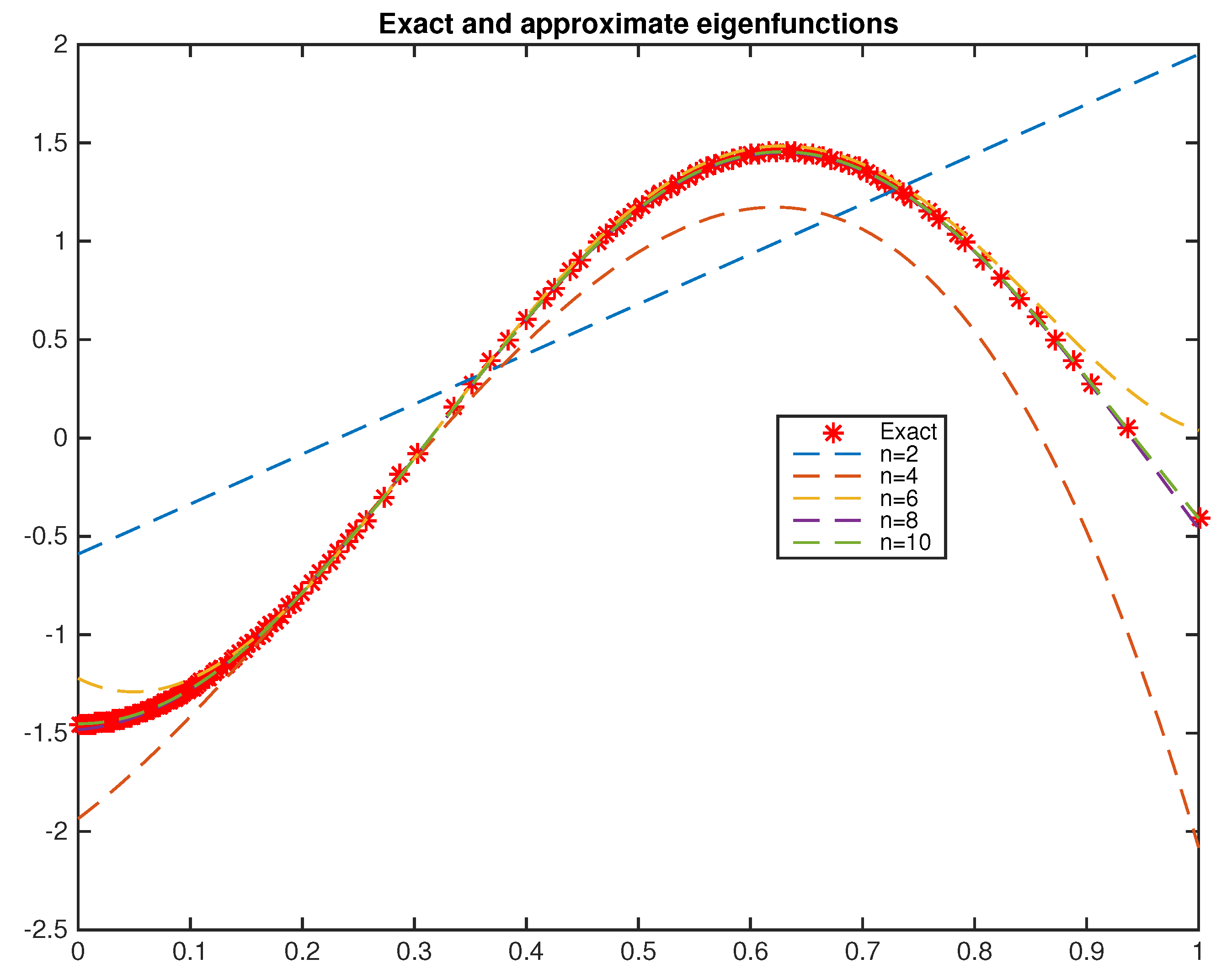
6. Numerical Implementations
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Gan, H.H.; Eu, B.C. Application of the integral equation theory of polymers: Distribution function, chemical potential, and mean expansion coefficient. J. Chem. Phys. 1993, 99, 4103–4111. [Google Scholar] [CrossRef]
- Cancés, E.; Mennucci, B. New applications of integral equations methods for solvation continuum models: Ionic solutions and liquid crystals. J. Math. Chem. 1998, 23, 309–326. [Google Scholar] [CrossRef]
- Buchukuri, T.; Chkadua, O.; Natroshvili, D. Mixed Boundary Value Problems of Thermopiezoelectricity for Solids with Interior Cracks. Integral Equ. Oper. Theory 2009, 64, 495–537. [Google Scholar] [CrossRef]
- Tuna, S.; Demiralp, M. Bivariate Enhanced Multivariance Products Representation (EMPR) at Zero Volume Limit via Geometric Separation. In Proceedings of the AIP Conference Proceedings, Potsdam, NY, USA, 19–24 July 2015; Volume 1702, pp. 759–762. [CrossRef]
- Tuna, S.; Demiralp, M. A Novel Piecewise Multivariate Function Approximation Method via Universal Matrix Representation. J. Math. Chem. 2013, 51, 1784–1801. [Google Scholar] [CrossRef]
- Debnath, L.; Mikusinski, P. Introduction to Hilbert Spaces with Applications; Elsevier: Burlington, MA, USA, 2005. [Google Scholar]
- Tricomi, F.G. Integral Equations; Interscience Publishers: New York, NY, USA, 1957. [Google Scholar]
- Porter, D.; Stirling, D.S. Integral Equations: A Practical Treatment from Spectral Theory to Applications; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin, Germany, 1995. [Google Scholar]
- Hinch, E.J. Perturbation Methods; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Holmes, M.H. Introduction to Perturbation Methods; Springer: New York, NY, USA, 1995. [Google Scholar]
- Trefethen, L.N.; Bau, D. Numerical Linear Algebra; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis; Brookes/Cole: Pacific Grove, CA, USA, 2010. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuna, S.; Demiralp, M. On Autonomy Imposition in Zero Interval Limit Perturbation Expansion for the Spectral Entities of Hilbert–Schmidt Integral Operators. Mathematics 2017, 5, 2. https://doi.org/10.3390/math5010002
Tuna S, Demiralp M. On Autonomy Imposition in Zero Interval Limit Perturbation Expansion for the Spectral Entities of Hilbert–Schmidt Integral Operators. Mathematics. 2017; 5(1):2. https://doi.org/10.3390/math5010002
Chicago/Turabian StyleTuna, Süha, and Metin Demiralp. 2017. "On Autonomy Imposition in Zero Interval Limit Perturbation Expansion for the Spectral Entities of Hilbert–Schmidt Integral Operators" Mathematics 5, no. 1: 2. https://doi.org/10.3390/math5010002




