Dialectical Multivalued Logic and Probabilistic Theory

Abstract

There are two probabilistic algebras: one for classical probability and the other for quantum mechanics. Naturally, it is the relation to the object that decides, as in the case of logic, which algebra is to be used. From a paraconsistent multivalued logic therefore, one can derive a probability theory, adding the correspondence between truth value and fortuity.

1. Introduction

When we toss a coin there are two possibilities: {heads} or {tails}. In the first event, we assign a probability value p and in the second a value q. In this case, p = q = 1/2. This means that for a sufficiently high number of tosses, half the time the result will be heads, and the other half it will be tails. In a (non-quantum) classic event like this, the numbers p and q are, generally, fractions less than unity. The location of the toss of a coin could be described by a combination of the two alternatives: p*{heads} + q*{tails}. In the quantum field, things are due to somewhat different probabilistic laws. Numbers p and q stop being fractions and become imaginary numbers (part real plus another imaginary part a with square root of −1) and the numbers are no longer called ‘chances’, but probability amplitudes, or just amplitudes. Events, while in that pure quantum state, are governed by probability amplitudes and have the form z = a + bi (where i is the square root of −1).

To find the real possibility when an event moves into the classic area is determined by the magnitude squared of the complex number, which is the square of the real part plus the square of the imaginary part: |z|² = a² + b² (module reads the square of z). In classical probability theory, when we want to represent the situation of the coin toss and the possibility of getting one outcome or another, we write: p*{heads} + q*{tails}. In this case, in which the sum of probabilities is 1, we will represent a certain event as (maximum probability = 1). If two runs require getting heads in the first and tails in the second, the representation would be: [p*{heads}] × [q*{tails}]. The disjunctive word “or”, becomes a sum, while the “and” becomes a product.

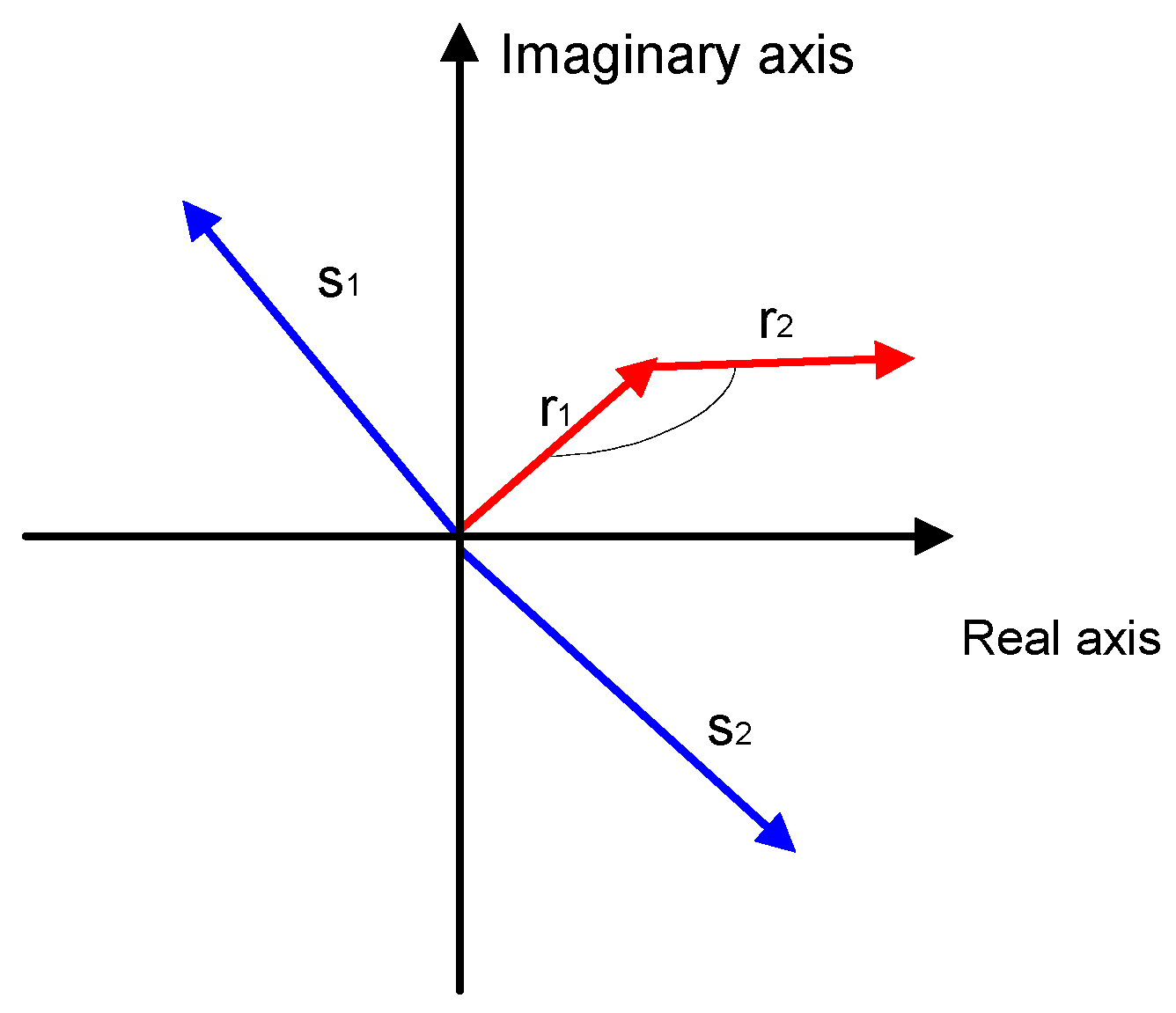
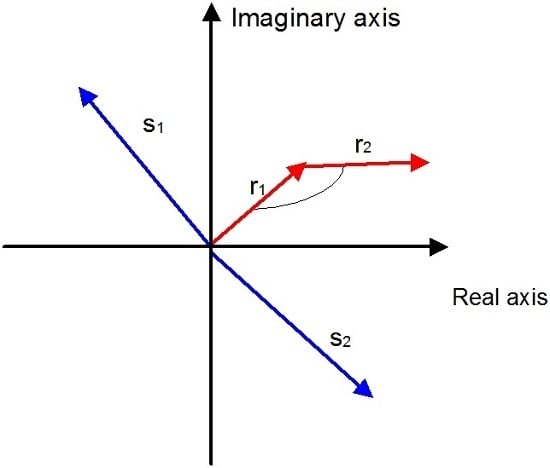
For amplitudes the same goes, but while normal probabilities naturally are summed as two simple fractional numbers, probability amplitudes are summed as vectors, and forces, as explained in Figure 1.

In our daily life, in the microphysical world probabilities offer a much poorer range than the range of quantum probability amplitudes. Again, imaginary numbers give us a little more to understand the strange and counterintuitive quantum world.

The isomorphism between a disjunctive logic and probability theory is defined by the following correspondences (

Table 1. Isomorphism between a disjunctive logic and probability theory.

Logic	Probability Theory
True	Necessary
False	Impossible
Approximate	Contingent or random
Truth value	Probability

).

From a paraconsistent multivalued logic, [1,2] a probability theory can be derived, adding a correspondence between value truth and fortuity. Regarding countable probabilities, fortuity is by definition a complex number whose squared modulus is a probability. In continuous probabilities, the fortuity density is a complex function of the actual random variable whose squared modulus is the probability density.

2. Probabilistic Axiomatics

We look to the axiomatic basis developed by Kolmogorov [3] for classical probability theory to generalize it to be extended to other probability theories. Furthermore, we will propose axioms directly in probabilistic language rather than ordinary language.

Let O be an abstract general object, such as the roll of a coin with its motion and stopping. Let x, y, z,…, be the characteristics of O, i.e., its attributes, that they are general and therefore required, for example the coin stops resting on one side. When O passes from a formal existence of a logical entity to a real physical existence, localized in space and time, that is, when O is updated and becomes an event, a general attribute x may take one or another of the particular mutually incompatible variants $x_1,x_2,...,x_k$; and attribute y may take one of the mutually incompatible variants $y_1,y_2,...,y_l$, etc. We will call $x_1,x_2,...,x_k,y_1,y_2,...,y_l$ the “elementary contingencies” of O. While attributes of O, as an abstract general object, they are possible or random. While attributes of O, which are realized in any actual time, they become “elementary events”.

Let E be the set of elementary contingencies (or elementary events) and F be a set containing the empty set, E and all parts of E are defined as follows: $F=\left\{\varnothing ,E,P(E)\right\}$.We will stick here to the finished sets E, they are sufficient for our logical study. Given that a general object is reproducible, in probability theory a repetition of N copies of an object O is often taken as an object of study, described as O^N. By numbering these copies with the index $\alpha$, the number of attributes $x_{\alpha },y_{\alpha }$ and that of their variants—$x_{\alpha i},y_{\alpha j}$, etc.—is multiplied by N. Note that this does not change the definitions of the sets E and F.

Every subset A of F, $A\subseteq F$ defines a contingency of the general object or an event of the updated object. We point out that, and according to Kolmogorov, for a set of contingencies to be realized, it is sufficient that at least one of its elements is realized. Thus, for O to be realized, it is sufficient that one of the elementary contingencies becomes an event.

E designates a set of elements $\varphi$ called “fortuitous”, identical to a set of truth values of multivalued logic. Let V be the function that transforms the truths into degrees of truth in multivalued logic.

The axioms are:

Axiom 1:

Any eventuality A has a fortuity $\varphi$ and a probability $p=V\left(\phi \right).$

Axiom 2 (Axiom of Necessity):

$p\left(E\right)=1.$

Axiom 3:

If A_i and A_j are two incompatible contingencies, the probability that either A_i or A_j indifferently is realized and worth $V\left({\phi }_i+{\phi }_j\right)$.

Kolmogorov adds to these axioms the definition of conditional probability that we will express as fortuitous as follows:

$${\phi }_i\left(A_j\right)=\frac{\phi \left(A_i\wedge A_j\right)}{\phi \left(A_i\right)}$$

(1)

Note that all elementary contingencies are a necessary attribute of the general object O. It is the same for all of their respective probabilities. Hence, it follows that statistical averages of all kinds are also necessary attributes of this general object.

Example 1:

Let O be a Gibbs thermodynamic system and the set of possible values ${\epsilon }_i$ (elementary contingencies) with the energy $\epsilon$ of a very small subsystem determined by the laws of physics, the Schrödinger equation for example. Probabilities $p\left({\epsilon }_i\right)$ are determined by another physical law, Boltzmann’s theorem $p\left({\epsilon }_i\right)=A{e}^{-\frac{{\epsilon }_i}{kT}}$, A and k are constants, T is the temperature.

3. Probabilities and Truth Values

Propositional algebra [1] takes into account only the truth value of propositions. A probability theory foregrounds its modality, that is, its necessity or contingency, its possibility or impossibility; and closely associated to its modality, its generality and its particularity, involving the categories of being and existence (possible, real, actual, contingency, and event). In probability theory, the truth value of the propositions is determined by the modality and related categories, which we mentioned in the preceding paragraphs.

Definition 1:

A statistical proposition is a proposition stating an event.

Let A be a contingency and $A^{°}$ be statistical proposition stating the realization of A. The verb tense in $A^{°}$ is either present, or past. A is an experimental constant, hence the adjective statistical. So, an updated object A can only be true or false and there is not a third possible value.

Consequence 1:

In relation to statistical propositions only classical logic is applied.

In the general object O, the truth value of $A^{°}$ is a random variable with only two possible values $v(A^{°})=0$ and $v(A^{°})=1$. To say that p(A) is the probability “of A is realized”, amounts to saying “$v(A^{°})=1$”. From where:

$$p\left(A\right)=p\left[v\left(A^{°}\right)=1\right]$$

(2)

Let $\Updownarrow$ be mutual exclusion applying to both incompatible contingencies A_i and A_j. J is “one or other of the two contingencies A_i and A_j, indifferently realized”:

$$J^{°}\iff A_i^{°}\Updownarrow A_j^{°}=1$$

(3)

Axiom 3 can then be written:

$$p\left[v\left(A_i^{°}\Updownarrow A_j^{°}\right)=1\right]=V\left({\phi }_i+{\phi }_j\right)$$

(4)

Definition 2:

A predictive proposition is a proposition that announces in advance an event.

We denote $\stackrel{⌣}{A}$ the predictive proposition announces that eventuality A will be realized. The verb tense in $\stackrel{⌣}{A}$ is therefore the future. $\stackrel{⌣}{A}$ is basically a bet.

Axiom 4:

The truth value $\alpha$ of a predictive proposition $\stackrel{⌣}{A}$, is equal to the fortuity of the contingency A, $\alpha (\stackrel{⌣}{A})=\phi \left(A\right)$.

From Axiom 1 and Axiom 4:

$$v\left(\stackrel{⌣}{A}\right)=p\left(A\right)=p\left[v\left(\stackrel{⌣}{A}\right)=1\right]$$

(5)

Consequence 2:

Predictive propositions are treated with a many-valued fuzzy logic [2].

Let $\Im$ be the complementarity. Applying this axiom to the relation (4):

$$p\left[v\left(A_i^{°}\Updownarrow A_j^{°}\right)=1\right]=v\left({\stackrel{⌣}{A}}_i\Im {\stackrel{⌣}{A}}_j\right)$$

(6)

Axiom 5:

A true statistic proposition $v(A^{°})=1$, is endowed with a fortuity $\phi$ and a probability $p\left[v\left(A^{°}\right)=1\right]=V\left(\phi \right)$.

Axiom 6:

$p\left[v\left(E^{°}\right)=1\right]=1$.

Axiom 7:

$\alpha \left(\stackrel{⌣}{A}\right)=\phi \left[v\left(A^{°}\right)=1\right]$, $\alpha$ is the truth value of $\stackrel{⌣}{A}$.

Axiom 8:

$\phi \left[v\left(A_i^{°}\Updownarrow A_j^{°}\right)=1\right]=\alpha \left({\stackrel{⌣}{A}}_i\Im {\stackrel{⌣}{A}}_j\right)$

To these axioms we add the definition of conditioned probability. To say that A_i and A_j are realized together, is equivalent to saying that $v\left(A_i^{°}\wedge A_j^{°}\right)=1$.

The definition is written thus:

Definition 3:

$${\mathsf{\phi }}_i\left[v\left(A_j^{°}\right)=1\right]=\frac{\mathsf{\phi }\left[v\left(A_i^{°}\wedge A_j^{°}\right)=1\right]}{\mathsf{\phi }\left[v\left(A_i^{°}\right)=1\right]}$$

(7)

${\mathsf{\phi }}_i$ is the conditional fortuity of A_j.

Proposition 1:

The truth value of the forecast of a conjunction is subject to the conditional probability.

Proof: 

Note $C\left(A_i,A_j\right)$ is the conjunction $A_i^{°}\wedge A_j^{°}$, and $\stackrel{⌣}{C}\left(A_i,A_j\right)$ is the forecast of the realization of $A_i^{°}\wedge A_j^{°}$.

From Axiom 4 and Definition 3:

$$v\left[\stackrel{⌣}{C}\left(A_i,A_j\right)\right]=p\left[v\left(A_i^{°}\wedge A_j^{°}\right)=1\right]=p\left(A_i\right)p\left(A_j\right)$$

(8)

Proposition 2:

The truth value of the conjunction of two predictions is not subject to the conditional probability.

Proof: 

Let ${\stackrel{⌣}{A}}_i\wedge {\stackrel{⌣}{A}}_j$ be the conjunction of predictions. The two propositions are independent bets one from the other, we have:

$$v\left({\stackrel{⌣}{A}}_i\wedge {\stackrel{⌣}{A}}_j\right)=p\left(A_i\right)p\left(A_j\right)$$

(9)

The need to distinguish a prediction of a conjunction and a conjunction of two predictions appears well if A_i and A_j are incompatible. Then $p_i\left(A_j\right)=0$, so that $v\left[\stackrel{⌣}{C}\left(A_i,A_j\right)\right]=0$. The forecasting of the realization of the conjunction cannot be as false as this realization is impossible. Instead, the bets ${\stackrel{⌣}{A}}_i$ and ${\stackrel{⌣}{A}}_j$ are not incompatible. A player can, for example, bet on roulette on two numbers at a time. This does not mean that it provides for a simultaneous realization, but it makes two bets at once, and their logical conjunction has a truth value, then $v({\stackrel{⌣}{A}}_i\wedge {\stackrel{⌣}{A}}_j)\ne 0$.

These are relationships between multivalued logic and theories of probabilities, between truth values and probabilities. These last two variables cannot be confused, although under the Axiom 3 they can be equal, since a truth value can be provided for a probability.

Consequence 3:

The probability is a value of necessity, not a truth value.

4. The Dialectic of Probability

If the fact A of a random process has the probability p, the negation of A (¬A) has the probability 1 − p and, in the case of maximum autonomy, the conjunction $A_i\wedge A_j$ has probability $p_i{p}_j.$ Now that is enough to justify the isomorphism between the algebra of classical probabilities and Boolean algebra. In addition, rather than accommodate the values 0 and 1, one can use the set [0, 1], that is, multivalued Boolean algebra.

According to References [1,2,4,5] probability theory as used in quantum physics is a paraconsistent dialectical multivalued logic.

Let P be a proposition belonging to a language L and ¬⃞P be its negation. To any proposition P is attributed a truth value that we will call v (P) = p, here p is 1 or 0, that is to say, p = 1 means P is true and p = 0 means it is false.

Definition 4:

The CO-contradiction (coincidentia oppositorum contradiction) is the compound proposition $P\wedge \neg P$ that is the logical conjunction “P and not P”.

In Aristotelian logics, P ∧ ¬P it is always considered false ∀Q y ∀q, P ∧ ¬P → Q and it has the value v(P ∧ ¬P → Q) = 1 − p(1 − p)(1 − q) = 1, that is it to say: P ∧ ¬P ⇒ Q.

Definition 5:

We define K(ℵ) as a Coincidentia oppositorum proposition that is a contradiction P ∧ ¬P whose truth value is always 1, i.e., v(P ∧ ¬P) = 1.

A coincidentia oppositorum proposition is formed by two poles: the pole of assertion P and the negative pole ¬P.

Definition 6:

A polar propositions is the proposition P and its negation ¬P; constituents of a coincidentia oppositorum proposition K(ℵ).

Definition 7:

u is a denier of the proposition A if the following three conditions are fulfilled:

a) 

$u\in E$

b) 

$V(u)=1;$ u has unitary truth value (from Axiom 6)

c) 

$u-p=p^{*}\in E$ (from Axiom 1)

In general, these three conditions can be satisfied by a set of deniers of A, then the contradictory ¬A has a priori, once p is fixed, a set of truth values p*(u); so the choice of a denier, in a problem of applied logic, will determine the truth value of the contradictory.

The determination of probabilities by complex numbers also led to another new feature called the Fourier correlation between two random variables one of which is necessarily continuous. It is called the Born-Fourier correlation, since Max Born was the first to use the Fourier correlation to give the theories of de Broglie and Schrödinger their probabilistic meaning.

Let x and v be two continuous random variables with fortuity densities of $\varphi \left(x\right)$ and $\psi \left(v\right)$. By definition, these variables are related by a Born-Fourier correlation if $\varphi$ and $\psi$ are reciprocal Fourier transforms of Fourier [6]:

$$\begin{array}{l}\varphi \left(x\right)=\frac{1}{\sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\psi \left(v\right)}{e}^{ixv}dv\\ \psi \left(v\right)=\frac{1}{\sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\varphi \left(x\right)}{e}^{ivx}dx\end{array}$$

The Parseval-Plancherel identity [7]:

$${{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\left|\varphi \left(x\right)\right|}}^{2}dx={{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\left|\psi \left(v\right)\right|}}^{2}dv$$

ensures that $\varphi$ and $\psi$ fulfil the requirements to be densities of fortuity; it is enough that their norms are equal to unity.

The mean squared deviations $\sigma \left(x\right)$ and $\sigma \left(v\right)$ of two variables the Fourier correlation, are necessarily linked by Heisenberg’s inequality:

$$\sigma \left(x\right)\cdot \sigma \left(v\right)\ge \frac{1}{2}$$

Logically, the Born-Fourier correlation should have been defined axiomatically by probabilistic mathematics. The characteristic Cauchy function, naturally leads to the Fourier transform of the probability density for a continuous variable. It is a pure historical accident that physicists found and studied this correlation. Paul Lévy [8] rediscovered and developed the theory of characteristic functions and then read Cauchy’s note in the French Academy of Sciences, which had been forgotten, even at the time when de Broglie, Schrodinger, and Born produced their work.

To the fact A is attributed a complex fortunity φ of a module belonging to [0, 1], and a probability $p={\left|\varphi \right|}^2.$ ¬A has a fortuity $\neg \varphi =u-\varphi$ where u is a denier such that ${\left|u\right|}^2=1$ and for a probability $\neg p={\left|u-\varphi \right|}^2$. The conjunction $A_i\wedge A_j$ has the probability ${\left|{\varphi }_i{\varphi }_j\right|}^2=p_i{p}_j$, in the case of maximum autonomy, as in classical probabilistic algebra. In this case, probabilistic quantum algebra has two new features:

(1) The achievement of total probability arises by adding fortuities and not probabilities. Thus, we have:

$${\left|\varphi +\neg \varphi \right|}^2=1$$

(10)

but:

$$p+\neg p={\left|\varphi \right|}^2+{\left|\neg \varphi \right|}^2\ne 1$$

(11)

Consider a practical example. We throw a die twice successively, the combination of 3 and 4 can be obtained by chance in two ways; either 3 followed by 4, or a 4 followed by 3. If p₁ and p₂ are the respective probabilities of each possibility, the probability of the combination (a 3 and a 4) is $p_1+p_2$. This comes from classical probability algebra.

Example 2:

A monokinetic beam of microphysical particles arrives on a diaphragm D with two striped thin slits F₁ and F₂ perpendicular to the figure’s plane. It then passes through a lens L, and is received on a screen E located in the focal plane. (Figure 2).

Reasoning in the context of Quantum Mechanics. The random variables by Fourier correlation are:

(a)

The crossing point P of a particle whose fortuity density $\phi \left(\overrightarrow{P}\right)$ is called a wave function.

(b)

The momentum $\overrightarrow{p}$of a particle with fortuity density $\psi \left(\overrightarrow{p}\right)$.

The statistical distribution of particles on E is the momentum after crossing the diaphragm. Upstream (of the diaphragm), the momentum ${\overrightarrow{p}}_0$ is the same for all the particles, it is not random.

Crossing the slots, the movement of the particles changes direction, so they shall exchange the amount of movement with the diaphragm, but without an exchange of energy. It is this that constitutes their diffraction. The experiment establishes that if one of the slots is closed, the distribution of particles on E is nearly uniform while if both slots are open, the distribution is radically different: that is, the particles accumulate at equidistant lines parallel to the slots (bright fringes) and are instead missing along lines which are inserted in the first (dark fringes). The Born-Fourier correlation is fully aware of the two distribution modes, but it leaves a feeling of misunderstanding and this is the tricky part. Indeed, as the fringes manifest themselves, there must be a huge number of particles reaching E. This number can be obtained as well in a very short time thanks to a powerful source that emits many particles in both in a very long time with an extremely low source that debited the particles one by one (diffraction experiments of photons or electrons one by one). The statistical distribution of E is the same in both cases; similarly, the statistic of a game of dice is the same if we throw consecutively the same die 1000 times, or throw 1000 identical dice in one moment. Therefore, in the design in the second case (launched particles one by one) a particle passes through the slot F₁. If F₂ is closed, it has equal chances of reaching any point M of E. If F₂ is open, on the contrary the chances become very unequal for reaching the different points M. In particular, the points on the dark fringes have zero chance of being reached by the particle. So, the random change of momentum that follows the F₁ crossing does not have the same probability when F₂ is open or closed. Note that when F₂ is located at a macroscopic distance from F₁, that is huge compared to the particle size. If one conceives of the microphysical object or micro-object as strictly localized, punctual at the macroscopic scale, and as moving in empty space, sort of physical nothingness, as does it the classical mechanics this influence at a great distance is very difficult to understand. If, as proposed by Schrödinger, one conceives of the influence as an extended and continuous wave, it is the effects on the particle that become incomprehensible. Unless we give up any attempt at an explanation, the only reasonable course seems to be thinking of a micro-object as composed of a point particle at the scale of our senses, which is concentrated in energy and inertia, and a having a sort of extended and continuous halo that surrounds it and which, while being devoid of energy and inertia itself, can serve as a mediator for an exchange of momentum between the corpuscle and another object. If this theory is adopted, the micro-object becomes a whole, endowed with opposite qualities—punctual and extended, discontinuous and continuous, inert and without inertia—which reports a dialectical logic.

From the mechanistic point of view, we can consider a micro-object reaches a point M on the plane E passing through F₁ or through F₂. Let P be the proposition “the particle passes through F₁” and ¬P be the proposition “the particle passes through F₂”. Then in the mechanistic point of view$v\left(P\Updownarrow \neg P\right)=1$. In Newtonian mechanics, we reason according to classic logic. From the point of view of quantum mechanics, the micro-object passed through both F₁ and F₂: $v\left(P\wedge \neg P\right)=1$. This constitutes a coincidentia oppositorum proposition and the reasoning follows dialectical logic.

However, the theory of probability which, by Fourier’s correlation, calculates the statistical distribution of particles such that it is observed experimentally on the photographic plate is not the classical theory, but a probability theory, isomorphic with dialectical logic. So, there is an inconsistency in the mechanistic and wave conceptions; they calculate with a dialectic probability theory while they argue with the logic of Aristotle. However, the inconsistency can be eliminated. Indeed $v\left(P\Updownarrow \neg P\right)=1$ in the classic sense, it is applied to the single particle and $v\left(P\wedge \neg P\right)=1$. It is applied to one halo, $v\left(P\Updownarrow \neg P\right)=1$ concerns the entire micro-object which passes through a slot or through another, but can also pass through both slots at once.

(2) Let σ be the standard deviation of a distribution of a random variable. This magnitude expresses the degree of contingency of the random variable. Indeed, σ² is the average of the squares of the differences x_i − x_m, i.e.,:

$${\sigma }^2=p_1{\left(x_1-x_m\right)}^2+p_2{\left(x_2-x_m\right)}^2+...+p_n{\left(x_n-x_m\right)}^2={\displaystyle \sum _{i=1}^n{p}_i}{\left(x_i-x_m\right)}^2$$

(12)

From this definition, it follows that if the variable x is necessary, σ is null and reciprocally, σ = 0 implies x is necessary. When σ is bigger, the values x_i are further away from x_m; so the contingent character of x is enhanced and this extends its field of compossibility. Novelty is a mode of correlation between two random variables x and q that are totally alien within classical probability algebra, and which has among others the following fact: The product ${\sigma }_x\times {\sigma }_q$ of the grades of contingency must be greater than a certain positive number. That is to say ${\sigma }_x\times {\sigma }_q>\epsilon ,\epsilon >0,\epsilon \in R.$ This number, and σ_x and σ_q, and the stated inequality, are all necessary characters within the random process and are part of an objective law of random processes. What is the content of this law? The inequality of x and q are needed at once, because if ${\sigma }_x=0={\sigma }_q$, then the inequality would not be satisfied, and the consequence is that if the degree of contingency of one of the two variables approaches zero, the degree of contingency of the other must increase so that inequality is maintained. That is, the pair of variables x and q contains an indelible randomness, which is characteristic of the process.

Example 3:

The oscillations of the nuclei of a diatomic molecule. We refer to the movement of a nucleus N relative to another stationary nucleus N, x is the abscissa of N on the line NN′ and q the momentum of N. The necessary inequality is:

$${\sigma }_x\times {\sigma }_p\ge \frac{\hslash }{2}$$

This inequality is called the Heisenberg inequality, where $\hslash$ is Planck’s constant, which is universal, i.e., independent of the nature of the particle and its mode of movement. The oscillation is random, indicating the autonomy of the particles that make up the molecule. With decreasing oscillation energy of the molecule, decreasing ${\sigma }_x$, the degree of contingency ${\sigma }_p$ increases, i.e., the random nature of the impulse is accentuated. Needless to say, chance is perfectly objective and internal to the molecule and entirely microphysical without any macroscopic origin and so much less human.

Compare these facts with a fortuitous corpuscular movement governed by statistical mechanics, which combines Newtonian mechanics with classical probability theory.

Example 4:

Imagine the case of a monatomic gas molecule. According to these traditional theories, the point M that this particle passes and its momentum p, are two independent random variables; no correlation links their degrees of contingency, so that one can reduce the degree of freedom of the contingency of M (by reducing, for example, the volume of the container) without thereby increasing the degree of contingency of p.

5. Conclusions

In respect of statistical modality, generality, and particularity, analytical concepts and synthetic concepts are opposed. The first is general and abstract, which means that it wants to ignore all the peculiarities (contingencies) of the object and it retains what is necessary. The second is concrete and general: to the abstract general concept, it adds and integrates all possible features; so necessarily it integrates the contingent and the random. According to analyses here of basic probabilistic concepts, the object O in probability theory is not analytic but synthetic.

Classical mechanics is an example of a purely analytical theory; it is deterministic, which means that it takes into consideration all the necessary relations implied. If one considers a roll of a die on a table and contemplates it resting on one face, one is not preoccupied with the other faces. On the contrary, the statistical scientist thinks of all six possibilities for the final position of the dice. The synthetic character of the probabilistic concept of the object explains a theory of derived probabilities, not from a purely analytical classical logic, but from a dialectical logic in which contradiction is not necessarily false.

Notwithstanding, the innovations introduced by quantum physics to probability theory, there is no change at all for the concepts of modality, chance, and probability. Considering Heisenberg’s inequality, neo-positivists have made a citadel of physical indeterminacy emphasizing that the greater physical error is due to the purely objective degree of contingency of a random microphysical magnitude, with the result of a measurement of magnitude which is objective too, but involving human intervention and, in any case, macroscopic. Thus the Copenhagen interpretation considers how assessment of our uncertainty is due to the inevitable imprecision of a macroscopic measure, touching the position x, or the momentum p of a particle, and not about characteristics inherent to this movement, microphysical and fortuitous, which feature independently of all measurement. However, the Copenhagen interpretation does nothing but strangely juxtapose the mathematical texts which say nothing about the characteristics that are independent of all measurement. On the contrary, in quantum mechanics as in every other field of statistical physics, the two sets contingency are independent in principle: those referring to the phenomena, being of much larger significance than the second set, the metrological. This is easy to demonstrate, for example in the case of a diffraction phenomenon. Consider the objectivity of the degrees of contingency and correlation in the diffraction of cosmic corpuscles through terrestrial crystalline rocks. This is a process that conforms to Heisenberg’s inequality, and was the case long before the appearance of man on Earth.

Because of this position, there is a confrontation between classical mechanics and quantum mechanics. The comparison of probabilistic mechanics (quantum mechanics) with deterministic mechanics (classical mechanics) is absurd. It comes from focusing on the internal fortuity of microphysical movement, and emphasizing metrological macroscopic random movement rather than any theory. Such confusion is the result of the lack of reflection on two main scientific problems: chance, and the link between what is macroscopic, observable, and measurable, and its object microphysical phenomena.

Heisenberg [9] did not want to consider pure contingency and emphasised the random-deterministic thesis of ignorance linked to a narrower positivism. He believed and continually repeated that the notions expressed by the non-mathematical language of physics are the result of experience of the phenomena of everyday life. The language of physics, therefore, is not perfectly suited to nature, but nevertheless, it is impossible to replace this language and we should not try. From the point of view of neo-positivists, reason cannot exceed experience. Such inadequacy is at the root of the statistical nature of quantum mechanics: one proceeds from chance to an epistemology. This was pointed out by the neo-positivists, stating that the probability function used by quantum mechanics combines elements that are entirely objective with statements about possibilities with subjective elements and with our incomplete knowledge of the process. It is their view that it is this latter incomplete knowledge of the process that implies the impossibility of predicting by using probability. As for the opponents of the Copenhagen school, usually none have rejected the interpretation of Heisenberg’s inequality principle based on the measurement, or at least of the interaction of, particles with a macroscopic body. Bohm [10,11] tried to save traditional determinism using “hidden parameters”. However, Blokhintsev [12,13] claimed objectivity and the need for probabilistic laws.