Continued-Fraction Expansion of Transport Coefficients with Fractional Calculus
Abstract
:1. Introduction
2. Methods
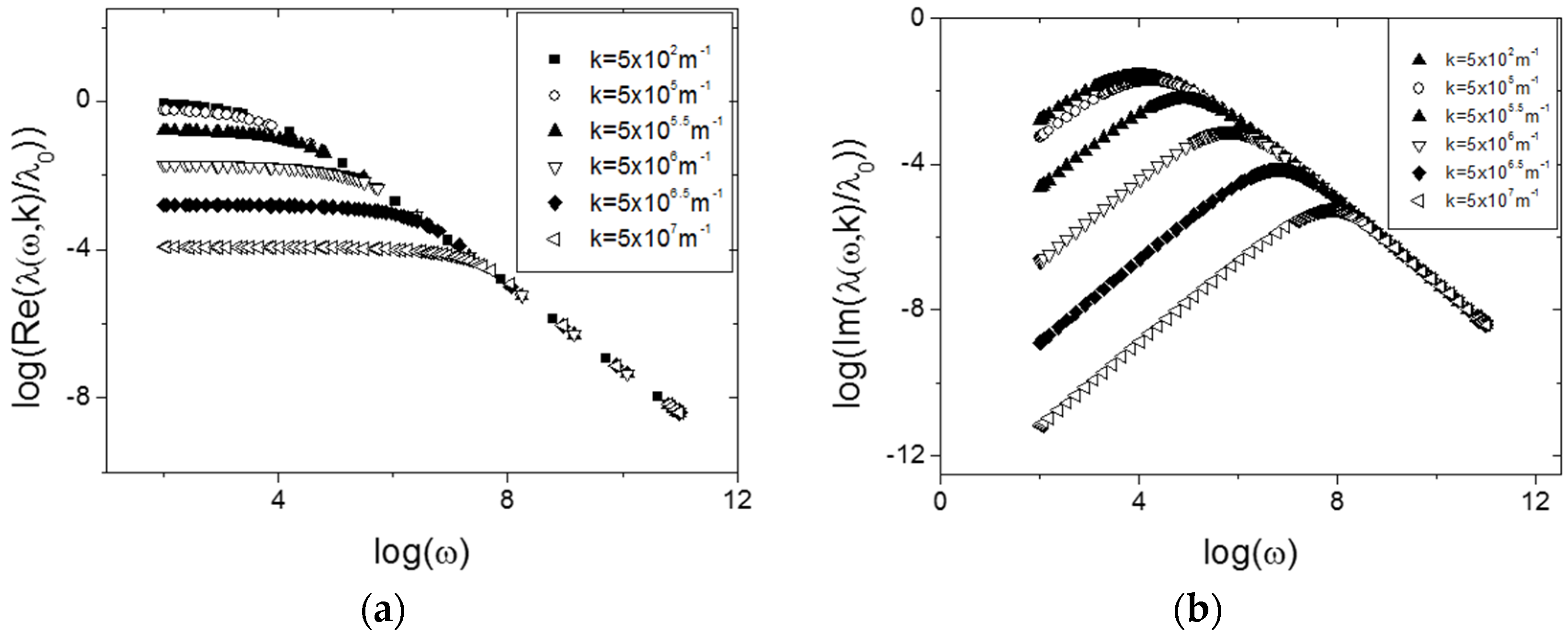
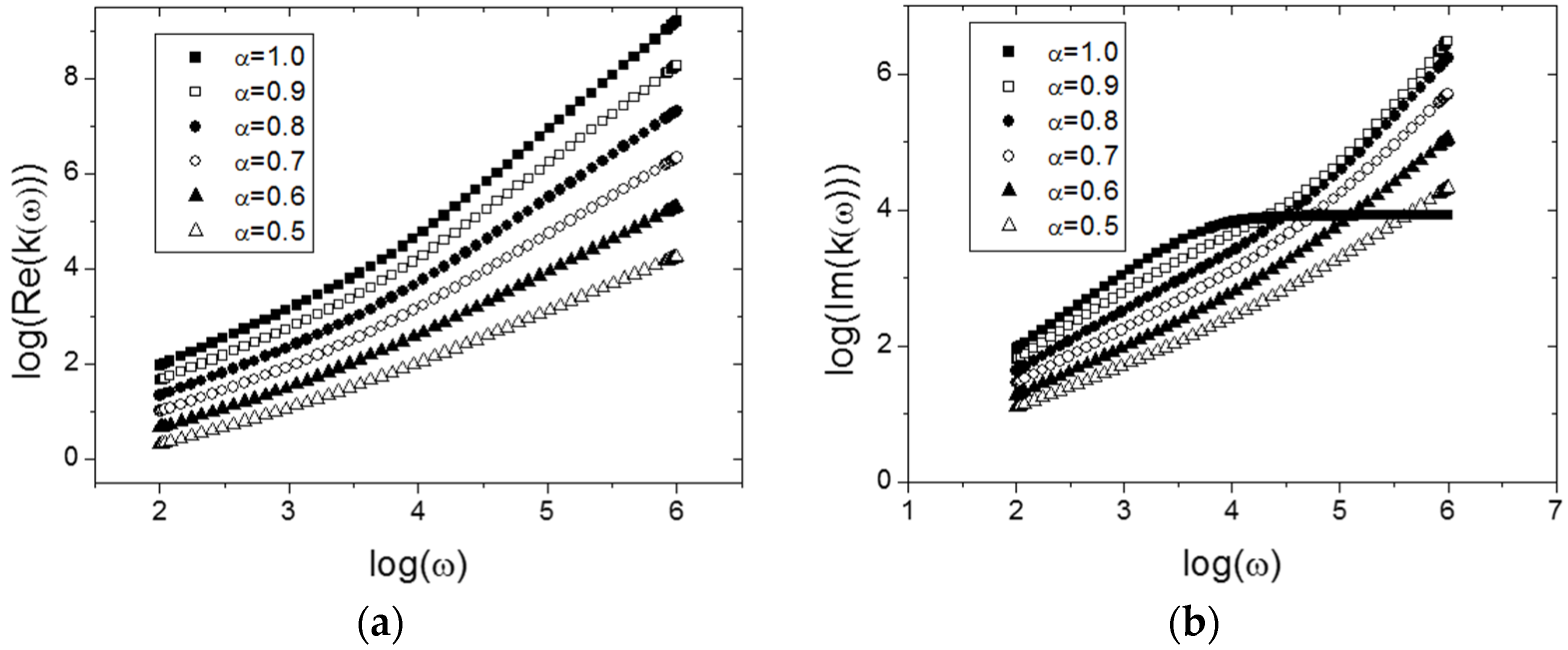
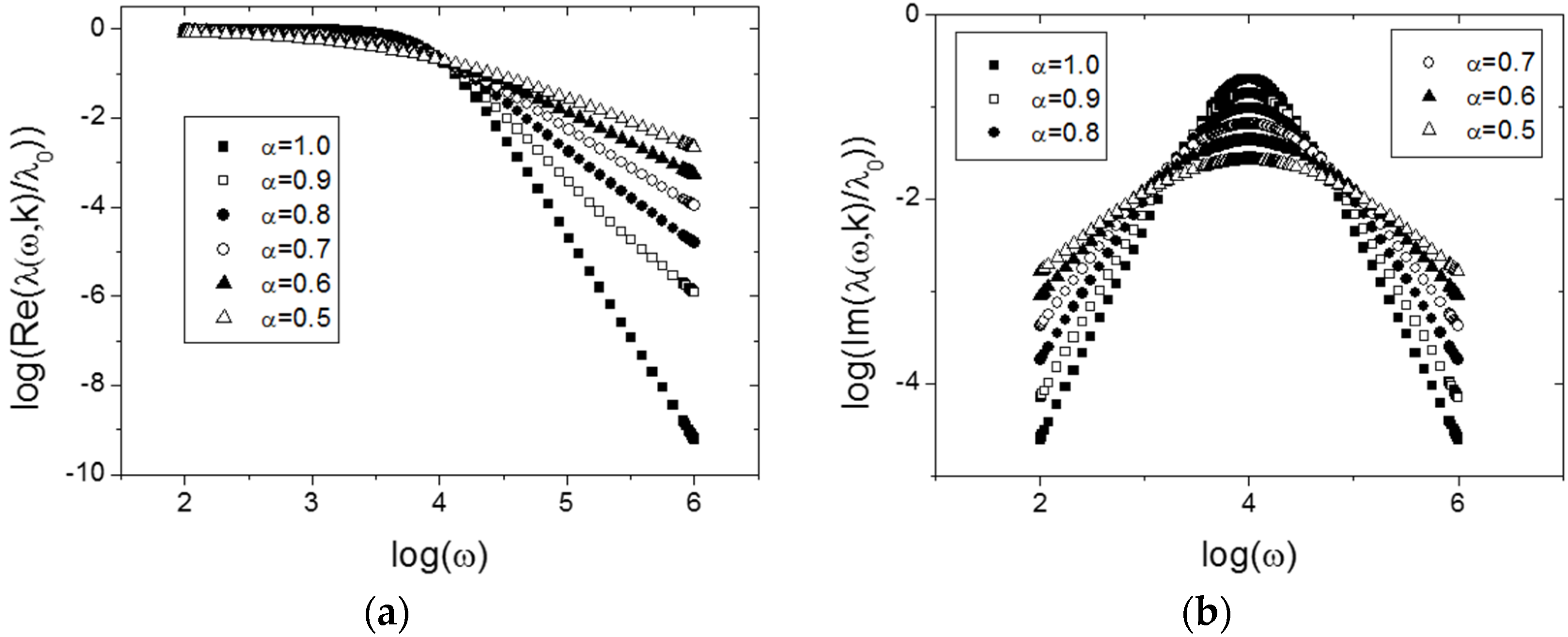
3. Results
The Relation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Dedeurwaerdere, T.; Casas-Vázquez, J.; Jou, D.; Lebon, G. Foundation and application of a mesoscopic thermodynamic theory of fast phenomenon. Phys. Rev. E 1996, 53, 498–506. [Google Scholar] [CrossRef]
- Cimmelli, V.A.; Sellitto, A.; Jou, D. Nonequilibrium temperatures, heat waves, and nonlinear heat transport equations. Phys. Rev. B 2010, 81, 054301. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Boon, J.P.; Yip, S. Molecular Hydrodynamics; Dover Publications: New York, NY, USA, 1991. [Google Scholar]
- Wyss, W. Fractional diffusion equation. J. Math. Phys. 1986, 27, 2782–2785. [Google Scholar] [CrossRef]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Fujita, Y. Integrodifferential equation which interpolates the heat equation and the wave equation (I). Osaka J. Math. 1990, 27, 309–321. [Google Scholar]
- Fujita, Y. Integrodifferential equation which interpolates the heat equation and the wave equation (II). Osaka J. Math. 1990, 27, 797–804. [Google Scholar]
- Anh, V.V.; Leonenko, N.N. Scaling laws for fractional diffusion-wave equation with singular data. Stat. Probab. Lett. 2000, 48, 239–252. [Google Scholar] [CrossRef]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: solutions and applications. Chaos 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Montroll, E.W.; Scher, H. Random walks on lattices. IV. Continuous-time walks and influence of absorbing boundaries. J. Stat. Phys. 1973, 9, 101. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. Anomalous diffusion spreads its wings. Phys. World 2005, 18, 29–32. [Google Scholar] [CrossRef]
- Lazopoulos, K. Non-local continuum mechanics and fractional calculus. Mech. Res. Commun. 2006, 33, 753–757. [Google Scholar] [CrossRef]
- Khamzin, A.A.; Nigmatullin, R.R.; Popov, I.I. Description of the anomalous dielectric relaxation in disordered systems in the frame of the Mori-Zwanzig formalism. J. Phys. Conf. Ser. 2012, 394, 012013. [Google Scholar] [CrossRef]
- Metzler, R.; Compte, A. Stochastic foundation of normal and anomalous Cattaneo-type transport. Phys. A 1999, 268, 454. [Google Scholar] [CrossRef]
- Metzler, R.; Nonnenmacher, T.F. Fractional diffusion, waiting-time distributions, and Cattaneo-type equations. Phys. Rev. E 1998, 57, 6409. [Google Scholar] [CrossRef]
- Orsingher, E.; Zhao, X. The space-fractional telegraph equation and the related fractional telegraph process. Chin. Ann. Math. 2003, 24, 1. [Google Scholar] [CrossRef]
- Orsingher, E.; Beghin, L. Time-fractional telegraph equations and telegraph processes with Brownian time. Probab. Theor. Relat. Fields 2004, 128, 141. [Google Scholar]
- Masoliver, J. Fractional telegrapher’s equation from fractional persistent random walks. Phys. Rev. E 2016, 93, 052107. [Google Scholar] [CrossRef] [PubMed]
- Khamzin, A.A.; Popov, I.I.; Nigmatullin, R.R. Correction of the power law of ac conductivity in ion-conducting materials due to the electrode polarization effect. Phys. Rev. E 2014, 89, 032303. [Google Scholar] [CrossRef] [PubMed]
- Meztler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Zingales, M. Fractional-order theory of heat transport in rigid bodies. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 3938–3953. [Google Scholar] [CrossRef]
- Deseri, L.; Zingales, Z. A mechanical picture of fractional-order Darcy equation. Commun. Nonlinear Sci. Numer. Simulat. 2015, 20, 940–949. [Google Scholar] [CrossRef]
- Ochoa-Tapia, J.A.; Valdés-Parada, F.J.; Alvarez-Ramirez, J. A fractional-order Darcy’s law. Phys. A 2007, 374, 1–14. [Google Scholar] [CrossRef]
- Gray, W.G.; Miller, C.T. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Adv. Water Resour. 2005, 28, 161–180. [Google Scholar] [CrossRef]
- Gray, W.G.; Miller, C.T. Introduction to the Thermodynamically Constrained Averaging Theory for Porous Medium Systems; Springer: New York, NY, USA, 2014. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- García-Bernabé, A.; Sanchis, M.J.; Díaz-Calleja, R.; del Castillo, L.F. Fractional Fokker-Planck equation approach for the interconversion between dielectric and mechanical measurements. J. Appl. Phys. 2009, 106, 014912. [Google Scholar] [CrossRef]
- Garcia-Bernabé, A.; Lidón-Roger, J.V.; Sanchis, M.J.; Díaz-Calleja, R.; del Castillo, L.F. Interconversion algorithm between mechanical and dielectric relaxation measurements for acetate of cis- and trans-2-phenyl-5-hydroxymethyl-1,3-dioxane. Phys. Rev. E 2015, 92, 042307–042315. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Grosso, C.; Moroni, S.; Pastore-Parravicini, G. The ordinary and matrix continued fractions in the theoretical analysis of Hermitian and relaxation operators. Appl. Num. Math. 1988, 4, 273–295. [Google Scholar] [CrossRef]
- Li, S.; Cao, B. Generalized variational principles for heat conduction models based on Laplace transforms. Int. J. Heat Mass Transfer. 2016, 103, 1176–1180. [Google Scholar]
- Jackson, A.S.; Rybak, I.; Helmig, R.; Gray, W.G.; Miller, C.T. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 9. Transition region models. Adv. Water Resour. 2012, 42, 71–90. [Google Scholar] [CrossRef]

| FLUX | Variables | Internal Energy Equation | Balance Equation |
|---|---|---|---|
| Heat Flux | Temperature T | ||
| Diffusive flux | Concentration ck | ||
| Electrical current | Charge density ze |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Bernabé, A.; Hernández, S.I.; Del Castillo, L.F.; Jou, D. Continued-Fraction Expansion of Transport Coefficients with Fractional Calculus. Mathematics 2016, 4, 67. https://doi.org/10.3390/math4040067
Garcia-Bernabé A, Hernández SI, Del Castillo LF, Jou D. Continued-Fraction Expansion of Transport Coefficients with Fractional Calculus. Mathematics. 2016; 4(4):67. https://doi.org/10.3390/math4040067
Chicago/Turabian StyleGarcia-Bernabé, Abel, S. I. Hernández, L. F. Del Castillo, and David Jou. 2016. "Continued-Fraction Expansion of Transport Coefficients with Fractional Calculus" Mathematics 4, no. 4: 67. https://doi.org/10.3390/math4040067
APA StyleGarcia-Bernabé, A., Hernández, S. I., Del Castillo, L. F., & Jou, D. (2016). Continued-Fraction Expansion of Transport Coefficients with Fractional Calculus. Mathematics, 4(4), 67. https://doi.org/10.3390/math4040067





