Uncertainty Relations for Quantum Coherence
Abstract
:1. Introduction
2. Uncertainty Like Relation for Quantum Coherence Expressed in Two Different Non-Commuting Bases
3. Uncertainty Like Relation for Quantum Coherence Expressed in Many Different Non-Commuting Bases
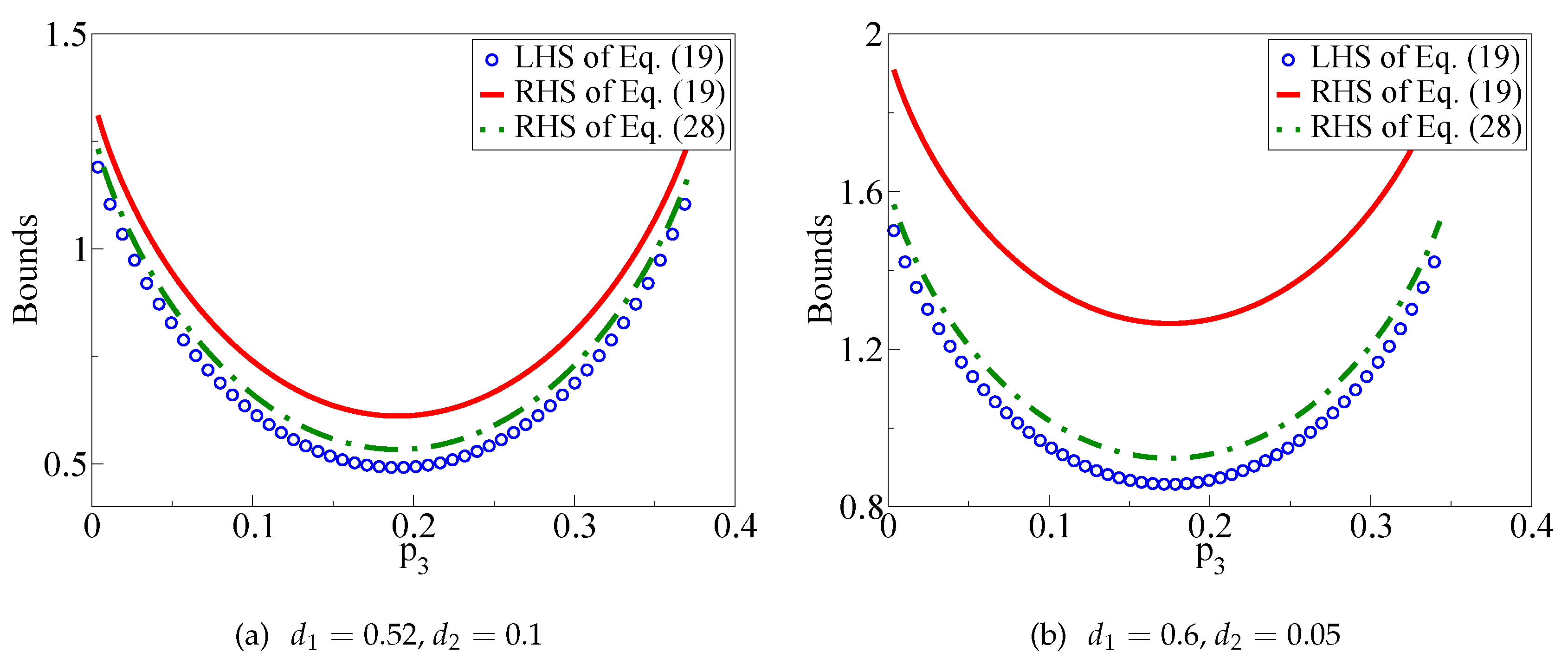
4. Complementarity Like Relation for Quantum Coherence for a Bipartite State
5. State Dependent Upper Bound for Coherence
6. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aberg, J. Quantifying Superposition. 2006. arXiv:quant-ph/0612146. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/quant-ph/0612146 (accessed 17 on December 2006).
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Girolami, D. Observable Measure of Quantum Coherence in Finite Dimensional Systems. Phys. Rev. Lett. 2014, 113, 170401. [Google Scholar] [CrossRef] [PubMed]
- Bromley, T.R.; Cianciaruso, M.; Adesso, G. Frozen Quantum Coherence. Phys. Rev. Lett. 2015, 114, 210401. [Google Scholar] [CrossRef] [PubMed]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring Quantum Coherence with Entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef] [PubMed]
- Xi, Z.; Li, Y.; Fan, H. Quantum coherence and correlations in quantum system. Sci. Rep. 2015, 5, 10922. [Google Scholar] [CrossRef] [PubMed]
- Winter, A.; Yang, D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.H.; Xi, Z.; Fan, H.; Li, Y. Fidelity and trace-norm distances for quantifying coherence. Phys. Rev. A 2015, 91, 042120. [Google Scholar] [CrossRef]
- Pires, D.P.; Céleri, L.C.; Soares-Pinto, D.O. Geometric lower bound for a quantum coherence measure. Phys. Rev. A 2015, 91, 042330. [Google Scholar] [CrossRef]
- Du, S.; Bai, Z.; Guo, Y. Conditions for coherence transformations under incoherent operations. Phys. Rev. A 2015, 91, 052120. [Google Scholar] [CrossRef]
- Yao, Y.; Xiao, X.; Ge, L.; Sun, C.P. Quantum coherence in multipartite systems. Phys. Rev. A 2015, 92, 022112. [Google Scholar] [CrossRef]
- Killoran, N.; Steinhoff, F.E.S.; Plenio, M.B. Converting Nonclassicality into Entanglement. Phys. Rev. Lett. 2016, 116, 080402. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Pati, A.K.; Wu, J. Interference visibility, entanglement, and quantum correlation. Phys. Rev. A 2015, 92, 022316. [Google Scholar] [CrossRef]
- Singh, U.; Bera, M.N.; Dhar, H.S.; Pati, A.K. Maximally coherent mixed states: Complementarity between maximal coherence and mixedness. Phys. Rev. A 2015, 91, 052115. [Google Scholar] [CrossRef]
- Singh, U.; Bera, M.N.; Misra, A.; Pati, A.K. Erasing Quantum Coherence: An Operational Approach. 2015. arXiv:1506.08186. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1506.08186 (accessed on 26 June 2015).
- Cheng, S.; Hall, M.J.W. Complementarity relations for quantum coherence. Phys. Rev. A 2015, 92, 042101. [Google Scholar] [CrossRef]
- Mondal, D.; Pramanik, T.; Pati, A.K. Steerability of Local Quantum Coherence. 2015. arXiv:1508.03770. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1508.03770 (accessed 24 September 2015).
- Mondal, D.; Datta, C.; Sazim, S. Quantum coherence sets the quantum speed limit for mixed states. Phys. Lett. A 2016, 380, 689–695. [Google Scholar] [CrossRef]
- Kumar, A. Quantum Coherence and Its Distribution. 2015. arXiv:1508.00262. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1508.00262 (accessed on 2 August 2015).
- Mani, A.; Karimipour, V. Cohering and decohering power of quantum channels. Phys. Rev. A 2015, 92, 032331. [Google Scholar] [CrossRef]
- Bu, K.; Zhang, L.; Wu, J. Cohering power of quantum operations. 2015. arXiv:1509.09109. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1509.09109 (accessed on 30 September 2015).
- Chitambar, E.; Streltsov, A.; Rana, S.; Bera, M.N.; Adesso, G.; Lewenstein, M. Assisted Distillation of Quantum Coherence. Phys. Rev. Lett. 2016, 116, 070402. [Google Scholar] [CrossRef] [PubMed]
- Streltsov, A.; Rana, S.; Bera, M.N.; Lewenstein, M. Hierarchies of incoherent quantum operations. 2015. arXiv:1509.07456. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1509.07456 (accessed on 24 September 2015).
- Chitambar, E.; Hsieh, M.-H. Relating the Resource Theories of Entanglement and Quantum Coherence. Phys. Rev. Lett. 2016, 117, 020402. [Google Scholar] [CrossRef]
- Streltsov, A. Genuine Quantum Coherence. 2015. arXiv:1511.08346. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1511.08346 (accessed on 26 November 2015).
- Bera, M.N.; Qureshi, T.; Siddiqui, M.A.; Pati, A.K. Duality of quantum coherence and path distinguishability. Phys. Rev. A 2015, 92, 012118. [Google Scholar] [CrossRef]
- Bagan, E.; Bergou, J.A.; Cottrell, S.S.; Hillery, M. Relations between Coherence and Path Information. Phys. Rev. Lett. 2016, 116, 160406. [Google Scholar] [CrossRef] [PubMed]
- Streltsov, A.; Chitambar, E.; Rana, S.; Bera, M.N.; Winter, A.; Lewenstein, M. Entanglement and Coherence in Quantum State Merging. Phys. Rev. Lett. 2016, 116, 240405. [Google Scholar] [CrossRef] [PubMed]
- Hillery, M. Coherence as a resource in decision problems: The Deutsch-Jozsa algorithm and a variation. Phys. Rev. A 2016, 93, 012111. [Google Scholar] [CrossRef]
- Rana, S.; Parashar, P.; Lewenstein, M. Trace-distance measure of coherence. Phys. Rev. A 2016, 93, 012110. [Google Scholar] [CrossRef]
- Rastegin, A.E. Quantum-coherence quantifiers based on the Tsallis relative α entropies. Phys. Rev. A 2016, 93, 032136. [Google Scholar] [CrossRef]
- Rodríguez-Rosario, C.A.; Frauenheim, T.; Aspuru-Guzik, A. Thermodynamics of quantum coherence. 2013. arXiv:1308.1245. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1308.1245 (accessed 6 August 2013).
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nanoscale thermodynamics. Nat. Commun. 2013, 4, 2059. [Google Scholar] [CrossRef] [PubMed]
- Skrzypczyk, P.; Short, A.J.; Popescu, S. Work extraction and thermodynamics for individual quantum systems. Nat. Commun. 2014, 5, 4185. [Google Scholar] [CrossRef] [PubMed]
- Narasimhachar, V.; Gour, G. Low-temperature thermodynamics with quantum coherence. Nat. Commun. 2015, 6, 7689. [Google Scholar] [CrossRef] [PubMed]
- Brandão, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef] [PubMed]
- Lostaglio, M.; Jennings, D.; Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef] [PubMed]
- Lostaglio, M.; Korzekwa, K.; Jennings, D.; Rudolph, T. Quantum Coherence, Time-Translation Symmetry, and Thermodynamics. Phys. Rev. X 2015, 5, 021001. [Google Scholar] [CrossRef]
- Ćwikliński, P.; Studziński, M.; Horodecki, M.; Oppenheim, J. Limitations on the Evolution of Quantum Coherences: Towards Fully Quantum Second Laws of Thermodynamics. Phys. Rev. Lett. 2015, 115, 210403. [Google Scholar] [CrossRef] [PubMed]
- Gardas, B.; Deffner, S. Thermodynamic universality of quantum Carnot engines. Phys. Rev. E 2015, 92, 042126. [Google Scholar] [CrossRef] [PubMed]
- Misra, A.; Singh, U.; Bera, M.N.; Rajagopal, A.K. Quantum Rényi relative entropies affirm universality of thermodynamics. Phys. Rev. E 2015, 92, 042161. [Google Scholar] [CrossRef] [PubMed]
- Goold, J.; Huber, M.; Riera, A.; del Rio, L.; Skrzypczyk, P. The role of quantum information in thermodynamics—A topical review. 2015. arXiv:1505.07835. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1505.07835 (accessed on 28 May 2015).
- Abbott, D.; Davies, P.C.W.; Pati, A.K. Quantum Aspects of Life; Imperial College Press: London, UK, 2008. [Google Scholar]
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: quantum networks and biomolecules. New J. Phys. 2008, 10, 113019. [Google Scholar] [CrossRef]
- Levi, F.; Mintert, F. A quantitative theory of coherent delocalization. New J. Phys. 2014, 16, 033007. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Aspuru-Guzik, A. Role of quantum coherence and environmental fluctuations in chromophoric energy transport. J. Phys. Chem. B 2009, 113, 9942. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S. Quantum coherence in biological systems. J. Phys. Conf. Ser. 2011, 302, 012037. [Google Scholar] [CrossRef]
- Li, C.M.; Lambert, N.; Chen, Y.N.; Chen, G.Y.; Nori, F. Witnessing Quantum Coherence: From solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef] [PubMed]
- Huelga, S.; Plenio, M. Vibrations, quanta and biology. Contemp. Phys. 2013, 54, 181–207. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 1927, 44, 326–352. [Google Scholar] [CrossRef]
- Robertson, H.P. The Uncertainty Principle. Phys. Rev. 1929, 34, 163–164. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Ber. Kgl. Akad. Wiss. Berlin 1930, 24, 296. [Google Scholar]
- Maccone, L.; Pati, A.K. Stronger Uncertainty Relations for All Incompatible Observables. Phys. Rev. Lett. 2014, 113, 260401. [Google Scholar] [CrossRef] [PubMed]
- Busch, P.; Heinonen, T.; Lahti, P. Heisenberg’s uncertainty principle. Phys. Rep. 2007, 452, 155–176. [Google Scholar] [CrossRef]
- Białynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129–132. [Google Scholar] [CrossRef]
- Deutsch, D. Uncertainty in Quantum Measurements. Phys. Rev. Lett. 1983, 50, 631–633. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J.B.M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 1988, 60, 1103–1106. [Google Scholar] [CrossRef] [PubMed]
- Berta, M.; Christandl, M.; Colbeck, R.; Renes, J.M.; Renner, R. The uncertainty principle in the presence of quantum memory. Nat. Phys. 2010, 6, 659–662. [Google Scholar] [CrossRef]
- Coles, P.J.; Berta, M.; Tomamichel, M.; Wehner, S. Entropic Uncertainty Relations and their Applications. 2015. arXiv:1511.04857. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1511.04857 (accessed on 16 November 2015).
- Lewenstein, M.; Sanpera, A. Separability and Entanglement of Composite Quantum Systems. Phys. Rev. Lett. 1998, 80, 2261–2264. [Google Scholar] [CrossRef]
- Pati, A.K.; Wilde, M.M.; Devi, A.R.U.; Rajagopal, A.K.; Sudha. Quantum discord and classical correlation can tighten the uncertainty principle in the presence of quantum memory. Phys. Rev. A 2012, 86, 042105. [Google Scholar] [CrossRef]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A Math. Gen. 2001, 34, 6899. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655–1707. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hu, M.L.; Fan, H. Competition between quantum correlations in the quantum-memory-assisted entropic uncertainty relation. Phys. Rev. A 2013, 87, 022314. [Google Scholar] [CrossRef]
- Liu, S.; Mu, L.Z.; Fan, H. Entropic uncertainty relations for multiple measurements. Phys. Rev. A 2015, 91, 042133. [Google Scholar] [CrossRef]
- Karnas, S.; Lewenstein, M. Separable approximations of density matrices of composite quantum systems. J. Phys. A Math. Gen. 2001, 34, 6919. [Google Scholar] [CrossRef]
- Akhtarshenas, S.J.; Jafarizadeh, M.A. Optimal Lewenstein-Sanpera decomposition for some bipartite systems. J. Phys. A Math. Gen. 2004, 37, 2965. [Google Scholar] [CrossRef]
- Thiang, G.C.; Raynal, P.; Englert, B.G. Optimal Lewenstein-Sanpera decomposition of two-qubit states using semidefinite programming. Phys. Rev. A 2009, 80, 052313. [Google Scholar] [CrossRef]
- Thiang, G.C. Degree of separability of bipartite quantum states. Phys. Rev. A 2010, 82, 012332. [Google Scholar] [CrossRef]
- Hill, S.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022–5025. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P. Reduction criterion of separability and limits for a class of distillation protocols. Phys. Rev. A 1999, 59, 4206–4216. [Google Scholar] [CrossRef]
- Fannes, M. A continuity property of the entropy density for spin lattice systems. Commun. Math. Phys. 1973, 31, 291–294. [Google Scholar] [CrossRef]
- Audenaert, K.M.R. A sharp continuity estimate for the von Neumann entropy. J. Phys. A Math. Theor. 2007, 40, 8127. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, U.; Pati, A.K.; Bera, M.N. Uncertainty Relations for Quantum Coherence. Mathematics 2016, 4, 47. https://doi.org/10.3390/math4030047
Singh U, Pati AK, Bera MN. Uncertainty Relations for Quantum Coherence. Mathematics. 2016; 4(3):47. https://doi.org/10.3390/math4030047
Chicago/Turabian StyleSingh, Uttam, Arun Kumar Pati, and Manabendra Nath Bera. 2016. "Uncertainty Relations for Quantum Coherence" Mathematics 4, no. 3: 47. https://doi.org/10.3390/math4030047
APA StyleSingh, U., Pati, A. K., & Bera, M. N. (2016). Uncertainty Relations for Quantum Coherence. Mathematics, 4(3), 47. https://doi.org/10.3390/math4030047





