Fourier Spectral Methods for Some Linear Stochastic Space-Fractional Partial Differential Equations
Abstract
:1. Introduction
2. Approximate White Noise and Regularity
3. Fourier Spectral Method
- 1.
- Let . We have:for some constants C and which depend on s and .
- 2.
- Let be defined by (12), then:
4. Numerical Simulations
function [u]=spde_oned_Gal(u0,x,T,N,kappa,W1,J, epsilon)
dt=T/N; Dt=kappa*dt; % kappa for the different time steps
N=T/Dt;
lambda= pi*[1:(J-1)]’; M= epsilon*lambda.^2; EE=1./(1+Dt*M);
for n=1:N
u0_hat=(sqrt(2)*J/2)^(-1)*dst(u0);
f_u0 = u0-u0.^3; % f(u) = u-u^3
f_u0_hat=(sqrt(2)*J/2)^(-1)*dst(f_u0);
W=W1(kappa*(n-1)+1,:); W=W’; % kappa for the different tim steps
G_hat=(sqrt(2)*J/2)^(-1)*dst(W);
u1_hat=(u0_hat + Dt*f_u0_hat + Dt*G_hat).*EE;
u1=(sqrt(2)*J/2)*idst(u1_hat);
u0=u1;
end
u=u1;
where W1 denotes the Brownian sheet generated by:
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Walsh, J.B. An introduction to stochastic partial differential equations. In École d’été de probabilités de Saint-Flour, XI-1984, volume 1180 of Lecture Notes in Math; Springer: Berlin, Germany, 1986; pp. 265–439. [Google Scholar]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional order governing equations of Lévy motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Biler, P.; Funaki, T.; Woyczynski, W.A. Fractal Burgers’ equations. J. Differ. Equ. 1998, 148, 9–46. [Google Scholar] [CrossRef]
- Caffarelli, L.A.; Vasseur, A. Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. Math. 2010, 171, 1903–1930. [Google Scholar] [CrossRef]
- Leoncini, X.; Zaslavsky, G.M. Jets, stickiness and anomalous transport. Phys. Rev. E 2002, 65, 046216. [Google Scholar] [CrossRef] [PubMed]
- Zaslavsky, G.M.; Abdullaev, S.S. Scaling property and anomalous transport of particals inside the stochastic layer. Phys. Rev. E 1995, 3901–3910. [Google Scholar] [CrossRef]
- Constantin, P.; Lai, M.C.; Sharma, R.; Tseng, Y.H.; Wu, J. New numerical results for the surface quasi-geostrophic equation. J. Sci. Comput. 2012, 50, 1–28. [Google Scholar] [CrossRef]
- Brzeźniak, Z.; Debbi, L.; Goldys, B. Ergodic properties of fractional stochastic Burgers Equations. Glob. Stoch. Anal. 2011, 1, 149–174. [Google Scholar]
- Debbi, L.; Dozzi, M. On the solutions of nonlinear stochastic fractional partial differential equations in one spatial dimension. Stoc. Proc. Appl. 2005, 115, 1764–1781. [Google Scholar] [CrossRef]
- Röckner, M.; Zhu, R.C.; Zhu, X.C. Local existence and non-explosion of solutions for stochastic fractional partial differential equations driven by multiplicative noise. Stoch. Process. Appl. 2014, 124, 1974–2002. [Google Scholar] [CrossRef]
- Debbi, L.; Dozzi, M. On a space discretization scheme for the fractional stochastic heat equations. 2011. arXiv:1102.4689v1. arXiv.org e-Print archive. http://arxiv.org/abs/1102.4689 (accessed on 23 February 2011).
- Allen, E.J.; Novosel, S.J.; Zhang, Z. Finite element and difference approximation of some linear stochastic partial differential equations. Stoch. Stoch. Rep. 1998, 64, 117–142. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, H.; Yin, H. Finite element methods for semilinear elliptic stochastic partial differential equations. Numer. Math. 2007, 106, 181–198. [Google Scholar] [CrossRef]
- Du, Q.; Zhang, T. Numerical approximation of some linear stochastic partial differential equations driven by special additive noises. SIAM J. Numer. Anal. 2002, 40, 1421–1445. [Google Scholar] [CrossRef]
- Katsoulakis, M.A.; Kossioris, G.T.; Lakkis, O. Noise regularization and computations for the 1-dimensional stochastic Allen-Cahn problem. Interfaces Free Bound. 2007, 9, 1–30. [Google Scholar] [CrossRef]
- Kossioris, G.T.; Zouraris, G.E. Fully-discrete finite element approximations for a fourth-order linear stochastic parabolic equation with additive space-time white noise. M2AN Math. Model. Numer. Anal. 2010, 44, 289–322. [Google Scholar] [CrossRef]
- Servadei, R.; Valdinoci, E. On the spectrum of two different fractional operators. Proc. R. Soc. Edinb. Sect. A 2014, 144, 831–855. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef] [Green Version]
- Baeumer, B.; Kovács, M.; Meerschaert, M.M. Fractional reproduction-dispersal equations and heavy tail dispersal kernels. Bull. Math. Biol. 2007, 69, 2281–2297. [Google Scholar] [CrossRef] [PubMed]
- Baeumer, B.; Kovács, M.; Meerschaert, M.M. Numerical solutions for fractional reaction-diffusion equations. Comput. Math. Appl. 2008, 55, 2212–2226. [Google Scholar] [CrossRef]
- Ilic, M.; liu, F.; Turner, I.; Anh, V. Numerical approximation of a fractional-in-space diffusion equation I. Frac. Calc. Appl. Anal. 2005, 8, 323–341. [Google Scholar]
- Ilic, M.; liu, F.; Turner, I.; Anh, V. Numerical approximation of a fractional-in-space diffusion equation II: With nonhomogeneous boundary conditions. Frac. Calc. Appl. Anal. 2006, 9, 333–349. [Google Scholar]
- Meerschaert, M.M.; Benson, D.A.; Baeumer, B. Multidimensional advection and fractional dispersion. Phys. Rev. E 1999, 59, 5026–5028. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Scheffler, H.; Tadjeran, C. Finite difference methods for two-dimensional fractional dispersion equation. J. Comput. Phys. 2006, 211, 249–261. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Anh, V. Numerical approximations and solution techniques for the space-time Riesz-Caputo fractional advection-diffusion equation. Numer. Algorithm. 2011, 56, 383–403. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Anh, V.; Turner, I. The fundamental solution and numerical solution of the Riesz fractional advection-dispersion equation. IMA J. Appl. Math. 2008, 73, 850–872. [Google Scholar] [CrossRef]
- Simpson, D.P.; Turner, I.W.; Ilic, M. A generalised matrix transfer technique for the numerical solution of fractional-in-space partial differential equations. SIAM J. Numer. Anal. 2007. submitted for publication. [Google Scholar]
- Tadjeran, C.; Meerschaert, M.M.; Scheffler, H. A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 2006, 213, 205–213. [Google Scholar] [CrossRef]
- Tadjeran, C.; Meerschaert, M.M. A second-order accurate numerical method for the two-dimensional fractional diffusion equation. J. Comput. Phys. 2007, 220, 813–823. [Google Scholar] [CrossRef]
- Deng, W. Finite element method for the space and time fractional Fokker-Planck equation. SIAM J. Numer. Anal. 2008, 47, 204–226. [Google Scholar] [CrossRef]
- Deng, W.; Hesthaven, J.S. Discontinuous Galerkin methods for fractional diffusion equations. ESAIM M2AN 2013, 47, 1845–1864. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Equ. 2006, 22, 558–576. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational solution of fractional advection dispersion equations on bounded domains in ℝd. Numer. Methods Partial Differ. Equ. 2007, 23, 256–281. [Google Scholar] [CrossRef]
- Ervin, V.J.; Heuer, N.; Roop, J.P. Numerical approximation of a time dependent nonlinear, space-fractional diffusion equation. SIAM J. Numer. Anal. 2007, 45, 572–591. [Google Scholar] [CrossRef]
- Fix, G.J.; Roop, J.P. Least squares finite-element solution of a fractional order two-point boundary value problem. Comput. Math. Appl. 2004, 48, 1017–1033. [Google Scholar] [CrossRef]
- Ford, N.J.; Xiao, J.; Yan, Y. A finite element method for time fractional partial differential equations. Fract. Calc. Appl. Anal. 2011, 14, 454–474. [Google Scholar] [CrossRef] [Green Version]
- Roop, J.P. Computational aspects of FEM approximation of fractional advection dispersion equations on bounded domains in ℝ2. J. Comput. Appl. Math. 2006, 193, 243–268. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Anh, V. Galerkin finite element approximations of symmetric space-fractional partial differential equations. Appl. Math. Comput. 2010, 217, 2534–2545. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, J.; Xu, Y. A finite element method for the multiterm time-space Riesz fractional advection-diffusion equations in finite domain. Abstr. Appl. Anal. 2013. [Google Scholar] [CrossRef]
- Li, X.J.; Xu, C.J. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Li, X.J.; Xu, C.J. Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation. Commun. Comput. Phys. 2010, 8, 1016–1051. [Google Scholar] [CrossRef]
- Burrage, K.; Hale, N.; Kay, D. An efficient implicit FEM scheme for fractional-in-space reaction-diffusion equations. SIAM J. Sci. Comput. 2012, 34, A2145–A2172. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Burrage, K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 2014. [Google Scholar] [CrossRef]
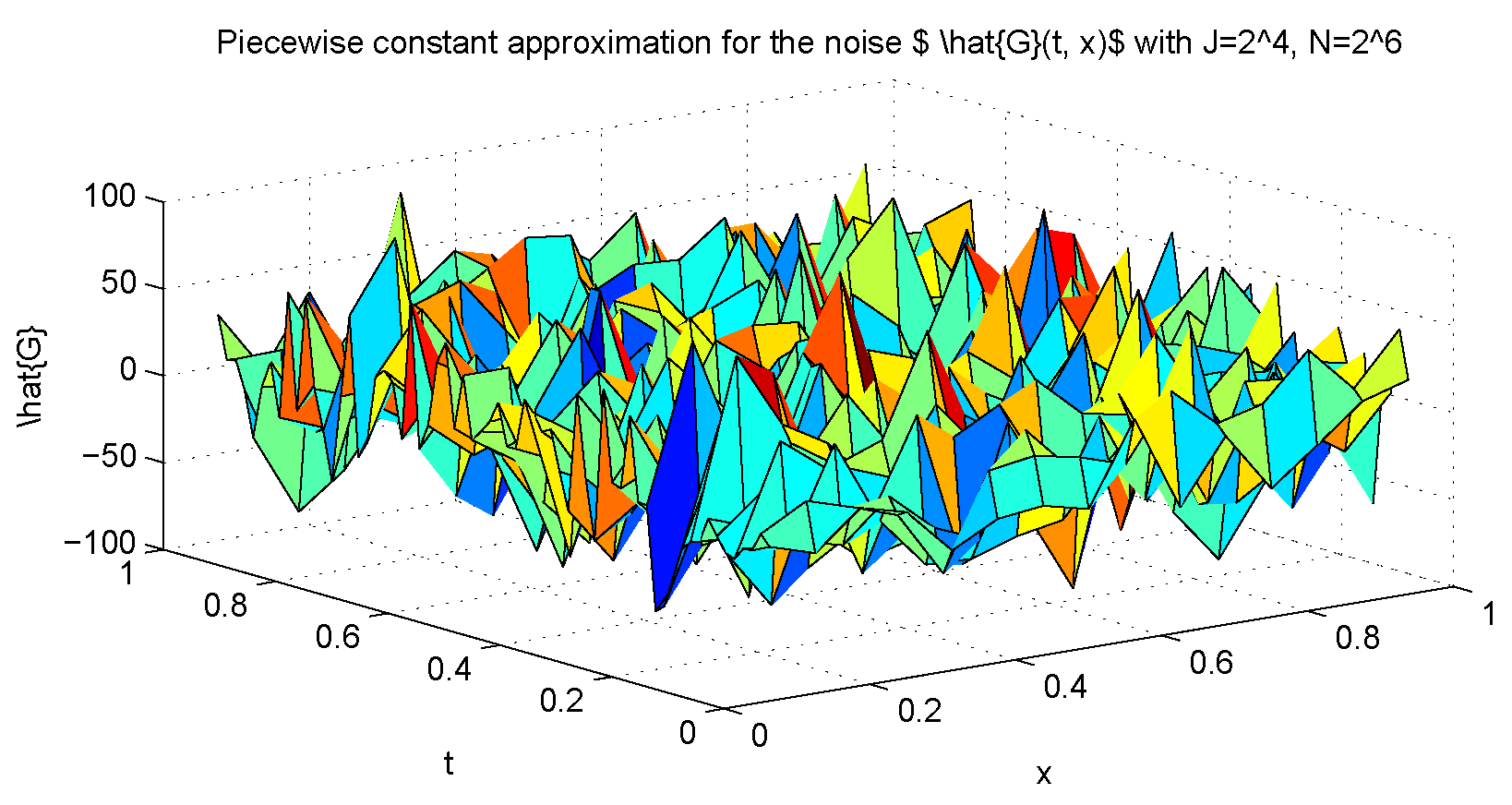
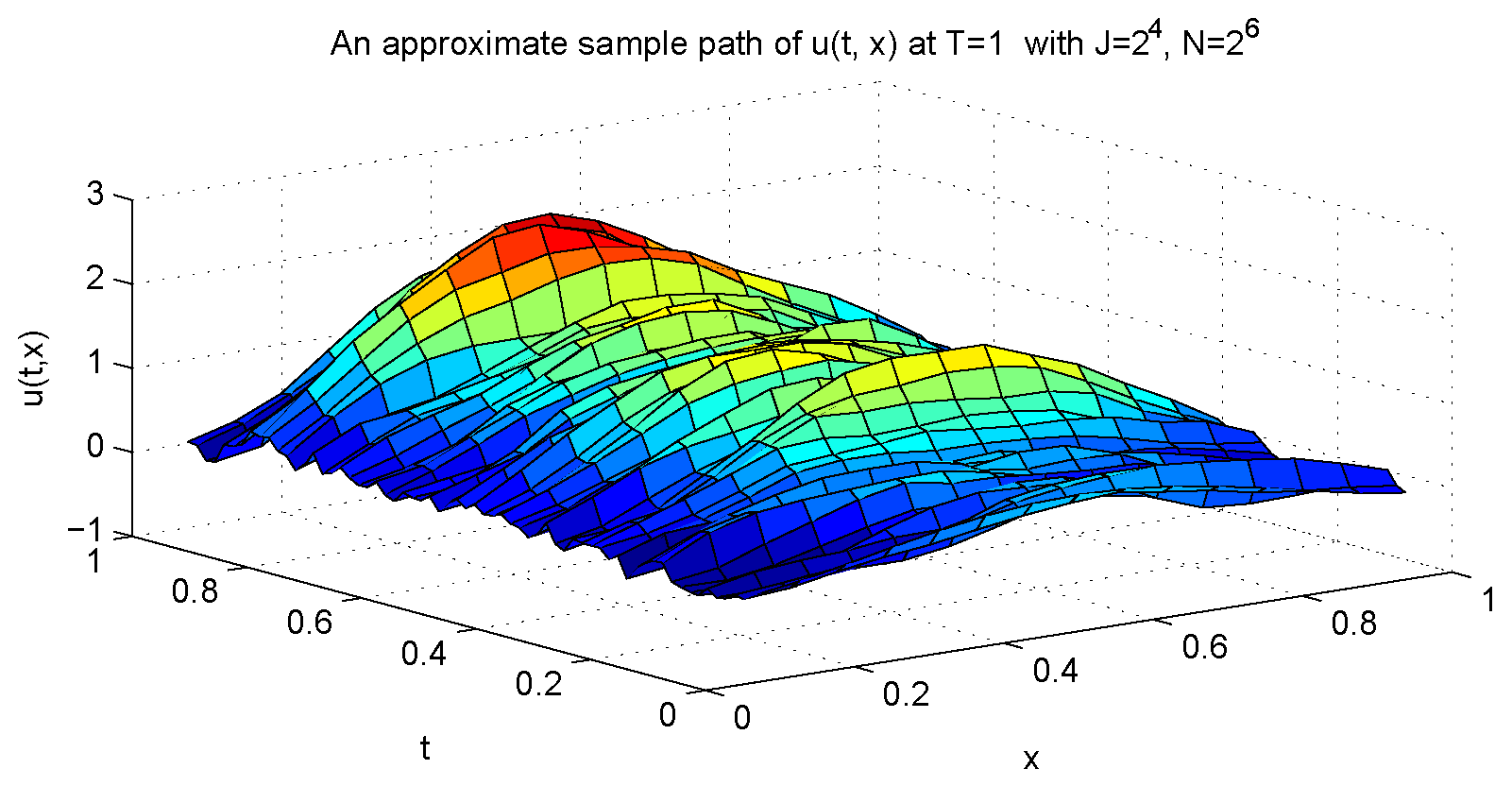
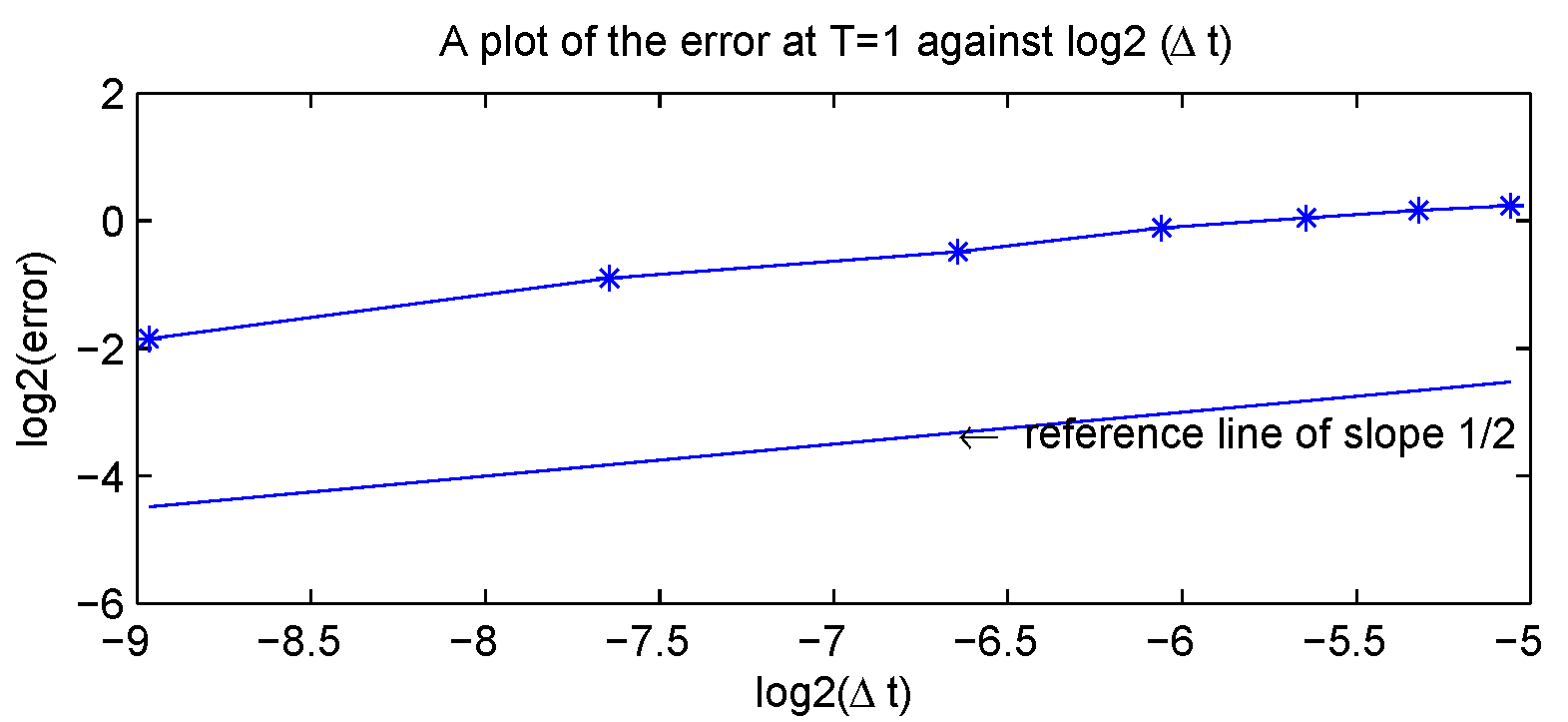
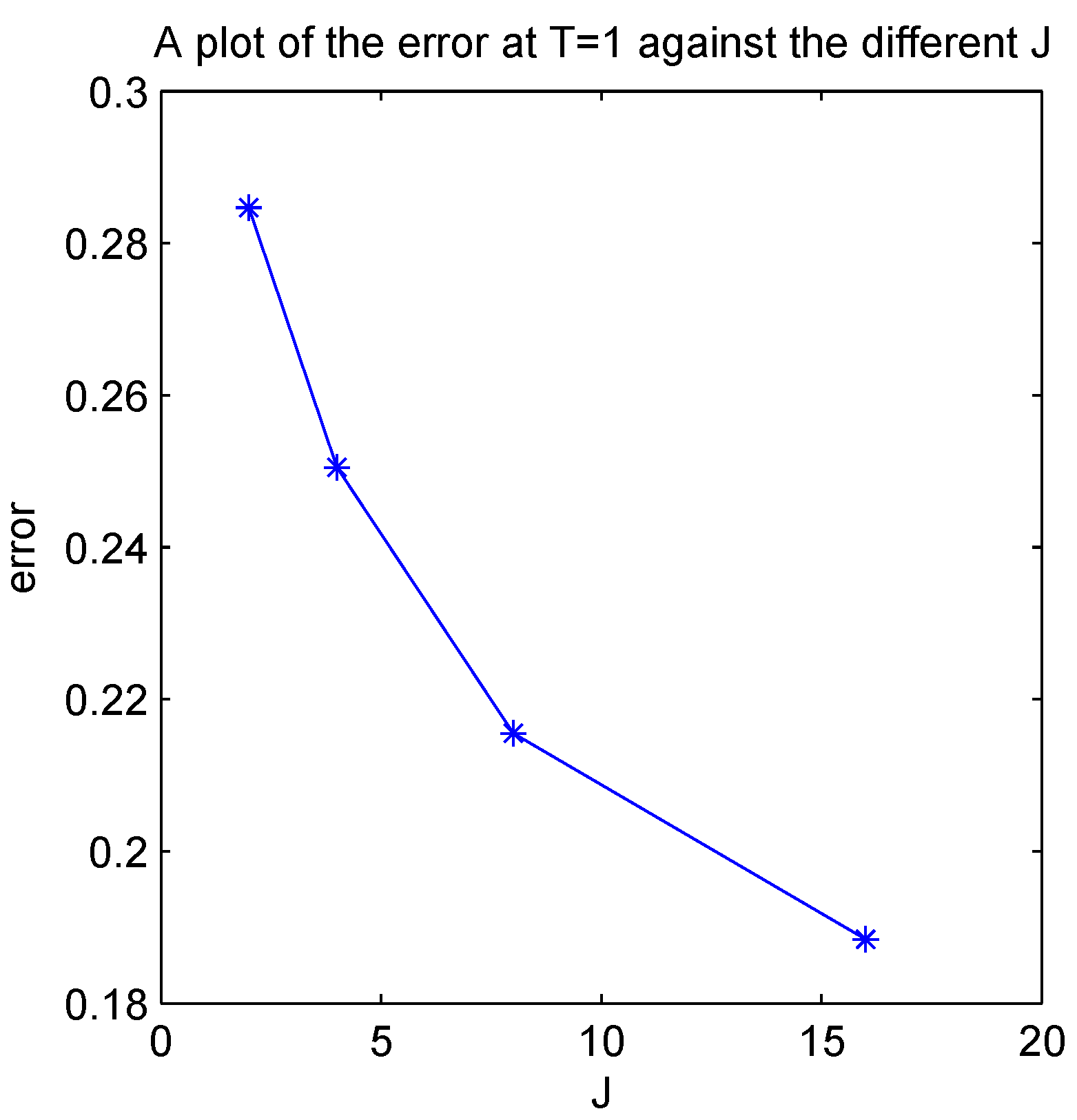
| 1/4 | 1/4 | 1.6108 | 2.6386 |
| 1/4 | 1/8 | 1.7003 | 2.9883 |
| 1/4 | 1/16 | 1.9051 | 3.6534 |
| 1/4 | 1/32 | 1.9051 | 3.6534 |
| 1/8 | 1/4 | 1.4838 | 2.5923 |
| 1/8 | 1/8 | 1.6574 | 2.7709 |
| 1/8 | 1/16 | 1.7323 | 2.7585 |
| 1/8 | 1/32 | 1.6676 | 2.8153 |
| 1/16 | 1/4 | 1.4681 | 2.3333 |
| 1/16 | 1/8 | 1.6097 | 2.6420 |
| 1/16 | 1/16 | 1.6110 | 2.5681 |
| 1/16 | 1/32 | 1.6133 | 2.8737 |
| 1/32 | 1/4 | 1.3605 | 2.4143 |
| 1/32 | 1/8 | 1.6099 | 2.6095 |
| 1/32 | 1/16 | 1.6839 | 2.7930 |
| 1/32 | 1/32 | 1.7061 | 2.8747 |
| -error | 0.2775 | 0.5355 | 0.7116 | 0.9249 | 1.0306 | 1.1159 | 1.1742 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Khan, M.; Yan, Y. Fourier Spectral Methods for Some Linear Stochastic Space-Fractional Partial Differential Equations. Mathematics 2016, 4, 45. https://doi.org/10.3390/math4030045
Liu Y, Khan M, Yan Y. Fourier Spectral Methods for Some Linear Stochastic Space-Fractional Partial Differential Equations. Mathematics. 2016; 4(3):45. https://doi.org/10.3390/math4030045
Chicago/Turabian StyleLiu, Yanmei, Monzorul Khan, and Yubin Yan. 2016. "Fourier Spectral Methods for Some Linear Stochastic Space-Fractional Partial Differential Equations" Mathematics 4, no. 3: 45. https://doi.org/10.3390/math4030045
APA StyleLiu, Y., Khan, M., & Yan, Y. (2016). Fourier Spectral Methods for Some Linear Stochastic Space-Fractional Partial Differential Equations. Mathematics, 4(3), 45. https://doi.org/10.3390/math4030045






