From Cayley-Dickson Algebras to Combinatorial Grassmannians
Abstract
:1. Introduction
2. Octonions and the Pasch -Configuration
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | −0 | −3 | +2 | −5 | +4 | +7 | −6 |
| 2 | +3 | −0 | −1 | −6 | −7 | +4 | +5 |
| 3 | −2 | +1 | −0 | −7 | +6 | −5 | +4 |
| 4 | +5 | +6 | +7 | −0 | −1 | −2 | −3 |
| 5 | −4 | +7 | −6 | +1 | −0 | +3 | −2 |
| 6 | −7 | −4 | +5 | +2 | −3 | −0 | +1 |
| 7 | +6 | −5 | −4 | +3 | +2 | −1 | −0 |




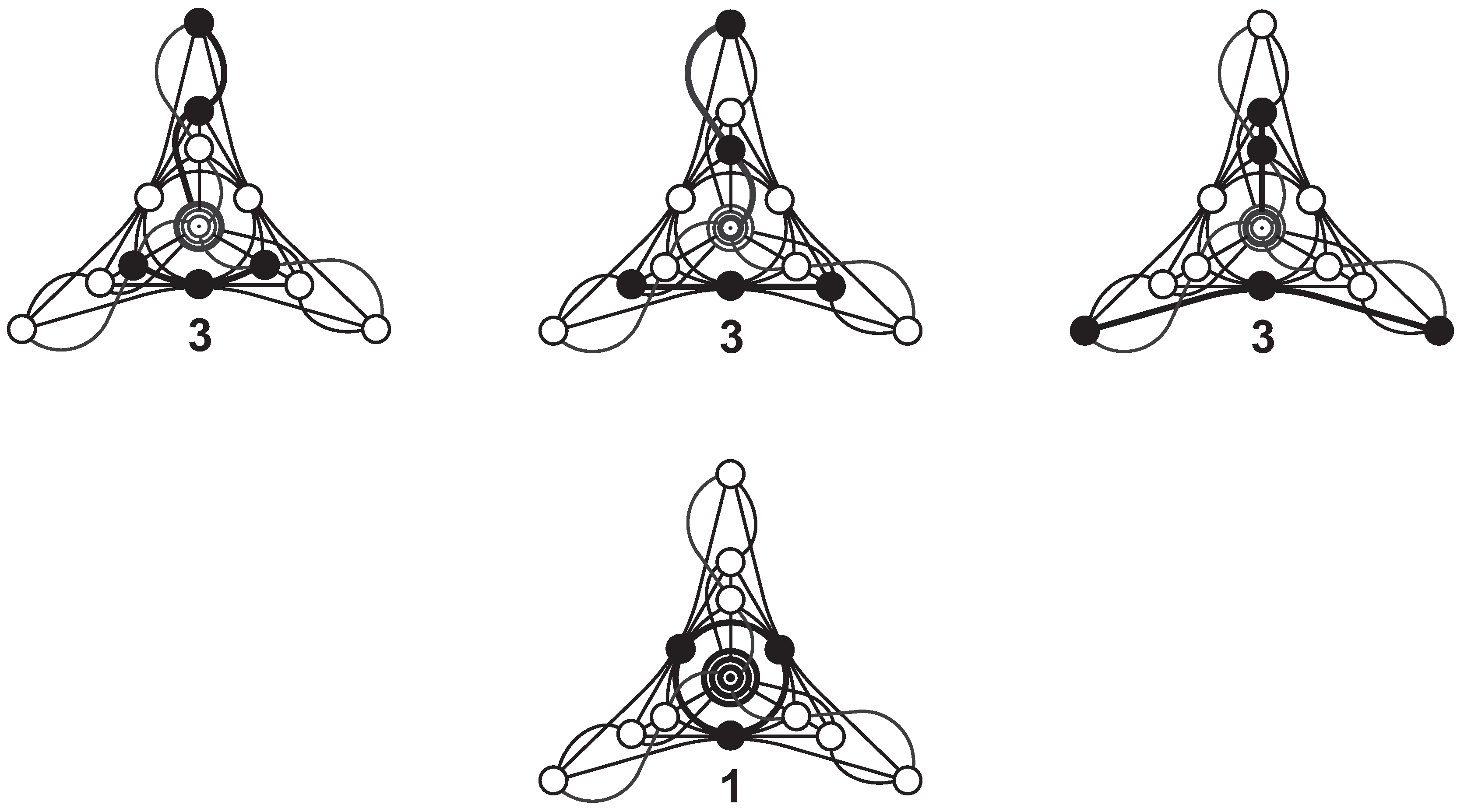
3. Sedenions and the Desargues -Configuration
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0 | −3 | +2 | −5 | +4 | +7 | −6 | −9 | +8 | +11 | −10 | +13 | −12 | −15 | +14 |
| 2 | +3 | −0 | −1 | −6 | −7 | +4 | +5 | −10 | −11 | +8 | +9 | +14 | +15 | −12 | −13 |
| 3 | −2 | +1 | −0 | −7 | +6 | −5 | +4 | −11 | +10 | −9 | +8 | +15 | −14 | +13 | −12 |
| 4 | +5 | +6 | +7 | −0 | −1 | −2 | −3 | −12 | −13 | −14 | −15 | +8 | +9 | +10 | +11 |
| 5 | −4 | +7 | −6 | +1 | −0 | +3 | −2 | −13 | +12 | −15 | +14 | −9 | +8 | −11 | +10 |
| 6 | −7 | −4 | +5 | +2 | −3 | −0 | +1 | −14 | +15 | +12 | −13 | −10 | +11 | +8 | −9 |
| 7 | +6 | −5 | −4 | +3 | +2 | −1 | −0 | −15 | −14 | +13 | +12 | −11 | −10 | +9 | +8 |
| 8 | +9 | +10 | +11 | +12 | +13 | +14 | +15 | −0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 |
| 9 | −8 | +11 | −10 | +13 | −12 | −15 | +14 | +1 | −0 | +3 | −2 | +5 | −4 | −7 | +6 |
| 10 | −11 | −8 | +9 | +14 | +15 | −12 | −13 | +2 | −3 | −0 | +1 | +6 | +7 | −4 | −5 |
| 11 | +10 | −9 | −8 | +15 | −14 | +13 | −12 | +3 | +2 | −1 | −0 | +7 | −6 | +5 | −4 |
| 12 | −13 | −14 | −15 | −8 | +9 | +10 | +11 | +4 | −5 | −6 | −7 | −0 | +1 | +2 | +3 |
| 13 | +12 | −15 | +14 | −9 | −8 | −11 | +10 | +5 | +4 | −7 | +6 | −1 | −0 | −3 | +2 |
| 14 | +15 | +12 | −13 | −10 | +11 | −8 | −9 | +6 | +7 | +4 | −5 | −2 | +3 | −0 | −1 |
| 15 | −14 | +13 | +12 | −11 | −10 | +9 | −8 | +7 | −6 | +5 | +4 | −3 | −2 | +1 | −0 |
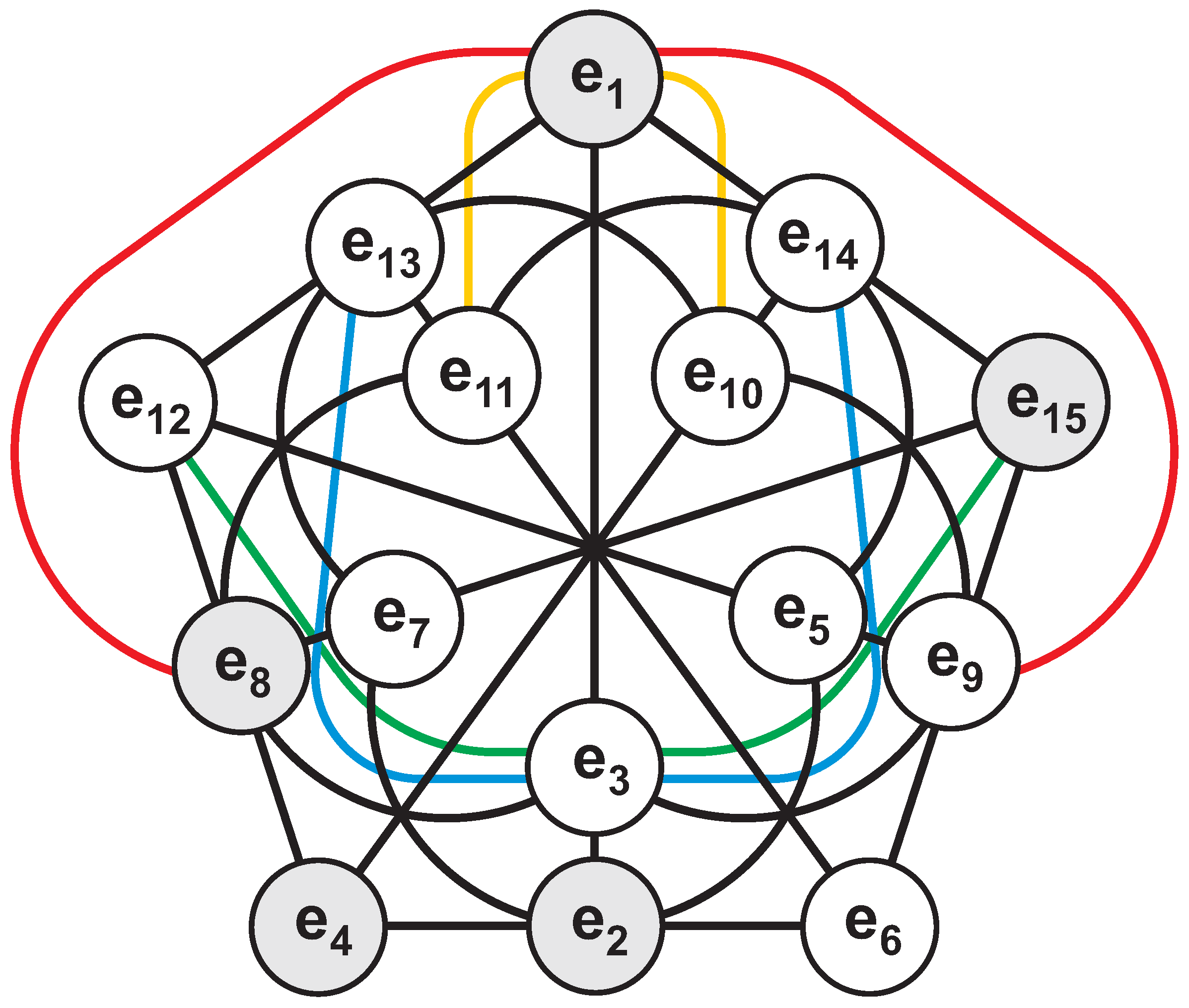

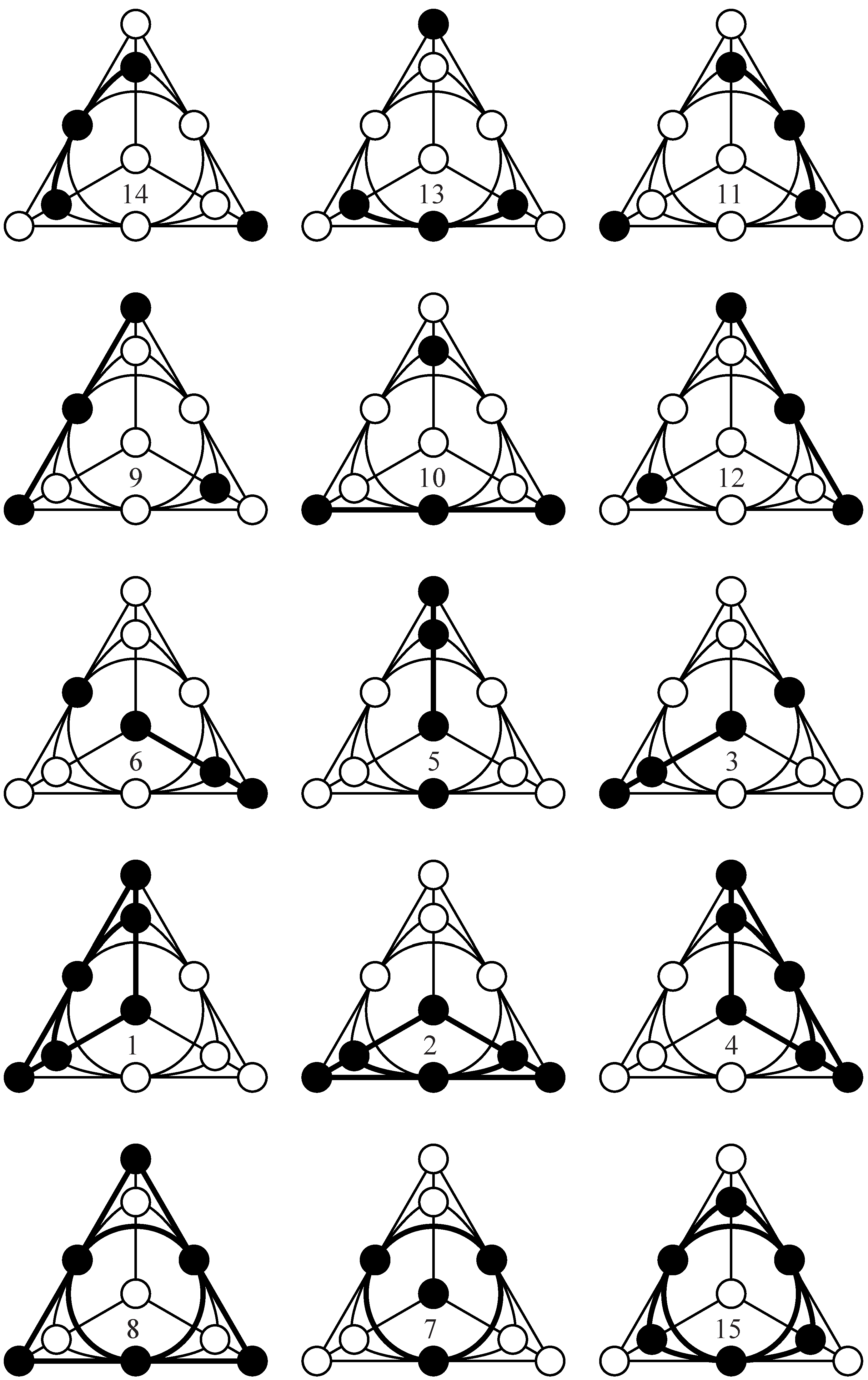


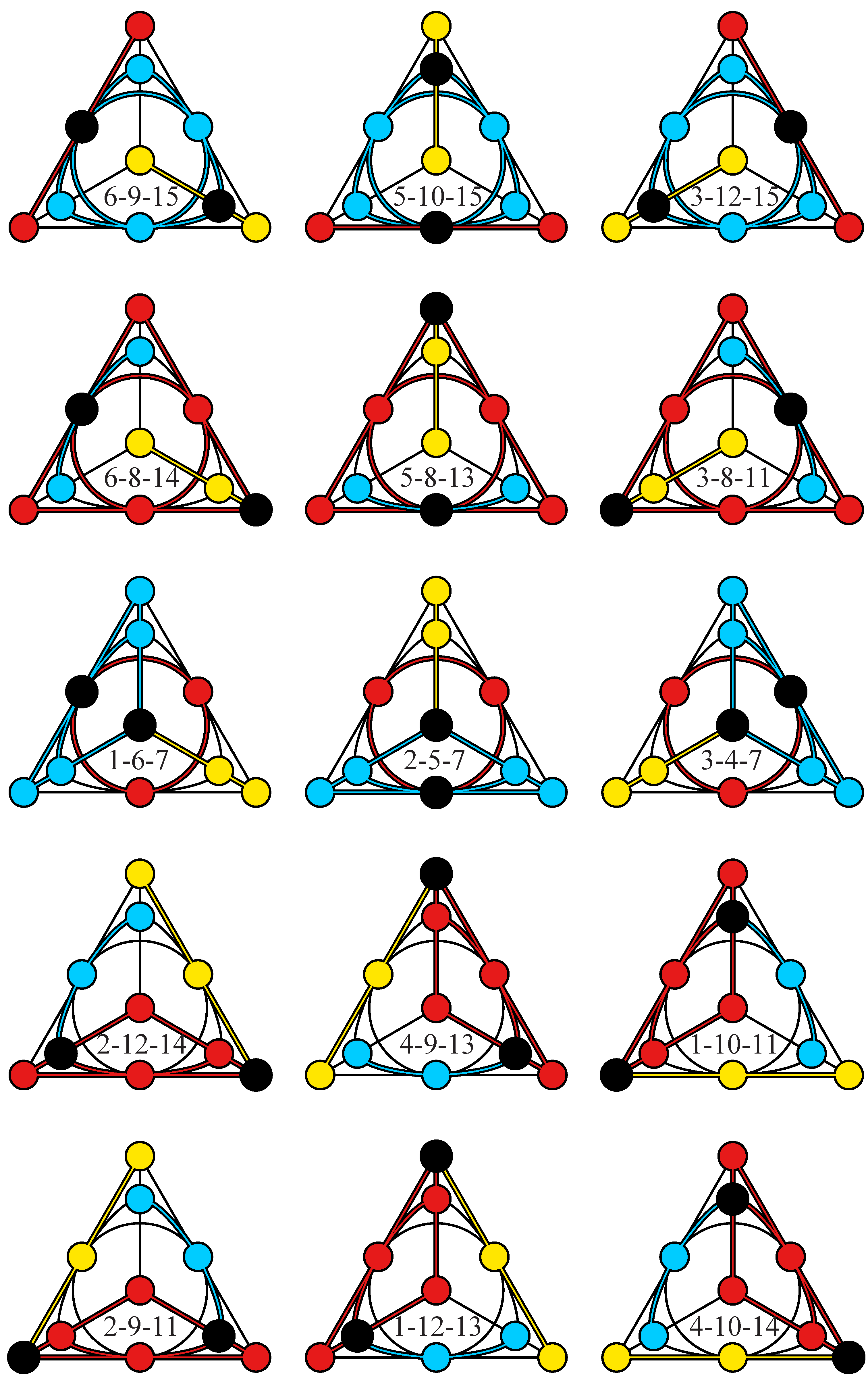
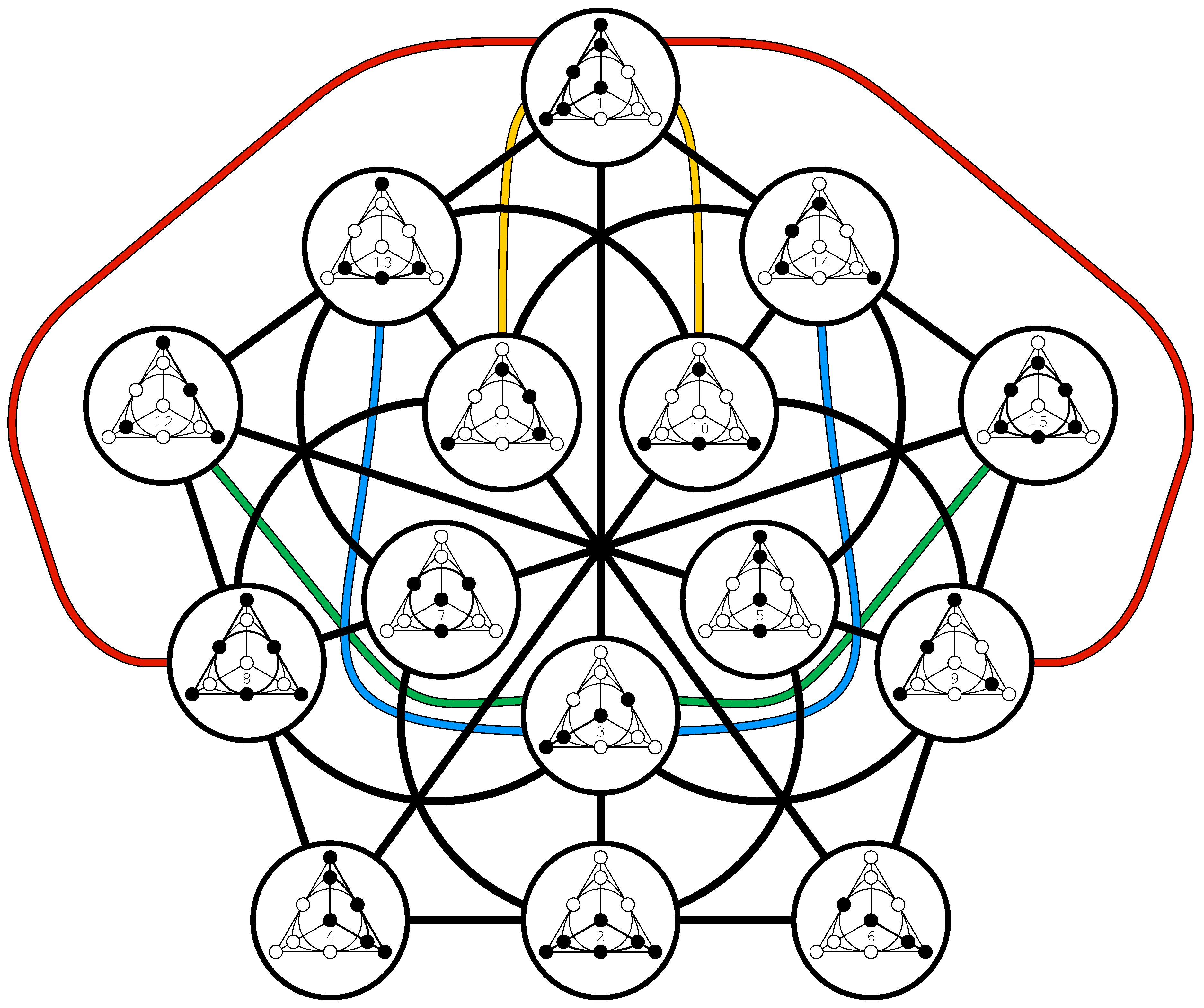
4. 32-Nions and the Cayley-Salmon -Configuration
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0 | −3 | +2 | −5 | +4 | +7 | −6 | −9 | +8 | +11 | −10 | +13 | −12 | −15 | +14 | |
| 2 | +3 | −0 | −1 | −6 | −7 | +4 | +5 | −10 | −11 | +8 | +9 | +14 | +15 | −12 | −13 | |
| 3 | −2 | +1 | −0 | −7 | +6 | −5 | +4 | −11 | +10 | −9 | +8 | +15 | −14 | +13 | −12 | |
| 4 | +5 | +6 | +7 | −0 | −1 | −2 | −3 | −12 | −13 | −14 | −15 | +8 | +9 | +10 | +11 | |
| 5 | −4 | +7 | −6 | +1 | −0 | +3 | −2 | −13 | +12 | −15 | +14 | −9 | +8 | −11 | +10 | |
| 6 | −7 | −4 | +5 | +2 | −3 | −0 | +1 | −14 | +15 | +12 | −13 | −10 | +11 | +8 | −9 | |
| 7 | +6 | −5 | −4 | +3 | +2 | −1 | −0 | −15 | −14 | +13 | +12 | −11 | −10 | +9 | +8 | |
| 8 | +9 | +10 | +11 | +12 | +13 | +14 | +15 | −0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | |
| 9 | −8 | +11 | −10 | +13 | −12 | −15 | +14 | +1 | −0 | +3 | −2 | +5 | −4 | −7 | +6 | |
| 10 | −11 | −8 | +9 | +14 | +15 | −12 | −13 | +2 | −3 | −0 | +1 | +6 | +7 | −4 | −5 | |
| 11 | +10 | −9 | −8 | +15 | −14 | +13 | −12 | +3 | +2 | −1 | −0 | +7 | −6 | +5 | −4 | |
| 12 | −13 | −14 | −15 | −8 | +9 | +10 | +11 | +4 | −5 | −6 | −7 | −0 | +1 | +2 | +3 | |
| 13 | +12 | −15 | +14 | −9 | −8 | −11 | +10 | +5 | +4 | −7 | +6 | −1 | −0 | −3 | +2 | |
| 14 | +15 | +12 | −13 | −10 | +11 | −8 | −9 | +6 | +7 | +4 | −5 | −2 | +3 | −0 | −1 | |
| 15 | −14 | +13 | +12 | −11 | −10 | +9 | −8 | +7 | −6 | +5 | +4 | −3 | −2 | +1 | −0 | |
| 16 | +17 | +18 | +19 | +20 | +21 | +22 | +23 | +24 | +25 | +26 | +27 | +28 | +29 | +30 | +31 | |
| 17 | −16 | +19 | −18 | +21 | −20 | −23 | +22 | +25 | −24 | −27 | +26 | −29 | +28 | +31 | −30 | |
| 18 | −19 | −16 | +17 | +22 | +23 | −20 | −21 | +26 | +27 | −24 | −25 | −30 | −31 | +28 | +29 | |
| 19 | +18 | −17 | −16 | +23 | −22 | +21 | −20 | +27 | −26 | +25 | −24 | −31 | +30 | −29 | +28 | |
| 20 | −21 | −22 | −23 | −16 | +17 | +18 | +19 | +28 | +29 | +30 | +31 | −24 | −25 | −26 | −27 | |
| 21 | +20 | −23 | +22 | −17 | −16 | −19 | +18 | +29 | −28 | +31 | −30 | +25 | −24 | +27 | −26 | |
| 22 | +23 | +20 | −21 | −18 | +19 | −16 | −17 | +30 | −31 | −28 | +29 | +26 | −27 | −24 | +25 | |
| 23 | −22 | +21 | +20 | −19 | −18 | +17 | −16 | +31 | +30 | −29 | −28 | +27 | +26 | −25 | −24 | |
| 24 | −25 | −26 | −27 | −28 | −29 | −30 | −31 | −16 | +17 | +18 | +19 | +20 | +21 | +22 | +23 | |
| 25 | +24 | −27 | +26 | −29 | +28 | +31 | −30 | −17 | −16 | −19 | +18 | −21 | +20 | +23 | −22 | |
| 26 | +27 | +24 | −25 | −30 | −31 | +28 | +29 | −18 | +19 | −16 | −17 | −22 | −23 | +20 | +21 | |
| 27 | −26 | +25 | +24 | −31 | +30 | −29 | +28 | −19 | −18 | +17 | −16 | −23 | +22 | −21 | +20 | |
| 28 | +29 | +30 | +31 | +24 | −25 | −26 | −27 | −20 | +21 | +22 | +23 | −16 | −17 | −18 | −19 | |
| 29 | −28 | +31 | −30 | +25 | +24 | +27 | −26 | −21 | −20 | +23 | −22 | +17 | −16 | +19 | −18 | |
| 30 | −31 | −28 | +29 | +26 | −27 | +24 | +25 | −22 | −23 | −20 | +21 | +18 | −19 | −16 | +17 | |
| 31 | +30 | −29 | −28 | +27 | +26 | −25 | +24 | −23 | +22 | −21 | −20 | +19 | +18 | −17 | −16 | |
| * | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| 1 | −17 | +16 | +19 | −18 | +21 | −20 | −23 | +22 | +25 | −24 | −27 | +26 | −29 | +28 | +31 | −30 |
| 2 | −18 | −19 | +16 | +17 | +22 | +23 | −20 | −21 | +26 | +27 | −24 | −25 | −30 | −31 | +28 | +29 |
| 3 | −19 | +18 | −17 | +16 | +23 | −22 | +21 | −20 | +27 | −26 | +25 | −24 | −31 | +30 | −29 | +28 |
| 4 | −20 | −21 | −22 | −23 | +16 | +17 | +18 | +19 | +28 | +29 | +30 | +31 | −24 | −25 | −26 | −27 |
| 5 | −21 | +20 | −23 | +22 | −17 | +16 | −19 | +18 | +29 | −28 | +31 | −30 | +25 | −24 | +27 | −26 |
| 6 | −22 | +23 | +20 | −21 | −18 | +19 | +16 | −17 | +30 | −31 | −28 | +29 | +26 | −27 | −24 | +25 |
| 7 | −23 | −22 | +21 | +20 | −19 | −18 | +17 | +16 | +31 | +30 | −29 | −28 | +27 | +26 | −25 | −24 |
| 8 | −24 | −25 | −26 | −27 | −28 | −29 | −30 | −31 | +16 | +17 | +18 | +19 | +20 | +21 | +22 | +23 |
| 9 | −25 | +24 | −27 | +26 | −29 | +28 | +31 | −30 | −17 | +16 | −19 | +18 | −21 | +20 | +23 | − 22 |
| 10 | −26 | +27 | +24 | −25 | −30 | −31 | +28 | +29 | −18 | +19 | +16 | −17 | −22 | −23 | +20 | +21 |
| 11 | −27 | −26 | +25 | +24 | −31 | +30 | −29 | +28 | −19 | −18 | +17 | +16 | −23 | +22 | −21 | +20 |
| 12 | −28 | +29 | +30 | +31 | +24 | −25 | −26 | −27 | −20 | +21 | +22 | +23 | +16 | −17 | −18 | −19 |
| 13 | −29 | −28 | +31 | −30 | +25 | +24 | +27 | −26 | −21 | −20 | +23 | −22 | +17 | +16 | +19 | −18 |
| 14 | −30 | −31 | −28 | +29 | +26 | −27 | +24 | +25 | −22 | −23 | −20 | +21 | +18 | −19 | +16 | +17 |
| 15 | −31 | +30 | −29 | −28 | +27 | +26 | −25 | +24 | −23 | +22 | −21 | −20 | +19 | +18 | −17 | +16 |
| 16 | −0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | −8 | −9 | −10 | −11 | −12 | −13 | −14 | −15 |
| 17 | +1 | −0 | +3 | −2 | +5 | −4 | −7 | +6 | +9 | −8 | −11 | +10 | −13 | +12 | +15 | −14 |
| 18 | +2 | −3 | −0 | +1 | +6 | +7 | −4 | −5 | +10 | +11 | −8 | −9 | −14 | −15 | +12 | +13 |
| 19 | +3 | +2 | −1 | −0 | +7 | −6 | +5 | −4 | +11 | −10 | +9 | −8 | −15 | +14 | −13 | +12 |
| 20 | +4 | −5 | −6 | −7 | −0 | +1 | +2 | +3 | +12 | +13 | +14 | +15 | −8 | −9 | −10 | −11 |
| 21 | +5 | +4 | −7 | +6 | −1 | −0 | −3 | +2 | +13 | −12 | +15 | −14 | +9 | −8 | +11 | −10 |
| 22 | +6 | +7 | +4 | −5 | −2 | +3 | −0 | −1 | +14 | −15 | −12 | +13 | +10 | −11 | −8 | +9 |
| 23 | +7 | −6 | +5 | +4 | −3 | −2 | +1 | −0 | +15 | +14 | −13 | −12 | +11 | +10 | −9 | −8 |
| 24 | +8 | −9 | −10 | −11 | −12 | −13 | −14 | −15 | −0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 |
| 25 | +9 | +8 | −11 | +10 | −13 | +12 | +15 | −14 | −1 | −0 | −3 | +2 | −5 | +4 | +7 | −6 |
| 26 | +10 | +11 | +8 | −9 | −14 | −15 | +12 | +13 | −2 | +3 | −0 | −1 | −6 | −7 | +4 | +5 |
| 27 | +11 | −10 | +9 | +8 | −15 | +14 | −13 | +12 | −3 | −2 | +1 | −0 | −7 | +6 | −5 | +4 |
| 28 | +12 | +13 | +14 | +15 | +8 | −9 | −10 | −11 | −4 | +5 | +6 | +7 | −0 | −1 | −2 | −3 |
| 29 | +13 | −12 | +15 | −14 | +9 | +8 | +11 | −10 | −5 | −4 | +7 | −6 | +1 | −0 | +3 | −2 |
| 30 | +14 | −15 | −12 | +13 | +10 | −11 | +8 | +9 | −6 | −7 | −4 | +5 | +2 | −3 | −0 | +1 |
| 31 | +15 | +14 | −13 | −12 | +11 | +10 | −9 | +8 | −7 | +6 | −5 | −4 | +3 | +2 | −1 | −0 |




5. 64-Nions and a -Configuration
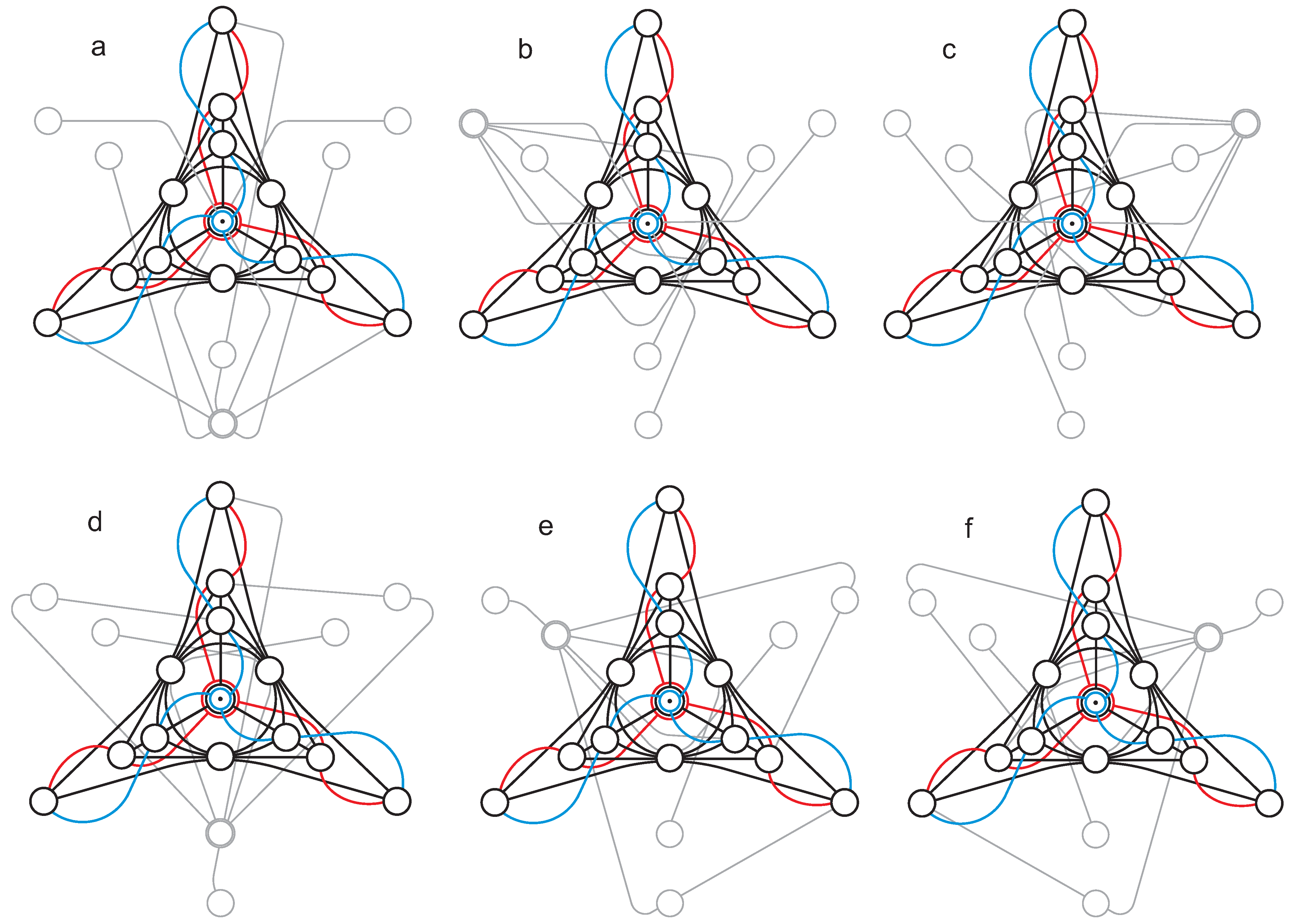
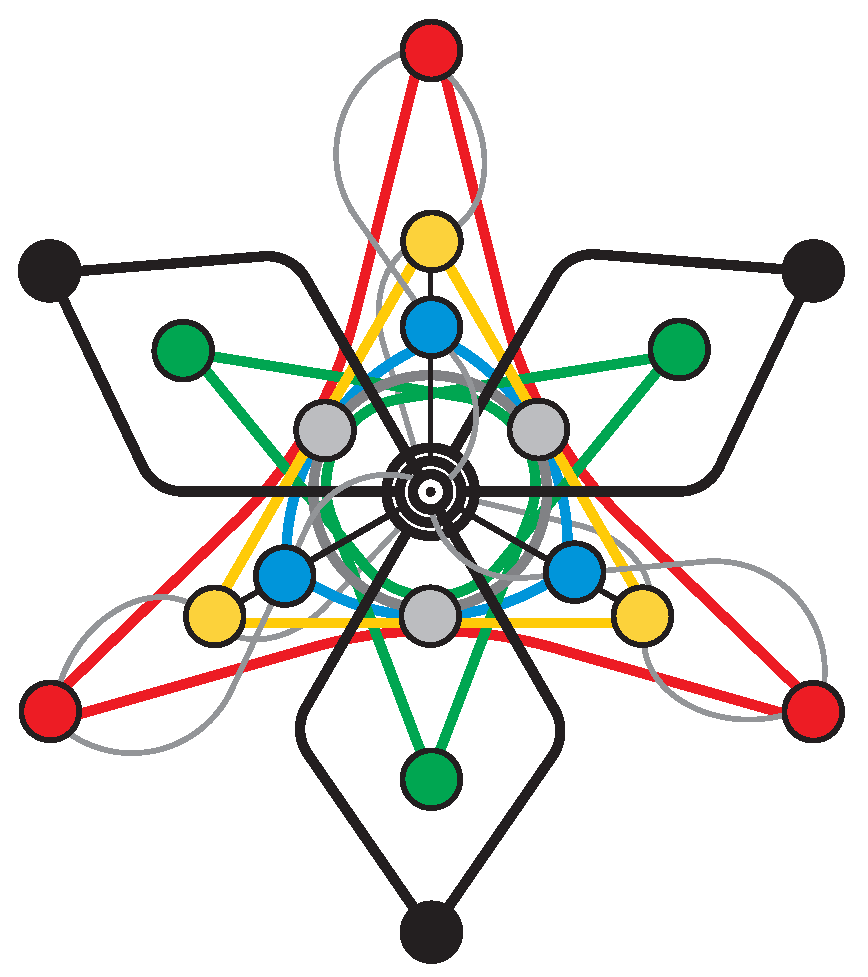
6. -Nions and a -Configuration

| : | ⌀, | ||
| : | , | ||
| : | , | , | |
| : | , | , | |
| : | , | , | , |
| : | , | , |
| : | , | , | , | …, |
| : | , | , | , | …, |

7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jacobson, N. Basic Algebra I; W. H. Freeman: San Francisco, CA, USA, 1974. [Google Scholar]
- Schafer, R.D. Introduction to Non-Associative Algebras; Dover: New York, NY, USA, 1995. [Google Scholar]
- Moreno, G. Hopf construction map in higher dimensions. Bol. Soc. Mat. Mex. 2004, 10, 383–397. [Google Scholar]
- Arndt, J. Matters Computational: Ideas, Algorithms, Source Code; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Arndt, J. The FXT Demos: Arithmetical Algorithms. Available online: http://jjj.de/fxt/demo/arith/index.html (accessed on 30 January 2014).
- Baez, J.C. The octonions. Bull. Am. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Culbert, C. Cayley-Dickson algebras and loops. J. Gen. Lie Theory Appl. 2007, 1, 1–17. [Google Scholar] [CrossRef]
- Shult, E.E. Points and Lines: Characterizing the Classical Geometries; Springer: Berlin, Germany, 2011. [Google Scholar]
- Grünbaum, B. Configurations of Points and Lines; Graduate Studies in Mathematics 103; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Buekenhout, F.; Cohen, A.M. Diagram Geometry: Related to Classical Groups and Buildings; Springer: Berlin, Germany, 2013. [Google Scholar]
- Grannell, M.J.; Griggs, T.S. The Pasch Configuration. Encyclopaedia of Mathematics. Available online: http://www.encyclopediaofmath.org/index.php/Pasch_configuration (accessed on 14 May 2014).
- Polster, B. A Geometrical Picture Book; Springer Verlag: New York, NY, USA, 1998. [Google Scholar]
- Pisanski, T.; Servatius, B. Configurations from a Graphical Viewpoint; Birkhäuser: Basel, Switzerland, 2013. [Google Scholar]
- Saniga, M.; Planat, M.; Pracna, P.; Havlicek, H. The Veldkamp space of two-qubits. SIGMA 2007, 3. [Google Scholar] [CrossRef]
- Fisher, J.C.; Fuller, N. The Complete Pascal Figure Graphically Presented. Available online: http://www.math.uregina.ca/˜fisher/Norma/paper.html (accessed on 14 May 2014).
- Lord, E. Symmetry and Pattern in Projective Geometry; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Conway, J.; Ryba, A. The Pascal mysticum demystified. Math. Intell. 2012, 34, 4–8. [Google Scholar] [CrossRef]
- Boben, M.; Gévay, G.; Pisanski, T. Danzer’s configuration revisited. Adv. Geom. 2015, 15, 393–408. [Google Scholar] [CrossRef]
- Arndt, J. TMP-Zero-Divisors. Available online: http://jjj.de/tmp-zero-divisors/mult-table-64-ions.txt (accessed on 30 January 2014).
- Prażmowska, M.; Prażmowski, K. Binomial Configurations Which Contain Complete Graphs: Kn-Subgraphs of a -Configuration. 2014. arXiv:1404.4064. Available online: http://arxiv.org/abs/1404.4064 (accessed on 17 May 2014).
- Petelczyc, K.; Prażmowska, M.; Prażmowski, K. A complete classification of the ()-configurations with at least three K5-graphs. Discret. Math. 2015, 338, 1243–1251. [Google Scholar] [CrossRef]
- Prażmowska, M. Multiple perspectives and generalizations of the Desargues configuration. Demonstr. Math. 2006, 39, 887–906. [Google Scholar]
- Prażmowska, M.; Prażmowski, K. A generalization of Desargues and Veronese configurations. Serdica Math. J. 2006, 32, 185–208. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saniga, M.; Holweck, F.; Pracna, P. From Cayley-Dickson Algebras to Combinatorial Grassmannians. Mathematics 2015, 3, 1192-1221. https://doi.org/10.3390/math3041192
Saniga M, Holweck F, Pracna P. From Cayley-Dickson Algebras to Combinatorial Grassmannians. Mathematics. 2015; 3(4):1192-1221. https://doi.org/10.3390/math3041192
Chicago/Turabian StyleSaniga, Metod, Frédéric Holweck, and Petr Pracna. 2015. "From Cayley-Dickson Algebras to Combinatorial Grassmannians" Mathematics 3, no. 4: 1192-1221. https://doi.org/10.3390/math3041192






