A Graphical Approach to a Model of a Neuronal Tree with a Variable Diameter
Abstract
:1. Introduction
2. Cable Equation with Varying Radius
2.1. Sealed end steady-state solutions
3. Cable Equations Defined on Cylindrical and Hyperbolic Compartments: Analytic, Asymptotic and Numerical Solutions
3.1. Cylinder
3.2. Hyperbola
3.3. General Case of Axial Symmetry
4. A Graphical Approach
4.1. Single Axially Symmetric Branch with Arbitrary Tapering
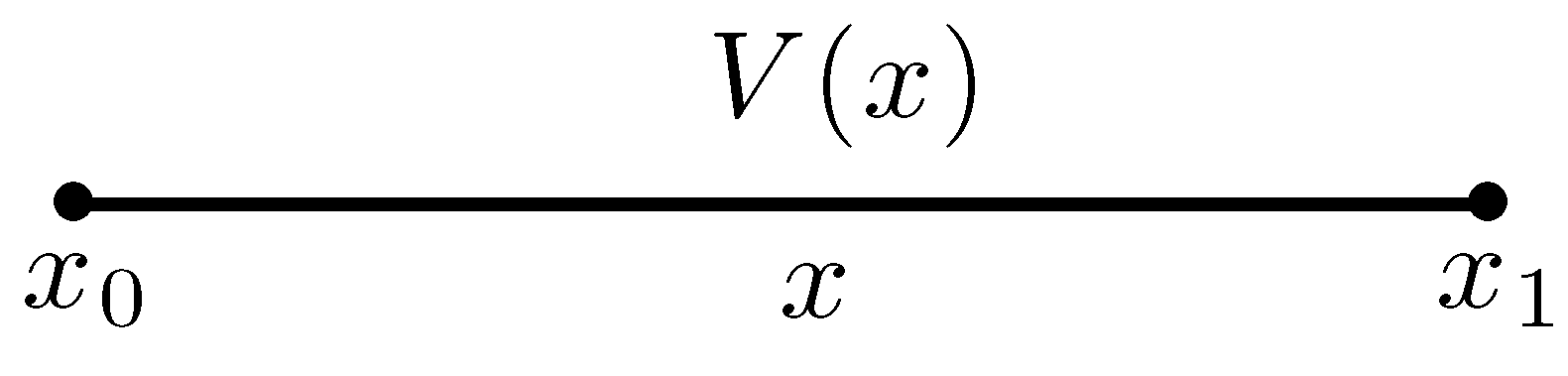
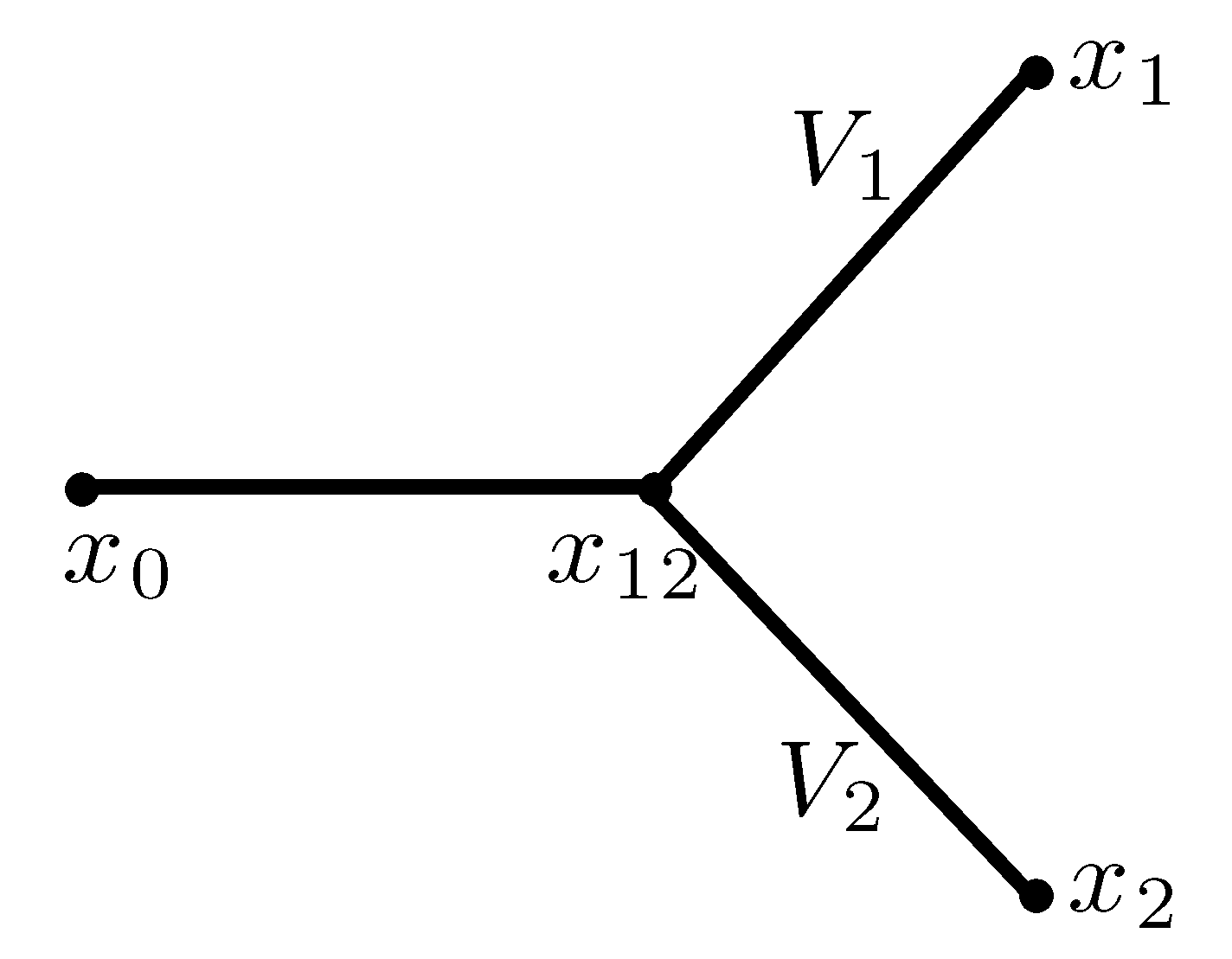
4.2. Junction of Three Branches with Different Types of Tapering
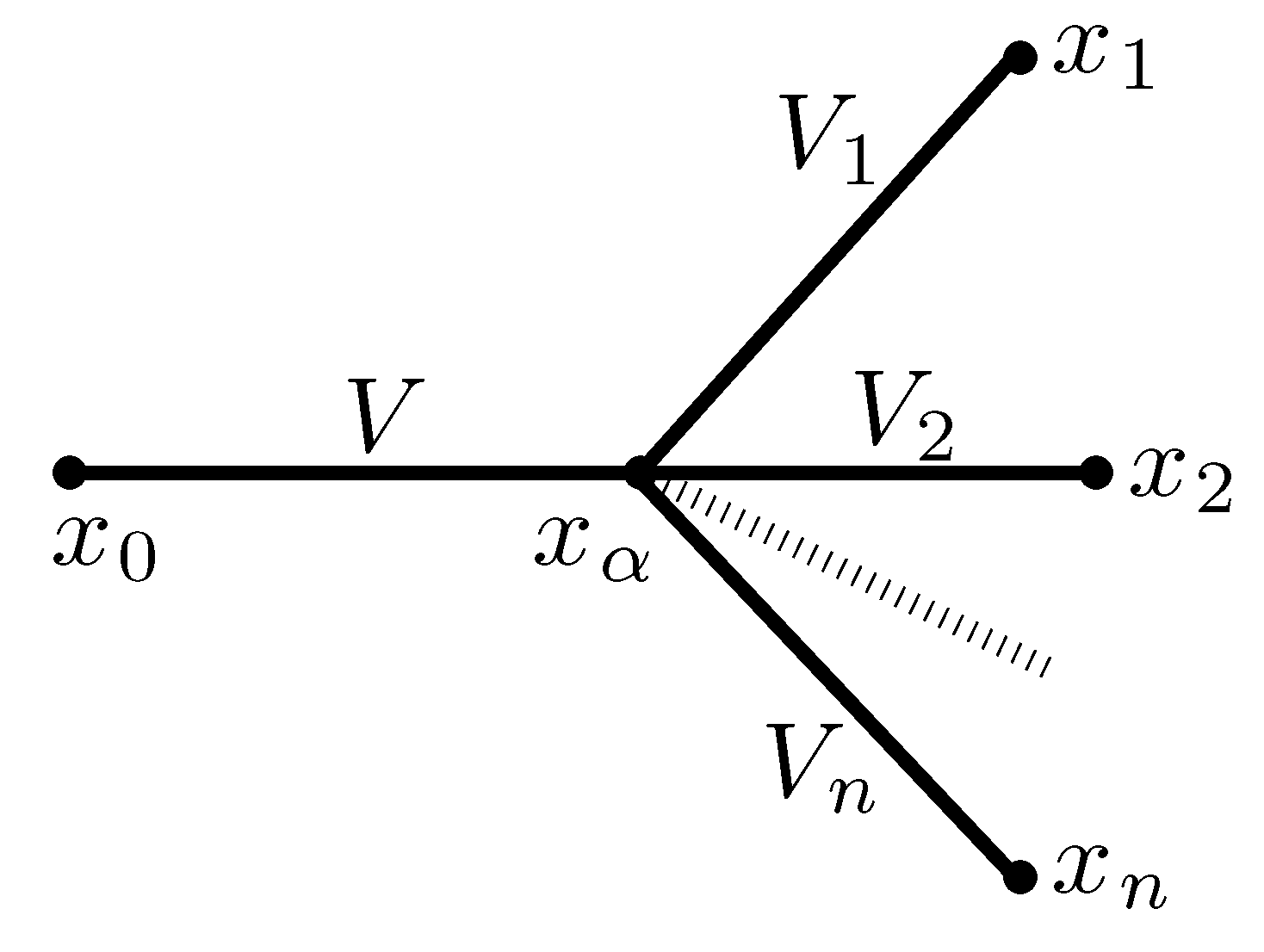
4.3. Junction of n-daughter branches
5. Examples
6. Transient Solutions
6.1. A Single Branch with Smooth Tapering
6.2. Single Branch with Piecewise Tapering
7. Summary
Acknowledgments
Appendix
A. Modified Orthogonality Relation
Conflicts of Interest
References
- Barret, J.N.; Crill, W.E. Influence of dendritic location and membrane properties on the effectiveness of synapses on cat motoneurones. J. Physiol. 1974, 239, 326–345. [Google Scholar] [CrossRef]
- Holmes, W.R.; Rall, W. Electrotonic length estimates in neurons with dendritic tapering or somatic shunt. J. Neurophysiol. 1992, 68, 1421–1437. [Google Scholar] [PubMed]
- Rall, W. Electrophysiology of a dendritic neuron model. Biophy. J. 1962, 2, 145–167. [Google Scholar] [CrossRef]
- Rall, W.; Burke, R.E.; Smith, T.G.; Nelson, P.G.; Frank, K. Dendritic location of synapses and possible mechanisms for the monosynaptic EPSP in motoneurons. J. Neurophysiol. 1967, 30, 884–915. [Google Scholar]
- Rall, W.; Shepherd, G.M.; Reese, T.S.; Brightman, M.W. Dendrodendritic synaptic pathway for inhibition in the olfactory bulb. Exp. Neurol. 1966, 14, 44–56. [Google Scholar] [CrossRef]
- Rinzel, J.; Wilfrid, R. Transient response in a dendritic neuron model for current injected at one branch. Biophy. J. 1974, 14, 759–790. [Google Scholar] [CrossRef]
- Stuart, G.J.; Häusser, M. Dendritic coincidence detection of EPSPs and action potentials. Nature Neurosci. 2001, 4, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Baer, S.M.; Tier, C. An analysis of a dentric neuron model with an active membrane site. J. Math. Biol. 1986, 23, 137–161. [Google Scholar] [CrossRef] [PubMed]
- Häusser, M.; Spruston, N.; Stuart, G.J. Diversity and dynamics of dendritic signaling. Science 2000, 290, 739–744. [Google Scholar] [CrossRef] [PubMed]
- Migliore, M.; Shepherd, G.M. Emerging rules for the distributions of active dendritic conductances. Nature Rev. Neurosci. 2002, 3, 362–370. [Google Scholar] [CrossRef] [PubMed]
- Sakatani, S.; Hirose, A. The influence of neuron shape changes on the firing characteristics. Neurocomputing 2003, 52, 355–362. [Google Scholar] [CrossRef]
- Vetter, P.; Ross, A.; Hausser, M. Propagation of action potential in dendrites depends on dendritic morphology. J. Neurophysiol. 2001, 85, 926–937. [Google Scholar] [PubMed]
- Kelvin, L. On the theory of the electric telegraph. Proc. Roy. Soc. (London) 1855, 7, 382. [Google Scholar]
- Rall, W. Branching dendritic trees and motoneurons membrane resistivity. Exp. Neurol. 1959, 1, 491–527. [Google Scholar] [CrossRef]
- Rall, W. Methods in Neuronal Modeling; MIT Press: Cambridge, MA, USA, 1989; pp. 9–92. [Google Scholar]
- Rall, W. Core conductor theory and cable properties of neurons. In Comprehensive Physiology; Wiley: Hoboken, NJ, USA, 2011; pp. 39–97. [Google Scholar]
- Rall, W. Membrane potential transients and membrane time constant of motoneurons. Exp. Neurol. 1960, 2, 503–532. [Google Scholar] [CrossRef]
- Rall, W. Theory of physiological properties of dendrites. Ann. N. Y. Acad. Sci. 1962, 96, 1071–1092. [Google Scholar] [CrossRef] [PubMed]
- Rall, W. Time constants and electrotonic length of membrane cylinders and neurons. Biophy. J. 1969, 9, 1483–1508. [Google Scholar] [CrossRef]
- Rall, W.; Rinzel, J. Branch input resistance and steady attenuation for input to one branch of a dendritic neuron model. Biophys. J. 1973, 13, 648–688. [Google Scholar] [CrossRef]
- Evans, J.D. Analytical solution of the cable equation with synaptic reversal potential for passive neurones with tip-to-tip dendrodendric coupling. Math. Biosci. 2005, 196, 125–152. [Google Scholar] [CrossRef] [PubMed]
- Ohme, M.; Schierwagen, A. An equivalent cable model for neuronal trees with active membrane. Biol. Cybernetics 1998, 78, 227–243. [Google Scholar] [CrossRef]
- Major, G.; Evans, J.D.; Jack, J.J. Solutions for transients in arbitrarily branching cables: I. Voltage recording with a somatic shunt. Biophy. J. 1993, 65, 423–449. [Google Scholar] [CrossRef]
- Major, G.; Evans, J.D.; Jack, J.J.B. Solutions for transients in arbitrarily branching cables: II. Voltage clamp theory. Biophy. J. 1993, 65, 450–468. [Google Scholar] [CrossRef]
- Major, G. Solutions for transients in arbitrarily branching cables: III. Voltage clamp problems. Biophy. J. 1993, 65, 469–491. [Google Scholar] [CrossRef]
- Major, G.; Evns, J.D. Solutions for transients in arbitrarily branching cables: IV. Nonuniform electrical parameters. Biophy. J. 1993, 66, 615–633. [Google Scholar] [CrossRef]
- Durand, D. The somatic shunt cable model for neurons. Biophys. J. 1984, 46, 645–653. [Google Scholar] [CrossRef]
- Evans, J.D.; Kember, G.C.; Major, G. Techniques for obtaining analytical solutions to the multicylinder somatic shunt cable model for passive neurones. Biophys. J. 1992, 63, 350–365. [Google Scholar] [CrossRef]
- Cox, S.J.; Raol, J.H. Recovering the passive properties of tapered dendrites from single and dual potential recordings. Math. Biosci. 2004, 190, 9–37. [Google Scholar] [CrossRef] [PubMed]
- Tsay, D.; Yuste, R. Role of dendritic spines in action potential backpropagation: A numerical simulation study. J. Neurophysiol. 2002, 88, 2834–2845. [Google Scholar] [CrossRef] [PubMed]
- Baer, S.; Tier, C. Techniques for obtaining analytical solutions for Rall’s model neuron. J. Neurosci. Methods 1987, 20, 151–166. [Google Scholar]
- Coombes, S.; Timofeeva, Y.; Svensson, C.M.; Lord, G.J.; Josić, K.; Cox, S.J.; Colbert, C.M. Branching dendrites with resonant membrane: A “sum-over-trips” approach. Biol. Cybernatics 2007, 97, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Roth, A.; Häusser, M. Compartmental models of rat cerebellar Purkinje cells based on simultaneous somatic and dendritic patch-clamp recordings. J. Physiol. 2001, 535, 445–472. [Google Scholar] [CrossRef] [PubMed]
- Häusser, M.; Mel, B. Dendrites: bug or feature? Curr. Opin. Neurobiol. 2003, 13, 372–383. [Google Scholar] [CrossRef]
- Krichmar, J.L.; Nasuto, S.J.; Scorcioni, R.; Washington, S.D.; Ascoli, G.A. Effects of dendritic morphology on CA3 pyramidal cell electrophysiology: A simulation study. Brain Res. 2002, 941, 11–28. [Google Scholar] [CrossRef]
- Mainen, Z.F.; Sejnowski, T.J. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 1996, 382, 363–366. [Google Scholar] [CrossRef] [PubMed]
- Nevian, T.; Larkum, M.E.; Polsky, A.; Schiller, J. Properties of basal dendrites of layer 5 pyramidal neurons: A direct patch-clamp recording study. Nature Neurosci. 2007, 10, 206–214. [Google Scholar] [CrossRef] [PubMed]
- Surkis, A.; Taylor, B.; Peskin, C.S.; Leonard, C.S. Quantitative morphology of physiologically identified and intracellularly labeled neurons from the guinea-pig laterodorsal tegmental nucleus in vitro. Neuroscience 1996, 74, 375–392. [Google Scholar] [CrossRef]
- Rall, W. Membrane time constant of motoneurons. Science 1957, 126, 454. [Google Scholar] [CrossRef] [PubMed]
- Abrikosov, A.A.; Gorkov, L.P.; Dzyaloshinski, I.E. Methods of Quantum Field Theory in Statistical Physics; Dover Publications: New York, NY, USA, 1963. [Google Scholar]
- Akhiezer, A.; Berestetskii, V.B. Quantum Electrodynamics; Interscience Publishers: New York, NY, USA, 1965. [Google Scholar]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Relativistic Quantum Theory; Pergamon Press: Oxford, UK, 1971. [Google Scholar]
- Feynman, R.P. The theory of positrons. Phys. Rev. 1949, 76, 749–759. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-time approach to quantum electrodynamics. Phys. Rev. 1949, 76, 769–789. [Google Scholar] [CrossRef]
- Feynman, R.P. QED: The Strange Theory of Light and Matter; Princeton, N.J., Ed.; Princeton University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Kaiser, D. Physics and Feynman’s diagrams. Am. Sci. 2005, 93, 156–165. [Google Scholar] [CrossRef]
- Mattuck, R.D. A Guide to Feynmann Diagrams in theMany-Body Problems; Dover Publications: New York, NY, USA, 1992. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1998; Volumes 1–3. [Google Scholar]
- Meiler, M.; Cordero-Soto, R.; Suslov, S.K. Solution of the Cauchy problem for a time-dependent Schrödinger equation. J. Math. Phys. 2008, 49, 072102. [Google Scholar] [CrossRef]
- Nikiforov, A.F.; Suslov, S.K.; Uvarov, V.B. Classical Orthogonal Polynomials of a Discrete Variable; Springer–Verlag: Berlin, Germany; New York, NY, USA, 1991. [Google Scholar]
- Smirnov, Y.F.; Shitikova, K.V. The method of Kharmonics and the shell model. Sov. J. Part. Nucl. 1977, 8, 344–370. [Google Scholar]
- Smorodinskii, Y.A. Trees and many-body problem. Izv. Vyssh. Uchebn. Zaved. Radiofiz. 1976, 19, 932–941. [Google Scholar] [CrossRef]
- Abbott, L.F. Simple diagrammatic rules for solving dendritic cable problems. Physica A 1992, 185, 343–356. [Google Scholar] [CrossRef]
- Chruściński, D.; Jurkowski, J. Memory in a nonlocally damped oscillator. In Proceedings of Quantum Bio-Informatics III From Quantum Information to Bio-Informatics, Tokyo, Japan, 11–14 March 2009.
- Cordero-Soto, R.; Lopez, R.M.; Suazo, E.; Suslov, S.K. Propagator of a charged particle with a spin in uniform magnetic and perpendicular electric fields. Lett. Math. Phys. 2008, 84, 159–178. [Google Scholar] [CrossRef]
- Cordero-Soto, R.; Suazo, E.; Suslov, S.K. Models of damped oscillators in quantum mechanics. J. Phy. Math. 2009, 1, S090603. [Google Scholar] [CrossRef]
- Cordero-Soto, R.; Suazo, E.; Suslov, S.K. Quantum integrals of motion for variable quadratic Hamiltonians. Ann. Phys. 2010, 315, 1884–1912. [Google Scholar] [CrossRef]
- Cordero-Soto, R.; Suslov, S.K. Time reversal for modified oscillators. Theo. Math. Phy. 2010, 162, 286–316. [Google Scholar] [CrossRef]
- Lanfear, N.; Suslov, S.K. The ime-dependent Schrödinger Equation, Riccati Equation and Airy Functions. Available online: http://arxiv.org/pdf/0903.3608.pdf (accessed on 22 April 2009).
- Suazo, E.; Suslov, S.K.; Vega-Guzmán, J.M. The Riccati differential equation and a diffusion-type equation. N. Y. J. Math. 2011, 17, 225–244. [Google Scholar]
- Suslov, S.K. Dynamical invariants for variable quadratic Hamiltonians. Phys. Scr. 2010, 81, 055006. [Google Scholar] [CrossRef]
- Jack, J.J.B.; Noble, D.; Tsien, R.W. Electric Current Flow in Excitable Cells; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Foster, A.; Hendryx, E.; Murillo, A.; Salas, M.; Morales-Butler, E.J.; Suslov, S.K.; Herrera-Valdez, M. Extensions of the Cable Equation Incorporating Spatial Dependent Variations in Nerve Cell Diameter. Available online: http://mtbi.asu.edu/research/archive (accessed on 31 August 2010).
- Churchill, R.V. Expansions in series of non-orthogonal functions. Bull. Amer. Math. Soc. 1942, 48, 143–149. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegan, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Andrews, G.E.; Askey, R.A.; Roy, R. Special Functions; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Askey, R.A. Orthogonal Polynomials and Special Functions. In Proceedings of the CBMS–NSF Regional Conferences Series in Applied Mathematics, SIAM, Philadelphia, PA, USA, 1 June 1975.
- Hartman, P. Ordinary Differential Equations; John Wiley & Sons: Baltimore, MA, USA, 1973. [Google Scholar]
- Kellogg, O.D. Note on closure of orthogonal sets. Bull. Amer. Math. Soc. 1921, 27, 165–169. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Fomin, S.V. Introductory Real Analysis; Dover: New York, NY, USA, 1970; pp. 1–365. [Google Scholar]
- Nikiforov, A.F. Lectures on Equations and Methods of Mathematical Physics; Intellect: Dolgoprudnii, Russia, 2009. (in Russian) [Google Scholar]
- Nikiforov, A.F.; Uvarov, V.B. Special Functions of Mathematical Physics; Birkhäuser: Basel, Boston, 1988. [Google Scholar]
- Reid, W.T. A boundary value problem assiciated with the calculus of variations. Am. J. Math. 1932, 54, 769–790. [Google Scholar] [CrossRef]
- Reid, W.T. Oscillation criteria for self-adjoint differential systems. Trans. Amer. Math. Soc. 1961, 101, 91–106. [Google Scholar] [CrossRef]
- Erdélyi, A. Higher Transcendental Functions, Volumes I–III; Erdélyi, A., Ed.; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Olver, F.W.J. Asymptotics and Special Functions; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Rainville, E.D. Special Functions; The Macmillan Company: New York, NY, USA, 1960. [Google Scholar]
- Vilenkin, N.Y. Special Functions and the Theory of Group Representations; American Mathematical Society: Providence, RI, USA, 1968. [Google Scholar]
- Watson, G.N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Herrera-Valdez, M.A.; Suslov, S.K.; Vega-Guzmán, J.M. A Graphical Approach to a Model of a Neuronal Tree with a Variable Diameter. Mathematics 2014, 2, 119-135. https://doi.org/10.3390/math2030119
Herrera-Valdez MA, Suslov SK, Vega-Guzmán JM. A Graphical Approach to a Model of a Neuronal Tree with a Variable Diameter. Mathematics. 2014; 2(3):119-135. https://doi.org/10.3390/math2030119
Chicago/Turabian StyleHerrera-Valdez, Marco A., Sergei K. Suslov, and José M. Vega-Guzmán. 2014. "A Graphical Approach to a Model of a Neuronal Tree with a Variable Diameter" Mathematics 2, no. 3: 119-135. https://doi.org/10.3390/math2030119
APA StyleHerrera-Valdez, M. A., Suslov, S. K., & Vega-Guzmán, J. M. (2014). A Graphical Approach to a Model of a Neuronal Tree with a Variable Diameter. Mathematics, 2(3), 119-135. https://doi.org/10.3390/math2030119




