Bounded Gaps between Products of Special Primes

Abstract

In their breakthrough paper in 2006, Goldston, Graham, Pintz and Yıldırım proved several results about bounded gaps between products of two distinct primes. Frank Thorne expanded on this result, proving bounded gaps in the set of square-free numbers with r prime factors for any $r\ge 2$, all of which are in a given set of primes. His results yield applications to the divisibility of class numbers and the triviality of ranks of elliptic curves. In this paper, we relax the condition on the number of prime factors and prove an analogous result using a modified approach. We then revisit Thorne’s applications and give a better bound in each case.

1. Introduction and Statement of Results

The celebrated twin prime conjecture predicts that there are infinitely many pairs of consecutive primes. While a proof of the conjecture seems to be out of reach by current methods, there has been a spate of recent advances concerning the weaker conjecture:

$$\underset{n\to \infty }{lim\; inf}(p_{n+1}-p_n)<\infty$$

In 2005, Goldston, Pintz and Yıldırım [1] proved that there exists infinitely many consecutive primes, which are much closer than average, that is,

$$\underset{n\to \infty }{lim\; inf}\frac{p_{n+1}-p_n}{log{p}_n}=0$$

Based on their methods, Zhang [2] showed that:

$$\underset{n\to \infty }{lim\; inf}(p_{n+1}-p_n)\le 7\times {10}^7$$

Maynard [3] improved the upper bound to 600 using a modified sieve method. The constant was subsequently improved to 252 by an ongoing polymath project [4].

In a similar vein, people have investigated related problems about “almost primes” or numbers with few prime factors. Chen [5] proved that there are infinitely many primes, p, such that $p+2$ has at most two distinct prime factors. In [6], Goldston, Graham, Pintz and Yıldırım (GGPY) considered the $E_2$ numbers, which are numbers with exactly two distinct prime factors, and showed that there are infinitely many pairs of $E_2$ numbers that are at most six apart.

Thorne [7] observed that the methods in [6] are highly adaptable, and generalized the result to $E_r$ numbers, which are numbers with exactly r distinct prime factors. In [7], he showed that given an infinite set of primes, $\mathcal{P}$, satisfying certain conditions, and positive integers ν and r with $r\ge 2$, there exists an effectively computable constant $C(r,\nu ,\mathcal{P})$, such that:

$$\underset{n\to \infty }{lim\; inf}(q_{n+1}-q_n)\le C(r,\nu ,\mathcal{P})$$

where $q_n$ is the n-th $E_r$ number, whose prime factors are all in $\mathcal{P}$.

Using this theorem, Thorne proved several corollaries. With a result by Soundararajan [8], he showed that there are infinitely many pairs of $E_2$ numbers, m and n, such that the class groups, $\mathrm{Cl}\left(\mathbb{Q}\left(\sqrt{-m}\right)\right)$ and $\mathrm{Cl}\left(\mathbb{Q}\left(\sqrt{-n}\right)\right)$, each contain elements of order four, with $|m-n|\le 64$. As a second application, he considered the quadratic twists of elliptic curves over $\mathbb{Q}$ without a $\mathbb{Q}$-rational torsion point of order two. Let $E/\mathbb{Q}$ be such an elliptic curve, $L(E,s)$ denote its Hasse–Weil L-function, $\mathrm{rk}\left(E\right):=\mathrm{rk}(E,\mathbb{Q})$ denote the rank of the group of rational points on E over $\mathbb{Q}$ and $E\left(D\right)$ denote the D-quadratic twist of E for a fundamental discriminant, D. Using the work of Ono [9], he showed that for “good” elliptic curve $E/\mathbb{Q}$ (defined as in [10]), there are infinitely many pairs of square-free numbers, m and n, such that $L\left(E\right(m),1)·L\left(E\right(n),1)\ne 0$, $\mathrm{rk}\left(E\right(m\left)\right)=\mathrm{rk}\left(E\right(n\left)\right)=0$ and $|m-n|\le C_E$ hold simultaneously for some absolute constant, $C_E$. For $E=X_0\left(11\right)$, Thorne obtained a bound of $C_E\le$ 6,152,146.

In this paper, we revisit Thorne’s examples and obtain stronger bounds by relaxing the $E_r$ condition to instead consider bounded gaps between square-free numbers with prime factors all in $\mathcal{P}$. In this case, we can prove an analogous general theorem with a better bound on the gaps.

Theorem 1. 

Suppose $\mathcal{P}$ is a set of primes with positive Frobenius density. Let ν be a positive integer; and let $q_n$ denote the n-th square-free number, whose prime factors are all in $\mathcal{P}$. Then:

$$\underset{n\to \infty }{lim\; inf}(q_{n+\nu }-q_n)\le C(\nu ,\mathcal{P})$$

Remark 1. 

Theorem 1 also holds for arbitrary sets of primes of positive density satisfying a Siegel–Walfisz-type condition (defined in Section 2).

We observe that if we remove the restriction on the number of prime divisors in each of Thorne’s examples, we can obtain better bounds. Replacing $E_2$ by a square-free number in his first example, we obtain the following twin prime-type result.

Corollary 1. 

There are infinitely many square-free numbers, n, such that the class groups, $\mathrm{Cl}\left(\mathbb{Q}\left(\sqrt{-n}\right)\right)$ and $\mathrm{Cl}\left(\mathbb{Q}\left(\sqrt{-n-8}\right)\right)$, each contain elements of order four.

In the second example, the bound, $C_E$, can be improved analogously. We give an explicit bound in the case when $E=X_0\left(11\right)$.

Corollary 2. 

Let $E:=X_0\left(11\right)$. Then, there are infinitely many pairs of square-free numbers, m and n, for which the following hold simultaneously:

 (i)

$L\left(E\right(m),1)·L\left(E\right(n),1)\ne 0$,

 (ii)

$\mathrm{rk}\left(E\right(m\left)\right)=\mathrm{rk}\left(E\right(n\left)\right)=0$,

 (iii)

$|m-n|\le 48$.

Remark 2. 

There are more general applications of Theorem 1. Thorne [7] described an application to the nonvanishing of Fourier coefficients of weight one newforms, where Theorem 1 can also be applied. If $f\left(z\right)={\sum }_{n=1}^{\infty }a\left(n\right)q^n$ is a newform of integer weight, then the set of integers, n, such that $a\left(n\right)$ is nonzero modulo ℓ has zero density for all prime ℓ by the theory of Deligne and Serre [11]. Nonetheless, our result shows that there are bounded gaps between such n for almost all ℓ, yielding better bounds than [7].

Our result also applies to the quadratic twists of elliptic curves over $\mathbb{Q}$ that have a given 2-Selmer ${\mathbb{F}}_2$-rank. If K is a number field, E is an elliptic curve over K and r is a suitable nonnegative integer, Mazur and Rubin [12] conjecture that for a positive proportion of quadratic extensions, $F/K$, the quadratic twist, $E^F$, of E by $F/K$ has the 2-Selmer rank r. Using ([12] (Proposition 4.2)), our result shows that for $K=\mathbb{Q}$, an elliptic curve, $E/\mathbb{Q}$, with no two-torsion points, and a given integer, $r\ge 0$, either no quadratic twists have 2-Selmer rank r or there are bounded gaps between the square-free numbers, d, such that $E\left(d\right)$ has 2-Selmer rank r.

2. Main Result

We borrow our notation from [6], using k to denote an integer greater than one, $\mathcal{L}=\{L_1,\dots ,L_k\}$ to denote an admissible k-tuple of linear forms (defined in Section 2.2) with $L_i\left(n\right):=a_{i}n+b_i$ for some $a_i,b_i\in \mathbb{Z},a_i>0$, and $\mathcal{P}$ to denote a set of primes with positive density α. The constants implied by “O” and “≪” may depend on k, $\mathcal{L}$ and $\mathcal{P}$. Let ${\tau }_k\left(n\right)$ denote the number of ways of writing n as a product of k factors and $\omega \left(n\right)$ denote the number of distinct prime factors of n. $\varphi \left(n\right)$ and $\mu \left(n\right)$ are the usual Euler and Möbius functions. N and R will denote real numbers regarded as tending to infinity, and we will always assume $R\le N^{1/2}$.

Given a set of primes, $\mathcal{P}$, with density α, we call a square-free number with prime factors only in $\mathcal{P}$ an $E_{\mathcal{P}}$ number . Let $\mathcal{P}\left(N\right)$ be the set of primes in $\mathcal{P}$ greater than $exp\left(\sqrt{logN}\right)$ and ${\xi }_{\mathcal{P}}$ be the characteristic function of all $E_{\mathcal{P}\left(N\right)}$ numbers. Given a positive integer, M, to be chosen later, let ${\delta }_m$ be the density of integers, n, congruent to m mod M in the set of $E_{\mathcal{P}}$ numbers and the minimum density δ of a set of linear forms, $\mathcal{L}$, be the minimum of ${\delta }_{b_j}$, $1\le j\le k$. We define:

$${\Delta }_{\mathcal{P},b}(N;q,a):=\sum _{\begin{array}{c}N<n\le 2N\\ n\equiv a\left(\mathrm{mod}q\right)\\ n\equiv b\left(\mathrm{mod}M\right)\end{array}}{\xi }_{\mathcal{P}}\left(n\right)-\frac{1}{\varphi \left(q\right)}\sum _{\begin{array}{c}N<n\le 2N\\ (n,q)=1\\ n\equiv b\left(\mathrm{mod}M\right)\end{array}}{\xi }_{\mathcal{P}}\left(n\right)$$

Following [7], we say that $\mathcal{P}$ satisfies a Siegel-Walfisz condition $SW\left(M\right)$ if for each b coprime to M and for any positive C,

$$\left|\sum _{\begin{array}{c}N<p\le 2N,p\in \mathcal{P}\\ p\equiv a\left(\mathrm{mod}q\right)\\ p\equiv b\left(\mathrm{mod}M\right)\end{array}}1-\frac{1}{\varphi \left(q\right)}\sum _{\begin{array}{c}N<p\le 2N,p\in \mathcal{P}\\ p\equiv b\left(\mathrm{mod}M\right)\end{array}}1\right|{\ll }_{A}N{log}^{-C}N$$

holds uniformly for all q with $(q,Ma)=1$.

We also recall that a set of primes, $\mathcal{P}$, has Frobenius densityα, $0<\alpha <1$ (cf. [13]), if there is a Galois extension, $K/\mathbb{Q}$, and a union of conjugacy classes, H, in $G=\mathrm{Gal}(K/\mathbb{Q})$, such that for all primes, p, sufficiently large, ${\mathrm{Frob}}_p\in H$ if and only if $p\in \mathcal{P}$, and $\#H/\#G=\alpha$.

Analogous to the approach in [6,7], Theorem 1 follows from the following main result.

Theorem 2. 

Let $\mathcal{P}$ be an infinite set of primes with positive Frobenius density $\alpha <1$ that satisfies $SW\left(M\right)$. Let $L_i\left(x\right)(1\le i\le k)$ be an M-admissible (defined in Section 2.2) k-tuple of linear forms with minimum density δ. There are at least $\nu +1$ forms among them that infinitely, often, simultaneously represent square-free numbers with prime factors all in $\mathcal{P}$, provided that:

$$k>\nu \frac{4^{1-\alpha }}{\delta \varphi \left(M\right)}\frac{\mathfrak{b}\left(1\right)}{\mathfrak{b}\left(k\right)}\Gamma \left(\alpha \right)\Gamma (2-\alpha )$$

where:

$$\mathfrak{b}\left(k\right):=\frac{\Gamma (1-\alpha )\Gamma \left(k\right(1-\alpha )+1)}{\Gamma \left(\right(k+1\left)\right(1-\alpha )+1))}=B(1-\alpha ,k(1-\alpha )+1)$$

Remark 3. 

Our method is not directly applicable in the case when $\alpha =1$. Nonetheless, if we take the limit, $\alpha \to 1$, on the right-hand side of the inequality, we get $k>\nu /\left(\delta \phi \right(M\left)\right)$. In practice, one can take a subset of $\mathcal{P}$ with Frobenius density close to one that satisfies $SW\left(M\right)$, so that the same k still satisfies the inequality in Theorem 2.

In the case when $k=2$ and $\nu =1$, we have the following twin prime-type result.

Corollary 3. 

Let $\mathcal{P}$ be an infinite set of primes with positive Frobenius density $\alpha <1$ that satisfies $SW\left(M\right)$. For any even number, d, let ${\delta }^{\prime }={max}_{m}min({\delta }_m,{\delta }_{m+d})$. Assume that:

$${\delta }^{\prime }\varphi \left(M\right)>2^{1-2\alpha }\frac{\mathfrak{b}\left(1\right)}{\mathfrak{b}\left(2\right)}\Gamma \left(\alpha \right)\Gamma (2-\alpha )$$

Then, there are infinitely many n for which n and $n+d$ are simultaneously square-free numbers with prime factors all in $\mathcal{P}$.

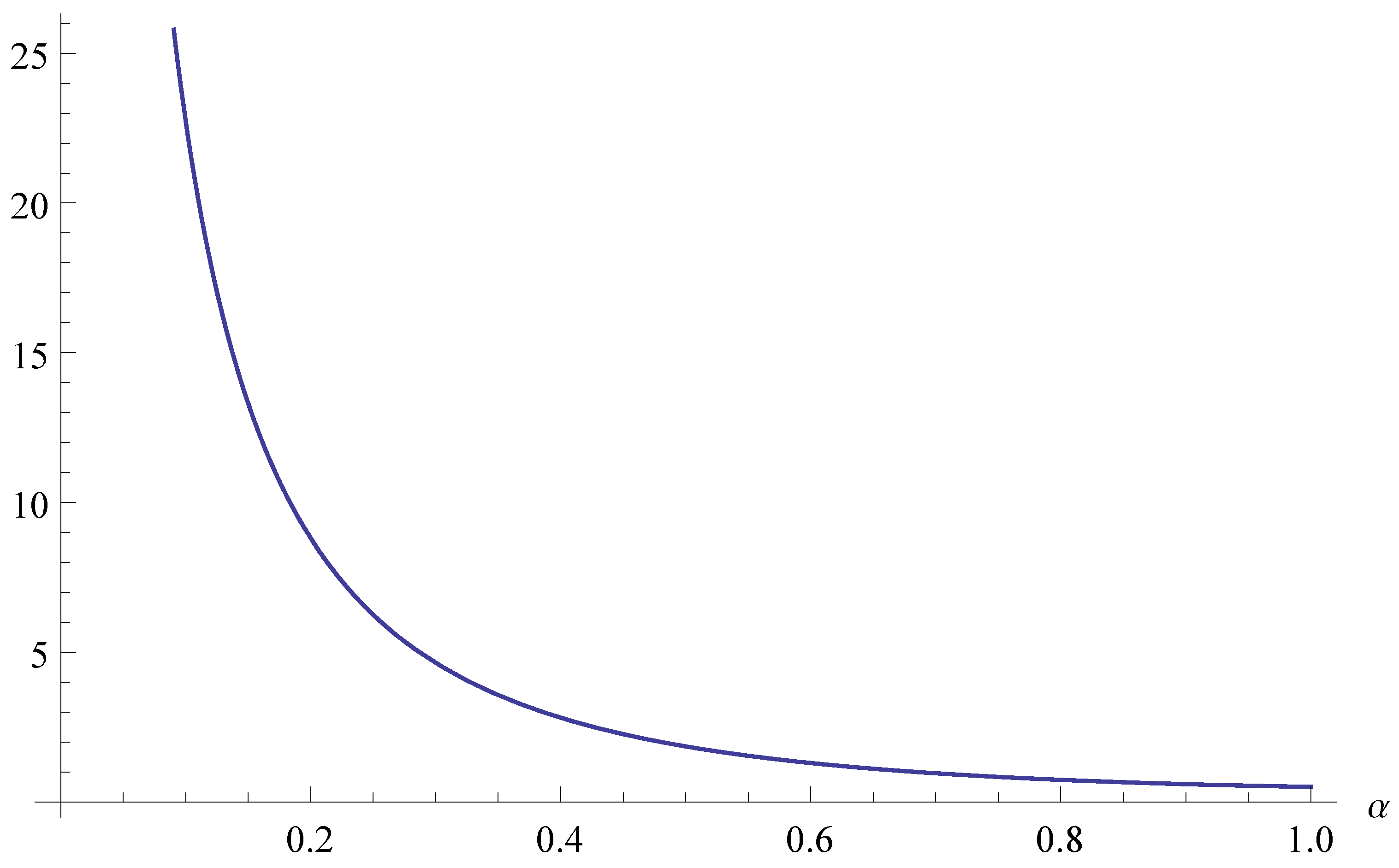
We have plotted the right-hand side of the inequality against α to illustrate the conditions under which one can obtain a twin prime-type result (Figure 1).

Figure 1. The right-hand side of Corollary 3 vs. α.

Figure 1. The right-hand side of Corollary 3 vs. α.

As another sample application of our theorem, we consider the problem of representing square-free integers by translates of tuples. This problem was actually answered by Hall [14], who even obtained an asymptotic expression for the number of such representations, but, by taking the limit, $\alpha \to 1$, in Theorem 2.1, we easily obtain the following corollary.

Corollary 4. 

Let $\{b_1,b_2,\dots ,b_k\}$ be an admissible k-tuple. Then, there are infinitely many n, such that all of the $n+b_i$ are simultaneously square-free.

Here, we recall from [1] that a k-tuple of integers is admissible if for all prime, p, they do not cover all the residue classes modulo p. We remark that admissibility is not a necessary condition for this corollary to hold, but it is a natural limit of our method.

2.1. The Level of Distribution of $E_{\mathcal{P}}$ Numbers

In this section, we will prove a Bombieri–Vinogradov-type result for $E_{\mathcal{P}}$ numbers if $\mathcal{P}$ satisfies $SW\left(M\right)$, generalizing a result of Orr [15]. More precisely, we shall show that the $E_{\mathcal{P}}$ numbers have a level of distribution $\vartheta =1/2$. We remark that a set, $\mathcal{P}$, with positive Frobenius density satisfies $SW\left(M\right)$ for some M as a consequence of Lemma 3.1 in [7].

Lemma 1. 

Suppose that $\mathcal{P}$ satisfies $SW\left(M\right)$ for some M. Then, for each b coprime to M and for any C, there exists some $B=B\left(C\right)>0$, such that:

$$\sum _{\begin{array}{c}q\le N^{1/2}{log}^{-B}N\\ (q,M)=1\end{array}}\underset{\begin{array}{c}a\\ (a,q)=1\end{array}}{max}\left|{\Delta }_{\mathcal{P},b}(N;q,a)\right|{\ll }_{C}N{log}^{-C}N$$

Proof. The result is a variant of Motohashi [16]. Similar results are also treated by Bombieri, Friedlander and Iwaniec [17]. We will use the modern treatment given by ([18] (Theorem 17.4)), following the approach of Thorne ([7] (Lemma 3.2)).

Let ${\xi }_{\mathcal{P},b}\left(n\right)$ be the characteristic function of $E_{\mathcal{P}\left(N\right)}$ numbers congruent to b modulo M and ${\chi }_{\mathcal{P},b}\left(n\right)$ be the characteristic function of primes in $\mathcal{P}\left(N\right)$ congruent to b modulo M. We further define ${\xi }_{\mathcal{P},b}^{\prime }\left(n\right)=\omega {\left(n\right)}^{-1}{\xi }_{\mathcal{P},b}\left(n\right)$. Borrowing the notation from [18], given an arithmetic function, $f\left(n\right)$, define:

$$D_f(N;q,a)=\sum _{\begin{array}{c}n\le N\\ n\equiv a\left(\mathrm{mod}q\right)\end{array}}f\left(n\right)-\frac{1}{\varphi \left(q\right)}\sum _{\begin{array}{c}n\le N\\ (n,q)=1\end{array}}f\left(n\right)$$

Finally, we let ${f|}_I$ denote the restriction of $f\left(n\right)$ to the interval, I, i.e., ${f|}_I\left(n\right)=f\left(n\right)$ if $n\in I$, ${f|}_I\left(n\right)=0$ otherwise. We first remark that:

$${\xi }_{\mathcal{P},b}=\sum _{ij\equiv b\left(\mathrm{mod}M\right)}{\xi }_{\mathcal{P},i}^{\prime }*{\chi }_{\mathcal{P},j},{\Delta }_{\mathcal{P},b}(N;q,a)=D_{{\xi }_{\mathcal{P},b}{|}_{[N,2N]}}(2N;q,a)$$

Hence, for $Q=N^{1/2}{log}^{-B}N$, where $B=B\left(C\right)$ will be chosen later,

$$\begin{array}{cc}\hfill \sum _{q\le Q}\underset{(a,q)=1}{max}\left|{\Delta }_{\mathcal{P},b}(N;q,a)\right|& =\sum _{q\le Q}\underset{(a,q)=1}{max}\left|D_{{\xi }_{\mathcal{P},b}{|}_{[N,2N]}}(2N;q,a)\right|\hfill \\ & \le \sum _{ij\equiv b\left(\mathrm{mod}M\right)}\sum _{q\le Q}\underset{(a,q)=1}{max}\left|D_{{\xi }_{\mathcal{P},i}^{\prime }*{\chi }_{\mathcal{P},j}{|}_{[N,2N]}}(2N;q,a)\right|\hfill \end{array}$$

Fixing $\epsilon >0$, we now split the interval $[x,2N/x]$ into intervals of the form $[t,(1+\epsilon \left)t\right)$, where $x=exp\left(\sqrt{logN}\right)$. The number of such intervals is $\ll \frac{logN}{\epsilon }$. Then, we remark that ${\sum }_t{\xi }_{\mathcal{P},i}^{\prime }{{|}_{[t,(1+\epsilon \left)t\right)}*{\chi }_{\mathcal{P},j}|}_{[N/t,\frac{2N}{(1+\epsilon )t}]}$ closely approximates ${\xi }_{\mathcal{P},i}^{\prime }*{\chi }_{\mathcal{P},j}{|}_{[N,2N]}$. Both functions are supported in $[N,2N]$ and identical on $\left[N\right(1+\epsilon ),2N/(1+\epsilon \left)\right]$. The differences on the intervals, $[N,N(1+\epsilon \left)\right)$ and $(2N/(1+\epsilon ),2N]$, contribute $\ll \epsilon N/\varphi \left(q\right)$ to each $D_{{\xi }_{\mathcal{P},i}^{\prime }*{\chi }_{\mathcal{P},j}{|}_{[N,2N]}}(2N;q,a)$. Summing over all $q\le Q$ and all pairs $(i,j)$, such that $ij\equiv b\left(\mathrm{mod}M\right)$, the total contribution of the error is:

$$\ll \epsilon N\sum _{q\le Q}\frac{1}{\varphi \left(q\right)}\ll \epsilon NlogN$$

On the other hand, we may apply Theorem 17.4 in [18] with $\alpha ={\xi }_{\mathcal{P},i}^{\prime }{|}_{[t,(1+\epsilon \left)t\right)}$ and $\beta ={\chi }_{\mathcal{P},j}{|}_{[N/t,\frac{2N}{(1+\epsilon )t}]}$. Note that Condition (17.13) on β is satisfied for some $\Delta {\ll }_U{log}^{-U}N$, since $\mathcal{P}$ satisfies the $SW\left(M\right)$ condition, and:

$$\left|\right|{\xi }_{\mathcal{P},i}^{\prime }{|}_{[t,(1+\epsilon \left)t\right)}\left|\right|\ll \frac{\sqrt{\epsilon t}}{{log}^{(1-\alpha )/2}\left(\epsilon t\right)},\left|\right|{\chi }_{\mathcal{P},j}{|}_{\left[N/t,\frac{2N}{(1+\epsilon )t}\right]}\left|\right|\sim {\left(\frac{\alpha (1-2\epsilon )N/t}{log\left(\right(1-2\epsilon )N/t)}\right)}^{1/2}$$

where:

$$\left|\right|f\left|\right|:={\left(\sum _{n}f{\left(n\right)}^2\right)}^{1/2}$$

Hence, the theorem gives (note that $x\gg {log}^{U}N$ for any $U>0$):

$$\sum _t\sum _{q\le Q}\underset{(a,q)=1}{max}\left|D_{{\xi }_{\mathcal{P},i}^{\prime }{{|}_{[t,(1+\epsilon \left)t\right)}*{\chi }_{\mathcal{P},j}|}_{[N/t,\frac{2N}{(1+\epsilon )t}]}}(2N;q,a)\right|\ll {\epsilon }^{-1/2}N{log}^{-B+2.5}N$$

We take $\epsilon ={log}^{-2B/3+1}N$, and sum over all the pairs $(i,j)$, such that $ij\equiv b\left(\mathrm{mod}M\right)$ to conclude that:

$$\sum _{q\le Q}\underset{(a,q)=1}{max}\left|{\Delta }_{\mathcal{P},b}(N;q,a)\right|\ll N{log}^{-2B/3+2}N$$

From there, taking $B=3C/2+3$ gives the desired result.

2.2. Linear Forms and Admissibility

Following [7] and [6], we will prove our results for k-tuples of linear forms:

$$L_i\left(x\right):=a_{i}x+b_i(1\le i\le k),a_i,b_i\in \mathbb{Z},a_i>0$$

We will prove that for any admissible k-tuple with k sufficiently large, there are infinitely many x for which several $L_i\left(x\right)$ simultaneously represent square-free numbers with all prime factors in $\mathcal{P}$. The basic setup is the same as [7]. We shall recall only the important notions and hypotheses in this section and refer our readers to ([7] (Section 2.2]) and ([6] (Section 3)) for a detailed exposition. As in [7] and [6], we define the quantities:

$$\begin{array}{c}\hfill P_{\mathcal{L}}\left(n\right):=\prod _{i=1}^k{L}_i\left(n\right),A:={\mathrm{lcm}}_i\left(a_i\right),\mathfrak{S}\left(\mathcal{L}\right):=\prod _{p\mid A}{\left(1-\frac{1}{p}\right)}^{-k}\prod _{p\nmid A}\left(1-\frac{k}{p}\right){\left(1-\frac{1}{p}\right)}^{-k}\end{array}$$

We recall from [7] the following admissibility constraint.

Definition 1. 

Given a positive integer, M, a k-tuple of linear forms $\mathcal{L}=\{L_1,\dots ,L_k\}$ is M-admissible if the following conditions hold simultaneously.

(i) 

For every prime, p, there exists an integer, $x_p$, such that ${\displaystyle p\nmid \prod _{i=1}^n(a_i{x}_p+b_i)}$;

 (ii)

for each i, M divides $a_i$;

 (iii)

for each i, M is coprime to $a_i/M$.

A k-tuple of linear forms, $\mathcal{L}$, is called admissible if it satisfies only (i). The above stronger admissibility constraint is introduced to incorporate the fact that $\mathcal{P}$ may fail to be well-distributed modulo M.

We will primarily consider the case when $a_1=\cdots =a_k=M$. Given a set of linear forms $\mathcal{L}=\{L_1,\dots ,L_k\}$ with $L_i\left(n\right)=a_{i}n+b_i$, remove finitely many primes from $\mathcal{P}$, so that $(A,p)=1$ for all $p\in \mathcal{P}$. Throughout the paper, we shall use ${\sum }^{\prime }$ for a sum over all the values relatively prime to A and any prime $p\in \mathcal{P}\left(N\right)$ (this is different from [7], which only requires the values to be relatively prime to A). As in [7] and [6], we may assume without loss of generality that M-admissibility can be replaced by a stronger condition, which we label Hypothesis $A\left(M\right)$. The justification for this hypothesis appears in [7].

Hypothesis $A\left(M\right)$. 

$\mathcal{L}=\{L_1,\dots ,L_k\}$ is an M-admissible k-tuple of linear forms. The functions $L_i\left(n\right)=a_{i}n+b_i(1\le i\le k)$ have integer coefficients with $a_i>0$. Each of the coefficients, $a_i$, is divisible by the same set of primes, none of which divides any of the $b_i$. If $i\ne j$, then any prime factor of $a_i{b}_j-a_j{b}_i$ divides each of the $a_i$.

2.3. Preliminary Lemmas

In this section, we shall provide the setup of the proof of the main theorem and prove a few key lemmas. We first recall a lemma from [6], which we shall use frequently in this section.

Lemma 2. 

([6] (Lemma 4)) Suppose that γ is a multiplicative function, and suppose that there are positive real numbers $\kappa ,A_1,A_2,L$, such that:

$$0\le \frac{\gamma \left(p\right)}{p}\le 1-\frac{1}{A_1}$$

and:

$$-L\le \sum _{w\le p<z}\frac{\gamma \left(p\right)logp}{p}-\kappa log\frac{z}{w}\le A_2$$

if $2\le w\le z$. Let g be the multiplicative function defined by:

$$g\left(d\right)=\prod _{p|d}\frac{\gamma \left(p\right)}{p-\gamma \left(p\right)}$$

Let:

$$c_{\gamma }:=\prod _p{\left(1-\frac{\gamma \left(p\right)}{p}\right)}^{-1}{\left(1-\frac{1}{p}\right)}^{\kappa }$$

Assume that $F:[0,1]\to \mathbb{R}$ is a piecewise differentiable function. Then:

$$\sum _{d<z}{\mu }^2\left(d\right)g\left(d\right)F\left(\frac{logz/d}{logz}\right)=c_{\gamma }\frac{{(logz)}^{\kappa }}{\Gamma \left(\kappa \right)}{\int }_0^{1}F(1-x)x^{\kappa -1}dx+O\left(c_{\gamma }LM\left(F\right){(logz)}^{\kappa -1}\right)$$

where: $M\left(F\right)=sup\left\{\right(\left|F\left(x\right)\right|+|F^{\prime }\left(x\right)\left|\right):0\le x\le 1\}$. The constant implied by “O” may depend on $A_1,A_2$ and κ, but it is independent of L and F.

Following the approach in [7] and [6], we shall consider the sum:

$$S:=\sum _{N<n\le 2N}\left(\sum _{i=1}^k{\xi }_{\mathcal{P}}\left(L_i\left(n\right)\right)-\nu \right){\left(\underset{d|P_{\mathcal{L}}\left(n\right)}{{\sum }^{\prime }}{\lambda }_d\right)}^2$$

where ${\lambda }_d$ are real numbers to be described later. As in [7] and [6], Theorem 2 will follow from the positivity of the sum, S.

Note that there is a key distinction between our definition of S and the definition in [7] and [6]. Here, we sum up ${\lambda }_d$ over only the square-free numbers, d, that are relatively prime to all the primes in $\mathcal{P}\left(N\right)$. Intuitively, this gives a bigger sieve weight to the values, n, where $P_{\mathcal{L}}\left(n\right)$ has many prime factors in $\mathcal{P}\left(N\right)$; hence, the positivity of S can be satisfied for smaller k. As we can see in the proof of Lemma 4, this change also simplifies the calculation of S.

Define:

$$\begin{array}{c}\hfill y_r=\left\{\begin{array}{cc}{\mu }^2\left(r\right)\mathfrak{S}\left(\mathcal{L}\right)\hfill & \text{if}r<R,(r,A)=1\text{and}(r,p)=1\text{for}\text{all}p\in \mathcal{P}\left(N\right)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.\end{array}$$

For each square-free number, d, let:

$$f\left(d\right):=\frac{d}{{\tau }_k\left(d\right)}=\prod _{p|d}\frac{p}{k},f_1:=f*\mu$$

The sieve weights, ${\lambda }_d$, are related to the quantities, $y_r$, by:

$${\lambda }_d=\mu \left(d\right)f\left(d\right)\underset{r}{{\sum }^{\prime }}\frac{y_{rd}}{f_1\left(rd\right)}$$

Then, by Möbius inversion, we have:

$$y_r=\mu \left(r\right)f_1\left(r\right)\underset{d}{{\sum }^{\prime }}\frac{{\lambda }_{dr}}{f\left(dr\right)}$$

Since the sum of ${\lambda }_d$ is taken over all the square-free numbers relatively prime to the primes in $\mathcal{P}\left(N\right)$, we take $y_r$ to be supported only on integers coprime to $\mathcal{P}\left(N\right)$, which implies that the ${\lambda }_d$ are also supported on integers coprime to $\mathcal{P}\left(N\right)$.

To determine S, we break the sum into parts and evaluate each of them individually. Let:

$$S_{1,j}:=\sum _{N<n\le 2N}{\xi }_{\mathcal{P}}\left(L_j\left(n\right)\right){\left(\underset{d|P_{\mathcal{L}}\left(n\right)}{{\sum }^{\prime }}{\lambda }_d\right)}^2\text{and}{S}_0:=\sum _{N<n\le 2N}{\left(\underset{d|P_{\mathcal{L}}\left(n\right)}{{\sum }^{\prime }}{\lambda }_d\right)}^2$$

Then:

$$S=\sum _{j=1}^k{S}_{1,j}-\nu S_0$$

We shall now estimate $S_0$ and $S_{1,j}$ in the following two lemmas.

Lemma 3. 

Suppose that $\mathcal{L}$ is a set of linear forms satisfying Hypothesis $A\left(M\right)$. There is a constant, C, such that if $R\le N^{1/2}{(logN)}^{-C}$, then:

$$S_0=\mathfrak{S}\left(\mathcal{L}\right)\prod _p{\left(1-\frac{1}{p}\right)}^{-k\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{k}{p}\right)\frac{N{(logR)}^{k(1-\alpha )}}{\Gamma \left(k\right(1-\alpha )+1)}+O\left(N{(logN)}^{k(1-\alpha )-1}\right)$$

Proof. From the definition of $S_0$, we have:

$$S_0=\underset{d,e}{{\sum }^{\prime }}{\lambda }_d{\lambda }_e\sum _{\begin{array}{c}N<n\le 2N\\ [d,e]|P_{\mathcal{L}}\left(n\right)\end{array}}1=N\underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e}{f\left(\right[d,e\left]\right)}+O\left(\underset{d,e}{{\sum }^{\prime }}\left|{\lambda }_d{\lambda }_e{r}_{[d,e]}\right|\right)$$

where for each square-free d with $(d,A)=1$ and $(d,p)=1$ for all $p\in \mathcal{P}$,

$$r_d:=\sum _{\begin{array}{c}N<n\le 2N\\ d|P_{\mathcal{L}}\left(n\right)\end{array}}1-\frac{N}{f\left(d\right)}$$

As in the proof of Theorem 7 in [6], note that the error term is $O\left(N\right)$ if $R\le N^{1/2}{(logN)}^{-3k}$. For the main term,

$$\begin{array}{cc}\hfill \underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e}{f\left(\right[d,e\left]\right)}& =\underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e}{f\left(d\right)f\left(e\right)}\sum _{r\left|\right(d,e)}{f}_1\left(r\right)=\underset{r}{{\sum }^{\prime }}{f}_1\left(r\right){\left(\underset{d}{{\sum }^{\prime }}\frac{{\lambda }_{dr}}{f\left(dr\right)}\right)}^2=\underset{r}{{\sum }^{\prime }}\frac{{\mu }^2\left(r\right)y_r^2}{f_1\left(r\right)}=\underset{r}{{\sum }^{\prime }}\frac{{\mu }^2\left(r\right)\mathfrak{S}{\left(\mathcal{L}\right)}^2}{f_1\left(r\right)}\hfill \end{array}$$

We use Lemma 2 with:

$$\begin{array}{c}\hfill \gamma \left(p\right)=\left\{\begin{array}{cc}k\hfill & \text{if}p\nmid A\text{and}p\notin \mathcal{P}\left(N\right)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.\end{array}$$

and $F\left(x\right)=1$. Then, $g\left(d\right)=f_1{\left(d\right)}^{-1}$. It can verified as in ([6] (Lemma 7)) that the conditions in Lemma 2 are satisfied with $\kappa =k(1-\alpha )$, using the fact that the Frobenius density of $\mathcal{P}\left(N\right)$ is $\alpha <1$. Then, the main term becomes:

$$\mathfrak{S}\left(\mathcal{L}\right)\prod _p{\left(1-\frac{1}{p}\right)}^{-k\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{k}{p}\right)\frac{N{(logR)}^{k(1-\alpha )}}{\Gamma \left(k\right(1-\alpha \left)\right)}{\int }_0^1{x}^{k(1-\alpha )-1}dx$$

with the desired error term. The result follows by evaluating the integral.     ☐

Remark 4. 

This argument breaks down when $\alpha =1$, since κ needs to be positive in order to apply Lemma 2. A similar phenomenon occurs in the proof of Lemma 4.

Lemma 4. 

Let $\mathcal{L}$ be a set of linear forms satisfying Hypothesis $A\left(M\right)$. There is a constant, C, such that if $R=N^{1/4}{(logN)}^{-C}$, then:

$$S_{1,j}\sim \frac{DN{(logR)}^{(k+1)(1-\alpha )}}{{log}^{1-\alpha }N}$$

where:

$$D:=\frac{\mathfrak{S}\left(\mathcal{L}\right){\delta }_{b_j}\varphi \left(M\right)c_{\mathcal{P}}\Gamma (2(1-\alpha )+1)}{\Gamma {(2-\alpha )}^2\Gamma ((k+1)(1-\alpha )+1)}\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha (k+1)}\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p}\right)\left(1-\frac{k}{p}\right)$$

and $c_{\mathcal{P}}=c_{\mathcal{P}}\left(N\right)>0$ satisfies:

$$\sum _{N<n\le 2N}{\xi }_{\mathcal{P}}\left(n\right)=\frac{c_{\mathcal{P}}N}{{log}^{1-\alpha }\left(N\right)}$$

Remark 5. 

The ratio, $c_{\mathcal{P}}\left(N\right)$, approaches a positive constant as N tends to infinity by Theorem 2.4 in [13].

Proof. From the definition of $S_{1,j}$, we have:

$$\begin{array}{cc}\hfill S_{1,j}& =\sum _{N<n\le 2N}{\xi }_{\mathcal{P}}\left(L_j\left(n\right)\right){\left(\underset{d|P_{\mathcal{L}}\left(n\right)}{{\sum }^{\prime }}{\lambda }_d\right)}^2=\underset{d,e}{{\sum }^{\prime }}{\lambda }_d{\lambda }_e\sum _{\begin{array}{c}N<n\le 2N\\ [d,e]|P_{\mathcal{L}}\left(n\right)/L_j\left(n\right)\end{array}}{\xi }_{\mathcal{P}}\left(L_j\left(n\right)\right)\hfill \end{array}$$

We remark that in the second equality, we have used the condition that $[d,e]$ is not divisible by any prime in $\mathcal{P}\left(N\right)$, and hence, the condition $[d,e]|P_{\mathcal{L}}\left(n\right)$ in the sum implies that $[d,e]|P_{\mathcal{L}}\left(n\right)/L_j\left(n\right)$ for nonzero ${\xi }_{\mathcal{P}}\left(L_j\left(n\right)\right)$. This contributes to the much simpler estimate of $S_{1,j}$ than that in [7].

Let ${\Omega }^{*}\left(x\right)$ denote the set of residue classes, a, modulo x, such that $x|P_{\mathcal{L}}\left(a\right)/L_j\left(a\right)$. Note that $|{\Omega }^{*}\left(x\right)|={\tau }_{k-1}\left(x\right)$ by Hypothesis $A\left(M\right)$ (cf. (4.4) in [7]). Then:

$$S_{1,j}=\underset{d,e}{\sum \prime }{\lambda }_d{\lambda }_e\sum _{a\in {\Omega }^{*}\left([d,e]\right)}\sum _{\begin{array}{c}N<n\le 2N\\ n\equiv a\left(\mathrm{mod}\right[d,e\left]\right)\end{array}}{\xi }_{\mathcal{P}}\left(L_j\left(n\right)\right)$$

Write $n^{\prime }=L_j\left(n\right)=a_{j}n+b_j$, then $a_{j}N+b_j<n^{\prime }\le 2a_{j}N+b_j$, with $n^{\prime }\equiv a{a}_j+b_j\left(\mathrm{mod}[d,e]\right)$ and $n^{\prime }\equiv b_j\left(\mathrm{mod}{a}_j\right)$. By assumption, the values, $[d,e],a_j/M,M$, are all coprime. Let $u_{d,e}=[d,e]a_j/M$. Then, we may use the Chinese Remainder Theorem to combine the congruence conditions modulo $[d,e]$ and $a_j/M$ into a single condition on $u_{d,e}$. Let ${\Omega }_1^{*}\left(x\right)$ denote the set of all possible residue classes of $n^{\prime }$ modulo x. Then:

$$S_{1,j}=\underset{d,e}{\sum \prime }{\lambda }_d{\lambda }_e\sum _{a^{\prime }\in {\Omega }_1^{*}\left(u_{d,e}\right)}\sum _{\begin{array}{c}{a}_{j}N+b_j<n^{\prime }\le 2a_{j}N+b_j\\ n^{\prime }\equiv a^{\prime }\left(\mathrm{mod}{u}_{d,e}\right)\\ n^{\prime }\equiv b_j\left(\mathrm{mod}M\right)\end{array}}{\xi }_{\mathcal{P}}\left(n^{\prime }\right)$$

Now, we decompose the inner sum:

$$\sum _{\begin{array}{c}{a}_{j}N+b_j<n^{\prime }\le 2a_{j}N+b_j\\ n^{\prime }\equiv a^{\prime }\left(\mathrm{mod}{u}_{d,e}\right)\\ n^{\prime }\equiv b_j\left(\mathrm{mod}M\right)\end{array}}{\xi }_{\mathcal{P}}\left(n^{\prime }\right)=\frac{1}{\varphi \left(u_{d,e}\right)}\sum _{\begin{array}{c}{a}_{j}N<n^{\prime }\le 2a_{j}N\\ n^{\prime }\equiv b_j\left(\mathrm{mod}M\right)\end{array}}{\xi }_{\mathcal{P}}\left(n^{\prime }\right)+{\Delta }_{\mathcal{P},b_j}(a_{j}N;u_{d,e},a^{\prime })+O_{b_j}\left(1\right)$$

Accordingly, we can decompose $S_{1,j}$ into its main term and error term $S_{1,j}=M_{1,j}+E_{1,j}$. Let ${\Delta }_{\mathcal{P},b_j}(X;u_{d,e}):={max}_{(a,u_{d,e})=1}\left|{\Delta }_{\mathcal{P},b_j}(X;u_{d,e},a)\right|.$ The error term can be estimated using Lemma 1 and Cauchy’s inequality as in the proof of Lemma 4.1 in [7]. Let $v=[d,e]$, then $u_{d,e}=a_{j}v/M$. Note that $|{\Omega }_1^{*}\left(u_{d,e}\right)|=|{\Omega }^{*}\left([d,e]\right)|={\tau }_{k-1}\left([d,e]\right)$. Moreover, by Hypothesis $A\left(M\right)$, we have $(a^{\prime },u_{d,e})=1$ for all $a^{\prime }\in {\Omega }_1^{*}\left(u_{d,e}\right)$. Hence:

$$\begin{array}{cc}\hfill E_{1,j}& =\underset{d,e}{{\sum }^{\prime }}{\lambda }_d{\lambda }_e\sum _{a^{\prime }\in {\Omega }_1^{*}\left(u_{d,e}\right)}({\Delta }_{\mathcal{P},b_j}(a_{j}N;u_{d,e},a^{\prime })+O_{b_j}\left(1\right))\hfill \\ & \le \underset{d,e}{{\sum }^{\prime }}{\lambda }_d{\lambda }_e{\tau }_{k-1}\left([d,e]\right)({\Delta }_{\mathcal{P},b_j}(a_{j}N;u_{d,e})+O\left(1\right))\hfill \\ & \ll {log}^{2k}N\sum _{v\le R^2}{(3k-3)}^{\omega \left(v\right)}{\Delta }_{\mathcal{P},b_j}\left(a_{j}N;\frac{a_{j}v}{M}\right)\hfill \\ & {\ll }_U\left({log}^{2k}N\right)\left(a_{j}N\right){log}^{-U}\left(a_{j}N\right)\hfill \\ & \ll N{log}^{2k-U}N\hfill \end{array}$$

for any U. To obtain the third line, we use the fact that $|{\lambda }_d|\ll {log}^{k}R\le {log}^{k}N$ by (4.3) of [6]. For the main term of $S_{1,j}$,

$$\begin{array}{ccc}\mathrm{(1)}& \hfill M_{1,j}& =& \underset{d,e}{{\sum }^{\prime }}{\lambda }_d{\lambda }_e\frac{{\tau }_{k-1}\left([d,e]\right)}{\varphi \left(u_{d,e}\right)}\sum _{\begin{array}{c}{a}_{j}N<n\le 2a_{j}N\\ n\equiv b_j\left(\mathrm{mod}M\right)\end{array}}{\xi }_{\mathcal{P}}\left(n\right)\hfill & \sim & {\delta }_{b_j}\frac{\varphi \left(M\right)}{\varphi \left(a_j\right)}\left(\sum _{a_{j}N<n\le 2a_{j}N}{\xi }_{\mathcal{P}}\left(n\right)\right)\underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e{\tau }_{k-1}\left([d,e]\right)}{\varphi \left(\right[d,e\left]\right)}\hfill \end{array}$$

where ${\delta }_{b_j}$ is the density of the elements congruent to $b_j$ mod M in the set of $E_{\mathcal{P}\left(N\right)}$ numbers.

Our next step is to evaluate the last sum. Let $f^{*}\left(n\right)=\varphi \left(n\right)/{\tau }_{k-1}\left(n\right)$ and $f_1^{*}=f^{*}*\mu$. Then:

$$\begin{array}{cc}\hfill \underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e{\tau }_{k-1}\left([d,e]\right)}{\varphi \left(\right[d,e\left]\right)}& =\underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e}{f^{*}\left([d,e]\right)}=\underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e}{f^{*}\left(d\right)f^{*}\left(e\right)}{f}^{*}\left((d,e)\right)\hfill \\ & =\underset{d,e}{{\sum }^{\prime }}\frac{{\lambda }_d{\lambda }_e}{f^{*}\left(d\right)f^{*}\left(e\right)}\sum _{r\left|\right(d,e)}{f}_1^{*}\left(r\right)\hfill \\ & =\underset{r}{{\sum }^{\prime }}{f}_1^{*}\left(r\right){\left(\underset{r|d}{{\sum }^{\prime }}\frac{{\lambda }_d}{f^{*}\left(d\right)}\right)}^2\hfill \\ & =\underset{r}{{\sum }^{\prime }}\frac{{\mu }^2\left(r\right)}{f_1^{*}\left(r\right)}{\left(y_r^{*}\right)}^2\hfill \end{array}$$

by an analogue of Lemma 6 in [6], where:

$$\begin{array}{cc}\hfill y_r^{*}& :=\frac{{\mu }^2\left(r\right)r}{\varphi \left(r\right)}\underset{m}{{\sum }^{\prime }}\frac{y_{mr}}{\varphi \left(m\right)}\hfill \end{array}$$

Thus:

$$\begin{array}{c}\hfill y_r^{*}=\frac{{\mu }^2\left(r\right)r\mathfrak{S}\left(\mathcal{L}\right)}{\varphi \left(r\right)}\underset{\begin{array}{c}m<R/r\\ (m,rA)=1\end{array}}{{\sum }^{\prime }}\frac{{\mu }^2\left(m\right)}{\varphi \left(m\right)}\end{array}$$

We use Lemma 2 with:

$$\begin{array}{c}\hfill \gamma \left(p\right)=\left\{\begin{array}{cc}1\hfill & \text{if}p\nmid rA\text{and}p\notin \mathcal{P}\left(N\right)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.\end{array}$$

and $F\left(x\right)=1$. Again, the conditions are verified as in ([6] (Lemma 7)) with $\kappa =1-\alpha$, giving:

$$c_{\gamma }=\frac{\varphi \left(rA\right)}{rA}\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p}\right)$$

Hence for square-free r with $(r,A)=1$ and $(r,p)=1$ for all $p\in \mathcal{P}\left(N\right)$,

$$\begin{array}{cc}\hfill y_r^{*}& \sim \frac{\varphi \left(A\right)\mathfrak{S}\left(\mathcal{L}\right)}{A}\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p}\right)\frac{{(logR/r)}^{1-\alpha }}{\Gamma (1-\alpha )}{\int }_0^1{x}^{-\alpha }dx\hfill \\ & =\frac{\varphi \left(A\right)\mathfrak{S}\left(\mathcal{L}\right)}{A}\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p}\right)\frac{{(logR)}^{1-\alpha }}{\Gamma (2-\alpha )}{\left(\frac{logR/r}{logR}\right)}^{1-\alpha }\hfill \end{array}$$

Thus:

$$\underset{r}{{\sum }^{\prime }}\frac{{\mu }^2\left(r\right)}{f_1^{*}\left(r\right)}{\left(y_r^{*}\right)}^2\sim \frac{\varphi {\left(A\right)}^2\mathfrak{S}{\left(\mathcal{L}\right)}^2}{A^2}\prod _p{\left(1-\frac{1}{p}\right)}^{-2\alpha }\prod _{p\in \mathcal{P}\left(N\right)}{\left(1-\frac{1}{p}\right)}^2\frac{{(logR)}^{2(1-\alpha )}}{\Gamma {(2-\alpha )}^2}\underset{r<R}{{\sum }^{\prime }}\frac{{\mu }^2\left(r\right)}{f_1^{*}\left(r\right)}{\left(\frac{logR/r}{logR}\right)}^{2(1-\alpha )}$$

We evaluate the last sum using Lemma 2, taking $F\left(x\right)=x^{2(1-\alpha )}$ and:

$$\begin{array}{c}\hfill \gamma \left(p\right)=\left\{\begin{array}{cc}{\displaystyle \frac{p(k-1)}{p-1}}\hfill & \text{if}p\nmid rA\text{and}p\notin \mathcal{P}\left(N\right)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.\end{array}$$

The conditions are satisfied when $\kappa =(k-1)(1-\alpha )$, as verified in ([6] [Lemma 8]). Then:

$$c_{\gamma }=\frac{1}{\mathfrak{S}\left(\mathcal{L}\right)}\frac{A}{\varphi \left(A\right)}\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha (k-1)}\prod _{p\in \mathcal{P}\left(N\right)}{\left(1-\frac{1}{p}\right)}^{-1}\left(1-\frac{k}{p}\right)$$

Hence:

$$\begin{array}{cc}& \underset{r}{{\sum }^{\prime }}\frac{{\mu }^2\left(r\right)}{f_1^{*}\left(r\right)}{\left(y_r^{*}\right)}^2\hfill \\ \hfill \sim & \frac{\varphi \left(A\right)\mathfrak{S}\left(\mathcal{L}\right)}{A}\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha (k+1)}\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p}\right)\left(1-\frac{k}{p}\right)\frac{{(logR)}^{(k+1)(1-\alpha )}\Gamma (2(1-\alpha )+1)}{\Gamma {(2-\alpha )}^2\Gamma ((k+1)(1-\alpha )+1)}\hfill \end{array}$$

Plugging the definition of $c_{\mathcal{P}}$ and this identity into (1), we have the desired result. Note that here we have used the fact that $a_j/\varphi \left(a_j\right)=A/\varphi \left(A\right)$ by Hypothesis $A\left(M\right)$.

2.4. Proof of Theorems 1 and 2

Proof of Theorem 2. Let $R=N^{1/4}{(logN)}^{-C}$, where C is the constant in Lemma 2.6. Noting that $4logR\sim logN$, we have, as $N\to \infty$,

$$S\ge \mathfrak{S}\left(\mathcal{L}\right)\prod _p{\left(1-\frac{1}{p}\right)}^{-k\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{k}{p}\right)\frac{N{(logR)}^{k(1-\alpha )}}{\Gamma \left(k\right(1-\alpha )+1)}(kD\left(k\right)-\nu )$$

where:

$$\begin{array}{cc}\hfill D\left(k\right)& :=\frac{c_{\mathcal{P}}\delta \varphi \left(M\right)}{4^{1-\alpha }}\frac{\Gamma \left(k\right(1-\alpha )+1)\Gamma \left(2\right(1-\alpha )+1)}{\Gamma {(2-\alpha )}^2\Gamma ((k+1)(1-\alpha )+1)}\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p}\right)\hfill \end{array}$$

Hence, S is positive for all large enough N if:

$$\begin{array}{c}\hfill kD\left(k\right)-\nu \iff k>\nu \frac{\mathfrak{b}\left(1\right)}{\mathfrak{b}\left(k\right)}\frac{4^{1-\alpha }}{c_{\mathcal{P}}\delta \varphi \left(M\right)}\frac{\Gamma (2-\alpha )}{\Pi }\end{array}$$

(2)

where:

$$\Pi :=\prod _p{\left(1-\frac{1}{p}\right)}^{-\alpha }\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p}\right)$$

and:

$$\mathfrak{b}\left(k\right):=\frac{\Gamma (1-\alpha )\Gamma \left(k\right(1-\alpha )+1)}{\Gamma \left(\right(k+1\left)\right(1-\alpha )+1))}=B(1-\alpha ,k(1-\alpha )+1)$$

is the beta function. Finally, by a variant of the Tauberian theorem ([19] (Theorem 2.4.1)), we deduce that:

$$c_{\mathcal{P}}\Pi \sim \frac{1}{{\zeta }_{\mathcal{P}\left(N\right)}\left(2\right)\Gamma \left(\alpha \right)}=\frac{1}{\Gamma \left(\alpha \right)}\prod _{p\in \mathcal{P}\left(N\right)}\left(1-\frac{1}{p^2}\right)$$

where, as we recall from Lemma 4, $c_{\mathcal{P}}=c_{\mathcal{P}}\left(N\right)>0$ is the function that satisfies:

$$\sum _{N<n\le 2N}{\xi }_{\mathcal{P}}\left(n\right)=\frac{c_{\mathcal{P}}N}{{log}^{1-\alpha }\left(N\right)}$$

For N large enough, the infinite product approaches one. Now, the result follows from Equation (2). ☐

Proof of Theorem 1. To derive Theorem 1.1 from our main theorem, we consider for given k and m a set of k primes, $b_1,...,b_k$, with the appropriate residue classes as needed. Then, $\{Mx+b_i\}$ forms an M-admissible k-tuple, which can be normalized to fit Hypothesis $A\left(M\right)$. This gives us the value, $b_k-b_1$, for the constant, $C(\nu ,\mathcal{P})$.

3. Discussion of Examples

In this section, we shall revisit two of the examples in [7]. We observe that both Theorem 1.2 and Corollary 1.3 in [7] rely on theorems that are not just applicable to $E_r$ numbers, but any square-free numbers whose prime factors satisfy a Chebotarëv condition. Therefore, Theorem 2 applies in these two examples, and we can get better bounds in both cases.

3.1. Example 1: Ideal Class Groups with Order Four Elements

We first recall a result of Soundararajan [8]. Proposition 1 and 2 in [8] show that for any positive square-free number $d\equiv 1$ (mod 8), whose prime factors are all congruent to $\pm 1$ (mod 8), the class group $\mathrm{Cl}\left(\mathbb{Q}\left(\sqrt{-d}\right)\right)$ contains an element of order four.

Applying Theorem 2 with $\nu =1$, $\alpha =1/2$, $\delta =1/2$ and $M=8$, the right-hand side of Theorem 2 is $1.850\dots <2$ when $k=2$. Hence, we may take $k=2$. Considering the eight-admissible two-tuple $\{8n+17,8n+25\}$, we obtain Corollary 1, which is an improvement on the bound in [7].

3.2. Example 2: Rank Zero Quadratic Twists of Modular Elliptic Curves

As in Section 6 of [7], we shall focus on the elliptic curve $E=X_0\left(11\right)$, recalling the setting from [9]. We take the cubic model of $X_0\left(11\right)$ to be:

$$y^2=f\left(x\right)=x^3-4x^2-160x-1264$$

The Galois representation:

$${\rho }_f:\mathrm{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\to {\mathrm{GL}}_2(\mathbb{Z}/2\mathbb{Z})$$

induced by the natural action of $\mathrm{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$ on the two-torsion points of $E(-11)$ has the property that:

$$\mathrm{tr}\left({\rho }_f\left({\mathrm{Frob}}_p\right)\right)\equiv a\left(p\right)\left(\mathrm{mod}2\right)$$

for all, except finitely many, primes, p. Here, $a\left(p\right)=p+1-\#E\left({\mathbb{F}}_p\right)$, and ${\mathrm{Frob}}_p$ is the Frobenius element at p in $\mathrm{Gal}\left(\mathbb{Q}\right[f\left(x\right)]/\mathbb{Q})$. Let S be the set of primes, p, such that $\mathrm{tr}\left({\rho }_f\left({\mathrm{Frob}}_p\right)\right)\equiv 1$ (mod 2). We remark that S is also the set of all primes p, such that $f\left(x\right)$ is irreducible mod p. Equation (1.4) and Theorem 1.1 of Boxer-Diao [10] establish that for any positive square-free number, d, with prime factors all in S, we have:

$$L\left(E\right(-d),1)\ne 0\text{and}\mathrm{rk}\left(E\right(-d),\mathbb{Q})=0$$

We note that $\mathrm{Gal}(\mathbb{Q}\left[f\left(x\right)\right]/\mathbb{Q})\cong S_3$; hence, the Chebotarëv density theorem shows that S has density $\alpha =1/3$. Murty and Murty’s theorem [20] now implies that S satisfies $SW\left(11\right)$, as analyzed in [7]. Furthermore, since $a\left(p\right)$ is odd only if $p=11$ or p is a quadratic residue mod 11 (cf. the proof of Corollary 1 in [9]) and these values distribute uniformly among the five quadratic residue classes, one may take $\delta =0.2$. Given $\nu =1$, $\alpha =1/3$, $\delta =0.2$ and $M=11$, the right-hand side of Theorem 2 is $7.771\dots <8$ when $k=8$. Hence, we may take $k=8$. One may check that the eight-tuple:

$$\{1,3,9,15,25,31,45,49\}$$

contains only quadratic residues mod 11 and, hence, forms an 11-admissible eight-tuple $\{11n+b_j\}$, such that $\delta \ge 0.2$. As a result, there are infinitely many pairs of square-free m and n with:

$$L\left(E\right(-m),1)·L\left(E\right(-n),1)\ne 0,\mathrm{rk}\left(E\right(-11m\left)\right)=\mathrm{rk}\left(E\right(-11n\left)\right)=0$$

and:

$$|m-n|\le 48$$