On V-Geometric Ergodicity Markov Chains of the Two-Inertia Systems
Abstract
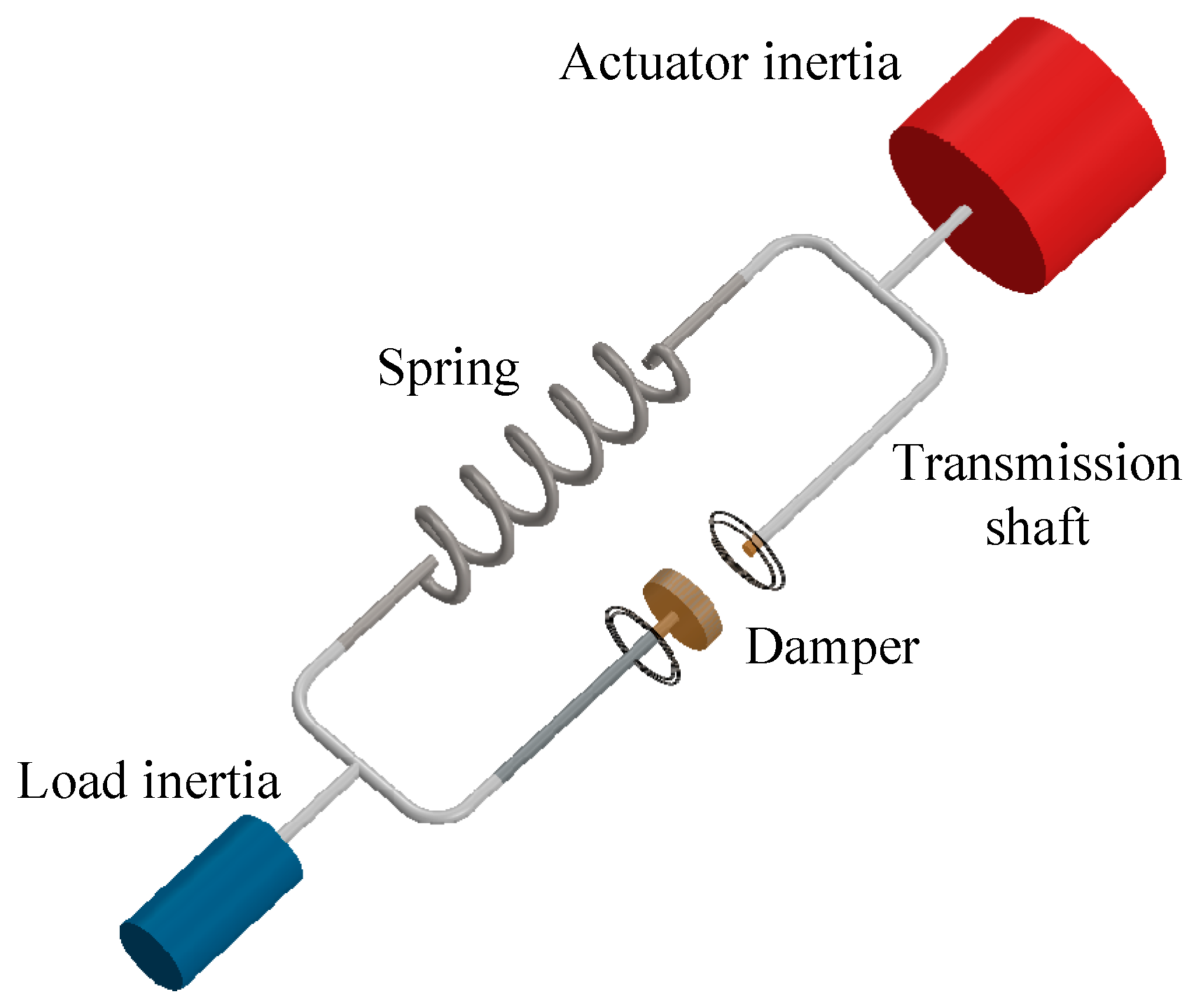
:1. Introduction
2. Existence of Invariant Measure
3. Main Findings
3.1. Conditions in Which Possesses an Invariant Measure
3.2. Approximation of by Utilizing Finite-Rank Operator
4. Evaluation of
5. Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
- (a)
- Assume that satisfies . If there exists such that one of the following conditions holds;, , then is null recurrent.
- (b)
- For given , assume . If there exists such that , , then is positive recurrent.
Appendix C
Appendix D
- (a)
- Then there exists a unique invariant measure .
- (b)
- For every real-valued function such that, then with probability 1,
Appendix E
- -
- Assumption (D)There exist and , .
- -
- Assumption (M), where is a small set and is a positive measure,
Appendix F
- (a)
- and ,
- (b)
- , and ,
- (c)
- and , then
References
- Hu, F.-R.; Hu, J.-S.; Kang, C.-H. On the two-inertia system: Analysis of the asymptotic behaviors to multiple feedback position control. Asian J. Control 2014, 16, 175–187. [Google Scholar] [CrossRef]
- Hu, F.-R.; Hu, J.-S. On the asymptotic behaviors of time homogeneous Markov chains in two-inertia systems. Microsyst. Technol. 2018, 24, 119–124. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Xu, J.; Chen, R.; Yang, H. Study of Dynamic Performance and Control Strategy of Variable Stiffness Actuator System Based on Two-Inertial-System. Mathematics 2023, 11, 1166. [Google Scholar] [CrossRef]
- Shang, D.; Li, X.; Yin, M.; Li, F. Vibration suppression for two-inertia system with variable-length flexible load based on neural network compensation sliding mode controller and angle-independent method. IEEE/ASME Trans. Mechatron. 2023, 28, 848–859. [Google Scholar] [CrossRef]
- Wang, S.; Yu, H.; Yu, J.; Gao, X. Adaptive neural funnel control for nonlinear two-inertia servo mechanisms with backlash. IEEE Access 2019, 7, 33338–33345. [Google Scholar] [CrossRef]
- Yokokura, Y.; Ohishi, K. Fine load-side acceleration control based on torsion torque sensing of two-inertia system. IEEE Trans. Ind. Electron. 2020, 67, 768–777. [Google Scholar] [CrossRef]
- Kawai, Y.; Yokokura, Y.; Ohishi, K.; Miyazaki, T. High-robust force control for environmental stiffness variation based on duality of two-inertia system. IEEE Trans. Ind. Electron. 2021, 68, 850–860. [Google Scholar] [CrossRef]
- Jung, H.; Jeon, K.; Kang, J.-G.; Oh, S. Iterative feedback tuning of cascade control of two-inertia system. IEEE Control Syst. Lett. 2021, 5, 785–790. [Google Scholar] [CrossRef]
- Biane, P. Intertwining of Markov semi-groups, some examples. Semin. Probab. Strasbg. 1995, 29, 30–36. [Google Scholar]
- Bhattacharya, N.; Waymire, E.C. Stochastic Processes with Applications; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Karlin, S.; Taylor, H.M. A Second Course in Stochastic Processes; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Kasahara, Y. Spectral theory of generalized second order differential operators and its applications to Markov processes. Jpn. J. Math. 1975, 1, 67–84. [Google Scholar] [CrossRef]
- Hu, F.-R. On Markov chains induced from stock processes having barriers in finance market. Osaka J. Math. 2002, 39, 487–509. [Google Scholar]
- Hu, F.-R. On convergent rates of ergodic Harris chains induced from diffusions. Taiwan. J. Math. 2006, 10, 651–668. [Google Scholar] [CrossRef]
- S, S.; Krishnamoorthy, A.; Kozyrev, D. A Two-Server Queue with Interdependence between Arrival and Service Processes. Mathematics 2023, 11, 4692. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Ning, R.; Chen, X. Joint Optimization of Maintenance and Spare Parts Inventory Strategies for Emergency Engineering Equipment Considering Demand Priorities. Mathematics 2023, 11, 3688. [Google Scholar] [CrossRef]
- Herve, L.; Ledoux, J. V-geometrical ergodicity of Markov kernels via finite-rank approximations. Electron. Commun. Probab. 2020, 23, 1–12. [Google Scholar] [CrossRef]
- Horsthemke, W.; Lefever, R. Noise-Induced Transitions: Theory and Applications in Physics, Chemistry, and Biology; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Tudorache, A.; Luca, R. Positive Solutions of a Fractional Boundary Value Problem with Sequential Derivatives. Symmetry 2021, 13, 1489. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, F.-R.; Hu, J.-S. On V-Geometric Ergodicity Markov Chains of the Two-Inertia Systems. Mathematics 2024, 12, 1492. https://doi.org/10.3390/math12101492
Hu F-R, Hu J-S. On V-Geometric Ergodicity Markov Chains of the Two-Inertia Systems. Mathematics. 2024; 12(10):1492. https://doi.org/10.3390/math12101492
Chicago/Turabian StyleHu, Feng-Rung, and Jia-Sheng Hu. 2024. "On V-Geometric Ergodicity Markov Chains of the Two-Inertia Systems" Mathematics 12, no. 10: 1492. https://doi.org/10.3390/math12101492




