DOA-Estimation Method Based on Improved Spatial-Smoothing Technique
Abstract
:1. Introduction
2. Signal Model
3. MUSIC Algorithm
4. Proposed Method
5. Experimental Analysis
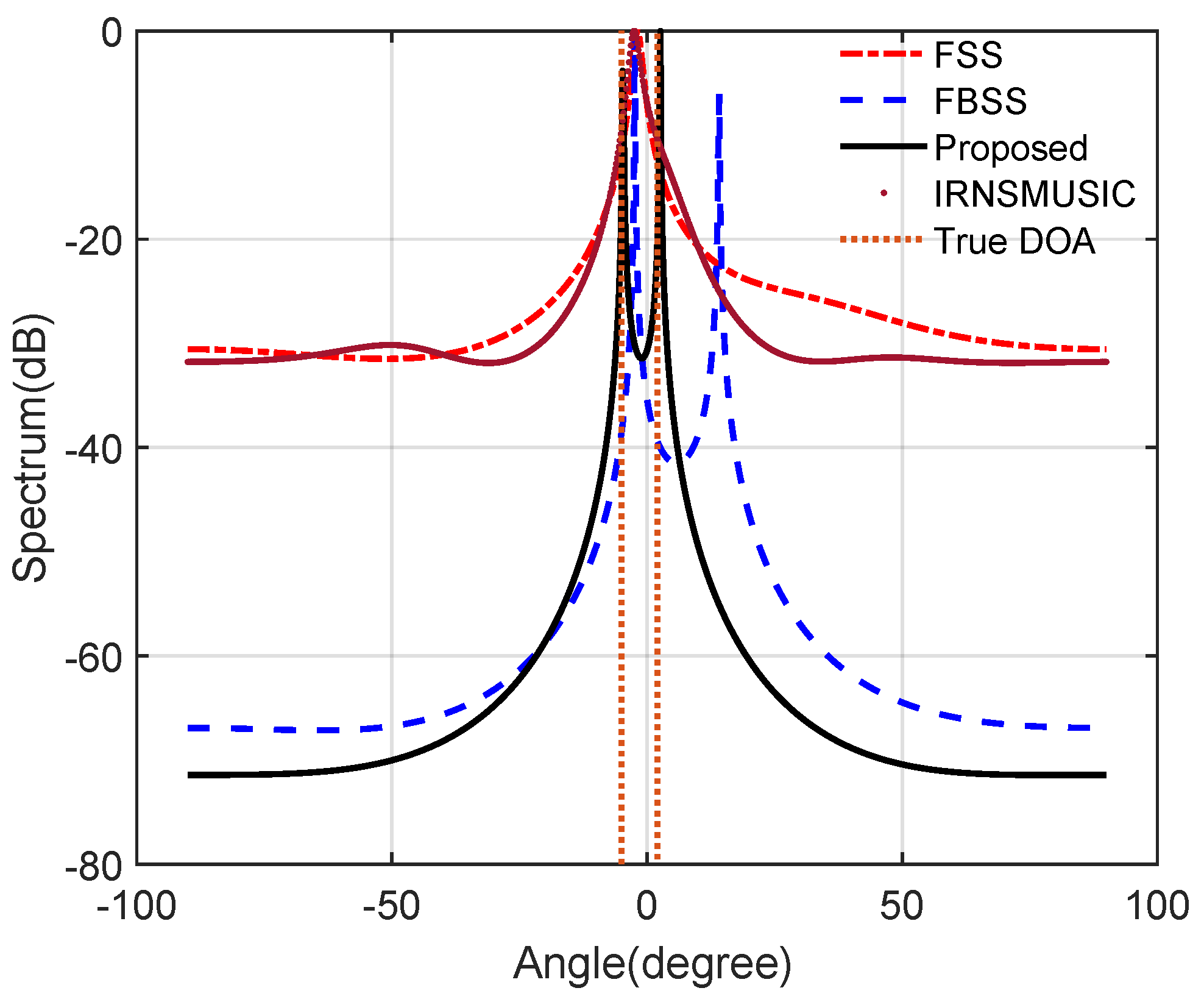
5.1. Simulation Experiment
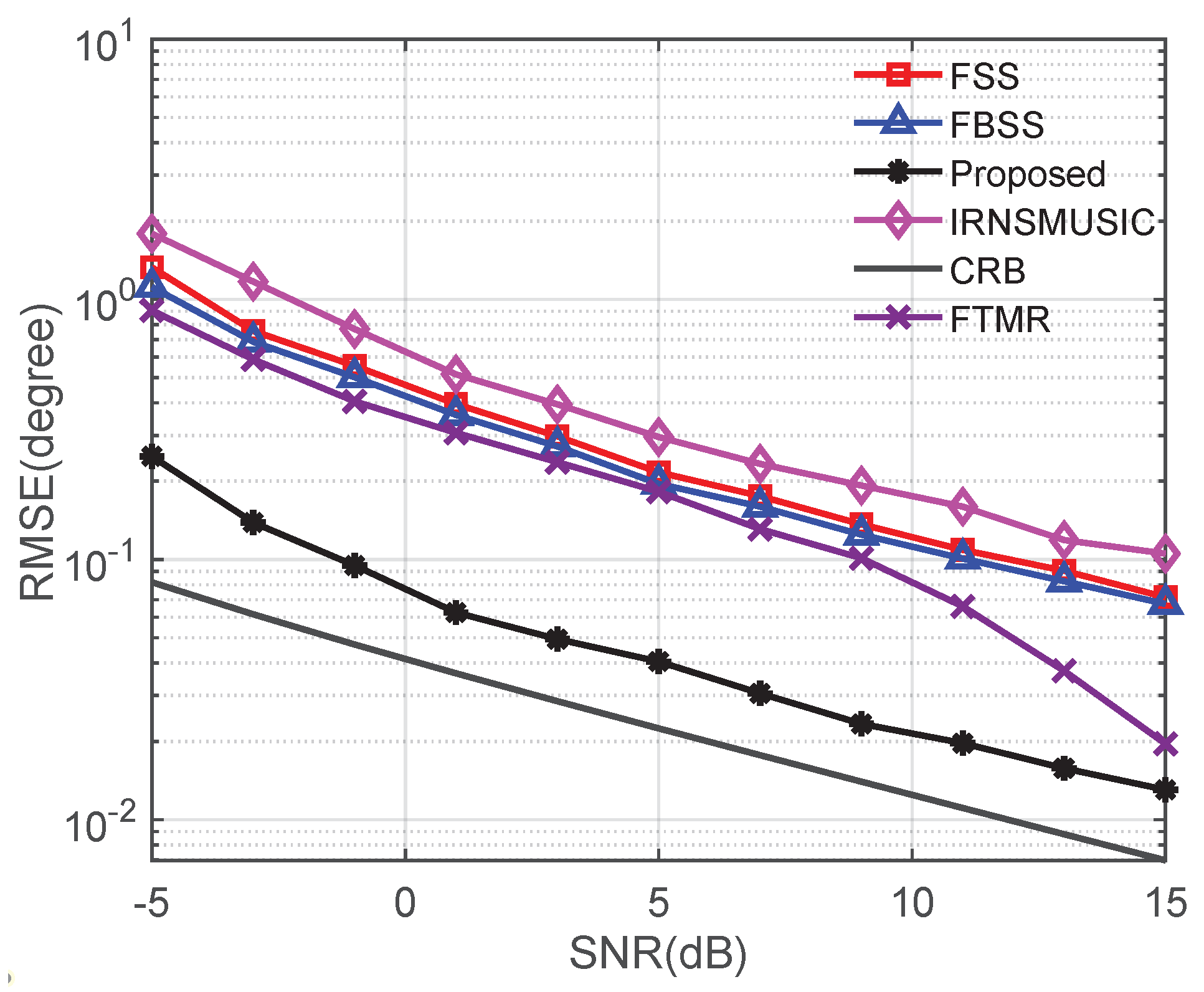
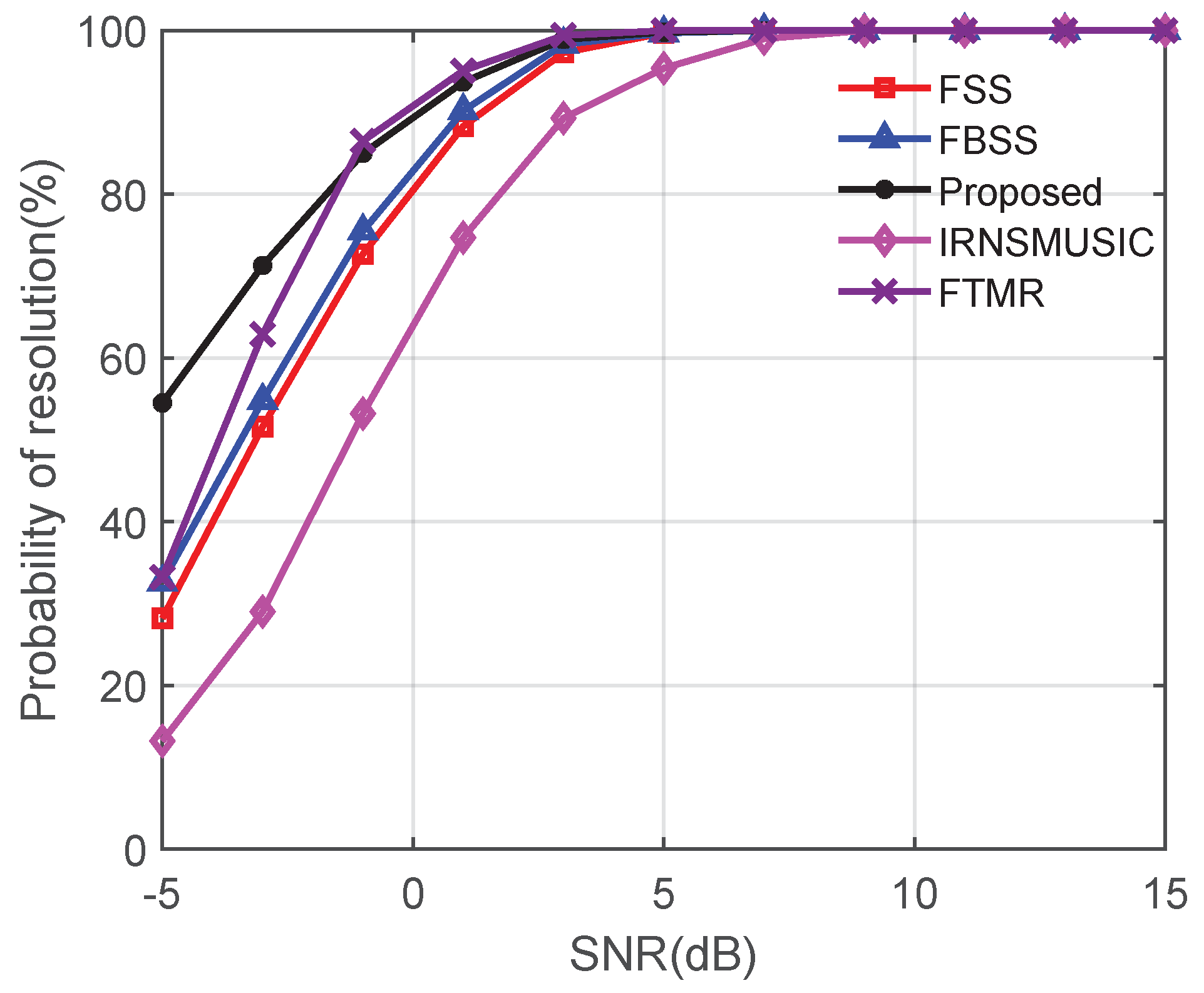
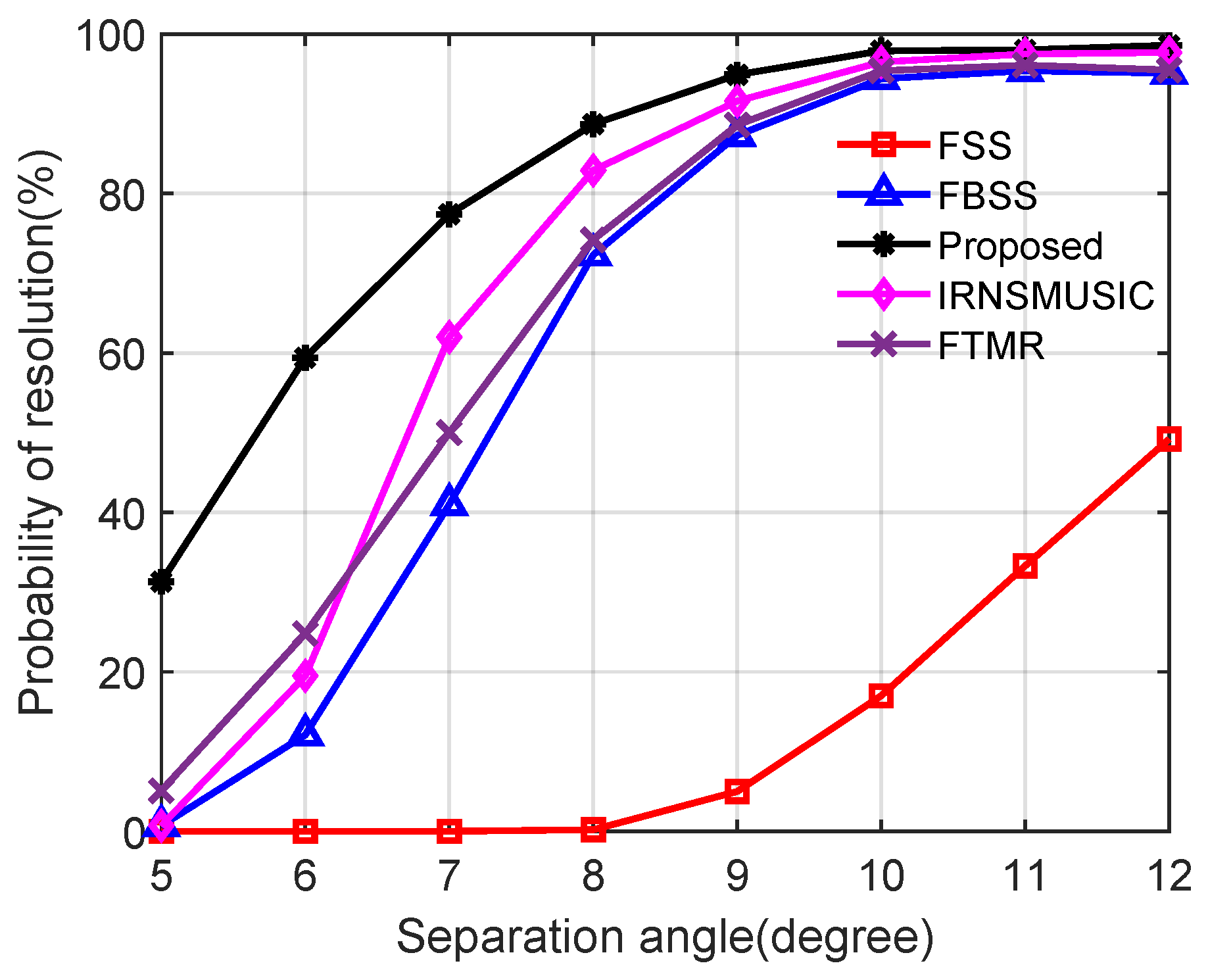
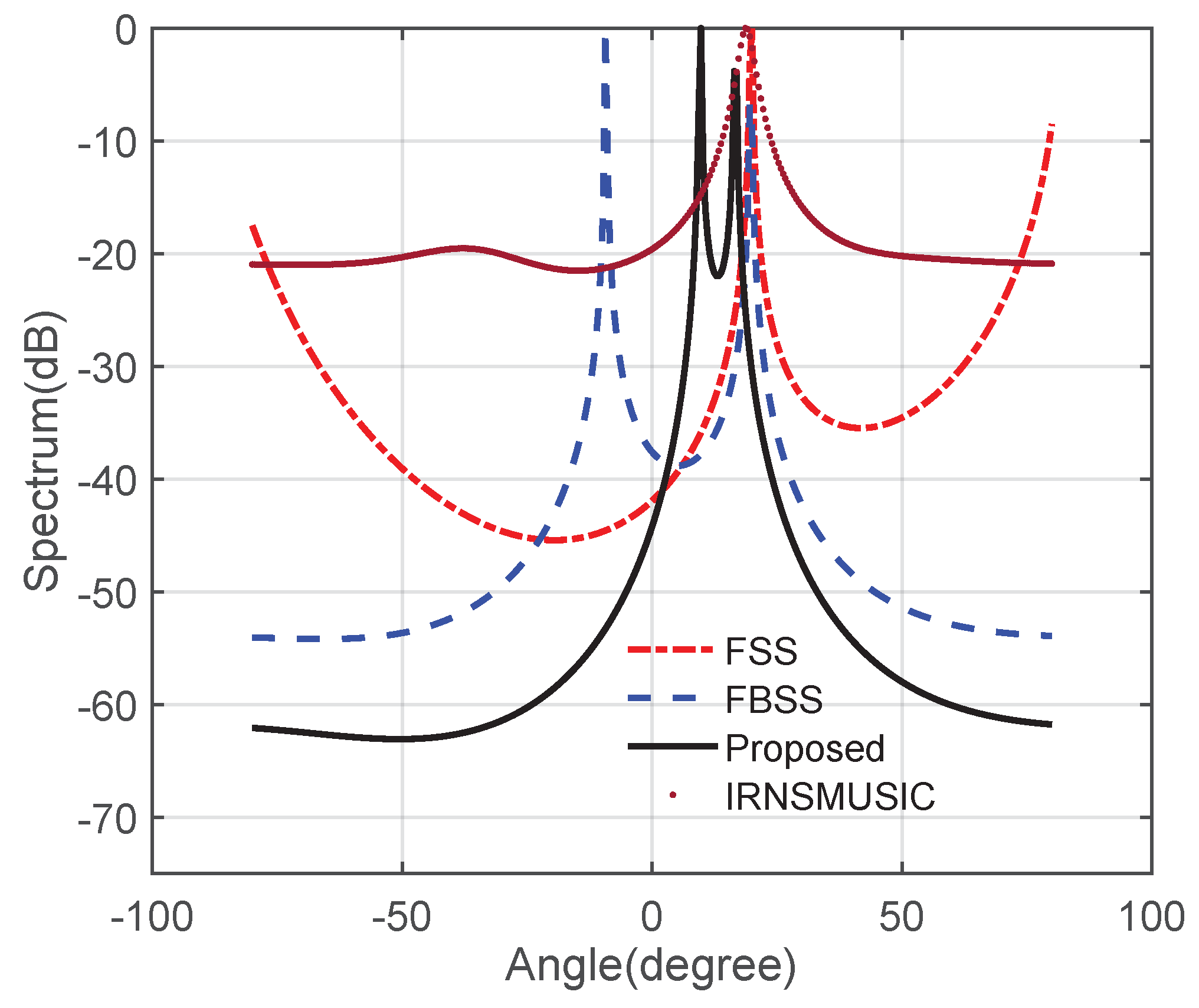
5.2. Performance Analysis
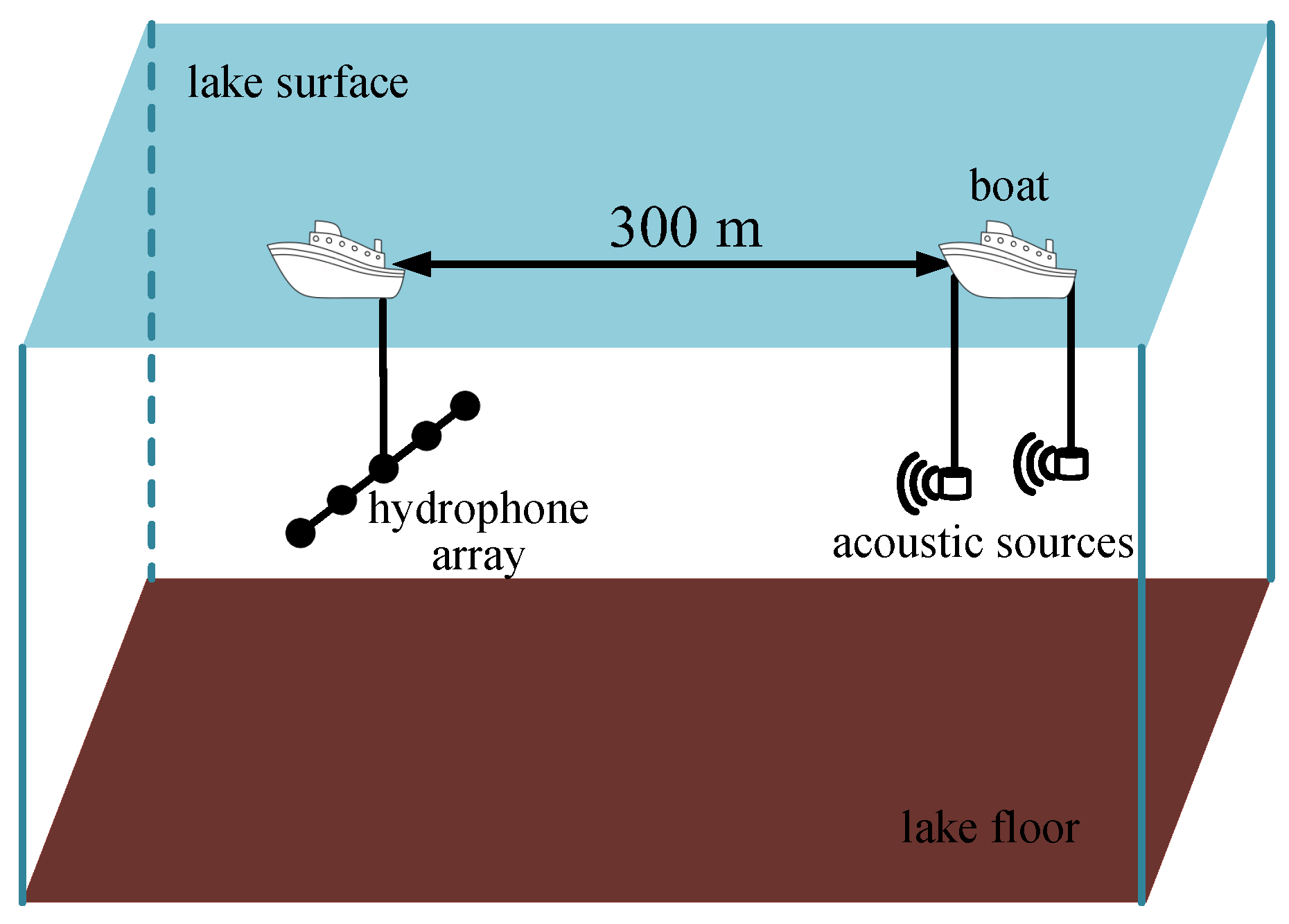
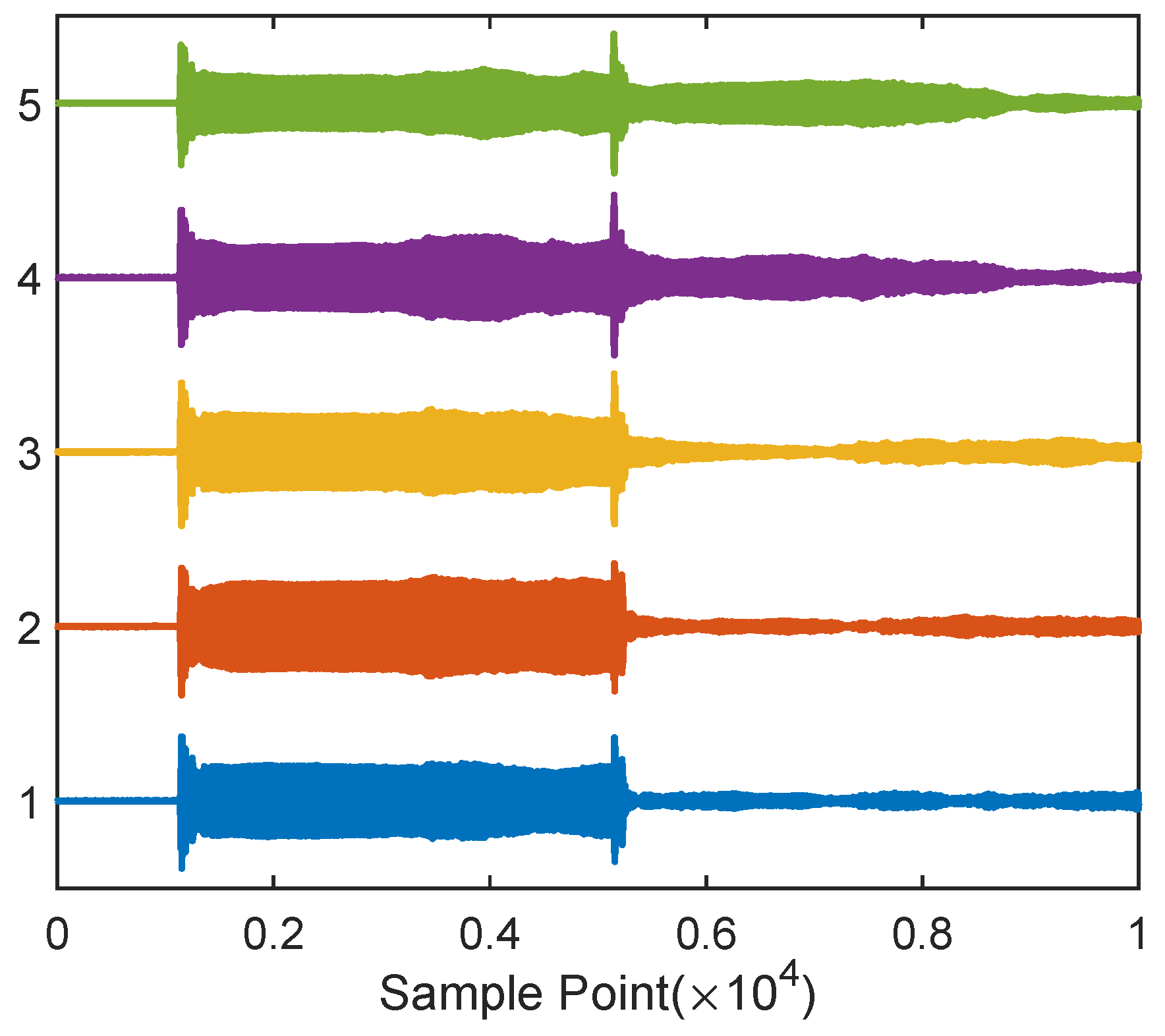
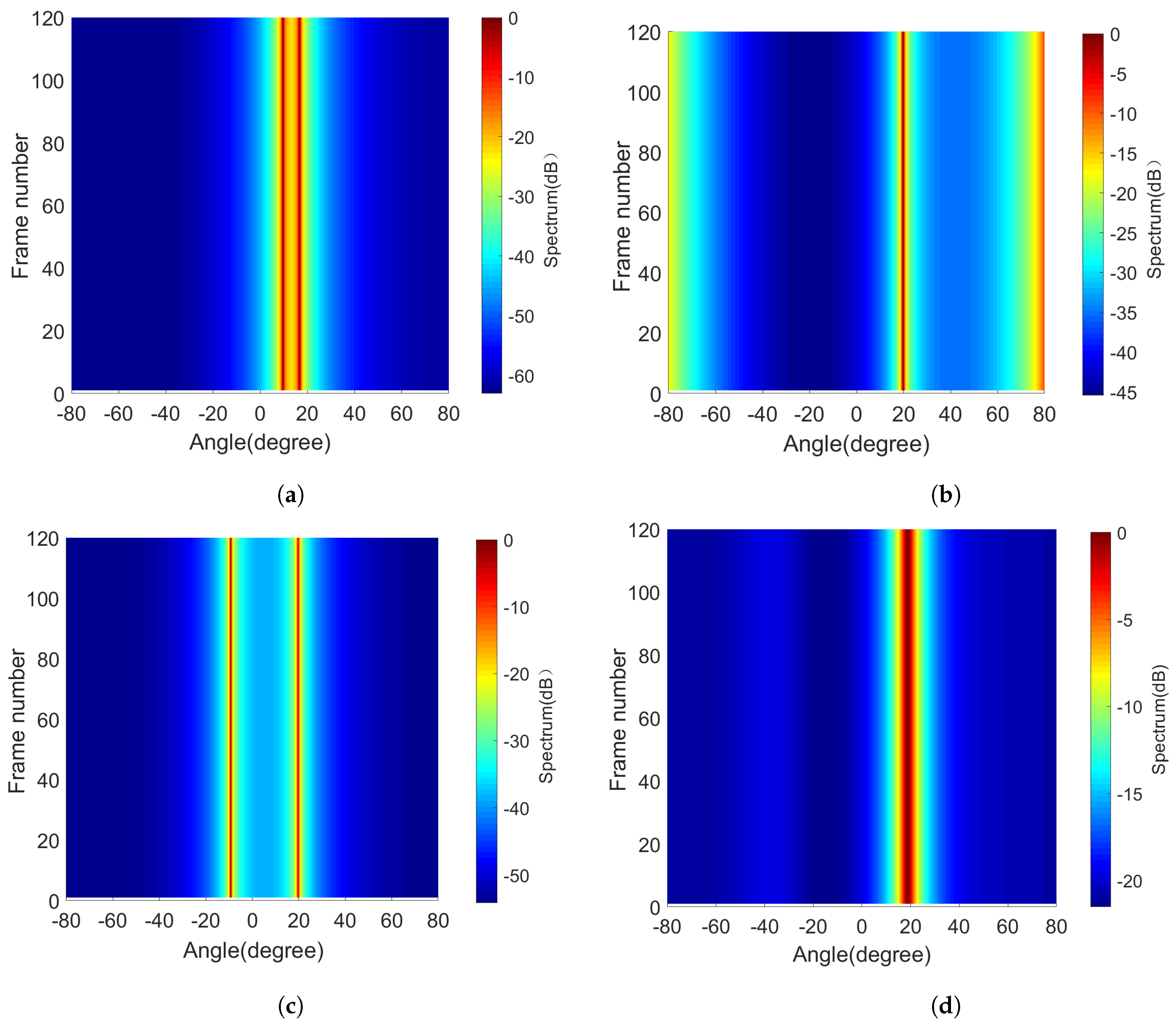
6. Lake-Test Data Processing
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, W.; Liu, H.; Chen, Z.; Yang, S.; Hu, Y.; Wen, F. Improved Amplitude-Phase Calibration Method of Nonlinear Array for Wide-Beam High-Frequency Surface Wave Radar. Remote Sens. 2023, 15, 4405. [Google Scholar] [CrossRef]
- Zhao, A.; Ma, L.; Ma, X.; Hui, J. An improved azimuth angle estimation method with a single acoustic vector sensor based on an active sonar detection system. Sensors 2017, 17, 412. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Shu, F.; Hu, J.; Yan, S.; Song, H.; Zhu, W.; Tian, D.; Song, Y.; Wang, J. Machine Learning Methods for Inferring the Number of UAV Emitters via Massive MIMO Receive Array. Drones 2023, 7, 256. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.H., III; Kailath, T. ESPRIT—Estimation of signal parameters via rotational invariance techniques. Opt. Eng. 1990, 29, 296–313. [Google Scholar] [CrossRef]
- Jeong, S.H.; Son, B.K.; Lee, J.H. Asymptotic performance analysis of the MUSIC algorithm for direction-of-arrival estimation. Appl. Sci. 2020, 10, 2063. [Google Scholar] [CrossRef]
- Hu, B.; Li, X.J.; Chong, P.H.J. Denoised modified incoherent signal subspace method for DOA of coherent signals. In Proceedings of the 2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP), Auckland, New Zealand, 5–8 August 2018; pp. 539–540. [Google Scholar] [CrossRef]
- Zhang, W.; Han, Y.; Jin, M.; Qiao, X. Multiple-Toeplitz matrices reconstruction algorithm for DOA estimation of coherent signals. IEEE Access 2019, 7, 49504–49512. [Google Scholar] [CrossRef]
- Qian, C.; Huang, L.; Zeng, W.J.; So, H.C. Direction-of-arrival estimation for coherent signals without knowledge of source number. IEEE Sens. J. 2014, 14, 3267–3273. [Google Scholar] [CrossRef]
- Han, F.M.; Zhang, X.D. An ESPRIT-like algorithm for coherent DOA estimation. IEEE Antennas Wirel. Propag. Lett. 2005, 4, 443–446. [Google Scholar] [CrossRef]
- Qi, B. DOA estimation of the coherent signals using beamspace matrix reconstruction. Signal Process. 2022, 191, 108349. [Google Scholar] [CrossRef]
- Sun, Z.G.; Bai, Q.S.; Bai, Y.Z.; Sun, R.C. Improved Weighted Spatial Smoothing Algorithm Based on Virtual Array Expansion. Syst. Eng. Electron. 2023, 45, 250–256. Available online: https://www.sys-ele.com/CN/Y2023/V45/I1/250 (accessed on 11 July 2023).
- Wen, J.; Liao, B.; Guo, C. Spatial smoothing based methods for direction-of-arrival estimation of coherent signals in nonuniform noise. Digit. Signal Process. 2017, 67, 116–122. [Google Scholar] [CrossRef]
- Li, H.S.; Shan, L.; ZHou, T. DOA estimation based on spatial smoothing for multi-beam bathymetric sonar coherent distributed sources. J. Vib. Shock 2014, 33, 138–142. [Google Scholar] [CrossRef]
- Tan, J.; Nie, Z.; Peng, S. Quadratic Forward/Backward Spatial Smoothing Polarization Smoothing MUSIC algorithm for Low Angle Estimation. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Qi, B.; Liu, D. An enhanced spatial smoothing algorithm for coherent signals DOA estimation. Eng. Comput. 2022, 39, 574–586. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Yang, X.; Xie, J.; Ng, B.W.H.; Zhang, P. Efficient cumulant-based methods for joint angle and frequency estimation using spatial-temporal smoothing. Electronics 2019, 8, 82. [Google Scholar] [CrossRef]
- Pillai, S.U.; Kwon, B.H. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Dong, M.; Zhang, S.; Wu, X.; Zhang, H. A high resolution spatial smoothing algorithm. In Proceedings of the 2007 International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 16–17 August 2007; pp. 1031–1034. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, X.G.; Liu, H.; Nguyen, A.H.; Khong, A.W. Iterative implementation method for robust target localization in a mixed interference environment. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Zamani, H.; Zayyani, H.; Marvasti, F. An iterative dictionary learning-based algorithm for DOA estimation. IEEE Commun. Lett. 2016, 20, 1784–1787. [Google Scholar] [CrossRef]
- Shi, Y.W.; Chen, M.; Shan, Z.T.; Shi, Y.R.; Shan, Z.B. Spatial smoothing technique for coherent signal DOA estimation based on eigen space MUSIC algorithm. J. Jilin Univ. (Eng. Technol. Ed.) 2017, 47, 268–273. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, F.H.; She, L.H.; Ping-Fan, L. DOA estimation of coherent signals based on reconstructed noise subspace. J. Northeast. Univ. (Nat. Sci.) 2021, 42, 1696–1700. [Google Scholar] [CrossRef]
- Stoica, P.; Larsson, E.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 148–150. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Wang, X.; Ding, L.; Jin, X.; Zhang, Q. DOA-Estimation Method Based on Improved Spatial-Smoothing Technique. Mathematics 2024, 12, 45. https://doi.org/10.3390/math12010045
Hou Y, Wang X, Ding L, Jin X, Zhang Q. DOA-Estimation Method Based on Improved Spatial-Smoothing Technique. Mathematics. 2024; 12(1):45. https://doi.org/10.3390/math12010045
Chicago/Turabian StyleHou, Yujun, Xuhu Wang, Lei Ding, Xu Jin, and Qunfei Zhang. 2024. "DOA-Estimation Method Based on Improved Spatial-Smoothing Technique" Mathematics 12, no. 1: 45. https://doi.org/10.3390/math12010045




