Discounted Risk-Sensitive Optimal Control of Switching Diffusions: Viscosity Solution and Numerical Approximation

Abstract

This work considers the infinite horizon discounted risk-sensitive optimal control problem for the switching diffusions with a compact control space and controlled through the drift; thus, the the generator of the switching diffusions also depends on the controls. Note that the running cost of interest can be unbounded, so a decent estimation on the value function is obtained, under suitable conditions. To solve such a risk-sensitive optimal control problem, we adopt the viscosity solution methods and propose a numerical approximation scheme. We can verify that the value function of the optimal control problem solves the optimality equation as the unique viscosity solution. The optimality equation is also called the Hamilton–Jacobi–Bellman (HJB) equation, which is a second-order partial differential equation (PDE). Since, the explicit solutions to such PDEs are usually difficult to obtain, the finite difference approximation scheme is derived to approximate the value function. As a byproduct, the $ϵ$-optimal control of finite difference type is also obtained.

1. Introduction

The past few decades have witnessed the emergence and development of optimal control problems with risk-sensitive criteria. The reason why risk-sensitive criteria are often desirable is that they can capture the effects of higher-order moments of the running costs in addition to their expectations. To the best of our knowledge, refs. [1,2] are the earliest works concerned with risk-sensitive optimal control problems. Since then, there has been a lot of research on risk-sensitive optimal control problems. For the discrete time controlled Markov chains, the risk-sensitive criteria have been studied in [3,4]; for the continuous time Markov chains with risk-sensitive criteria see [5,6,7,8] and the reference therein; for piecewise deterministic Markov decision processes see [9] and the reference therein; for the controlled diffusions with risk-sensitive criteria, we refer the readers to [10,11,12,13]. Besides the theoretical improvement, it has also has found applications in Q-learning [14], finance [15], insurance [16], missile guidance [17], and many other applications.

As to controlled switching diffusion, it has been paid much attention in theory and application in recent years. The state of such process consists of a continuous part and a discrete part at the same time. Usually, the discrete part of the state is modelled by a continuous time Markov chain with finite states. So much effort has been spent to learn more about the properties of the processes, for instance [18,19] and the reference therein. Much of the study originated from applications arising in manufacturing systems [20,21], filtering [22], and financial engineering [23]. For more general theory on such hybrid systems, we refer the readers to [24,25]. While [24] concerns the case when the generator of the continuous time Markov chain is independent of the continuous part of the state, and [25] studies the case when the generator of the continuous time Markov chain depends on the continuous part of the state. Such models can be widely used in many practical applications. For example, [26] applies the switching diffusions to the ecosystems and let the discrete part of the state represent the random environment. Within the framework of financial applications, the discrete part of the state is usually used to capture the market environment, say bull or bear, see [27].

However, to the best of our knowledge, there is little literature on controlled switching diffusions with risk-sensitive criteria. The risk-sensitive optimal control problem to the controlled switching diffusions is of interest and such an issue has not received so much attention, which motivates us to consider such topics. In this work, we are going to study the infinite horizon discounted risk-sensitive optimal control problem based on the controlled switching diffusions. To be specific, we work on the process $\left(X\right(t),\alpha (t\left)\right)$ with $X\left(t\right)$ being the continuous part of the state and $\alpha \left(t\right)$ being the discrete part, which is governed by (1) and (2). Based on the controlled switching diffusion $\left(X\right(t),\alpha (t\left)\right)$ defined above, we are going to minimize

$$J(\theta ,x,\alpha ,u(·))=\frac{1}{\theta }log\left\{E\left[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),u\left(t\right))dt\right)\right]\right\},$$

with $\theta \in (0,1]$ being the risk factor and $\rho >0$ being the discount factor. Define the value function as follows,

$$V(\theta ,x,\alpha )=\underset{u(·)}{inf}J(\theta ,x,\alpha ,u(·)).$$

Our aim is to find the optimal control $u^{*}(·)$ such that $V(\theta ,x,\alpha )=J(\theta ,x,\alpha ,u^{*}(·))$. Since the logarithm function is increasing, to simplify the calculation, we only need to minimize the following functional

$$I(\theta ,x,\alpha ,u(·))=E\left[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),u\left(t\right))dt\right)\right],$$

The corresponding value function is

$$W(\theta ,x,\alpha )=\underset{u(·)}{inf}I(\theta ,x,\alpha ,u(·)).$$

Similarly, if there exists a control $u^{*}(·)$ such that $W(\theta ,x,\alpha )=I(\theta ,x,\alpha ,u^{*}(·))$, we call it optimal. It is easy to know that if $u^{*}(·)$ such that $W(\theta ,x,\alpha )=I(\theta ,x,\alpha ,u^{*}(·))$, then we can also obtain $V(\theta ,x,\alpha )=J(\theta ,x,\alpha ,u^{*}(·))$, and vice versa. Therefore, it is sufficient to work on the optimization problem with exponential utility.

To solve such problem, similar to the risk neutral case, see [20,27], we should find suitable characterizations to the value function $W(\theta ,x,\alpha )$ and the optimal control $u^{*}(·)$. Due to the dynamic program principle, such characterizations are usually given via the associated optimality equation, or the HJB equation. Thus we formally derive the associated HJB equation and rigorously prove that the value function $W(\theta ,x,\alpha )$ of the optimization problem solves the associated HJB equation as the unique viscosity solution. We will see that such equation is a second-order partial differential equation. The viscosity solution is one of the commonly used weak solutions for this kind of equation; we recommend [27,28,29] and the reference therein for readers who are not familiar with the concept of viscosity solutions. In particular, the development of viscosity solutions is briefly introduced in reference [28].

As is well known, explicit solutions to such HJB equations are usually difficult to obtain, so we turn to study the numerical solutions. Finite difference approximation scheme is a tool of commonly used. Moreover, associated with the viscosity solution method, we can also give the convergence analysis to the finite difference approximation scheme. As a byproduct, through the convergence analysis of the approximation scheme we can obtain the $ϵ$-optimal control of finite difference type.

This work has the following contributions: (a) We propose a suitable condition to give a decent estimation on the value function of concerned with unbounded running cost. Unlike in [10], we do not need the near-monotonicity condition as the structural assumption on the running cost function. Further, compared with the assumptions adopted in [10], under our assumption we can also drop the requirement that the coefficients of the systems should be bounded. (b) We construct an appropriate truncation function to reduce the proof of the global comparison theorem to the local case. To be specific, the difficulty of verifying the uniqueness of viscosity solution is to prove the corresponding comparison theorem, and the large obstacle of proving the corresponding comparison theorem is to construct the corresponding truncation function. (c) We construct a finite difference approximation scheme to approach the value function, and as a byproduct, we can obtain the existence of $ϵ$-optimal control of finite difference type. This kind of idea can be extended to treat the optimal control of controlled (switching) diffusions with other criteria.

The rest of the work is organized as follows: In Section 2, we introduce the mathematical background and arise the optimization problem. In Section 3, we derive the associated HJB equation and show that the value function to the optimization problem solves the associated HJB equation as the unique viscosity solution. In Section 4, we construct the finite difference approximation scheme and give its convergence analysis, as a byproduct, we also show the existence of $ϵ$-optimal control of finite difference type.

2. The Model

In this work, the underlying process $\left(X\right(t),\alpha (t\left)\right)$ is defined on the complete filtered probability space $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},P)$ and governed by the following system,

$$dX\left(t\right)=b\left(X\right(t),\alpha (t),u(t\left)\right)dt+\sigma \left(X\right(t),\alpha (t\left)\right)dB\left(t\right),\left(X\right(0),\alpha (0\left)\right)=(x,\alpha ),$$

(1)

$$P(\alpha (t+\delta )=j|\alpha \left(t\right)=i,X\left(s\right),\alpha \left(s\right),s\le t)=q_{ij}(X\left(t\right),u\left(t\right))\delta +o\left(\delta \right),i\ne j,$$

(2)

with $\delta >0$ arbitrarily small. $(X\left(t\right),\alpha \left(t\right))\in {\mathbb{R}}^r\times \mathcal{M}$, with $\mathcal{M}=\{1,2,\cdots ,m\}$ be a finite set. $b(·,·,·):{\mathbb{R}}^r\times \mathcal{M}\times \mathbb{U}\to {\mathbb{R}}^r$ and $\sigma (·,·):{\mathbb{R}}^r\times \mathcal{M}\to {\mathbb{R}}^{r\times r}$ are drift term and diffusion term, respectively. $Q(x,u)=\left(q_{ij}(x,u)\right)\in {\mathbb{R}}^{m\times m}$ is the generator of the process of Markov regime switching. The control process ${\left\{u\left(t\right)\right\}}_{t\ge 0}$ is taking value in $\mathbb{U}$, which is a given compact metric space. $B\left(t\right)$ is a standard Brownian motion.

Remark 1.

The probability space $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},P)$ mentioned above is constructed in the following way. Firstly, for fixed $x\in {\mathbb{R}}^r$, define

$$p(t,x,y)={\left(2\pi t\right)}^{-r/2}exp\left\{-\frac{{|x-y|}^2}{2t}\right\},$$

for $y\in {\mathbb{R}}^r,t>0$. If $0\le t_1\le t_2\le \cdots \le t_k$, define a measure ${\nu }_{t_1,\cdots ,t_k}$ on ${\mathbb{R}}^{rk}$ by

$$\begin{array}{cc}& {\nu }_{t_1,\cdots ,t_k}(F_1\times \cdots \times F_k)\hfill \\ \hfill =& {\int }_{F_1\times \cdots \times F_k}p(t_1,x,x_1)p(t_2-t_1,x_1,x_2)\cdots p(t_k-t_{k-1},x_{k-1},x_k)d{x}_1\cdots d{x}_k,\hfill \end{array}$$

where $F_i,i=1,2,\cdots ,k$, are members of $\mathcal{B}\left({\mathbb{R}}^r\right)$, the Borel σ-field of ${\mathbb{R}}^r$. Additionally, we use the convention that $p(0,x,y)dy={\delta }_x\left(y\right)$. Then by verifying that ${\nu }_{t_1,\cdots ,t_k}$ satisfies the consistent properties and the Kolmogorov’s extension theorem (see [30] (p. 11, Theorem 2.1.5) and the reference therein), there exists a probability space $({\Omega }^B,{\mathcal{F}}^B,P^B)$ and a stochastic process ${\left\{B\left(t\right)\right\}}_{t\ge 0}$ on ${\Omega }^B$ such that

$$P^B(B\left(t_1\right)\in F_1,\cdots ,B\left(t_k\right)\in F_k)={\nu }_{t_1,\cdots ,t_k}(F_1\times \cdots \times F_k).$$

In fact, ${\left\{B\left(t\right)\right\}}_{t\ge 0}$ is a standard Brownian motion.

Moreover, Let λ be the Lebesgue measure on $({\mathbb{R}}_{+}\times \mathbb{R},\mathcal{B}({\mathbb{R}}_{+}\times \mathbb{R}))$ such that $\lambda (dt\times dz)=dt\times m\left(dz\right)$, where m is the Lebesgue measure on $\mathbb{R}$. For arbitrary $A\in \mathcal{B}({\mathbb{R}}_{+}\times \mathbb{R})$ and $\lambda \left(A\right)<\infty$, let

$$p_A\left(n\right)=e^{-\lambda \left(A\right)}\frac{{\left[\lambda \left(A\right)\right]}^n}{n!},n=0,1,2,\cdots .$$

If $\lambda \left(A\right)=\infty$, then let

$$p_A(\infty )=1.$$

It is easy to know that $p_A$ is a probability measure on ${\overline{Z}}_{+}=Z_{+}\cup \{\infty \}$. Moreover, for each $k\in Z_{+}/\left\{0\right\}$, $A_i\in \mathcal{B}({\mathbb{R}}_{+}\times \mathbb{R})$, and $\lambda \left(A_i\right)<\infty$, $(i=1,2,\cdots ,k)$ and $i_j\in {\overline{Z}}_{+}$, $(j=1,2,\cdots ,k)$, define the following finite dimensional distribution on ${\left({\overline{Z}}_{+}\right)}^k$

$$p_{A_1,\cdots ,A_k}(i_1,\cdots ,i_k)={\Pi }_{n=1}^k{p}_{A_n}\left(i_n\right).$$

Then by verifying the above finite dimensional distribution admits several consistent properties, the existence theorem of Poisson random measure (see in [31] [Chapter 11]) ensures that there exists a probability space $({\Omega }^{\mathfrak{p}},{\mathcal{F}}^{\mathfrak{p}},P^{\mathfrak{p}})$ and a process of Poisson random measure $\mathfrak{p}(dt,dz)$ defined on ${\Omega }^{\mathfrak{p}}$ with intensity $dt\times m\left(dz\right)$, where $m\left(dz\right)$ denotes the Lebesgue measure on $\mathbb{R}$, such that, for each $k\in Z_{+}/\left\{0\right\}$, $A_i\in \mathcal{B}({\mathbb{R}}_{+}\times \mathbb{R})$ and $\lambda \left(A_i\right)<\infty$, for $i=1,2,\cdots ,k$,

$$P^{\mathfrak{p}}(\mathfrak{p}\left(A_j\right)=i_j,j=1,2,\cdots ,k)=p_{A_1,\cdots ,A_k}(i_1,\cdots ,i_k).$$

Then by letting $(\Omega ,\mathcal{F},P):=({\Omega }^B\times {\Omega }^{\mathfrak{p}},{\mathcal{F}}^B\times {\mathcal{F}}^{\mathfrak{p}},P^B\times P^{\mathfrak{p}})$ and ${\mathcal{F}}_t=\sigma \{B\left(s\right),\mathfrak{p}(E,F),(E,F)\in$$\mathcal{B}\left(\right[0,s\left)\right)\times \mathcal{B}\left(\mathbb{R}\right),0\le s\le t\}$, we have actually constructed the complete filtered probability space $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},P)$. Throughout the work, we assume that the Poisson random measure $\mathfrak{p}(dt,dz)$ is independent of the Brownian motion $B(·)$.

In order to get convenient compactness property, we introduce the notion of relaxed control. Let $\Pi =\left\{\pi \right(t)\in \mathcal{P}(\mathbb{U}),t\ge 0\}$, with $\mathcal{P}\left(\mathbb{U}\right)$ being the space of all probability measures defined on the control space $\mathbb{U}$. In particular, $u\left(t\right)$ is equivalent to ${\delta }_{u\left(t\right)}$, with $\delta$ be the Dirac measure, for each $t\ge 0$. To proceed, we also need the following definition of admissible control.

Definition 1.

We say that a relaxed control $\pi \in \Pi$ is admissible if $\pi \left(t\right)$ is ${\mathcal{F}}_t$-adapted measurable and the σ-fields ${\mathcal{F}}_t^{\pi }$ and ${\mathcal{F}}_{[t,\infty )}^{B,\mathfrak{p}}$ are independent, with ${\mathcal{F}}_t^{\pi }=\sigma \{\pi \left(s\right),s\le t\}$ and ${\mathcal{F}}_{[t,\infty )}^{B,\mathfrak{p}}=\sigma \{B\left(s\right)-B\left(t\right),\mathfrak{p}(E,F),E\in \mathcal{B}\left([s,\infty )\right),F\in \mathcal{B}\left(\mathbb{R}\right),s\ge t\}$.

Denote by ${\Pi }_A$ the collecton of all admissible controls. Furthermore, if $\pi \left(t\right)=\phi \left(X\right(t),\alpha (t\left)\right)$ for a measurable function $\phi :{\mathbb{R}}^r\times \mathcal{M}\to \mathcal{P}\left(\mathbb{U}\right)$, the admissible control $\pi =\left\{\pi \right(t),t\ge 0\}$ is called a stationary Markov control. We use ${\Pi }_{RM}$ to represent the family of all stationary Markov controls. Moreover, we call $u(·)$ or $\pi (·)={\delta }_{u(·)}$ the non-randomized stationary Markov control, if $u\left(t\right)=\varphi \left(X\right(t),\alpha (t\left)\right)$ and $\varphi :{\mathbb{R}}^r\times \mathcal{M}\to \mathbb{U}$ is measurable for all $t\ge 0$. Denote all such controls by ${\Pi }_{DM}$. Obviously, ${\Pi }_{DM}\subset {\Pi }_{RM}\subset {\Pi }_A\subset \Pi$.

In order to guarantee that the system (1) and (2) admits a unique solution, we need the following assumption.

Assumption 1.

(i) 

$Q(x,u)=\left(q_{ij}(x,u)\right)\in {\mathbb{R}}^{m\times m}$ with $q_{ij}(x,u)\ge 0$($i\ne j$), for all $(x,u)\in {\mathbb{R}}^r\times \mathbb{U}$, and ${\sum }_{j=1}^m{q}_{ij}(x,u)=0$ for all $i\in \mathcal{M}$. Additionally, $q_{ij}(x,u)$ is bounded continuous function for all $i,j\in \mathcal{M}$

(ii) 

The drift term $b(·,·,·)$ and the diffusion term $\sigma (·,·)$ are continuous functions. Moreover, both of them are Lipschitz continuous in their first component, uniformly for all $\alpha \in \mathcal{M}$ and $u\in \mathbb{U}$, with Lipschitz constant $k_0>0$.

(iii) 

The system is non-degenerate, i.e., $\sigma {\sigma }^T\ge k_{1}I$ for suitable constant $k_1>0$, where $I\in {\mathbb{R}}^{r\times r}$ represents the identity matrix.

Associated with the assumptions above, we can get the following conclusion.

Theorem 1.

Suppose that the Assumption 1 holds, then the system (1) and (2) admits an unique strong solution $\left(X\right(·),\alpha (·\left)\right)$ for a given control $\pi \in {\Pi }_{RM}$, which is a Feller process and the associated operator is given by

$${\mathcal{L}}^{\pi }f(x,\alpha )={\int }_{\mathbb{U}}{\mathcal{L}}^{u}f(x,\alpha )\pi \left(du\right|x,\alpha ),\pi \in {\Pi }_{RM}$$

where

$${\mathcal{L}}^{u}f(x,\alpha )=\sum _{l=1}^r{b}_l(x,\alpha ,u)\frac{\partial f(x,\alpha )}{\partial x_l}+\frac{1}{2}\sum _{l,k=1}^r{a}_{lk}(x,\alpha )\frac{{\partial }^{2}f(x,\alpha )}{\partial x_l\partial x_k}+\sum _{j=1}^m{q}_{\alpha j}(x,u)f(x,j),$$

(3)

with $a(x,\alpha )=\sigma (x,\alpha ){\sigma }^T(x,\alpha )\in {\mathbb{R}}^{r\times r}$ and $f\in C^{2,0}({\mathbb{R}}^r\times \mathcal{M})$, which is the space consisting of all real-valued functions, which are twice continuously differentiable with respect to x and continuous with respect to α.

Proof 1.

As well known, the Markov regime switching process $\alpha (·)$ can be represented by the stochastic integral with respect to the forementioned Poisson random measure $\mathfrak{p}(dt,dz)$ as given is Remark 1. Then for $\pi =\{\pi \left(t\right),t\ge 0\}\in {\Pi }_{RM}$, (1) and (2) have the following equivalent form

$$\begin{array}{cc}\hfill dX\left(t\right)& {\displaystyle =b\left(X\right(t),\alpha (t),\pi (t\left)\right)dt+\sigma \left(X\right(t),\alpha (t\left)\right)dB\left(t\right),}\hfill \\ \hfill d\alpha \left(t\right)& {\displaystyle ={\int }_{\mathbb{R}}h(X\left(t\right),\alpha (t-),\pi \left(t\right),z)\mathfrak{p}(dt,dz),}\hfill \end{array}$$

(4)

with initial state $\left(X\right(0),\alpha (0\left)\right)=(x,\alpha )$. For more details, we refer the readers to [25,32], [Chapter 2] and the reference therein. Thus the result follows by ([20] Theorem 2.1). □

The Risk-Sensitive Criterion

Now, we are going to introduce the risk-sensitive criterion. For $\theta \in (0,1]$ and $\rho >0$, define

$$J(\theta ,x,\alpha ,\pi )=\frac{1}{\theta }log\left\{E\left[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)\right]\right\},$$

where $c(x,\alpha ,\pi (·)):={\int }_{\mathbb{U}}c(x,\alpha ,u)\pi \left(du\right|x,\alpha )$ for all control $\pi \in {\Pi }_{RM}$, θ is the risk-sensitive parameter and ρ is the given discount factor. We are going to minimize $J(\theta ,x,\alpha ,\pi )$ over ${\Pi }_{RM}$. Let the value function be defined as follows,

$$V(\theta ,x,\alpha ):=\underset{\pi \in {\Pi }_{RM}}{inf}J(\theta ,x,\alpha ,\pi ).$$

The aim is to find a suitable control ${\pi }^{*}\in {\Pi }_{RM}$ such that $V(\theta ,x,\alpha )=J(\theta ,x,\alpha ,{\pi }^{*})$, we call such ${\pi }^{*}$ the optimal control. As mentioned in the introduction, to simplify the calculation, we need to work with the following auxiliary functional

$$I(\theta ,x,\alpha ,\pi )=E\left[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)\right],$$

The corresponding value function is

$$W(\theta ,x,\alpha )=\underset{\pi \in {\Pi }_{RM}}{inf}I(\theta ,x,\alpha ,\pi ).$$

Since the logarithm function is an increasing function, thus the optimal control to the auxiliary problem is also optimal to the original risk-sensitive problem. Henceforth, we only need to work with $W(\theta ,x,\alpha )$.

To proceed we need the following assumption to ensure that the value function W is well defined, which means that it admits a certain property of boundness.

Assumption 2.

Suppose that the following conditions hold.

(i) 

The running cost function $c(x,\alpha ,u)$ is continuous in $(x,\alpha ,u)$, and ${sup}_{\pi }\left|c(x,\alpha ,\pi (·))\right|\le M_0\omega (x,\alpha )$, for suitable $M_0>0$, where $\omega :{\mathbb{R}}^r\times \mathcal{M}\to {\mathbb{R}}^{+}$ is a given positive function and twice continuously differentiable in $x\in {\mathbb{R}}^r$ for each $\alpha \in \mathcal{M}$, and $\omega (x,\alpha )\ge 1$, for all $(x,\alpha )\in {\mathbb{R}}^r\times \mathcal{M}$.

(ii) 

There have two constants $A,\tilde{A}>0$ such that $\rho >A>0$ and

$${\mathcal{L}}^u\omega (x,\alpha )+\frac{1}{2}\sum _{l,k=1}^r{a}_{l,k}(x,\alpha )\frac{\partial \omega (x,\alpha )}{\partial x_l}\frac{\partial \omega (x,\alpha )}{\partial x_k}\le A\omega (x,\alpha )+\tilde{A}.$$

(iii) 

And assume that

$$E\left\{exp\left[\frac{1}{2}{\int }_0^{\infty }{\left(e^{-As}\partial \omega (X\left(s\right),\alpha \left(s\right))\sigma (X\left(s\right),\alpha \left(s\right))\right)}^{2}ds\right]\right\}<\infty ,$$

(5)

with ${(\partial \omega (x,\alpha )\sigma (x,\alpha ))}_k={\sum }_{l=1}^r\frac{\partial \omega (x,\alpha )}{\partial x_l}{\sigma }_{lk}(x,\alpha )$.

Henceforth, we denote $\partial \omega (x,\alpha )\sigma (x,\alpha )$ or its suitable variants $\partial \omega \left(X\right(s),\alpha (s\left)\right)\sigma \left(X\right(s),\alpha (s\left)\right)$ by $\partial \omega \sigma$, for simplicity.

Remark 2.

Since the function ω can be unbounded, thus $c(x,\alpha ,u)$ can also be unbounded. Unlike in [10], we do not need the structural assumption on the running cost function, which is known as near-monotonicity, and we also do not assume the cofficients of the diffusion to be bounded.

Under the assumption above, we can show that the value functions are well defined. In fact, we can obtain the following conclusion.

Proposition 1.

Under the Assumption 2, we have

$$W(\theta ,x,\alpha )\le M_{1}exp\left\{M_2\omega (x,\alpha )\right\},$$

with $M_1=exp\left\{{\displaystyle \frac{M_0}{\rho -A}}\right\}$ and $M_2=2max\left\{{\displaystyle \frac{M_0}{\rho -A}},{\displaystyle \frac{M_0\tilde{A}}{\rho (\rho -A)}}\right\}$.

Proof 2.

Let $f(t,x,\alpha )=e^{-At}\omega (x,\alpha )$, then by using the Itô’s formula we have

$$\begin{array}{cc}& {\displaystyle e^{-At}\omega (X\left(t\right),\alpha \left(t\right))}\hfill \\ \hfill =& {\displaystyle \omega (x,\alpha )+{\int }_0^t{e}^{-As}\left[{\mathcal{L}}^u\omega (X\left(s\right),\alpha \left(s\right))-A\omega (X\left(s\right),\alpha \left(s\right))\right]ds+{\int }_0^t{e}^{-As}\partial \omega ·\sigma dB\left(s\right)}\hfill \\ \hfill =& {\displaystyle \omega (x,\alpha )+{\int }_0^t{e}^{-As}\left[{\mathcal{L}}^u\omega (X\left(s\right),\alpha \left(s\right))-A\omega (X\left(s\right),\alpha \left(s\right))\right]ds+\frac{1}{2}{\int }_0^t{\left(e^{-As}\partial \omega ·\sigma \right)}^{2}ds}\hfill \\ & {\displaystyle +{\int }_0^t{e}^{-As}\partial \omega ·\sigma dB\left(s\right)-\frac{1}{2}{\int }_0^t{\left(e^{-As}\partial \omega ·\sigma \right)}^{2}ds}\hfill \\ \hfill \le & {\displaystyle \omega (x,\alpha )+{\int }_0^t{e}^{-As}\tilde{A}ds+{\int }_0^t{e}^{-As}\partial \omega ·\sigma dB\left(s\right)-\frac{1}{2}{\int }_0^t{\left(e^{-As}\partial \omega ·\sigma \right)}^{2}ds}\hfill \end{array}$$

(6)

Thus

$$\omega (X\left(t\right),\alpha \left(t\right))\le e^{At}\omega (x,\alpha )+\frac{\tilde{A}}{A}(e^{At}-1)+e^{At}{Z}_t$$

(7)

with

$$Z_t={\int }_0^t{e}^{-As}\partial \omega ·\sigma dB\left(s\right)-\frac{1}{2}{\int }_0^t{\left(e^{-As}\partial \omega ·\sigma \right)}^{2}ds$$

(8)

In addition, we have

$$\begin{array}{cc}& {\displaystyle E\left\{exp\left[\theta {\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right]\right\}}\hfill \\ \hfill \le & {\displaystyle E\left\{exp\left[\theta {\int }_0^{\infty }{e}^{-\rho t}\left|c(X\left(t\right),\alpha \left(t\right),\pi (·))\right|dt\right]\right\}}\hfill \\ \hfill \le & {\displaystyle E\left\{exp\left[{\int }_0^{\infty }{e}^{-\rho t}{M}_0\omega (X\left(t\right),\alpha \left(t\right))dt\right]\right\}\hspace{1em}(\mathrm{by} \mathrm{Assumption} 2\left(\mathrm{i}\right) \mathrm{and} \theta \le 1)}\hfill \\ \hfill \le & {\displaystyle E\left\{exp\left[{\int }_0^{\infty }{e}^{-\rho t}{M}_0\left(e^{At}\omega (x,\alpha )+\frac{\tilde{A}}{A}(e^{At}-1)\right)dt\right]\right\}}\hfill \\ & {\displaystyle \times E\left\{exp\left[{\int }_0^{\infty }{e}^{-\rho t}{M}_0\left(e^{At}{Z}_t\right)dt\right]\right\}.}\hfill \end{array}$$

(9)

Furthermore, note that $\rho >A$, by direct calculation, we can derive that

$$\begin{array}{cc}& {\displaystyle E\left\{exp\left[{\int }_0^{\infty }{e}^{-\rho t}{M}_0\left(e^{At}\omega (x,\alpha )+\frac{\tilde{A}}{A}(e^{At}-1)\right)dt\right]\right\}}\hfill \\ \hfill =& {\displaystyle {\displaystyle \frac{M_0}{\rho -A}}\omega (x,\alpha )+{\displaystyle \frac{M_0\tilde{A}}{\rho (\rho -A)}}}\hfill \\ \hfill \le & {\displaystyle M_2\omega (x,\alpha )(\mathrm{by}\omega (x,\alpha )\ge 1),}\hfill \end{array}$$

with $M_2:=2max\left\{{\displaystyle \frac{M_0}{\rho -A}},{\displaystyle \frac{M_0\tilde{A}}{\rho (\rho -A)}}\right\}$.

Moreover, by letting $\nu \left(dt\right):=(\rho -A)e^{-(\rho -A)t}dt$, and noting that it is a probability measure on $[0,\infty )$, we can derive that

$$\begin{array}{cc}& {\displaystyle E\left\{exp\left[{\int }_0^{\infty }{e}^{-\rho t}{M}_0\left(e^{At}{Z}_t\right)dt\right]\right\}}\hfill \\ \hfill =& {\displaystyle E\left\{exp\left[{\int }_0^{\infty }{\displaystyle \frac{M_0}{\rho -A}}{Z}_t\nu \left(dt\right)\right]\right\}}\hfill \\ \hfill \le & {\displaystyle E\left\{{\int }_0^{\infty }exp\left[{\displaystyle \frac{M_0}{\rho -A}}{Z}_t\right]\nu \left(dt\right)\right\}}\hfill \\ \hfill =& {\displaystyle {\int }_0^{\infty }exp\left[{\displaystyle \frac{M_0}{\rho -A}}\right]E\left[e^{Z_t}\right]\nu \left(dt\right).}\hfill \end{array}$$

By the condition (5), we can derive that $Z_t$ is an exponential martingale and

$$E\left[e^{Z_t}\right]=E\left[e^{Z_0}\right]=1.$$

Thus we have

$$E\left\{exp\left[{\int }_0^{\infty }{e}^{-\rho t}{M}_0\left(e^{At}{Z}_t\right)dt\right]\right\}=exp\left[{\displaystyle \frac{M_0}{\rho -A}}\right]=:M_1.$$

Therefore, we can conclude that

$$W(\theta ,x,\alpha )\le M_{1}exp\left\{M_2\omega (x,\alpha )\right\},$$

for all $\theta \in (0,1]$, with $M_1=exp\left[{\displaystyle \frac{M_0}{\rho -A}}\right]$ and $M_2=2max\left\{{\displaystyle \frac{M_0}{\rho -A}},{\displaystyle \frac{M_0\tilde{A}}{\rho (\rho -A)}}\right\}$. We are done. □

Let $\tilde{\omega }(x,\alpha )=exp\left\{M_2\omega (x,\alpha )\right\}$. Now, we can introduce the $\tilde{\omega }$-norm and the definition of $\tilde{\omega }$ bounded. A function $\psi :(0,1]\times {\mathbb{R}}^r\times \mathcal{M}\to \mathbb{R}$, is called $\tilde{\omega }$-bounded if

$${\parallel \psi \parallel }_{\tilde{\omega }}:=\underset{(\theta ,x,\alpha )\in {\mathbb{R}}^r\times \mathcal{M}}{sup}\frac{\left|\psi \right(\theta ,x,\alpha \left)\right|}{\tilde{\omega }(x,\alpha )}<\infty .$$

Then, we can see that W is a member of $B_{\tilde{\omega }}((0,1]\times {\mathbb{R}}^r\times \mathcal{M})$, the collection of all $\tilde{\omega }$-bounded real valued functions defined on $(0,1]\times {\mathbb{R}}^r\times \mathcal{M}$, which is a Banach space. Thus, the value function W is well defined. For simplicity, henceforth, let ${\mathcal{Q}}_0:=(0,1]\times {\mathbb{R}}^r\times \mathcal{M}$, then $B_{\tilde{\omega }}((0,1]\times {\mathbb{R}}^r\times \mathcal{M})$ can be simply denoted by $B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$.

To proceed, we need to illustrate that the set of models which satisfy Assumptions 1 and 2 is nonempty. We show this fact by giving a representative example.

Example 1.

For simplicity, we consider the one-dimensional Ornstein–Uhlenbeck type process with regime switching. Let $\left(X\right(t),\alpha (t\left)\right)\in \mathbb{R}\times \mathcal{M}$, with $\mathcal{M}=\{1,2\}$, and

$$dX\left(t\right)=\left(\mu \right(\alpha \left(t\right))+u(t\left)\right)X\left(t\right)dt+\sigma \left(\alpha \right(t\left)\right)dB\left(t\right)$$

(10)

$$Q(x,u)=\left(\begin{array}{cc}{q}_{11}(x,u)& -q_{11}(x,u)\\ -q_{22}(x,u)& q_{22}(x,u)\end{array}\right)$$

(11)

with $q_{ii}<0,\left|q_{ii}\right|<\infty ,i=1,2$ and $\mathbb{U}=[0,U_0]$, and consider the functional

$$I(\theta ,x,\alpha ,\pi (·))=E\left[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)\right],$$

with $c(x,\alpha ,u)=x+\alpha +u$, and $\rho >{\mu }_M+U_0$, with ${\sigma }_M=max\{\sigma \left(1\right),\sigma \left(2\right)\},{\mu }_M=max\{\mu \left(1\right),$$\mu \left(2\right)\}$.

It is obvious to know that Assumption 1 holds and by taking $\omega (x,\alpha )=x+\alpha +1$, it is easy to verify that Assumption 2 (i) and (ii) also hold with $A={\mu }_M+U_0<\rho$, $\tilde{A}=max\left\{\right|q_{11}|,|q_{22}\left|\right\}$ and $M_0=max\{U_0,1\}$. Now it remains to verify that Assumption 2 (iii) also holds. In fact,

$$\begin{array}{cc}& {\displaystyle E\left\{exp\left[\frac{1}{2}{\int }_0^{\infty }{\left(e^{-As}\partial \omega (X\left(s\right),\alpha \left(s\right))\sigma (X\left(s\right),\alpha \left(s\right))\right)}^{2}ds\right]\right\}}\hfill \\ \hfill =& {\displaystyle E\left\{exp\left[\frac{1}{2}{\int }_0^{\infty }(e^{-2As}\sigma {\left(\alpha \left(s\right)\right)}^{2}ds\right]\right\}}\hfill \\ \hfill \le & {\displaystyle exp\left[\frac{1}{2}{\int }_0^{\infty }{e}^{-2As}{\sigma }_M^{2}ds\right]}\hfill \\ \hfill =& {\displaystyle exp\left[{\displaystyle \frac{{\sigma }_M^2}{4A}}\right]<\infty .}\hfill \end{array}$$

Therefore, Assumption 2 (iii) has been verified.

To conclude this section, now we formally derive the HJB equation for W. For any $T>0$ and given Markov control $\pi \in {\Pi }_{RM}$, it is easy to know that

$$\begin{array}{cc}& {\displaystyle W(\theta ,x,\alpha )}\hfill \\ \hfill =& {\displaystyle \underset{\pi \in {\Pi }_{RM}}{inf}I(\theta ,x,\alpha ,\pi )}\hfill \\ \hfill =& {\displaystyle \underset{\pi \in {\Pi }_{RM}}{inf}E\left[exp\left(\theta {\int }_0^T{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt+\theta {\int }_T^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)\right]}\hfill \\ \hfill =& {\displaystyle \underset{\pi \in {\Pi }_{RM}}{inf}E\{exp\left(\theta {\int }_0^T{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)}\hfill \\ & {\displaystyle \times E_{\left(X\right(T),\alpha (T\left)\right)}\left[exp\left(\theta e^{-\rho T}{\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)\right]\}.}\hfill \end{array}$$

Thus, formally we have

$$W(\theta ,x,\alpha )=\underset{\pi \in {\Pi }_{RM}}{inf}E\left\{exp\left(\theta {\int }_0^T{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)W(\theta e^{-\rho T},X\left(T\right),\alpha \left(T\right))\right\},$$

(12)

then by using Itô’s formula for $exp\left(\theta {\int }_0^T{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)W(\theta e^{-\rho T},X\left(T\right),\alpha \left(T\right))$, and letting T approach 0, we obtain

$$-\theta \rho \frac{\partial W(\theta ,x,\alpha )}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta c(x,\alpha ,u)W(\theta ,x,\alpha )+{\mathcal{L}}^{u}W(\theta ,x,\alpha )\}=0.$$

(13)

Remark 3.

In fact, (12) is the direct consequence of the multiplicative dynamic programming principle, whose proof can be find in [12] and the reference therein.

Later in this work, we will show that the value function W is the unique viscosity solution to the associated HJB equation and construct a decent approximation scheme to such equation. As a byproduct, we can also obtain the existence of the $ϵ$-optimal control of finite difference type.

3. The Main Results

3.1. The Optimality Equation and Viscosity Property

One of the main result of this work is to verify that W is the unique viscosity solution of the following optimality equation, also called the HJB equation:

$$-\theta \rho \frac{\partial \varphi (\theta ,x,\alpha )}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta c(x,\alpha ,u)\varphi (\theta ,x,\alpha )+{\mathcal{L}}^u\varphi (\theta ,x,\alpha )\}=0.$$

(14)

Before giving the definition of viscosity solution, we introduce two notations, $C\left({\mathcal{Q}}_0\right)$ the set of all continuous real-valued functions on ${\mathcal{Q}}_0$, and $C^{1,2,0}\left({\mathcal{Q}}_0\right)$ the collection of all real-valued functions on ${\mathcal{Q}}_0$, which are continuously differentiable, twice continuously differentiable and continuous with respect to its corresponding components.

Definition 2.

(i) 

If $w(\theta ,x,\alpha )\in C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$ such that

$$-\theta \rho \frac{\partial \psi ({\theta }_0,x_0,{\alpha }_0)}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta c({\theta }_0,x_0,{\alpha }_0)\psi ({\theta }_0,x_0,{\alpha }_0)+{\mathcal{L}}^u\psi ({\theta }_0,x_0,{\alpha }_0)\}\ge 0,$$

at every $({\theta }_0,x_0,{\alpha }_0)\in {\mathcal{Q}}_0$ which is a maximum of $w-\psi$, with $w({\theta }_0,x_0,{\alpha }_0)=\psi ({\theta }_0,x_0,{\alpha }_0)$, whenever $\psi (\theta ,x,\alpha )\in C^{1,2,0}\left({\mathcal{Q}}_0\right)$ and ${lim}_{t\to \infty }\psi (\theta e^{-\rho t},x,\alpha )=1$, then we say that w is a viscosity subsolution of (14) on ${\mathcal{Q}}_0$.

(ii) 

If $w(\theta ,x,\alpha )\in C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$ such that

$$-\theta \rho \frac{\partial \psi ({\theta }_0,x_0,{\alpha }_0)}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta c({\theta }_0,x_0,{\alpha }_0)\psi ({\theta }_0,x_0,{\alpha }_0)+{\mathcal{L}}^u\psi ({\theta }_0,x_0,{\alpha }_0)\}\le 0,$$

at every $({\theta }_0,x_0,{\alpha }_0)\in {\mathcal{Q}}_0$ which is a minimum of $w-\psi$, with $w({\theta }_0,x_0,{\alpha }_0)=\psi ({\theta }_0,x_0,{\alpha }_0)$, whenever $\psi (\theta ,x,\alpha )\in C^{1,2,0}\left({\mathcal{Q}}_0\right)$ and ${lim}_{t\to \infty }\psi (\theta e^{-\rho t},x,\alpha )=1$, then we say that w is a viscosity supsolution of (14) on ${\mathcal{Q}}_0$.

(iii) 

We say that w is a viscosity solution of (14) on ${\mathcal{Q}}_0$ if it is both a viscosity subsolution and a viscosity supsolution of (14).

In order to show that $W(\theta ,x,\alpha )$ is the unique viscosity solution to the corresponding HJB equation, we define the following operator on $C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$,

$${\mathcal{T}}_t\varphi (\theta ,x,\alpha )=\underset{\pi \in {\Pi }_{RM}}{min}{E}_{(x,\alpha )}^{\pi }\left\{exp\left(\theta {\int }_0^t{e}^{-\rho s}c(X\left(s\right),\alpha \left(s\right),\pi \left(s\right))ds\right)\varphi (\theta e^{-\rho t},X\left(t\right),\alpha \left(t\right))\right\},$$

where $E_{(x,\alpha )}^{\pi }\left[f(X\left(t\right),\alpha \left(t\right))\right]=E\left[f(X\left(t\right),\alpha \left(t\right))\right]$ for every bounded function f on ${\mathcal{Q}}_0$, with $E_{(x,\alpha )}^{\pi }$ be the expectation operator with respect to $P_{(x,\alpha )}^{\pi }$, the probability law deduced by $\left(X\right(t),\alpha (t\left)\right)$, the process corresponding to control π and initial state $(x,\alpha )$. E is the expectation operator with respect to the given probability measure P.

To proceed, we first need to verify that the operator has the following properties. Set

$$\mathcal{H}(\theta ,x,\alpha ,\psi ,D_{\theta }\psi ,D_x\psi ,D_x^2\psi )=-\theta \rho \frac{\partial \psi (\theta ,x,\alpha )}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta c(x,\alpha ,u)\psi (\theta ,x,\alpha )+{\mathcal{L}}^u\psi (\theta ,x,\alpha )\}.$$

Lemma 1.

If Assumptions 1 and 2 hold, then we have the following conclusions:

(i) 

${\mathcal{T}}_0\varphi (\theta ,x,\alpha )=\varphi (\theta ,x,\alpha )$, for all $\varphi \in C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$;

(ii) 

${\mathcal{T}}_t\varphi (\theta ,x,\alpha )\le {\mathcal{T}}_t\psi (\theta ,x,\alpha )$, if $\varphi \le \psi$, with $\varphi ,\psi \in C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$;

(iii) 

and for each $\psi (\theta ,x,\alpha )\in C^{1,2,0}\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$, we have

$$\underset{r\downarrow 0}{lim}\frac{1}{r}({\mathcal{T}}_r\psi (\theta ,x,\alpha )-\psi (\theta ,x,\alpha ))=\mathcal{H}(\theta ,x,\alpha ,\psi ,D_{\theta }\psi ,D_x\psi ,D_x^2\psi ).$$

Proof 3.

The conclusions (i) and (ii) are obvious by the definition. Now, the verification of conclusion (iii) remains. For fixed $u\in \mathbb{U}$, let $\pi (·)={\delta }_u(·)$, thus by definition, it is easy to obtain that

$$\begin{array}{cc}& {\displaystyle \frac{1}{r}({\mathcal{T}}_r\psi (\theta ,x,\alpha )-\psi (\theta ,x,\alpha ))}\hfill \\ \hfill \le & {\displaystyle \frac{1}{r}\left\{E_{(x,\alpha )}^u\left[exp\left(\theta {\int }_0^r{e}^{-\rho s}c(X\left(s\right),\alpha \left(s\right),u)ds\right)\psi (\theta e^{-\rho r},X\left(r\right),\alpha \left(r\right))\right]-\psi (\theta ,x,\alpha )\right\}.}\hfill \end{array}$$

Let $f(r,X\left(r\right),\alpha \left(r\right)):=exp\left(\theta {\int }_0^r{e}^{-\rho s}c(X\left(s\right),\alpha \left(s\right),u)ds\right)\psi (\theta e^{-\rho r},X\left(r\right),\alpha \left(r\right))$, by Itô’s formula, we have

$$\begin{array}{cc}& {\displaystyle E\left[f(r,X(r),\alpha (r\left)\right)\right]-f(0,x,\alpha )}\hfill \\ \hfill =& {\displaystyle E\left\{{\int }_0^r\left[\frac{\partial }{\partial s}f(s,X\left(s\right),\alpha \left(s\right))+{\mathcal{L}}^{u}f(s,X\left(s\right),u)\right]ds\right\}}\hfill \\ \hfill =& {\displaystyle E\{{\int }_0^{r}exp\left(\theta {\int }_0^s{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),u)dt\right)[\theta (-\rho )e^{-\rho s}\frac{\partial }{\partial \theta }\psi (\theta e^{-\rho s},X\left(s\right),\alpha \left(s\right))}\hfill \\ & {\displaystyle +\psi (\theta e^{-\rho s},X\left(s\right),\alpha \left(s\right))\theta e^{-\rho s}c(X\left(s\right),\alpha \left(s\right),u)}\hfill \\ & {\displaystyle +{\mathcal{L}}^u\psi (\theta e^{-\rho s},X\left(s\right),\alpha \left(s\right))\left]ds\right\}.}\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}& {\displaystyle \underset{r\downarrow 0}{lim}\frac{1}{r}({\mathcal{T}}_r\psi (\theta ,x,\alpha )-\psi (\theta ,x,\alpha ))}\hfill \\ \hfill \le & {\displaystyle \theta (-\rho )\frac{\partial }{\partial \theta }\psi (\theta ,x,\alpha )+\psi (\theta ,x,\alpha )\theta c(x,\alpha ,u)+{\mathcal{L}}^u\psi (\theta ,x,\alpha ).}\hfill \end{array}$$

Moreover, we have

$$\begin{array}{cc}& {\displaystyle \underset{r\downarrow 0}{lim}\frac{1}{r}({\mathcal{T}}_r\psi (\theta ,x,\alpha )-\psi (\theta ,x,\alpha ))}\hfill \\ \hfill \le & {\displaystyle \theta (-\rho )\frac{\partial }{\partial \theta }\psi (\theta ,x,\alpha )+\underset{u\in \mathbb{U}}{min}\left\{\psi (\theta ,x,\alpha )\theta c(x,\alpha ,u)+{\mathcal{L}}^u\psi (\theta ,x,\alpha )\right\}.}\hfill \end{array}$$

On the other hand, let $\left\{r_n\right\}$ be a sequence of positive numbers, such that $r_n<r_m$ for $n>m$ and ${lim}_{n\to \infty }{r}_n=0$. Obviously, for given $r_n$, we have a control ${\pi }_n(·):={\pi }_{r_n}(·)\in {\Pi }_{RM}$ such that

$$\begin{array}{cc}& {\displaystyle {\mathcal{T}}_{r_n}\psi (\theta ,x,\alpha )+{\left(r_n\right)}^2}\hfill \\ \hfill \ge & {\displaystyle E\left\{exp\left(\theta {\int }_0^{r_n}{e}^{-\rho s}c(X_n\left(s\right),{\alpha }_n\left(s\right),{\pi }_n\left(s\right))ds\right)\psi (\theta e^{-\rho r_n},X_n\left(r_n\right),{\alpha }_n\left(r_n\right))\right\},}\hfill \end{array}$$

with $(X_n(·),{\alpha }_n(·)),n\ge 1$ be the process corresponding to the control ${\pi }_n(·)$ and initial state $(x,\alpha )$.

Let ${\pi }_n\left(0\right)\equiv {\delta }_u$ for all $n\ge 1$, with u arbitrarily taken from $\mathbb{U}$ and assume that $\left\{{\pi }_n(·)\right\}$ convergents to $\pi :={\pi }_{\infty }\in {\Pi }_{RM}$, with ${\pi }_{\infty }\left(0\right)={\delta }_u$. Then we can derive that

$$\begin{array}{cc}& {\displaystyle \frac{1}{r_n}({\mathcal{T}}_{r_n}\psi (\theta ,x,\alpha )-\psi (\theta ,x,\alpha ))}\hfill \\ \hfill \ge & {\displaystyle \frac{1}{r_n}\{E\left\{exp\left(\theta {\int }_0^{r_n}{e}^{-\rho s}c(X_n\left(s\right),{\alpha }_n\left(s\right),{\pi }_n\left(s\right))ds\right)\psi (\theta e^{-\rho r_n},X_n\left(r_n\right),{\alpha }_n\left(r_n\right))\right\}}\hfill \\ & {\displaystyle -\psi (\theta ,x,\alpha )\}-r_n.}\hfill \end{array}$$

By Itô’s formula, we have

$$\begin{array}{cc}& {\displaystyle E\left\{exp\left(\theta {\int }_0^{r_n}{e}^{-\rho s}c(X_n\left(s\right),{\alpha }_n\left(s\right),{\pi }_n\left(s\right))ds\right)\psi (\theta e^{-\rho r_n},X_n\left(r_n\right),{\alpha }_n\left(r_n\right))\right\}-\psi (\theta ,x,\alpha )}\hfill \\ \hfill =& {\displaystyle E\{{\int }_0^{r_n}exp\left(\theta {\int }_0^s{e}^{-\rho t}c(X_n\left(t\right),{\alpha }_n\left(t\right),{\pi }_n\left(t\right))dt\right)[\theta (-\rho )e^{-\rho s}\frac{\partial }{\partial \theta }\psi (\theta e^{-\rho s},X_n\left(s\right),{\alpha }_n\left(s\right))}\hfill \\ & {\displaystyle +\psi (\theta e^{-\rho s},X_n\left(s\right),{\alpha }_n\left(s\right))\theta e^{-\rho s}c(X_n\left(s\right),{\alpha }_n\left(s\right),{\pi }_n\left(s\right))}\hfill \\ & {\displaystyle +{\mathcal{L}}^{{\pi }_n}\psi (\theta e^{-\rho s},X_n\left(s\right),{\alpha }_n\left(s\right))\left]ds\right\}.}\hfill \end{array}$$

Since $\psi \in C^{1,2,0}\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$, and the fact that $r_n>0$ small enough, there exists a ${\xi }_n\in [0,r_n]$ such that

$$\begin{array}{cc}& {\displaystyle \underset{n\to \infty }{lim}\frac{1}{r_n}E\{{\int }_0^{r_n}exp\left(\theta {\int }_0^s{e}^{-\rho t}c(X_n\left(t\right),{\alpha }_n\left(t\right),{\pi }_n\left(t\right))dt\right)}\hfill \\ & {\displaystyle [\theta (-\rho )e^{-\rho s}\frac{\partial }{\partial \theta }\psi (\theta e^{-\rho s},X_n\left(s\right),{\alpha }_n\left(s\right))+\psi (\theta e^{-\rho s},X_n\left(s\right),{\alpha }_n\left(s\right))\theta e^{-\rho s}c(X_n\left(s\right),{\alpha }_n\left(s\right),{\pi }_n\left(s\right))}\hfill \\ & {\displaystyle +{\mathcal{L}}^{{\pi }_n}\psi (\theta e^{-\rho s},X_n\left(s\right),{\alpha }_n\left(s\right))\left]ds\right\}}\hfill \\ \hfill =& {\displaystyle \underset{n\to \infty }{lim}E\{exp\left(\theta {\int }_0^{{\xi }_n}{e}^{-\rho t}c(X_n\left({\xi }_n\right),{\alpha }_n\left({\xi }_n\right),{\pi }_n\left({\xi }_n\right))dt\right)}\hfill \\ & {\displaystyle [\theta (-\rho )e^{-\rho {\xi }_n}\frac{\partial }{\partial \theta }\psi (\theta e^{-\rho {\xi }_n},X_n\left({\xi }_n\right),{\alpha }_n\left({\xi }_n\right))}\hfill \\ & {\displaystyle +\psi (\theta e^{-\rho {\xi }_n},X_n\left({\xi }_n\right),{\alpha }_n\left({\xi }_n\right))\theta e^{-\rho {\xi }_n}c(X_n\left({\xi }_n\right),{\alpha }_n\left({\xi }_n\right),{\pi }_n\left({\xi }_n\right))}\hfill \\ & {\displaystyle +{\mathcal{L}}^{{\pi }_n}\psi (\theta e^{-\rho {\xi }_n},X_n\left({\xi }_n\right),{\alpha }_n\left({\xi }_n\right))\left]\right\}}\hfill \\ \hfill =& {\displaystyle \theta (-\rho )\frac{\partial }{\partial \theta }\psi (\theta ,x,\alpha )+\psi (\theta ,x,\alpha )\theta c(x,\alpha ,u)+{\mathcal{L}}^u\psi (\theta ,x,\alpha ).}\hfill \end{array}$$

So we have

$$\begin{array}{cc}& {\displaystyle \underset{r_n\downarrow 0}{lim}\frac{1}{r_n}({\mathcal{T}}_r\psi (\theta ,x,\alpha )-\psi (\theta ,x,\alpha ))}\hfill \\ \hfill \ge & {\displaystyle \theta (-\rho )\frac{\partial }{\partial \theta }\psi (\theta ,x,\alpha )+\psi (\theta ,x,\alpha )\theta c(x,\alpha ,u)+{\mathcal{L}}^u\psi (\theta ,x,\alpha )}\hfill \\ \hfill \ge & {\displaystyle \theta (-\rho )\frac{\partial }{\partial \theta }\psi (\theta ,x,\alpha )+\underset{u\in \mathbb{U}}{min}\{\psi (\theta ,x,\alpha )\theta c(x,\alpha ,u)+{\mathcal{L}}^u\psi (\theta ,x,\alpha )\}.}\hfill \end{array}$$

Thus, the result follows. □

Now we can give one of the main results of this work.

Theorem 2.

Under Assumptions 1 and 2, the value function $W(\theta ,x,\alpha )$ is the unique positive viscosity solution of the HJB Equation (14).

Proof 4.

Firstly, we should show that the value function W is continuous in $(\theta ,x,\alpha )$. It should be pointed out that the continuity of W with respect to α is in the topological sense. Let

$$I^M(\theta ,x,\alpha ,\pi )=E\left[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}(c(X\left(t\right),\alpha \left(t\right),\pi (·))\wedge M)dt\right)\right],$$

for given $\pi (·)$ with $c(x,\alpha ,u)\wedge M:=min\left\{c\right(x,\alpha ,u),M\}$. By the estimation in Proposition 1, there is no doubt that ${lim}_{M\to \infty }{I}^M(\theta ,x,\alpha ,\pi )=I(\theta ,x,\alpha ,\pi )$. By the Feller property of the process $\left(X\right(t),\alpha (t\left)\right)$, it is obvious that $I^M(\theta ,x,\alpha ,\pi )$ is continuous in $(\theta ,x,\alpha )$ for given π. Then, associated with the following inequality

$$\begin{array}{cc}& {\displaystyle \left|I\right(\theta ,x,\alpha ,\pi )-I(\theta ,y,\alpha ,\pi \left)\right|}\hfill \\ \hfill \le & {\displaystyle |I(\theta ,x,\alpha ,\pi )-I^M(\theta ,x,\alpha ,\pi )|+|I^M(\theta ,x,\alpha ,\pi )-I^M(\theta ,y,\alpha ,\pi )|+|I^M(\theta ,y,\alpha ,\pi )-I(\theta ,y,\alpha ,\pi )|,}\hfill \end{array}$$

we conclude that $I(\theta ,x,\alpha ,\pi )$ is continuous in $(\theta ,x,\alpha )$, for given π. Then, it follows that $W(\theta ,x,\alpha )$ is continuous in $(\theta ,x,\alpha )$.

Now, we can verify that W solves the HJB Equation (14) as a viscosity solution. Let $\psi \in C^{1,2,0}\left({\mathcal{Q}}_0\right)$ and ${lim}_{t\to \infty }\psi (\theta e^{-\rho t},x,\alpha )=1$. Denote by $({\theta }_0,x_0,{\alpha }_0)$ the maximizer of $W-\psi$, with $W({\theta }_0,x_0,{\alpha }_0)=\psi ({\theta }_0,x_0,{\alpha }_0)$. Then, $\psi (\theta ,x,\alpha )\ge W(\theta ,x,\alpha )$, and associated with Lemma 1 and (12), we can derive that

$$\begin{array}{cc}\hfill {\mathcal{T}}_r\psi (\theta ,x,\alpha )\ge & {\displaystyle {\mathcal{T}}_{r}W(\theta ,x,\alpha )=W(\theta ,x,\alpha ).}\hfill \end{array}$$

Furthermore, we can obtain that

$$\mathcal{H}({\theta }_0,x_0,{\alpha }_0,\psi ,D_{\theta }\psi ,D_x\psi ,D_x^2\psi )=\underset{r\downarrow 0}{lim}\frac{1}{r}({\mathcal{T}}_r\psi ({\theta }_0,x_0,{\alpha }_0)-\psi ({\theta }_0,x_0,{\alpha }_0))\ge 0,$$

thus, W is the subsolution of the HJB Equation (14). Similarly, we can also verify that W is also a supsolution of the HJB equation. Then we conclude that W is a viscosity solution of the HJB equation.

As to the uniqueness, it is the direct consequence of the following comparison result. □

3.2. Comparison Result

In order to prove the uniqueness, we need some more preparations as follows. Let ${\mathcal{Q}}_R^{\nu }=[\nu ,1]\times B_R\times \mathcal{M}$, where $B_R$ is the open ball in ${\mathbb{R}}^r$ with radius R and $\nu >0$ is arbitrarily small. Suppose that $w(\theta ,x,\alpha )\in C^{1,2,0}\left(\overline{{\mathcal{Q}}_0}\right)$ is a classical solution of the HJB equation, i.e.,

$$-\theta \rho \frac{\partial w(\theta ,x,\alpha )}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta c(x,\alpha ,u)w(\theta ,x,\alpha )+{\mathcal{L}}^{u}w(\theta ,x,\alpha )\}=0,$$

(15)

Let ${\xi }^R(\theta ,x)\in C^{1,2}([\nu ,1]\times {\overline{B}}_R)$ the space of all real-valued functions defined on $[\nu ,1]\times {\overline{B}}_R$, which are continuously differentiable with respect to θ and twice continuously differentiable with respect to x. Further, we assume that ${\xi }^R>0$, for all $(\theta ,x)\in [\nu ,1]\times {\overline{B}}_R$, with ν arbitrarily small. Moreover, ${lim}_{R\to \infty }{\xi }^R(\theta ,x)=1$ for all $(\theta ,x)\in [\nu ,1]\times B_R$ and ${lim}_{R\to \infty }{\xi }^R(\theta ,x)=0$ for all $(\theta ,x)\in [\nu ,1]\times \partial B_R$. Set

$$\widehat{w}(\theta ,x,\alpha )={\xi }^{R}w(\theta ,x,\alpha ),(\theta ,x,\alpha )\in (0,1]\times {\overline{B}}_R\times \mathcal{M}.$$

Let $(D_{\theta }\varphi ,D_x\varphi )=({\varphi }_{\theta },{\varphi }_{x_1},\cdots ,{\varphi }_{x_r})$ and $D_x^2\varphi =\left({\varphi }_{x_i{x}_j}\right),i,j=1,2,\cdots ,r$, with $\varphi ={\xi }^R,w$ or $\widehat{w}$. Then, we can directly calculate that

$${\widehat{w}}_{\theta }={\xi }_{\theta }^{R}w+{\xi }^R{w}_{\theta },{\widehat{w}}_{x_i}={\xi }^R{w}_{x_i}+{\xi }_{x_i}^{R}w,$$

and

$${\widehat{w}}_{x_i{x}_j}={\xi }^R{w}_{x_i{x}_j}+{\xi }_{x_i}^R{w}_{x_j}+{\xi }_{x_j}^R{w}_{x_i}+{\xi }_{x_i{x}_j}^{R}w.$$

Multiplying the HJB Equation (15) by ${\xi }^R(\theta ,x)$ we have

$$-\theta \rho {\xi }^R(\theta ,x)\frac{\partial w(\theta ,x,\alpha )}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\left\{{\xi }^R(\theta ,x)\left[\theta c(x,\alpha ,u)w(\theta ,x,\alpha )+{\mathcal{L}}^{u}w(\theta ,x,\alpha )\right]\right\}=0.$$

(16)

Note that

$${\xi }^R{w}_{\theta }={\widehat{w}}_{\theta }-w{\xi }_{\theta }^R,{\xi }^R{w}_{x_i}={\widehat{w}}_{x_i}-w{\xi }_{x_i}^R,$$

and

$$\begin{array}{cc}\hfill {\xi }^R{w}_{x_i{x}_j}=& {\displaystyle {\widehat{w}}_{x_i{x}_j}-w{\xi }_{x_i{x}_j}^R-{\xi }_{x_i}^R{w}_{x_j}-{\xi }_{x_j}^R{w}_{x_i}}\hfill \\ \hfill =& {\displaystyle {\widehat{w}}_{x_i{x}_j}-w{\xi }_{x_i{x}_j}^R-\frac{{\xi }_{x_i}^R}{{\xi }^R}{\widehat{w}}_{x_j}-\frac{{\xi }_{x_j}^R}{{\xi }^R}{\widehat{w}}_{x_i}+2w\frac{{\xi }_{x_i}^R{\xi }_{x_j}^R}{{\xi }^R},}\hfill \end{array}$$

we can derive that

$$-\theta \rho \frac{\partial \widehat{w}(\theta ,x,\alpha )}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta \widehat{c}(x,\alpha ,u)\widehat{w}(\theta ,x,\alpha )+{\widehat{\mathcal{L}}}^u\widehat{w}(\theta ,x,\alpha )\}=-\theta \rho {\xi }_{\theta }^{R}w,$$

(17)

with

$$\widehat{c}:=c(x,\alpha ,u)-\frac{1}{{\xi }^R}\left(\sum _{l=1}^r{b}_l(x,\alpha ,u){\xi }_{x_l}^R+\frac{1}{2}\sum _{l,k=1}^r{a}_{lk}(x,\alpha ){\xi }_{x_l{x}_k}^R\right),$$

and

$${\widehat{\mathcal{L}}}^u:=\sum _{l=1}^r{\widehat{b}}_l(x,\alpha ,u)\frac{\partial }{\partial x_l}+\frac{1}{2}\sum _{l,k=1}^r{a}_{l,k}(x,\alpha )\frac{{\partial }^2}{\partial x_l\partial x_k}+\sum _{j=1}^m{q}_{\alpha j}(x,u),$$

where

$${\widehat{b}}_l(x,\alpha ,u):=b_l(x,\alpha ,u)-\frac{1}{{\xi }^R}\sum _{k=1}^r{a}_{lk}(x,\alpha ){\xi }_{x_k}^R.$$

In order to show that the value function W is the unique viscosity solution of the HJB Equation (14) in ${\mathcal{Q}}_0$, we only need to show the following comparison result. To proceed, let $\varphi (x,\alpha ):=W(1,x,\alpha ),(x,\alpha )\in {\mathbb{R}}^r\times \mathcal{M}$.

Theorem 3.

Assume that Assumptions 1 and 2 hold. Let $w,v\in C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$ be the viscosity subsolution and viscosity supsolution of the HJB Equation (14) in ${\mathcal{Q}}_0$, respectively. And suppose that $w>0$ and $v>0$ for all $(\theta ,x,\alpha )\in {\mathcal{Q}}_0$ with $w(1,x,\alpha )=v(1,x,\alpha )=\varphi (x,\alpha )$. Then, we have

$$\underset{{\mathcal{Q}}_0}{sup}(w-v)=\underset{{\mathbb{R}}^r\times \mathcal{M}}{sup}(w(1,x,\alpha )-v(1,x,\alpha )).$$

Proof 5.

Set

$${\zeta }^R\left(x\right)=exp\left\{\frac{1}{R}\right\}-exp\left\{{\left|x\right|}^2-R^2\right\},x\in {\overline{B}}_R.$$

Then it is easy to note that ${\zeta }^R\in C^2\left({\overline{B}}_R\right)$ and ${\zeta }^R>0$, for all $x\in {\overline{B}}_R$ with ν arbitrarily small. We can also verify that ${lim}_{R\to \infty }{\zeta }^R\left(x\right)=1$, for all $x\in B_R$ and ${lim}_{R\to \infty }{\zeta }^R\left(x\right)=0$, for all $x\in \partial B_R$. Denote

$$w^R(\theta ,x,\alpha )={\zeta }^R\left(x\right)exp\left\{-\frac{K_2\theta }{R}\right\}w(\theta ,x,\alpha ),K_2>0.$$

Suppose that ${\psi }^R(\theta ,x,\alpha )\in C^{1,2,0}\left(\overline{{\mathcal{Q}}_R^{\nu }}\right)\bigcap B_{\tilde{\omega }}\left(\overline{{\mathcal{Q}}_R^{\nu }}\right)$ and ${lim}_{t\to \infty }{lim}_{R\to \infty }{\psi }^R(\theta e^{-\rho t},x,\alpha )=1$ for all $(\theta ,x,\alpha )\in {\mathcal{Q}}_R$, and $w^R-{\psi }^R$ has a maximum at $({\theta }_0,x_0,{\alpha }_0)\in {\mathcal{Q}}_R$ with $w^R({\theta }_0,x_0,{\alpha }_0)={\psi }^R({\theta }_0,x_0,{\alpha }_0)$. Let $\psi (\theta ,x,\alpha )={\psi }^R(\theta ,x,\alpha )exp\left\{\frac{K_2\theta }{R}\right\}/{\zeta }^R$. Thus it is easy to verify that $\psi (\theta ,x,\alpha )\in C^{1,2,0}\left(\overline{{\mathcal{Q}}_R^{\nu }}\right)\bigcap B_{\tilde{\omega }}\left(\overline{{\mathcal{Q}}_R^{\nu }}\right)$ and ${lim}_{t\to \infty }\psi (\theta e^{-\rho t},x,\alpha )=1$ for all $(\theta ,x,\alpha )\in {\mathcal{Q}}_R$, and $w-\psi$ has a maximum at $({\theta }_0,x_0,{\alpha }_0)\in {\mathcal{Q}}_R$ with $w({\theta }_0,x_0,{\alpha }_0)=\psi ({\theta }_0,x_0,{\alpha }_0)$. Since $w(\theta ,x,\alpha )$ is a viscosity subsolution of the HJB Equation (14), by definition we have

$$-\theta \rho \frac{\partial \psi ({\theta }_0,x_0,{\alpha }_0)}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta c({\theta }_0,x_0,{\alpha }_0)\psi ({\theta }_0,x_0,{\alpha }_0)+{\mathcal{L}}^u\psi ({\theta }_0,x_0,{\alpha }_0)\}\ge 0,$$

Note that ${\psi }^R(\theta ,x,\alpha )={\zeta }^{R}exp\left\{-\frac{K_2\theta }{R}\right\}\psi (\theta ,x,\alpha )$, and the calculations preceding the theorem, we can verify that

$$\begin{array}{cc}& {\displaystyle -\theta \rho \frac{\partial {\psi }^R({\theta }_0,x_0,{\alpha }_0)}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta \widehat{c}({\theta }_0,x_0,{\alpha }_0){\psi }^R({\theta }_0,x_0,{\alpha }_0)+\widehat{{\mathcal{L}}^u}{\psi }^R({\theta }_0,x_0,{\alpha }_0)\}}\hfill \\ & {\displaystyle \ge \theta \rho exp\left\{-\frac{K_2\theta }{R}\right\}w({\theta }_0,x_0,{\alpha }_0)\frac{K_2}{R}{\zeta }^R\ge 0.}\hfill \end{array}$$

Since the constant $K_2>0$, we conclude that $w^R$ is the viscosity subsolution of the the following modified HJB equation

$$-\theta \rho \frac{\partial \psi (\theta ,x,\alpha )}{\partial \theta }+\underset{u\in \mathbb{U}}{inf}\{\theta \widehat{c}(\theta ,x,\alpha )\psi (\theta ,x,\alpha )+\widehat{{\mathcal{L}}^u}\psi (\theta ,x,\alpha )\}=0,$$

(18)

on ${\mathcal{Q}}_R$. Similarly, we can also verify that

$$v^R={\zeta }^{R}exp\left(\theta \frac{K_3}{R}\right)v(\theta ,x,\alpha ),$$

with given constant $K_3>0$, is the viscosity supsolution of the modified HJB Equation (18) on ${\mathcal{Q}}_R$. Then, by Lemma A1, we obtain that

$$\underset{\overline{{\mathcal{Q}}_R^{\nu }}}{sup}(w^R-v^R)=\underset{{\partial }^{*}{Q}_R^{\nu }}{sup}(w^R-v^R),$$

(19)

with ${\partial }^{*}{\mathcal{Q}}_R^{\nu }:=([\nu ,1]\times \partial B_R)\cup (\left\{1\right\}\times B_R)$. Note that $w^R,v^R$ approach $w,v$ uniformly on bounded subsets of $\overline{{\mathcal{Q}}_0}$ as $R\to \infty$, respectively. Moreover, since ${lim}_{R\to \infty }{\zeta }^R\left(x\right)=0$, for all $x\in \partial B_R$, we have

$$\underset{R\to \infty }{lim}\underset{[\nu ,1]\times \partial B_R}{sup}{w}^R-v^R\le \underset{R\to \infty }{lim}\tilde{M}{(\parallel w\parallel }_{\tilde{\omega }}+{\parallel v\parallel }_{\tilde{\omega }}){\zeta }^R\left(x\right)=0,$$

for a suitable constant $\tilde{M}$. Since $\nu >0$ can be arbitrarily small, the result follows by letting R approaches to infinity in (19). □

4. The Approximation Scheme

In order to solve the HJB equation numerically, we are going to introduce the finite difference approximation scheme. For numerical purpose, we only need to work on the case with the cutoff as follows,

$$I^M(\theta ,x,\alpha ,\pi )=E\left[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}\left(c\left(X\right(t),\alpha (t),\pi (·\left)\right)\wedge M\right)dt\right)\right],$$

for given $\pi (·)$, and we can also define

$$W^M(\theta ,x,\alpha )=\underset{\pi \in {\Pi }_{RM}}{inf}{I}^M(\theta ,x,\alpha ,\pi ).$$

By the estimation in Proposition 1, we can conclude that $W^M\to W$, as $M\to \infty$. This means that it is enough to work with $W^M$ when constructing the approximation scheme. To proceed, we set

$${\Delta }_{\theta }^{-}{W}^M=\frac{W^M(\theta ,x,\alpha )-W^M(\theta -h,x,\alpha )}{h},$$

$${\Delta }_{x_i}^{+}{W}^M=\frac{W^M(\theta ,x+\delta e_i,\alpha )-W^M(\theta ,x,\alpha )}{\delta },$$

$${\Delta }_{x_i}^{-}{W}^M=\frac{W^M(\theta ,x,\alpha )-W^M(\theta ,x-\delta e_i,\alpha )}{\delta },$$

$${\Delta }_{x_i}^2{W}^M=\frac{W^M(\theta ,x+\delta e_i,\alpha )+W^M(\theta ,x-\delta e_i,\alpha )-2W^M(\theta ,x,\alpha )}{{\delta }^2},$$

$$\begin{array}{cc}& {\displaystyle {\Delta }_{x_i{x}_j}^{+}{W}^M}\hfill \\ \hfill =& {\displaystyle \frac{2W^M(\theta ,x,\alpha )+W^M(\theta ,x+\delta e_i+\delta e_j,\alpha )+W^M(\theta ,x-\delta e_i-\delta e_j,\alpha )}{2{\delta }^2}}\hfill \\ & {\displaystyle -\frac{W^M(\theta ,x+\delta e_i,\alpha )+W^M(\theta ,x-\delta e_i,\alpha )+W^M(\theta ,x+\delta e_j,\alpha )+W^M(\theta ,x-\delta e_j,\alpha )}{2{\delta }^2},}\hfill \end{array}$$

$$\begin{array}{cc}& {\displaystyle {\Delta }_{x_i{x}_j}^{-}{W}^M}\hfill \\ \hfill =& {\displaystyle -\frac{2W^M(\theta ,x,\alpha )+W^M(\theta ,x+\delta e_i+\delta e_j,\alpha )+W^M(\theta ,x-\delta e_i-\delta e_j,\alpha )}{2{\delta }^2}}\hfill \\ & {\displaystyle +\frac{W^M(\theta ,x+\delta e_i,\alpha )+W^M(\theta ,x-\delta e_i,\alpha )+W^M(\theta ,x+\delta e_j,\alpha )+W^M(\theta ,x-\delta e_j,\alpha )}{2{\delta }^2},}\hfill \end{array}$$

Replacing the derivatives by their corresponding finite difference quotients, and rearranging the terms we have the following approximation scheme

$$\begin{array}{cc}& {\displaystyle W_{h,\delta }^M(\theta ,x,\alpha )}\hfill \\ \hfill =& {\displaystyle \underset{u\in \mathbb{U}}{inf}\left\{C{(h,\delta ,x,\alpha ,u)}^{-1}\right[\frac{\theta }{h}{W}_{h,\delta }^M(\theta -h,x,\alpha )+\sum _{l=1}^r(C_l^{+}(h,\delta ,x,\alpha ,u)W_{h,\delta }^M(\theta ,x+\delta e_l,\alpha )}\hfill \\ & {\displaystyle +C_l^{-}(h,\delta ,x,\alpha ,u)W_{h,\delta }^M(\theta ,x-\delta e_l,\alpha )+\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}|}{2{\delta }^2}{W}_{h,\delta }^M(\theta ,x+\delta e_l+\delta e_k,\alpha )}\hfill \\ & {\displaystyle +\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}|}{2{\delta }^2}{W}_{h,\delta }^M(\theta ,x-\delta e_l-\delta e_k,\alpha ))+\sum _{j\ne \alpha }{q}_{\alpha j}(x,u)W_{h,\delta }^M(\theta ,x,j)]\},}\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill C(h,\delta ,x,\alpha ,u)& {\displaystyle :=\frac{\theta \rho }{h}-\theta (c(x,\alpha ,u)\wedge M)-q_{\alpha \alpha }}\hfill \\ & {\displaystyle +\sum _{l=1}^r\left(\frac{|b_l(x,\alpha ,u)|}{\delta }+\frac{|a_{ll}(x,\alpha )|}{{\delta }^2}-\frac{{\sum }_{k\ne l}\left|a_{lk}(x,\alpha )\right|}{2{\delta }^2}\right),}\hfill \end{array}$$

and

$$C_l^{+}(h,\delta ,x,\alpha ,u):=\frac{b_l^{+}(x,\alpha ,u)}{\delta }+\frac{a_{ll}(x,\alpha )}{2{\delta }^2}-\frac{{\sum }_{k\ne l}\left|a_{lk}(x,\alpha )\right|}{2{\delta }^2},$$

$$C_l^{-}(h,\delta ,x,\alpha ,u):=\frac{b_l^{-}(x,\alpha ,u)}{\delta }+\frac{a_{ll}(x,\alpha )}{2{\delta }^2}-\frac{{\sum }_{k\ne l}\left|a_{lk}(x,\alpha )\right|}{2{\delta }^2}.$$

To proceed, we should first show that the above approximation scheme makes sense. To show this, for given $h,\delta >0$, we need to verify that $C(h,\delta ,x,\alpha ,u)\ne 0$ for all $(x,\alpha ,u)$. We also need the following assumption.

Assumption 3.

Supposing that

$$a_{ll}(x,\alpha )-\sum _{k\ne l}\left|a_{lk}(x,\alpha )\right|\ge 0.$$

Then under Assumptions 1 and 3, we can derive that $C(h,\delta ,x,\alpha ,u)\ne 0$. In fact, by Assumption 1 (i) and the fact that $q_{\alpha \alpha }<0$, we have $\tilde{M}>-q_{\alpha \alpha }(x,u)>0$ for suitable constant $\tilde{M}$ and all x and u. Additionally, by Assumption 3 we conclude that

$$\sum _{l=1}^r\left(\frac{|b_l(x,\alpha ,u)|}{\delta }+\frac{|a_{ll}(x,\alpha )|}{{\delta }^2}-\frac{{\sum }_{k\ne l}\left|a_{lk}(x,\alpha )\right|}{2{\delta }^2}\right)>0.$$

Moreover, if we choose that $h=\frac{\rho }{M+1}$, then it is easy to have $c(x,\alpha ,u)\wedge M<\frac{\rho }{h}=M+1$, thus $\frac{\theta \rho }{h}-\theta (c(x,\alpha ,u)\wedge M)>0$, for all $x,\alpha ,u$. Based on the statement above we conclude that

$$C(h,\delta ,x,\alpha ,u)>0.$$

Thus, the approximation scheme constructed above is well defined. Furthermore, we also know that the value of h can be chosen such that $h\to 0$, as $M\to \infty$. Moreover, we can also choose the value of δ such that $\delta \to 0$ as $M\to \infty$. Then $h,\delta \to 0$ is equivalent to $M\to \infty$.

Let

$$\begin{array}{cc}& {\displaystyle \mathcal{S}(h,\delta ,\theta ,x,\alpha ,t,v)}\hfill \\ \hfill =& {\displaystyle \underset{u\in \mathbb{U}}{inf}\{-C(h,\delta ,x,\alpha ,u)t+[\frac{\theta }{h}v(\theta -h,x,\alpha )+\sum _{l=1}^r(C_l^{+}(h,\delta ,x,\alpha ,u)v(\theta ,x+\delta e_l,\alpha )}\hfill \\ & {\displaystyle +C_l^{-}(h,\delta ,x,\alpha ,u)v(\theta ,x-\delta e_l,\alpha )+\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}v(\theta ,x+\delta e_l+\delta e_k,\alpha )}\hfill \\ & {\displaystyle +\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}v(\theta ,x-\delta e_l-\delta e_k,\alpha ))+\sum _{j\ne \alpha }{q}_{\alpha j}(x,u)v(\theta ,x,j)]\}.}\hfill \end{array}$$

Then the approximation scheme can be rewritten as

$$\mathcal{S}(h,\delta ,\theta ,x,\alpha ,W_{h,\delta }^M(\theta ,x,\alpha ),W_{h,\delta }^M)=0.$$

Because of Assumption 3, it is easy to derive that the coefficients of v is positive. Thus, we can easily verify that $\mathcal{S}(h,\delta ,\theta ,x,\alpha ,t,v)$ is monotone in v, i.e., for arbitrary $t\in \mathbb{R}$, $h,\delta \in (0,1)$, $(\theta ,x,\alpha )\in {\mathcal{Q}}_0$,

$$\mathcal{S}(h,\delta ,\theta ,x,\alpha ,t,v)\le \mathcal{S}(h,\delta ,\theta ,x,\alpha ,t,w),$$

with $v\le w$ and $v,w\in C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$. In addition, we can also verify that $\mathcal{S}(h,\delta ,\theta ,x,\alpha ,t,v)$ is consistent which means that

$$\begin{array}{cc}& {\displaystyle \underset{ϵ\to 0,h\downarrow 0,\delta \downarrow 0,\zeta \to \theta ,\xi \to x}{lim}\mathcal{S}(h,\delta ,\theta ,x,\alpha ,v(\zeta ,\xi ,\alpha )+ϵ,v+ϵ)}\hfill \\ \hfill =& {\displaystyle \mathcal{H}(\theta ,x,\alpha ,v(\theta ,x,\alpha ),D_{\theta }v(\theta ,x,\alpha ),D_{x}v(\theta ,x,\alpha ),D_x^{2}v(\theta ,x,\alpha ))}\hfill \end{array}$$

Now we are going to verify the stability. Let ${\mathcal{O}}_{h,\delta }:{\left(C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)\right)}^m\to {\left(C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)\right)}^m$, such that

$${\mathcal{O}}_{h,\delta }(v(\theta ,x,1),\cdots ,v(\theta ,x,m))=({\mathcal{G}}_{h,\delta }^{1}v(\theta ,x,1),\cdots ,{\mathcal{G}}_{h,\delta }^{m}v(\theta ,x,m)),$$

with

$$\begin{array}{cc}& {\displaystyle {\mathcal{G}}_{h,\delta }^{\alpha }v(\theta ,x,\alpha )}\hfill \\ \hfill =& {\displaystyle \underset{u\in \mathbb{U}}{inf}\left\{C{(h,\delta ,x,\alpha ,u)}^{-1}\right[\frac{\theta }{h}v(\theta -h,x,\alpha )+\sum _{l=1}^r(C_l^{+}(h,\delta ,x,\alpha ,u)v(\theta ,x+\delta e_l,\alpha )}\hfill \\ & {\displaystyle +C_l^{-}(h,\delta ,x,\alpha ,u)v(\theta ,x-\delta e_l,\alpha )+\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}v(\theta ,x+\delta e_l+\delta e_k,\alpha )}\hfill \\ & {\displaystyle +\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}v(\theta ,x-\delta e_l-\delta e_k,\alpha ))+\sum _{j\ne \alpha }{q}_{\alpha j}(x,u)v(\theta ,x,j)]\}.}\hfill \end{array}$$

If we claim that ${\mathcal{O}}_{h,\delta }$ is a strict contraction mapping, the stability can be verified. Thus we need to show that there exists a constant $\kappa \in (0,1)$ such that

$$\parallel {\mathcal{O}}_{h,\delta }v-{\mathcal{O}}_{h,\delta }w\parallel \le \kappa \parallel v-w\parallel ,$$

for all $v,w\in C\left({\mathcal{Q}}_0\right)\bigcap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$. Note that

$$|{\mathcal{O}}_{h,\delta }v-{\mathcal{O}}_{h,\delta }{w|}^2\le |{\mathcal{G}}_{h,\delta }^{1}v(\theta ,x,1)-{\mathcal{G}}_{h,\delta }^1{w(\theta ,x,1)|}^2+\cdots +{|{\mathcal{G}}_{h,\delta }^{m}v(\theta ,x,m)-{\mathcal{G}}_{h,\delta }^{m}w(\theta ,x,m)|}^2,$$

and

$$\begin{array}{cc}& {\displaystyle {\mathcal{G}}_{h,\delta }^{\alpha }v(\theta ,x,\alpha )-{\mathcal{G}}_{h,\delta }^{\alpha }w(\theta ,x,\alpha )}\hfill \\ \hfill =& {\displaystyle \underset{u\in \mathbb{U}}{inf}\left\{C{(h,\delta ,x,\alpha ,u)}^{-1}\right[\frac{\theta }{h}v(\theta -h,x,\alpha )+\sum _{l=1}^r(C_l^{+}(h,\delta ,x,\alpha ,u)v(\theta ,x+\delta e_l,\alpha )}\hfill \\ & {\displaystyle +C_l^{-}(h,\delta ,x,\alpha ,u)v(\theta ,x-\delta e_l,\alpha )+\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}v(\theta ,x+\delta e_l+\delta e_k,\alpha )}\hfill \\ & {\displaystyle +\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}v(\theta ,x-\delta e_l-\delta e_k,\alpha ))+\sum _{j\ne \alpha }{q}_{\alpha j}(x,u)v(\theta ,x,j)]\}}\hfill \\ & {\displaystyle -\underset{u\in \mathbb{U}}{inf}\left\{C{(h,\delta ,x,\alpha ,u)}^{-1}\right[\frac{\theta }{h}w(\theta -h,x,\alpha )+\sum _{l=1}^r(C_l^{+}(h,\delta ,x,\alpha ,u)w(\theta ,x+\delta e_l,\alpha )}\hfill \\ & {\displaystyle +C_l^{-}(h,\delta ,x,\alpha ,u)w(\theta ,x-\delta e_l,\alpha )+\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}w(\theta ,x+\delta e_l+\delta e_k,\alpha )}\hfill \\ & {\displaystyle +\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}w(\theta ,x-\delta e_l-\delta e_k,\alpha ))+\sum _{j\ne \alpha }{q}_{\alpha j}(x,u)w(\theta ,x,j)]\},}\hfill \end{array}$$

thus

$$\left|{\mathcal{G}}_{h,\delta }^{\alpha }v(\theta ,x,\alpha )-{\mathcal{G}}_{h,\delta }^{\alpha }w(\theta ,x,\alpha )\right|\le \underset{u\in \mathbb{U}}{max}\left\{F_{h,\delta }(x,\alpha ,u)\right\}{\parallel v-w\parallel }_{\tilde{\omega }}\tilde{\omega }(x,\alpha ),$$

with

$$F_{h,\delta }(x,\alpha ,u)=\frac{\frac{\theta }{h}+{\sum }_{l=1}^r\left(C_l^{+}(h,\delta ,x,\alpha ,u)+C_l^{-}(h,\delta ,x,\alpha ,u)+{\sum }_{k\ne l}^r\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}\right)}{C(h,\delta ,x,\alpha ,u)}.$$

Since we can choose that $h=\frac{\rho }{M+1}$, thus it is easy to know that

$$\frac{\theta }{h}<\frac{\theta \rho }{h}-\theta (c(x,\alpha ,u)\wedge M),$$

for all $(x,\alpha ,u)$. Furthermore, we can derive that

$$\underset{u\in \mathbb{U}}{max}\left\{F_{h,\delta }(x,\alpha ,u)\right\}<1.$$

Thus, let $\kappa ={max}_{u\in \mathbb{U}}\left\{F_{h,\delta }\left(u\right)\right\}$ we have

$$\parallel {\mathcal{O}}_{h,\delta }v-{\mathcal{O}}_{h,\delta }{w\parallel }_{\tilde{\omega }}\le \kappa {\parallel v-w\parallel }_{\tilde{\omega }},$$

for all $v,w\in C\left({\mathcal{Q}}_0\right)\cap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$. This means that ${\mathcal{O}}_{h,\delta }$ is a strict contraction mapping. Then, there is a unique fixed point to ${\mathcal{O}}_{h,\delta }$, by the Banach fixed point theorem. We denote it by $v_{h,\delta }$. Moreover, we define

$$v^{*}(\theta ,x,\alpha )=\underset{(\zeta ,\xi )\to (\theta ,x)}{lim}\underset{h,\delta \downarrow 0}{sup}{v}_{h,\delta }(\zeta ,\xi ,\alpha ),$$

and

$$v_{*}(\theta ,x,\alpha )=\underset{(\zeta ,\xi )\to (\theta ,x)}{lim}\underset{h,\delta \downarrow 0}{inf}{v}_{h,\delta }(\zeta ,\xi ,\alpha ).$$

Note that $h,\delta \to 0$ is equivalent to $M\to \infty$. If we can verify that $v^{*}$ and $v_{*}$ are sub- and supersolutions of the HJB Equation (14), respectively, then the result that follows is associated with the comparison result. In fact, as in [27], we can show that

$$\mathcal{H}({\theta }_0,x_0,{\alpha }_0,\phi ({\theta }_0,x_0,{\alpha }_0),D_{\theta }\phi ({\theta }_0,x_0,{\alpha }_0),D_x\phi ({\theta }_0,x_0,{\alpha }_0),D_x^2\phi ({\theta }_0,x_0,{\alpha }_0))\ge 0,$$

for any test function $\phi \in C^{1,2,0}\left({\mathcal{Q}}_0\right)\cap B_{\tilde{\omega }}\left({\mathcal{Q}}_0\right)$ such that $({\theta }_0,x_0,{\alpha }_0)$ is a strictly local maximum of $v^{*}-\phi$ with $v^{*}({\theta }_0,x_0,{\alpha }_0)=\phi ({\theta }_0,x_0,{\alpha }_0)$. Since the proofs are alike, we omit the details. Based on the statement above, we can obtain the following conclusion.

Theorem 4.

The solution $v_{h,\delta }$ of the approximation scheme $\mathcal{S}$ converges to the unique viscosity solution of the HJB Equation (14).

4.1. Existence of $ϵ$-Optimal Controls of Finite-Difference-Type

In this section, we will first introduce the definition of the so-said ϵ-optimal control and talk about its existence. Let

$$\begin{array}{cc}& {\displaystyle {\overline{H}}_{W_M^{h,\delta }}(\theta ,x,\alpha ,u)}\hfill \\ \hfill :=& {\displaystyle C{(h,\delta ,\theta ,x,\alpha ,u)}^{-1}[\frac{\theta }{h}{W}_M^{h,\delta }(\theta -h,x,\alpha )+\sum _{l=1}^r(C_l^{+}(h,\delta ,\theta ,x,\alpha ,u)W_M^{h,\delta }(\theta ,x+\delta e_l,\alpha )}\hfill \\ & {\displaystyle +C_l^{-}(h,\delta ,\theta ,x,\alpha ,u)W_M^{h,\delta }(\theta ,x-\delta e_l,\alpha )+\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}{W}_M^{h,\delta }(\theta ,x+\delta e_l+\delta e_k,\alpha )}\hfill \\ & {\displaystyle +\frac{1}{2}\sum _{k\ne l}\frac{|a_{lk}(x,\alpha )|}{2{\delta }^2}{W}_M^{h,\delta }(\theta ,x-\delta e_l-\delta e_k,\alpha ))+\sum _{j\ne \alpha }{q}_{\alpha j}(x,u)W_M^{h,\delta }(\theta ,x,j)],}\hfill \end{array}$$

with $W_M^{h,\delta }$ such that $\mathcal{S}(h,\delta ,\theta ,x,\alpha ,W_M^{h,\delta }(\theta ,x,\alpha ),W_M^{h,\delta })=0$.

Definition 3.

We call $u_{h,\delta }^{*}(\theta ,x,\alpha )$ the ϵ-optimal control, if there exists a pair of constants $(h_{ϵ},{\delta }_{ϵ})$ such that $h\le h_{ϵ},\delta \le {\delta }_{ϵ}$ and

$${\overline{H}}_{W_M^{h,\delta }}(\theta ,x,\alpha ,u_{h,\delta }^{*})=\underset{u\in \mathbb{U}}{inf}\left\{{\overline{H}}_{W_M^{h,\delta }}(\theta ,x,\alpha ,u)\right\}.$$

Now, we first illustrate why such controls are called ϵ-optimal controls. Note that $h,\delta \to 0$ is equivalent to $M\to \infty$ and $u_{h,\delta }^{*}(\theta ,x,\alpha )$ is corresponding to $W_M^{h,\delta }(\theta ,x,\alpha )$. By Theorem 4, we know that for arbitrary $ϵ>0$, there exists a constant $M_0>0$ such that for all $M>M_0$,

$$|W_M^{h,\delta }-W|<ϵ.$$

Thus, it is understandable to say that $u_{h,\delta }^{*}(\theta ,x,\alpha )$ is the ϵ-optimal control.

Lemma 2.

Under Assumptions 1–3, there always exist ϵ-optimal controls.

Proof 6.

If Assumptions 1–3 are all satisfied. Then it is easy to find that ${\overline{H}}_{W_M^{h,\delta }}(\theta ,x,\alpha ,u)$ is continuous in u, for given $(h,\delta ,\theta ,x,\alpha )$. Note that we assume that $\mathbb{U}$ is compact. Thus it is obvious that there exist a control $u_{h,\delta }^{*}(\theta ,x,\alpha )$, such that

$${\overline{H}}_{W_M^{h,\delta }}(\theta ,x,\alpha ,u_{h,\delta }^{*})=\underset{u\in \mathbb{U}}{inf}\left\{{\overline{H}}_{W_M^{h,\delta }}(\theta ,x,\alpha ,u)\right\}.$$

Thus the result follows. □

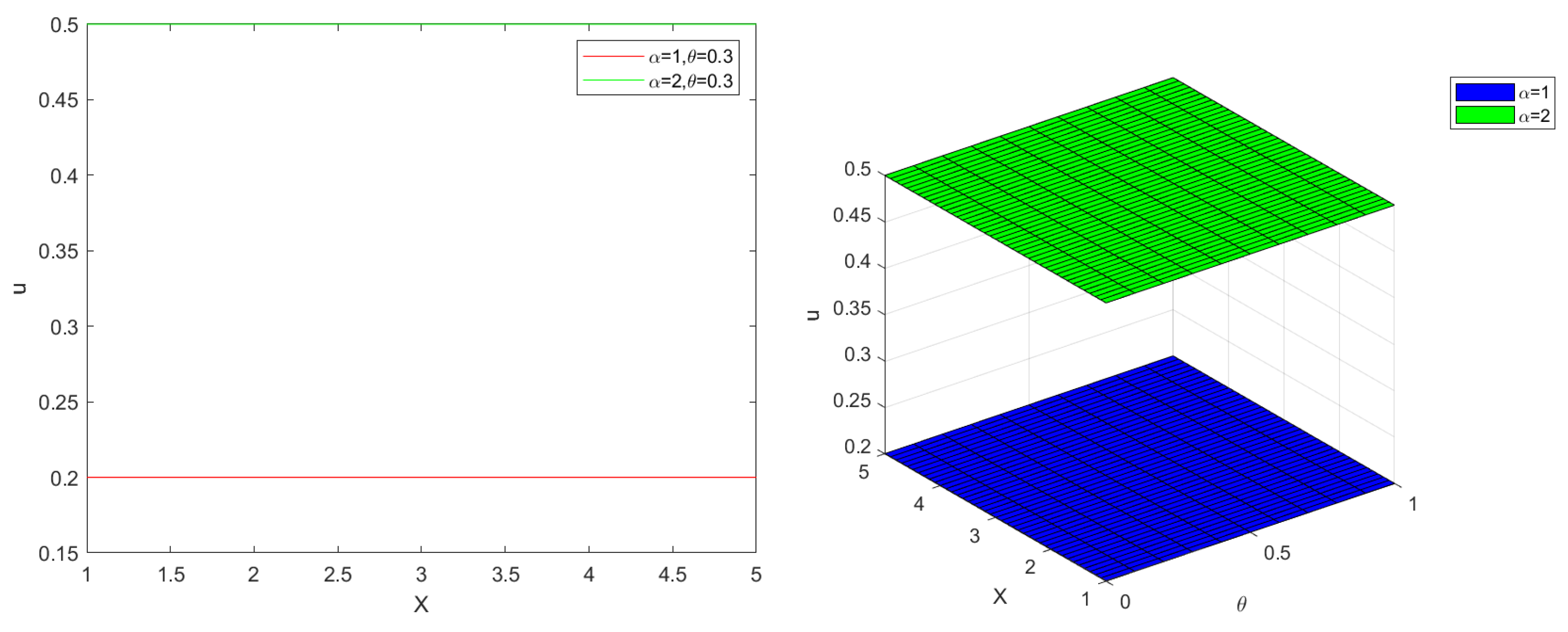
4.2. Numerical Simulation

In order to demonstrate our theoretical results, we will give a numerical simulation example in this section. We consider the one-dimensional stochastic process with regime switching given in Example 1. Let $\left(X\right(t),\alpha (t\left)\right)\in \mathbb{R}\times \mathcal{M}$, with $\mathcal{M}=1,2$, and

$$dX\left(t\right)=\left(\mu \right(\alpha \left(t\right))+u(t\left)\right)X\left(t\right)dt+\sigma \left(\alpha \right(t\left)\right)dB\left(t\right),$$

(20)

$$Q(x,u)=\left(\begin{array}{cc}{q}_{11}(x,u)& -q_{11}(x,u)\\ -q_{22}(x,u)& q_{22}(x,u)\end{array}\right),$$

(21)

with $q_{ii}<0$, $|q_{ii}|<\infty$, $i=1,2$ and $\mathbb{U}=[0,U_0]$, consider the functional

$$I(\theta ,x,\alpha ,\pi (·)))=E[exp\left(\theta {\int }_0^{\infty }{e}^{-\rho t}c(X\left(t\right),\alpha \left(t\right),\pi (·))dt\right)],$$

(22)

with $c(x,\alpha ,u)=x+\alpha +u$, and $\rho >{\mu }_M+U_0$, with ${\sigma }_M=max\{\sigma \left(1\right),\sigma \left(2\right)\}$, ${\mu }_M=max\{\mu \left(1\right),\mu \left(2\right)\}$.

Previously, we have verified that the model in Example 1 satisfies the assumptions proposed in this paper, so based on the approximation scheme in the previous section, for the one-dimensional example mentioned above, we can obtain the following iterative format of the value function with $\alpha ,j=1,2$ and $\alpha \ne j$,

$$\begin{array}{cc}\hfill W_{h,\delta }^M(\theta ,x,\alpha )=& \underset{u\in U}{inf}\left\{C{(h,\delta ,x,\alpha ,u)}^{-1}\right[\frac{\theta }{h}{W}_{h,\delta }^M(\theta -h,x,\alpha )+C_l^{+}(h,\delta ,x,\alpha ,u)W_{h,\delta }^M(\theta ,x+\delta ,\alpha )\hfill \\ & +C_l^{-}(h,\delta ,x,\alpha ,u)W_{h,\delta }^M(\theta ,x-\delta ,\alpha )+q_{\alpha j}{W}_{h,\delta }^M(\theta ,x,j)\left]\right\},\hfill \end{array}$$

(23)

with

$$C(h,\delta ,x,\alpha ,u)=\frac{\theta \rho }{h}-\theta (c(x,\alpha ,u)\wedge M)-q_{\alpha \alpha }+\frac{|b_l(x,\alpha ,u)|}{\delta }+\frac{|a_{ll}(x,\alpha )|}{{\delta }^2},$$

(24)

$$C_l^{+}(h,\delta ,x,\alpha ,u)=\frac{b_l^{+}(x,\alpha ,u)}{\delta }+\frac{a_{ll}(x,\alpha )}{2{\delta }^2},$$

(25)

$$C_l^{-}(h,\delta ,x,\alpha ,u)=\frac{b_l^{-}(x,\alpha ,u)}{\delta }+\frac{a_{ll}(x,\alpha )}{2{\delta }^2},$$

(26)

and

$$b_l(x,\alpha ,u)=(\mu (\alpha \left(t\right)+u\left(t\right))X\left(t\right),a_{ll}(x,\alpha )=\sigma \left(\alpha \left(t\right)\right)$$

(27)

$$b_l^{+}(x,\alpha ,u)=max\{b_l(x,\alpha ,u),0\},b_l^{-}(x,\alpha ,u)=max\{-b_l(x,\alpha ,u),0\}$$

(28)

Furthermore, we choose the appropriate parameters for this example as follows, $\delta =0.1$, h=0.1, $M=5$, $\mu \left(1\right)=-0.2$, $\mu \left(2\right)=0.2$, $\sigma \left(1\right)=-0.1$, $\sigma \left(2\right)=0.1$, $\rho =0.8$, $u\in \mathbb{U}=[0,U_0]=[0,0.5]$, thus the following condition $\rho >{\mu }_M+U_0$ holds. The interval of θ is selected as $[0,1]$, and we set $q_{11}=-u$, $q_{12}=u$, $q_{21}=2u$, $q_{22}=-2u$.

According to the iterative format and parameter settings mentioned above, we conduct the numerical experiments by using the Matlab software (latest version R2023b) to obtain the following results:

In Figure 1, we can observe that the value function decreases with respect to X, and increases with respect to θ, and it can also be observed that the value function at state 2 is significantly larger than the value function at state 1.

Figure 2 shows that the ϵ-optimal control $\mathsf{\mu }$ remains almost constant with the change of X, and the control in state 2 is larger than that in state 1.

5. Discussion

This work considers the controlled switching diffusions with infinite horizon discounted risk-sensitive criterion. The associated HJB equation has been derived. Since the explicit solution to such an equation is not easy to obtain, we figure out a numerical approximation scheme through the finite difference method. However, there is still an open problem. As to the existence of optimal control, in the risk-neutral case [20,27], the occupation measure method is usually used. By introducing the occupation measure method, one can pose the risk-neutral optimal control problem as a convex optimization problem. Moreover, as in [29] (Chapter 2, Section 5), except for the conditions similar to Assumption 1, by supposing that the pair of functions, consisting of the coefficients of the dynamic system and the running cost, maps the control space $\mathbb{U}$ into a convex set, one can show the existence of the optimal control for the controlled diffusion model. Such a technique can also be extended to deal with the risk-neutral optimal control problem within the controlled switching diffusion model. However, it seems that such methods can not be directly used to handle the risk-sensitive case. Thus, we need to find other ways to show the existence of optimal control to the risk-sensitive optimal control problem to the controlled switching model. Open problem: We guess that $u_{h,\delta }^{*}(\theta ,x,\alpha )$ is the approximation of the optimal control when $h,\delta$ approach 0, under suitable conditions.