Stability of Vertical Rotations of an Axisymmetric Ellipsoid on a Vibrating Plane
Abstract
:1. Introduction
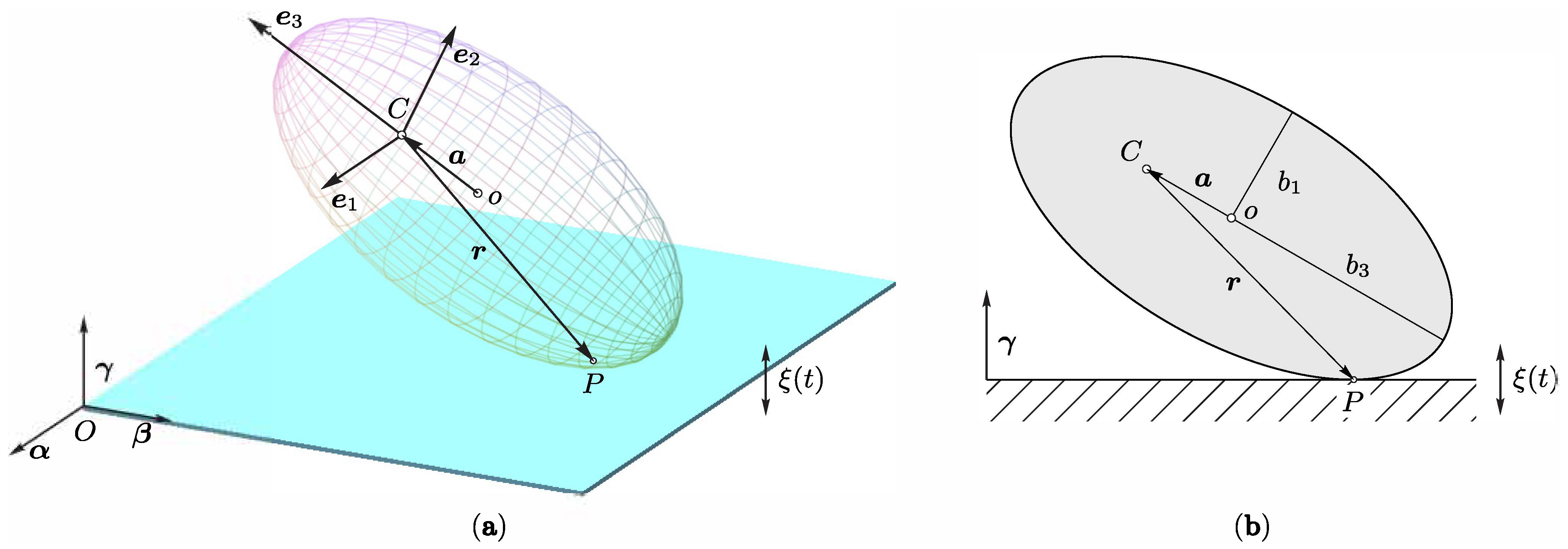
2. Equations of Motion
2.1. Model Assumptions
- The ellipsoid moves with one point in contact with the supporting plane without losing contact with it;
- The velocity of the point of contact P of the ellipsoid with the supporting plane is zero;
- In the general case, the center of mass of the ellipsoid is offset from its geometric center and lies on its symmetry axis;
- The supporting plane performs vertical periodic oscillations according to the law .
2.2. Configuration Space and Kinematic Relations
- –
- A fixed (inertial) coordinate system with unit vectors , where is the vertical unit vector;
- –
- A moving coordinate system with unit vectors attached to the ellipsoid, with origin at its center of mass C and with the axis directed along the symmetry axis.
2.3. Constraint Equations and Dynamical Equations
2.4. Averaged Equations of Motion
3. Integrability of the Averaged System (18)
3.1. Invariants
3.2. Reduction by the Symmetry Field
3.3. Additional Integrals of Motion and Reduction to a System with One Degree of Freedom
4. Vertical Rotations and Analysis of Their Stability
4.1. Vertical Rotations of an Ellipsoid
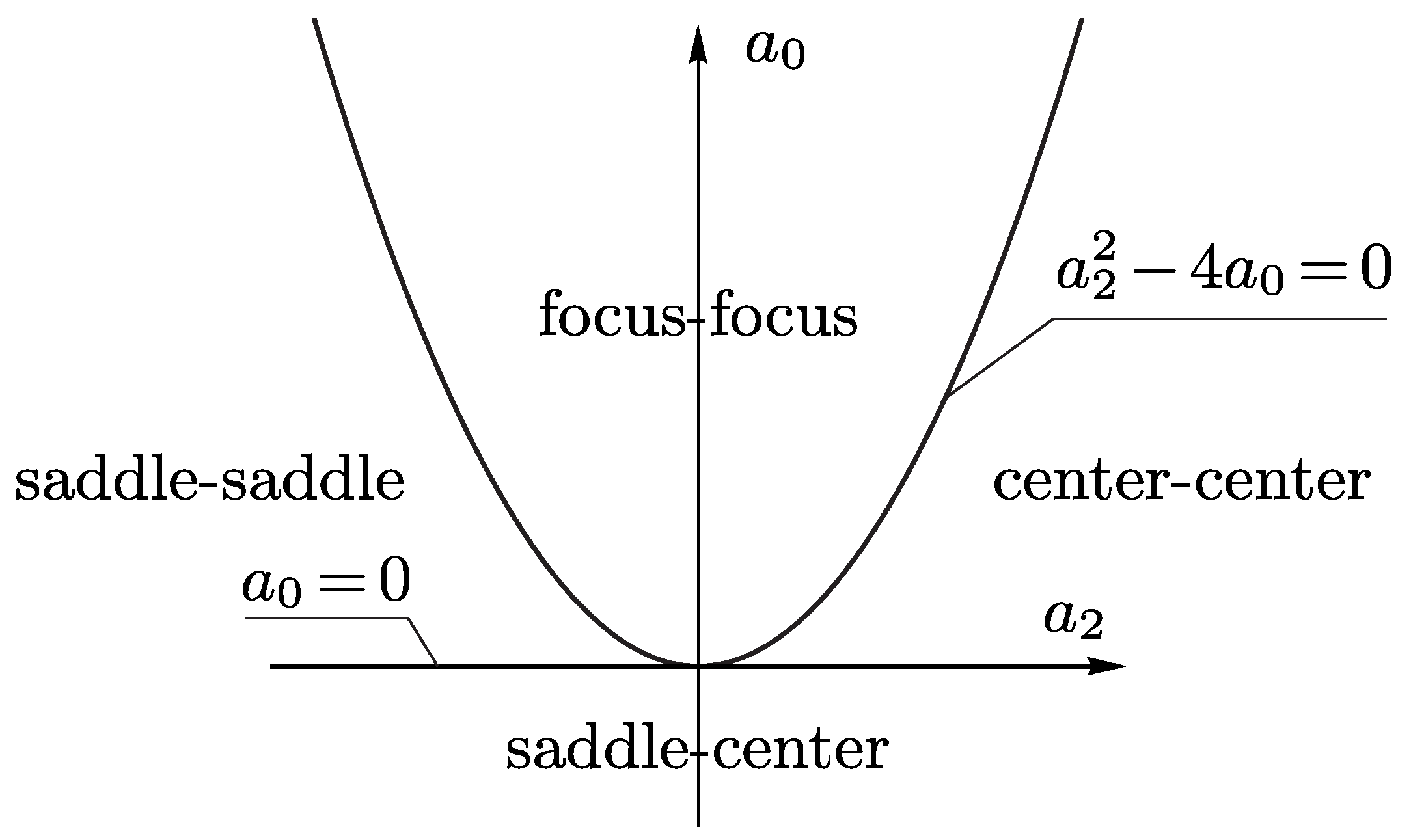
4.2. Linear Stability of Vertical Rotations
- Coefficients of the characteristic equation
4.2.1. Stability of Vertical Rotations in the Absence of a Vibrational Potential
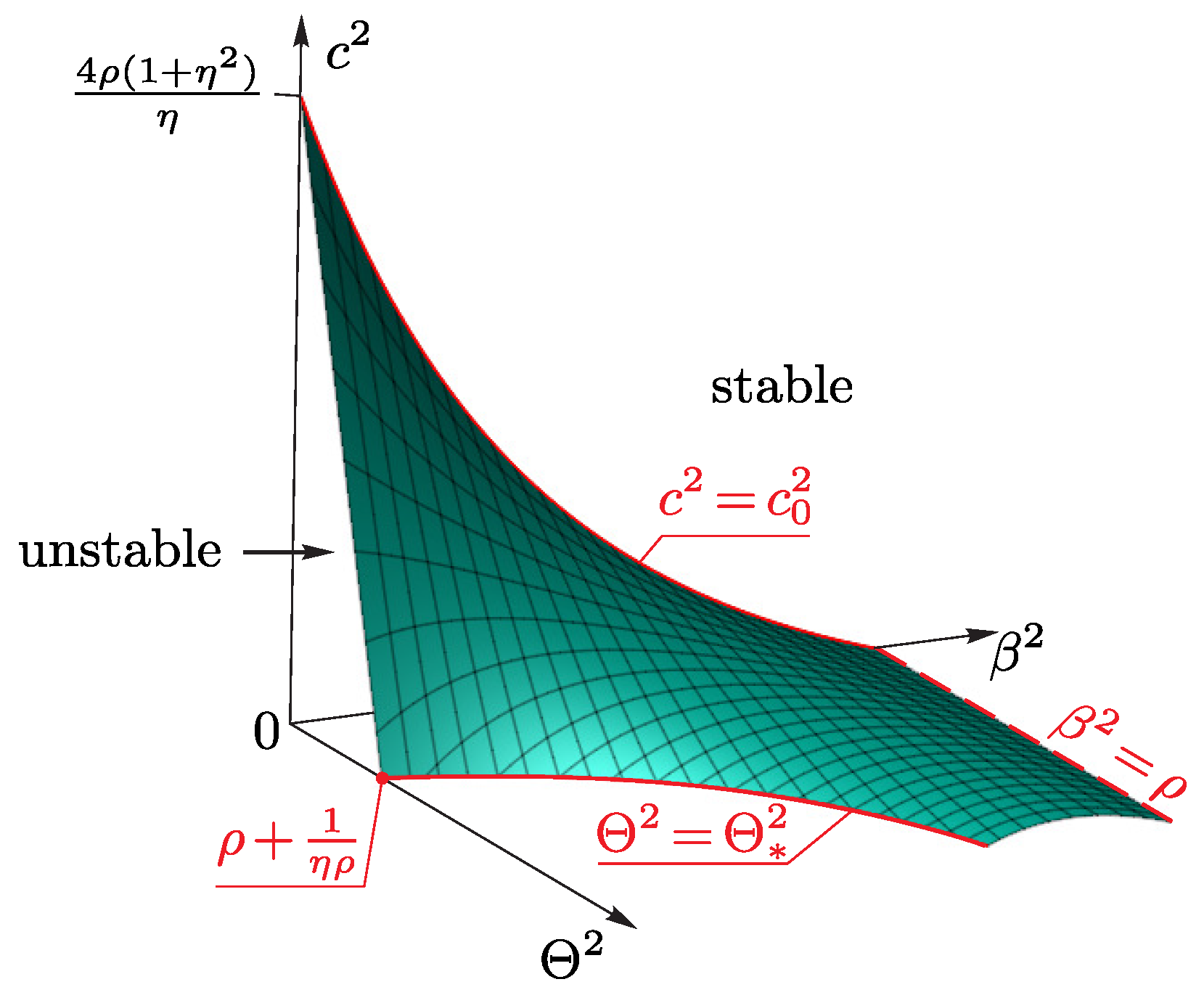
4.2.2. Stability of Vertical Rotations in the Presence of a Vibrational Potential
- When , the vertical rotations are stable for any values of the angular momentum and for any parameters of oscillations of ;
- When , the vertical rotations become stable for smaller values of the angular momentum than those in the absence of vibrations;
- There exists a critical value of such that, when the inequalityis satisfied, the vertical position of the ellipsoid becomes stable even without rotation ().
4.3. Analysis of Reaction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kapitza, P. A pendulum with oscillating suspension. Uspekhi Fiz. Nauk 1951, 44, 7–20. [Google Scholar] [CrossRef]
- Kapitza, P. Dynamic stability of a pendulum when its point of suspension vibrates. Sov. Phys. JETP 1951, 21, 588–597. [Google Scholar]
- Stephenson, A. On a new type of dynamical stability. Mem. Proc. Manch. Lit. Phil. Sci. 1908, 52, 1–10. [Google Scholar]
- Bardin, B.S.; Markeyev, A.P. The stability of the equilibrium of a pendulum for vertical oscillations of the point of suspension. J. Appl. Math. Mech. 1995, 59, 879–886. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Di Massa, G. Sphere rolling on a moving surface: Application of the fundamental equation of constrained motion. Simul. Model. Pract. Theory 2011, 19, 1118–1138. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Kudra, G. Dynamics of a wobblestone lying on vibrating platform modified by magnetic interactions. Procedia IUTAM 2017, 22, 229–236. [Google Scholar] [CrossRef]
- Borisov, A.V.; Ivanov, A.P. Dynamics of the Tippe Top on a Vibrating Base. Regul. Chaotic Dyn. 2020, 25, 707–715. [Google Scholar] [CrossRef]
- Kilin, A.A.; Pivovarova, E.N. Nonintegrability of the problem of a spherical top rolling on a vibrating plane. Vestnik Udmurt. Univ. Mat. Mekhanika Komp Yuternye Nauk. 2020, 30, 628–644. [Google Scholar] [CrossRef]
- Kilin, A.A.; Pivovarova, E.N. Stability and stabilization of steady rotations of a spherical robot on a vibrating base. Regul. Chaotic Dyn. 2020, 25, 729–752. [Google Scholar] [CrossRef]
- Borisov, A.V.; Ivanov, A.P. A Top on a Vibrating Base: New Integrable Problem of Nonholonomic Mechanics. Regul. Chaotic Dyn. 2022, 27, 2–10. [Google Scholar] [CrossRef]
- Kilin, A.A.; Pivovarova, E.N. A Particular Integrable Case in the Nonautonomous Problem of a Chaplygin Sphere Rolling on a Vibrating Plane. Regul. Chaotic Dyn. 2021, 26, 775–786. [Google Scholar] [CrossRef]
- Kilin, A.A.; Pivovarova, E.N. Motion control of the spherical robot rolling on a vibrating plane. Appl. Math. Model. 2022, 109, 492–508. [Google Scholar] [CrossRef]
- Markeyev, A.P. The equations of the approximate theory of the motion of a rigid body with a vibrating suspension point. J. Appl. Math. Mech. 2011, 75, 132–139. [Google Scholar] [CrossRef]
- Ryabov, P.E.; Sokolov, S.V. Bifurcation Diagram of the Model of a Lagrange Top with a Vibrating Suspension Point. Mathematics 2023, 11, 533. [Google Scholar] [CrossRef]
- Karapetian, A. On stability of steady motions of a heavy solid body on an absolutely smooth horizontal plane. J. Appl. Math. Mech. 1981, 45, 368–373. [Google Scholar] [CrossRef]
- Karapetyan, A.; Rumyantsev, V. Stability of Conservative and Dissipative Systems. In Advances in Science and Technology. Series General Mechanics; Vsesoyuz. Inst. Nauch. Tekhn. Inform.: Moscow, Russia, 1983; Volume 6. [Google Scholar]
- Markeev, A.; Moshchuk, N. Qualitative analysis of motion of a heavy solid body on a smooth horizontal plane. J. Appl. Math. Mech. 1983, 47, 22–26. [Google Scholar] [CrossRef]
- Rumiantsev, V. Stability of rotation of a heavy gyrostat on a horizontal plane. Mech. Solids 1980, 15, 1–10. [Google Scholar]
- Karapetyan, A.; Rubanovskii, V. The bifurcation and stability of permanent rotations of a heavy triaxial ellipsoid on a smooth plane. J. Appl. Math. Mech. 1987, 51, 202–208. [Google Scholar] [CrossRef]
- Ivochkin, M.Y. Topological analysis of the motion of an ellipsoid on a smooth plane. Sb. Math. 2008, 199, 871. [Google Scholar] [CrossRef]
- Rauch-Wojciechowski, S.; Przybylska, M. On Dynamics of Jellet’s Egg. Asymptotic Solutions Revisited. Regul. Chaotic Dyn. 2020, 25, 40–58. [Google Scholar] [CrossRef]
- Bou-Rabee, N.M.; Marsden, J.E.; Romero, L.A. A geometric treatment of Jellett’s egg. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. Appl. Math. Mech. 2005, 85, 618–642. [Google Scholar] [CrossRef]
- Mindlin, I. The stability of the motion of a heavy solid of revolution on a horizontal plane. Inzh. Zh 1964, 4, 225–230. [Google Scholar]
- Mindlin, I.; Pozharitskii, G. On the stability of steady motions of a heavy body of revolution on an absolutely rough horizontal plane. J. Appl. Math. Mech. 1965, 29, 879–883. [Google Scholar] [CrossRef]
- Markeev, A. On the motion of a heavy homogeneous ellipsoid on a fixed horizontal plane. J. Appl. Math. Mech. 1982, 46, 438–449. [Google Scholar] [CrossRef]
- Markeev, A. The rolling of an ellipsoid on a horizontal plane. Mekhanika Tverd. Tela 1983, 18, 53–62. [Google Scholar]
- Karapetyan, A. Families of permanent rotations of triaxial ellipsoid on rough horizontal plane and their branchings. In Actual Problems of Classical and Celestial Mechanics; OOO “El’f” Ltd.: Moscow, Russia, 1998; pp. 46–51. [Google Scholar]
- Bizyaev, I.A.; Mamaev, I.S. Permanent Rotations in Nonholonomic Mechanics. Omnirotational Ellipsoid. Regul. Chaotic Dyn. 2022, 27, 587–612. [Google Scholar] [CrossRef]
- Tkhai, V. Instability of permanent rotations of a heavy homogeneous ellipsoid of revolution on an absolutely rough plane. Ross. Akad. Nauk Izv. Mekhanika Tverd. Tela 1992, 2, 25–30. [Google Scholar]
- Glukhikh, Y.; Tkhai, V.; Chevallier, D. On the Stability of Permanent Rotations of a Heavy Homogeneous Ellipsoid on the Rough Plane. In Problems of Studying the Stability and Stabilization of Motion; CC RAS: Moscow, Russia, 2000; pp. 87–104. [Google Scholar]
- Bolsinov, A.V.; Kilin, A.A.; Kazakov, A.O. Topological monodromy as an obstruction to Hamiltonization of nonholonomic systems: Pro or contra? J. Geom. Phys. 2015, 87, 61–75. [Google Scholar] [CrossRef]
- Poincaré, H. Sur le forme nouvelle des equations de la mecanique. C. R. Acad. Sci. Paris 1901, 132, 369–371. [Google Scholar]
- Borisov, A.V.; Mamaev, I.S. Rigid Body Dynamics. In De Gruyter Studies in Mathematical Physics; De Gruyter: Berlin, Germany, 2018; Volume 57. [Google Scholar]
- Neimark, J.I.; Fufaev, N.A. Dynamics of Nonholonomic Systems; American Mathematical Society: Providence, RI, USA, 2004; Volume 33. [Google Scholar]
- Bogolyubov, N.; Mitropolskiy, Y. Asymptotic Methods in the Theory of Nonlinear Oscillations; Nauka: Moscow, Russia, 1974. [Google Scholar]
- Chaplygin, S.A. On a motion of a heavy body of revolution on a horizontal plane. Regul. Chaotic Dyn. 2002, 7, 119–130. [Google Scholar] [CrossRef]
- Borisov, A.; Mamaev, I. The Rolling Motion of a Rigid Body on a Plane and a Sphere. Hierarchy of Dynamics. Regul. Chaotic Dyn. 2002, 7, 177–200. [Google Scholar] [CrossRef]
- Routh, E.J. The Advanced Part of a Treatise on the Dynamics of a System of Rigid Bodies; Macmillan and Co.: London, UK, 1892. [Google Scholar]
- Borisov, A.V.; Mamaev, I.S.; Kilin, A.A. Dynamics of rolling disk. Regul. Chaotic Dyn. 2003, 8, 201–212. [Google Scholar] [CrossRef]
- Markeev, A.P. The Dynamics of a Body Contacting a Rigid Surface; Nauka: Moscow, Russia, 1992; p. 336. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kilin, A.A.; Pivovarova, E.N. Stability of Vertical Rotations of an Axisymmetric Ellipsoid on a Vibrating Plane. Mathematics 2023, 11, 3948. https://doi.org/10.3390/math11183948
Kilin AA, Pivovarova EN. Stability of Vertical Rotations of an Axisymmetric Ellipsoid on a Vibrating Plane. Mathematics. 2023; 11(18):3948. https://doi.org/10.3390/math11183948
Chicago/Turabian StyleKilin, Alexander A., and Elena N. Pivovarova. 2023. "Stability of Vertical Rotations of an Axisymmetric Ellipsoid on a Vibrating Plane" Mathematics 11, no. 18: 3948. https://doi.org/10.3390/math11183948




