The Problems of Dimension Four, and Some Ramifications

Abstract

In this short note, I present a very quick review of the peculiarities of dimension four in geometric topology. I consider, in particular, the role of geometric simple connectivity (which means handle decomposition without handles of index one) for both closed manifolds and open manifolds and for finitely presented groups, together with some of recent developments in geometric group theory.

1. Introduction

Since about 1950, geometric topology has seen spectacular advances. However, deep mysteries still remain, exactly in dimension four—the present main topic in this short paper. In addition, since geometric topology is very closely related to group theory, I discuss that as well here.

As soon as we are in dimensions strictly larger than three, there are three related contexts in which manifolds can be studied: differentiable (DIFF), piecewise linear (PL) and topological (TOP). We cannot go here into the deep interconnections between these three distinct categories, and to a large extent, I restrict the discussion here to the DIFF case; whenever not, this is explicitly stated. Of course, DIFF means $C^{\infty }$.

I think that at the origin of this topic is the famous Poincaré Conjecture [1] from 1904, stating that each closed simply connected 3-manifold is homeomorphic to the 3-sphere ${\mathbb{S}}^3$. In the 1930s, this was extended to the generalized Poincaré Conjecture: each closed n-manifold homotopically equivalent to ${\mathbb{S}}^n$ is actually homeomorphic to ${\mathbb{S}}^n$.

Very soon, mathematicians found out that as soon as one gets to n equals 3, things get very hard, and it was believed that difficulties only increased with dimensions. However, in about 1957, there was a big breakthrough that totally changed the perspective. Steve Smale discovered that in dimensions 5 and more, things become even easier, and so he proved the generalized Poincaré Conjecture in dimensions $n\ge 5$ [2,3].

Soon, John Stallings found a different approach for the same problem [4]; many big breakthroughs followed (see for instance [5,6]), and high-dimensional topology became a rather well understood topic.

For further purposes, I only mention here another related important theorem of Stallings [7]: there is a unique DIFF structure on the Euclidean space ${\mathbb{R}}^n$, for any $n\ge 5$. More generally, John Milnor and Michel Kervaire [8,9] showed that, in those dimensions, the possible DIFF structures are actually controlled by algebraic topology.

Then, around 1983, Mike Freedman proved the 4-dimensional TOP Poincaré Conjecture, and then he also essentially cleaned up the structure of compact, simply connected 4-manifolds in the TOP case [10,11].

Next, using Freedman’s work and also the equations of Yang-Mills from quantum field theory, Simon Donaldson showed, among many other things, that there are even uncountably many DIFF structures on the 4-dimensional Euclidean space ${\mathbb{R}}^4$ [12,13].

Finally, in 2002–2003, Grisha Perelman, using the Ricci flow, a nonlinear partial differential equation in infinite dimensions stemming from differential geometry, proved the 3-dimensional Poincaré Conjecture and, at the same time, Thurston’s Conjecture on the geometrization of all closed 3-manifolds [14,15,16].

This is a very brief account of the glamorous successes of geometric topology, too brief indeed and incomplete, but sufficient to understand how things have been in recent decades. Now, we can move to the open problems.

2. Open Problems and Dimension Four

The first problem (the very obvious one) is the DIFF 4-dimensional Poincaré Conjecture. This is still a deep mystery, and the fact is that dimension four is really very special.

Here below, I present a list of items that make dimension four really very different from all the others.

(A) Already in Smale’s work cited above, the notion of geometric simple connectivity (GSC) arose, which I very briefly explain now (more about it is written in the Appendix at the end of the paper).

The notion of handle-body decomposition is equivalent to a Morse function where higher index singularities occur only for higher values of the function. A handle of index $\lambda$ (a $\lambda$-handle), is a copy of

$$B^{\lambda }\times B^{n-\lambda }$$

that is attached to some union of lower index handles, along $\partial B^{\lambda }\times B^{n-\lambda }$, and a manifold is geometrically simply connected if it admits a handle-body decomposition where all the 1-handles are cancellable by appropriate 2-handles; in the Appendix to the paper, I offer a more precise definition.

In any case, we have an obvious implication

$$GSC\Rightarrow {\pi }_1=0,$$

but what about the converse implication?

Here is the complete answer for compact n-manifolds:

(A1) For $n\ge 5$, the answer is yes, ${\pi }_1=0$ implies GSC. This was actually one of the main steps in Smale’s proof of the high-dimensional Poincaré Conjecture.

(A2) For $n=4$, the answer is no. Very explicitly, the Po-Mazur manifolds, which are non-trivial factors of the 5-ball discovered long ago by the present author and by Barry Mazur [17,18] and which clearly are simply-connected, were shown many years later not to be GSC by Andrew Casson. He never published his argument, but many people knew about it, and personally, I learned it from Mike Freedman.

(A3) Finally, for n equal 3, the answer is again yes. Very explicitly, the corresponding implication is equivalent to the original Poincaré Conjecture, proved by Perelman [14,15,16].

Similar results to (A1) and (A3) are true for open manifolds, provided one adds the condition of simple connectivity at infinity (a space is said to be simply connected at infinity if loops close to infinity can be collapsed to a point still staying close to infinity); see here, for instance, the paper by Po-Tanasi [19].

When one moves then to the non-compact manifolds with a non-empty boundary, then we enter largely uncharted territory, except for the very special spaces endowed with high symmetry coming from geometric group theory. This is a territory which, together with others, I have explored a great deal, and we return to it later.

(B) When we go to the issue of DIFF structures versus TOP structures on a given n-manifold, then dimension four is again very special.

For the dimensions $n=1,2$ or 3, on a given manifold, one can largely ignore the distinction between the two, while for $n\ge 5$, the difference between DIFF and TOP is controlled by algebraic topology.

On the other hand, when we move to dimension four, the situation is completely different. The uncountable infinity of different DIFF structures on ${\mathbb{R}}^4$, already mentioned earlier, lays this in front of us. Clearly, algebraic topology is powerless here; is there maybe some still-to-be-discovered quantum topology that could help us here? I certainly do not know, and I do not know either whether there is some earthly connection between the present item (B) and the previous one (A). However, there is a connection between our (B) and the next item (C).

(C) It is only in dimension four that the Yang-Mills equations (and hence the Maxwell equations) make sense. This is so because only in dimension four is the Hodge dual of a 2-form again a 2-form. Of course, some people might add that four is the dimension of our space-time, but that argument does not very much appeal to me.

(D) Largely connected with the Poincaré Conjecture is the classical Schoenflies problem, of about the same vintage. The issue here is whether an ${\mathbb{S}}^{n-1}$ embedded in ${\mathbb{S}}^n$ divides it into two copies of ${\mathbb{B}}^n$.

Again, of course, there are the contexts DIFF, PL and TOP. In any case, since the 1920s, things were clear for n equal to three or less, and complete mystery lay beyond that. Then, in the late 1950s, a few years before Smale, came the big breakthrough of Barry Mazur [20,21], who was barely 18 at that time. Below is what Barry proved.

If $X^n$ is any of the two manifolds into which ${\mathbb{S}}^{n-1}$ divides ${\mathbb{S}}^n$, then we have a homeomorphism f from $X^n-\{$a boundary point} to ${\mathbb{B}}^n-\{$a boundary point}, extending of course to the boundary point as well, and this f is infinitely differentiable, except maybe at that boundary point.

A few years later, using the heaviest artillery of high-dimensional topology, Smale and Milnor-Kervaire proved that for dimensions n equal to 5 or more, the map f is $C^{\infty }$ even at that boundary point.

Hence, if $n\ge 5$, via Mazur, Smale and Milnor-Kervaire, we have that

$$X^n\underset{DIFF}{=}{\mathbb{B}}^n,$$

holding actually for all dimensions, EXCEPT for n = 4, where it is still a big open mystery!

I have managed to prove that in the 4-dimensional Schoenflies context, the Schoenflies ball $X^4$ is GSC [22]. Now, if we would manage to show that any DIFF compact 4-manifold homotopically equivalent to the 4-ball is GSC, this would be a big step towards the DIFF 4- dimensional Poincaré Conjecture; see [23]. Personally, I have some doubts concerning the truth of the conjecture in question.

For more details on the topology of dimension 4 and its particularities, we refer to the classic books by Akbulut [24], Freedman-Quinn [11], Gompf-Stipsicz [25] and Scorpan [26].

3. Discrete Groups

We end this short review paper with some words concerning geometric group theory—a topic that is very closely connected with the things we have just discussed.

It concerns finitely presented groups (no other ones will be considered here) and the geometric and topological properties of the universal covering spaces of the compact spaces having as fundamental group, the group in question. According to the viewpoint of the quasi-isometries of Misha Gromov [27], the groups and those universal covering spaces are in fact equivalent objects, and so many topological properties make sense for groups as well (see e.g., [28,29]).

Now, when Grisha Perelman proved the Poincaré Conjecture and Thurston’s geometrization, this had very important consequences for group theory as well. For instance, it actually implied that any fundamental group of a compact 3-manifold is simply connected at infinity, whereas, on the other hand, this turns out to be a very rare property among discrete groups [30].

However, in the realm of group theory, descending from the old classical work of Max Dehn, there is the notion of quasi-simple filtration (QSF), which for fundamental groups of 3-manifolds is equivalent to simple connectivity at infinity; in the appendix here below, I define QSF rigorously.

A few years ago, I managed to prove that all groups are QSF; see here the trilogy [31,32,33] and also the review papers by Daniele Otera and myself [34,35]. Now, GSC also makes sense for groups, and it is a stronger property than QSF.

Louis Funar, Daniele Otera and myself are currently working on a project to show that all groups are actually GSC, continuing our previous research in this direction [36,37]. On this topic, see also my forthcoming paper “On the Whitehead nightmare and related topics” which will appear in an issue of the European Mathematical Journal dedicated to the 80th birthday of the recent Abel prize winner Dennis Sullivan.

4. Appendix (Explaining Some Technical Terms)

4.1. On GSC

For a manifold $M^n$ of dimension n, we consider a decomposition starting with an n-ball if $M^n$ is compact, or with a regular neighborhood of an infinite tree if $M^n$ is not; then, in increasing order of indices $\lambda$ come handles

$$H^{\lambda }=B^{\lambda }\times B^{n-\lambda },(\partial H^{\lambda }=\partial B^{\lambda }\times B^{n-\lambda }\cup B^{\lambda }\times \partial B^{n-\lambda }),$$

with $\partial B^{\lambda }\times B^{n-\lambda }$ being the attaching zone to lower index handles and $B^{\lambda }\times \partial B^{n-\lambda }$ being the “lateral surface”. For two handles $H_{\alpha }^2, H_{\beta }^1$, we consider the incidence number $a_{\alpha ,\beta }$, which counts how many times the attaching zone of the 2-handle goes through the lateral surface of the 1-handle; no signs are involved here.

We say that the manifold $M^n$ is GSC if for the family of 1-handles

$$\sum _{i\in I}{H}_i^1$$

we can find a family of 2-handles ${\sum }_{j\in J}{H}_j^2$ with $I\approx J$, such that the corresponding geometric incidence matrix $a_{ji}$ has the property “easy id + nilpotent” (equivalent to id + nilpotent in the finite case), namely

$$a_{ji}={\delta }_{ji}+b_{ji},b_{ji}\in {\mathbb{Z}}_{+},\mathrm{with}{b}_{ji}>0\Rightarrow j>i.$$

For more detailed information about this fundamental notion in geometric topology, low-dimensional topology and geometric group theory, see [19,28,38,39].

4.2. On Yang-Mills Equations

We consider a closed oriented 4-manifold $M^4$ endowed with a complex bundle of structure group G, having a connection A. This comes with a curvature form $F_A$ with values in the 2-forms

$$\mathrm{\Omega }(M^4,\mathcal{L}G).$$

With this, we have Bianchi’s theorem

$$d_A{F}_A=0.$$

If ★ is the Hodge operator between 2-forms, we also have the Yang-Mills equations (written here without the source term), namely

$$d_A★F_A=0.$$

In a more basic form, this means (with $ϵ=$ charge, $\mathcal{I}=$ current (or source)) that

$$\partial F_{\mu \nu }/\partial x_{\nu }+2ϵ[A_{\nu }\times F_{\mu \nu }]+{\mathcal{I}}_{\mu }=0.$$

The unknown here is the connection A, and as soon as G involves two dimensions or more, the equations are non-linear. For $G=U\left(1\right)$, we find Maxwell.

Note also that the Yang-Mills equations are at the core of the Standard Model of elementary particles, but that is another story. For all the details of this interesting field, we refer the reader to and recommend Donaldson’s wonderful book [13].

4.3. On QSF

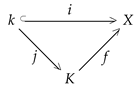
A locally compact complex X is QSF (quasi-simply filtrated) if for every compact subset k of X there is some abstract simply connected finite complex K coming with a commutative diagram where j is an inclusion map, and f is some simplicial map satisfying the Dehn-type property $j\left(k\right)\cap M_2\left(f\right)=\varnothing$ (where $M_2\left(f\right)\subset K$ denotes the set of double points of f).

This notion was introduced by Stephen Brick and Mike Mihalik in [40] (but see also [28,29,41]), and they also proved the following useful concepts:

• If $K_1$ and $K_2$ are two finite complexes with the same fundamental group G, then ${\tilde{K}}_1$ if QSF if and only if ${\tilde{K}}_2$ is QSF. In this case we say that the group G is QSF.
• For fundamental groups of finite 3-complexes, QSF is equivalent to simple connectivity at infinity.

5. Conclusions

In this short survey paper, we have stressed once again that four-dimensional topology is very special indeed and deserves to be further studied in depth. In addition, in dimension 4, as far as geometric topology is concerned, there are still big questions waiting to be explored and solved. Furthermore, all these questions concern several distinct branches of mathematics: we have differential geometry and topology, calculus, Riemannian geometry, geometric topology, global analysis, combinatorial topology, algebraic topology, wild topology, group theory, geometric group theory, mathematical physics, theoretical physics and partial differential equations. It is a rich and vast research area, with connections to the real world and applications in physics.