Distributed Finite-Time and Fixed-Time Nash Equilibrium Seeking for Non-Cooperative Game with Input Saturation

Abstract

In this paper, a modified distributed Nash equilibrium seeking problem with input saturation has been investigated. The payoff function of each player is related to the communication topology, which is closer to the actual scenes. The sigmoid function is utilized to limit the range of the input. Through the network communication between players and the gradient of the players’ payoff functions, the finite-time and fixed-time distributed Nash equilibrium seeking protocols with input saturation are given. Using the Lyapunov stability analysis, it is determined that the action of each player converges to the Nash equilibrium if all the players update their action according to the proposed algorithms. The numerical simulations are also provided to testify the algorithms.

1. Introduction

In past decade, significant attention has been drawn to the study on Nash equilibrium seeking for non-cooperative games due to its wide applications in resource allocation [1,2], sensor network [3,4,5], smart grid [6,7], social science [8] and so on. In noncooperative games, the payoff function of each player is determined by the actions of all players [9]. However, it is difficult to build communication between every two players in many engineering systems. Thus, distributed Nash equilibrium seeking algorithms receive much attention of researchers [10,11,12,13,14,15,16,17,18,19,20,21].

An asynchronous gossip-based strategy for Nash equilibrium seeking was presented in [10]. Ref. [11] exploited distributed Nash equilibrium seeking protocols for both quadratic and nonquadratic payoff functions by utilizing the estimates of all players’ actions for each player. Ref. [12] proposed a distributed averaging integral algorithm, which does not require the algebraic connectivity of the graph. Distributed event-triggered algorithms with weaker step-size condition for searching for Nash equilibrium were considered in [13]. The authors of [14] exploited algorithms with time-varying payoff function subject to a convex constraint. In [15], the authors solved the distributed Nash equilibrium seeking problem with shared coupling constraints through a doubly augmented operator splitting method. Ref. [16] designed algorithms on a time-varying communication network based on partial-decision information. [17] proposed the protocol for high-order systems with convex separable coupling constraints. Distributed Nash equilibrium seeking algorithms under heterogeneous Euler–Lagrange systems were exploited in [18]. Ref. [19] utilized a hybrid system approach to handle the distributed Nash equilibrium seeking problem with persistent attacks. The authors of [20] adopted the event-triggered method to reduce the communication frequency between players for distributed Nash equilibrium seeking protocols under strongly connected graphs. The authors of [21] presented distributed algorithms which utilize optimal responses instead of the payoff functions’ gradients to update the actions of players.

Finite-time and fixed-time control approaches [22,23] have attracted much interest from researchers, as they are expected to provide a stable control system in a finite settling time for many engineering systems. Finite-time or fixed-time control systems for multi-agent systems and distributed optimization have been fully studied [24,25,26,27,28,29]; however, there are few results concerning finite-time or fixed-time distributed Nash equilibrium seeking algorithms [30]. At the same time, input saturation is also a common and practical phenomenon due to the physical limitations. The authors of [31] designed the distributed Nash equilibrium algorithms with bounded controls. Nevertheless, the abovementioned results about bounded controls just utilize the piecewise functions, which makes that the control input does not change when the input saturation occurs.

Input saturation is a common non-linear phenomenon that occurs when the input signal to a system exceeds a certain limit or boundary. In other words, input saturation occurs when the input signal is too large to be processed or measured by the system, and the system’s response becomes limited or constrained as a result. Input saturation is an important phenomenon to consider when designing and analyzing systems, especially those that involve processing and measuring signals. Considering input saturation and its effects can help improve the performance and stability of systems in various applications. However, most of the existing results [20,31] do not take this into consideration or use the piecewise function to achieve bounded control.

Existing results solving distributed Nash equilibrium seeking problems directly apply the conception of generalized Nash equilibrium(GNE) to distributed systems [10,11,12,13,14,15,16,17,18,19,20,21,32,33]. However, the payoff function of each player is determined by the actions of all players. For generalized Nash equilibrium, players in the distributed system can just “perceive” their neighbors. Whether it is proper to directly extend generalized Nash equilibrium to distributed systems is worth considering. For example, in a distributed system, player 2 is not a neighbor of player 1, while player 1 has to make player 2 who “doesn’t exist” in its perspective affect its payoff function and predict the action of player 2.

Motivated by what mentioned above, a modified Nash equilibrium problem for distributed systems is investigated in this paper. We propose both the finite-time and fixed-time protocols solving this modified problem with input saturation. The main contribution of this paper is threefold.

(1) Different from most of the existing results, we assume that actions of the current player and its neighbors determine the payoff function of each player, which means that the payoff function is affected by the communication network.

(2) Distributed finite-time and fixed-time Nash equilibrium seeking algorithms with input saturation are exploited based on the modified problem. The convergence conditions are also given with use of Lyapunov stability analysis and the property of the sigmoid function.

(3) The sigmoid function is utilized to design the algorithm with input saturation. Compared to the method of attaining bounded control in [31], the sigmoid function is smooth and the deadband of the piecewise function is avoided.

The rest of the paper is organized as follows. In Section 2, we formulate the modified distributed Nash equilibrium seeking problem with input saturation. The distributed finite-time algorithm used to search for Nash equilibrium is provided in Section 3. In Section 4, the distributed fixed-time protocol with bounded control is presented. In Section 5, numerical simulations are given to testify the results in this paper. Finally, we provide the conclusion and future work direction in Section 6.

Notations: $B^T$ represents the transpose of the matrix B. ${\mathbf{1}}_n$ and ${\mathbf{0}}_n$ are the column vectors of n ones and n zeros, respectively. $I_n$ denotes the $n\times n$ identity matrix. $sig{(\mathbf{y})}^{\alpha }={[sig{(y_1)}^{\alpha },\dots ,sig{(y_m)}^{\alpha }]}^T$, where $sig{(z)}^{\alpha }={|z|}^{\alpha }sgn(z)$ and $sgn(·)$ denotes the standard sign function. The compact set is denoted by C. The real number is denoted by $\mathbb{R}$. ⊗ represents the Kronecker product.

2. Preliminaries and Problem Formulation

In this section, the distributed Nash equilibrium problem under undirected and connected graphs with input saturation is formulated. Some related conceptions, assumptions and lemmas are also provided.

2.1. Problem Formulation

Consider a game with n players. The set of players is denoted by $\upsilon =\{1,2,...,n\}$, $f_i(g_i(\mathbf{x}))$ represents the payoff function of player i, where $g_i(\mathbf{x})={[l_{i1}\ast x_1,l_{i2}\ast x_2,\dots ,l_{in}\ast x_n]}^T$, $l_{ij}$ denotes the element of the Laplacian matrix L, $\mathbf{x}=[x_1,x_2,\dots ,x_n]$ stands for the vector of the players’ actions, $x_i\in {\mathbb{R}}^m$ is the action of player i and m is the dimension of $x_i$. In the game, each player aims to

$$\underset{x_i}{min}{f}_i(g_i(\mathbf{x})).$$

The distributed algorithm is proposed to make all the players find Nash equilibrium through the action exchange between players under undirected and connected graphs with input saturation when Nash equilibrium of the game exists.

Remark 1.

Existing results about distributed Nash equilibrium algorithms extend generalized Nash equilibrium to distributed systems directly and assume that the payoff function of each agent is determined by all the players and are designed to estimate the decisions of all the player. However, each player can not perceive any other players except itself and its neighbors in the distributed algorithms normally. So it is more reasonable and realistic that the payoff function of each player is determined by itself and its neighbors. In this paper, the payoff function of each player is related to the communication topology, which means that the payoff function of each player is determined by itself and its neighbors.

2.2. Graph Theory

Let $\mathcal{G}=(\upsilon ,\epsilon )$ be a graph, where $\upsilon =\{1,\dots ,N\}$ is the node set and $\epsilon \subseteq \upsilon \times \upsilon$ is the edge set. An edge from i to j is denoted by $(i,j)$, which means that player i can transmit information to player i. The graph is undirected if $\left(i,j\right)\in \epsilon$ for anytime $\left(j,i\right)\in \epsilon$. The graph is unilaterally connected if there exists a sequence of directed path to go from at least one of the nodes to the other for any two nodes. The graph is strongly connected if there exists at least one path between any two nodes. $A=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ is a weighted adjacency matrix related to $\mathcal{G}$, such that $a_{ij}=1$ if $\left(j,i\right)\in \epsilon$; otherwise, $a_{ij}=0$. $D=diag\left\{d_1,\dots ,d_n\right\}\in {\mathbb{R}}^{n\times n}$ denotes the degree matrix of the graph $\mathcal{G}$, where $d_i={\sum }_{j=1}^N{a}_{ij}$. The Laplacian matrix of $\mathcal{G}$ is described as $L=D-A$. $sgn(·)$ represents the signum function. $sig{(x)}^a\Delta qsgn(x){|x|}^a$.

2.3. Nash Equilibrium

An action profile ${\mathbf{x}}^{*}=(x_i^{*},{\mathbf{x}}_{-i}^{*})$ is a Nash equilibrium if, for all $x_i$

$$f_i(x_i^{*},{\mathbf{x}}_{-i}^{*})\le f_i(x_i,{\mathbf{x}}_{-i}^{*}),\forall i\in \upsilon .$$

(1)

, where ${\mathbf{x}}_{-i}={[x_1,x_2,\dots ,x_{i-1},x_{i+1},\dots ,x_N]}^T$.

2.4. Lemmas and Assumptions

Lemma 1.

Ref. [34] $\forall x_1,\dots ,x_n\in \mathbb{R}$, $({\displaystyle \sum _{i=1}^n}|x_i{|)}^q\le {\displaystyle \sum _{i=1}^n}{|x_i|}^q$ if $0<q\le 1$, and $({\displaystyle \sum _{i=1}^n}|x_i{|)}^q\le n^{q-1}{\displaystyle \sum _{i=1}^n}{|x_i|}^q$ if $q>1$.

Lemma 2.

Ref. [31] Considering the following system $\dot{x}=f(x,t)$, where $x\in {\mathbb{R}}^m$, $f({\mathbf{0}}_m,t)={\mathbf{0}}_m$, $f(x,t):U\to {\mathbb{R}}^m$ is continuous on an open neighborhood $U\subseteq {\mathbb{R}}^m$ of the origin.

(i) If there exists a positive-definite function $V(x,t)$, such that

$$\begin{array}{c}\hfill \dot{V}(x,t)\le -c{V}^{\alpha }(x,t)\end{array}$$

where $c>0$ and $0<\alpha <1$. Then, $V(x,t)$ approaches zero in finite time, and the finite time T is estimated by

$$T\le T_{max}:=\frac{V{(x(t_0),t_0)}^{1-\alpha }}{c(1-\alpha )}$$

($ii$) If there exists a positive-definite function $V(x,t)$, such that

$$\begin{array}{c}\hfill \dot{V}(x,t)\le -{(c_1{V}^{\beta }(x,t)+c_2{V}^{\gamma }(x,t))}^{c_3}\end{array}$$

where $c_1,c_2,c_3,\beta ,\gamma >0$, $0<c_3\beta <1$ and $c_3\gamma >1$. Then, $V(x,t)$ approaches zero in fixed time, and the fixed time T is estimated by

$$T\le T_{max}:=\frac{1}{{c_1}^{c_3}(1-c_3\beta )}+\frac{1}{{c_2}^{c_3}(c_3\gamma -1)}$$

Lemma 3.

$\forall x\in \mathbb{R}$, $e^x-1>=x$ and the equal sign holds if and only if $x=0$. $sgn(e^x-1)=sgn(x)$.

Proof. 

Let $f(x)=e^x-1-x$, the plot of $f(x)$ is shown in Figure 1. It follows that $f^{\prime }(x)=e^x-1$, and it is obtained that $f^{\prime }(x)=0$ if and only if $x=0$, which indicates that $f(0)=e^0-1-0=0$ is the minimum value of $f(x)$. Thus, $e^x-1>=x$ and the equal sign holds if and only if $x=0$. Notice that $e^x-1>0$ if and only if $x>0$, $e^x-1=0$ if and only if $x=0$ and $e^x-1<0$ if and only if $x<0$, we have $sgn(e^x-1)=sgn(x)$. The proof is complete. □

Assumption 1.

The graph of the communication topology is undirected and connected.

Assumption 2.

The payoff function of each player $f_i(\mathbf{x})$ is twice-continuously differentiable.

Assumption 3.

The payoff function of each player $f_i(\mathbf{x})$ is ${\omega }_i$-strongly convex (${\omega }_i>0$) for $x_i$, which means that it satisfies ${\left(z-x\right)}^T\left(\nabla f_i\left(z\right)-\nabla f_i\left(x\right)\right)\ge {\omega }_i{∥z-x∥}^2$, for all $x,z\in C$.

Assumption 4.

For each $i\in \upsilon$, $\frac{\partial f_i(\mathbf{x})}{\partial x_i}$ is Lipschitz continuous, which means

$$||\frac{\partial f_i(\mathbf{x})}{\partial x_i}-\frac{\partial f_i(\mathbf{z})}{\partial z_i}||\le {\theta }_i||\mathbf{x}-\mathbf{z}||,$$

(2)

for all $\mathbf{x},\mathbf{z}\in {\mathbb{R}}^N$.

3. Distributed Finite-Time Nash Equilibrium Seeking Protocol with Input Saturation

In this section, a distributed finite-time Nash equilibrium protocol under undirected and connected graphs with input saturation is given.

Players update their actions by the following equations

$$\begin{array}{cc}\hfill & {\dot{x}}_i=-k_{i}sig{(y_i)}^{\alpha },\hfill \\ \hfill & y_i=\frac{2}{1+e^{-z_i}}-1,\hfill \\ \hfill & z_i=\frac{\partial f_i(g_i(\mathbf{x}))}{\partial x_i},\hfill \end{array}$$

(3)

where $k_i>0$ is the possible maximum input for player i, $\alpha <1$ is a positive parameter.

Theorem 1.

Suppose Assumptions 1–4 are satisfied; the players update their action according to (3). Then, the actions of all the players converge globally to the Nash equilibrium ${\mathbf{x}}^{*}$ with input limit $k_i$ in finite time.

Proof. 

With Assumption 3, it follows that the Nash equilibrium point for the game is unique. Notice that $y_i$ monotonically increases with the increase in $z_i$. Thus, the control system (3) is stable if and only if the equation $\frac{\partial f_i(g_i(\mathbf{x}))}{\partial x_i}={\mathbf{0}}_m$ is satisfied for all $i\in \upsilon$, which means $\mathbf{x}={\mathbf{x}}^{*}$.

Finite time: Take the candidate Lyapunov function as $V_i=\frac{1}{2}||x_i-x_i^{*}{||}_2^2$; it follows that

$$\begin{array}{cc}\hfill {\dot{V}}_i& =-k_i{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sig{(y_i^j)}^{\alpha }\hfill \\ \hfill & =-k_i{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sig{(\frac{2}{1+e^{-z_i^j}}-1)}^{\alpha }\hfill \\ \hfill & =-k_i{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sgn(\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}){|\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}|}^{\alpha }.\hfill \end{array}$$

(4)

With Lemma 3, it follows that

$$\begin{array}{c}\hfill sgn(\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}})=sgn(\frac{z_i^j}{1+e^{-z_i^j}})=sgn(z_i^j).\end{array}$$

(5)

From Assumption 3 and 4, we have

$$\begin{array}{cc}\hfill (x_i^j-x_i^{*,j})sgn(z_i^j)& =(x_i^j-x_i^{*,j})\frac{z_i^j}{|z_i^j|}=(x_i^j-x_i^{*,j})\frac{z_i^j-z_i^j}{|z_i^{*,j}|}\ge {\omega }_i\frac{{(x_i^j-x_i^{*,j})}^2}{|z_i^j|}\ge {\omega }_i\frac{{(x_i^j-x_i^{*,j})}^2}{{\theta }_i|x_i^j-x_i^{*,j}|}.\hfill \end{array}$$

(6)

We have $|z_i^j|\le {\theta }_i|x_i^j-x_i^{*,j}|\le {\theta }_i\eta$ with Assumption 4, where $\eta >0$ is the upper bound of $|x_i^j-x_i^{*,j}|$. It follows that

$$\begin{array}{c}\hfill |\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}|\ge \kappa |z_i^j|,\end{array}$$

(7)

where $\kappa =\frac{1-e^{-{\theta }_i\eta }}{{\theta }_i\eta (1+e^{-{\theta }_i\eta })}$. With Lemma 3, it follows that $\kappa >0$. Combining (4)–(7), yield

$$\begin{array}{cc}\hfill {\dot{V}}_i& \le -k_i{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sgn(z_i^j){|\kappa z_i^j|}^{\alpha }\hfill \\ \hfill & \le -k_i{\kappa }^{\alpha }{\displaystyle \sum _{j=1}^m}{\omega }_i\frac{{(x_i^j-x_i^{*,j})}^2}{{\theta }_i|x_i^j-x_i^{*,j}|}{|{\omega }_i(x_i^j-x_i^{*,j})|}^{\alpha }\hfill \\ \hfill & =-\frac{k_i{\kappa }^{\alpha }{\omega }_i^{1+\alpha }}{{\theta }_i}{\displaystyle \sum _{j=1}^m}{|x_i^j-x_i^{*,j}|}^{\alpha +1}.\hfill \end{array}$$

(8)

Since $0<\alpha <1$, according to Lemma 1, it follows that

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j=1}^m}|x_i^j-x_i^{*,j}{|}^{\alpha +1}={\displaystyle \sum _{j=1}^m}(|x_i^j-x_i^{*,j}{|}^2{)}^{\frac{\alpha +1}{2}}\ge ({\displaystyle \sum _{j=1}^m}|x_i^j-x_i^{*,j}{{|}^2)}^{\frac{\alpha +1}{2}}=2V_i^{\frac{\alpha +1}{2}}.\hfill \end{array}$$

(9)

From (8) and (9), we have

$${\dot{V}}_i\le -c{V}_i^{\frac{\alpha +1}{2}},$$

where $c=\frac{2k_i{\kappa }^{\alpha }{\omega }_i^{1+\alpha }}{{\theta }_i}$. From Lemma 2, it is determined that the actions of all the players converge to the Nash equilibrium ${\mathbf{x}}^{*}$ in finite time.

Input limit: Let $f(x)=\frac{2}{1+e^{-x}}-1$, the plot of $f(x)$ is shown in Figure 2. Notice that (1) $x\to -\infty \Rightarrow f(x)\to -1$; (2) $x\to \infty \Rightarrow f(x)\to 1$; (3) $f(x)$ is a monotonically increasing function. It follows $f(x)\in (-1,1)$, which means $y_i^j\in (-1,1),\forall i\in \upsilon$. Consequently, ${\dot{x}}_i^j\in (-k_i,k_i)$ is obtained. The proof is complete. □

Remark 2.

In this paper, the sigmoid function is utilized to limit the range of the input. Compared to the method used in [31] to realize bounded control, the advantages of the sigmoid function are threefold. (1) The sigmoid function is continuous and smooth, which makes the actuator achieve a better control effect. (2) Due to the property of the sigmoid function, the deadband of the bounded control system is avoided. (3) The definition domain and the value domain of the sigmoid function correspond one to one. If the sensor is accurate enough, we can get the input before saturation handling from the input processed by sigmoid function so as to observe the control system better.

4. Distributed Fixed-Time Nash Equilibrium Seeking Protocol sith Input Saturation

In Theorem 1, the finite-time distributed Nash equilibrium seeking protocol under undirected and connected with bounded control is investigated. The fixed-time case is studied in this section.

The actions of players are determined using the following equations

$$\begin{array}{cc}\hfill & {\dot{x}}_i=-\frac{k_i}{2}(sig{(y_i)}^{\alpha }+sig{(y_i)}^{\beta }),\hfill \\ \hfill & y_i=\frac{2}{1+e^{-z_i}}-1,\hfill \\ \hfill & z_i=\frac{\partial f_i(g_i(\mathbf{x}))}{\partial x_i},\hfill \end{array}$$

(10)

where $0<\alpha <1$, $\beta >1$ and $k_i>0$ are the possible maximum inputs for player i.

Theorem 2.

Suppose that Assumptions 1–4 are satisfied, and the players update their action according to (10). Then, the actions of all the players converge globally to the Nash equilibrium ${\mathbf{x}}^{*}$ with input limit $k_i$ in fixed time $T_{max}=\frac{2}{c_1(1-\alpha )}+\frac{2}{c_2(\beta -1)}$.

Proof. 

Similar to the analysis in Theorem 1, the control system (10) is stable if and only if the equation $\frac{\partial f_i(g_i(\mathbf{x}))}{\partial x_i}={\mathbf{0}}_m$ is satisfied for all $i\in \upsilon$, which means $\mathbf{x}={\mathbf{x}}^{*}$.

Fixed time: The candidate Lyapunov function is selected as $V_i=\frac{1}{2}||x_i-x_i^{*}{||}_2^2$, and it follows that

$$\begin{array}{cc}\hfill \dot{V_i}& =-\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sig{(y_i^j)}^{\alpha }-\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sig{(y_i^j)}^{\beta }\hfill \\ \hfill & =-\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sig{(\frac{2}{1+e^{-z_i^j}}-1)}^{\alpha }\hfill \\ \hfill & -\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sig{(\frac{2}{1+e^{-z_i^j}}-1)}^{\beta }\hfill \\ \hfill & =-\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sgn(\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}){|\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}|}^{\alpha }\hfill \\ \hfill & -\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sgn(\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}){|\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}|}^{\beta }.\hfill \end{array}$$

(11)

With Lemma 3 and Assumption 3 and 4, it follows that

$$\begin{array}{c}\hfill sgn(\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}})=sgn(\frac{z_i^j}{1+e^{-z_i^j}})=sgn(z_i^j).\end{array}$$

(12)

$$\begin{array}{cc}\hfill (x_i^j-x_i^{*,j})sgn(z_i^j)& =(x_i^j-x_i^{*,j})\frac{z_i^j}{|z_i^j|}=(x_i^j-x_i^{*,j})\frac{z_i^j-z_i^j}{|z_i^{*,j}|}\ge {\omega }_i\frac{{(x_i^j-x_i^{*,j})}^2}{|z_i^j|}\ge {\omega }_i\frac{{(x_i^j-x_i^{*,j})}^2}{{\theta }_i|x_i^j-x_i^{*,j}|}.\hfill \end{array}$$

(13)

$$\begin{array}{c}\hfill |z_i^j|\le {\theta }_i|x_i^j-x_i^{*,j}|\le {\theta }_i\eta \end{array}$$

where $\eta >0$ is the upper bound of $|x_i^j-x_i^{*,j}|$, it is obtained that

$$\begin{array}{c}\hfill |\frac{1-e^{-z_i^j}}{1+e^{-z_i^j}}|\ge \kappa |z_i^j|,\end{array}$$

(14)

where $\kappa =\frac{1-e^{-{\theta }_i\eta }}{{\theta }_i\eta (1+e^{-{\theta }_i\eta })}$. Combining with (11)–(14), we have

$$\begin{array}{cc}\hfill \dot{V_i}& \le -\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sgn(z_i^j)|\kappa z_i^j{|}^{\alpha }-\frac{k_i}{2}{\displaystyle \sum _{j=1}^m}(x_i^j-x_i^{*,j})sgn(z_i^j){|\kappa z_i^j|}^{\beta }\hfill \\ \hfill & \le -\frac{k_i}{2}{\kappa }^{\alpha }{\displaystyle \sum _{j=1}^m}{\omega }_i\frac{{(x_i^j-x_i^{*,j})}^2}{{\theta }_i|x_i^j-x_i^{*,j}|}{|{\omega }_i(x_i^j-x_i^{*,j})|}^{\alpha }\hfill \\ \hfill & -\frac{k_i}{2}{\kappa }^{\beta }{\displaystyle \sum _{j=1}^m}{\omega }_i\frac{{(x_i^j-x_i^{*,j})}^2}{{\theta }_i|x_i^j-x_i^{*,j}|}{|{\omega }_i(x_i^j-x_i^{*,j})|}^{\beta }\hfill \\ \hfill & =-\frac{k_i{\kappa }^{\alpha }{\omega }_i^{1+\alpha }}{2{\theta }_i}{\displaystyle \sum _{j=1}^m}|x_i^j-x_i^{*,j}{|}^{\alpha +1}-\frac{k_i{\kappa }^{\beta }{\omega }_i^{1+\beta }}{2{\theta }_i}{\displaystyle \sum _{j=1}^m}{|x_i^j-x_i^{*,j}|}^{\beta +1}\hfill \end{array}$$

(15)

With Lemma 1, it follows that

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j=1}^m}|x_i^j-x_i^{*,j}{|}^{\alpha +1}={\displaystyle \sum _{j=1}^m}(|x_i^j-x_i^{*,j}{|}^2{)}^{\frac{\alpha +1}{2}}\ge ({\displaystyle \sum _{j=1}^m}|x_i^j-x_i^{*,j}{{|}^2)}^{\frac{\alpha +1}{2}}=2V_i^{\frac{\alpha +1}{2}},\hfill \\ \hfill & {\displaystyle \sum _{j=1}^m}|x_i^j-x_i^{*,j}{|}^{\beta +1}={\displaystyle \sum _{j=1}^m}(|x_i^j-x_i^{*,j}{|}^2{)}^{\frac{\beta +1}{2}}\ge ({\displaystyle \sum _{j=1}^m}{m}^{\frac{\beta -1}{2}}|x_i^j-x_i^{*,j}{{|}^2)}^{\frac{\beta +1}{2}}=2m^{\frac{\beta -1}{2}}{V}_i^{\frac{\beta +1}{2}}.\hfill \end{array}$$

(16)

From (15) and (16), yield

$$\begin{array}{c}\hfill \dot{V_i}\le -c_1{V}_i^{\frac{\alpha +1}{2}}-c_2{V}_i^{\frac{\beta +1}{2}},\end{array}$$

where $c_1=\frac{2k_i{\kappa }^{\alpha }{\omega }_i^{1+\alpha }}{{\theta }_i}$, $c_2=\frac{2k_i{m}^{\frac{\beta -1}{2}}{\kappa }^{\beta }{\omega }_i^{1+\beta }}{{\theta }_i}$. Using Lemma 2, it follows that the action of each player converges to the Nash equilibrium in fixed time with the setting time $T_{max}=\frac{1}{c_1(1-\frac{\alpha +1}{2})}+\frac{1}{c_2(\frac{\beta +1}{2}-1)}=\frac{2}{c_1(1-\alpha )}+\frac{2}{c_2(\beta -1)}$.

Input limit: Based on Theorem 1, we have $y_i^j\in (-1,1),\forall i\in \upsilon$. Notice that $f(x)={sgn(a)|a|}^x\in (-1,1)$ if $a\in (-1,1)$ and $x>0$. Thus, it follows that ${\dot{x}}_i^j\in (-k_i,k_i)$; the proof is complete. □

Remark 3.

In this paper, the payoff function of each player is relative to the communication topology. An example is provided to illustrate how the communication topology affects the payoff function and Nash equilibrium. The communication topology of three players is shown in Figure 3. Player 1 is the neighbor of player 2, player 2 is the neighbor of player 3, and player 3 is the neighbor of player 1. The corresponding Laplacian matrix of the communication topology is

$$L=\left[\begin{array}{ccc}1& 0& -1\\ -1& 1& 0\\ 0& -1& 1\end{array}\right]$$

It follows that

$$\begin{array}{c}\hfill g_1(\mathbf{x})={[l_{11}\ast x_1,l_{12}\ast x_2,l_{13}\ast x_3]}^T={[x_1,0,-x_3]}^T,\\ \hfill g_2(\mathbf{x})={[l_{21}\ast x_1,l_{22}\ast x_2,l_{23}\ast x_3]}^T={[-x_1,x_2,0]}^T,\\ \hfill g_3(\mathbf{x})={[l_{31}\ast x_1,l_{32}\ast x_2,l_{33}\ast x_3]}^T={[0,-x_2,x_3]}^T.\end{array}$$

The payoff functions of the players are designed as

$$\begin{array}{cc}\hfill f_1(g_1(\mathbf{x}))& =f_1({[x_1,0,-x_3]}^T)={(x_1-3x_3)}^2,\hfill \\ \hfill f_2(g_2(\mathbf{x}))& =f_2({[-x_1,x_2,0]}^T)={(x_2-x_1)}^2,\hfill \\ \hfill f_3(g_3(\mathbf{x}))& =f_3({[0,-x_2,x_3]}^T)={(x_3-2x_2)}^2.\hfill \end{array}$$

The payoff function of each player is just determined by the actions of itself and its neighbors, which is more consistent with the actual situation. Player i searches for the action that can minimize their payoff function along the decreasing direction of the partial derivative, $i=1,2,3$. At the same time, the actions of their neighbors also affect the action of player i. Finally, the actions of all players reach a balance; that is, the distributed Nash equilibrium mentioned in this paper is achieved.

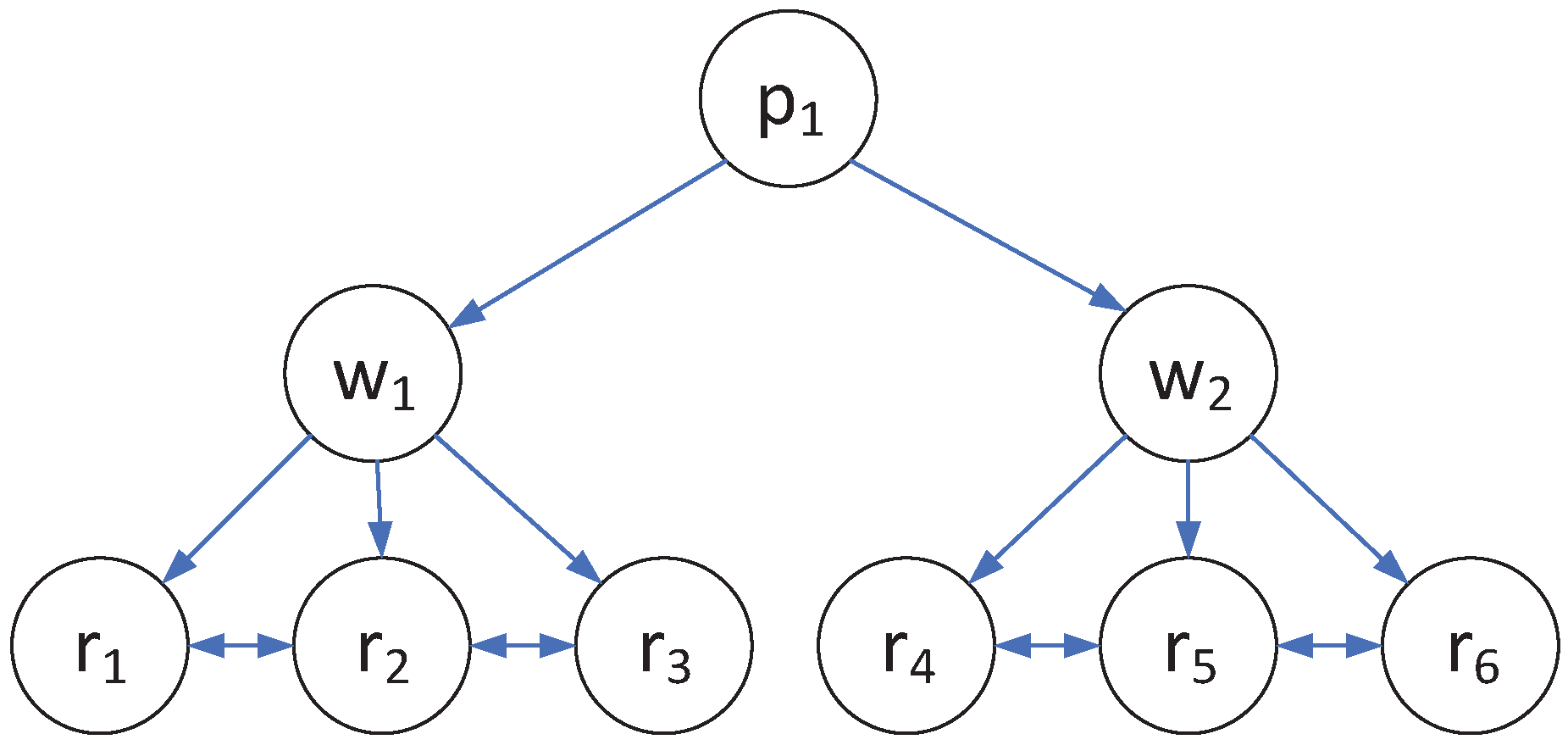
Remark 4.

Although this paper studies the modified distributed Nash equilibrium seeking under undirected and connected graphs, the results in this paper can also extend to the case under unilateral connected graphs. Different from the distributed Nash equilibrium seeking problem studied in [11,12,13,14,15], the payoff function of each player in this paper is determined by the actions of the player and their neighbors, and the condition of undirected and connected needed to estimate the actions of all the player can be weakened for unilateral connected graphs. An example is given as follows to illustrate the application of unilateral connected graphs in non-cooperative games and the modified distributed Nash equilibrium problem in realistic situations.

 Example 1:

The diagram of commodity sales network is shown in Figure 4. $p_i$, $w_i$ and $r_i$ represent producers, wholesalers and retailers, respectively. We use the distributed Nash seeking equilibrium problem under unilateral connected graphs to build the model of the commodity price changing. The producer $p_1$ sells the good to the wholesalers at the price $l_1$, the wholesalers $w_i$ sells the good to the retailers $r_j(j=1,\dots ,6)$ at the price $m_i$, $i=1,2$. Notice that the price of the good for the retailers selling to the customers is affected by its neighbors’ prices and upstream prices due to the market regulation. The modified distributed Nash equilibrium problem in this paper can explain some practical problems to a certain extent.

5. Simulation

In this section, numerical examples are given to validate the finite-time and fixed-time distributed Nash equilibrium seeking protocols with input saturation under undirected and connected graphs.

The communication topology between players is shown in Figure 5. The Laplacian matrix of the communication topology is

$$L=\left[\begin{array}{cccccc}2& -1& 0& 0& 0& -1\\ -1& 2& -1& 0& 0& 0\\ 0& -1& 2& -1& 0& 0\\ 0& 0& -1& 2& -1& 0\\ 0& 0& 0& -1& 2& -1\\ -1& 0& 0& 0& -1& 2\end{array}\right]$$

It follows

$$\begin{array}{cc}\hfill & g_1(\mathbf{x})={[2x_1,-x_2,0,0,0,-x_6]}^T,\hfill \\ \hfill & g_2(\mathbf{x})={[-x_1,2x_2,-x_3,0,0,0]}^T,\hfill \\ \hfill & g_3(\mathbf{x})={[0,-x_2,2x_3,-x_4,0,0]}^T,\hfill \\ \hfill & g_4(\mathbf{x})={[0,0,-x_3,2x_4,-x_5,0]}^T,\hfill \\ \hfill & g_5(\mathbf{x})={[0,0,0,-x_4,2x_5,-x_6]}^T,\hfill \\ \hfill & g_6(\mathbf{x})={[-x_1,0,0,0,-x_5,2x_6]}^T.\hfill \end{array}$$

With the communication topology and $g_i(\mathbf{x})$, the payoff functions of the players are designed as

$$\begin{array}{cc}\hfill & f_1(g_1(\mathbf{x}))={(x_1-2x_2+3)}^2+cos(6x_1{x}_6)\hfill \\ \hfill & f_2(g_2(\mathbf{x}))={(x_2-x_1)}^2+{(x_2+3x_3)}^2\hfill \\ \hfill & f_3(g_3(\mathbf{x}))={(x_3-2x_2)}^2+{(x_3+4x_4)}^2\hfill \\ \hfill & f_4(g_4(\mathbf{x}))={(x_4-3x_3)}^2+{(x_4+5x_5)}^2\hfill \\ \hfill & f_5(g_5(\mathbf{x}))={(x_5-4x_4)}^2+{(x_5+6x_6)}^2\hfill \\ \hfill & f_6(g_6(\mathbf{x}))={(x_6-5x_5)}^2+{(x_6+x_1)}^2.\hfill \end{array}$$

The initial actions of the players are set as $\mathbf{x}(0)$ $={[1,2,0,-1,0,0]}^T$. It is derived that the unique Nash equilibrium is ${\mathbf{x}}^{*}={[-4.2038,-0.5853,-1.0110,-0.6918,0.3725]}^T$, based on direct calculation. For comparison, the normal distributed Nash equilibrium seeking algorithm without finite-time and fixed-time handling is given as follows:

$$\begin{array}{cc}\hfill & {\dot{x}}_i=-k_i{y}_i,\hfill \\ \hfill & y_i=\frac{2}{1+e^{-z_i}}-1,\hfill \\ \hfill & z_i=\frac{\partial f_i(g_i(\mathbf{x}))}{\partial x_i},\hfill \end{array}$$

(17)

the distributed fixed-time Nash equilibrium seeking algorithm with input saturation using piecewise function is given as follows:

$$\begin{array}{cc}\hfill & {\dot{x}}_i=-\frac{k_i}{2}(sig{(z_i)}^{\alpha }+sig{(z_i)}^{\beta }),\hfill \\ \hfill & z_i={\Phi }_{{\Delta }_i}(\frac{\partial f_i(g_i(\mathbf{x}))}{\partial x_i}).\hfill \end{array}$$

(18)

where ${\Delta }_i>0$, ${\Phi }_{{\Delta }_i}:R^m\to R^m$ is a saturation function with a saturation level ${\Delta }_i$, which means, for $q={[q_1,q_2,\dots ,q_m]}^T\in R^m$,

$$\begin{array}{cc}\hfill & {\Phi }_{{\Delta }_i}(q)={[{\Phi }_{{\Delta }_1}(q_1),{\Phi }_{{\Delta }_2}(q_2),\dots ,{\Phi }_{{\Delta }_m}(q_m)]}^T\in R^m,\hfill \\ \hfill & {\Phi }_{{\Delta }_i}(q_i)=sgn(q_i)min\{|s_i|,{\Delta }_i\},i=1,2,\dots ,m.\hfill \end{array}$$

Take the parameters as $k_1=1,k_2=1.5,k_3=2,$ $k_4=2.5,k_5=3,k_6=3.5$, $\alpha =0.8$, $\beta =1.05$. Plots of players’ actions under algorithms (3), (10), (17) and (18) are shown in Figure 6, Figure 7, Figure 8 and Figure 9, respectively. The convergence times of the three algorithms are $16.24$ s, $27.35$ s, $32.64$ s and $14.52$ s, respectively, which means the finite-time algorithm (3) and the fixed-time algorithm (10) have more advantages in terms of convergence speed and time compared with the normal algorithm (17). As for the input limit, trajectories of the input states under (3), (10), (17) and (18) are given in Figure 10, Figure 11, Figure 12 and Figure 13, respectively. The input ${\dot{x}}_i$ ranges from $-k_i$ to $k_i$ all the time for all $i=1,2,\dots ,6$. Compared with the input plot in Figure 13, although $\dot{x_i}$ in Figure 11 spends more time to change to zero due to the transformation of sigmoid function, the plot in Figure 11 is smoother and avoids the deadband. The algorithms realize the distributed Nash equilibrium seeking with input saturation in finite time and fixed time.

6. Conclusions

This paper investigates a modified distributed Nash equilibrium seeking problem. The payoff function of each player is determined by the actions of the player and their neighbors. A finite-time protocol and a fixed-time protocol with input saturation are proposed. The sigmoid function is utilized to limit the range of the inputs for the player. The proposed algorithms are theoretically verified using Lyapunov stability analysis. Finally, numerical simulations are given to validate the algorithm; the convergence time of finite-time, fixed-time and normal algorithms is given to illustrate the advantages of the proposed algorithms. Future work will include designing distributed Nash equilibrium algorithms with switching topologies and communication delay.