1. Introduction
One lesson to be recalled from the recent subprime mortgage crisis concerns the major importance of the link between the housing market and macroeconomic stability. As witnessed by the U.S. subprime mortgage crisis of 2007/2008, significant macroeconomic downside risk may loom if housing markets collapse. Supporting this view, the results of empirical research by Cecchetti [
1] indicate that house price booms deteriorate growth prospects and create substantial risks of very bad macroeconomic outcomes. A boom in the housing market may reflect speculative exuberance and herding of investors. A natural question is whether such herding, to the extent that it occurred, was driven by herding in the forecasts of professional housing market forecasters. While much research has been done in recent literature to study herding of, for example, stock market forecasters [
2,
3] and oil-price forecasters [
4], empirical evidence on herding behavior of professional housing market forecasters is relatively scarce. In fact, earlier researchers have focused on concepts like housing market efficiency and rationality of forecasts. For example, Grimes
et al. [
5] study housing market efficiency and overshooting of house prices based on regional data for New Zealand. Song
et al. [
6] and Aggarwal and Mohanty [
7] analyze the rationality of forecasts of U.S. housing starts published in the Money Market Services. Hott [
8] reports that fluctuations in actual house prices exceed fluctuations in “fundamental” house prices. None of the mentioned studies, however, uses cross-sectional micro data on house prices and housing starts to test for herding or anti-herding of forecasters. Laster
et al. [
9] show, in the context of a game-theoretic model, how the form of forecasters’ loss function may give rise to forecaster (anti-)herding. In their model, forecasters sell their forecasts to two groups of customers. The first group of customers buys forecasts from a forecaster who has published the most accurate forecasts over a longer period. The second group of customers buys forecasts from a forecaster who published the most accurate forecast in the last period. If several forecasters published the most accurate forecast, these forecasters share the revenues from the second group of customers. As a result, forecasters have a strong incentive to publish “extreme” forecasts (that is, to differentiate their forecasts from the forecasts of others).
Only in recent research Pierdzioch
et al. [
10,
11] have studied herding behavior of professional housing market forecasters. Following their analysis, we implemented a robust empirical test developed by Bernhardt
et al. [
2] to study whether professional housing market forecasters did, in fact, herd. In order to implement this test, we used the
Wall Street Journal (WSJ) survey data on forecasts of house prices and housing starts for the period 2006–2012. The WSJ survey data contain, for different forecast horizons, forecasts of a large group of individual forecasters, allowing forecaster interactions (herding and anti-herding) to be analyzed at the micro level. We go beyond the research by Pierdzioch
et al. [
10,
11] in that our data set also contains forecasts of changes in house prices, whereas they have studied only housing starts and housing approvals. While housing starts and housing approvals summarize the stance and prospect of housing markets, house prices are more important in terms of, for example, balance-sheet effects. Balance-sheet effects, in turn, have been one major channel through which the current crisis propagated from housing markets to other sectors. We, therefore, deem it an important contribution of this research that we analyze for the first time whether signs of forecaster (anti-)herding can be detected in forecasts of changes in house prices. Importantly, our empirical study is based on recent data that cover the period of time during which U.S. house prices boomed, and the period of time of the eventual burst of the house price rally following the Lehman collapse and the U.S. subprime mortgage crisis. Corroborating results of earlier research, our empirical results do not provide evidence of forecaster herding. On the contrary, we find evidence of forecaster
anti-herding in case of forecasts of both changes in house prices and housing starts. Evidence of forecaster anti-herding indicates that professional housing market forecasters deliberately placed their forecasts away from the cross-sectional consensus forecast. Evidence of forecaster anti-herding is less strong with regard to forecasts of housing starts after the Lehman collapse, indicating that the prevalence of forecaster anti-herding changes over time.
In
Section 2, we describe the data that we used in our empirical analysis. In
Section 3, we describe the test for forecaster (anti-)herding developed by Bernhardt
et al. [
2], and we report our results. In
Section 4, we offer some concluding remarks.
2. The Data
The WSJ conducts, on a monthly basis (during the time period that we analyze), a questionnaire survey of professional forecasters. Professional forecasters are asked about their forecasts of several important financial U.S. variables. When the questionnaire survey was launched in 1981, the focus was on the expected development of the Fed prime rate. In later years, the number of economic variables covered by the questionnaire survey has increased considerably. For example, since January 1985, participants have also been asked to forecast the GNP growth rate and, since 1991, the GDP growth rate. The inflation rate and the unemployment rate have been incorporated into the questionnaire survey since 1989. Additionally, since 2002, the WSJ has published forecasts of the Federal Funds Rate. Since August 2006, the questionnaire survey includes data on forecasts of changes in house prices and forecasts of housing starts for the current year and the next year. Until August 2012, 68 forecasters have participated in the WSJ questionnaire surveys yielding more than
![Ijfs 01 00016 i003]()
forecasts.
The WSJ survey data have been used in several earlier empirical studies. The research questions analyzed in earlier empirical studies, however, significantly differ from our research question. For example, Greer [
12] analyzes whether the forecasters accurately predict the direction of change of yields on 30-year U.S. Treasury bonds correctly and finds some evidence that this is indeed the case. Cho and Hersch [
13] analyze whether the characteristics of forecasters help to explain forecast accuracy (
i.e., the size of the forecast error) and/or the forecast bias (
i.e., the sign of the forecast error). While the authors find that characteristics of forecasters do not help to explain forecast accuracy, some characteristics like the professional experience of a forecaster with the Federal Reserve System seem to have power for explaining the forecast direction error. Kolb and Stekler [
14] report a high degree of heterogeneity of WSJ forecasts, implying that standard central moments (mean, median) do not adequately describe the rich cross-sectional structure of forecasts. Eisenbeis
et al. [
15] analyze the methodology used by the WSJ to construct an overall ranking of forecasters. Because the WSJ ranks the forecasts on the sum of the weighted absolute percentage deviation from the actual realized value of each series, this methodology neglects correlations among the forecasted variables. Mitchell and Pearce [
16] analyze the unbiasedness and forecast accuracy of individual forecasters with respect to their interest rate and exchange rate forecasts. They find that several forecasters form biased forecasts, and that most forecasters cannot out-predict a random walk model.
The WSJ survey data have several interesting features. First, the WSJ is the only survey covering house price forecasts. It publishes forecasts of changes in house prices and housing starts made by a large number of individual forecasters, and not only the mean forecast used in other studies [
6,
7]. Second, the WSJ publishes individual forecasts together with the names of forecasters and the institutions at which they work, implying that forecaster reputation may be linked to forecast accuracy. A link between forecaster reputation and forecast accuracy may strengthen incentives of survey participants to submit their best rather than their strategic forecast [
17], or it may strengthen incentives to strategically deviate from the “consensus” forecast and to “lean against the trend”. Strategic deviations from the consensus forecast may result in systematic forecaster “anti-herding”. Laster
et al. [
9] develop a theoretical model that illustrates how anti-herding of forecasters can easily arise in a game-theoretic model of forecaster interaction. Third, forecasters who participate in the WSJ questionnaire survey not only take a stance on the direction of change of a variable but also forecast the level of a variable. Fourth, the WSJ survey data contain information on forecasts formed by private-sector forecasters rather information on forecasts of international institutions. The forecasts published by international institutions may have characteristics that differ quite substantially from the characteristics of private-sector forecasters. For example, Batchelor [
18] shows that private-sector forecasts are less biased and more accurate in terms of mean absolute error and root mean square error than forecasts published by the OECD and the IMF. Fifth, the WSJ conducts the questionnaire surveys at a monthly basis, implying that the data are available at a relatively high frequency, where the data are readily available to the public and the participating forecasters. This makes it possible to analyze interactions among forecasters. Sixth, the WSJ survey data cover the duration of the U.S. subprime mortgage crisis, rendering it possible to analyze forecasts of changes in house prices and housing starts in times of financial and economic distress. Finally, the WSJ survey data contain forecasts for different forecast horizons, that is, for the current year and the next year. Therefore, we can analyze short-term forecasts and medium-term forecasts (that is, the forecast horizons vary between one and twelve months for short-term forecasts and between 13 and 24 months for next-year forecasts).
Table 1 provides summary statistics of the WSJ survey data. The sample period is from August 2006 to August 2012. Because the sample period covers the period of financial market jitters following the U.S. subprime mortgage crisis, it is not surprising that forecasters expected on average house prices to decrease by about
![Ijfs 01 00016 i004]()
percent (p.a.). The actual house prices decreased by
![Ijfs 01 00016 i005]()
percent. Medium-term forecasts indicate that forecasters expected on average a slight increase in house prices by
![Ijfs 01 00016 i006]()
percent. With regard to medium-term prospects for house prices, forecasters thus were on average more optimistic. Similarly, forecasters expected on average housing starts of about
![Ijfs 01 00016 i007]()
million units (p.a.), where the actual number of housing starts was about
![Ijfs 01 00016 i008]()
million units. The medium-term forecast (
![Ijfs 01 00016 i009]()
million units) again is slightly larger than the short-term forecast.
Figure 1 (change in house prices) and
Figure 2 (housing starts) illustrate that one should not only focus on the cross-sectional, time-averaged mean values of forecasts. A characteristic feature of the WSJ data is that forecasts witness a characteristic cross-sectional dispersion of forecasts of both changes in house price and housing starts. In
Figure 1 and
Figure 2, the cross-sectional heterogeneity of forecasts is measured in terms of the cross-sectional range of forecasts (shaded areas). Cross-sectional dispersion of forecasts of, for example, exchange rates has been widely documented in recent literature (see, for example [
19]). Pierdzioch
et al. [
10,
11] have documented cross-sectional dispersion of forecasts of housing starts and housing approvals. To the best of our knowledge, the cross-sectional dispersion of forecasts of changes in house prices has not been documented in earlier literature. Given the substantial cross-sectional dispersion of the WSJ data, we used in our empirical analysis individual forecasts of changes in house prices and housing starts rather than cross-sectional mean values.
Table 1.
Summary Statistics of the Survey Data (2006–2012).
Table 1.
Summary Statistics of the Survey Data (2006–2012).
| Panel A: Forecasts of House Prices (percentage change p.a.) |
| Short-Term | Medium-Term | Actual |
| Mean | –2.259 | 0.134 | –2.626 |
| Standard Deviation | (0.066) | (0.060) | (0.055) |
| Observations | 3,524 | 3,171 | 68 |
| Panel B: Forecasts of Housing Starts (in million units) |
| Short-Term | Medium-Term | Actual |
| Mean | 0.884 | 1.031 | 0.840 |
| Standard Deviation | (0.006) | (0.006) | (0.005) |
| Observations | 3,648 | 3,240 | 68 |
Figure 1.
Expected and Actual Change in House Prices.
Figure 1.
Expected and Actual Change in House Prices.
In addition to the cross-sectional dispersion of the WSJ data,
Figure 1 and
Figure 2 plot time series of (i) the cross-sectional mean values of the forecasts of changes in house prices and forecasts of housing starts (dashed lines); and, (ii) the actual relative change in house prices and the actual housing starts (solid lines). The cross-sectional mean values of changes in house prices and housing starts move in tandem with the respective actual values, at least as results for end-of-year values are concerned. This result is in line with economic intuition because forecast accuracy should increase as the forecast horizon decreases.
Figure 2.
Expected and Actual Housing Starts.
Figure 2.
Expected and Actual Housing Starts.
3. (Anti-)Herding of Forecasters
The significant cross-sectional dispersion of forecasts of changes in house prices and of forecasts of housing starts gives rise to the question whether herding (or anti-herding) of forecasters helps to explain this dispersion. Herding of forecasters arises if forecasters deliberately center their forecasts around a consensus forecast. The consensus forecast can be represented by the cross-sectional mean of the forecasts made by forecasters who participate, in a given forecasting cycle, in a questionnaire survey. Anti-herding, in contrast, arises if forecasts try to differentiate forecasts by deliberately placing their forecast farther away from the consensus forecast. This definition of forecaster (anti-) herding should make clear that our analysis concerns the cross-sectional herding (or anti-herding) of forecasters. In earlier empirical research, researchers have used the term “herding” to characterize the time-series properties of forecasts. Our use of the term herding, thus, should not be confused with the terminology used by other researchers who have used the term herding to describe, for example, trend-extrapolative forecasts in a time-series context.
We used a test that has recently been developed by Bernhardt
et al. [
2] to analyze whether forecasters (anti-)herd. Using this test ensures that our results can be readily compared with results reported recently by Pierdzioch
et al. [
10,
11]. The test is easy to implement, the economic interpretation of the test results is straightforward, and the test is robust to various types of specification errors. The mechanics of the test can be illustrated by considering a forecaster who forms an efficient private forecast of house prices or housing starts. The forecaster derives her private forecast by applying her optimal forecasting model, and by using all information available to her at the time she forms the forecast. Her private forecast, thus, should be unbiased, and the probability that her unbiased private forecast overshoots or undershoots the future house price should be
![Ijfs 01 00016 i011]()
.
The published forecast may differ from the private forecast if the published forecast is influenced by the consensus forecast. In the case of herding, a forecaster places her published forecast closer to the consensus forecast than warranted by her private forecast. The published forecast will be biased towards the consensus forecast. In case the private forecast exceeds the consensus forecast, the published forecast thus will be smaller than the private forecast. The probability of undershooting is then smaller than 0.5. In a similar vein, if the private forecast is smaller than the consensus forecast, the probability that future house prices or future housing starts overshoot the published forecast is also smaller than 0.5. In contrast, in the case of anti-herding, the published forecast will be farther away from the consensus forecast than the private forecast. The result is that the probability of undershooting and the probability of overshooting will be larger than 0.5.
The probabilities of undershooting and overshooting (computed as the relative frequencies of events, using data for all forecasters) can be used to develop a simple test of herding and anti-herding. Under the null hypothesis that forecasters neither herd nor anti-herd, the probability,
![Ijfs 01 00016 i012]()
, that forecasts of future house prices or housing starts (
![Ijfs 01 00016 i013]()
, where
![Ijfs 01 00016 i014]()
is a forecaster index) overshoot (undershoot) future house prices or housing starts (
![Ijfs 01 00016 i015]()
) should be 0.5, regardless of the consensus forecast (
![Ijfs 01 00016 i016]()
). The conditional probability of undershooting in the case forecasts exceed the consensus forecast should be
and the conditional probability of overshooting in the case forecasts are smaller than the consensus forecast should be
In the case of herding, published forecasts will center around the consensus forecast, implying that the conditional probabilities should be smaller than 0.5. In the case of anti-herding, the published forecasts will be farther away from the consensus forecast, and the conditional probabilities should be larger than 0.5. The test statistic,
![Ijfs 01 00016 i019]()
, defined as the arithmetic average of the sample estimates of the two conditional probabilities, should assume the value
![Ijfs 01 00016 i020]()
in the case case of unbiased forecasts, the value
![Ijfs 01 00016 i021]()
in the case of herding, and the value
![Ijfs 01 00016 i022]()
in the case of anti-herding. (For a graphical illustration of how forecaster (anti-)herding affects the undershooting and overshooting probabilities, See Pierdzioch
et al. [
4].) Bernhardt
et al. [
2] show that the test statistic
![Ijfs 01 00016 i019]()
, asymptotically has a normal sampling distribution. They also demonstrate that, due to the averaging of conditional probabilities, the test statistic,
![Ijfs 01 00016 i019]()
, is robust to phenomena like, for example, correlated forecast errors and optimism or pessimism among forecasters. Such phenomena make it more difficult to reject the null hypothesis of unbiased forecasts.
The results summarized in
Table 2 show that the test statistic,
![Ijfs 01 00016 i019]()
, significantly exceeds the value
![Ijfs 01 00016 i011]()
, providing strong evidence of forecaster anti-herding. (The number of observations is slightly smaller than in
Table 1 because some forecasts are equal to the subsequently realized value, that is,
![Ijfs 01 00016 i023]()
. Equations (1) and (2) show that such forecasts were dropped from the analysis.) The evidence of anti-herding is strong regardless of the forecast horizon and regardless of whether we studied forecasts of changes in house prices or housing starts. We computed the test statistic,
![Ijfs 01 00016 i019]()
, using the consensus of the previous period,
![Ijfs 01 00016 i024]()
, because forecasters deliver their forecasts simultaneously, implying that the contemporaneous consensus forecast may not be in forecasters information set. More precisely, we used the forecast from the predecessor survey to compute the consensus forecast. As for January forecasts, we used the medium-term December forecasts to compute the consensus forecast. (We also found strong evidence of forecaster anti-herding when we used the contemporaneous consensus forecast to compute the test statistic,
![Ijfs 01 00016 i019]()
. Results are not reported, but available upon request.)
Table 2.
Test for Herding.
Table 2.
Test for Herding.
| Panel A: Short-Term Forecasts of House Prices |
| ![Ijfs 01 00016 i025]() | ![Ijfs 01 00016 i026]() |
![Ijfs 01 00016 i027]() | 633 / 35.1 % | 1,341 / 78.3 % |
![Ijfs 01 00016 i028]() | 1,171 / 64.9 % | 371 / 21.7 % |
| Sum | 1,804 / 100.0 % | 1,712 / 100.0 % |
| S-Stat | 0.716 | |
| Stand. Error | 0.0084 |
| Lower 99 % | 0.694 |
| Upper 99 % | 0.738 |
| Observations | 3,516 |
| Panel B: Medium-Term Forecasts of House Price |
| ![Ijfs 01 00016 i025]() | ![Ijfs 01 00016 i026]() |
![Ijfs 01 00016 i027]() | 795 / 57.4 % | 1,341 / 85.3 % |
![Ijfs 01 00016 i028]() | 589 / 42.6 % | 232 / 14.7 % |
| Sum | 1,384 / 100.0 % | 1,573 / 100.0 % |
| S-Stat | 0.639 | |
| Stand. Error | 0.0092 | |
| Lower 99 % | 0.615 | |
| Upper 99 % | 0.663 | |
| Observations | 2,957 | |
| Panel C: Short-Term Forecasts of Housing Starts |
| ![Ijfs 01 00016 i025]() | ![Ijfs 01 00016 i026]() |
![Ijfs 01 00016 i027]() | 972 / 49.4 % | 1,266 / 85.3 % |
![Ijfs 01 00016 i028]() | 995 / 50.6 % | 219 / 14.7 % |
| Sum | 1,967 / 100.0 % | 1,485 / 100.0 % |
| S-Stat | 0.679 | |
| Stand. Error | 0.0086 | |
| Lower 99 % | 0.657 | |
| Upper 99 % | 0.702 | |
| Observations | 3,452 | |
| Panel D: Medium-Term Forecasts of Housing Starts |
| ![Ijfs 01 00016 i025]() | ![Ijfs 01 00016 i026]() |
![Ijfs 01 00016 i027]() | 1,153 / 72.8 % | 1,336 / 96.6 % |
![Ijfs 01 00016 i028]() | 430 / 27.2 % | 47 / 3.4 % |
| Sum | 1,583 / 100.0 % | 1,383 / 100.0 % |
| S-Stat | 0.619 | |
| Stand. Error | 0.0092 | |
| Lower 99 % | 0.595 | |
| Upper 99 % | 0.643 | |
| Observations | 2,966 | |
To analyze the impact of the Lehman collapse on expectation formation in the housing market, we split the sample period into two subsample periods in
Table 3 and
Table 4: a pre-Lehman collapse subsample period, and a post-Lehman collapse subsample period. The results confirm that forecasters of changes in house prices anti-herd before and after the Lehman collapse. Interestingly, forecaster anti-herding tends to be more pronounced in the period before the Lehman collapse with regard to housing starts. For medium-term forecasts of housing starts, the herding statistic even becomes only marginally significant in the post-Lehman sample. While the interpretation of this result should not be stretched too far, it may reflect that the strategic interactions between forecasters of housing starts have become weaker after the collapse of Lehman brothers, and after the housing rally pricked.
Table 3.
Test for Herding before Lehman.
Table 4.
Test for Herding after Lehman collapse.
As yet another robustness test, we tested whether forecaster (anti-)herding is stable over the forecasting cycle. To this end, we computed the test statistic,
![Ijfs 01 00016 i019]()
, for each month separately (that is, for forecasts made in January, forecasts made in February, ...), where we used data from the previous month to compute the consensus forecast.
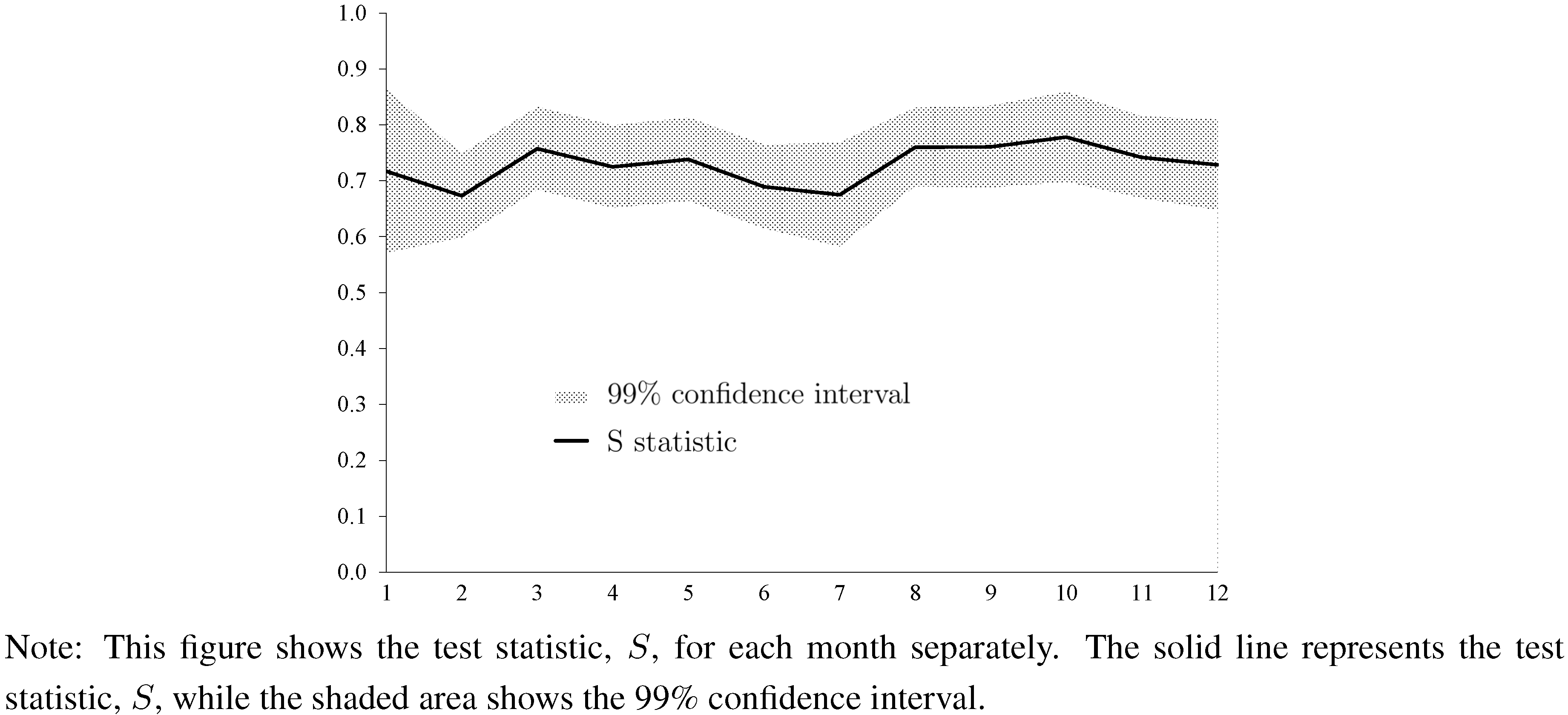
Figure 3 and
Figure 4 report the results based on the current-year forecasts. (We do not present results for the next-year forecasts because we do not have a consensus forecast for next-year forecasts in January. Results for next-year forecasts are qualitatively similar and are available upon request.) Results show strong evidence of forecaster anti-herding for all months in the case of forecasts of house price changes. The test statistic,
![Ijfs 01 00016 i019]()
, always settles above the 0.5 line. Concerning current-year forecasts of housing starts, we also find strong evidence of forecaster anti-herding, but the results are somewhat more variable across months as compared with forecasts of changes of house prices. December forecasts are not significantly different from 0.5.
Figure 3.
Test Statistic for Every Month (Changes of House Prices, Current-Year Forecasts).
Figure 3.
Test Statistic for Every Month (Changes of House Prices, Current-Year Forecasts).
Figure 4.
Test Statistic for Every Month (Housing Starts, Current-Year Forecasts).
Figure 4.
Test Statistic for Every Month (Housing Starts, Current-Year Forecasts).
 forecasts.
forecasts. percent (p.a.). The actual house prices decreased by
percent (p.a.). The actual house prices decreased by  percent. Medium-term forecasts indicate that forecasters expected on average a slight increase in house prices by
percent. Medium-term forecasts indicate that forecasters expected on average a slight increase in house prices by  percent. With regard to medium-term prospects for house prices, forecasters thus were on average more optimistic. Similarly, forecasters expected on average housing starts of about
percent. With regard to medium-term prospects for house prices, forecasters thus were on average more optimistic. Similarly, forecasters expected on average housing starts of about  million units (p.a.), where the actual number of housing starts was about
million units (p.a.), where the actual number of housing starts was about  million units. The medium-term forecast (
million units. The medium-term forecast (  million units) again is slightly larger than the short-term forecast.
million units) again is slightly larger than the short-term forecast.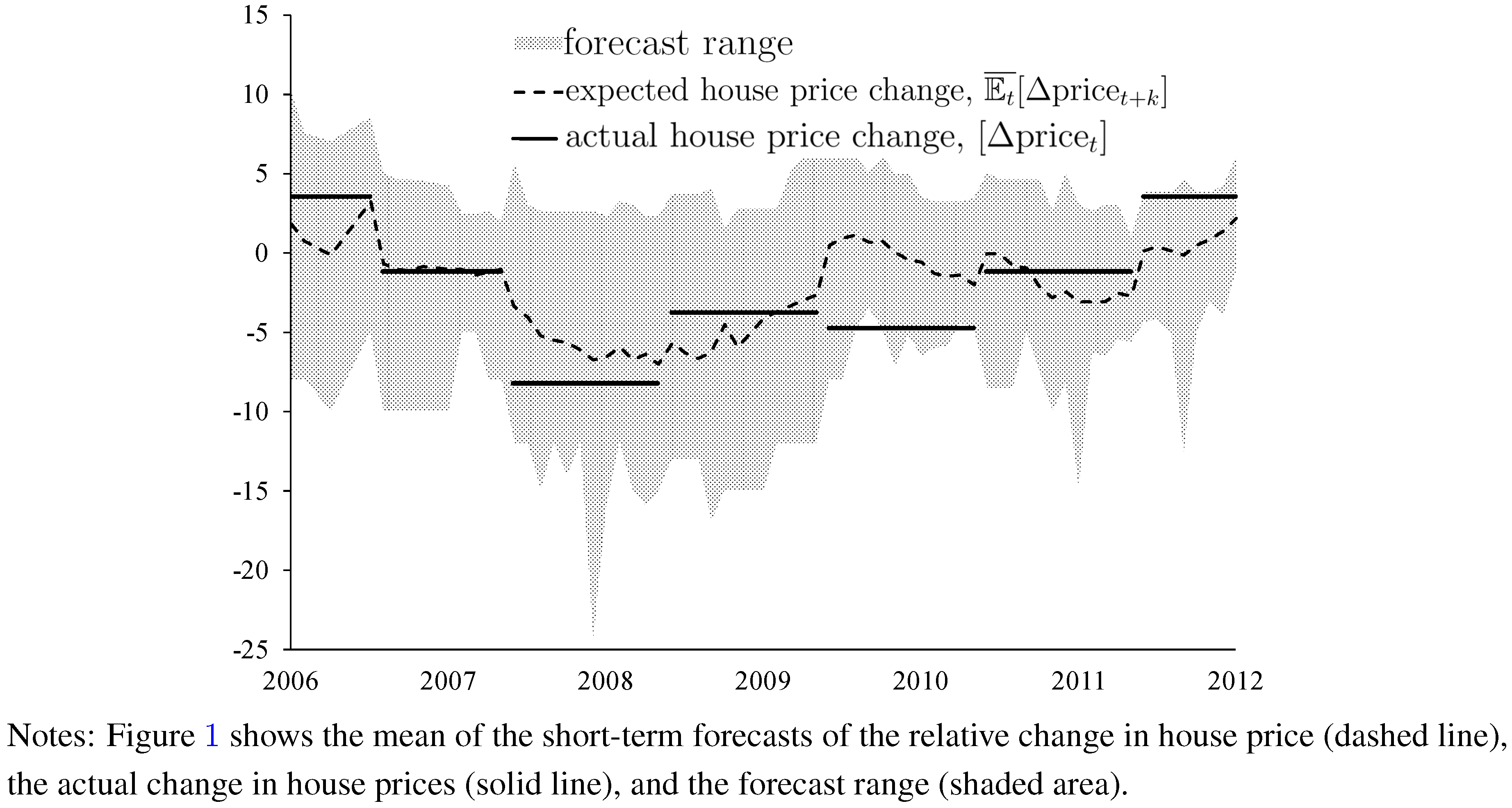

 .
. , that forecasts of future house prices or housing starts (
, that forecasts of future house prices or housing starts (  , where
, where  is a forecaster index) overshoot (undershoot) future house prices or housing starts (
is a forecaster index) overshoot (undershoot) future house prices or housing starts (  ) should be 0.5, regardless of the consensus forecast (
) should be 0.5, regardless of the consensus forecast (  ). The conditional probability of undershooting in the case forecasts exceed the consensus forecast should be
). The conditional probability of undershooting in the case forecasts exceed the consensus forecast should be


 , defined as the arithmetic average of the sample estimates of the two conditional probabilities, should assume the value
, defined as the arithmetic average of the sample estimates of the two conditional probabilities, should assume the value  in the case case of unbiased forecasts, the value
in the case case of unbiased forecasts, the value  in the case of herding, and the value
in the case of herding, and the value  in the case of anti-herding. (For a graphical illustration of how forecaster (anti-)herding affects the undershooting and overshooting probabilities, See Pierdzioch et al. [4].) Bernhardt et al. [2] show that the test statistic
in the case of anti-herding. (For a graphical illustration of how forecaster (anti-)herding affects the undershooting and overshooting probabilities, See Pierdzioch et al. [4].) Bernhardt et al. [2] show that the test statistic  , asymptotically has a normal sampling distribution. They also demonstrate that, due to the averaging of conditional probabilities, the test statistic,
, asymptotically has a normal sampling distribution. They also demonstrate that, due to the averaging of conditional probabilities, the test statistic,  , is robust to phenomena like, for example, correlated forecast errors and optimism or pessimism among forecasters. Such phenomena make it more difficult to reject the null hypothesis of unbiased forecasts.
, is robust to phenomena like, for example, correlated forecast errors and optimism or pessimism among forecasters. Such phenomena make it more difficult to reject the null hypothesis of unbiased forecasts. , significantly exceeds the value
, significantly exceeds the value  , providing strong evidence of forecaster anti-herding. (The number of observations is slightly smaller than in Table 1 because some forecasts are equal to the subsequently realized value, that is,
, providing strong evidence of forecaster anti-herding. (The number of observations is slightly smaller than in Table 1 because some forecasts are equal to the subsequently realized value, that is,  . Equations (1) and (2) show that such forecasts were dropped from the analysis.) The evidence of anti-herding is strong regardless of the forecast horizon and regardless of whether we studied forecasts of changes in house prices or housing starts. We computed the test statistic,
. Equations (1) and (2) show that such forecasts were dropped from the analysis.) The evidence of anti-herding is strong regardless of the forecast horizon and regardless of whether we studied forecasts of changes in house prices or housing starts. We computed the test statistic,  , using the consensus of the previous period,
, using the consensus of the previous period,  , because forecasters deliver their forecasts simultaneously, implying that the contemporaneous consensus forecast may not be in forecasters information set. More precisely, we used the forecast from the predecessor survey to compute the consensus forecast. As for January forecasts, we used the medium-term December forecasts to compute the consensus forecast. (We also found strong evidence of forecaster anti-herding when we used the contemporaneous consensus forecast to compute the test statistic,
, because forecasters deliver their forecasts simultaneously, implying that the contemporaneous consensus forecast may not be in forecasters information set. More precisely, we used the forecast from the predecessor survey to compute the consensus forecast. As for January forecasts, we used the medium-term December forecasts to compute the consensus forecast. (We also found strong evidence of forecaster anti-herding when we used the contemporaneous consensus forecast to compute the test statistic,  . Results are not reported, but available upon request.)
. Results are not reported, but available upon request.)















































 , for each month separately (that is, for forecasts made in January, forecasts made in February, ...), where we used data from the previous month to compute the consensus forecast. Figure 3 and Figure 4 report the results based on the current-year forecasts. (We do not present results for the next-year forecasts because we do not have a consensus forecast for next-year forecasts in January. Results for next-year forecasts are qualitatively similar and are available upon request.) Results show strong evidence of forecaster anti-herding for all months in the case of forecasts of house price changes. The test statistic,
, for each month separately (that is, for forecasts made in January, forecasts made in February, ...), where we used data from the previous month to compute the consensus forecast. Figure 3 and Figure 4 report the results based on the current-year forecasts. (We do not present results for the next-year forecasts because we do not have a consensus forecast for next-year forecasts in January. Results for next-year forecasts are qualitatively similar and are available upon request.) Results show strong evidence of forecaster anti-herding for all months in the case of forecasts of house price changes. The test statistic,  , always settles above the 0.5 line. Concerning current-year forecasts of housing starts, we also find strong evidence of forecaster anti-herding, but the results are somewhat more variable across months as compared with forecasts of changes of house prices. December forecasts are not significantly different from 0.5.
, always settles above the 0.5 line. Concerning current-year forecasts of housing starts, we also find strong evidence of forecaster anti-herding, but the results are somewhat more variable across months as compared with forecasts of changes of house prices. December forecasts are not significantly different from 0.5.