A Nonlinear Ultrasonic Modulation Method for Crack Detection in Turbine Blades
Abstract
:1. Introduction
2. Global Nonlinearity Parameter
- A longitudinal plane wave propagates in a thin circular rod.
- Attenuation is neglected.
2.1. Validation of the Use of the One-Dimensional Wave Equation
2.2. Amplitude Summing Method
3. Numerical Simulation
3.1. Modelling
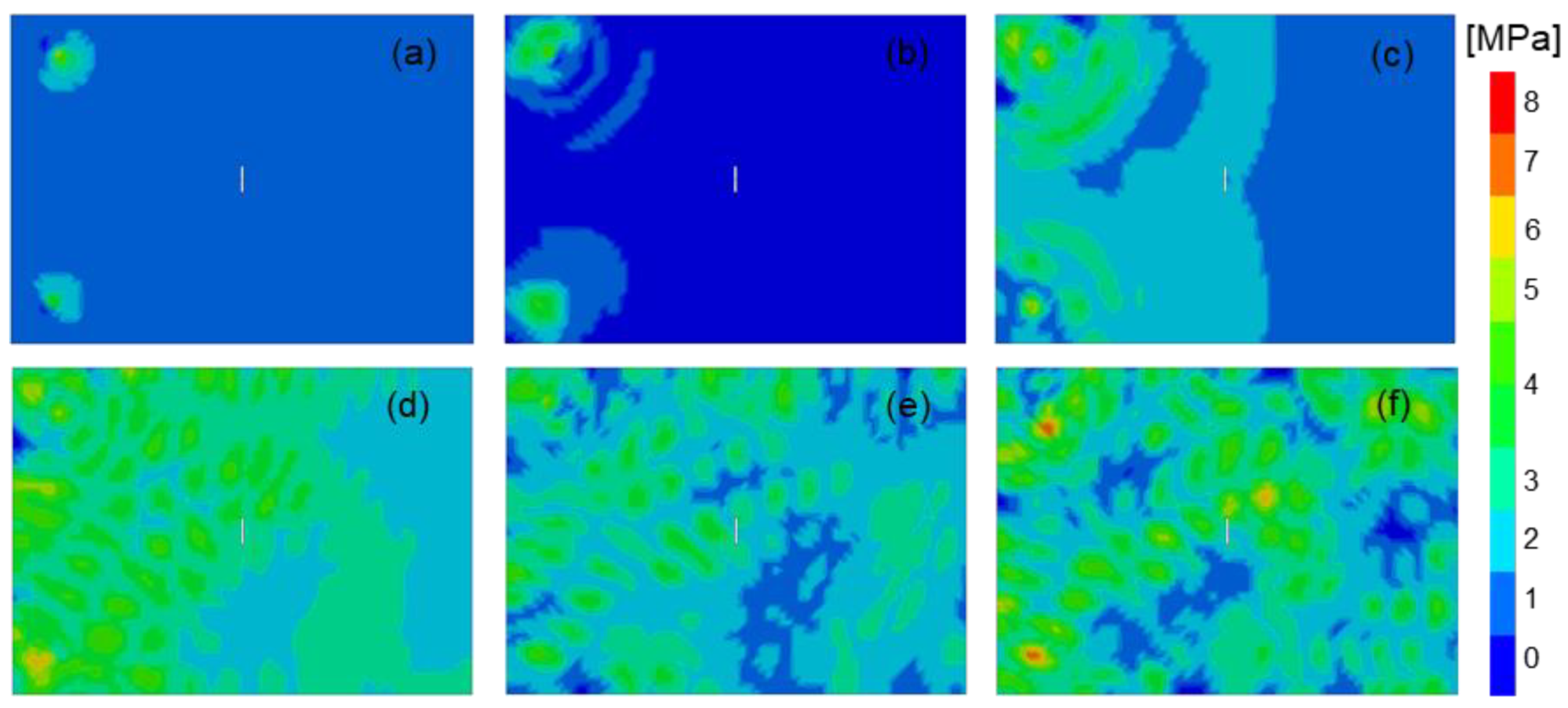
3.2. Results and Discussion
4. Experimental Validation
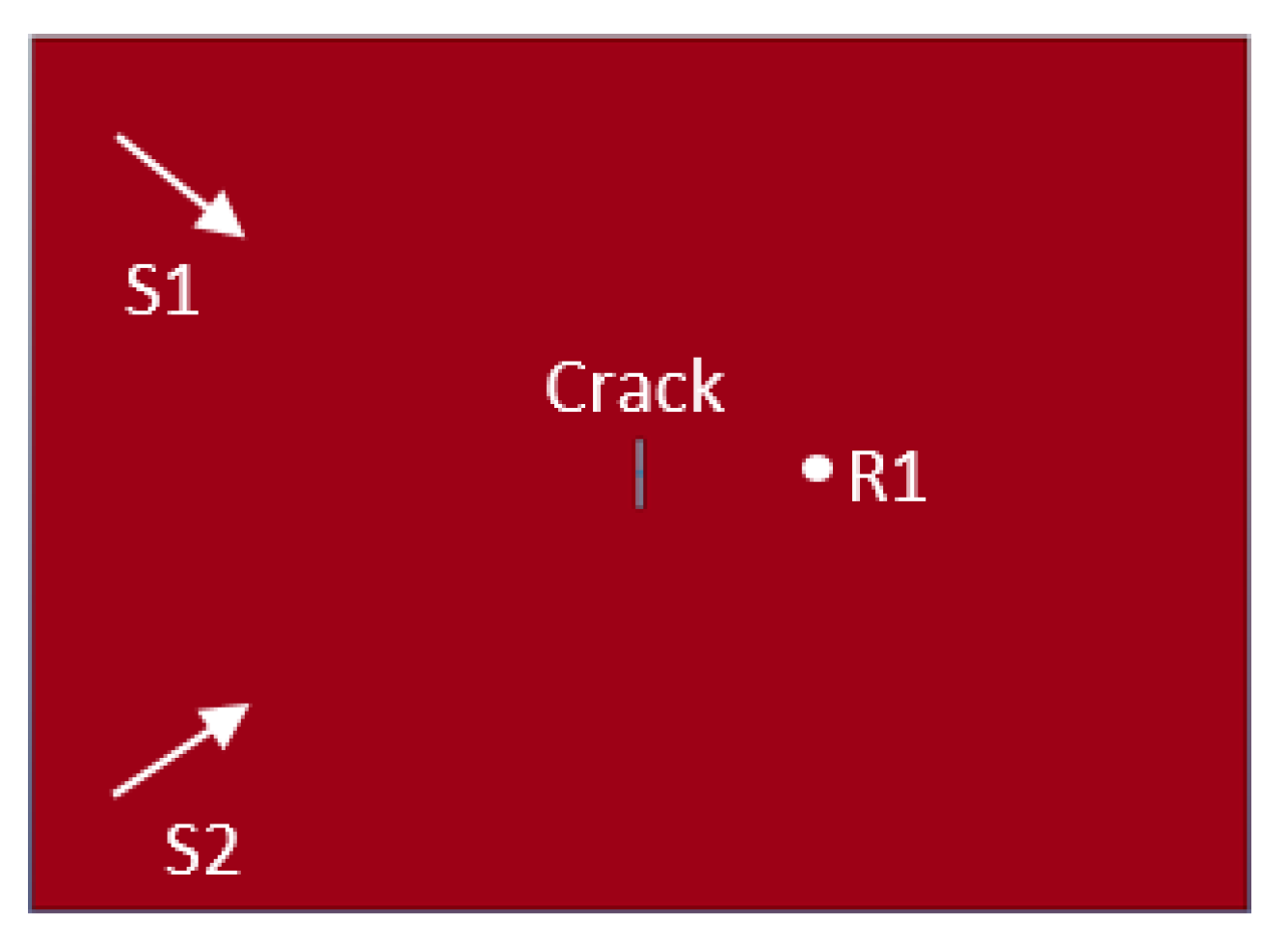
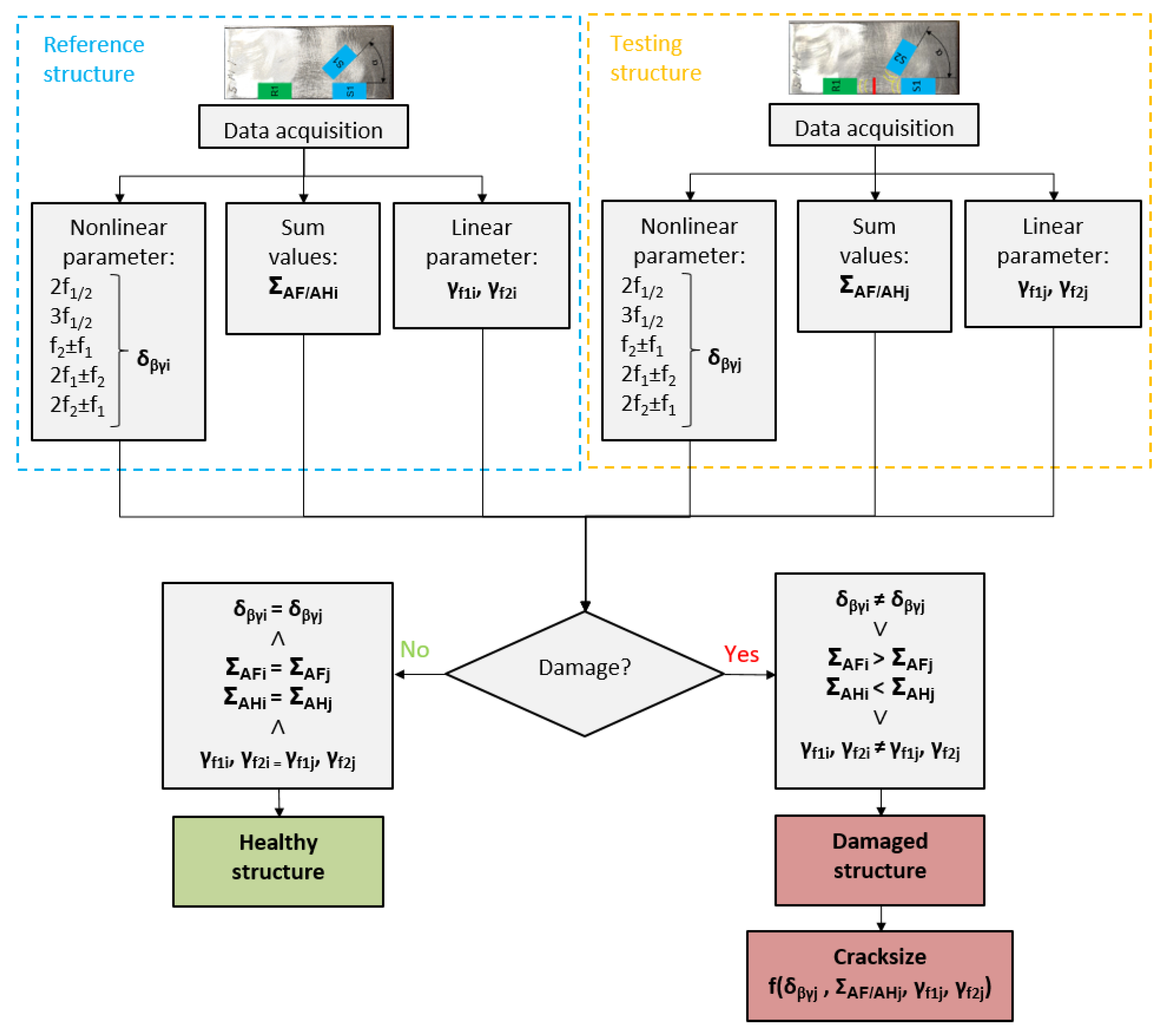
4.1. Damage Detection Methodology
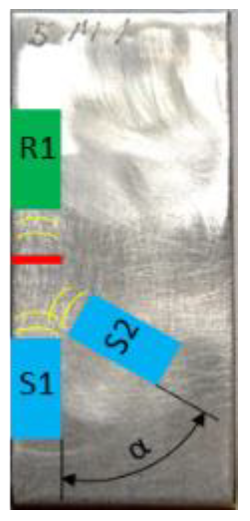
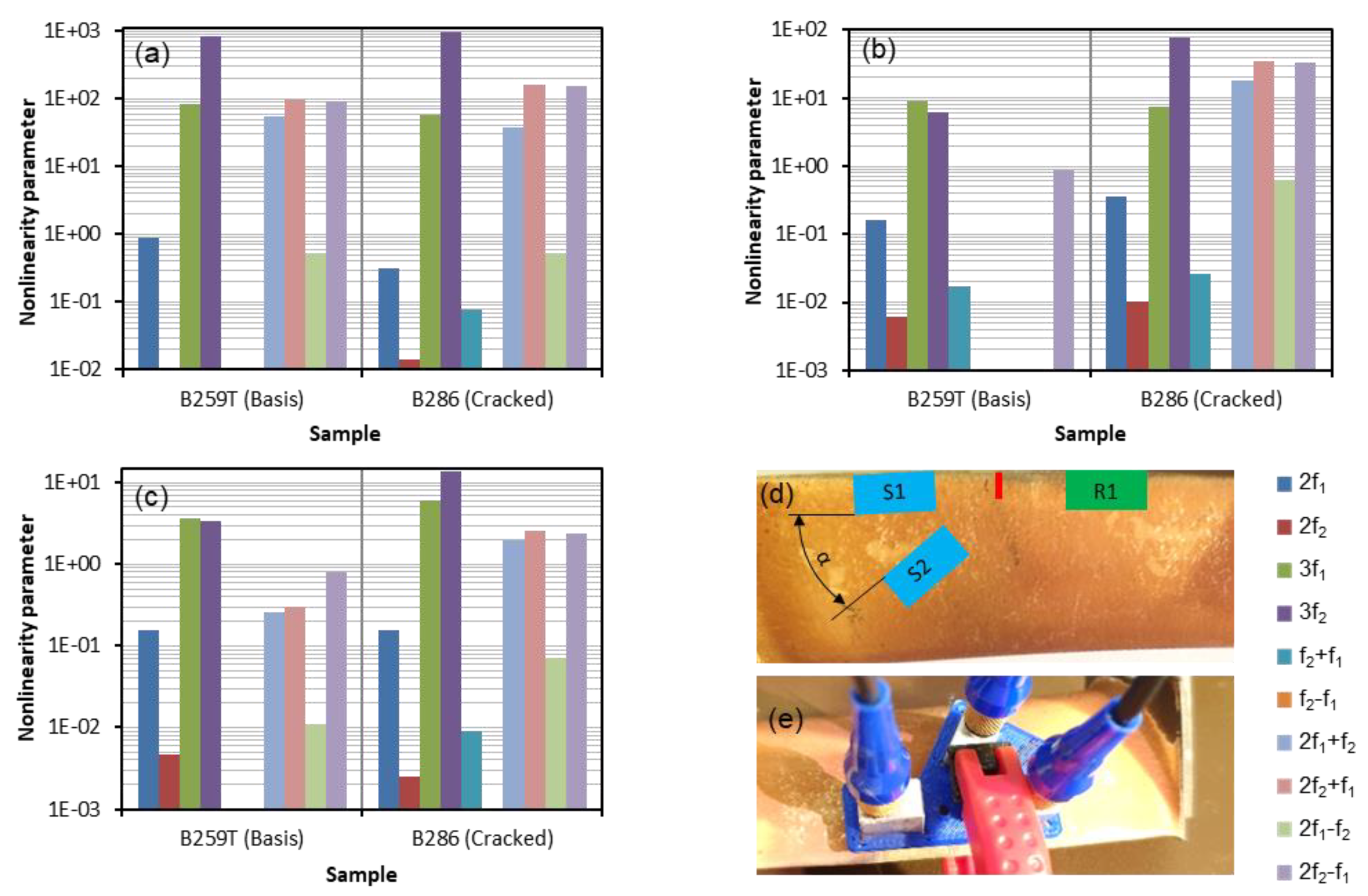
4.2. Plate Samples—Welded
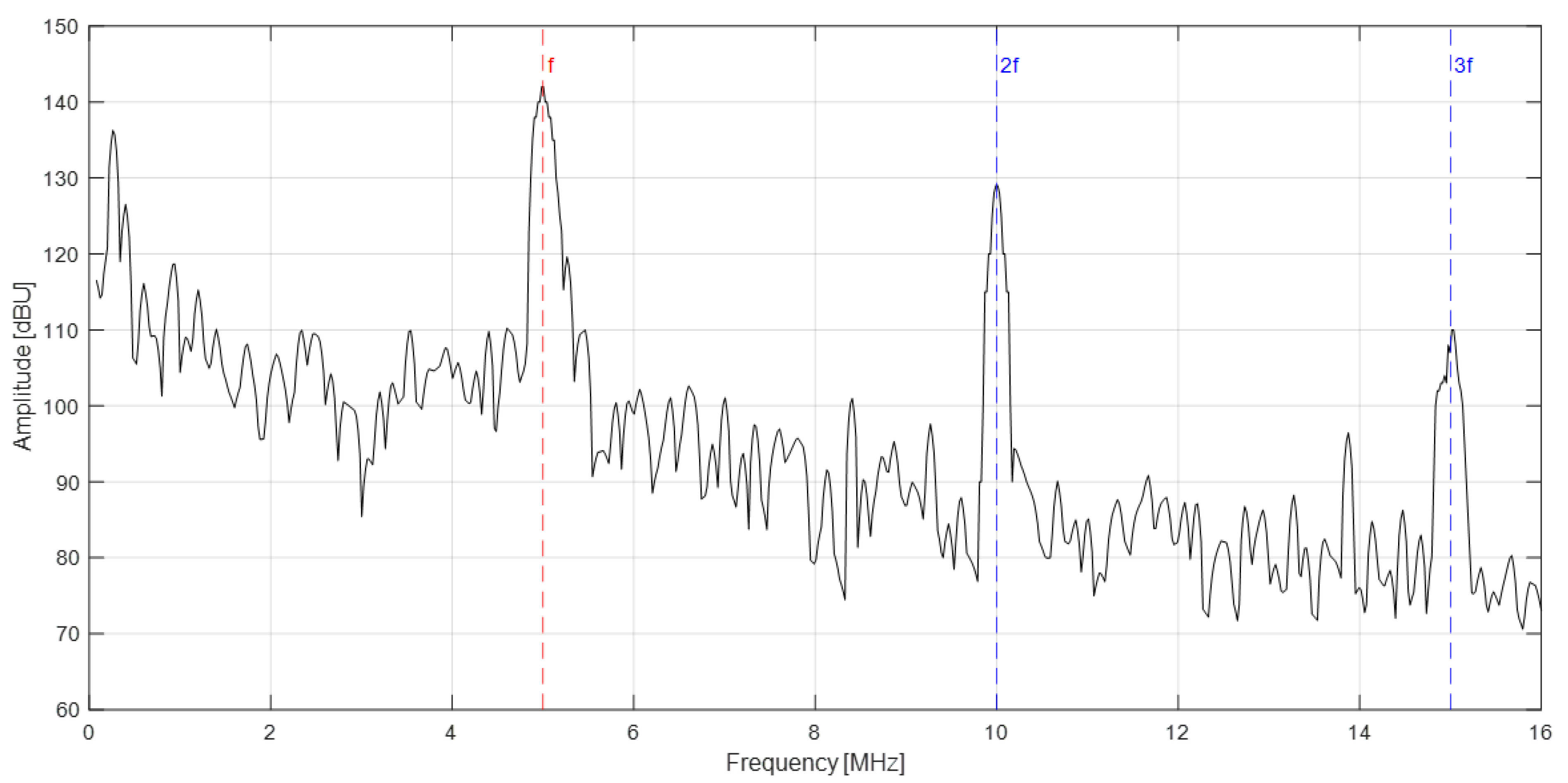
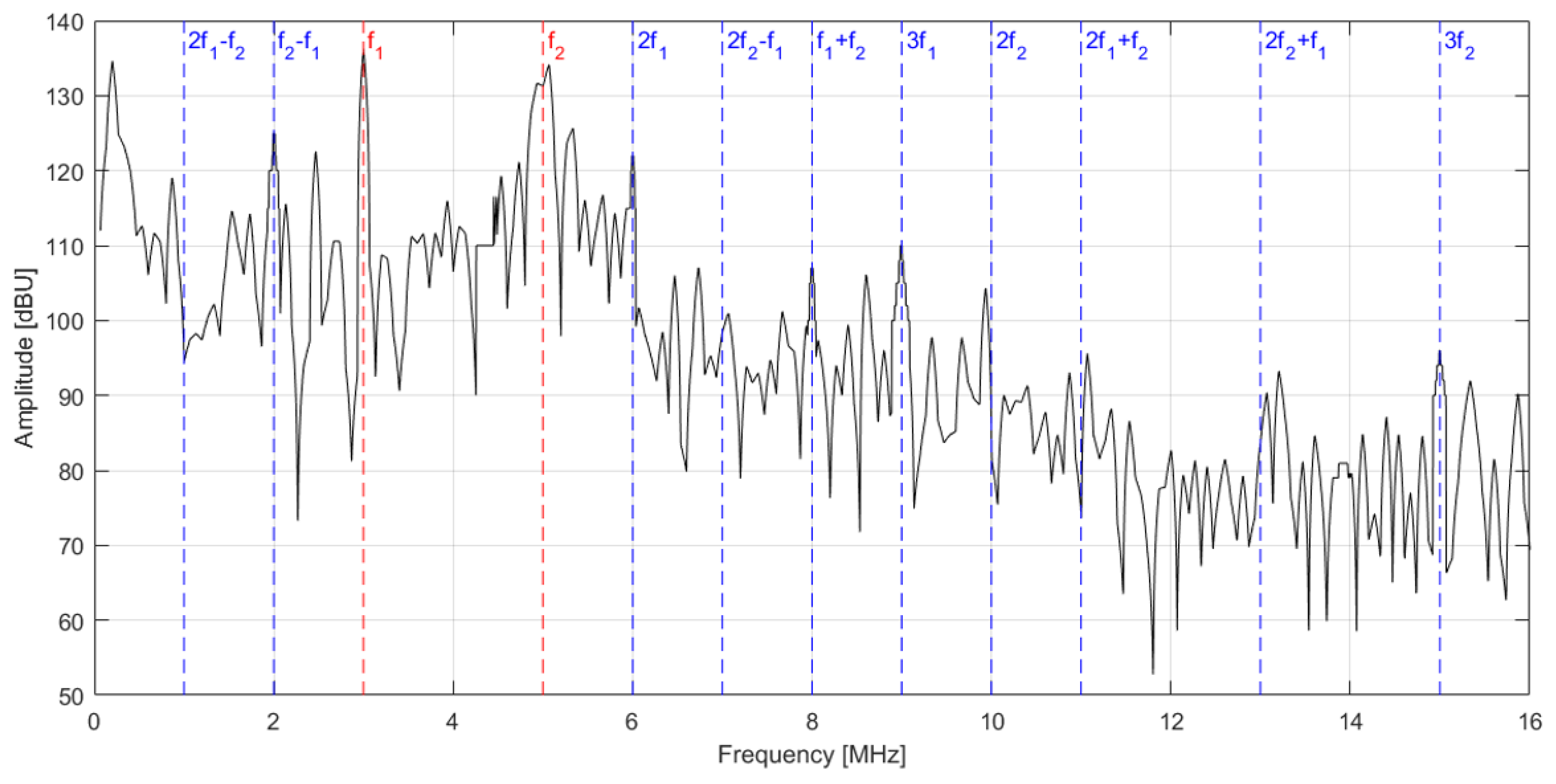
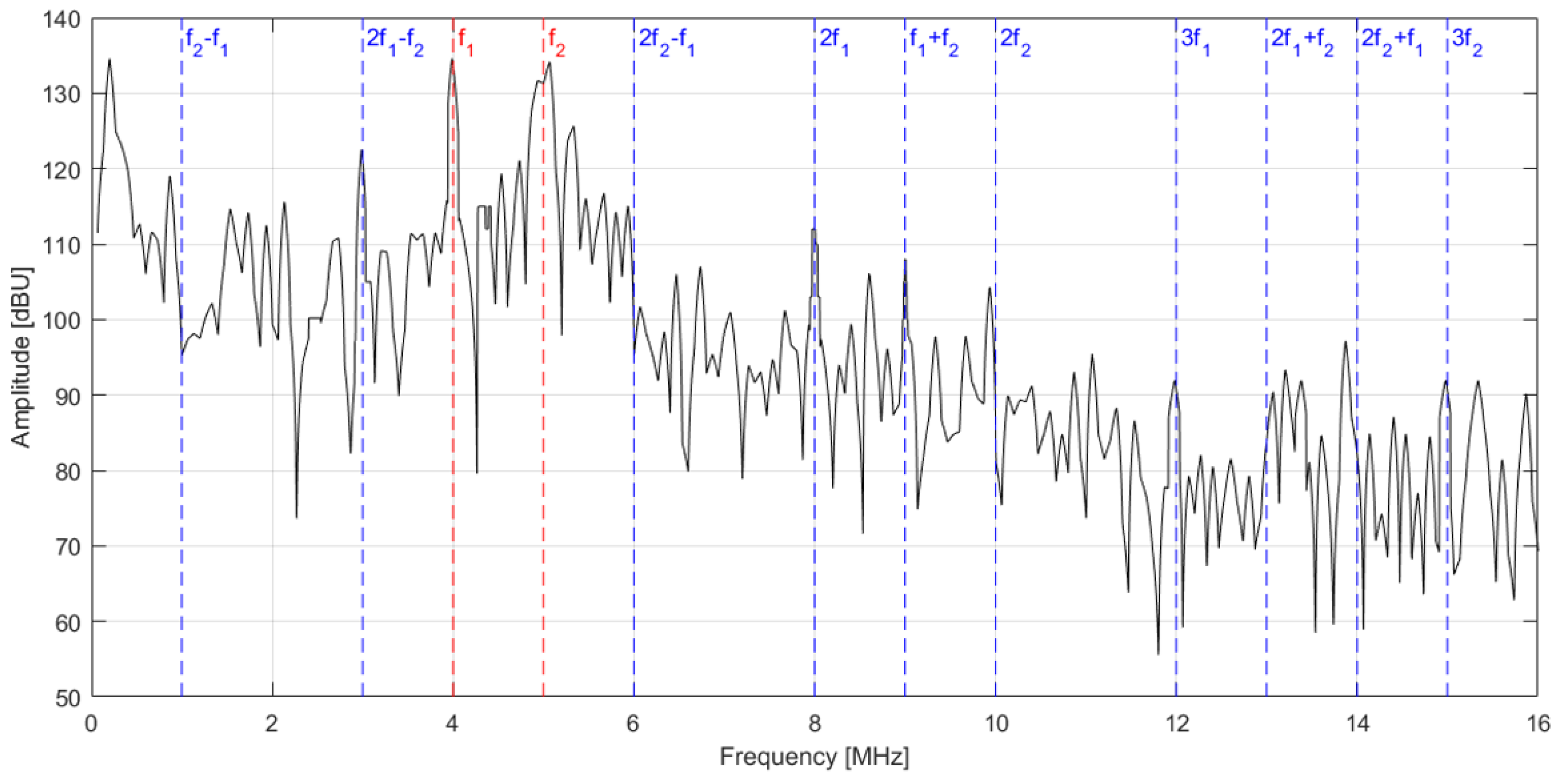
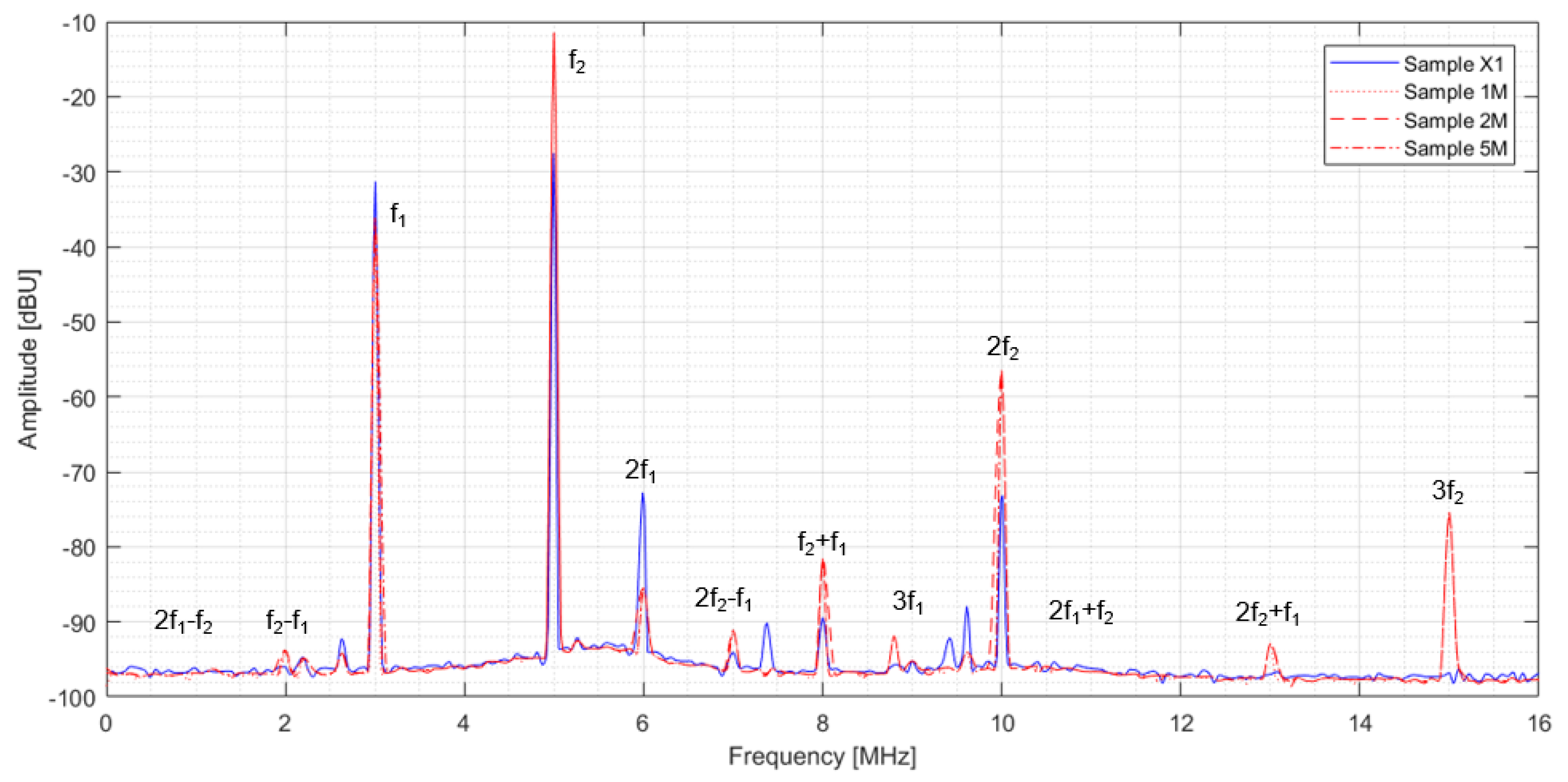
4.2.1. Evidence Higher Harmonic Frequencies
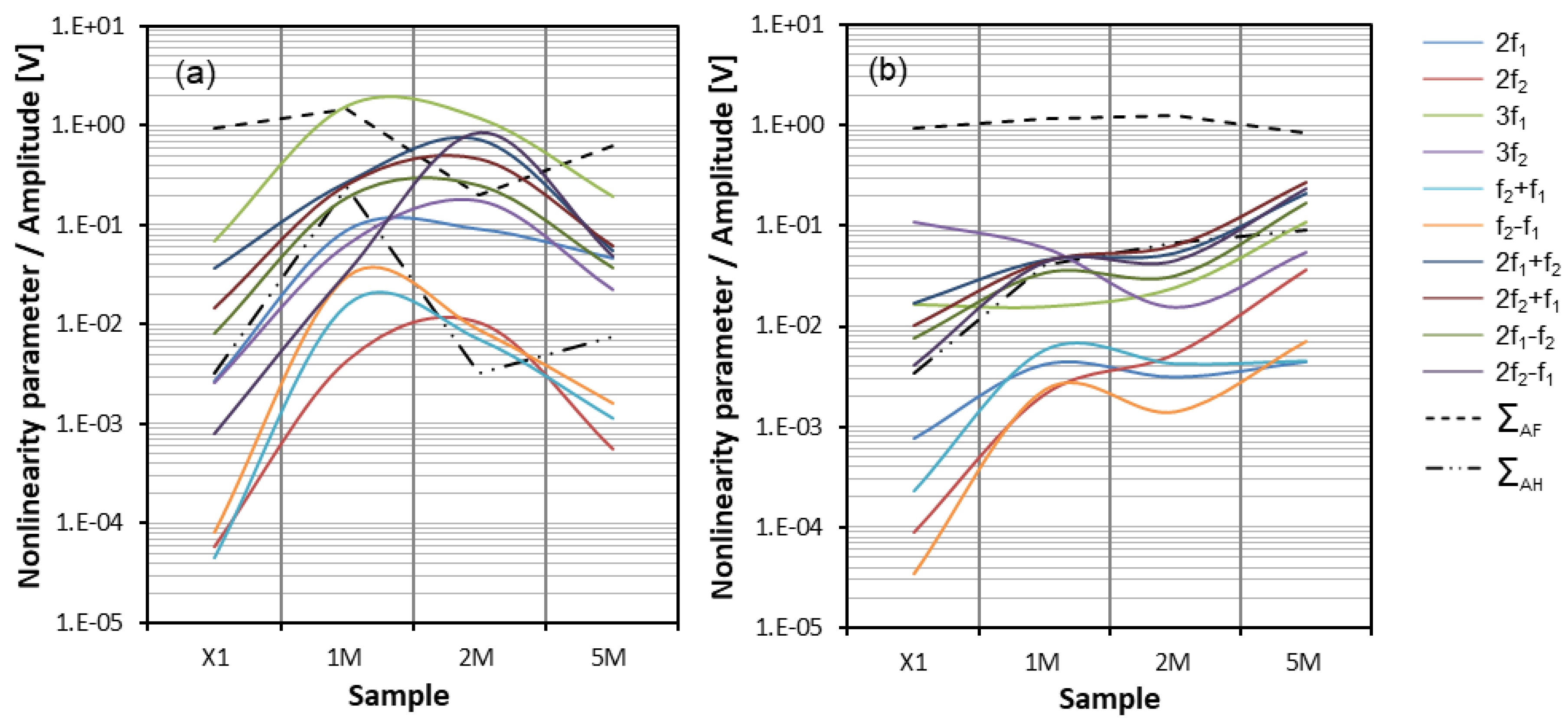
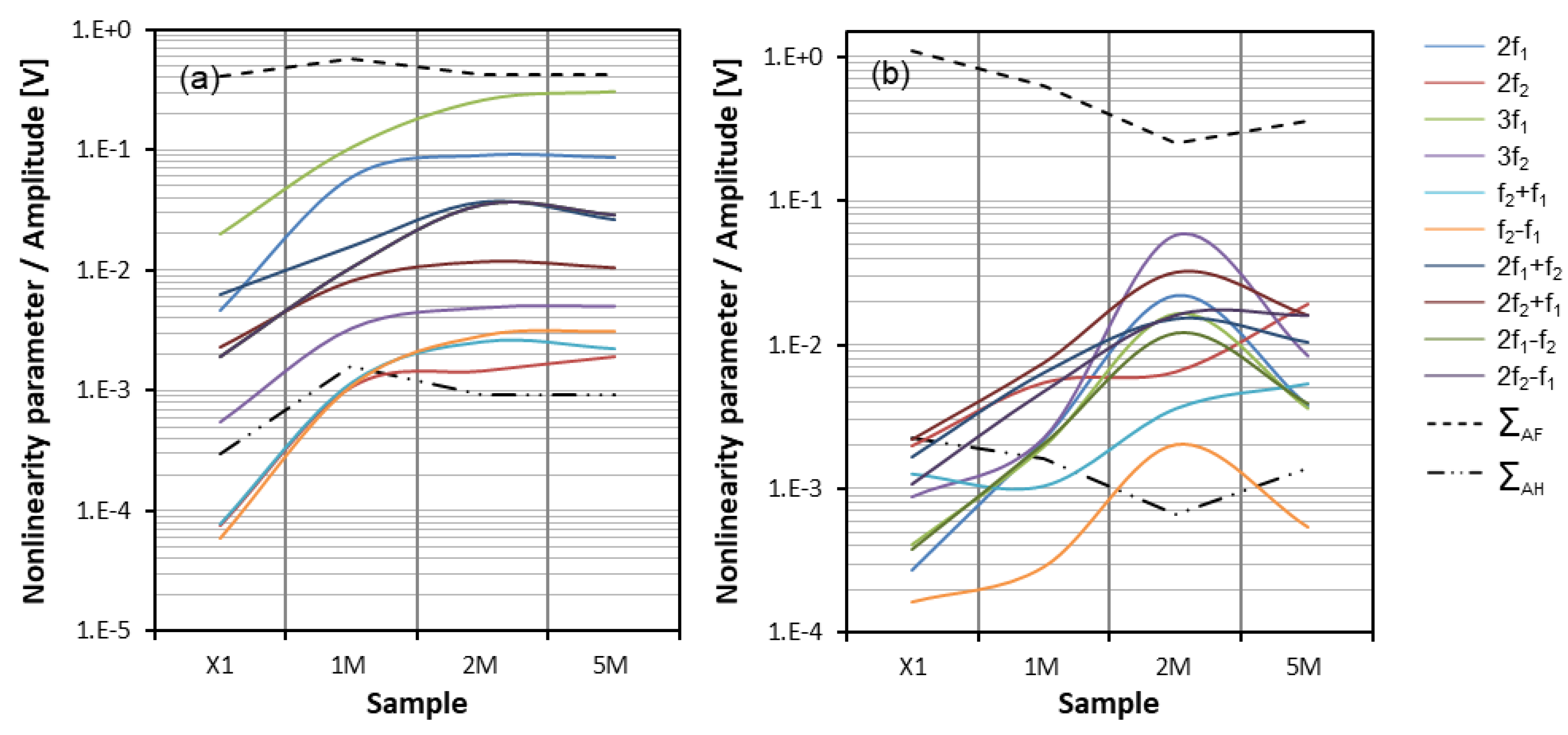
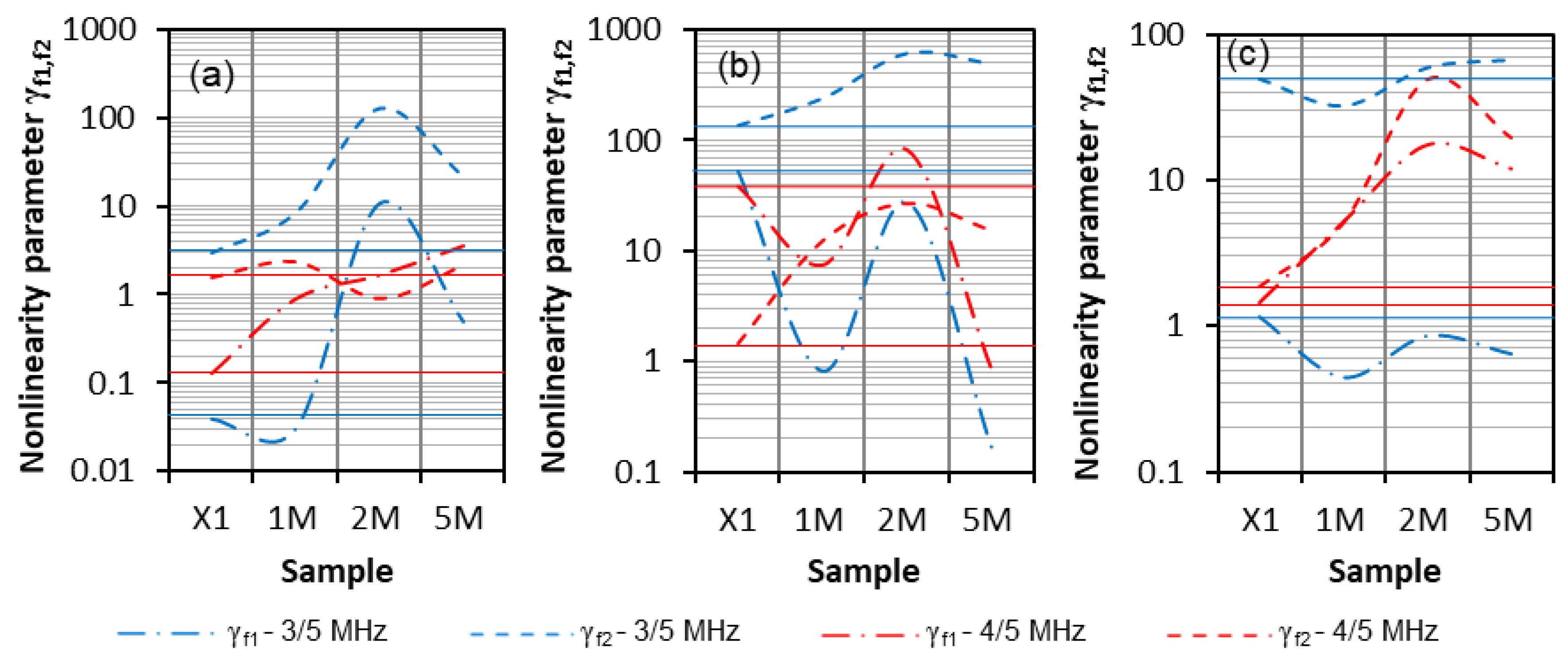
4.2.2. Results and Discussion—Central Defect
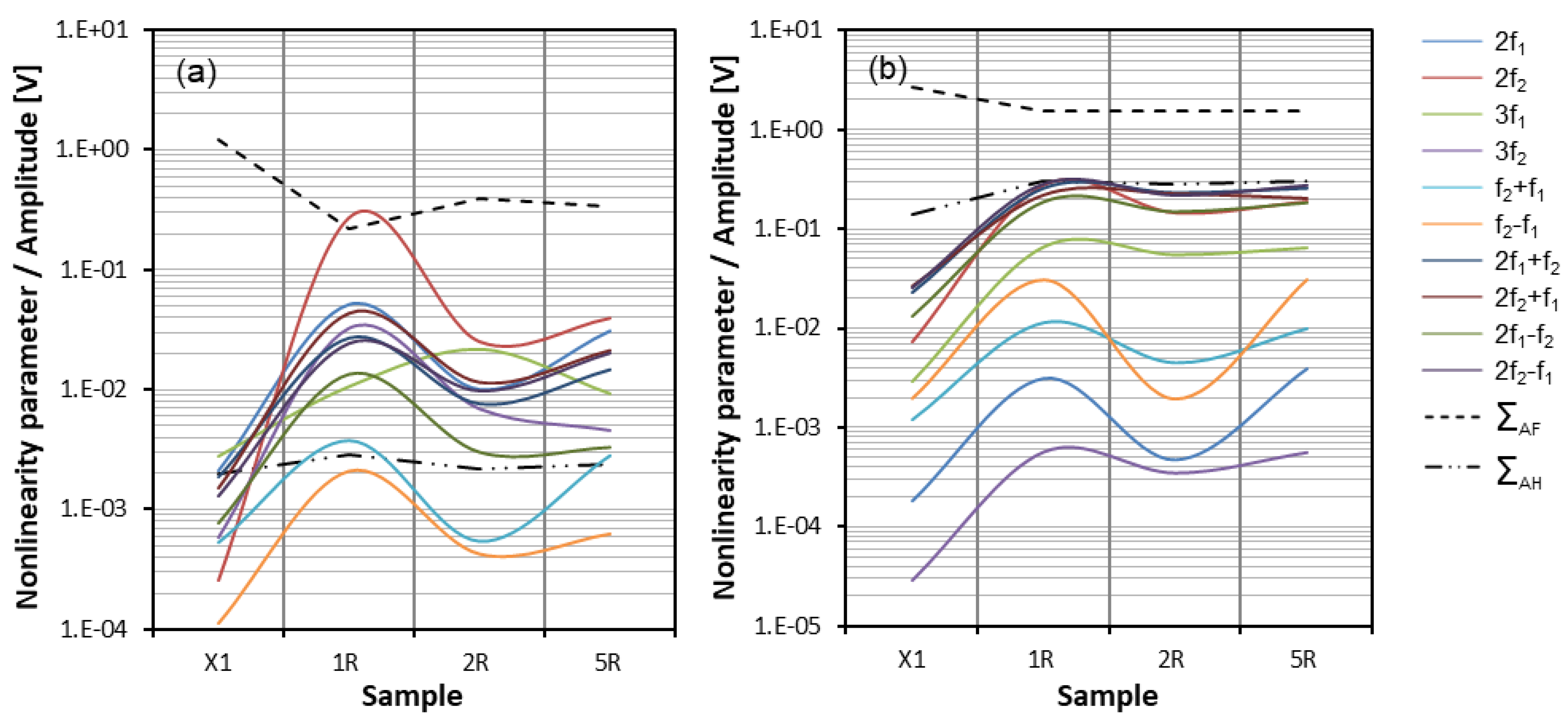
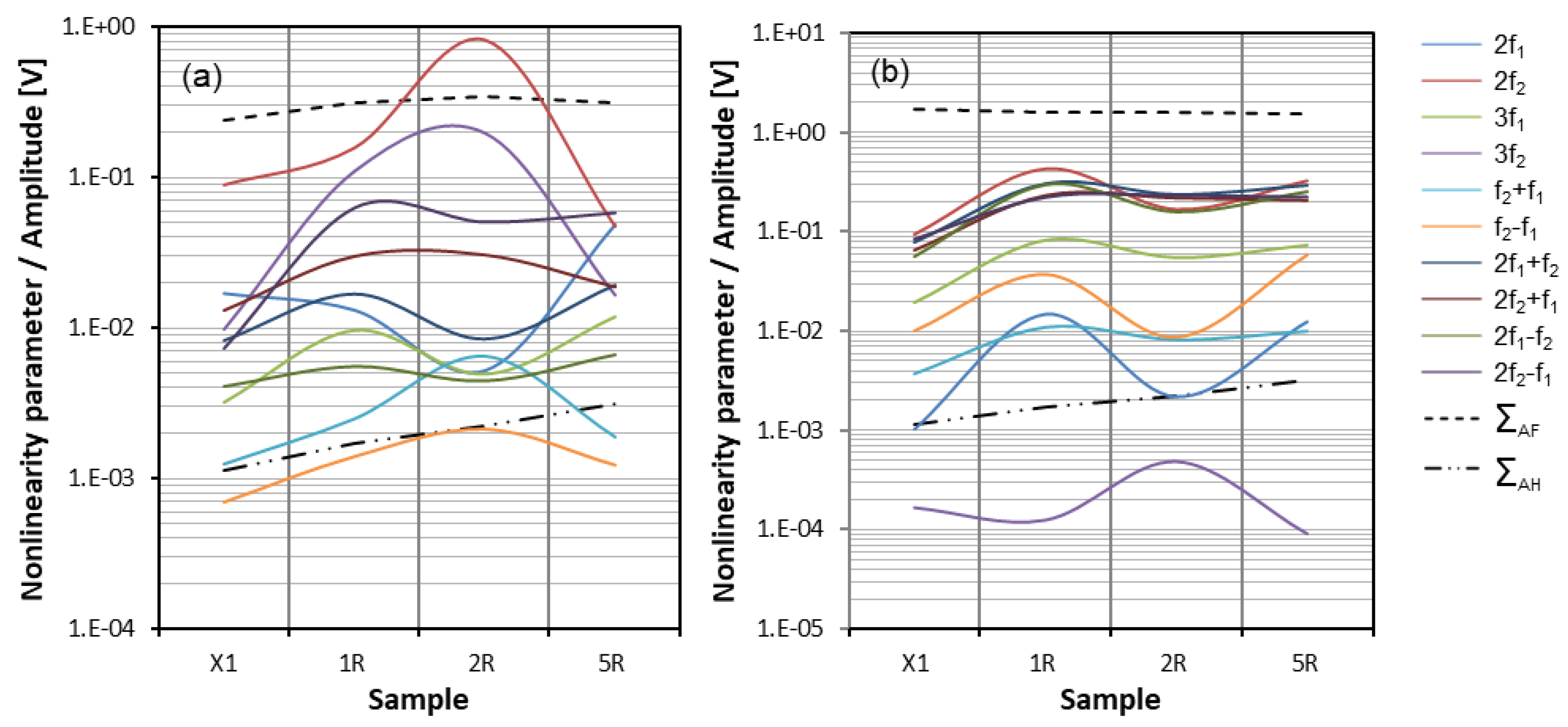
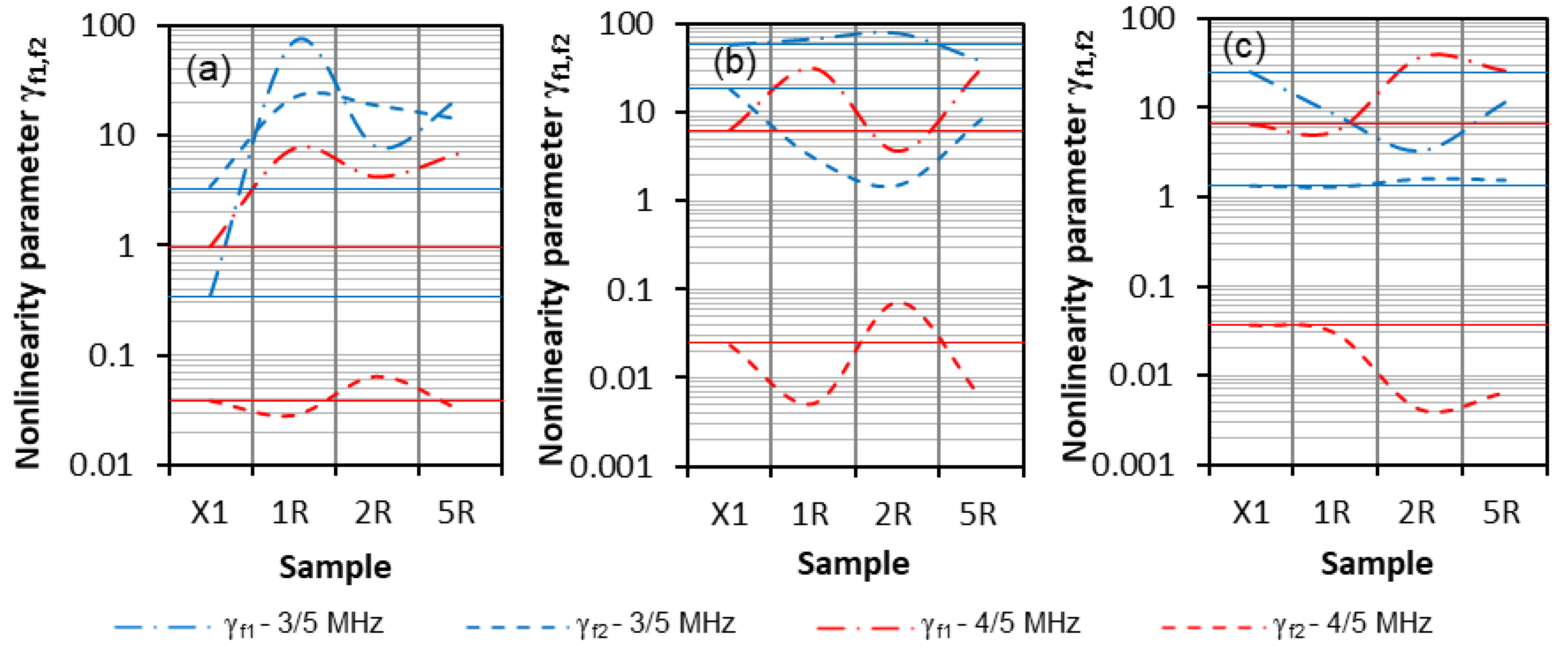
4.2.3. Results and Discussion—Lateral Defect
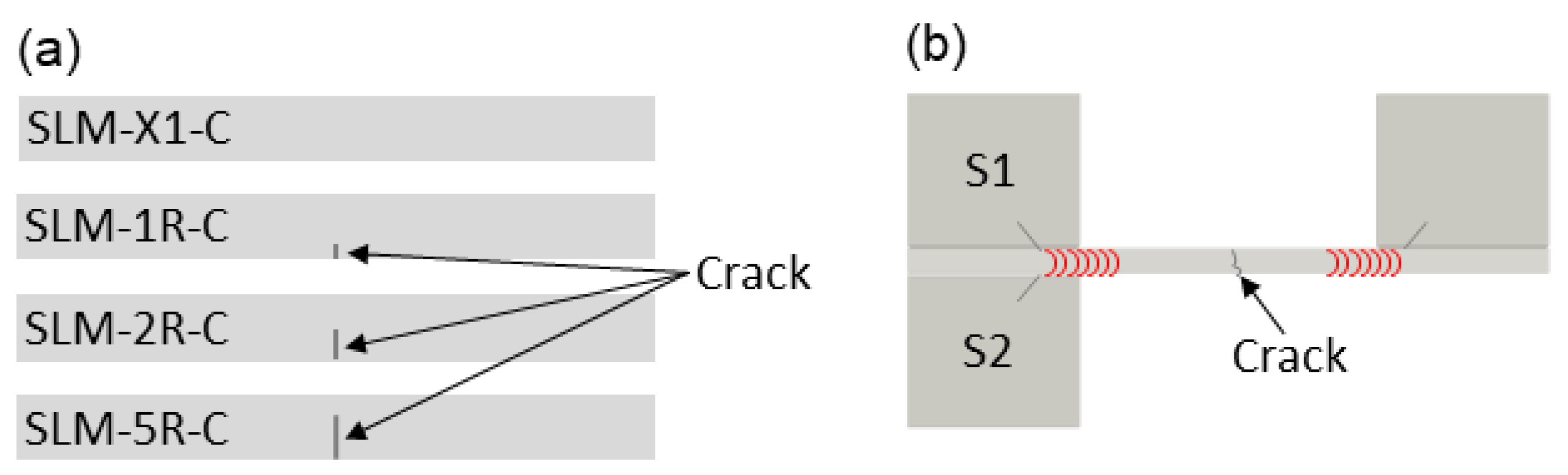
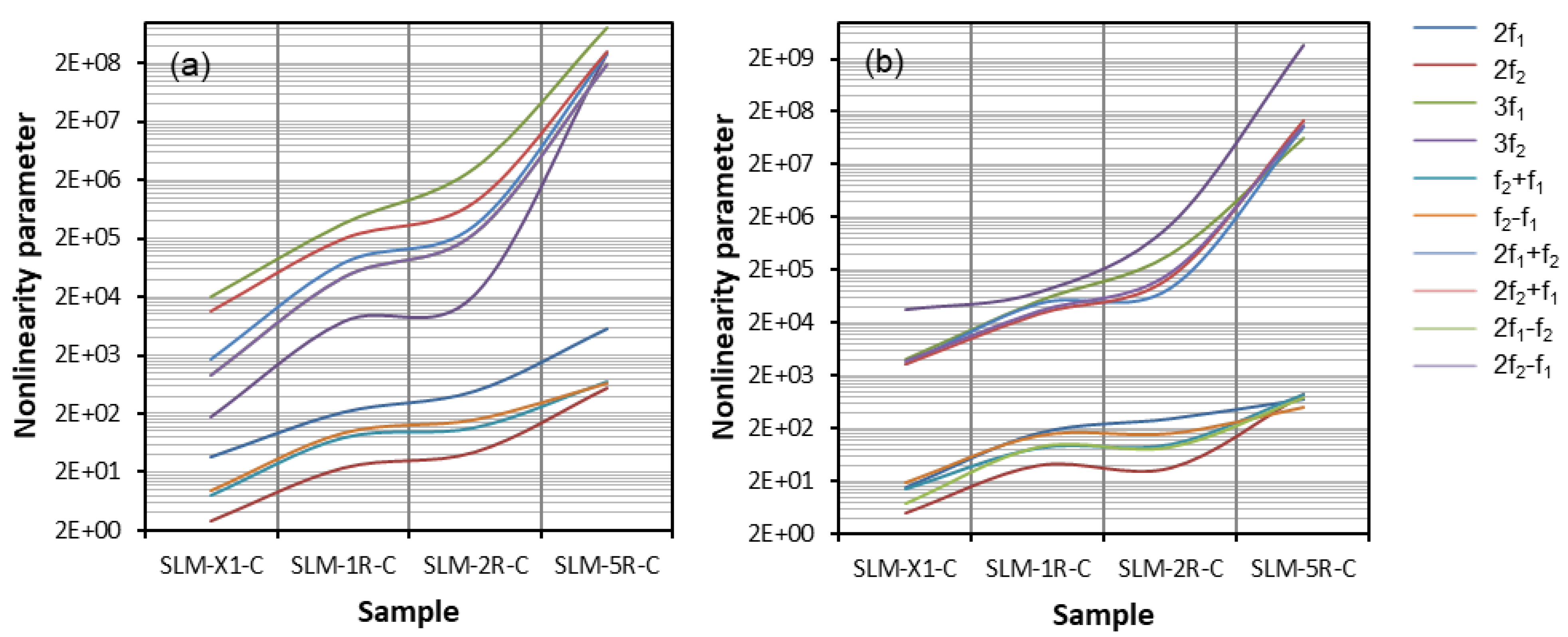
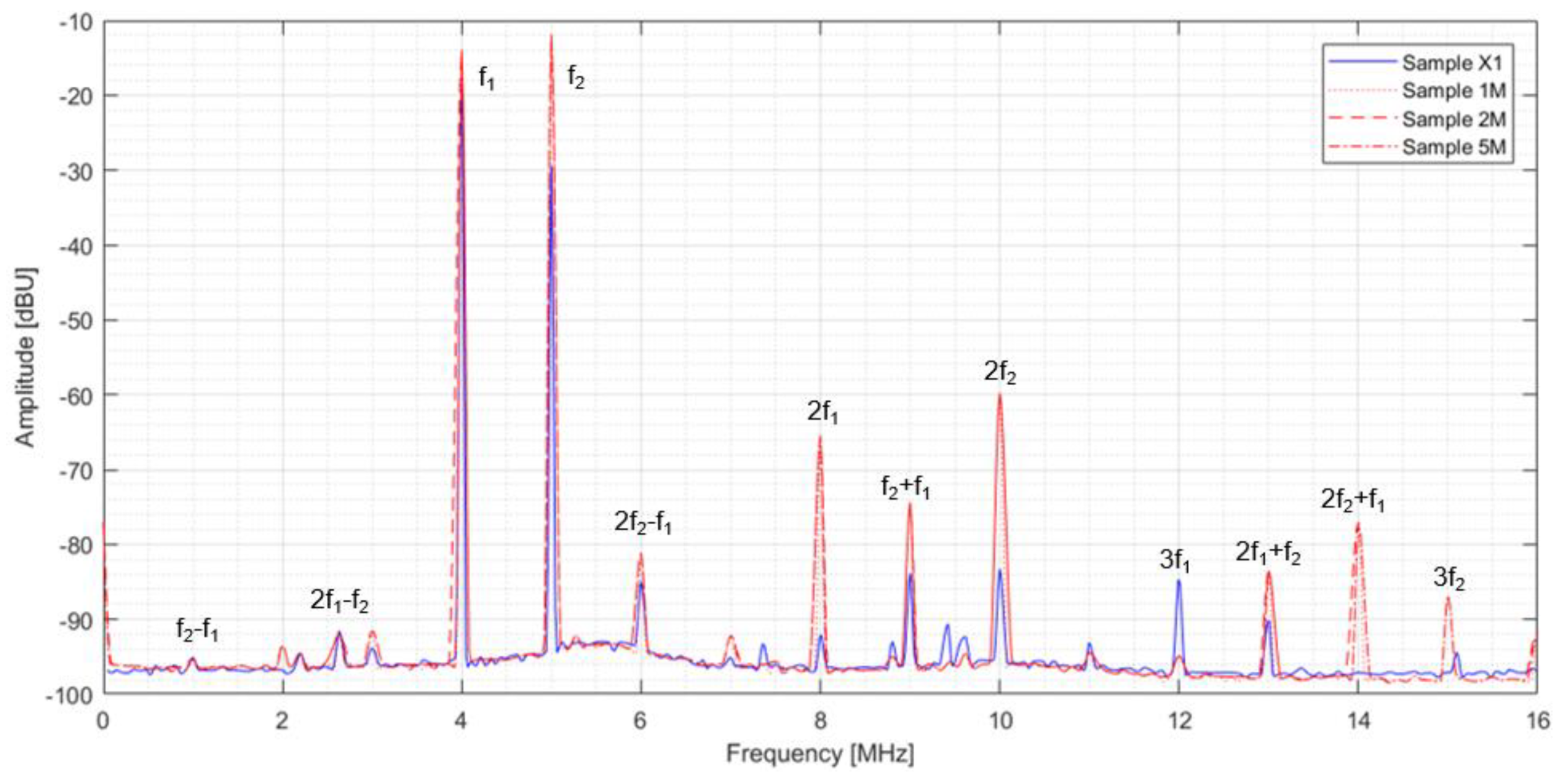
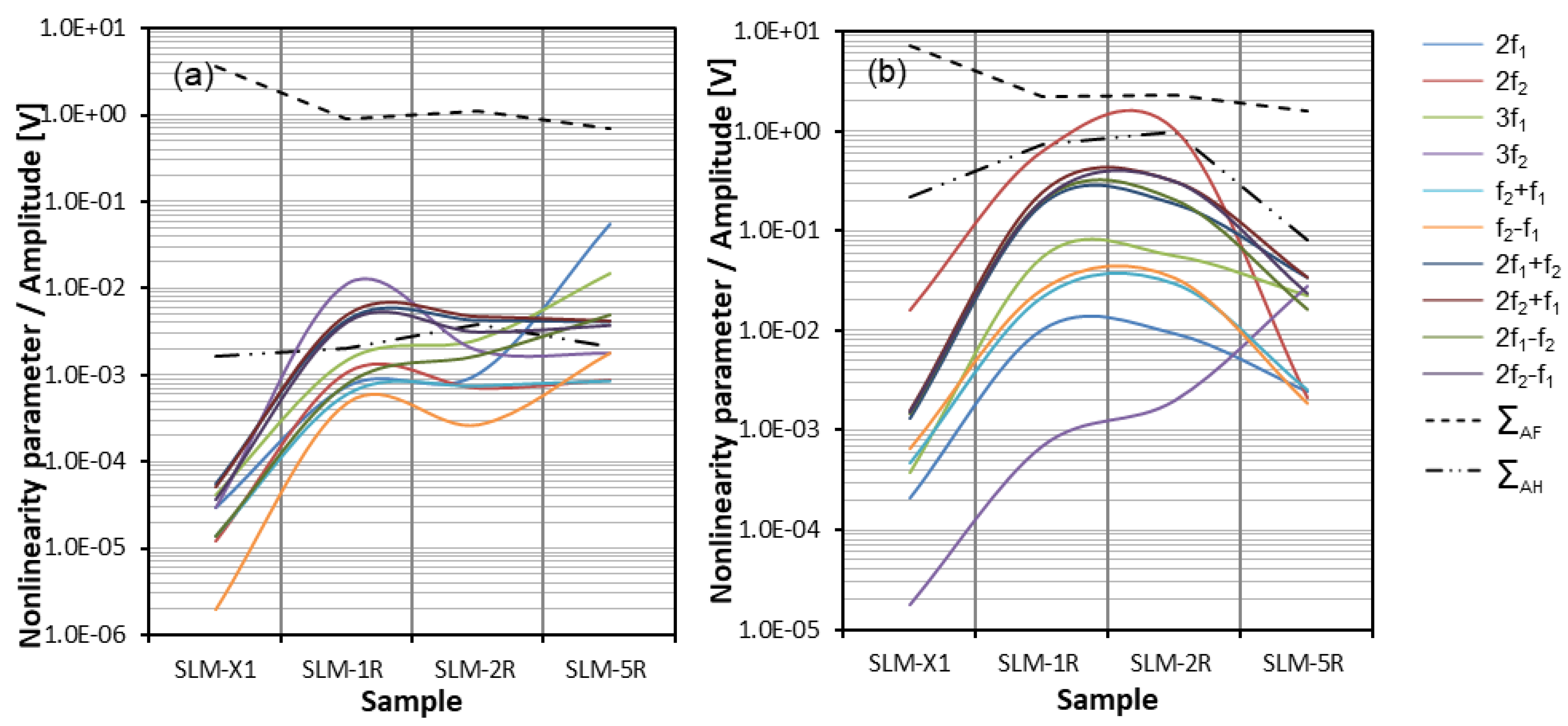
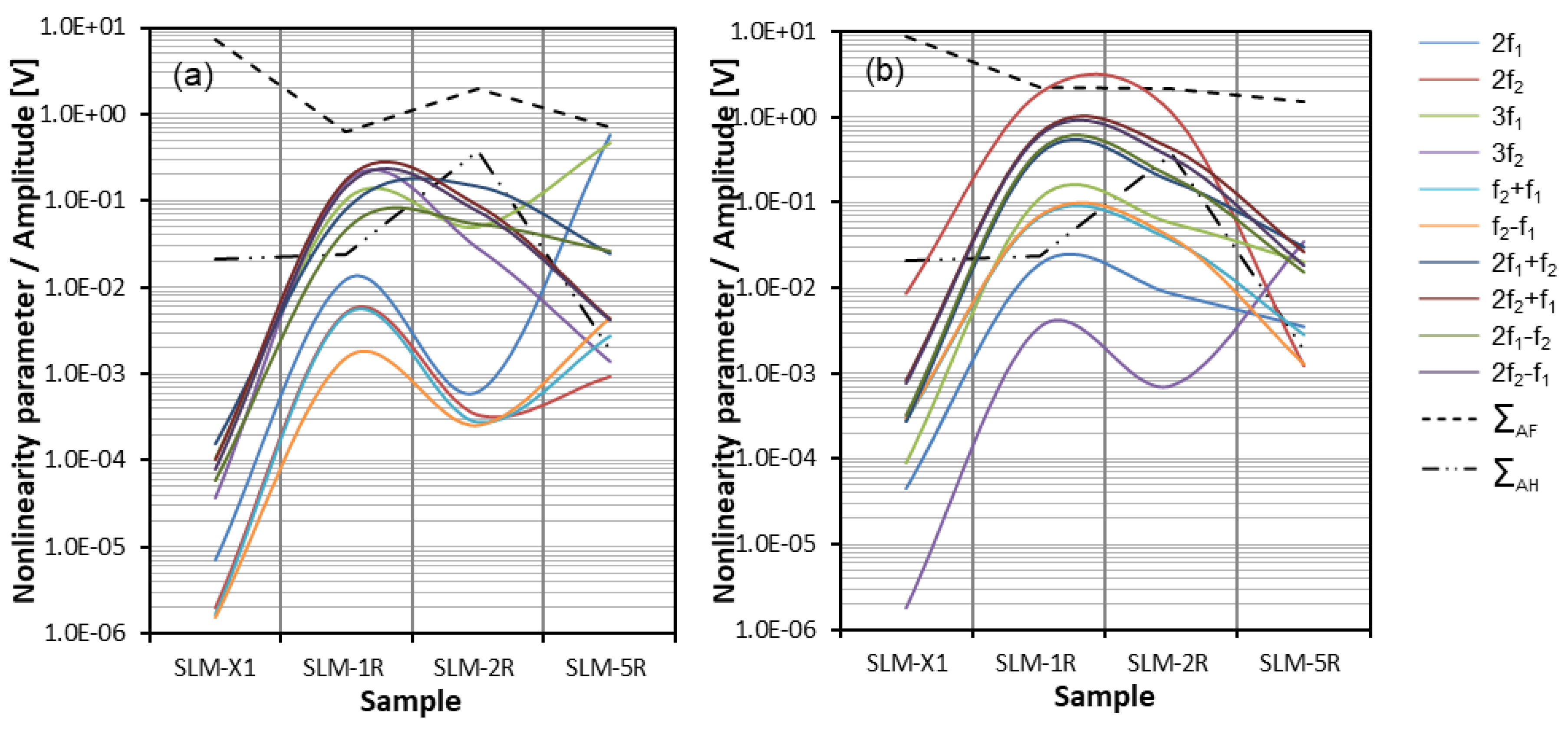
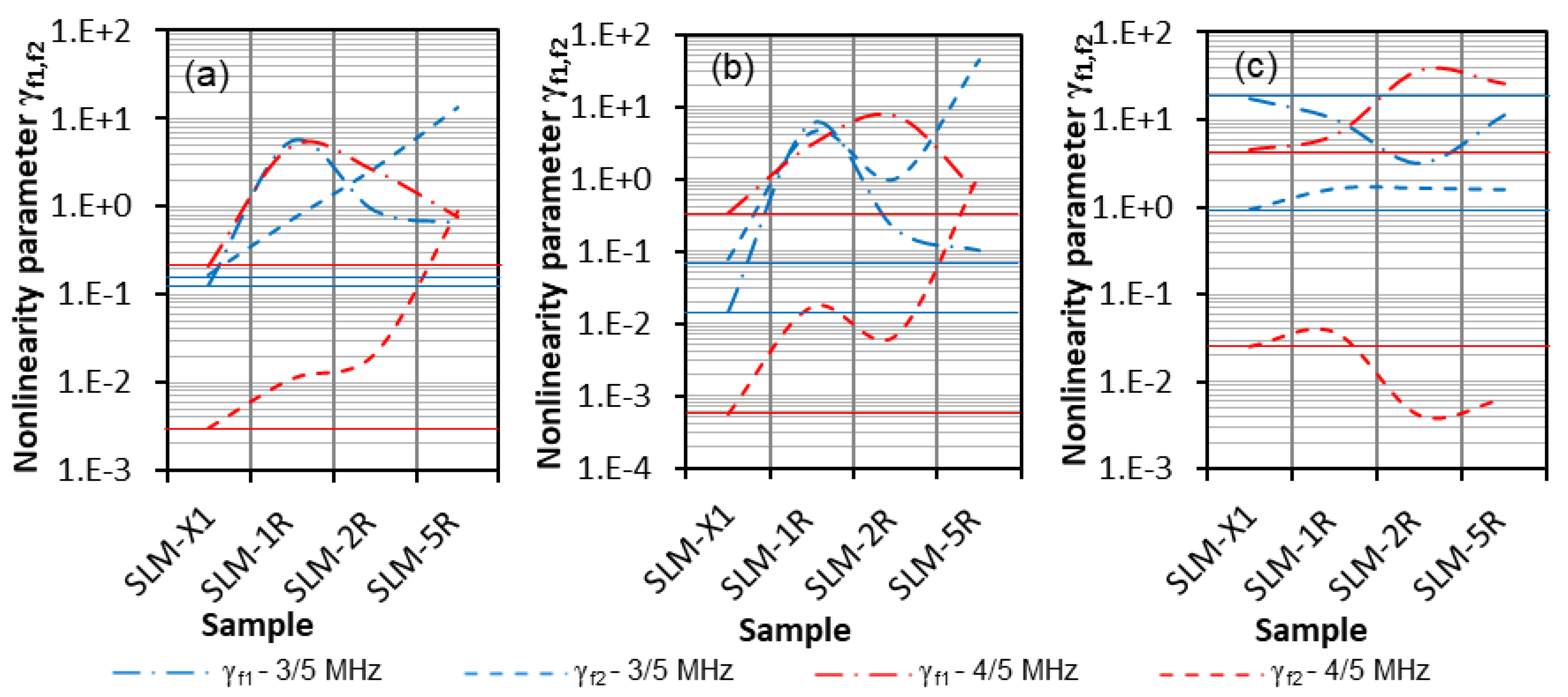
4.3. Plate Samples—SLM Manufactured
Results and Discussion
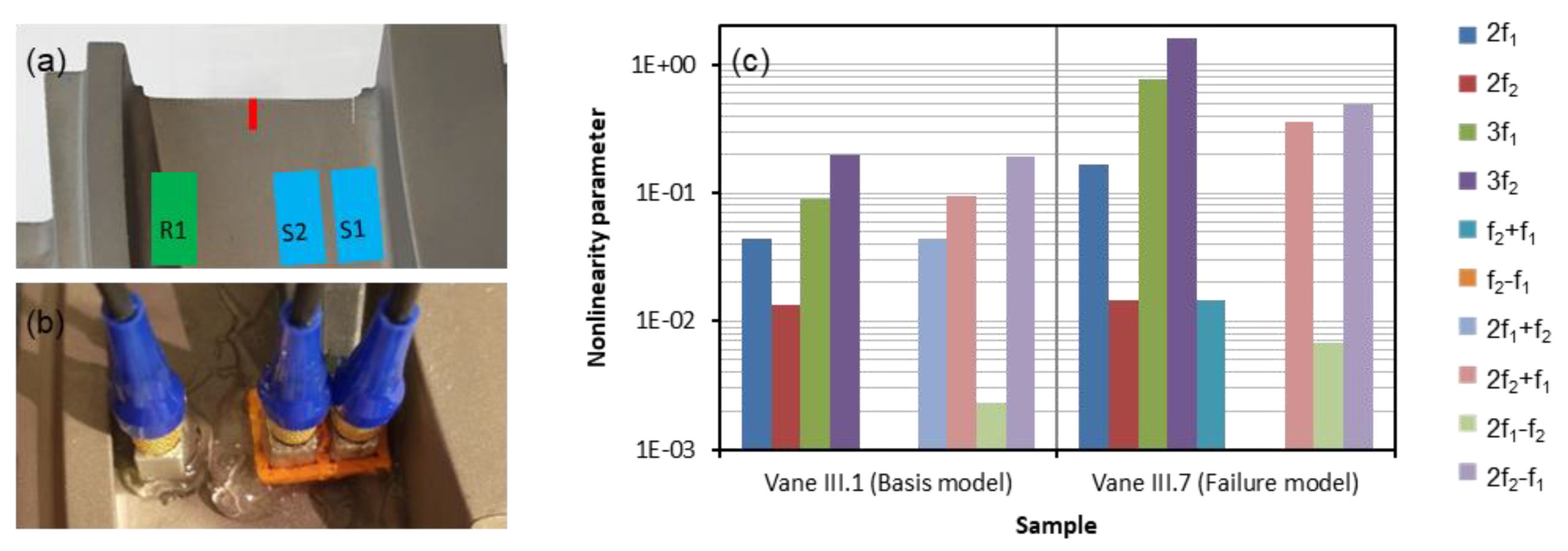
4.4. Turbine Vane
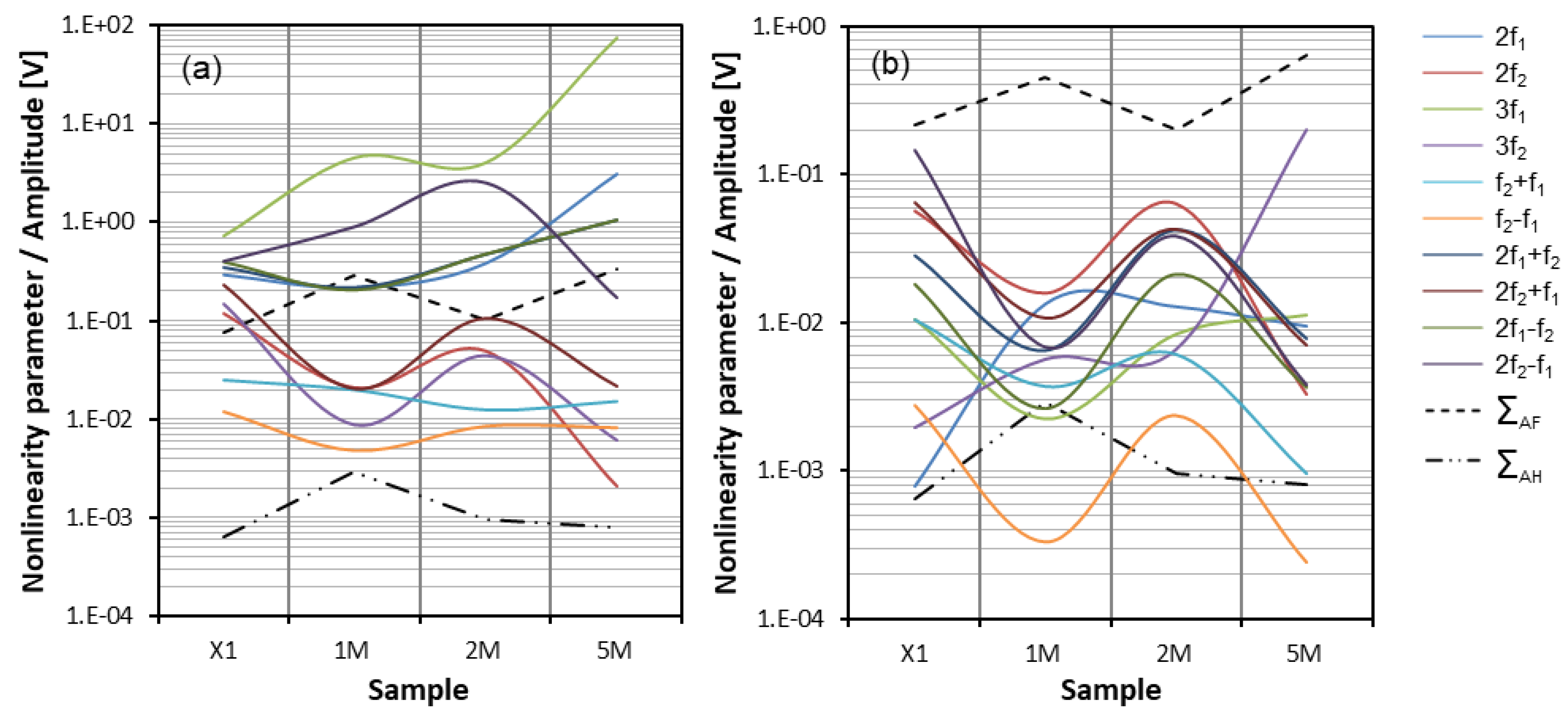
Results and Discussion
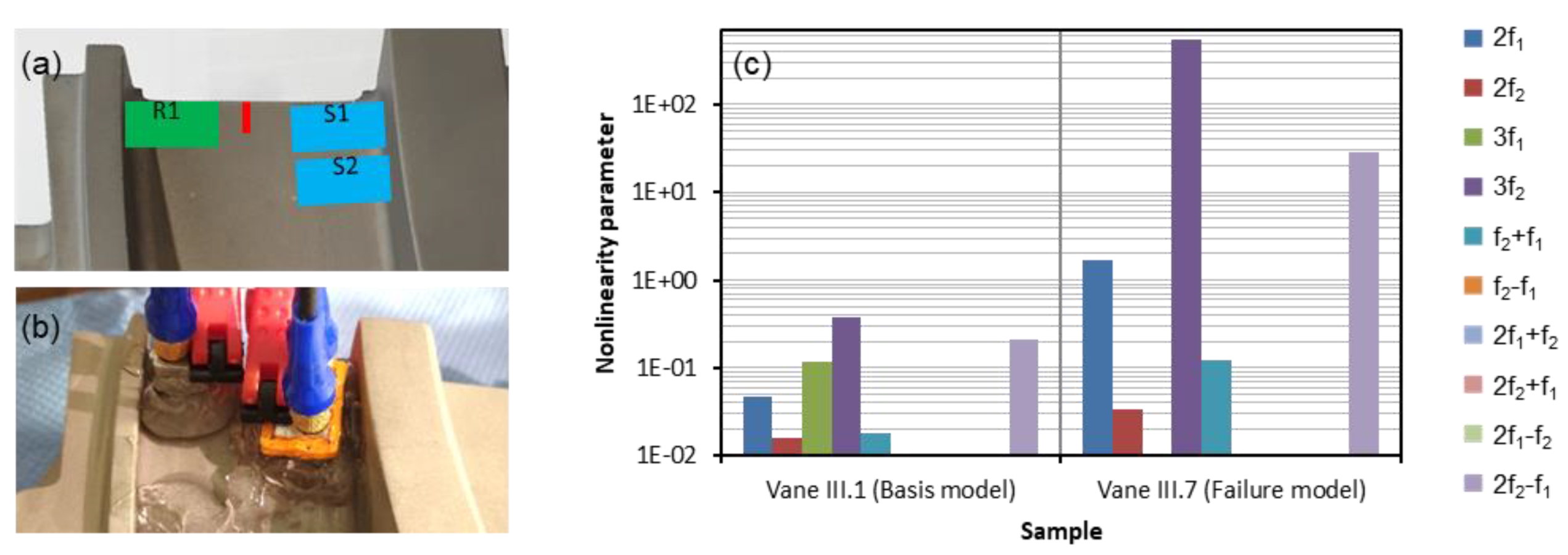
4.5. Turbine Blade
Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Z.L.; Achenbach, J.D. Reflection and Transmission of Rayleigh Surface Waves by a Material Interphase. J. Appl. Mech. 1991, 58, 688. [Google Scholar] [CrossRef]
- Achenbach, J.D.; Lin, W.; Keer, L.M. Mathematical Modelling of Ultrasonic Wave Scattering by sub-Surface Cracks. Ultrasonics 1986, 24, 207–215. [Google Scholar] [CrossRef]
- Angel, Y.C.; Achenbach, J.D. Reflection and Transmission of Obliquely Incident Rayleigh Waves by a Surface-Breaking Crack. Acoust. Soc. Am. 1983, 74, S87. [Google Scholar] [CrossRef]
- Hikata, A.; Chick, B.B.; Elbaum, C. Dislocation Contribution to the Second Harmonic Generation of Ultrasonic Waves. J. Appl. Phys. 1965, 36, 229–236. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear Ultrasonic Characterization of Fatigue Microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Mitra, M.; Gopalakrishnan, S. Guided Wave Based Structural Health Monitoring: A Review. Smart Mater. Struct. 2016, 25, 53001. [Google Scholar] [CrossRef]
- Cho, H.; Lissenden, C.J. Structural Health Monitoring of Fatigue Crack Growth in Plate Structures with Ultrasonic Guided Waves. Struct. Health Monit. 2012, 11, 393–404. [Google Scholar] [CrossRef]
- Chan, H.; Masserey, B.; Fromme, P. High Frequency Guided Ultrasonic Waves for Hidden Fatigue Crack Growth Monitoring in multi-Layer Model Aerospace Structures. Smart Mater. Struct. 2015, 24, 25037. [Google Scholar] [CrossRef] [Green Version]
- Masserey, B.; Fromme, P. Analysis of High Frequency Guided Wave Scattering at a Fastener Hole with a View to Fatigue Crack Detection. Ultrasonics 2017, 76, 78–86. [Google Scholar] [CrossRef]
- Masserey, B.; Fromme, P. Fatigue Crack Growth Monitoring Using High-Frequency Guided Waves. Struct. Health Monit. 2013, 12, 484–493. [Google Scholar] [CrossRef] [Green Version]
- Masserey, B.; Fromme, P. Noncontact monitoring of fatigue crack growth using high frequency guided waves. In Proceedings of the SPIE 9061, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2014, Bellingham, WA, USA, 8 March 2014. [Google Scholar]
- Broda, D.; Staszewski, W.J.; Martowicz, A.; Uhl, T.; Silberschmidt, V.V. Modelling of Nonlinear Crack—Wave Interactions for Damage Detection Based on Ultrasound—A Review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Guan, L.; Zou, M.; Wan, X.; Li, Y. Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique. Appl. Sci. 2020, 10, 2135. [Google Scholar] [CrossRef] [Green Version]
- Lim, H.J.; Sohn, H. Online Fatigue Crack Prognosis Using Nonlinear Ultrasonic Modulation. Struct. Health Monit. 2019, 18, 1889–1902. [Google Scholar] [CrossRef]
- Mihara, T.; Konishi, G.; Miura, Y.; Ishida, H. Accurate sizing of closed crack using nonlinear ultrasound of space with high voltage transformer pulser technique. In Proceedings of the American Institute of Physics Conference, Baltimore, MD, USA, 21–26 July 2013; AIP Publishing LLC: Melville, NY, USA, 2014; pp. 727–732. [Google Scholar]
- Moll, J.; Kexel, C.; Pötzsch, S.; Rennoch, M.; Herrmann, A.S. Temperature Affected Guided Wave Propagation in a Composite Plate Complementing the Open Guided Waves Platform. Sci. Data 2019, 6, 191. [Google Scholar] [CrossRef] [PubMed]
- Pan, Q.; Pan, R.; Shao, C.; Chang, M.; Xu, X. Research Review of Principles and Methods for Ultrasonic Measurement of Axial Stress in Bolts. Chin. J. Mech. Eng. 2020, 33, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Jhang, K.-Y.; Kim, K.-C. Evaluation of Material Degradation Using Nonlinear Acoustic Effect. Ultrasonics 1999, 37, 39–44. [Google Scholar] [CrossRef]
- Frouin, J.; Sathish, S.; Matikas, T.E.; Na, J.K. Ultrasonic Linear and Nonlinear Behavior of Fatigued Ti–6Al–4V. J. Mater. Res. 1999, 14, 1295–1298. [Google Scholar] [CrossRef]
- Rothenfusser, M.; Mayr, M.; Baumann, J. Acoustic Nonlinearities in Adhesive Joints. Ultrasonics 2000, 38, 322–326. [Google Scholar] [CrossRef]
- Yost, W.T. Nonlinear ultrasonic pulsed measurements and applications to metal processing and fatigue. In Proceedings of the 27th Annual Review of Progress in Quantitative Nondestructive Evaluation, Ames, IA, USA, 16–20 July 2000; AIP: Melville, NY, USA, 2000; pp. 1268–1275. [Google Scholar]
- Boccardi, S.; Callá, D.B.; Ciampa, F.; Meo, M. Nonlinear Elastic multi-Path Reciprocal Method for Damage Localisation in Composite Materials. Ultrasonics 2018, 82, 239–245. [Google Scholar] [CrossRef] [Green Version]
- Jeong, H.; Nahm, S.-H.; Jhang, K.-Y.; Nam, Y.-H. A Nondestructive Method for Estimation of the Fracture Toughness of CrMoV Rotor Steels Based on Ultrasonic Nonlinearity. Ultrasonics 2003, 41, 543–549. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Johnson, P.A. Dynamic nonlinear elasticity in geomaterials. La Rivista del Nuovo Cimento 2001, 24, 1–46. [Google Scholar]
- Straka, L.; Yagodzinskyy, Y.; Landa, M.; Hänninen, H. Detection of Structural Damage of Aluminum Alloy 6082 Using Elastic Wave Modulation Spectroscopy. NDT & E Int. 2008, 41, 554–563. [Google Scholar]
- Malfense Fierro, G.P.; Meo, M. Residual Fatigue Life Estimation Using a Nonlinear Ultrasound Modulation Method. Smart Mater. Struct. 2015, 24, 25040. [Google Scholar] [CrossRef]
- Malfense Fierro, G.P.; Meo, M. Nonlinear Imaging (NIM) of Flaws in a Complex Composite Stiffened Panel Using a Constructive Nonlinear Array (CNA) Technique. Ultrasonics 2017, 74, 30–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malfense Fierro, G.P. Development of Nonlinear Ultrasound Techniques for Multidisciplinary Engineering Applications. Ph.D. Thesis, University of Bath, Bath, UK, 2014. [Google Scholar]
- Jingpin, J.; Xiangji, M.; Cunfu, H.; Bin, W. Nonlinear Lamb Wave-Mixing Technique for micro-Crack Detection in Plates. NDT & E Int. 2017, 85, 63–71. [Google Scholar]
- Amura, M.; Meo, M.; Amerini, F. Baseline-free Estimation of Residual Fatigue Life Using a Third Order Acoustic Nonlinear Parameter. Acoust. Soc. Am. 2011, 130, 1829–1837. [Google Scholar] [CrossRef] [Green Version]
- TenCate, J.A.; van den Abeele, K.E.A.; Shankland, T.J.; Johnson, P.A. Laboratory Study of Linear and Nonlinear Elastic Pulse Propagation in Sandstone. J. Acoust. Soc. Am. 1996, 100, 1383–1391. [Google Scholar] [CrossRef] [Green Version]
- Bermes, C.; Kim, J.-Y.; Qu, J.; Jacobs, L.J. Nonlinear Lamb Waves for the Detection of Material Nonlinearity. Mech. Syst. Signal Process. 2008, 22, 638–646. [Google Scholar] [CrossRef]
- Herrmann, J.; Kim, J.-Y.; Jacobs, L.J.; Qu, J.; Littles, J.W.; Savage, M.F. Assessment of Material Damage in a Nickel-Base Superalloy Using Nonlinear Rayleigh Surface Waves. J. Appl. Phys. 2006, 99, 124913. [Google Scholar] [CrossRef]
- Markovic, N.; Stojic, D.; Cvetkovic, R.; Radojicic, V.; Conic, S. Numerical Modeling of Ultrasonic Wave Propagation-by Using of Explicit FEM in ABAQUS. Facta Univ. Ser. Archit. Civ. Eng. 2018, 16, 135–147. [Google Scholar] [CrossRef]
- Schwarz, C.; Werner, E.; Dirschmid, H.J. 1D Wave Propagation in a Rod: Analytic Treatment for non-Trivial Boundary Conditions. Proc. Appl. Math. Mech. 2010, 10, 525–526. [Google Scholar] [CrossRef]
- Cui, Z.; Huang, Y. Discussion on Acoustic Databases in LS-DYNA. 2017. Available online: http://www.lstc.com/sites/default/files/marketing/new_features/12_Acoustic_Databases_ZheCui_2017_01.pdf (accessed on 8 March 2020).
- Maraghechi, B.; Hasani, M.H.; Kolios, M.C.; Tavakkoli, J. Temperature Dependence of Acoustic Harmonics Generated by Nonlinear Ultrasound Wave Propagation in Water at Various Frequencies. J. Acoust. Soc. Am. 2016, 139, 2475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, B.; Zhao, X.; Li, S.; Han, C.; Wei, Q.; Wen, S.; Liu, J.; Shi, Y. Differences in Microstructure and Properties between Selective Laser Melting and Traditional Manufacturing for Fabrication of Metal Parts: A Review. Front. Mech. Eng. 2015, 10, 111–125. [Google Scholar] [CrossRef]









| Mode | Frequency |
|---|---|
| n1 | f1 |
| n2 | f2 |
| n3 | 2f1 |
| n4 | 2f2 |
| n5 | 3f1 |
| n6 | 3f2 |
| n7 | f2 + f1 |
| n8 | f2 − f1 |
| n9 | 2f1 + f2 |
| n10 | 2f1 − f2 |
| n11 | 2f2 + f1 |
| n12 | 2f2 − f1 |
| Material | Inconel 718 |
|---|---|
| Density, ρ | 8.2 kg/dm3 |
| Speed of sound, c | 5820 m/s |
| Young’s modulus, E | 205,000 MPa |
| Poisson’s ratio, υ | 0.292 |
| Specimen | Crack Length | Crack Position |
|---|---|---|
| X1 | - | - |
| 1M | 1 mm | Centre |
| 1R | 1 mm | Lateral |
| 2M | 2 mm | Centre |
| 2R | 2 mm | Lateral |
| 5M | 5 mm | Centre |
| 5R | 5 mm | Lateral |
| Specimen | Crack Length | Crack Position |
|---|---|---|
| SLM-X1 | - | - |
| SLM-1R | 1 mm | Lateral |
| SLM-2R | 2 mm | Lateral |
| SLM-5R | 5 mm | Lateral |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mevissen, F.; Meo, M. A Nonlinear Ultrasonic Modulation Method for Crack Detection in Turbine Blades. Aerospace 2020, 7, 72. https://doi.org/10.3390/aerospace7060072
Mevissen F, Meo M. A Nonlinear Ultrasonic Modulation Method for Crack Detection in Turbine Blades. Aerospace. 2020; 7(6):72. https://doi.org/10.3390/aerospace7060072
Chicago/Turabian StyleMevissen, Frank, and Michele Meo. 2020. "A Nonlinear Ultrasonic Modulation Method for Crack Detection in Turbine Blades" Aerospace 7, no. 6: 72. https://doi.org/10.3390/aerospace7060072





