Single-Sensor Acoustic Emission Source Localization in Plate-Like Structures Using Deep Learning †
Abstract
:1. Introduction
2. Deep Learning Architectures
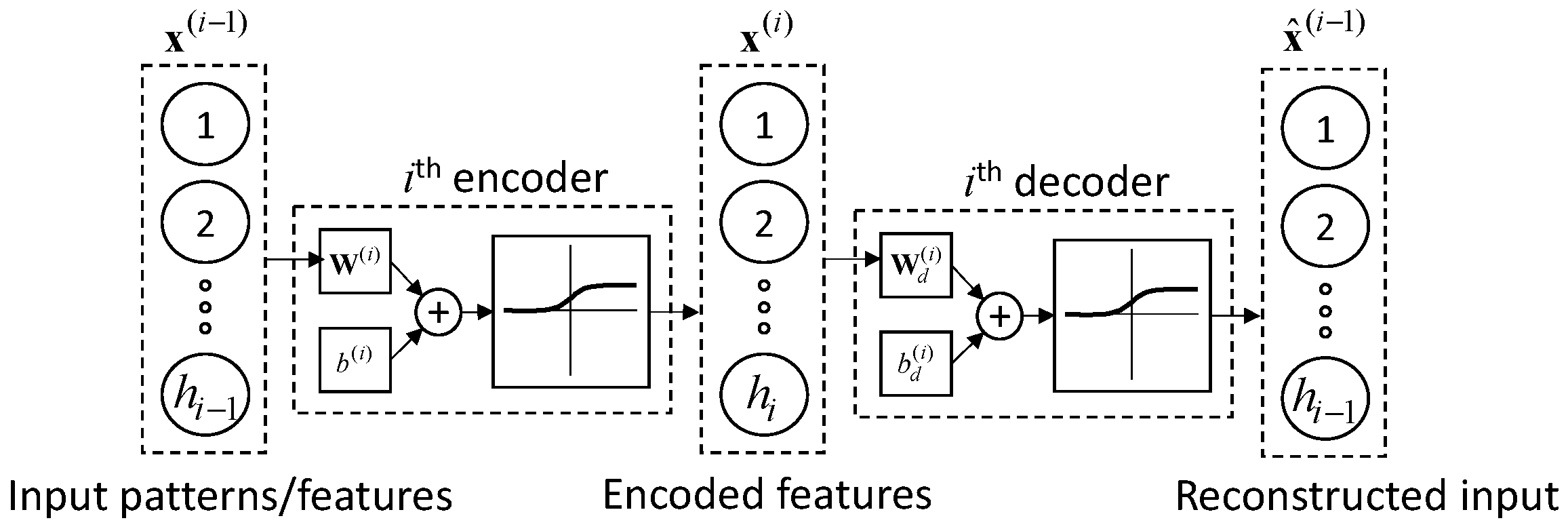
2.1. Stacked Autoencoders
2.1.1. Autoencoders
2.1.2. Softmax Layer
2.1.3. Fine-Tuning
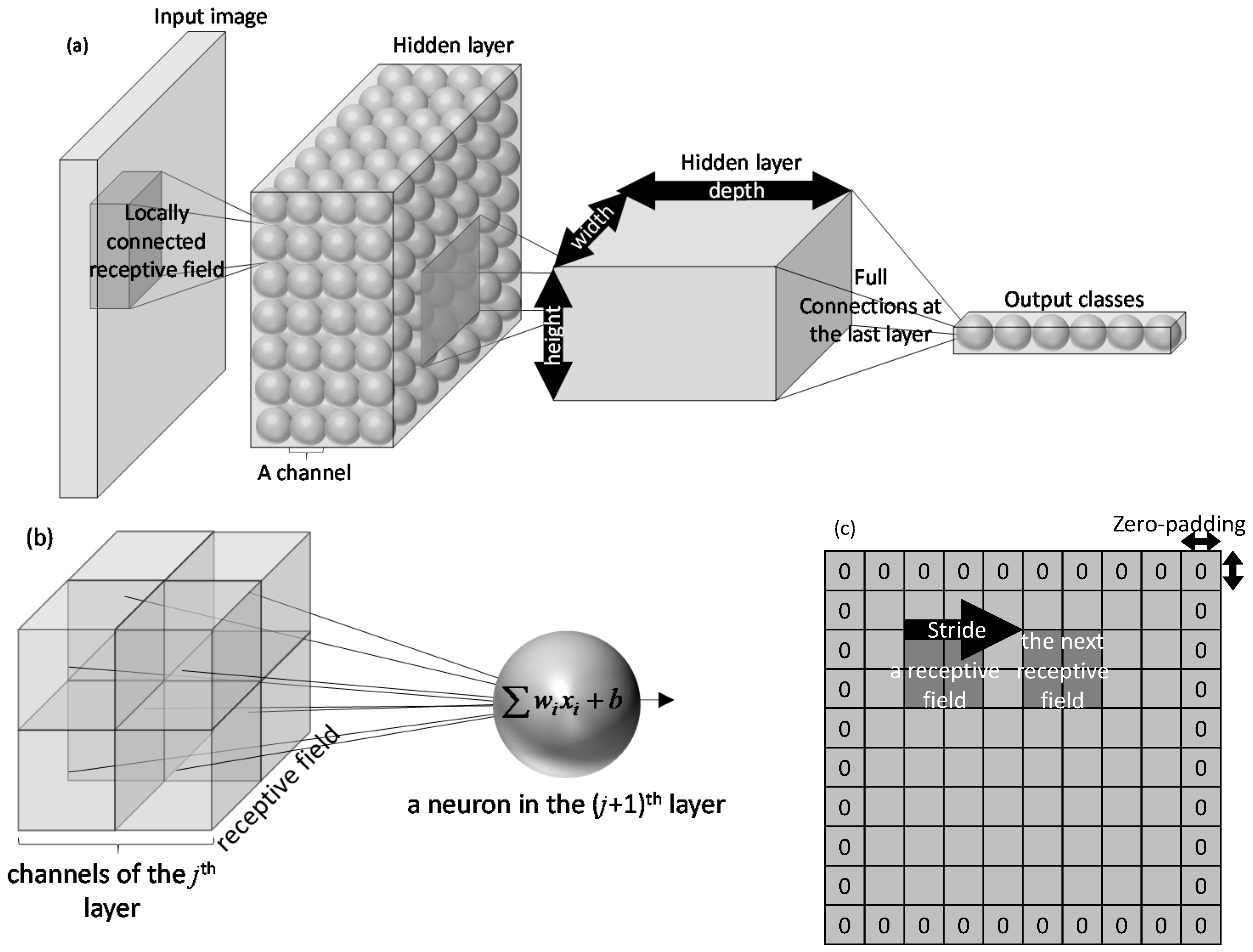
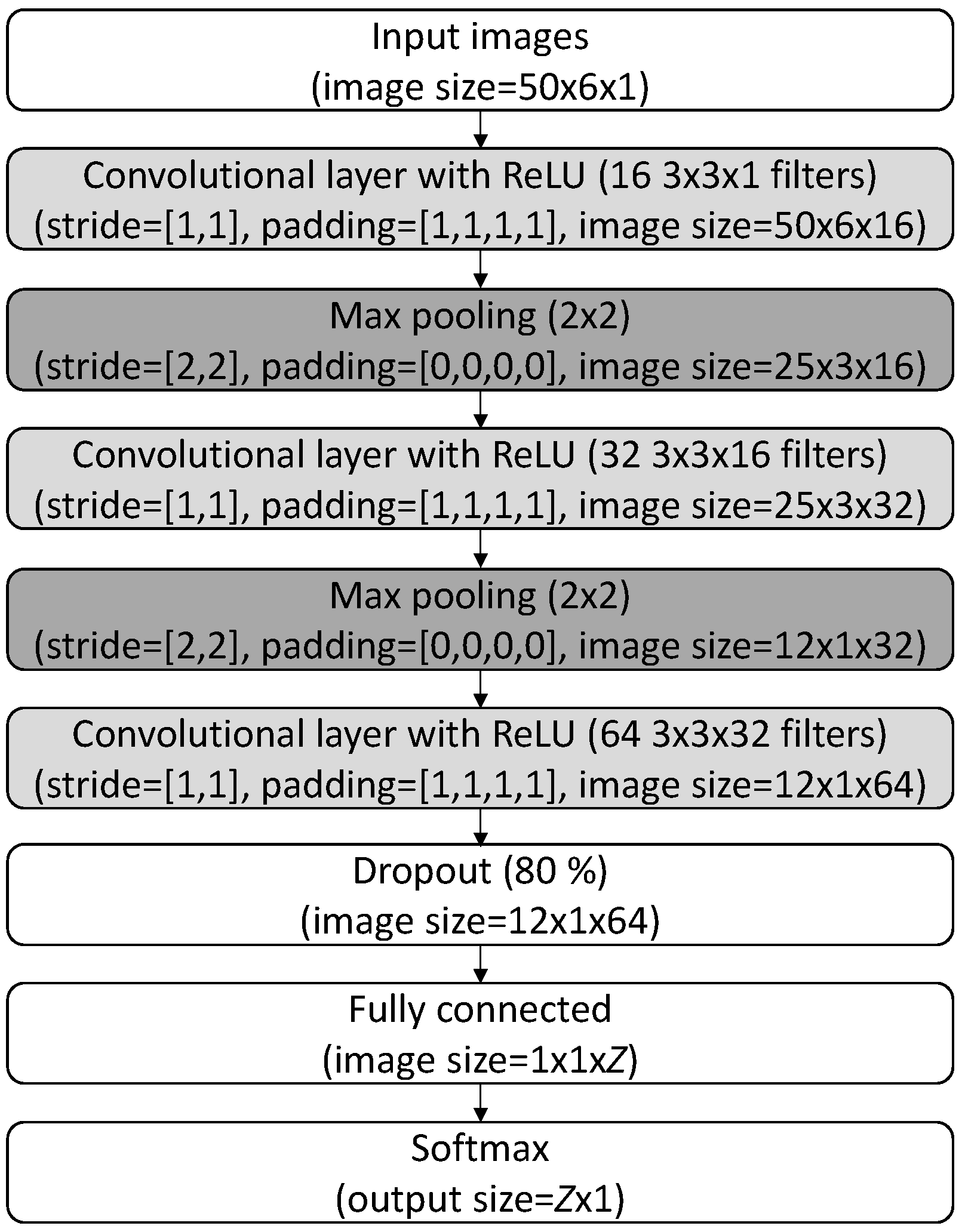
2.2. Convolutional Neural Networks
2.2.1. Convolutional Layer
2.2.2. Max-Pooling Layer
2.2.3. Fully Connected Layer
2.2.4. Visualizing the Inception of a Convolutional Neural Network
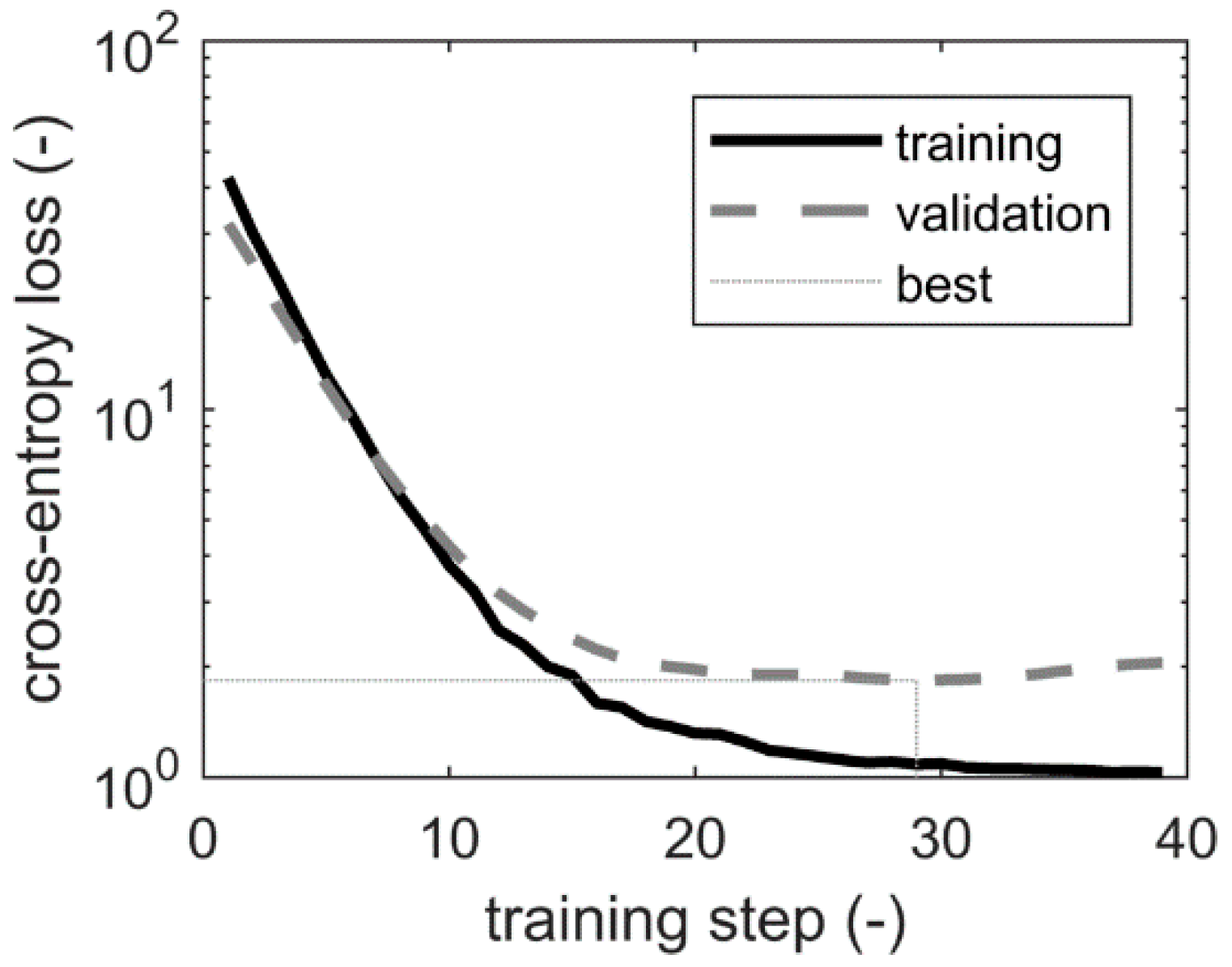
2.3. Overfitting Mitigation in Training Deep Netwoprks
3. Acoustic Emission Source Localization with Deep Learning
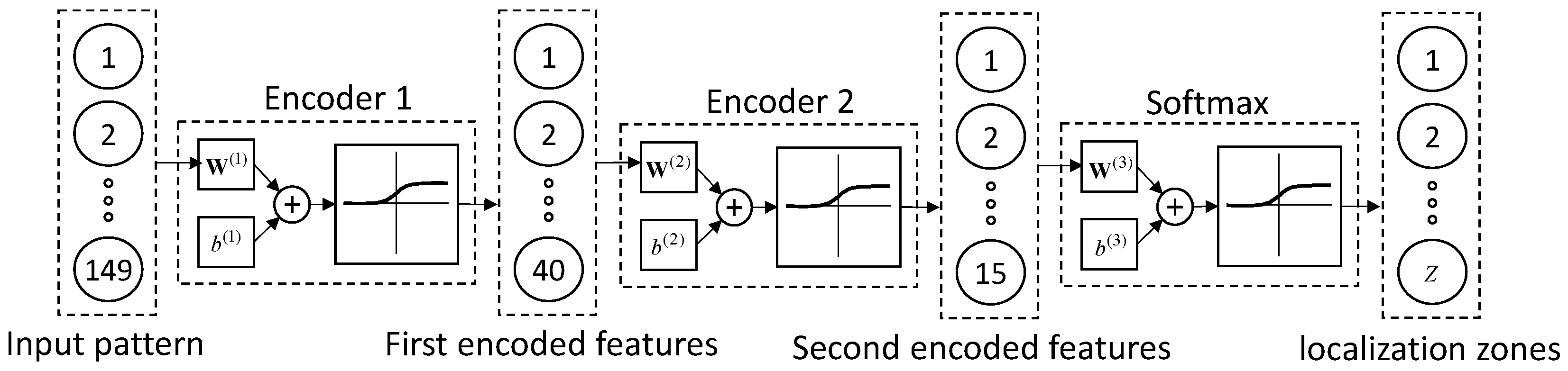
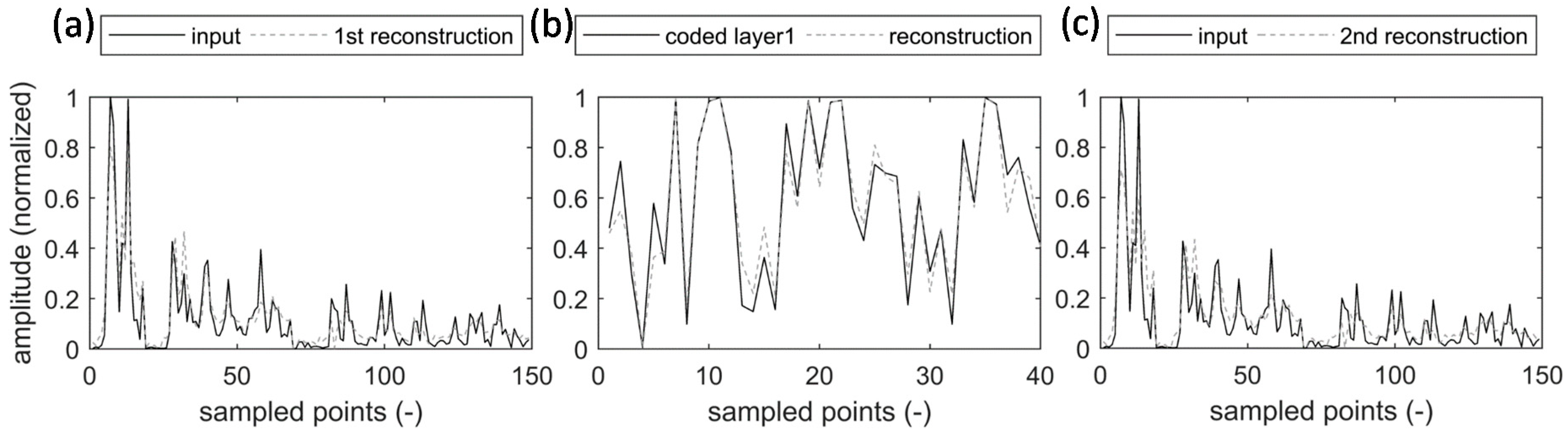
3.1. Stacked Autoencoders
3.2. Convolutional Neural Networks
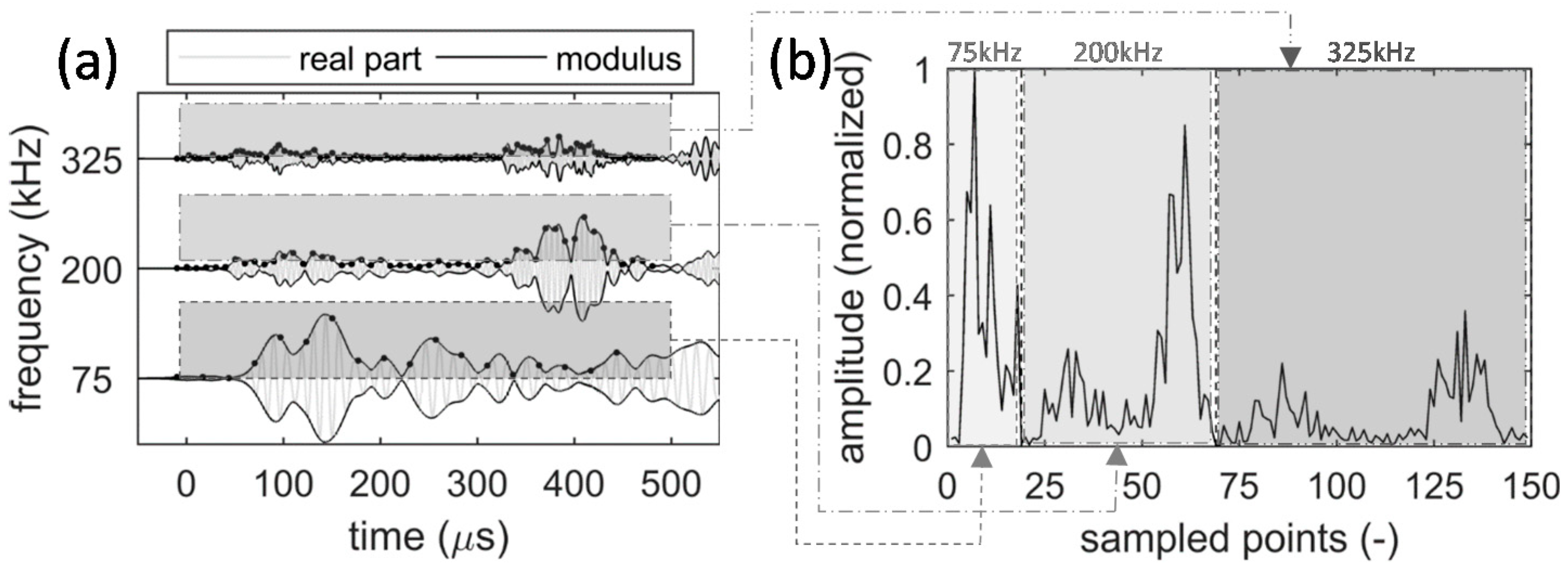
4. Experiments
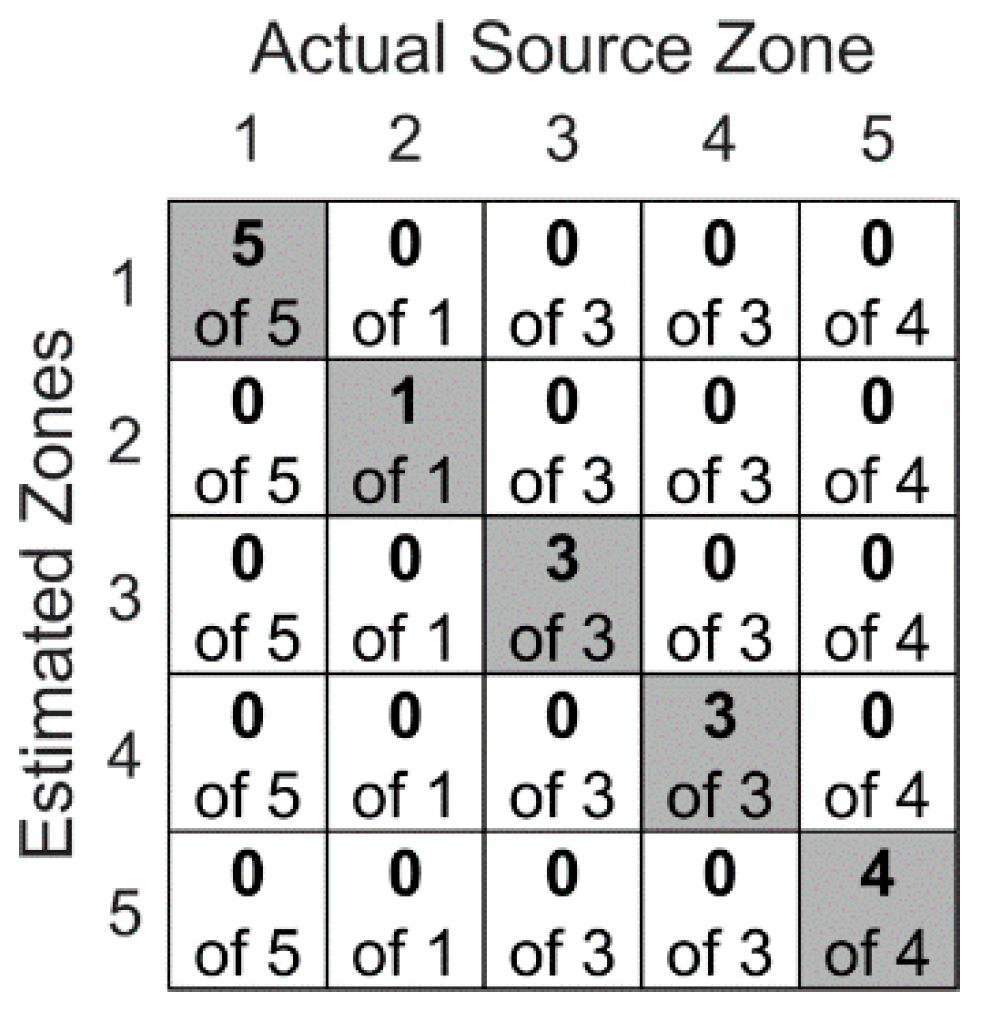
5. Results
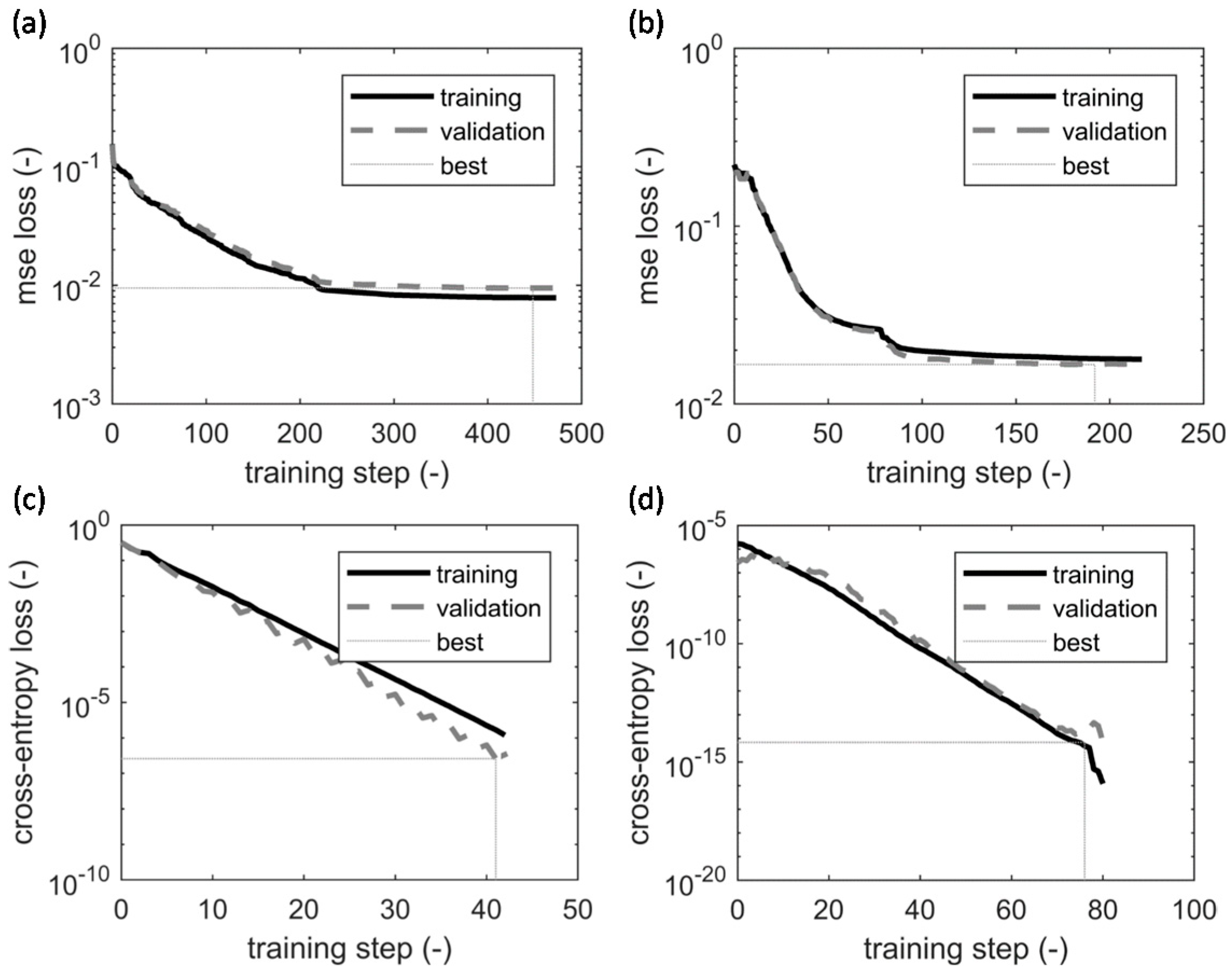
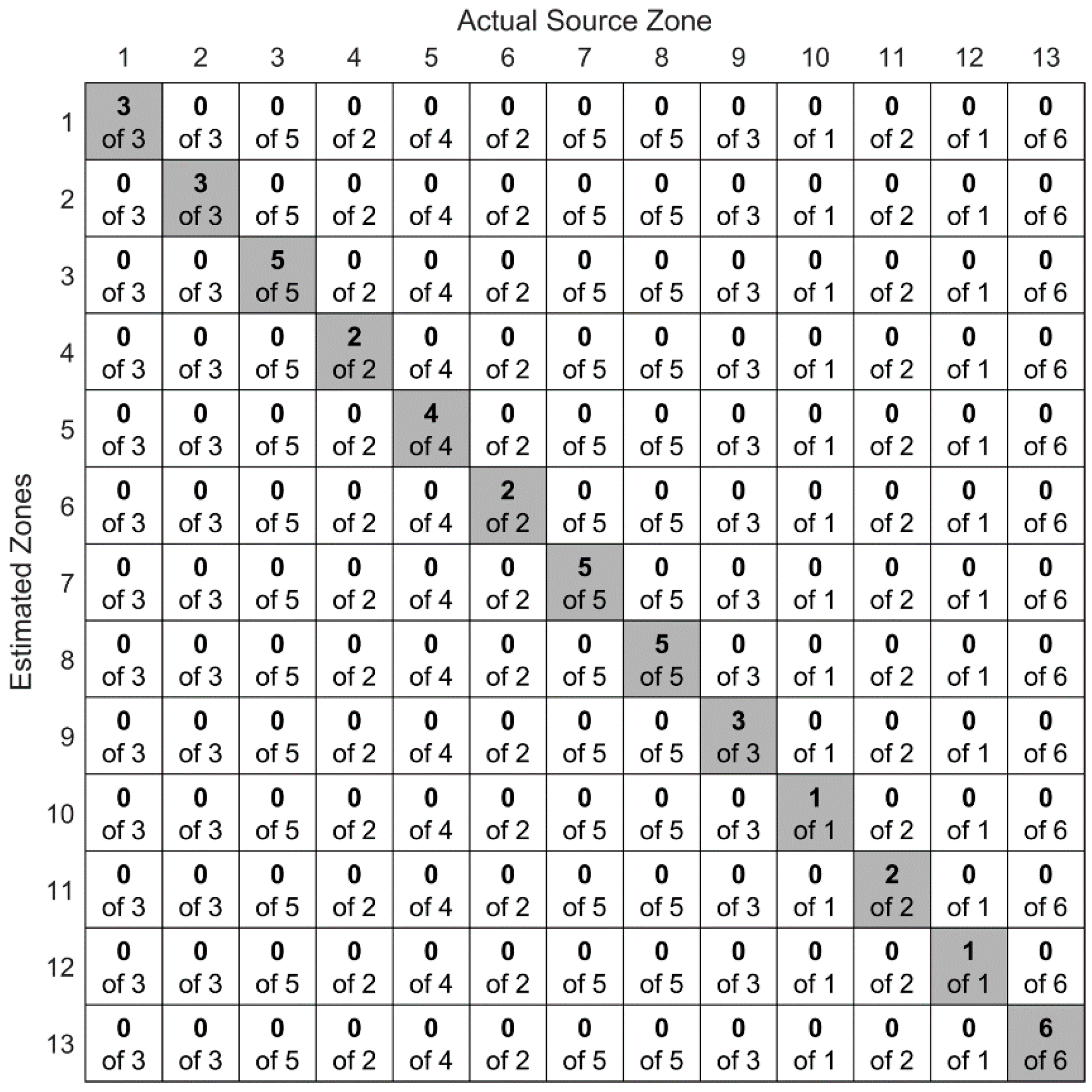
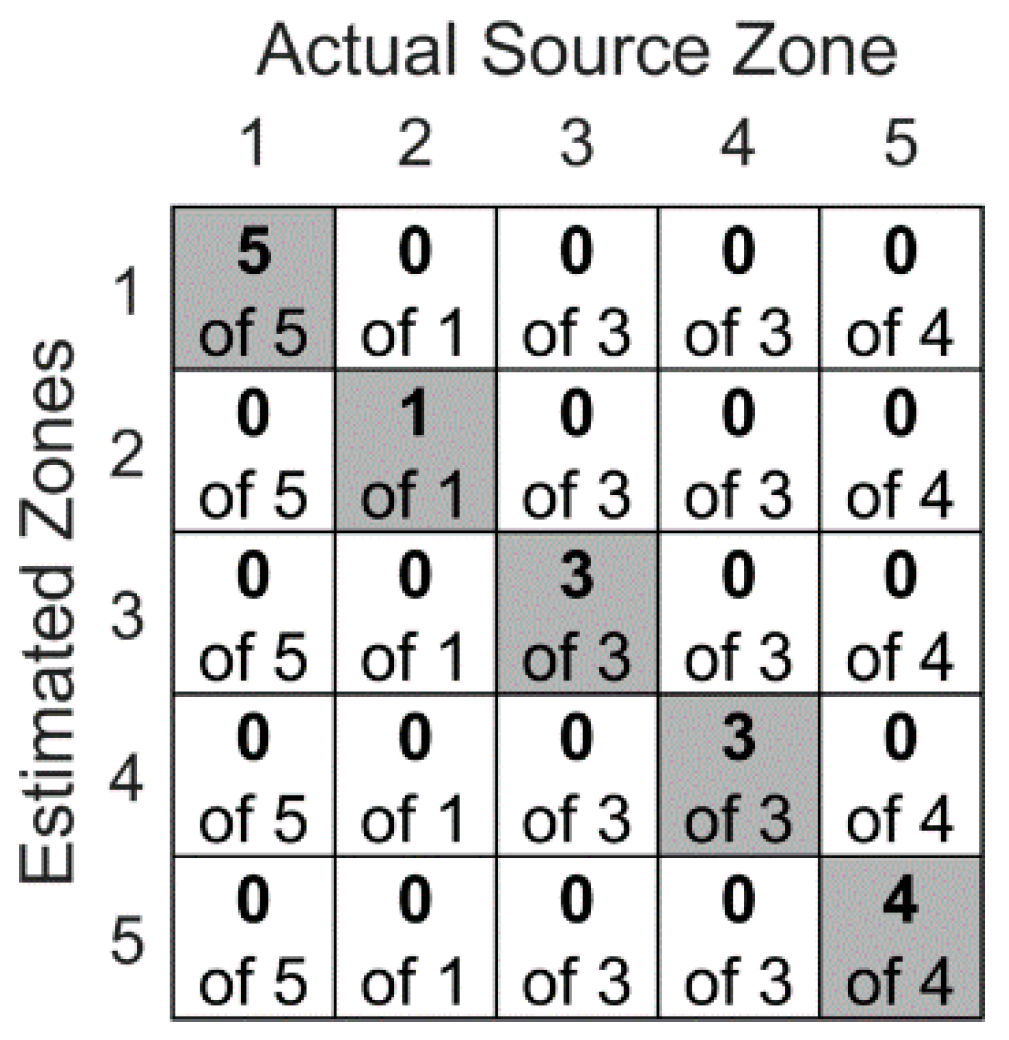
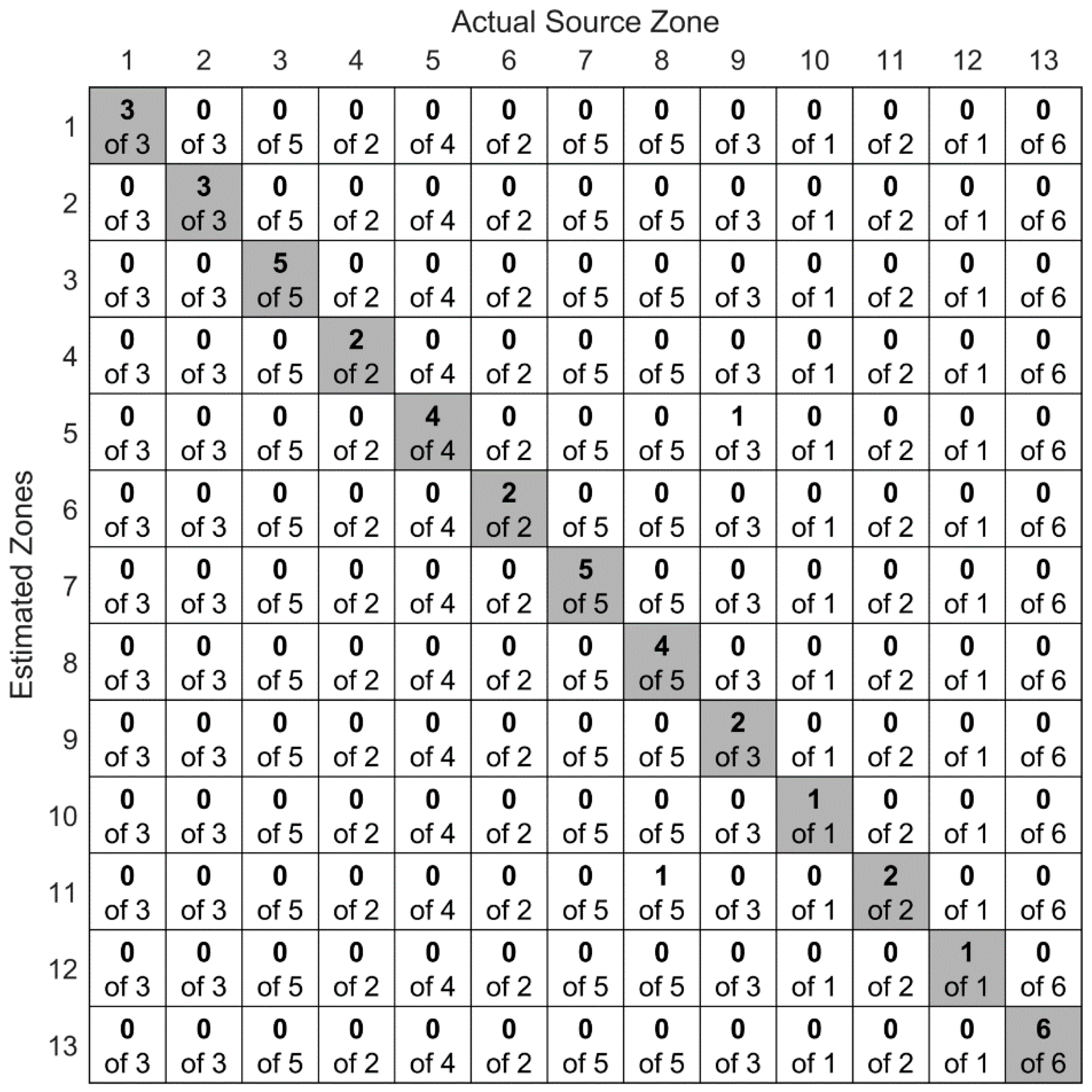
5.1. Stacked Autoencoders
5.2. Convolutional Neural Networks
6. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wilson, H.A.; Goldfein, D.L. USAF Posture Statement Fiscal Year 2018; Department of the Air Force: Washington, DC, USA, 2017. [Google Scholar]
- Encyclopedia of Structural Health Monitoring; Boller, C.; Chang, F.; Fujino, Y. (Eds.) John Wiley and Sons, Ltd.: Chichester, UK, 2009. [Google Scholar]
- Nicolas, M.; Sullivan, R.; Richards, W. Large Scale Applications Using FBG Sensors: Determination of In-Flight Loads and Shape of a Composite Aircraft Wing. Aerospace 2016, 3, 18. [Google Scholar] [CrossRef]
- Kundu, T. Acoustic source localization. Ultrasonics 2014, 54, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Kundu, T.; Das, S.; Jata, K.V. Point of impact prediction in isotropic and anisotropic plates from the acoustic emission data. J. Acoust. Soc. Am. 2007, 122, 2057–2066. [Google Scholar] [CrossRef] [PubMed]
- Kundu, T.; Yang, X.; Nakatani, H.; Takeda, N. A two-step hybrid technique for accurately localizing acoustic source in anisotropic structures without knowing their material properties. Ultrasonics 2015, 56, 271–278. [Google Scholar] [CrossRef] [PubMed]
- Sen, N.; Kundu, T. A new wave front shape-based approach for acoustic source localization in an anisotropic plate without knowing its material properties. Ultrasonics 2018. [Google Scholar] [CrossRef] [PubMed]
- Dubuc, B.; Ebrahimkhanlou, A.; Salamone, S. Simultaneous Localization and Classification of Acoustic Emission Sources in Plates Using a Guided Wave-Based Sparse Reconstruction. In Proceedings of the 11th International Workshop on Structural Health Monitoring, Real-Time Material State Awareness and Data-Driven Safety Assurance, Stanford, CA, USA, 12–14 September 2017; Chang, F.-K., Fotis, K., Eds.; Destech Publications: Stanford, CA, USA, 2017; Volume 1, pp. 1779–1787. [Google Scholar]
- Prosser, W.H.; Hamstad, M.A.; Gary, J.; O’Gallagher, A. Reflections of AE Waves in Finite Plates: Finite Element Modeling and Experimental Measurements. J. Acoust. Emiss. 1999, 17, 37–47. [Google Scholar]
- Hamstad, M.A.; Gallagher, A.O.; Gary, J. Effects of lateral plate dimensions on acoustic emission signals from dipole sources. J. Acoust. Emiss. 2001, 19, 258–274. [Google Scholar]
- Hamstad, M.A.; Downs, K.S.; O’Gallagher, A. Practical aspects of acoustic emission source location by a wavelet transform. J. Acoust. Emiss. 2003, 21, 70–94. [Google Scholar]
- Farhangdoust, S.; Younesian, D.; Esmailzadeh, E. Interaction of Higher Modes in Nonlinear Free Vibration of Stiffened Rectangular Plates. In Proceedings of the ASME 29th Conference on Mechanical Vibration and Noise, Cleveland, OH, USA, 6–9 August 2017; ASME: Cleveland, OH, USA, 2017; Volume 8, p. V008T12A043. [Google Scholar]
- Bhuiyan, M.Y.; Haider, M.F.; Poddar, B.; Giurgiutiu, V. Guided wave crack detection and size estimation in stiffened structures. In Proceedings of the SPIE Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, Civil Infrastructure, and Transportation XII, Denver, CO, USA, 4–8 March 2018; Shull, P.J., Ed.; SPIE: Denver, CO, USA, 2018; p. 91. [Google Scholar]
- Carpenter, S.H.; Gonnan, M.R. A Waveform Investigation of the Acoustic Emission Generated during the Deformation and Cracking of 7075 Aluminum. J. Acoust. Emiss. 1995, S01–S07. [Google Scholar]
- Achdjian, H.; Moulin, E.; Benmeddour, F.; Assaad, J.; Chehami, L. Source Localisation in a Reverberant Plate Using Average Coda Properties and Early Signal Strength. Acta Acust. United Acust. 2014, 100, 834–841. [Google Scholar] [CrossRef]
- Ernst, R.; Zwimpfer, F.; Dual, J. One sensor acoustic emission localization in plates. Ultrasonics 2016, 64, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Toyama, N.; Koo, J.-H.; Oishi, R.; Enoki, M.; Kishi, T. Two-dimensional AE source location with two sensors in thin CFRP plates. J. Mater. Sci. Lett. 2001, 20, 1823–1825. [Google Scholar] [CrossRef]
- Jiao, J.; Wu, B.; He, C. Acoustic emission source location methods using mode and frequency analysis. Struct. Control Health Monit. 2008, 15, 642–651. [Google Scholar] [CrossRef]
- Holford, K.M.; Carter, D. Acoustic Emission Source Location. Key Eng. Mater. 1999, 167–168, 162–171. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Salamone, S. Acoustic emission source localization in thin metallic plates: A single-sensor approach based on based on multimodal edge reflections. Ultrasonics 2017, 78, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimkhanlou, A.; Salamone, S. A probabilistic framework for single-sensor acoustic emission source localization in thin metallic plates. Smart Mater. Struct. 2017, 26, 95026. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Salamone, S. Probabilistic location estimation of acoustic emission sources in isotropic plates with one sensor. In Proceedings of the SPIE, Health Monitoring of Structural and Biological Systems, Portland, OR, USA, 25–29 March 2017; Kundu, T., Ed.; SPIE: Portland, OR, USA, 2017; Volume 10170, p. 1017029. [Google Scholar]
- Ebrahimkhanlou, A.; Dubuc, B.; Salamone, S. Damage localization in metallic plate structures using edge-reflected lamb waves. Smart Mater. Struct. 2016, 25, 85035. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Salamone, S. A Deep Learning Approach for Single-sensor Acoustic Emission Source Localization in Plate-like Structures. In Proceedings of the 11th International Workshop on Structural Health Monitoring: Real-Time Material State Awareness and Data-Driven Safety Assurance, Stanford, CA, USA, 12–14 September 2017; Chang, F.-K., Fotis, K., Eds.; Destech Publications: Stanford, CA, USA, 2017; Volume 2, pp. 2139–2146. [Google Scholar]
- Hsu, N.N. Acoustic Emissions Simulator. US Patent 4018084 A, 19 April 1977. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 0262035618. [Google Scholar]
- Sharif-Khodaei, Z.; Ghajari, M.; Aliabadi, M.H. Determination of impact location on composite stiffened panels. Smart Mater. Struct. 2012, 21, 105026. [Google Scholar] [CrossRef]
- Al-Jumaili, S.K.; Pearson, M.R.; Holford, K.M.; Eaton, M.J.; Pullin, R. Acoustic emission source location in complex structures using full automatic delta T mapping technique. Mech. Syst. Signal Process. 2016, 72–73, 513–524. [Google Scholar] [CrossRef]
- Li, C.; Sanchez, R.-V.; Zurita, G.; Cerrada, M.; Cabrera, D.; Vásquez, R.E. Gearbox fault diagnosis based on based on deep random forest fusion of acoustic and vibratory signals. Mech. Syst. Signal Process. 2016, 76–77, 283–293. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- He, M.; He, D. Deep Learning Based Approach for Bearing Fault Diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th international conference on Machine learning (ICML ’08), Helsinki, Finland, 5–9 July 2008; ACM Press: New York, NY, USA, 2008; pp. 1096–1103. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 15, 1–9. [Google Scholar] [CrossRef]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Bishop, M.C. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006; ISBN 9780387310732. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the 14th International Conference on Artifcial Intelligence and Statistics (AISTATS) 2011, Fort Lauderdale, FL, USA, 11–13 April 2011; Volume 15, pp. 315–323. [Google Scholar]
- Alexander, M.; Olah, C.; Tyka, M. Inceptionism: Going Deeper into Neural Networks. Available online: https://research.googleblog.com/2015/06/inceptionism-going-deeper-into-neural.html (accessed on 21 April 2018).
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the Computer Vision ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2014; Volume 8689, pp. 818–833. [Google Scholar] [CrossRef]
- Agarwal, A.; Negahban, S.N.; Wainwright, M.J. Noisy matrix decomposition via convex relaxation: Optimal rates in high dimensions. J. Mach. Learn. Res. 2011, 15, 1929–1958. [Google Scholar] [CrossRef]
- Sarrafi, A.; Poozesh, P.; Niezrecki, C.; Mao, Z. Mode extraction on wind turbine blades via phase-based video motion estimation. In Proceedings of the SPIE, Smart Materials and Nondestructive Evaluation for Energy Systems, Portland, OR, USA, 25–29 March 2017; Meyendorf, N.G., Ed.; SPIE: Portland, OR, USA, 2017; p. 101710E. [Google Scholar]
- Mostavi, A.; Kamali, N.; Tehrani, N.; Chi, S.-W.; Ozevin, D.; Indacochea, J.E. Wavelet-based-based harmonics decomposition of ultrasonic signal in assessment of plastic strain in aluminum. Measurement 2017, 106, 66–78. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Dubuc, B.; Salamone, S. A guided ultrasonic imaging approach in isotropic plate structures using edge reflections. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, Vegas, NV, USA, 20–24 March 2016; Lynch, J.P., Ed.; SPIE: Vegas, NV, USA, 2016; Volume 9803. [Google Scholar]
- Sarrafi, A.; Mao, Z.; Niezrecki, C.; Poozesh, P. Vibration-based damage detection in wind turbine blades using Phase-based Motion Estimation and motion magnification. J. Sound Vib. 2018, 421, 300–318. [Google Scholar] [CrossRef]
- Sarrafi, A.; Mao, Z. Structural operating deflection shape estimation via a hybrid computer-vision algorithm. In Proceedings of the SPIE, Health Monitoring of Structural and Biological Systems XII, Devor, CO, USA, 5 March 2018; Kundu, T., Ed.; SPIE: Devor, CO, USA, 2018; p. 94. [Google Scholar]
- Mohammadi-Ghazi, R.; Marzouk, Y.M.; Büyüköztürk, O. Conditional classifiers and boosted conditional Gaussian mixture model for novelty detection. Pattern Recognit. 2018. [Google Scholar] [CrossRef]
- Sarrafi, A.; Niezrecki, C.; Poozesh, P.; Mao, Z. Applying video magnification for vision-based operating deflection shape evaluation on a wind turbine blade cross-section. In Proceedings of the SPIE, Health Monitoring of Structural and Biological Systems XII, Devor, CO, USA, 5 March 2018; Kundu, T., Ed.; SPIE: Devor, CO, USA, 2018; p. 21. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Ebrahimkhanlou, A.; Salamone, S. Single-sensor acoustic emission source localization in plate-like structures: A deep learning approach. In Proceedings of the SPIE, Health Monitoring of Structural and Biological Systems, Devor, CO, USA, 5 March 2018. [Google Scholar]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebrahimkhanlou, A.; Salamone, S. Single-Sensor Acoustic Emission Source Localization in Plate-Like Structures Using Deep Learning. Aerospace 2018, 5, 50. https://doi.org/10.3390/aerospace5020050
Ebrahimkhanlou A, Salamone S. Single-Sensor Acoustic Emission Source Localization in Plate-Like Structures Using Deep Learning. Aerospace. 2018; 5(2):50. https://doi.org/10.3390/aerospace5020050
Chicago/Turabian StyleEbrahimkhanlou, Arvin, and Salvatore Salamone. 2018. "Single-Sensor Acoustic Emission Source Localization in Plate-Like Structures Using Deep Learning" Aerospace 5, no. 2: 50. https://doi.org/10.3390/aerospace5020050




