Energy-Dynamics Resulting in Turbulent and Acoustic Phenomena in an Underexpanded Jet
Abstract
:1. Introduction
2. Physical Problem and Methodology
2.1. Flowfield Parameters
2.2. Numerical Technique for the Navier-Stokes Solver
2.3. Validation
2.4. Energy-Based Decomposition: Momentum Potential Theory
2.4.1. Theoretical Considerations in MPT
2.4.2. Numerical Implementation of MPT
- The mean solenoidal field, in Equation (3), is calculated as the average of instantaneous from the LES.
- The source term for the total scalar potential in Equation (4), , is obtained from the LES data, by obtaining the time-derivative of instantaneous density. This Poisson equation is then solved to obtain the total scalar potential, .
- The source term for the acoustic scalar potential in Equation (5), , is also calculated from the LES data, by obtaining the time-derivative of instantaneous pressure. Solution of this Poisson equation yields the acoustic scalar potential, .
- The thermal scalar potential is obtained using the relation, .
- Finally, the fluctuating solenoidal component is obtained as, .
3. Results
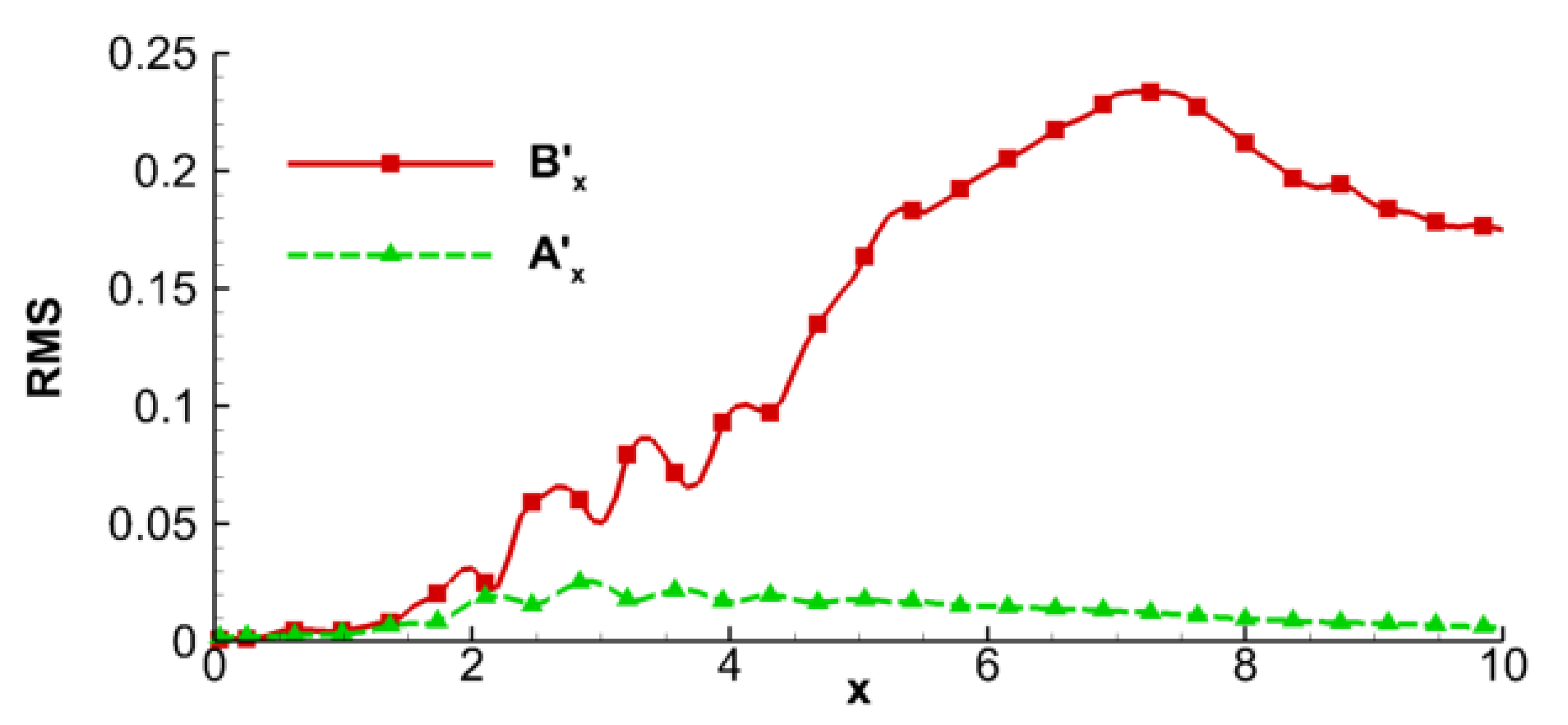
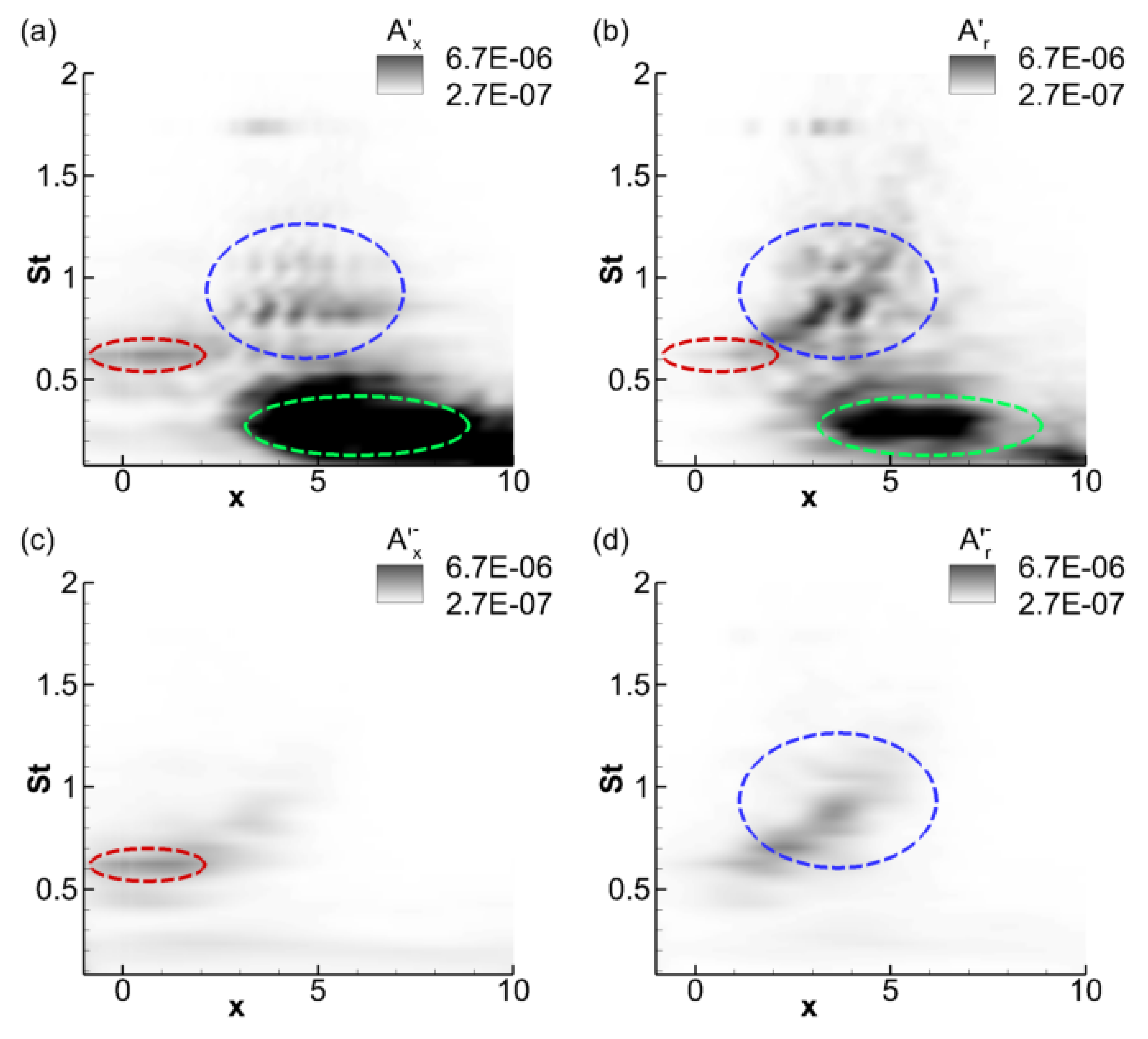
3.1. Fluid-Thermodynamic Modal Features
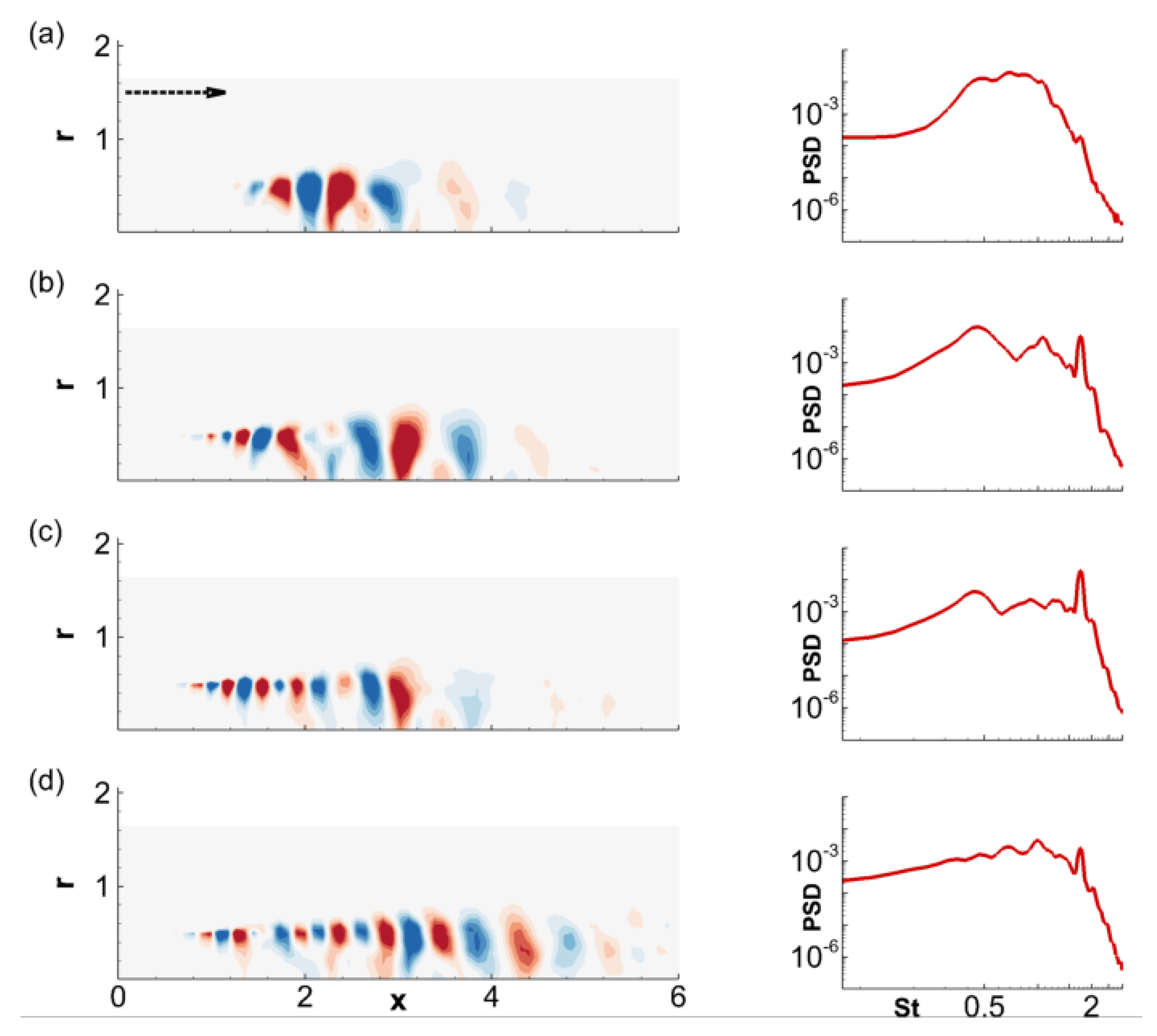
3.2. Relationship of Nearfield Pressure and the Acoustic Mode
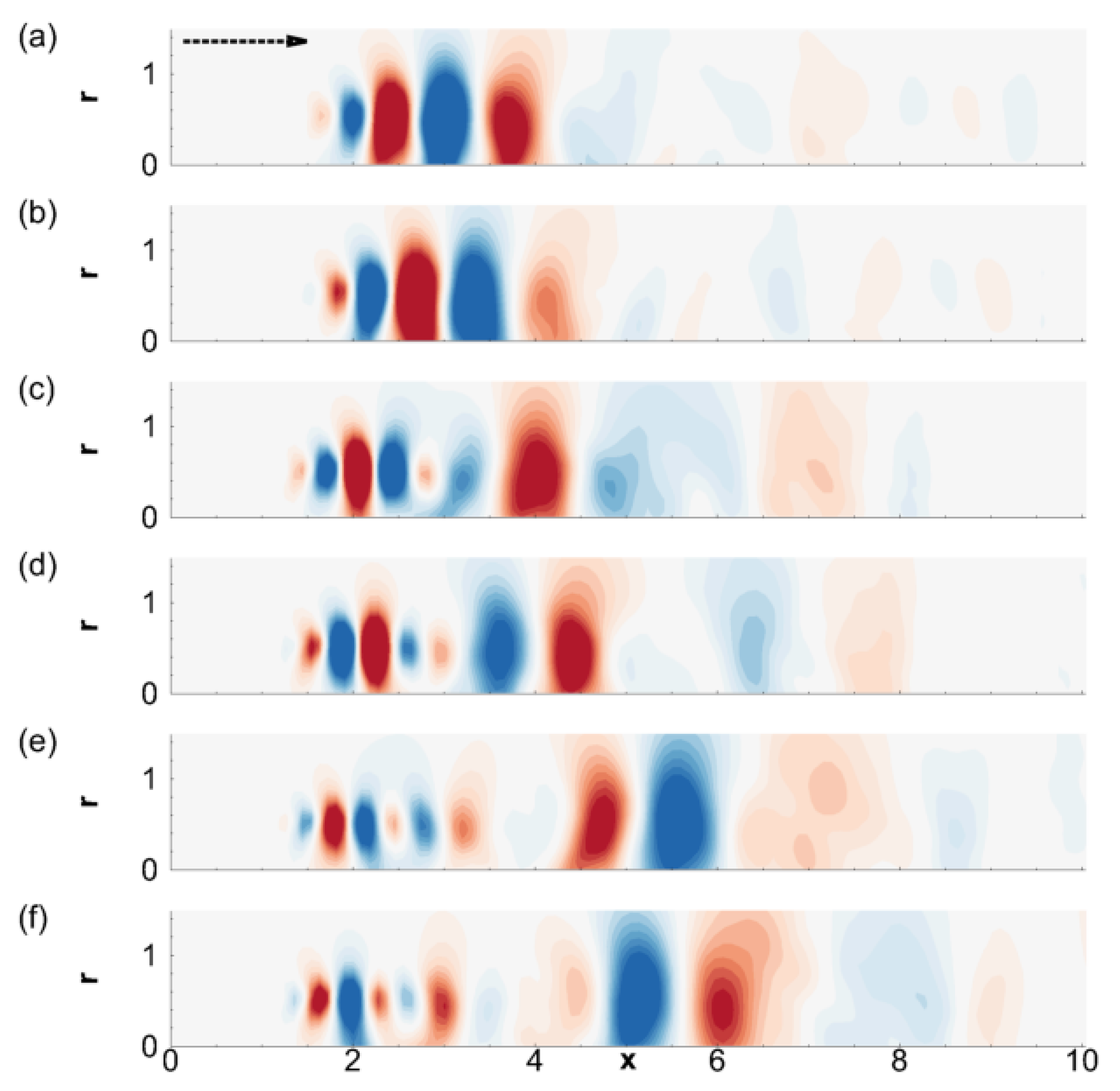
3.3. Shock-Cell Dynamics and Their Acoustic Imprint
3.4. Predictive Advantages of the Acoustic Mode
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Suzuki, T. Wave-Packet Representation of Shock-Cell Noise for a Single Round Jet. AIAA J. 2016, 54, 3903–3917. [Google Scholar] [CrossRef]
- Panda, J.; Seasholtz, R.G. Measurement of shock structure and shock–vortex interaction in underexpanded jets using Rayleigh scattering. Phys. Fluids 1999, 11, 3761–3777. [Google Scholar] [CrossRef]
- Owston, R.; Magi, V.; Abraham, J. Fuel-Air Mixing Characteristics of DI Hydrogen Jets. SAE Int. J. Eng. 2009, 1, 693–712. [Google Scholar] [CrossRef]
- Adamson, T.C.; Nicholls, J.A. On the structure of jets from highly underexpanded nozzles into still air. J. Aerosp. Sci. 1959, 26, 16–24. [Google Scholar] [CrossRef]
- Bonelli, F.; Viggiano, A.; Magi, V. A numerical analysis of hydrogen underexpanded jets under real gas assumption. J. Fluids Eng. 2013, 135, 121101. [Google Scholar] [CrossRef]
- Avital, G.; Cohen, Y.; Gamss, L.; Kanelbaum, Y.; Macales, J.; Trieman, B.; Yaniv, S.; Lev, M.; Stricker, J.; Sternlieb, A. Experimental and computational study of infrared emission from underexpanded rocket exhaust plumes. J. Thermophys. Heat Transf. 2001, 15, 377–383. [Google Scholar] [CrossRef]
- Norum, T.D.; Seiner, J.M. Measurements of Mean Static Pressure and Far Field Acoustics of Shock Containing Supersonic Jets; NASA Technical Report; NASA Langley Research Center: Hampton, VA, USA, September 1982.
- André, B.; Castelain, T.; Bailly, C. Experimental exploration of underexpanded supersonic jets. Shock Waves 2014, 24, 21–32. [Google Scholar] [CrossRef]
- Raman, G. Supersonic jet screech: Half-century from Powell to the present. J Sound Vib. 1999, 225, 543–571. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Viswanathan, K.; Ahuja, K.K.; Panda, J. The sources of jet noise: Experimental evidence. J. Fluid Mech. 2008, 615, 253–292. [Google Scholar] [CrossRef]
- Tam, C.K.W. Jet noise generated by large-scale coherent motion. In Aeroacoustics of Flight Vehicles: Theory and Practice. Volume 1: Noise Sources; NASA Langley Research Center, Aeroacoustics of Flight Vehicles: Hampton, VA, USA, 1991; Volume 1. [Google Scholar]
- Tam, C.K.W. Supersonic jet noise. Ann. Rev. Fluid Mech. 1995, 27, 17–43. [Google Scholar] [CrossRef]
- Powell, A. On the mechanism of choked jet noise. Proc. Phys. Soc. Sect. B 1953, 66, 1039. [Google Scholar] [CrossRef]
- Harper-Bourne, M. The noise from shock waves in supersonic jets. AGARD-CP-131 1973, 11, 1–13. [Google Scholar]
- Tam, C.K.W.; Tanna, H.K. Shock associated noise of supersonic jets from convergent-divergent nozzles. J. Sound Vib. 1982, 81, 337–358. [Google Scholar] [CrossRef]
- Magstadt, A.S.; Berry, M.G.; Berger, Z.P.; Shea, P.R.; Ruscher, C.J.; Gogineni, S.P.; Glauser, M.N. Flow Structures Associated with Turbulent Mixing Noise and Screech Tones in Axisymmetric Jets. Flow Turbul. Combust. 2017, 98, 725–750. [Google Scholar] [CrossRef]
- Freund, J.B. Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 2001, 438, 277–305. [Google Scholar] [CrossRef]
- Freund, J.B.; Lele, S.K.; Moin, P. Numerical simulation of a Mach 1.92 turbulent jet and its sound field. AIAA J. 2000, 38, 2023–2031. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Computation of a high Reynolds number jet and its radiated noise using large eddy simulation based on explicit filtering. Comput. fluids 2006, 35, 1344–1358. [Google Scholar] [CrossRef]
- Schulze, J.; Sesterhenn, J. Numerical simulation of supersonic jet-noise. Proc. Appl. Math. Mech. 2008, 8, 10703–10704. [Google Scholar] [CrossRef]
- Bodony, D.J.; Lele, S.K. On using large-eddy simulation for the prediction of noise from cold and heated turbulent jets. Phys. Fluids 2005, 17, 085103. [Google Scholar] [CrossRef]
- Bonelli, F.; Viggiano, A.; Magi, V. How does a high density ratio affect the near-and intermediate-field of high-Re hydrogen jets? Int. J. Hydrogen Energy 2016, 41, 15007–15025. [Google Scholar] [CrossRef]
- Gaitonde, D.V.; Samimy, M. Coherent structures in plasma-actuator controlled supersonic jets: Axisymmetric and mixed azimuthal modes. Phys. Fluids 2011, 23, 095104. [Google Scholar] [CrossRef]
- Nichols, J.; Ham, F.; Lele, S.; Bridges, J. Aeroacoustics of a supersonic rectangular jet: Experiments and LES predictions. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee, 9–12 January 2012. [Google Scholar]
- Li, X.; Zhou, R.; Yao, W.; Fan, X. Flow characteristic of highly underexpanded jets from various nozzle geometries. Appl. Therm. Eng. 2017, 125, 240–253. [Google Scholar] [CrossRef]
- Morris, P.J.; Miller, S.A.E. Prediction of broadband shock-associated noise using Reynolds-averaged Navier-Stokes computational fluid dynamics. AIAA J. 2010, 48, 2931–2944. [Google Scholar] [CrossRef]
- Suzuki, T.; Lele, S.K. Shock leakage through an unsteady vortex-laden mixing layer: Application to jet screech. J. Fluid Mech. 2003, 490, 139–167. [Google Scholar] [CrossRef]
- Doak, P.E. Momentum potential theory of energy flux carried by momentum fluctuations. J. Sound Vib. 1989, 131, 67–90. [Google Scholar] [CrossRef]
- Goldstein, M.E. On Identifying the Sound Sources in a Turbulent Flow; NASA Technical Report; NASA Glenn Research Center: Cleveland, OH, USA, 2008.
- Jordan, P.; Daviller, G.; Comte, P. Doak’s momentum potential theory of energy flux used to study a solenoidal wavepacket. J. Sound Vib. 2013, 332, 3924–3936. [Google Scholar] [CrossRef]
- Unnikrishnan, S.; Gaitonde, D.V. Acoustic, hydrodynamic and thermal modes in a supersonic cold jet. J. Fluid Mech. 2016, 800, 387–432. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. An analysis of the correlations between the turbulent flow and the sound pressure fields of subsonic jets. J. Fluid Mech. 2007, 583, 71–97. [Google Scholar] [CrossRef]
- Panda, J.; Seasholtz, R.G. Experimental investigation of density fluctuations in high-speed jets and correlation with generated noise. J. Fluid Mech. 2002, 450, 97–130. [Google Scholar] [CrossRef]
- Arroyo, C.P.; Daviller, G.; Puigt, G.; Airiau, C. Shock-cell noise of supersonic under expanded jets. In Proceedings of the 50th 3AF International Conference on Applied Aerodynamics, Toulouse, France, 29 March–1 April 2015. [Google Scholar]
- Sinayoko, S.; Agarwal, A.; Sandberg, R.D. On wavenumber spectra for sound within subsonic jets. arXiv, 2013; arXiv:1311.5358. [Google Scholar]
- Grizzi, S.; Camussi, R.; Di Marco, A. Experimental Investigation of pressure fluctuations in the near field of subsonic jets at different Mach and Reynolds numbers. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference, Colorado Springs, CO, USA, 4–6 June 2012. [Google Scholar]
- Krothapalli, A.; Hsia, Y.; Baganoff, D.; Karamcheti, K. The role of screech tones in mixing of an underexpanded rectangular jet. J. Sound Vib. 1986, 106, 119–143. [Google Scholar] [CrossRef]
- Tam, C.K.W. Stochastic model theory of broadband shock associated noise from supersonic jets. J. Sound Vib. 1987, 116, 265–302. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation; House Nauka: Moscow, USSR, 1967; pp. 166–178. [Google Scholar]
- Lighthill, M.J. On Sound Generated Aerodynamically: I. General Theory. Proc. R. Soc. Lond. A 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Lighthill, M.J. On Sound Generated Aerodynamically: II. Turbulence as a Source of Sound. Proc. R. Soc. Lond. A 1954, 222, 1–32. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.E. The noise from turbulence convected at high speed. Philos. Trans. R. Soc. Lond. A 1963, 255, 469–503. [Google Scholar] [CrossRef]
- Shea, P.R.; Berger, Z.P.; Berry, M.G.; Glauser, M.N.; Gogineni, S. Low-dimensional modeling of a Mach 0.6 axisymmetric jet. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MA, USA, 13–17 January 2014. [Google Scholar]
- Gaitonde, D.V. Analysis of the near field in a plasma-actuator-controlled supersonic jet. J. Propuls. Power 2012, 28, 281–292. [Google Scholar] [CrossRef]
- Speth, R.L.; Gaitonde, D.V. Parametric Study of a Mach 1.3 Cold Jet Excited by the Flapping Mode Using Plasma Actuators. Comput. Fluids 2013, 84, 16–34. [Google Scholar] [CrossRef]
- González, D.R.; Speth, R.L.; Gaitonde, D.V.; Lewis, M.J. Finite-time Lyapunov exponent-based analysis for compressible flows. Chaos Int. J. Nonlinear Sci. 2016, 26, 083112. [Google Scholar] [CrossRef] [PubMed]
- Steger, J.L. Implicit finite-difference simulation of flow about arbitrary two-dimensional geometries. AiAA J. 1978, 16, 679–686. [Google Scholar] [CrossRef]
- Vinokur, M. Conservation equations of gasdynamics in curvilinear coordinate systems. J. Comput. Phys. 1974, 14, 105–125. [Google Scholar] [CrossRef]
- Rizzetta, D.P.; Visbal, M.R. Large-eddy simulation of plasma-based turbulent boundary-layer separation control. AIAA J. 2010, 48, 2793–2810. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann Solvers, Parameter Vectors and Difference Schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservation Difference Scheme V, A Second-Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Pulliam, T.H.; Chaussee, D.S. A Diagonal Form of an Implicit Approximate-Factorization Algorithm. J. Comp. Phys. 1981, 39, 347–363. [Google Scholar] [CrossRef]
- Beam, R.; Warming, R. An Implicit Factored Scheme for the Compressible Navier-Stokes Equations. AIAA J. 1978, 16, 393–402. [Google Scholar] [CrossRef]
- Goparaju, K.; Gaitonde, D.V. Large-Eddy Simulation of Plasma-Based Active Control on Imperfectly Expanded Jets. J. Fluids Eng. 2016, 138, 071101. [Google Scholar] [CrossRef]
- Berger, Z.P. The Effects of Active Flow Control on High-Speed Jet Flow Physics and Noise. Ph.D. Thesis, Syracuse University, New York, NY, USA, 2014. [Google Scholar]
- Powell, A. On Prandtl’s formulas for supersonic jet cell length. Int. J. Aeroacoust. 2010, 9, 207–236. [Google Scholar] [CrossRef]
- Kovásznay, L.S.G. Turbulence in supersonic flow. J. Aeronaut. Sc. 1953, 20, 657–674. [Google Scholar] [CrossRef]
- Truesdell, C. Intrinsic Equations of Spatial Gas Flow. ZAMM-J. Appl. Math. Mech. Z. Angew. Math. Mech. 1960, 40, 9–14. [Google Scholar] [CrossRef]
- Doak, P.E. Fluctuating total enthalpy as a generalized acoustic field. Acoust. Phys. 1995, 41, 677–685. [Google Scholar] [CrossRef]
- Doak, P.E. Fluctuating total enthalpy as the basic generalized acoustic field. Theor. Comput. Fluid Dyn. 1998, 10, 115–133. [Google Scholar] [CrossRef]
- Van der Vorst, H.A. Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Seiner, J. Advances in high speed jet aeroacoustics. In Proceedings of the 9th Aeroacoustics Conference, Williamsburg, VA, USA, 10–15 October 1984; p. 2275. [Google Scholar]
- Bodony, D.; Ryu, J.; Ray, P.; Lele, S. Investigating broadband shock-associated noise of axisymmetric jets using large-eddy simulation. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006. [Google Scholar]
- Hileman, J.; Samimy, M. Turbulence structures and the acoustic far field of a Mach 1.3 jet. AIAA J. 2001, 39, 1716–1727. [Google Scholar] [CrossRef]
- Kearney-Fischer, M.; Sinha, A.; Samimy, M. Intermittent nature of subsonic jet noise. AIAA J. 2013, 51, 1142–1155. [Google Scholar] [CrossRef]
- Samimy, M.; Kim, J.H.; Kastner, J.; Adamovich, I.; Utkin, Y. Active control of high-speed and high-Reynolds-number jets using plasma actuators. J. Fluid Mech. 2007, 578, 305–330. [Google Scholar] [CrossRef]
- Berland, J.; Bogey, C.; Bailly, C. Large eddy simulation of screech tone generation in a planar underexpanded jet. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006. [Google Scholar]
- Arroyo, C.P.; Daviller, G.; Puigt, G.; Airiau, C.; Moreau, S. Identification of temporal and spatial signatures of broadband shock-associated noise. Shock Waves 2018, 1–18. [Google Scholar] [CrossRef]
- Howe, M.S.; Ffowcs, J.E. On the noise generated by an imperfectly expanded supersonic jet. Philos. Trans. R. Soc. Lond. A 1978, 289, 271–314. [Google Scholar] [CrossRef]
- Lo, S.C.; Aikens, K.M.; Blaisdell, G.A.; Lyrintzis, A.S. Numerical investigation of 3-D supersonic jet flows using large-eddy simulation. Int. J. Aeroacoust. 2012, 11, 783–812. [Google Scholar] [CrossRef]
- Sinha, A.; Rodríguez, D.; Brès, G.A.; Colonius, T. Wavepacket models for supersonic jet noise. J. Fluid Mech. 2014, 742, 71–95. [Google Scholar] [CrossRef]
- Bailly, C.; André, B.; Castelain, T.; Henry, C.; Bodard, G.; Porta, M. An analysis of shock noise components. AerospaceLab 2014, 1–8. [Google Scholar] [CrossRef]
- Magstadt, A.S.; Berry, M.G.; Berger, Z.P.; Shea, P.R.; Glauser, M.N.; Ruscher, C.J.; Gogineni, S. An investigation of sonic & supersonic axisymmetric jets: correlations between flow physics and far-field noise. In Proceedings of the 9th International Symposium on Turbulence and Shear Flow Phenomena, Melbourne, Australia, 30 June–1 July 2015. [Google Scholar]
- Savarese, A.; Jordan, P.; Girard, S.; Collin, E.; Porta, M.; Gervais, Y. Experimental study of shock-cell noise in underexpanded supersonic jets. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, AIAA Paper 2013–2080, Berlin, Germany, 27–29 May 2013. [Google Scholar]
- Tam, C.K.W. Broadband shock associated noise from supersonic jets measured by a ground observer. AIAA J. 1992, 30, 2395–2401. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. II. Symmetries and transformations. Q. Appl. Math. 1987, 45, 573–582. [Google Scholar] [CrossRef]
- Norum, T.D.; Seiner, J.M. Broadband shock noise from supersonic jets. AIAA journal 1982, 20, 68–73. [Google Scholar]
- Cavalieri, A.V.G.; Jordan, P.; Agarwal, A.; Gervais, Y. Jittering wave-packet models for subsonic jet noise. J. Sound Vib. 2011, 330, 4474–4492. [Google Scholar] [CrossRef]










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sasidharan Nair, U.; Goparaju, K.; Gaitonde, D. Energy-Dynamics Resulting in Turbulent and Acoustic Phenomena in an Underexpanded Jet. Aerospace 2018, 5, 49. https://doi.org/10.3390/aerospace5020049
Sasidharan Nair U, Goparaju K, Gaitonde D. Energy-Dynamics Resulting in Turbulent and Acoustic Phenomena in an Underexpanded Jet. Aerospace. 2018; 5(2):49. https://doi.org/10.3390/aerospace5020049
Chicago/Turabian StyleSasidharan Nair, Unnikrishnan, Kalyan Goparaju, and Datta Gaitonde. 2018. "Energy-Dynamics Resulting in Turbulent and Acoustic Phenomena in an Underexpanded Jet" Aerospace 5, no. 2: 49. https://doi.org/10.3390/aerospace5020049



