Development and Demonstration of a Novel Test Bench for the Experimental Validation of Fuselage Stiffened Panel Simulations
Abstract
:1. Introduction
2. Description of the Specimen and Experimental Facility
3. Setup and Calibration of the Load Introduction and Inspection Devices
4. Description of the Finite Element Model (FEM)
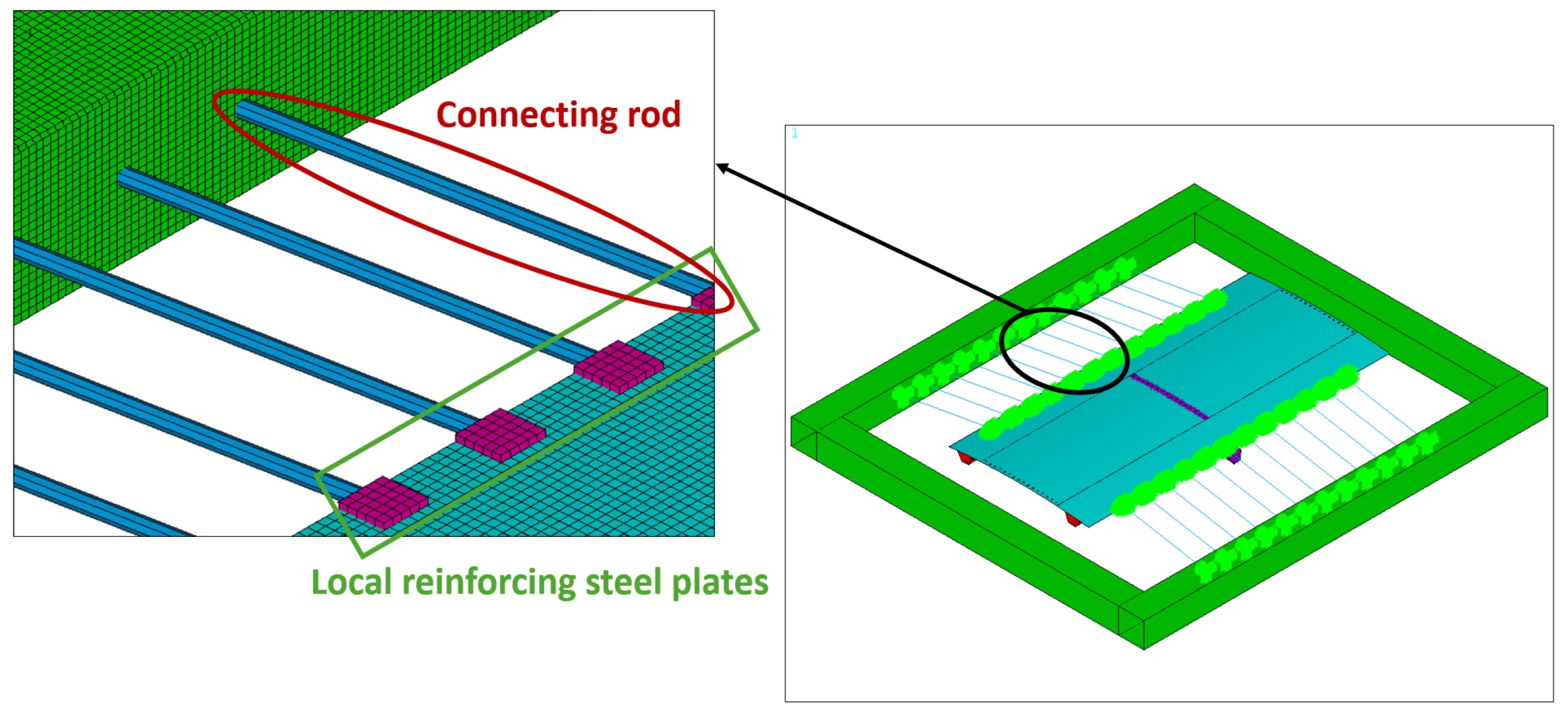
4.1. Development of the Finite Element Model
4.2. Discrepancies in the Experimental Installation in Comparison to the Original Design and Modifications Made on the FEM
5. Validation of the Numerical Simulation and Correlation with Experimental Results
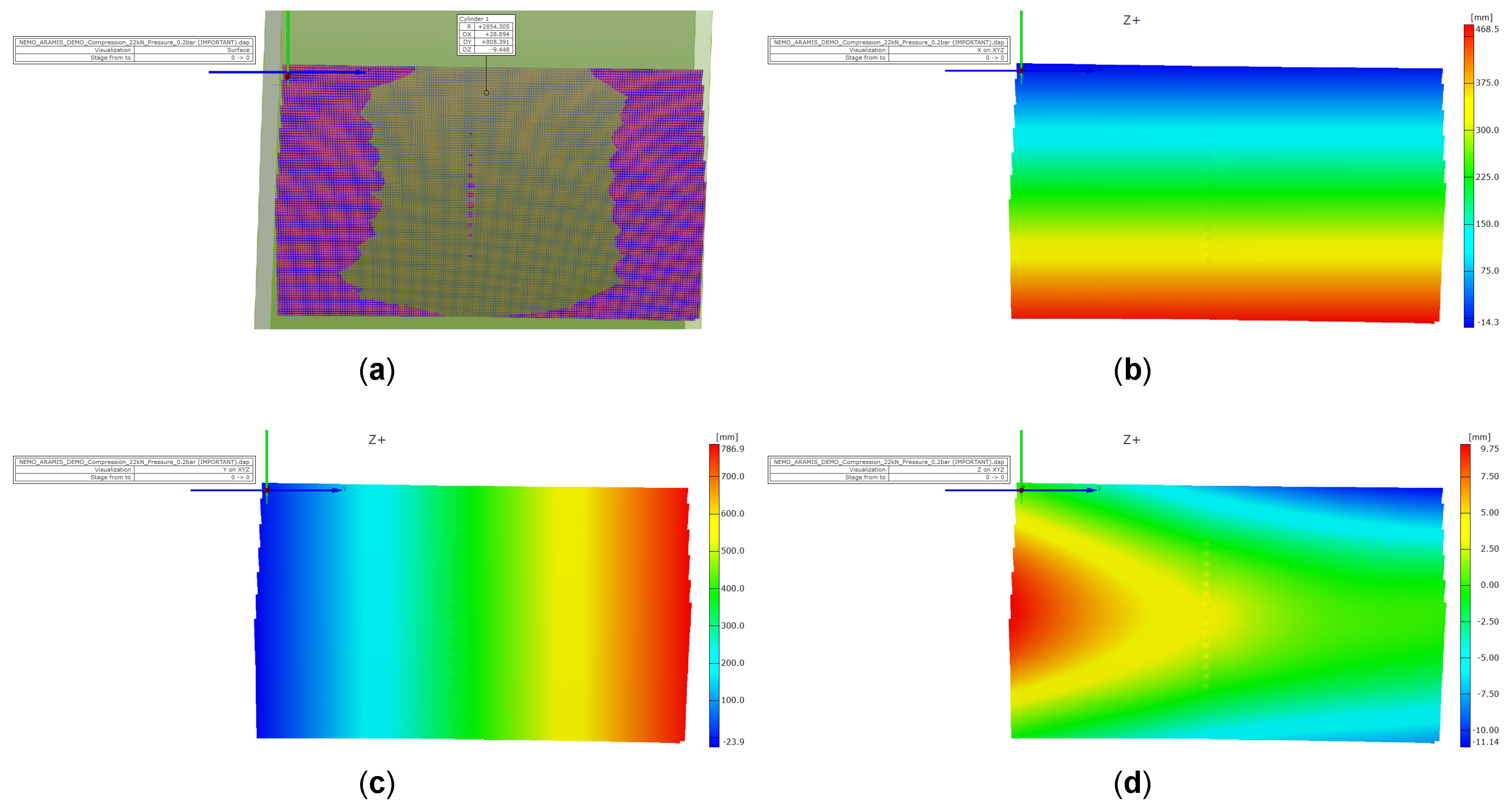
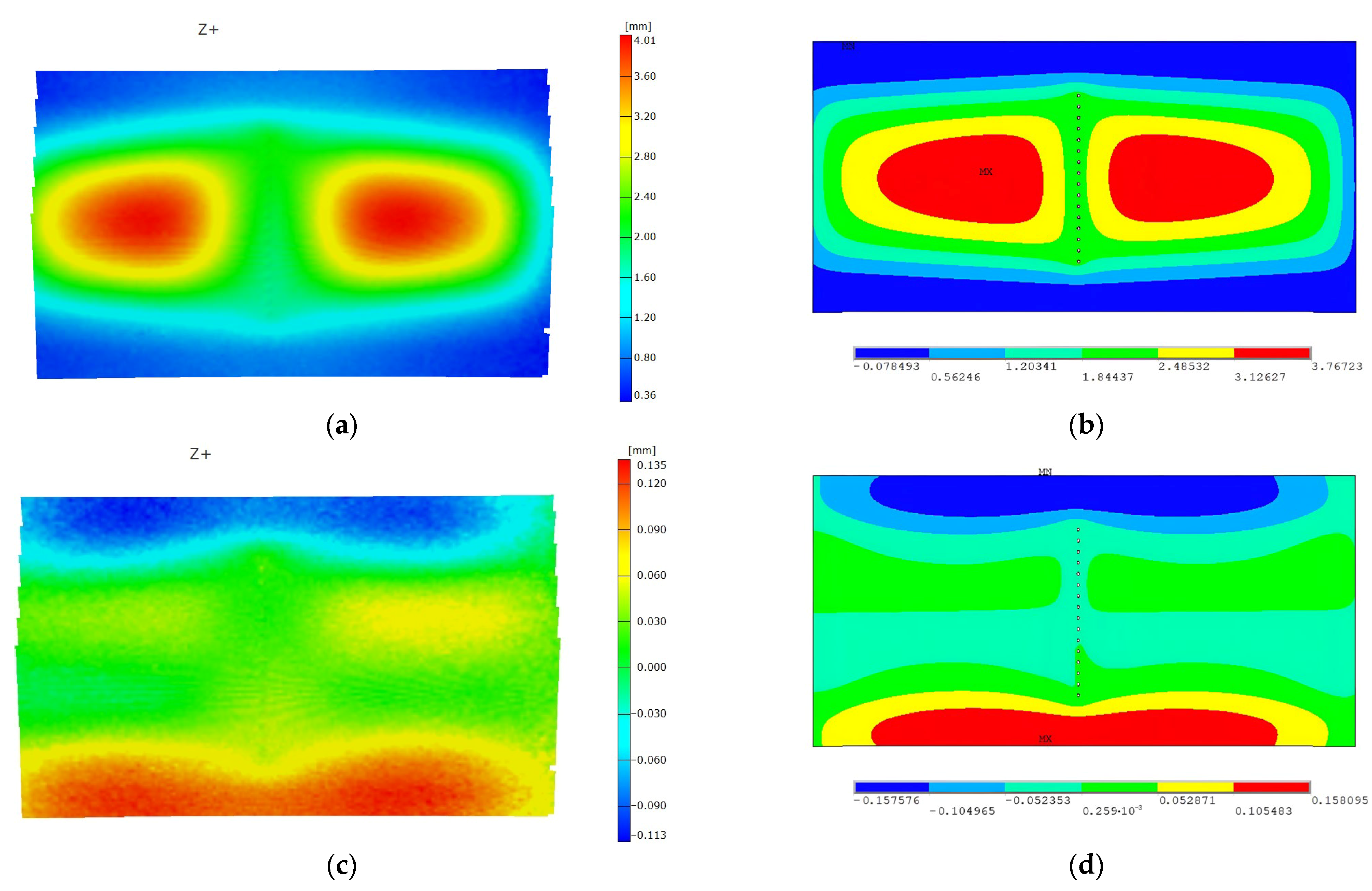
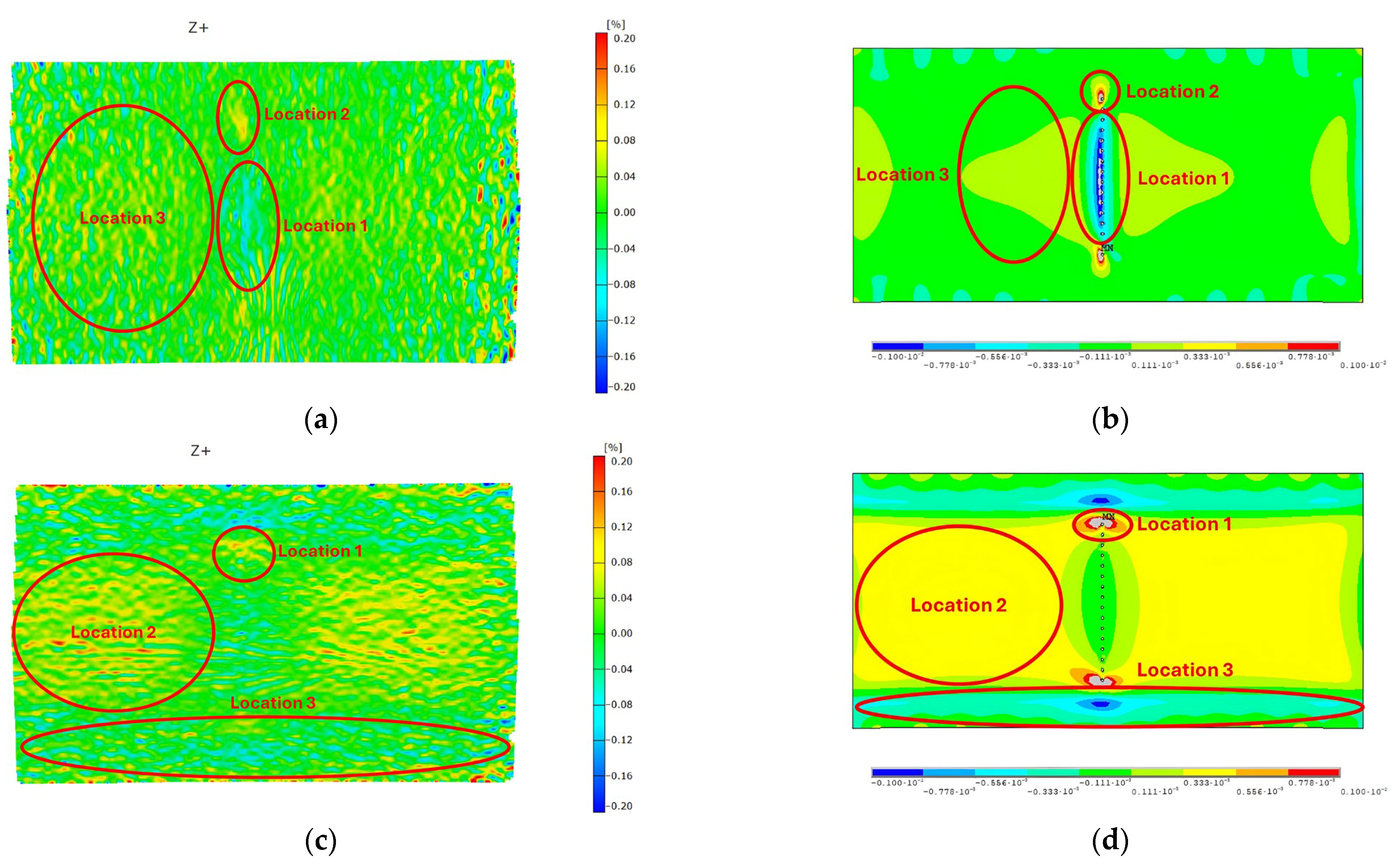
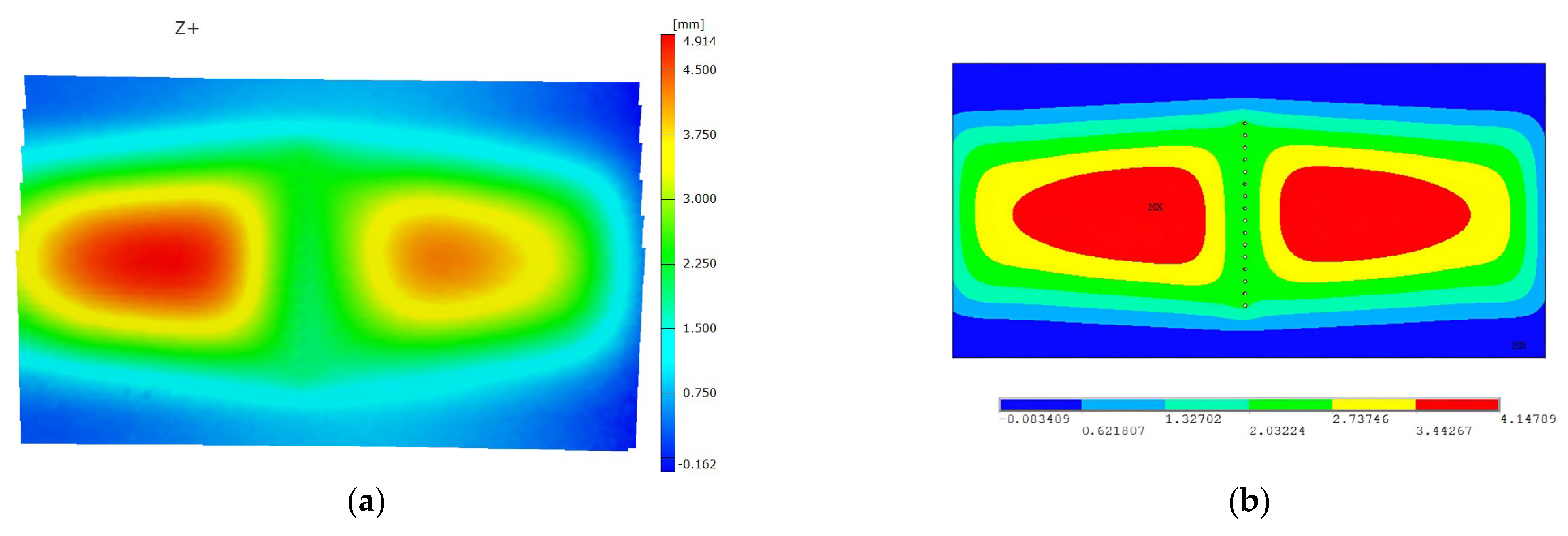
5.1. Load Case 1: Internal Pressure
5.2. Load Case 2: Linear Compression up to 11.5 kN
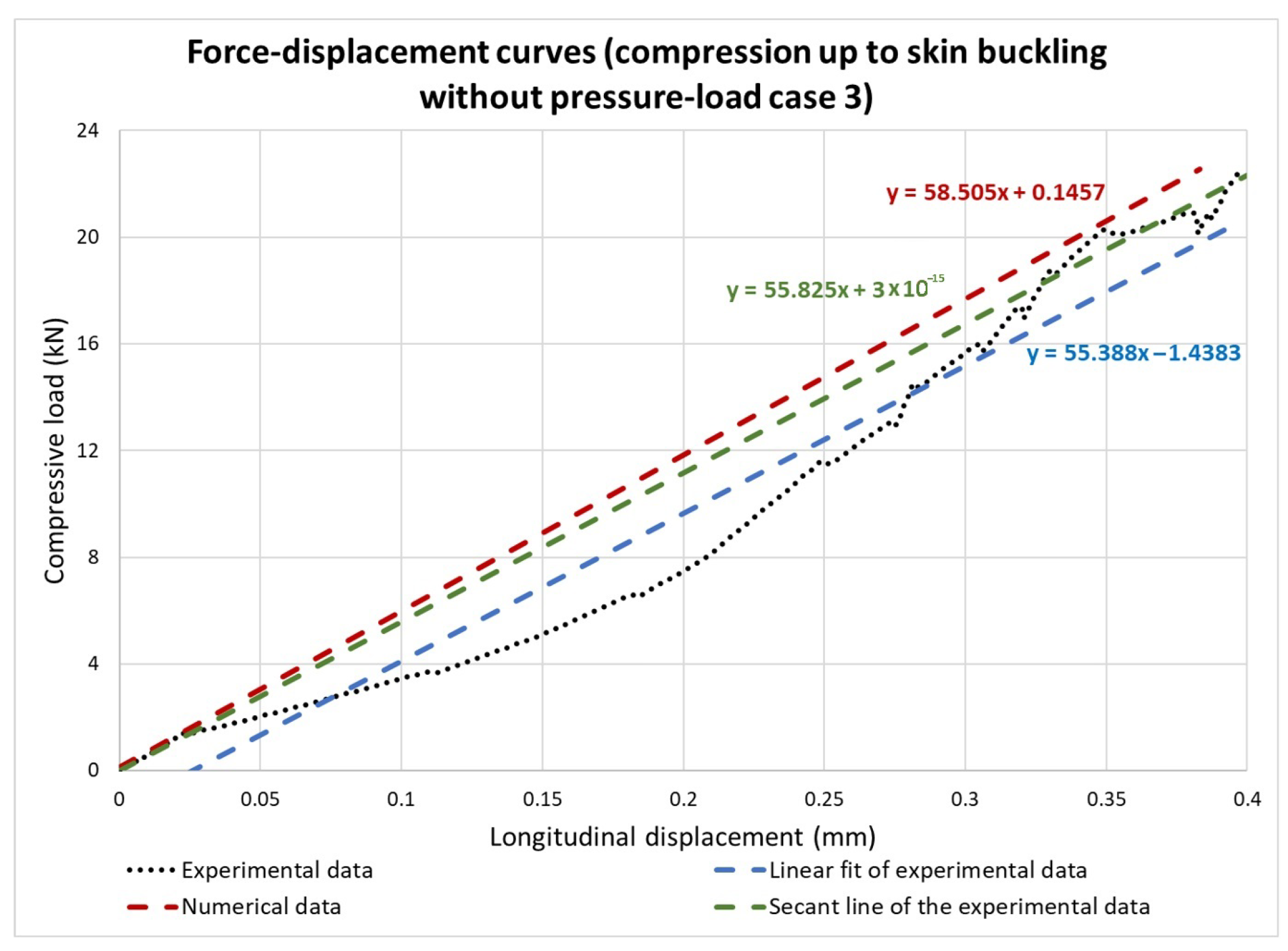
5.3. Load Case 3: Buckling Caused by Uniaxial Compression
5.4. Load Case 4: Combined Loading Case (Compression and Internal Pressure)
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harris, C.E.; Starnes, J.H., Jr.; Shuart, M.J. Design and Manufacturing of Aerospace Composite Structures, State-of-the-Art Assessment. J. Aircr. 2002, 39, 545–560. [Google Scholar] [CrossRef]
- Jones, R.; Peng, D. A Building Block Approach to Sustainment and Durability Assessment: Experiment and Analysis. Compr. Struct. Integr. 2023, 7, 73–101. [Google Scholar] [CrossRef]
- Markus, W. Building Block Approach for Development of Structural Health Monitoring Technologies Using Idealized Demonstrators. 2022. Available online: https://resolver.obvsg.at/urn:nbn:at:at-ubl:1-53692 (accessed on 2 March 2025).
- Tropis, A.; Thomas, M.; Bounie, J.L.; Lafon, P. Certification of the Composite Outer Wing of the ATR72. Proc. Inst. Mech. Eng. Part G 1995, 209, 327–339. [Google Scholar] [CrossRef]
- Hamm, K.R.; Phillips, D.R.; Imtiaz, K.S.; Raju, I.S. Revisiting Building Block Approaches for Structures. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Rouse, M.; Jegley, D.; McGowan, D.; Bush, H.; Waters, W. Utilization of the Building-Block Approach in Structural Mechanics Research. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005. [Google Scholar] [CrossRef]
- Hiken, A. The Evolution of the Composite Fuselage—A Manufacturing Perspective. SAE Int. J. Aerosp. 2017, 10, 77–91. [Google Scholar] [CrossRef]
- Zhu, L.; Li, N.; Childs, P.R.N. Light-weighting in aerospace component and system design. Propuls. Power Res. 2018, 7, 103–119. [Google Scholar] [CrossRef]
- Kirubakaran, R.; Lokesharun, D.; Rajkumar, S.; Anand, R. Aircraft Wing Weight Optimization by Composite Material Structure Design Configuration. IOSR J. Mech. Civ. Eng. 2017, 14, 71–80. [Google Scholar]
- Zaragkas, T.; Psarras, S.; Sotiriadis, G.; Kostopoulos, V. Experimental Building Block Approach and Numerical Modelling of CF-LMPAEK. In Proceedings of the 11th International Conference on Composite Testing and Model Identification, Girona, Spain, 31 May–2 June 2023. [Google Scholar]
- Soden, P.D.; Hinton, M.J.; Kaddour, A.S. Lamina properties, lay-up configurations and loading conditions for a range of fibre reinforced composite laminates. In Failure Criteria in Fibre-Reinforced-Polymer Composites; Elsevier: Amsterdam, The Netherlands, 2004; Chapter 2.1; pp. 30–51. [Google Scholar] [CrossRef]
- Wright, T.; Hyder, I.; Daniels, M.; Kim, D.; Parmigiani, J.P. Effects of material property variation in composite panels. Aircr. Eng. Aerosp. Technol. 2017, 89, 274–279. [Google Scholar] [CrossRef]
- Warzok, F. Experimental and Numerical Characterisation of Fatigue Damage in Z-Pinned Composite Structures. Ph.D. Thesis, University of Bristol, Bristol, UK, 14 November 2017. [Google Scholar]
- Zhong, Z.; Wang, F.; Kong, F.; Chen, Y. Study of fatigue damage behavior in off-axis CFRP composites using digital image correlation technology. Heliyon 2024, 10, 3. [Google Scholar] [CrossRef]
- Riccio, A.; Castaldo, R.; Palumbo, C.; Russo, A. Delamination Effect on the Buckling Behaviour of Carbon–Epoxy Composite Typical Aeronautical Panels. Appl. Sci. 2023, 13, 4358. [Google Scholar] [CrossRef]
- Best, R.; Fleischer, T.; Götze, M.; Sachse, M.; Semsch, M. A Test Concept for Future Aircraft Fuselage Panels. In Proceedings of the ICAF 2009, Bridging the Gap between Theory and Operational Practice, Dordrecht, The Netherlands, 27–29 May 2009; pp. 3–14. [Google Scholar] [CrossRef]
- Zucco, G.; Oliveri, V.; Peeters, D.; Telford, R.; Clancy, G.J.; McHale, C.; Rouhi, M.; O’Higgins, R.; Young, T.M.; Weaver, P.M. Static Test of a Thermoplastic Composite Wingbox Under Shear and Bending Moment. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 7 January 2018. [Google Scholar] [CrossRef]
- Kordas, P.D.; Lampeas, G.N. Numerical and experimental investigation of a metallic fuselage stiffened panel loaded with a representative fuselage fatigue spectrum. Int. J. Fatigue 2024, 182, 108217. [Google Scholar] [CrossRef]
- Kordas, P.; Fotopoulos, K.; Lampeas, G.; Karelas, E.; Louizos, E. Design and development of an experimental bench concept for testing of fuselage stiffened panels, using a virtual testing methodology. Aircr. Eng. Aerosp. Technol. 2023, 96, 14–26. [Google Scholar] [CrossRef]
- Ostergaard, M.; Ibbotson, A.; Roux, O.; Prior, A. Virtual testing of aircraft structures. CEAS Aeronaut. J. 2011, 1, 83–103. [Google Scholar] [CrossRef]
- Lampeas, G.; Carelas, E.; Kordas, P.; Karanika, A.; Fotopoulos, K. Experimental validation of aircraft fuselage sections by testing at the stiffened panel level. In Proceedings of the Aerospace Europe Conference 2023—10th EUCASS—9th CEAS, Lausanne, Switzerland, 9–13 July 2023. [Google Scholar] [CrossRef]
- Stamatelos, D.G.; Lampeas, G.N.; Tserpes, K.I. Analytical calculation of local buckling and post-buckling behaviour of isotropic and orthotropic stiffened panels. Thin-Walled Struct. 2011, 49, 422–430. [Google Scholar] [CrossRef]
- Bisagni, C.; Vescovini, R. Analytical formulation for local buckling and post-buckling analysis of stiffened laminated panels. Thin-Walled Struct. 2009, 47, 318–334. [Google Scholar] [CrossRef]
- Fan, S.; Kroeplin, B.; Geier, B. Buckling, postbuckling and failure behavior of composite-stiffened panels under axial compression. In Proceedings of the Structural Dynamics and Materials Conference, Dallas, TX, USA, 13–15 April 1992. [Google Scholar] [CrossRef]
- Kumar, N.J.; Babu, P.R.; Pandu, R. Investigations on Buckling Behaviour of Laminated Curved Composite Stiffened Panels. Appl. Compos. Mater. 2014, 21, 359–376. [Google Scholar] [CrossRef]
- Ambur, D.R.; Jaunky, N.; Hilburger, M.H. Progressive failure studies of stiffened panels subjected to shear loading. Compos. Struct. 2004, 65, 129–142. [Google Scholar] [CrossRef]
- Psihoyos, H.; Fotopoulos, K.; Lampeas, G.; Waleson, J.; Brethouwer, M.; Romano, B.; Pearson, D. Development of a numerical methodology for the analysis of the post-buckling and failure behavior of butt-joint stiffened thermoplastic composite panels. Eng. Fail. Anal. 2024, 160, 108193. [Google Scholar] [CrossRef]
- Bin Kamarudin, M.N.; Mohamed Ali, J.S.; Aabid, A.; Ibrahim, Y.E. Buckling Analysis of a Thin-Walled Structure Using Finite Element Method and Design of Experiments. Aerospace 2022, 9, 541. [Google Scholar] [CrossRef]
- Zumaquero, P.L.; Correa, E.; Justo, J.; París, F. Transverse biaxial tests on long fibre reinforced composites. Compos. Struct. 2022, 297, 115868. [Google Scholar] [CrossRef]
- Rouse, W.J.; van den Brink, W.M.; Maas, R. Validation and correlation of aircraft composite fuselage structure models. In Proceedings of the ECCOMAS-2016 Congress, Hersonissos, Greece, 5–10 June 2016. [Google Scholar]
- Rouchon, J. Certification of Large Airplane Composite Structures. 1990. Available online: https://www.icas.org/ICAS_ARCHIVE/ICAS1990/ICAS-90-1.8.1.pdf (accessed on 25 February 2025).
- Guyett, P.; Cardrick, A. The certification of composite airframe structures. Aeronaut. J. 2016, 84, 188–203. [Google Scholar] [CrossRef]
- Hombergsmeier, E. Review of Aeronautical Fatigue Investigations in Germany during the Period April 2017 to March 2019; CTO Office, Central Research & Technology, Airbus; International Committee on Aeronautical Fatigue: Köln, Germany, 2019. [Google Scholar]
- PERI Philippines Formwork Scaffolding Engineering. Available online: https://www.peri.com.ph/projects/working-scaffold-airbus-germany.html (accessed on 18 December 2024).
- Völkerink, O.; Hühne, C. Virtual testing for design and certification of (fusion) bonded longitudinal joints in a fibre composite fuselage: A proposal using FEM-based progressive damage analysis. Compos. Part C Open Access 2022, 7, 100236. [Google Scholar] [CrossRef]
- Mauery, T.; Alonso, J.; Cary, A.; Lee, V.; Malecki, R.; Mavriplis, D.; Medic, G.; Schaefer, J.; Slotnick, J. A Guide for Aircraft Certification by Analysis; NASA/CR-20210015404; Langley Research Center: Hampton, VA, USA, 2021. [Google Scholar]
- Prior, A. Dassault Systèmes, Nonlinear simulation of large scale aircraft structures—Implications for certification methodology and high performance computing infrastructure. In Proceedings of the NAFEMS World Congress, Crete, Greece, 16–19 June 2009. [Google Scholar]
- Prior, A. Dassault Systèmes, Simulating damage and failure in aircraft structures. In Proceedings of the RAeS Conference: Challenges for the Next Generation-Concept to Disposal, Liverpool, UK, 14–16 October 2008. [Google Scholar]
- Grotto, F.; Peta, O.; Bouvet, C.; Castanié, B.; Serra, J. Testing Structural Elements under Multiaxial Loading: A Numerical Model of the Bench to Understand and Predict Complex Boundary Conditions. Aerospace 2024, 11, 68. [Google Scholar] [CrossRef]
- Ge, D.; Mo, Y.; He, B.; Wu, Y.; Du, X. Experimental and numerical investigation of stiffened composite curved panel under shear and in-plane bending. Compos. Struct. 2016, 137, 185–195. [Google Scholar] [CrossRef]
- Kordas, P.D.; Lampeas, G.N.; Fotopoulos, K.T. Numerical Investigation of an Experimental Setup for Thermoplastic Fuselage Panel Testing in Combined Loading. Aerospace 2024, 11, 175. [Google Scholar] [CrossRef]
- Aircraft Pressurization Systems. Integrated Publishing, Inc. Available online: https://www.tpub.com/ase2/75.htm. (accessed on 25 February 2025).
- Vescovini, R.; Bisagni, C. Semi-analytical buckling analysis of omega stiffened panels under multi-axial loads. Compos. Struct. 2015, 120, 285–299. [Google Scholar] [CrossRef]
- Qi, L. A Study of the Buckling Behavior of Stiffened Panels under Compression and Lateral Pressure. Master’s Thesis, Faculty of Aerospace Engineering, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Paik, J.; Kim, B.J. Ultimate strength formulations for stiffened panels under combined axial load, in-plane bending and lateral pressure: A benchmark study. Thin-Walled Struct. 2002, 40, 45–83. [Google Scholar] [CrossRef]
- Rouse, M.; Young, R.; Gehrki, R. Structural Stability of a Stiffened Aluminum Fuselage Panel Subjected to Combined Mechanical and Internal Pressure Loads. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar] [CrossRef]

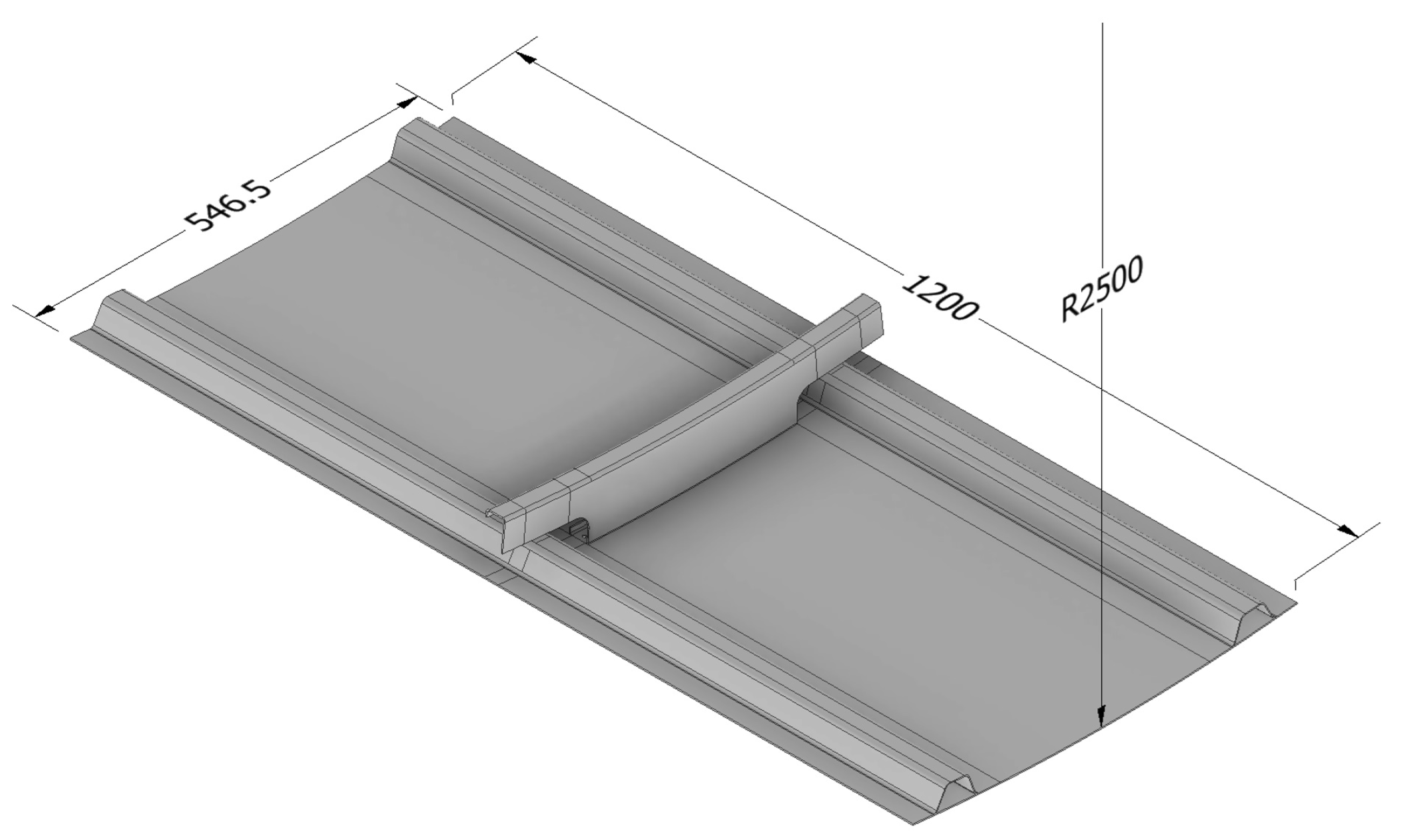




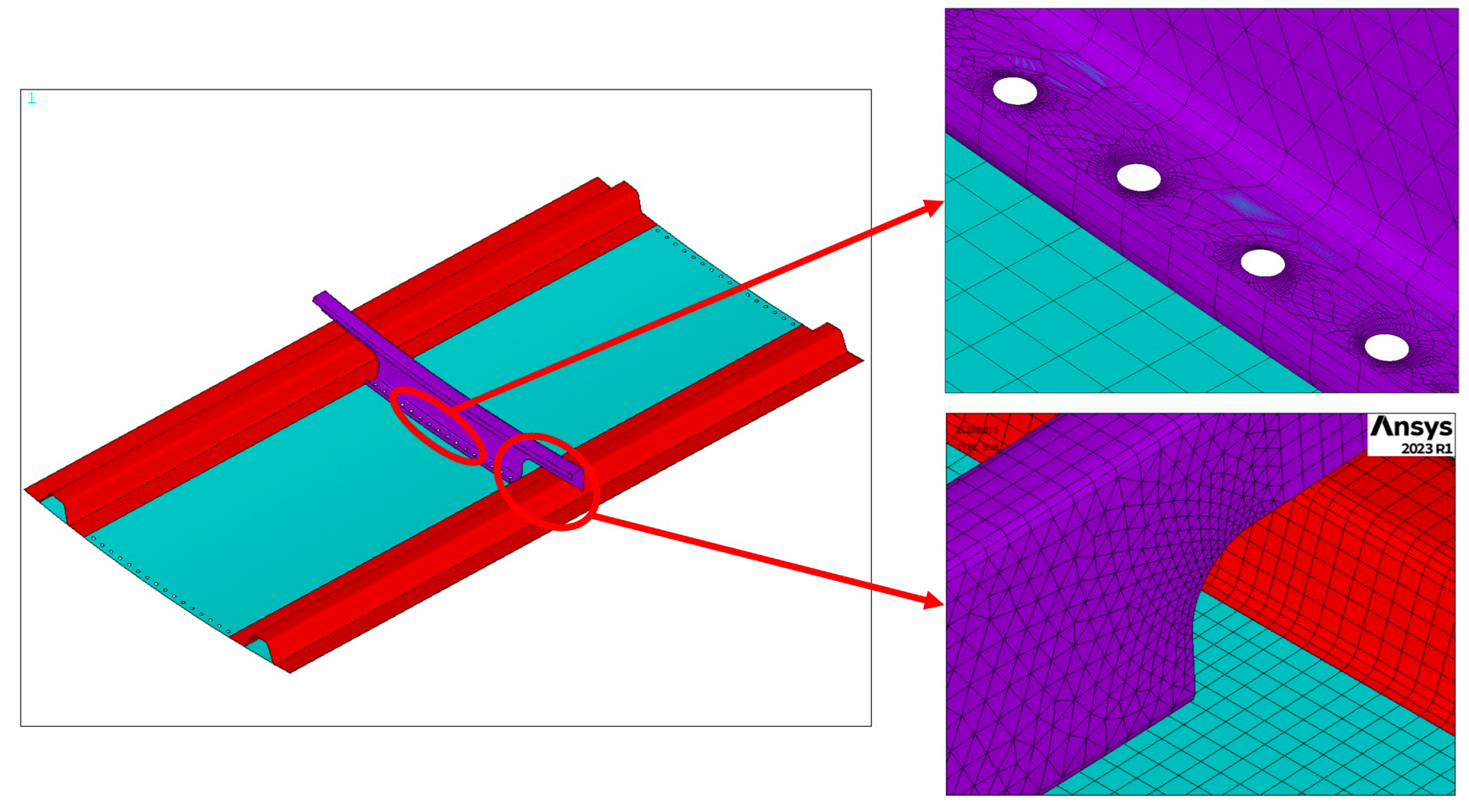










| Materials and Thicknesses of the Investigated Panel | |||
|---|---|---|---|
| Component | Material | Lamination | Thickness (mm) |
| Skin | LMPAEK composite | [+45/−45/90/0/90/0/90/−45/+45] | 1.8 |
| Stringer | Toughened epoxy composite | [45/−45/0/90/0/−45/45] | 1.3 |
| Frame | 7000 series aluminum alloy | - | 2 |
| Adhesive film | FM 300-2 epoxy resin system | - | - |
| EN6115 Bolts | Alloy steel 4340 | - | - |
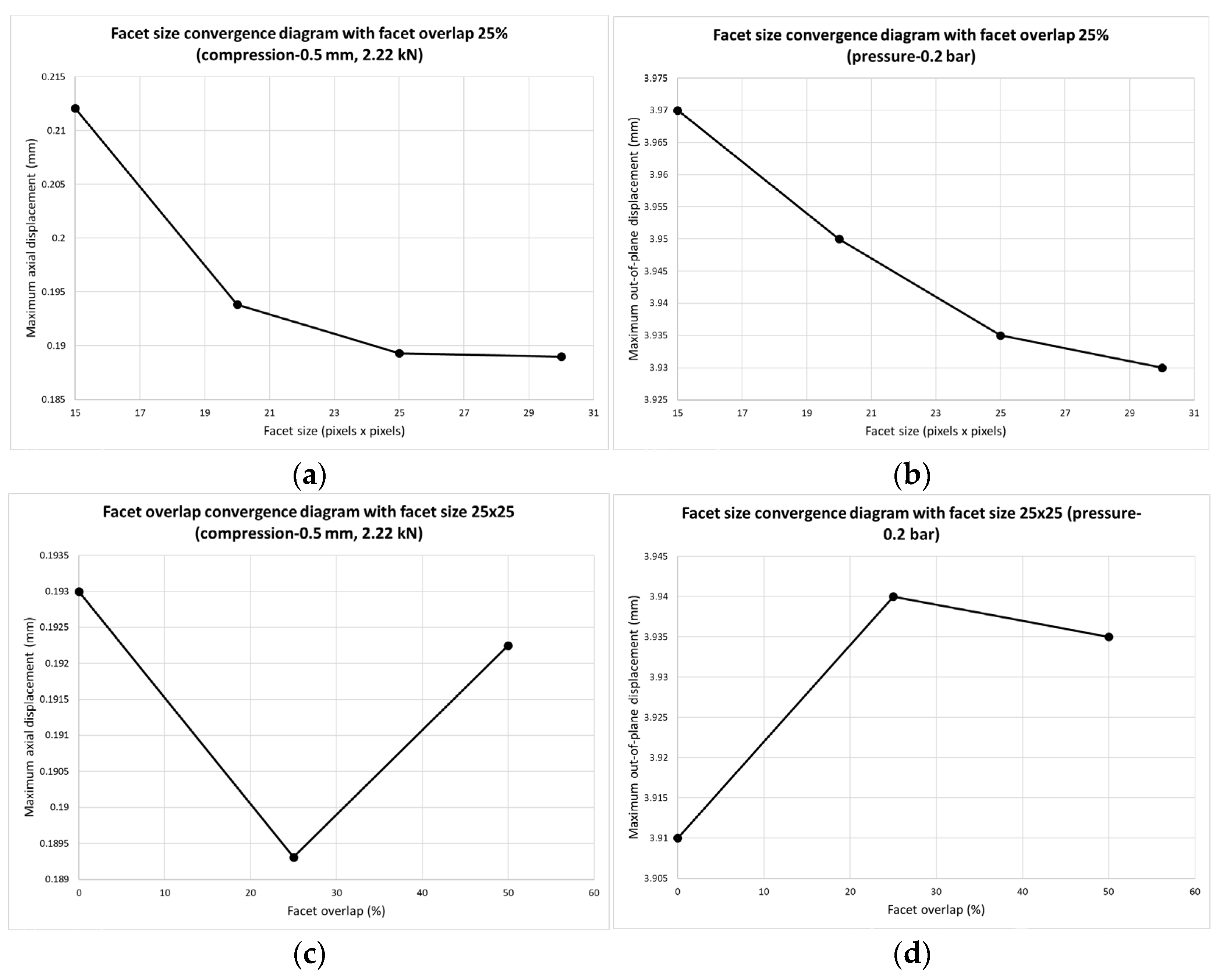
| Facet Size Convergence Study (25% Facet Overlap) | ||||
| Load Case | 15 × 15 Pixels | 20 × 20 Pixels | 25 × 25 Pixels | 30 × 30 Pixels |
| Compression (2.2 kN) | 0.212 mm | 0.194 mm | 0.18931 mm | 0.189 mm |
| Lateral pressure (0.2 bar) | 3.97 mm | 3.95 mm | 3.935 mm | 3.93 mm |
| Facet Overlap Convergence Study (25 × 25 Pixel Facet Size) | ||||
| Load Case | 0% | 25% | 50% | - |
| Compression (2.2 kN) | 0.193 mm | 0.18931 mm | 0.19225 mm | - |
| Lateral pressure (0.2 bar) | 3.91 mm | 3.935 mm | 3.93 mm | - |
| Pressure-Only Load Case—Displacements (mm) | ||
| Result Type | Out-of-Plane (max.) | Transverse (max. and min.) |
| Finite element model | 4.01 | 0.158 and −0.157 |
| Experiment | 3.77 | 0.135 and −0.113 |
| Percentile deviation (%) | 6.4% | 17% and 39.8% |
| Pressure-Only Load Case—Strains (%) | ||
| Longitudinal | Transverse | |
| Finite element model | −0.1% (location 1), 0.1% (location 2) | 0.1% (location 1), −0.778% (location 3) |
| Experiment | −0.12% (location 1), 0.08% (location 2) | 0.12% (location 1), −0.08% (location 3) |
| Percentile deviation (%) | 16.7%, 25% | 16.7%, 2.7% |
| Compression-Only Load Case | |||
|---|---|---|---|
| Longitudinal Displacement (mm) | Critical Buckling Load (kN) | Longitudinal Stiffness (kN/mm) | |
| Finite element model | −0.396 | 21.23 (first eigenvalue), 21.83 (second eigenvalue, 23 (non-linear analysis) | 58.5 |
| Experiment | −0.4 | 22.4 | 55.5 (average) |
| Percentile deviation (%) | 1% | 5.2%, 2.5%, 2.7% | 5.2% |
| Combined Compression and Pressure Load Case Strains (%)—Approximations at Each Location | |||
|---|---|---|---|
| Longitudinal | Transverse | Equivalent von Mises | |
| Finite element model | 0.157% (location 1) | 0.157% (location 1), −0.1% (location 3) | 0.23% (location 1) |
| Experiment | 0.16% (location 1) | 0.16% (location 1), −0.08% (location 3) | 0.27% (location 1) |
| Percentile deviation (%) | 2.5% | 2.5%, 25% | 14.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kordas, P.D.; Fotopoulos, K.T.; Lampeas, G.N. Development and Demonstration of a Novel Test Bench for the Experimental Validation of Fuselage Stiffened Panel Simulations. Aerospace 2025, 12, 263. https://doi.org/10.3390/aerospace12030263
Kordas PD, Fotopoulos KT, Lampeas GN. Development and Demonstration of a Novel Test Bench for the Experimental Validation of Fuselage Stiffened Panel Simulations. Aerospace. 2025; 12(3):263. https://doi.org/10.3390/aerospace12030263
Chicago/Turabian StyleKordas, Panagiotis D., Konstantinos T. Fotopoulos, and George N. Lampeas. 2025. "Development and Demonstration of a Novel Test Bench for the Experimental Validation of Fuselage Stiffened Panel Simulations" Aerospace 12, no. 3: 263. https://doi.org/10.3390/aerospace12030263
APA StyleKordas, P. D., Fotopoulos, K. T., & Lampeas, G. N. (2025). Development and Demonstration of a Novel Test Bench for the Experimental Validation of Fuselage Stiffened Panel Simulations. Aerospace, 12(3), 263. https://doi.org/10.3390/aerospace12030263








