Multiscale Aeroelastic Optimization Method for Wing Structure and Material
Abstract
:1. Introduction
2. Methods
2.1. Homogenization Method
2.2. Parameterized Level-Set Methods
2.3. Multiscale Aeroelastic Optimization Method for Wing Structure and Material
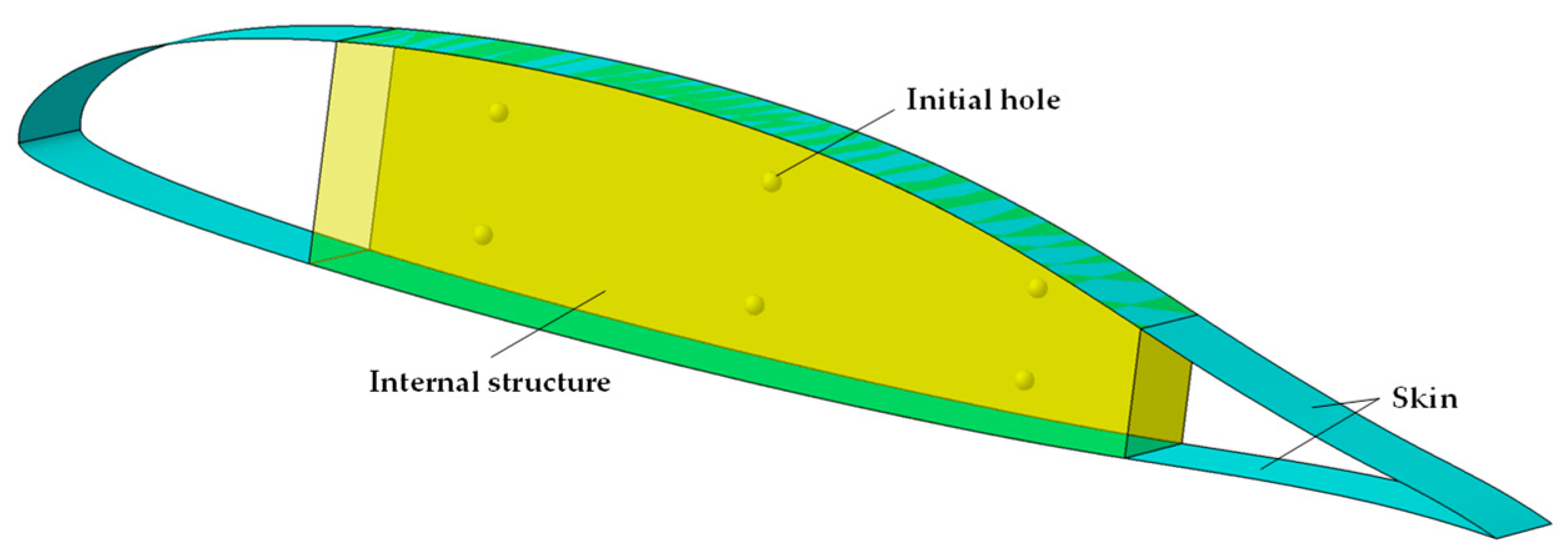
2.3.1. Macro- and Microstructure Design Variables
2.3.2. Optimization Model
2.3.3. Sensitivity Analysis
3. Results
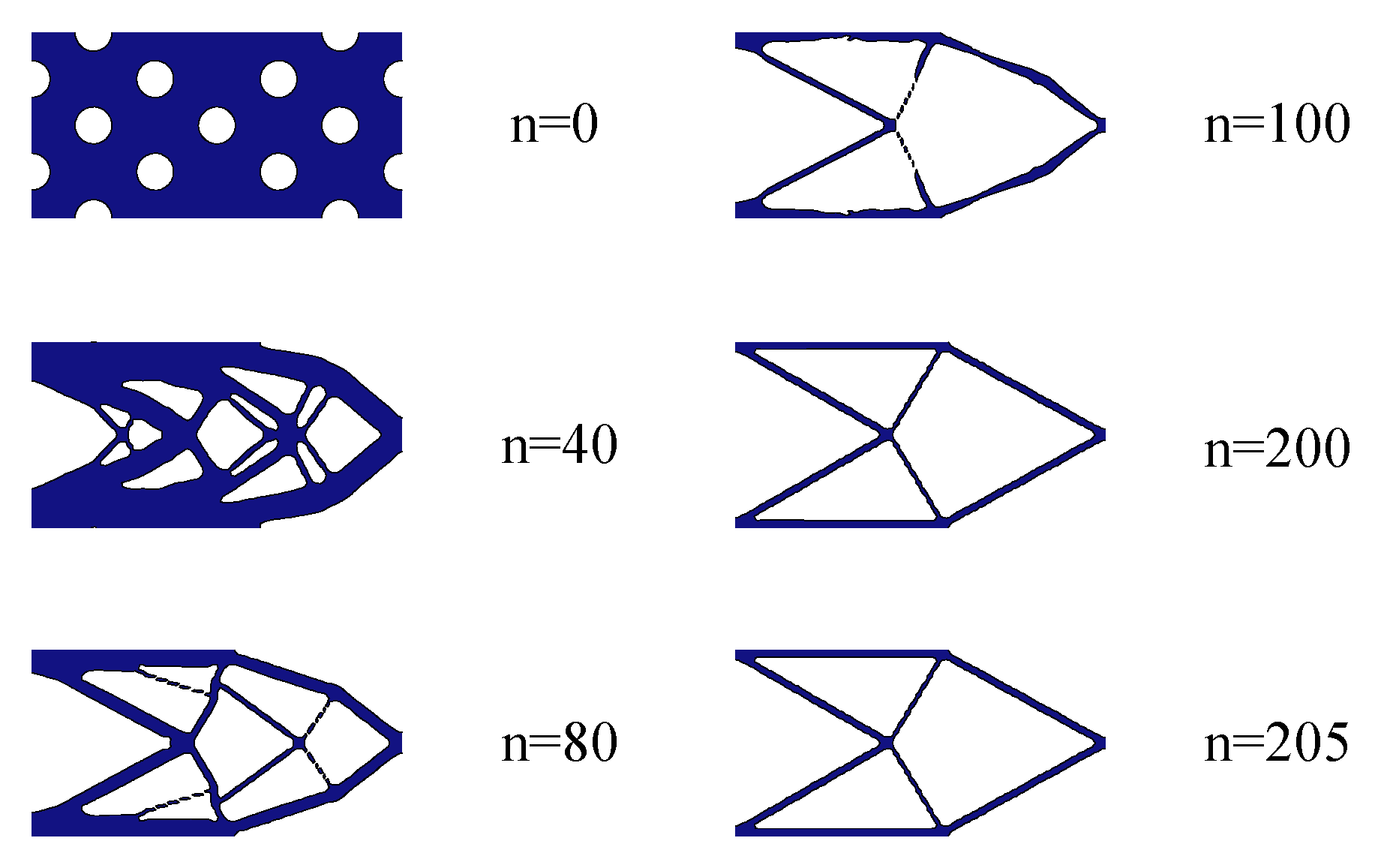
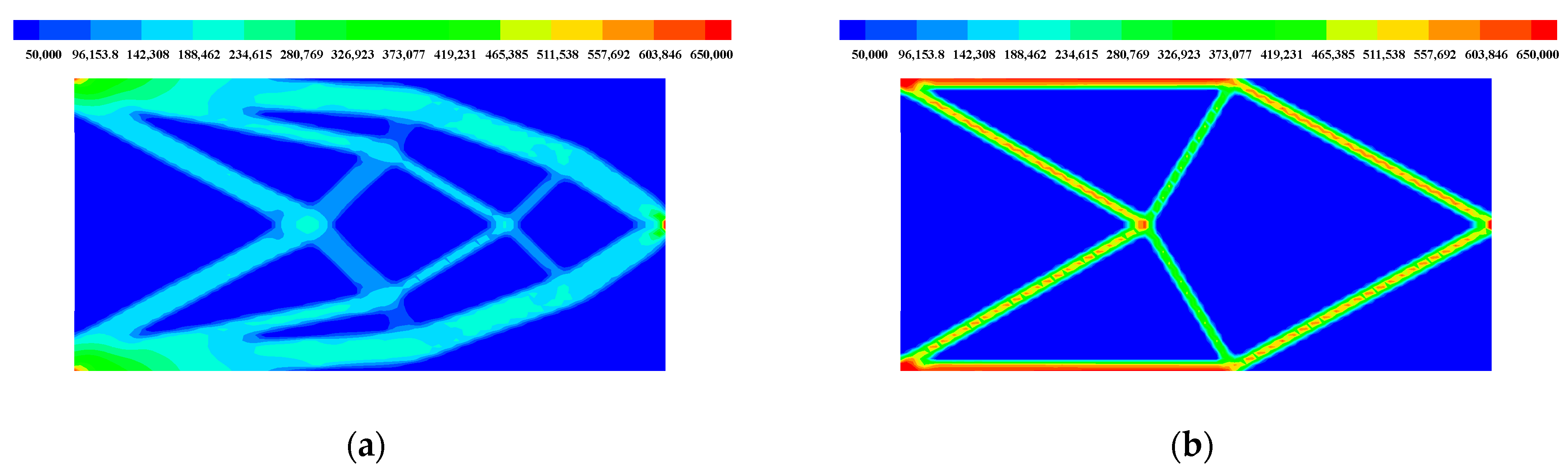
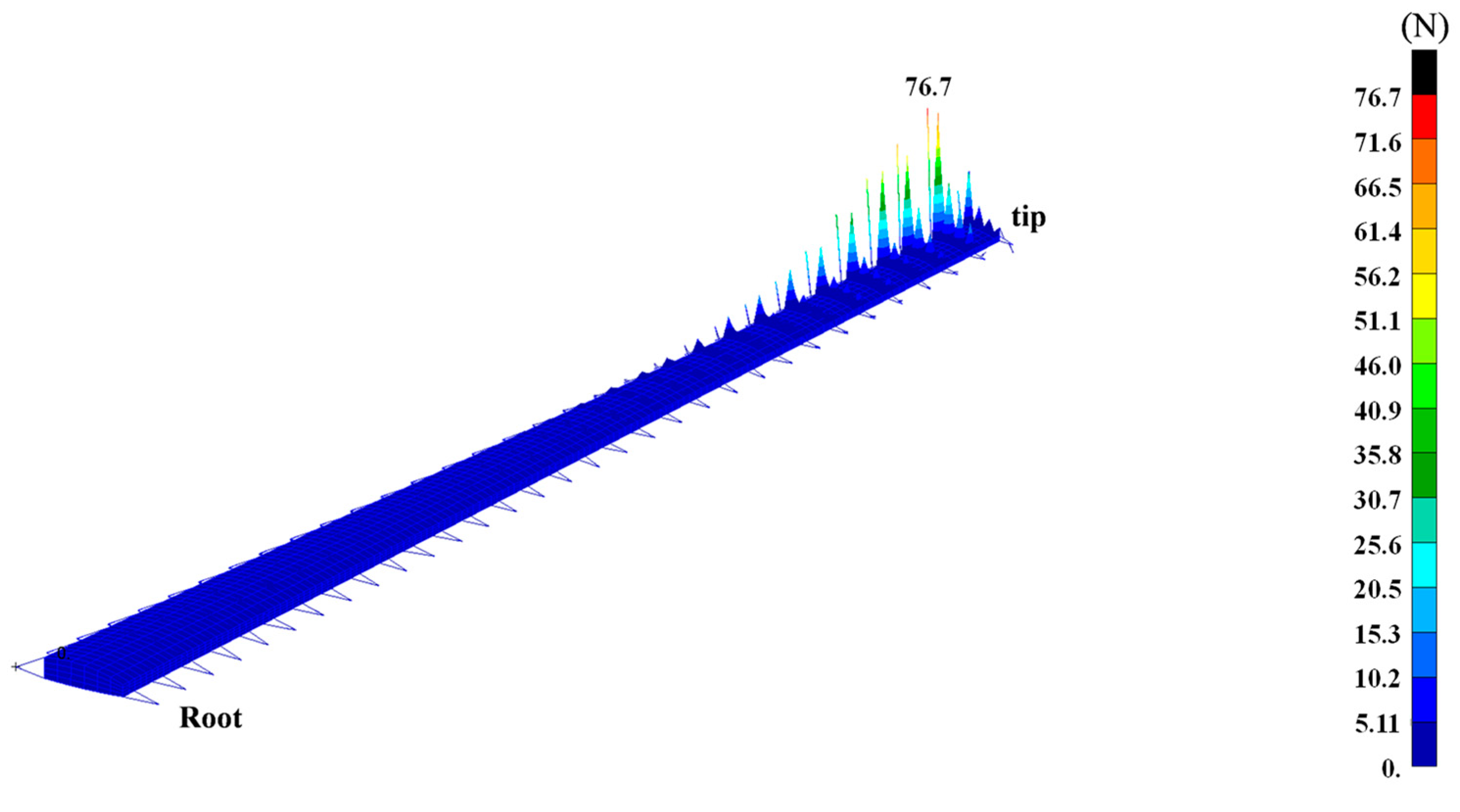
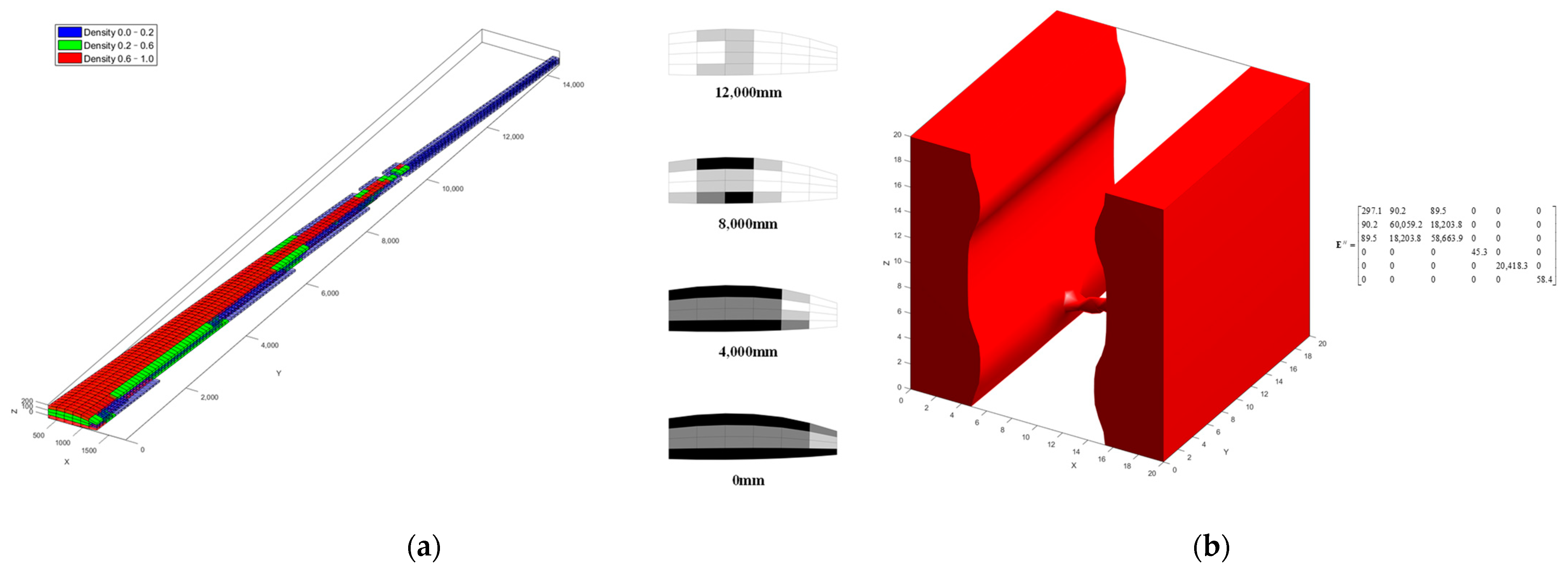
3.1. Cantilever Beam
3.2. Multiscale Optimization of Structure and Materials for Wings with Large Aspect Ratios
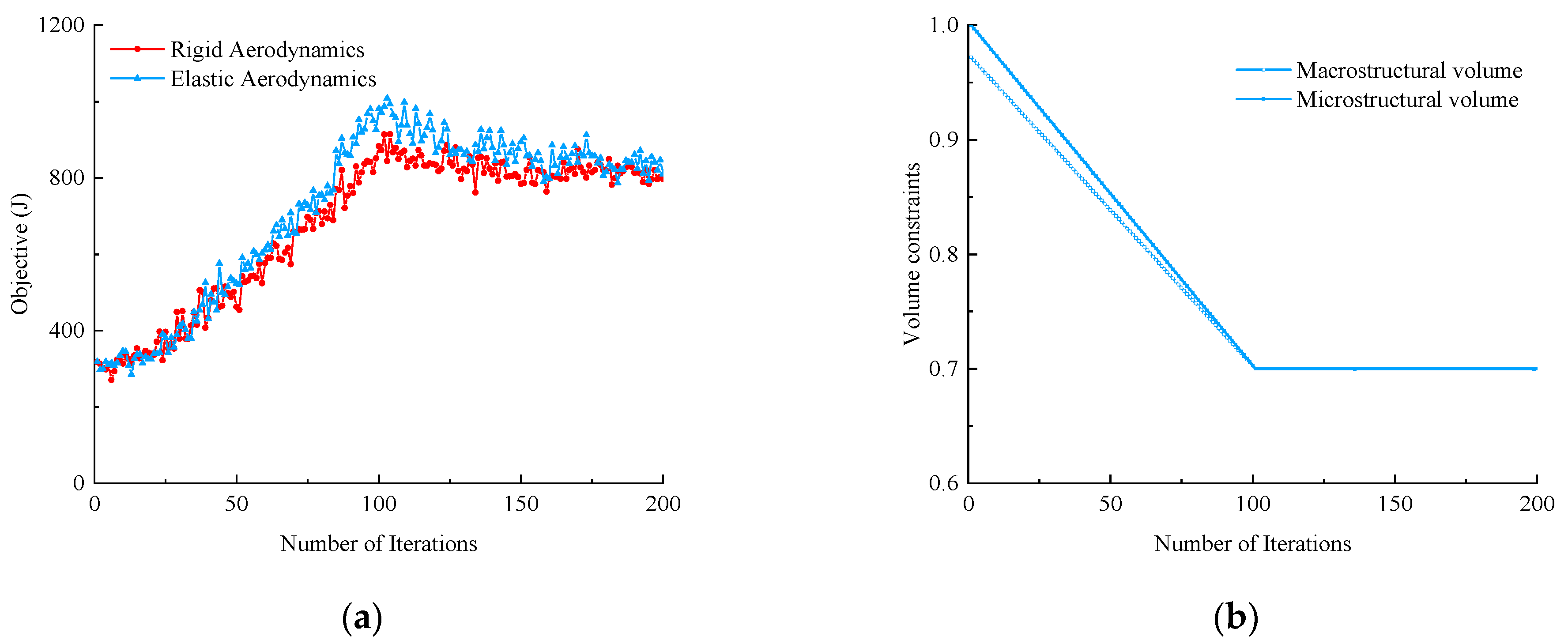
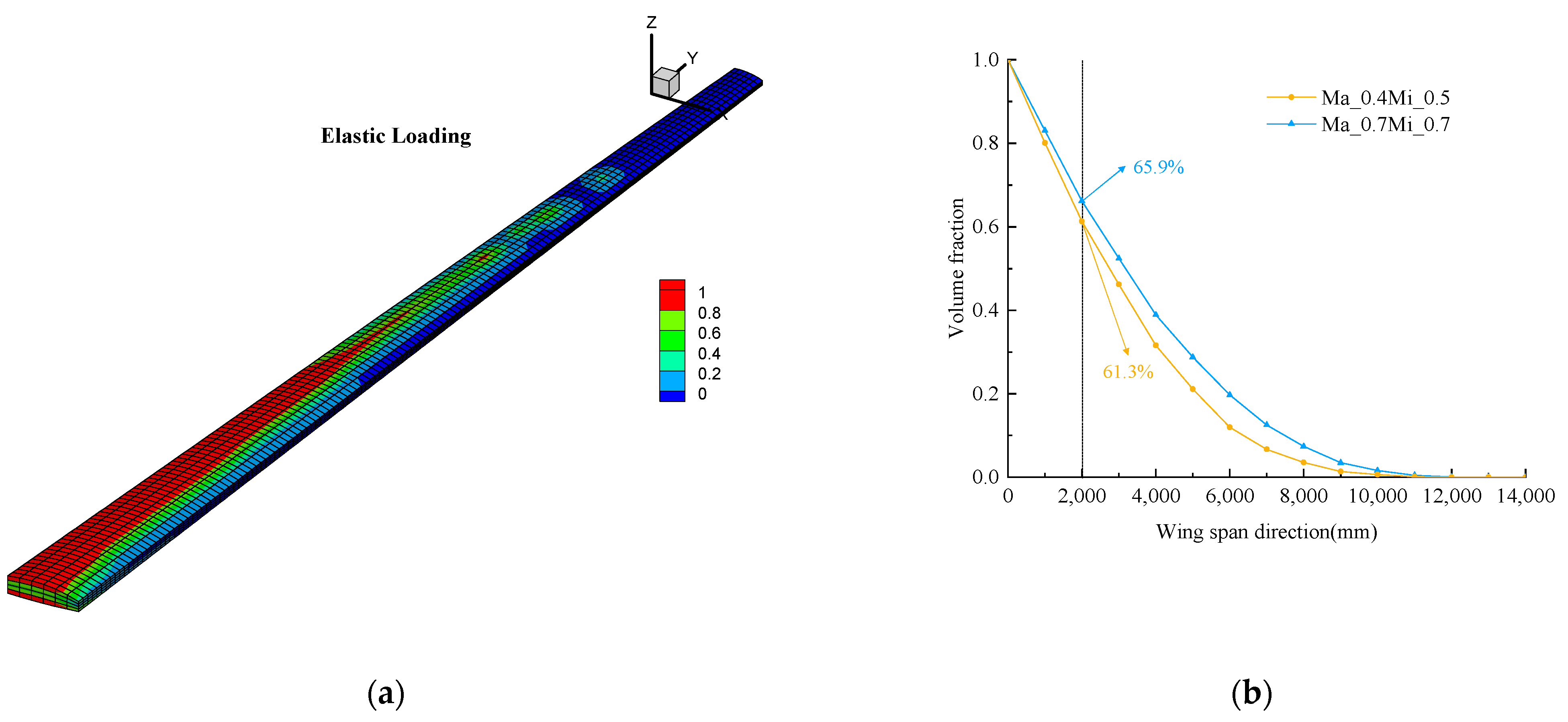
3.2.1. Multiscale Aeroelastic Optimization of Wing Structure and Material under Rigid and Elastic Loading
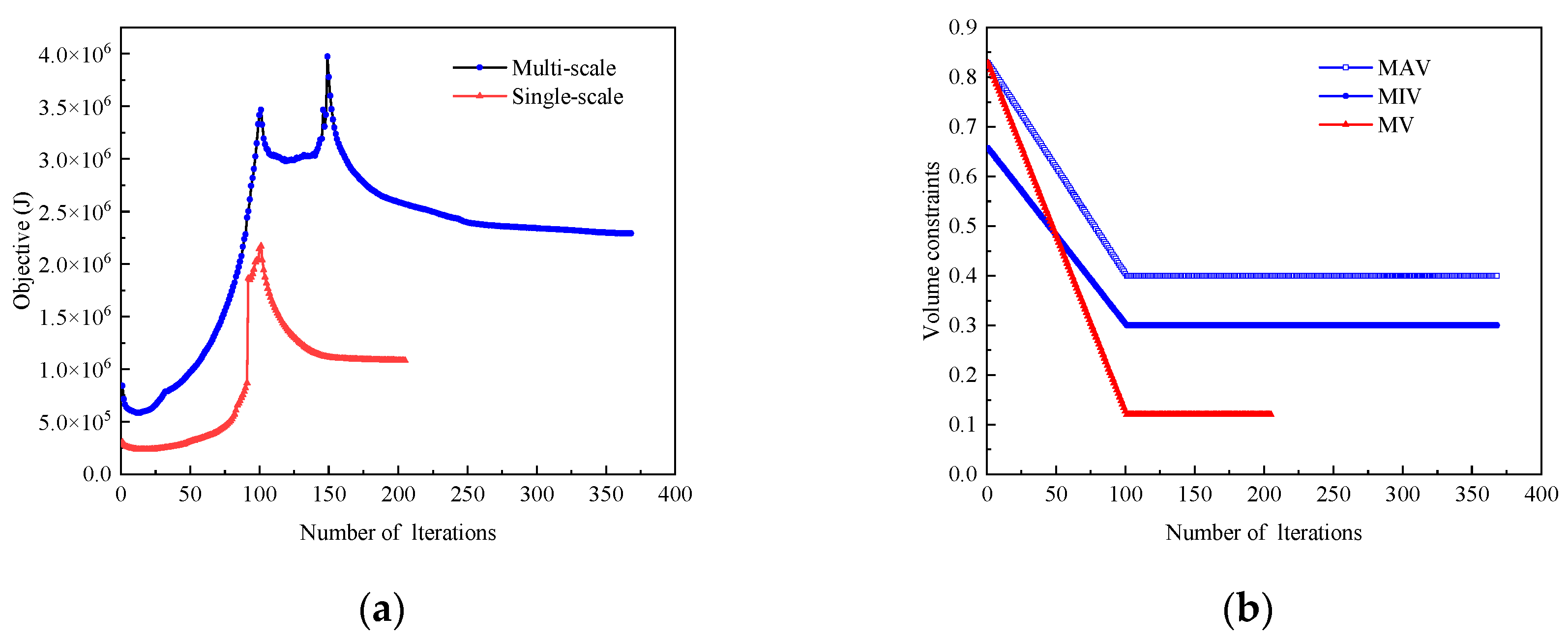
3.2.2. Multiscale Optimization of Wing Structure and Material with Different Volume Constraints
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kilimtzidis, S.; Kostopoulos, V. Static Aeroelastic Optimization of High-Aspect-Ratio Composite Aircraft Wings via Surrogate Modeling. Aerospace 2023, 10, 251. [Google Scholar] [CrossRef]
- Wang, X.; Wan, Z.; Liu, Z.; Yang, C. Integrated optimization on aerodynamics-structure coupling and flight stability of a large airplane in preliminary design. Chin. J. Aeronaut. 2018, 31, 1258–1272. [Google Scholar] [CrossRef]
- Kafkas, A.; Kilimtzidis, S.; Kotzakolios, A.; Kostopoulos, V.; Lampeas, G. Multi-Fidelity Optimization of a Composite Airliner Wing Subject to Structural and Aeroelastic Constraints. Aerospace 2021, 8, 398. [Google Scholar] [CrossRef]
- Guo, L.; Tao, J.; Wang, C.; Zhang, M.; Sun, G. Fuel efficiency optimization of high-aspect-ratio aircraft via variable camber technology considering aeroelasticity. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 782–793. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Wan, Z.; Wang, Z. Aeroelastic Topology Optimization of Wing Structure Based on Moving Boundary Meshfree Method. Symmetry 2022, 14, 1154. [Google Scholar] [CrossRef]
- Otomori, M.; Yamada, T.; Izui, K.; Nishiwaki, S. Matlab code for a level set-based topology optimization method using a reaction diffusion equation. Struct. Multidiscip. Optim. 2014, 51, 1159–1172. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Bendsøe, M.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2010, 43, 1–16. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.-M. Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X. A level set method for structural topology optimization. Adv. Eng. Softw. 2004, 35, 415–441. [Google Scholar] [CrossRef]
- Wang, S.; Wang, M.Y. Radial basis functions and level set method for structural topology optimization. Int. J. Numer. Methods Eng. 2006, 65, 2060–2090. [Google Scholar] [CrossRef]
- Gao, J.; Li, H.; Luo, Z.; Gao, L.; Li, P. Topology Optimization of Micro-Structured Materials Featured with the Specific Mechanical Properties. Int. J. Comput. Methods 2019, 17, 1850144. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, Ultrastiff Mechanical Metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.; Guedes, J.M.; Bendsoe, M.P. Hierarchical optimization of material and structure. Struct. Multidiscip. Optim. 2002, 24, 1–10. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Xia, L.; Gao, L. Concurrent topology optimization of multiscale composite structures in Matlab. Struct. Multidiscip. Optim. 2019, 60, 2621–2651. [Google Scholar] [CrossRef]
- Cramer, N.B.; Cellucci, D.W.; Formoso, O.B.; Gregg, C.E.; Jenett, B.E.; Kim, J.H.; Lendraitis, M.; Swei, S.S.; Trinh, G.T.; Trinh, K.V.; et al. Elastic Shape Morphing of Ultralight Structures by Programmable Assembly. Smart Mater. Struct. 2019, 28, 055006. [Google Scholar] [CrossRef]
- Cramer, N.B.; Kim, J.; Jenett, B.; Cheung, K.C.; Swei, S. Simulated Scalability of Discrete Lattice Materials Substructures to Commercial Scale Aircraft. In Proceedings of the Aiaa Aviation 2020 Forum, Virtual Event, 15–19 June 2020. [Google Scholar]
- Queheillalt, D.T.; Carbajal, G.; Peterson, G.P.; Wadley, H.N.G. A multifunctional heat pipe sandwich panel structure. Int. J. Heat Mass Transf. 2008, 51, 312–326. [Google Scholar] [CrossRef]
- Jenett, B.; Calisch, S.; Cellucci, D.; Cramer, N.; Gershenfeld, N.; Swei, S.; Cheung, K.C. Digital Morphing Wing: Active Wing Shaping Concept Using Composite Lattice-Based Cellular Structures. Soft Robot. 2017, 4, 33–48. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C.; Zhang, W. Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components. Chin. J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology optimization I—Homogenization theory for media with periodic structure. Comput. Struct. 1998, 69, 707–717. [Google Scholar] [CrossRef]
- Xia, Z.; Zhou, C.; Yong, Q.; Wang, X. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites. Int. J. Solids Struct. 2006, 43, 266–278. [Google Scholar] [CrossRef]
- Gao, J.; Li, H.; Gao, L.; Xiao, M. Topological shape optimization of 3D micro-structured materials using energy-based homogenization method. Adv. Eng. Softw. 2018, 116, 89–102. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Luo, Z.; Tong, L.; Kang, Z. A level set method for structural shape and topology optimization using radial basis functions. Comput. Struct. 2009, 87, 425–434. [Google Scholar] [CrossRef]
- Li, E.; Zhang, Z.; Chang, C.C.; Liu, G.R.; Li, Q. Numerical homogenization for incompressible materials using selective smoothed finite element method. Compos. Struct. 2015, 123, 216–232. [Google Scholar] [CrossRef]
- Li, H.; Gao, L.; Xiao, M.; Gao, J.; Chen, H.; Zhang, F.; Meng, W. Topological shape optimization design of continuum structures via an effective level set method. Cogent Eng. 2016, 3, 1250430. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, J.; Kang, Z. Level set-based topology optimization with overhang constraint: Towards support-free additive manufacturing. Comput. Methods Appl. Mech. Eng. 2018, 339, 591–614. [Google Scholar] [CrossRef]
- Kim, N.H.; Dong, T.; Weinberg, D.; Dalidd, J. Generalized Optimality Criteria Method for Topology Optimization. Appl. Sci. 2021, 11, 3175. [Google Scholar] [CrossRef]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for Additive Manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Im, S.; Kim, E.; Park, K.; Lee, D.-H.; Chang, S.; Cho, M. Surrogate Model Considering Trim Condition for Design Optimization of High-Aspect-Ratio Flexible Wing. Int. J. Aeronaut. Space Sci. 2022, 23, 288–302. [Google Scholar] [CrossRef]

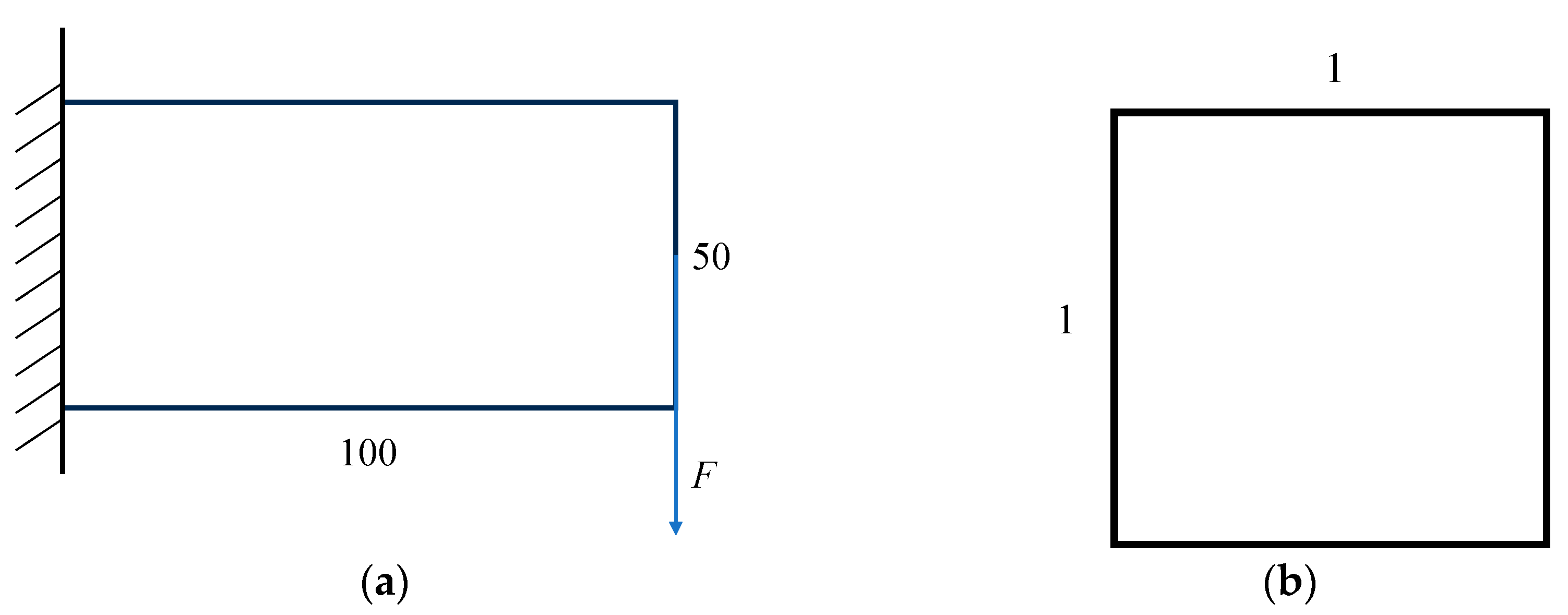



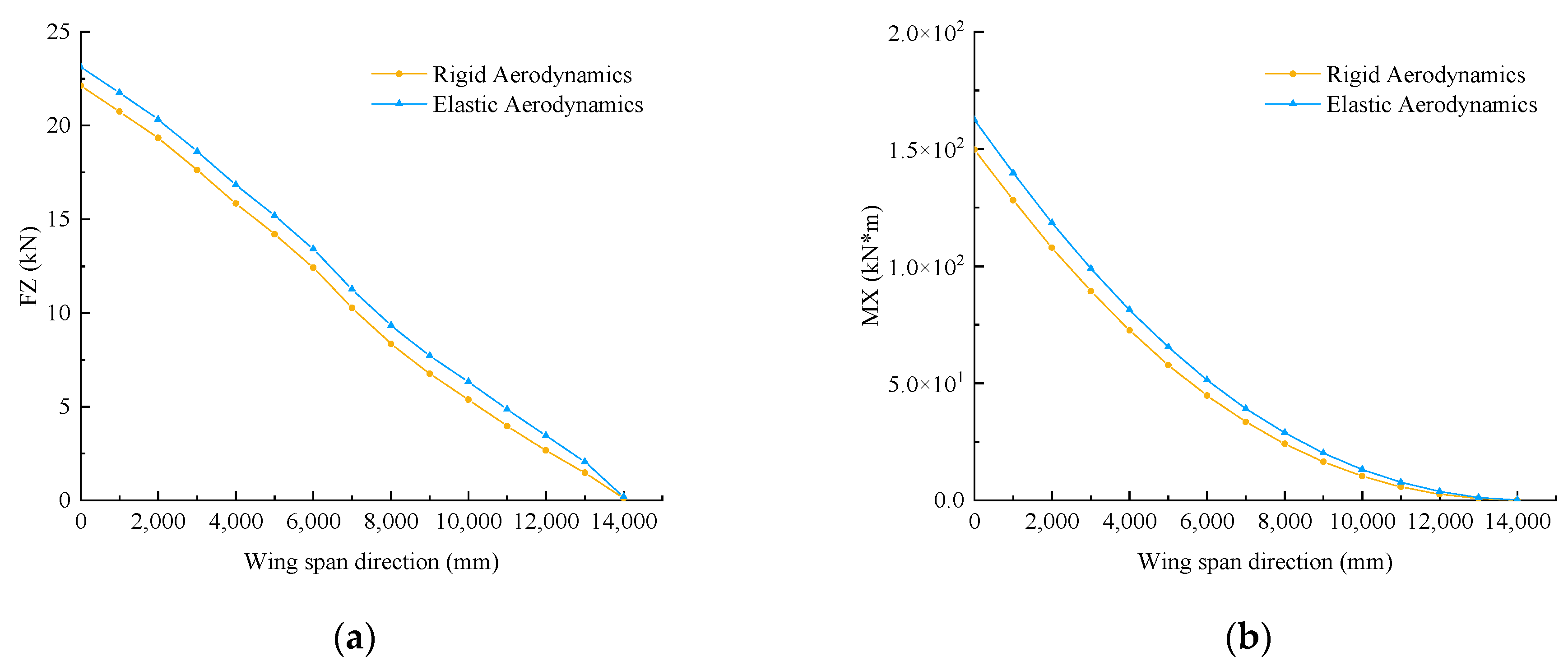
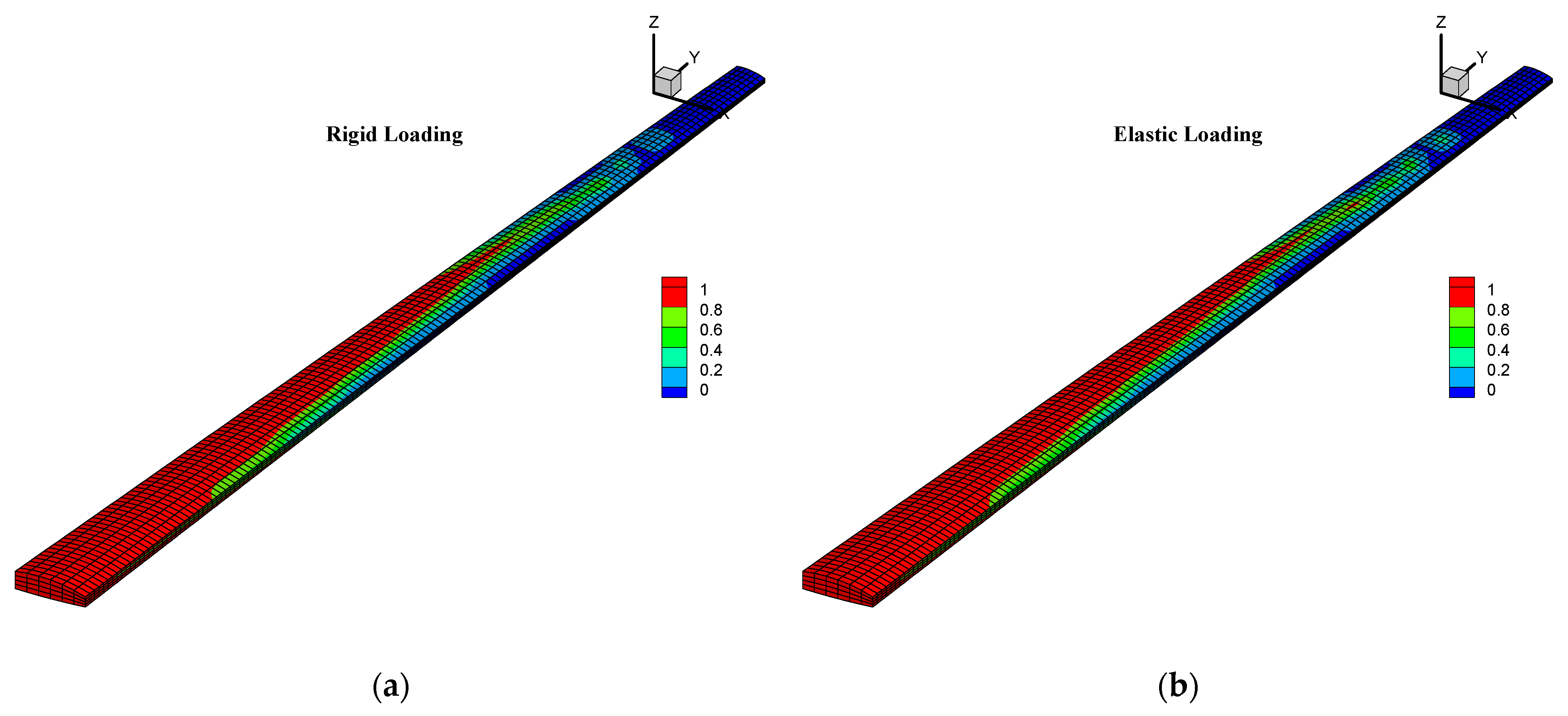
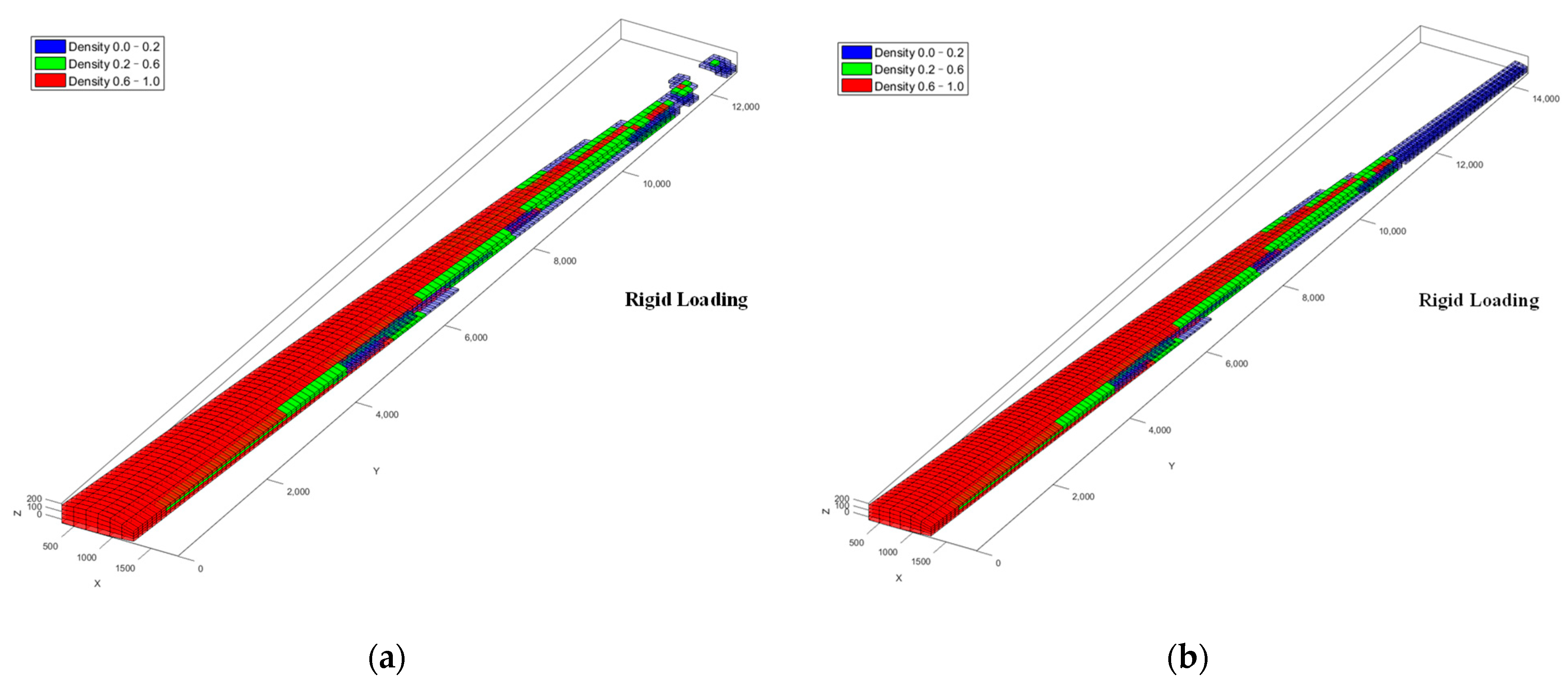

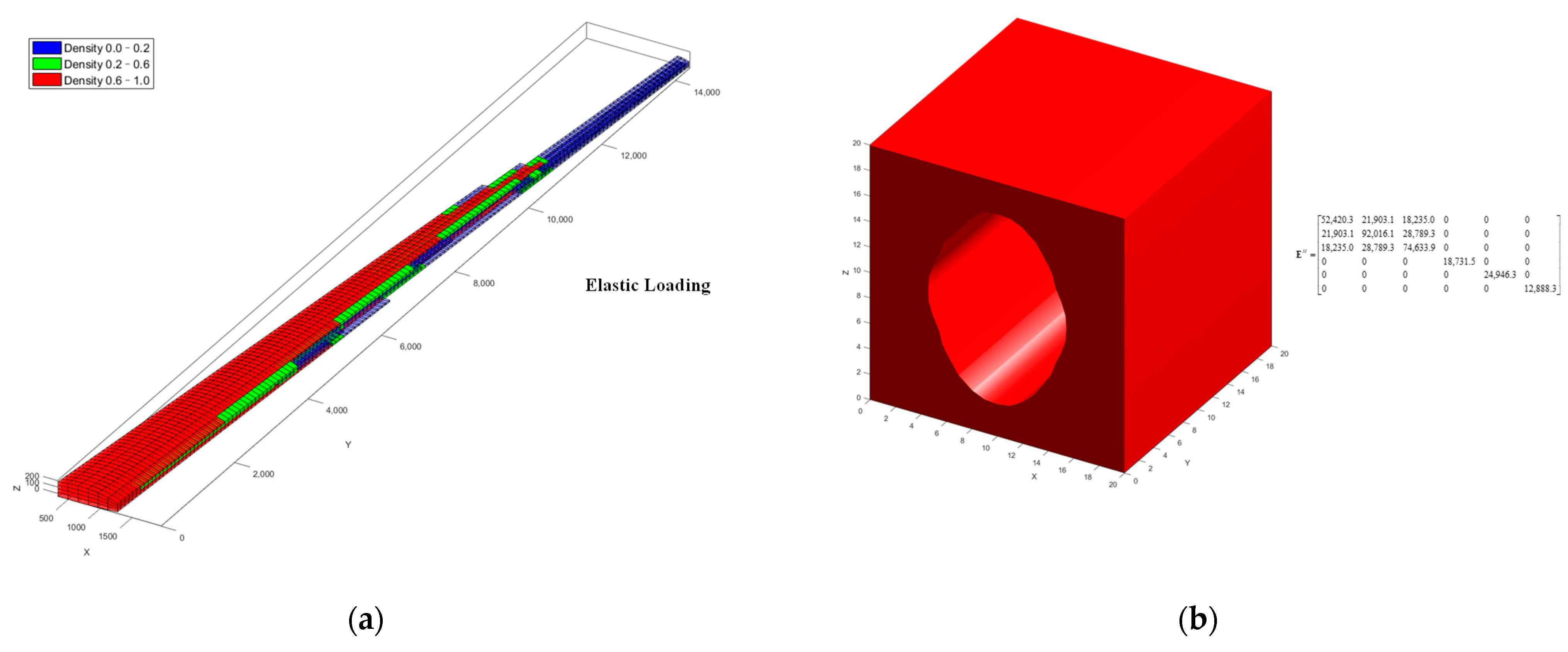
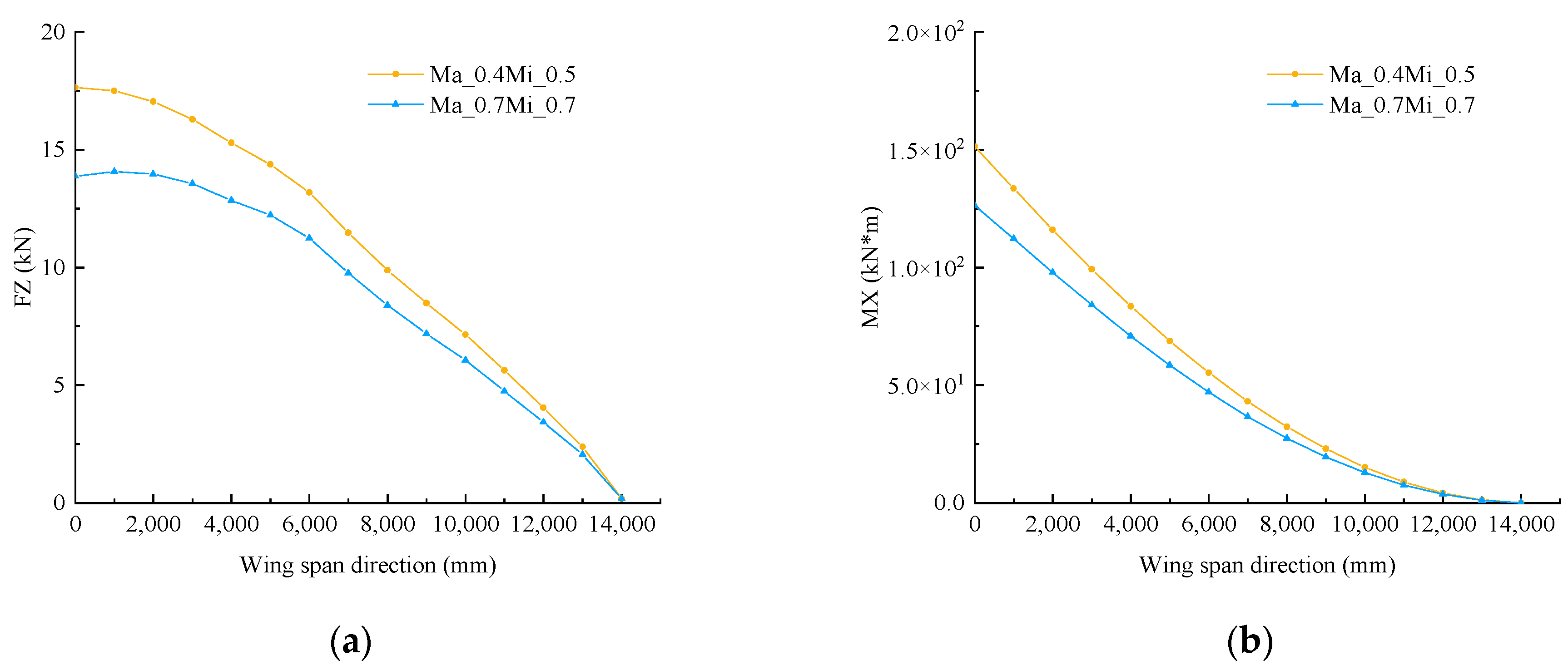
| Optimization Structure | Post-Processing Structure | |
|---|---|---|
| Compliance (J) | 7.62 × 102 | 8.47 × 102 |
| Mass ratio | 49% | 49% |
| Ma_0.7Mi_0.7 (Rigid) | Ma_0.7Mi_0.7 (Elastic) | Ma_0.4Mi_0.5 (Elastic) | |
|---|---|---|---|
| Compliance (J) | 7.62 × 102 | 7.87 × 102 | 1.54 × 103 |
| Mass ratio | 49% | 49% | 20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Yang, C.; Wang, X.; Wan, Z.; Li, C. Multiscale Aeroelastic Optimization Method for Wing Structure and Material. Aerospace 2023, 10, 866. https://doi.org/10.3390/aerospace10100866
Li K, Yang C, Wang X, Wan Z, Li C. Multiscale Aeroelastic Optimization Method for Wing Structure and Material. Aerospace. 2023; 10(10):866. https://doi.org/10.3390/aerospace10100866
Chicago/Turabian StyleLi, Keyu, Chao Yang, Xiaozhe Wang, Zhiqiang Wan, and Chang Li. 2023. "Multiscale Aeroelastic Optimization Method for Wing Structure and Material" Aerospace 10, no. 10: 866. https://doi.org/10.3390/aerospace10100866





