Robust Flight Control Design to Minimize Aircraft Loss-of-Control Incidents

Abstract

A pseudo-sliding mode control synthesis procedure discussed previously in the literature is applied to the design of a control system for a nonlinear model of the NASA Langley Generic Transport Model. The complete vehicle model is included as an appendix. The goal of the design effort is the synthesis of a robust control system to minimize aircraft loss-of-control by preserving fundamental pilot input—system response characteristics across the flight envelope, here including the possibility of actuator damage. The design is carried out completely in the frequency domain and is described by a ten-step synthesis procedure, also previously introduced it the literature. Five different flight tasks are considered in computer simulations of the completed design demonstrating the stability and performance robustness of the control system.

1. Introduction

Transport aircraft loss-of-control (LOC) incidents are a continuing problem in aviation safety [1,2]. There is growing interest in the design and validation of robust flight control systems to alleviate the severity of LOC incidents, e.g., [3,4]. A majority of these control designs are adaptive in nature. It is of interest to explore the feasibility of employing non-adaptive systems in this role. The research described herein employs frequency-domain sliding mode control to provide a robust flight control system for a model of the NASA Langley Generic Transport Model (GTM) [5], shown in Figure 1. Although referred to as a “model” the vehicle is actually a 5% dynamically-scaled version of a commercial transport. The frequency-domain sliding mode control approach has been applied in a number of instances in the literature, e.g., [6,7,8,9,10,11,12,13]. The contribution of the present study lies in the application of the frequency-domain sliding mode control to an existing flight vehicle (GTM) which has been the subject of other studies, e.g., [14] and in which a set of nonlinear dynamics have been explicitly and succinctly described [15]. The philosophy behind the approach espoused herein is that the preservation of fundamental pilot input—system response characteristics throughout the flight envelope is important, indeed vital, in preventing LOC events. Obviously, this is not a novel viewpoint. Indeed, it is shared by researchers developing model reference adaptive control designs, e.g., [14]. Among other potential outcomes, sudden changes in aircraft response characteristics can create “triggering events” leading to pilot-induced oscillations (PIOs) [16]. Quoting findings and recommendations from [16]:

“Finding 1-1 Adverse (PIO) events are fundamentally interactive and occur during highly demanding tasks when environmental, pilot, or aircraft dynamic changes create or trigger mismatches between actual and expected aircraft responses (emphasis added).”

“Recommendation 4-3 Organizations should adopt and implement minimization techniques in design and development policies, processes, and procedures. These techniques should be tailored and routinely updated to accommodate applications of newly developed technologies (emphasis added).”

Figure 1. The NASA generic transport model.

Figure 1. The NASA generic transport model.

The paper is organized as follows: Section 2 and the Appendix describe the nonlinear GTM model. Section 3 outlines the frequency-domain sliding mode design procedure, and then applies the procedure to the design of a flight control system for the GTM vehicle. The reader is reminded that the introductory material of Section 3 has appeared before in the literature, e.g., [13]. Section 4 discusses the design of the outer-loop compensation elements. Section 5 provides computer simulations of five tasks for the GTM vehicle. Section 6 provides a discussion of the results. Section 7 provides conclusions to the study.

2. Vehicle Model

The appendix provides a nonlinear model of the vehicle in question, the NASA Langley GTM. These dynamics are taken directly from [15] and repeated here for the convenience of the reader. The study of [10] was devoted to bifurcation analyses of the nonlinear model, with applications to the study of LOC events. The Appendix also includes elevator, aileron and rudder actuator models (including amplitude and rate limits) obtained from [17]. The inclusion of these models allows the reader to (1) replicate the results of the author and/or (2) compare the results with competitive designs.

3. Frequency Domain Sliding Model Control System Design

3.1. The Design Procedure

The design procedure for the frequency-domain sliding mode control approach has been thoroughly described in the literature, e.g., [13]. For the sake of completeness, it will be repeated here:

(1)

A vehicle model is obtained. If the vehicle in question is nonlinear, a linearized version is obtained for initiating the SMC design. Actuator dynamics are ignored at this stage. The linearization here is only evoked to allow classical frequency-domain design techniques to be employed in the synthesis procedure to be described.

(2)

A square control structure is identified. The design requires that no transmission zeros lie in the right-half plane and any uncontrollable states must be asymptotically stable. These requirements are similar to those employed in feedback linearization designs. Observability of the linear model must be in evidence to accommodate the observer design to be discussed in Step (7). The control loop structure in the square system is based upon a simple premise. Consider a square structure containing “m” control loops eventually driving a single control variable u_c. Define the inner-most loop as loop “1”, with the next being “m − 1”, etc. The transfer function of the linearized vehicle model for the control loop “1” should have a relative order of unity. The command variable in the “m − n” loop is, over a limited but important frequency range, the approximate integral of the command variable in the “m − (n + 1)” loop. Sequential loop closure design like that just described is certainly not novel, e.g., [18]. Its use here, however, forms the basis of the step-by-step design procedure being described.

Rules (3)–(10) refer to the inner-most control loops in the square structure.

(3)

Sliding mode control is limited to the inner-most control loops in the structure. The control law for each of these loops is given by

(1)

and the sliding manifolds σ for each control channel are selected.

a)

σ for any channel is derived from a tracking error expression such as

(2)

where ξ is the relative order of the system. Here e(t)^ξ-i refers the (ξ-i)^th derivative of e(t). An integral term also appears in Equation (2) to counter the steady-state bias often created with the inclusion of a boundary layer.

b)

Recognizing that a boundary layer is to be implemented, the control law is expressed as a linear transfer function,

(3)

The parameters K_i are chosen to provide “desirable” properties in the frequency domain. This means creating a loop transmission with broad K/s-like characteristics around crossover. The minimum K_ρ is that which permits pure gain or PI compensation in the frequency range at and beyond which ξ = 1, while exhibiting adequate gain and phase margins.

(4)

With the K_{( - )} values just determined, the existence of sliding behavior is verified through computer simulation. A convenient and practical choice for ρ is the amplitude limit of the actuator for the loop in question. Thus u_c(t) is the output of a relay element with limits of ±ρ.

(5)

A boundary layer is included in the controller to eliminate the high-frequency switching in the control variable(s) u_c(t).

(6)

Actuator dynamics are now included in the computer simulation. Instability will typically result. This condition highlights the effect of so-called “parasitic dynamics” in the SMC design procedure.

(7)

Asymptotic observers are created for each channel with actuator dynamics still eliminated in the observer design. The eigenvalues of the observers are selected as real and (approximately) equal, and are determined by either maximizing the stability margins evident in “effective” unity feedback loop transmissions L_eq, e.g., [13], or simply by selecting the eigenvalues near the bandwidth of the actuators.

(8)

To increase robustness, “hedge” dynamics can be created in which an additional loop is closed in parallel with the observer. Briefly, the hedge dynamics further decrease the destabilizing effects of the actuator in the loop in question. The method for choosing hedge dynamics can be found in [10] and will be summarized here. Hedge dynamics are created from a Bode diagram of the hedge dynamics transfer function G_hedge as follows: The magnitude plot of the hedge dynamics should exhibit (a) a +20 dB/dec slope at low frequencies, (b) a −20ξ dB/dec slope at frequencies near the actuator bandwidth, where ξ is the relative order of the vehicle dynamics in the loop in question (excluding actuators), and (c) a (−20ξ – 20) dB/dec slope at high frequencies. The gain value is chosen so that the magnitude of the Bode diagram of the hedge dynamics equals that of the transfer function of the appropriate observer output to SMC output near the natural frequency of the appropriate actuator [10].

(9)

In some applications, the addition of a rate-feedback loop in the inner-most control loops to which FDSMC is being applied can be considered. This was done, for example in [19]. Here “rate” refers to the fact that the derivative of the output of the inner-most feedback loop is utilized. In this case, it would be pitch and roll acceleration.

(10)

If desired, the observer(s) of Step (7) can be scheduled with flight condition.

3.2. Design Specifics for the GTM Vehicle

(1)

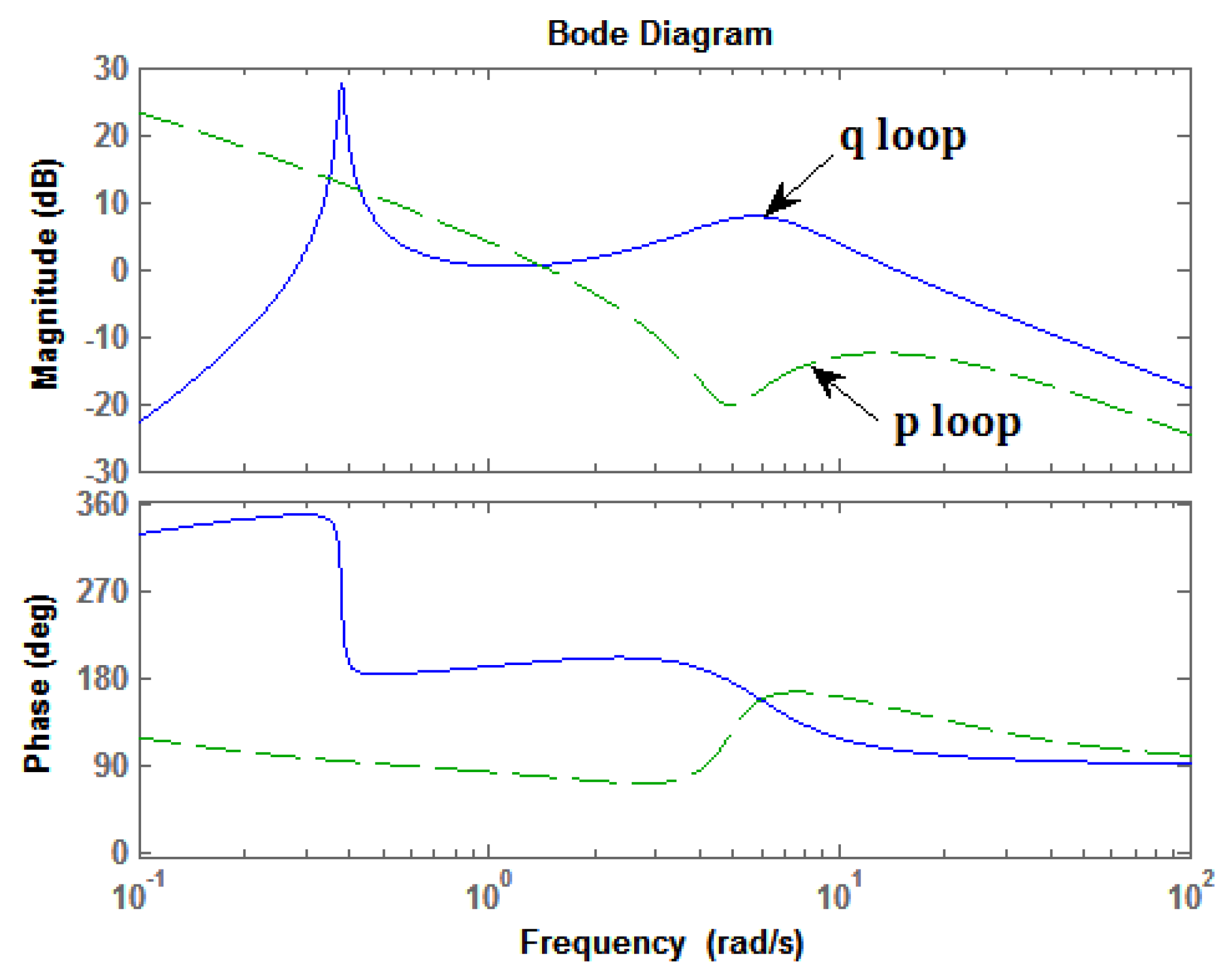
The vehicle model in the Appendix was mechanized in Simulink^® and linearized about a flight condition of steady-wings-level flight at a trim velocity of 110 ft/s. This step required an estimation of trim values of pitch attitude, θ₀, angle of attack, α₀, thrust level, T₀, and elevator angle, δe₀. These were estimated as: θ₀ = 5/57.3 rad, α₀ = 5/57.3 rad, T₀ = 5 lbf, δe₀ = 0 rad. The results of [15] provided guidance in choosing these values. It should be emphasized that after the SMC design is complete, the initial trim value can be obtained exactly, as the final SMC controller will “self-trim” in simulation. For reference, the following pitch and roll-rate open-loop transfer functions were obtained at this stage:

(4)

(5)

The reader will recognize typical modal characteristics in Equations (4) and (5), i.e., short period, phugoid, roll subsidence, spiral, and Dutch-roll modes [20]. Also note the non-minimum phase zero in Equation (5), not uncommon in such transfer functions [21].

Figure 2 shows the Bode diagrams of the transfer functions of Equations (4) and (5), indicating relative orders of 1 (−20 dB/dec magnitude slopes beyond 10 rad/s).

Figure 2. Bode Diagrams for the Transfer Functions of Equations (4) and (5).

Figure 2. Bode Diagrams for the Transfer Functions of Equations (4) and (5).

(2)

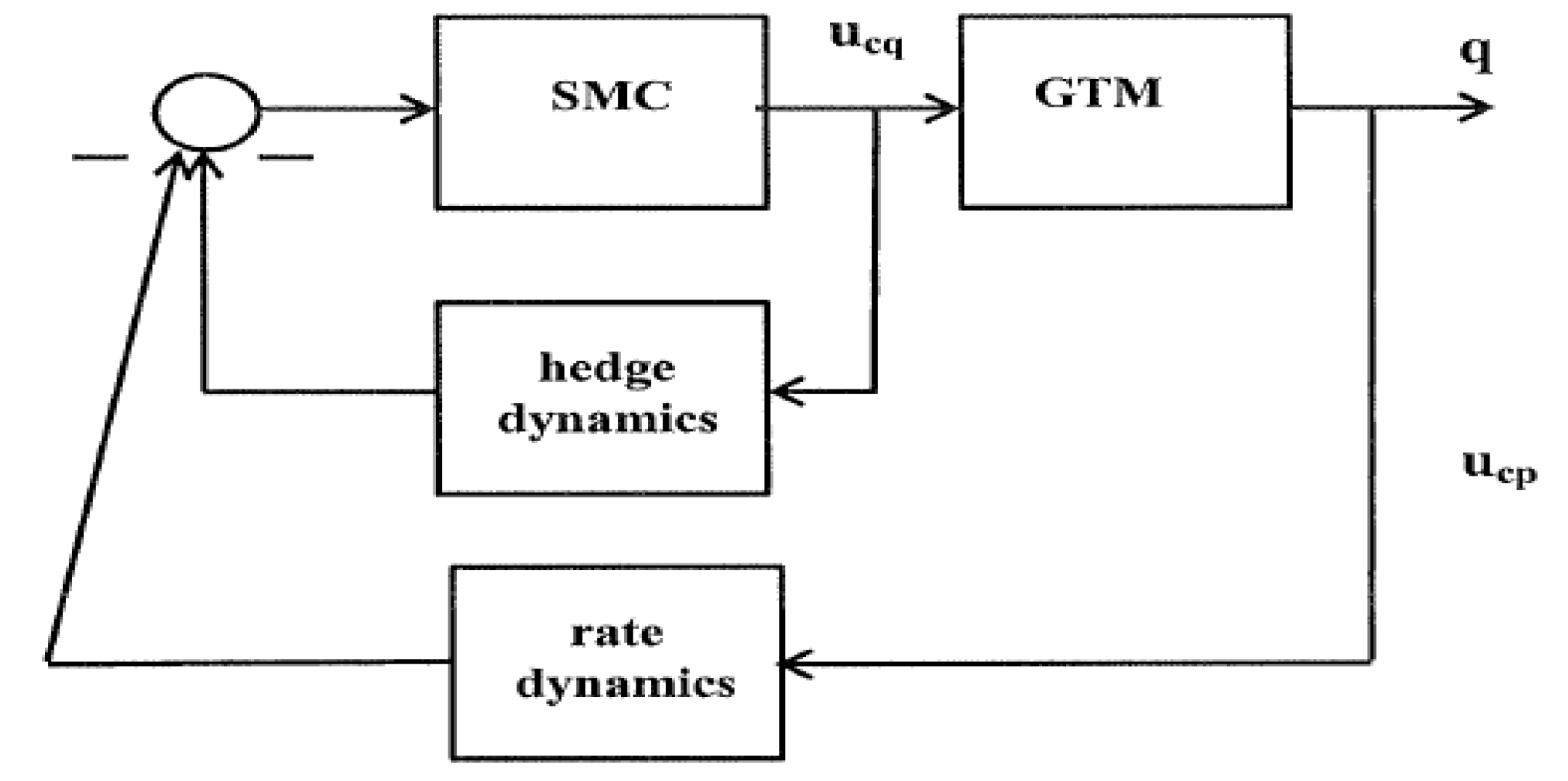
The control structure to be used is shown in simplified form in Figure 3. Note that no yaw control system is to be created. In terms of pilot control of a full-scale aircraft, the system of Figure 3 would define flight-path control with the cockpit column, roll-rate control with the wheel, auto-throttles controlling airspeed, with bare-airframe dynamics in response to pedal inputs.

Figure 3. The control system architecture.

Figure 3. The control system architecture.

(3)

The sliding manifolds for the q and p loops, as interpreted in the frequency domain can be given by

(6)

(7)

The simplicity of these compensators should be noted. To accommodate the non-minimum phase characteristics of Equation (5), “regulated variables” were employed for the feedback variable in the p loop p(t) + 0.5r(t). Regulated variables were also used in the study of [22]. The gains shown in Equations (6) and (7) result in crossover frequencies of 20 rad/s. The author would point out that this value is reasonable for a 5% scaled aircraft.

(4)

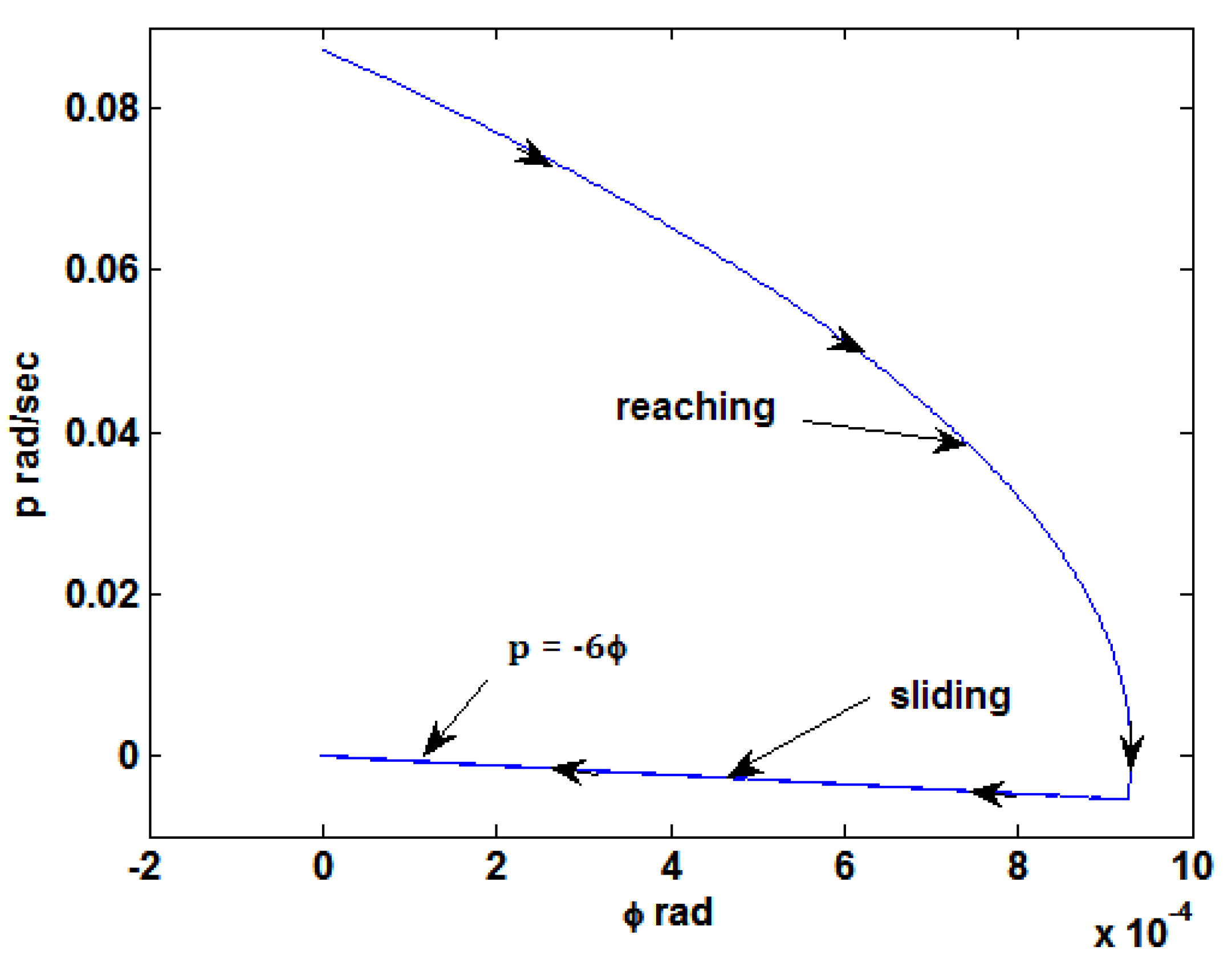
By introducing initial conditions of 5/57.3 rad/s in the q-loop and −5/57.3 rad/s in the p-loop sliding behavior was verified. That is, “reaching” and “sliding” behavior was noted along with “infinite frequency” switching in the outputs of the signum elements. Figure 4 shows the reaching and sliding behavior in the p loop. Note that for sliding behavior, the numerator of Equation (7) is zero, i.e., p(t) = −6φ(t) on the sliding surface [23].

Figure 4. Reaching and sliding behavior in the p loop.

Figure 4. Reaching and sliding behavior in the p loop.

(5)

A boundary layer was included in the q and p loops to eliminate the high-frequency switching characteristic of SMC systems. The signum elements in the q and p loops were removed. As in other applications of the methodology, e.g., [13], no saturation elements were included. This leads to an accurate description of the methodology as pseudo-sliding mode control.

(6)

Actuator dynamics were next included. Due to the relative high-frequency bandwidth of the actuators, instability was avoided in this case. Nonetheless, asymptotic observers were created for the q and p loops to ensure robustness in the presence of the actuator dynamics. A single observer was utilized with inputs consisting of φ, θ, ψ, p, q, r and the outputs of all the inner-loop compensators. The eigenvalues were selected as λ = −75, −75.1, −75.2,…,−75.8, just beyond the actuator bandwidths of 62.8 rad/s.

(7)

Hedge dynamics were created in the q and p loops as follows:

(8)

(9)

where u_cq and u_cp are the output of the elements in Equations (6) and (7).

(8)

Rate feedback loops were included in the q and p loops as follows:

(10)

(11)

Figure 5 shows the manner in which the hedge and rate-feedback dynamics were employed, in this case, for the q loop. As an example, Figure 6 shows the result of adding the rate feedback loop to the loop transmission of the p loop. The phase difference in Figure 6 merely represents a 360 deg shift. A significant reduction in phase lag at high frequency can be seen.

Figure 5. Hedge and rate dynamics placement.

Figure 5. Hedge and rate dynamics placement.

Figure 6. Effect of rate-loop closure in loop transmission of p loop.

Figure 6. Effect of rate-loop closure in loop transmission of p loop.

(9)

For the purposes of this study, two flight conditions were considered, both at sea level, one at 110 ft/s and one at 220 ft/s. The asymptotic observers were scheduled with respect to these flight conditions.

4. Design of Outer-Loop Compensators

The four non-SMC compensators in Figure 3 were created using classical loop-shaping principles, i.e., ensuring K/s-like characteristics in the loop transmissions and separating the crossover frequencies of each sequential loop by at least a factor of 3. The resulting compensation elements are given in Equation (12).

(12)

The simplicity of these elements is worthy of note as each is either a pure gain or PI controller.

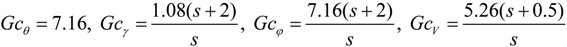
5. Computer Simulation of the Design

5.1. Sensor Noise and Unmodeled Time Delays

Additive sensor noise was included in each of the response variables used in the observers. The noise was created by passing white noise second-order filters with break frequencies of 10 rad/s. The root-mean square noise levels were 0.1 deg, 0.1 deg/s on vehicle attitudes and attitude rates, respectively. In addition, unmodeled time delays of 0.2 s were introduced at the input of each actuator.

5.2. Task 1 and Actuator Damage

A computer simulation of the nonlinear vehicle and control system was undertaken with the following task:

(1)

Command flight path angle γ = 0 deg.

(2)

Command velocity V_c = 110 ft/s

(3)

Command velocity perturbations around trim ΔV_c = 15 sin(0.1 t) ft/s

(4)

Command roll attitude φ_c = 10 sin(t) deg and simultaneous rudder input δ_r = 5 sin(t) deg. The roll and rudder commands were deliberately designed to produce positive (negative) sideslip β, with positive (negative) roll attitude φ. These inputs were included to excite the nonlinearities in the vehicle model. While decidedly atypical pilot inputs, they have been seen in piloted simulations involving crosswind landings [24].

To emulate damage to the elevator and aileron actuators, at 30 s into a 180 s run the effectiveness of the actuators was reduced by 25% and a 0.5 deg backlash element was introduced in the outer loop of the actuator mechanization. Simultaneously a −10 deg elevator bias (trailing edge up) was introduced.

Figure 7 and Figure 8 show the vehicle responses and longitudinal control/thrust inputs. Note that the angle of attack reaches approximately 10 deg in Figure 7. Figure 8 indicates that the elevator bias was immediately compensated by the SMC system. By way of comparison, Figure 9 and Figure 10 show the vehicle responses and longitudinal control/thrust inputs when no actuator damage was considered. It is interesting to note that the vehicle responses in the two cases are essentially identical.

Figure 7. Vehicle responses for Task 1.

Figure 7. Vehicle responses for Task 1.

Figure 8. Elevator and thrust inputs for Task 1.

Figure 8. Elevator and thrust inputs for Task 1.

Figure 9. Vehicle responses for Task 1 with no actuator damage.

Figure 9. Vehicle responses for Task 1 with no actuator damage.

Figure 10. Elevator and thrust inputs for Task 1 with no actuator damage.

Figure 10. Elevator and thrust inputs for Task 1 with no actuator damage.

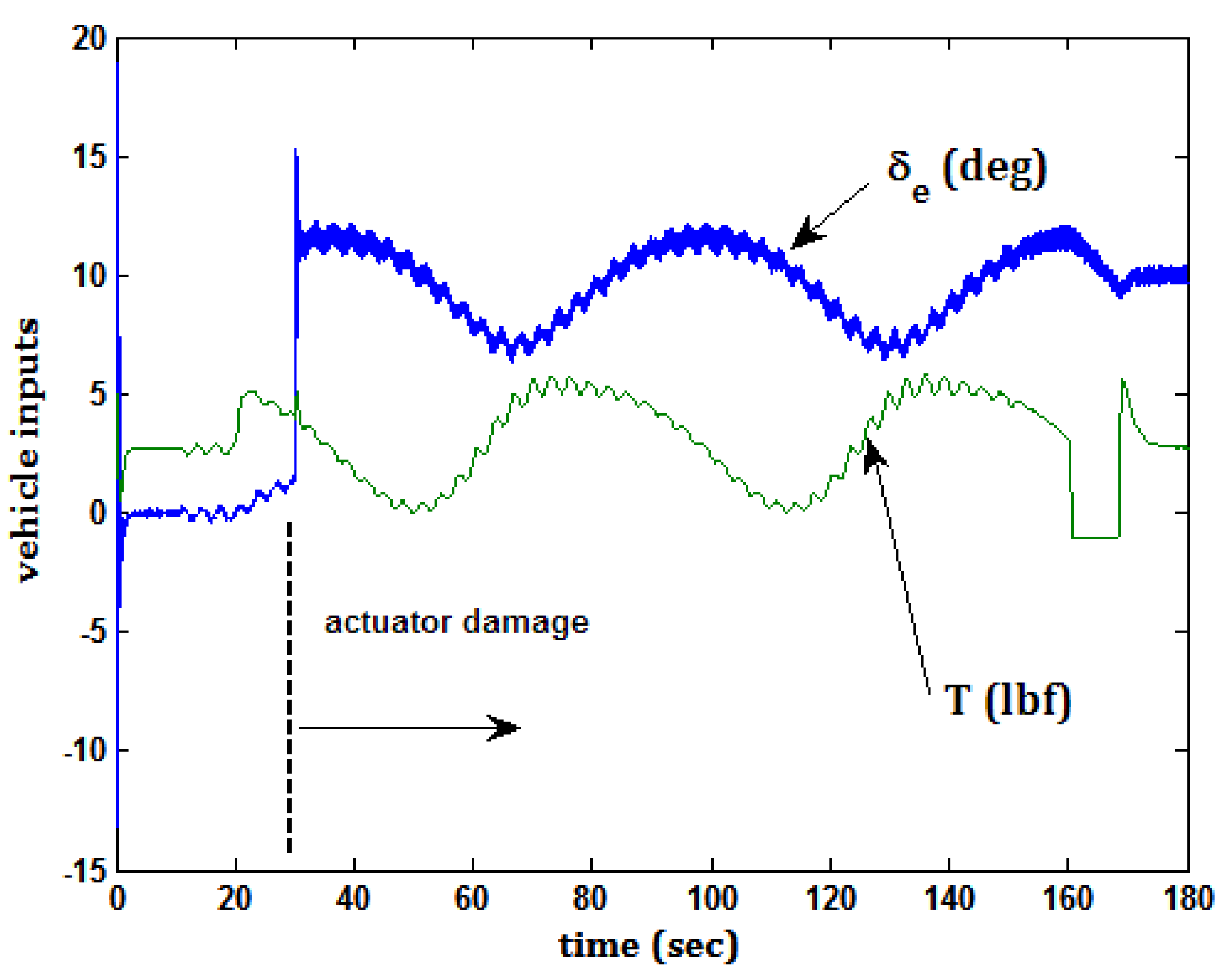
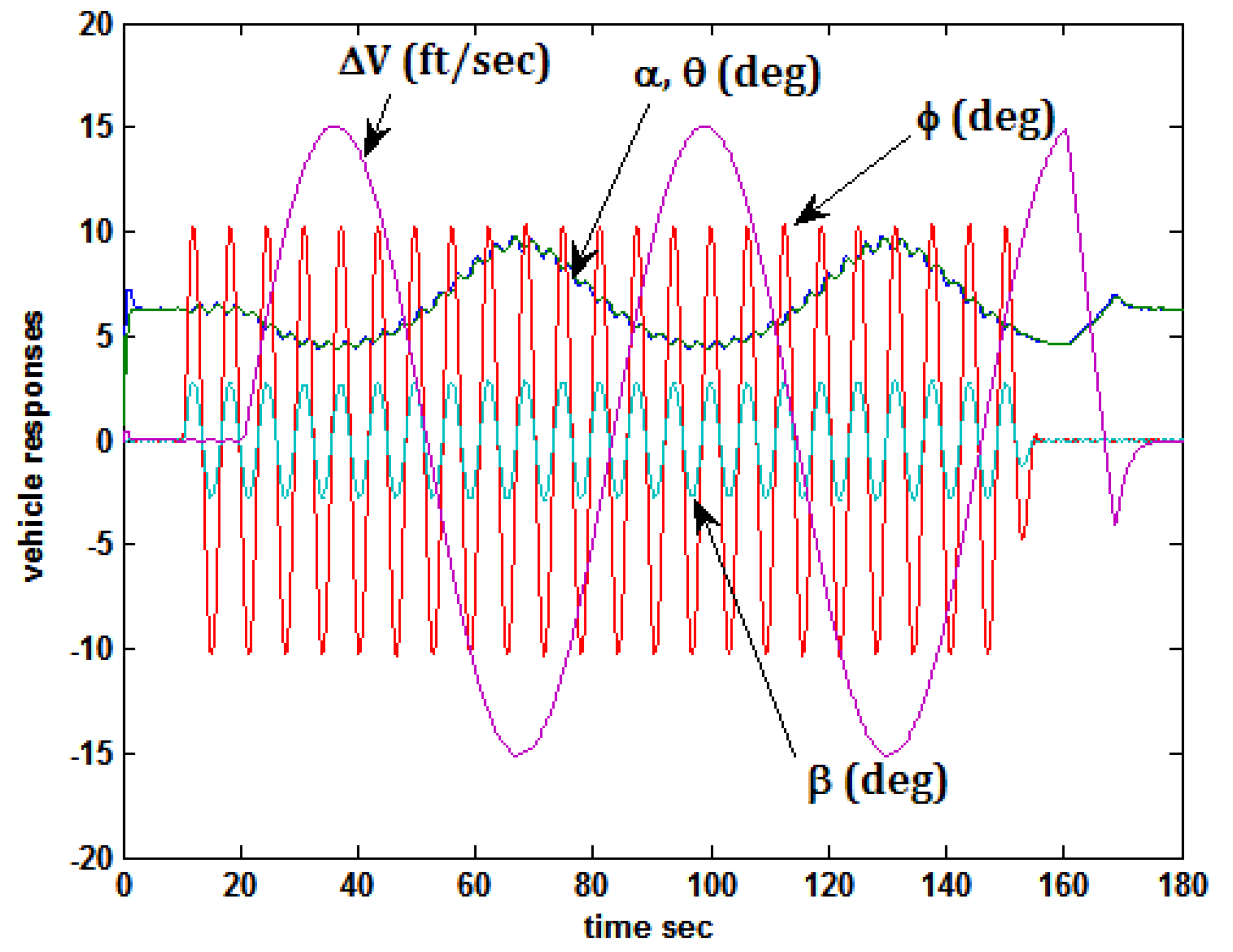
5.3. Task 2 and Actuator Damage

The scenario of Task 1 was repeated, with the command velocity V_c = 220 ft/s. Figure 11 and Figure 12 show the results. Note in Figure 13 that δ_e – 10 (deg) has been plotted to prevent overlap with the thrust time history. The very active elevator inputs are attributable to the effect of the actuator backlash element at the higher airspeed.

Figure 11. Vehicle responses for Task 2.

Figure 11. Vehicle responses for Task 2.

Figure 12. Elevator and thrust inputs for Task 2.

Figure 12. Elevator and thrust inputs for Task 2.

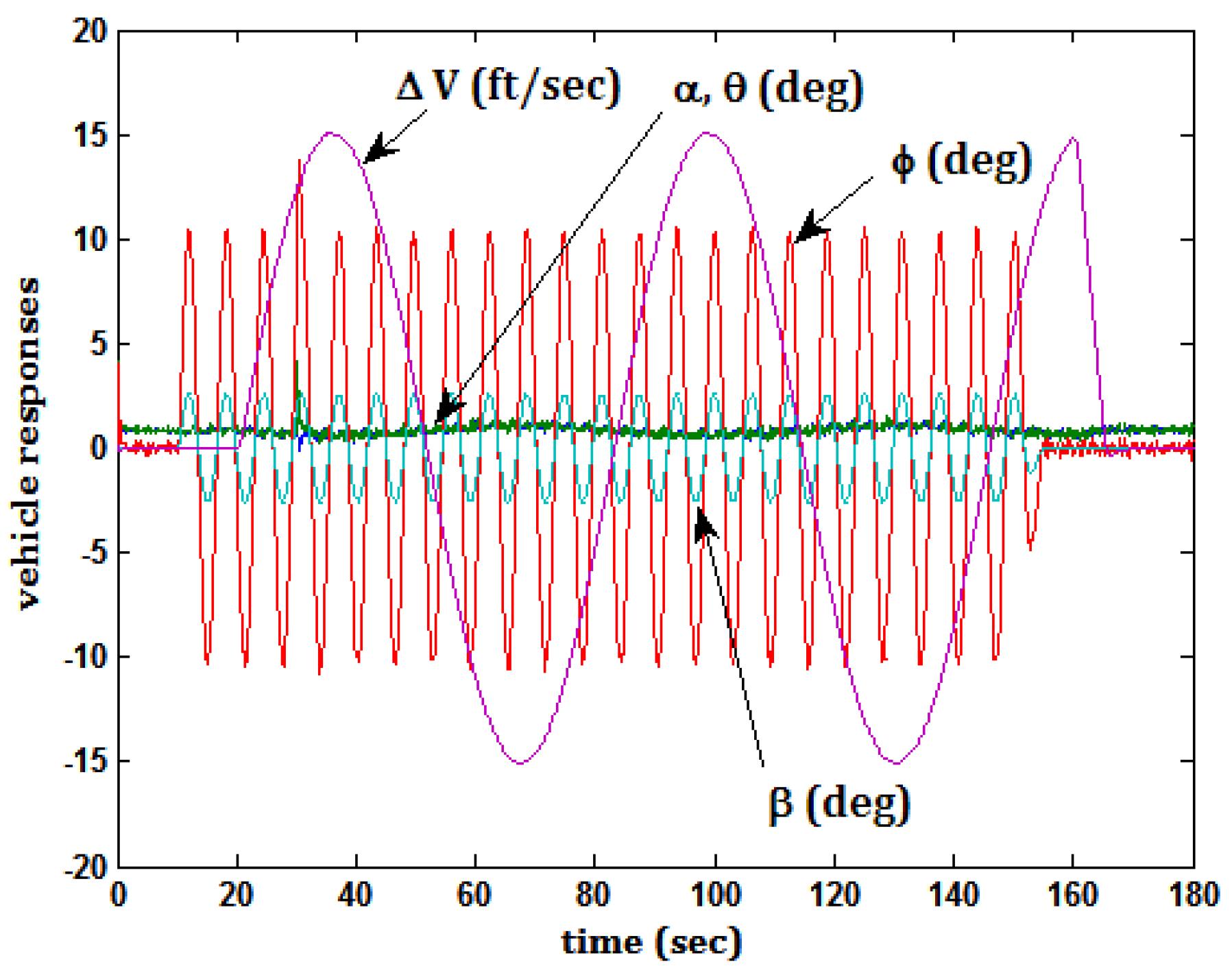
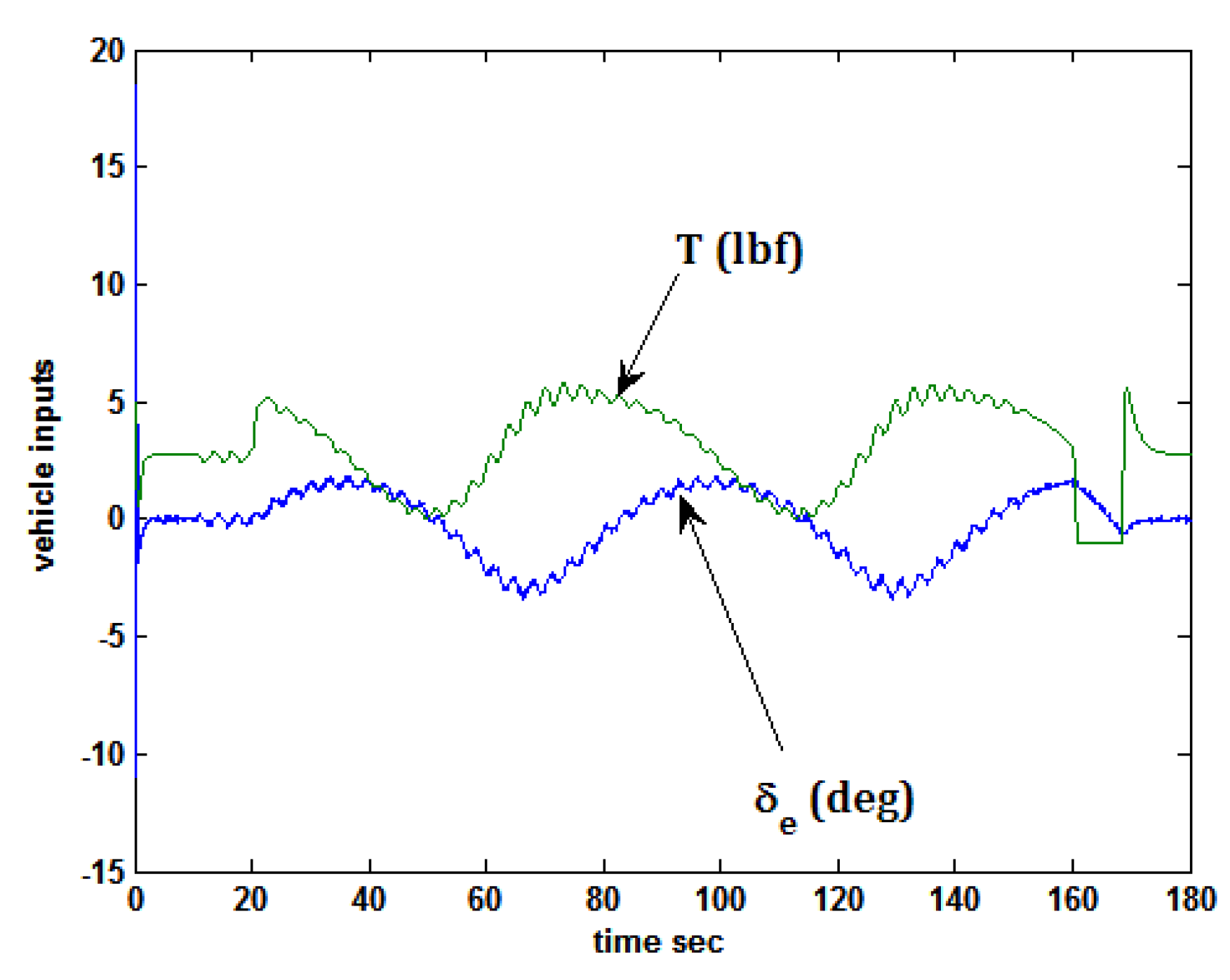
5.4. Task 3 and Actuator Damage

Task 3 consisted of the following

(1)

Command flight path angle γ = 2.5 deg.

(2)

Command velocity V_c = 110 ft/s

(3)

Command velocity perturbation around trim ΔV_c = −22.5 ft/s

(4)

Command roll attitude φ_c = 10 sin(t) deg and simultaneous rudder input δ_r = 5 sin(t) deg.

The actuator damage described in Section 6 was also included. Figure 13 and Figure 14 show the results. Note in Figure 14 that the angle of attack is approaching 13 deg, quite near stall for this vehicle [25].

Figure 13. Vehicle responses for Task 3.

Figure 13. Vehicle responses for Task 3.

Figure 14. Elevator and thrust inputs for Task 3.

Figure 14. Elevator and thrust inputs for Task 3.

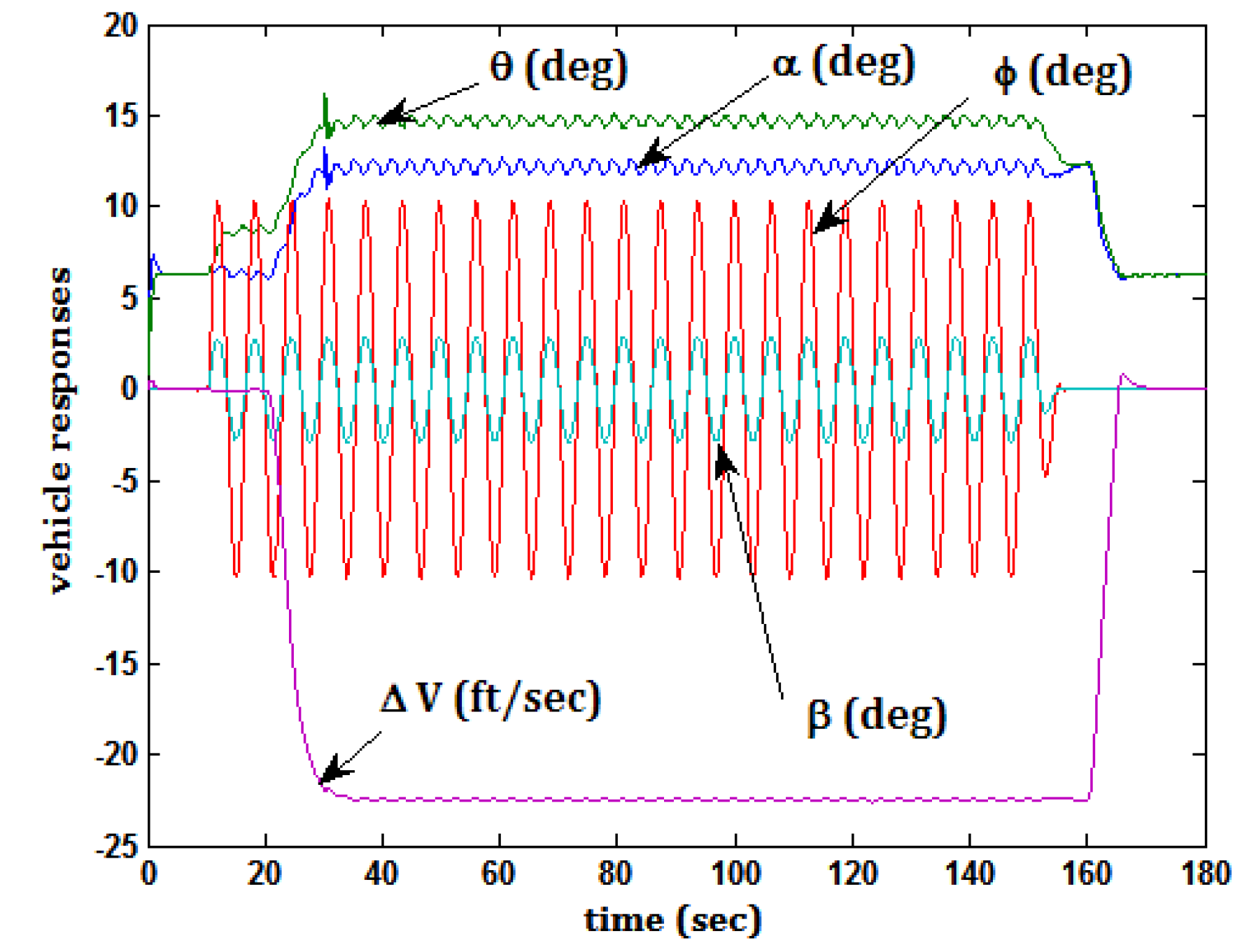
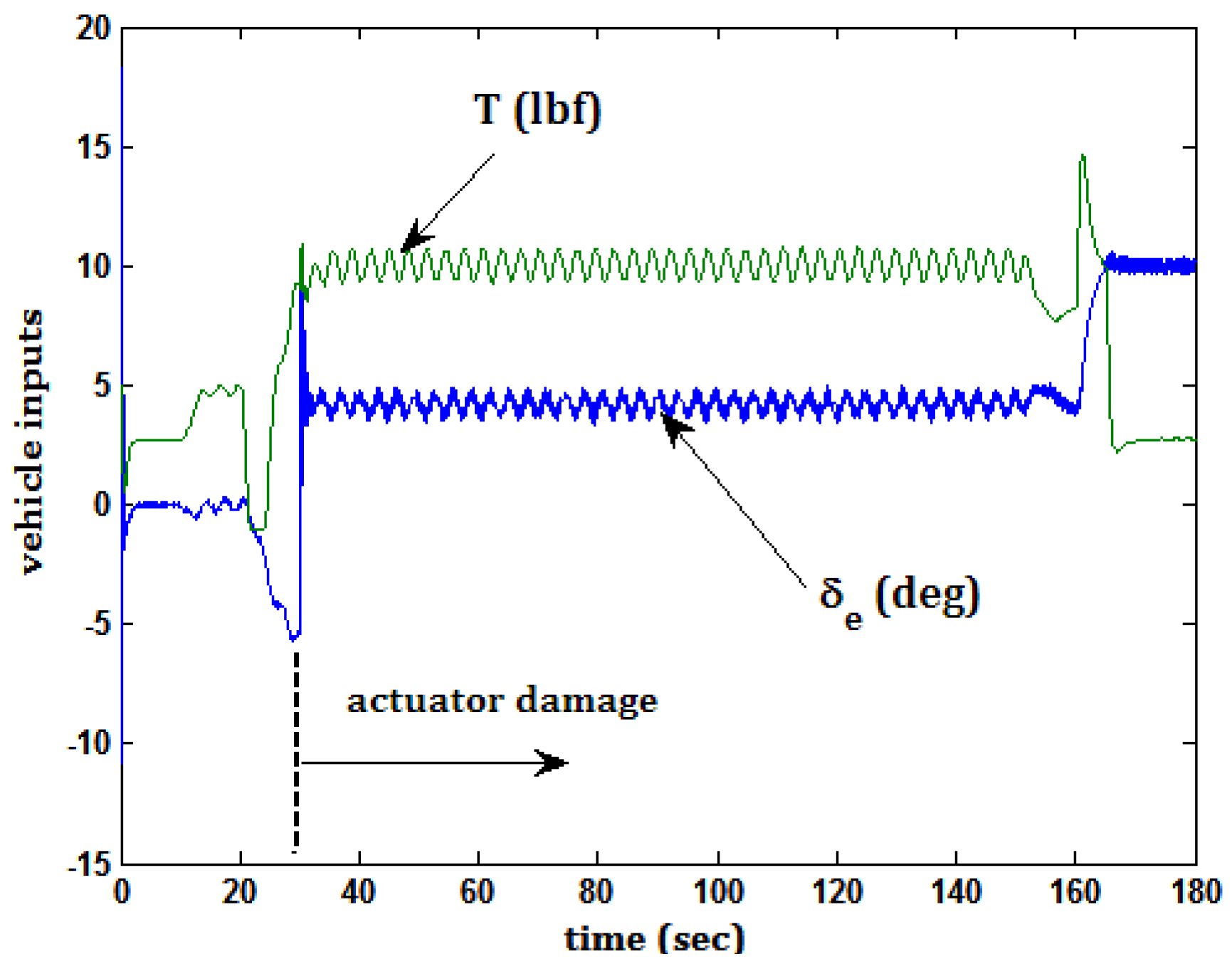
5.5. Task 4 and Actuator Damage

Task 4 was identical to Task 3 with the following two exceptions:

(1)

Command velocity perturbation around trim ΔV_c = −7.5 ft/s

(2)

Air density in the vehicle model was set to a value appropriate for an altitude of 10,000 ft (ρ = 0.0017556 slugs/ft³). The author is aware that the vehicle in question was not intended to operate at this altitude. The inclusion of this flight condition, however, provides an opportunity to evaluate the robustness of the SMC design.

The necessity of reducing the magnitude ΔV_c from that of Task 3 was necessary to prevent stall at the higher simulated altitude. Figure 15 and Figure 16 show the vehicle responses and inputs. The maximum angle of attack in the task was approximately 12 deg.

Figure 15. Vehicle responses for Task 4.

Figure 15. Vehicle responses for Task 4.

Figure 16. Elevator and thrust inputs for Task 4.

Figure 16. Elevator and thrust inputs for Task 4.

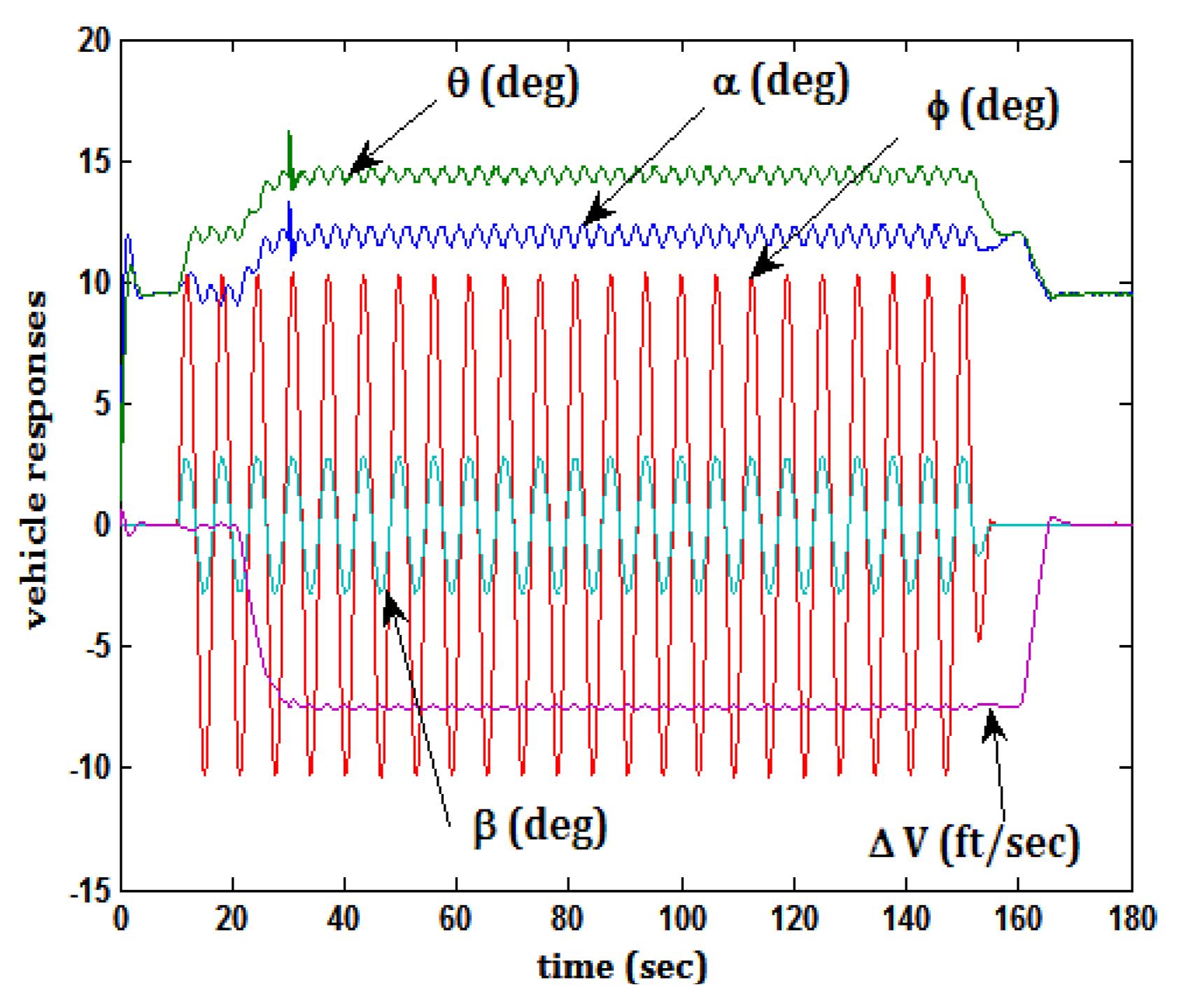
5.6. Task 5 and Actuator Damage

Task 5 was identical to Task 4 save that the trim airspeed was 220 ft/s. Figure 17 and Figure 18 show the simulation results. Again, the elevator activity is attributable to the higher airspeed and actuator damage.

Figure 17. Vehicle responses for Task 5.

Figure 17. Vehicle responses for Task 5.

Figure 18. Elevator and thrust inputs for Task 5.

Figure 18. Elevator and thrust inputs for Task 5.

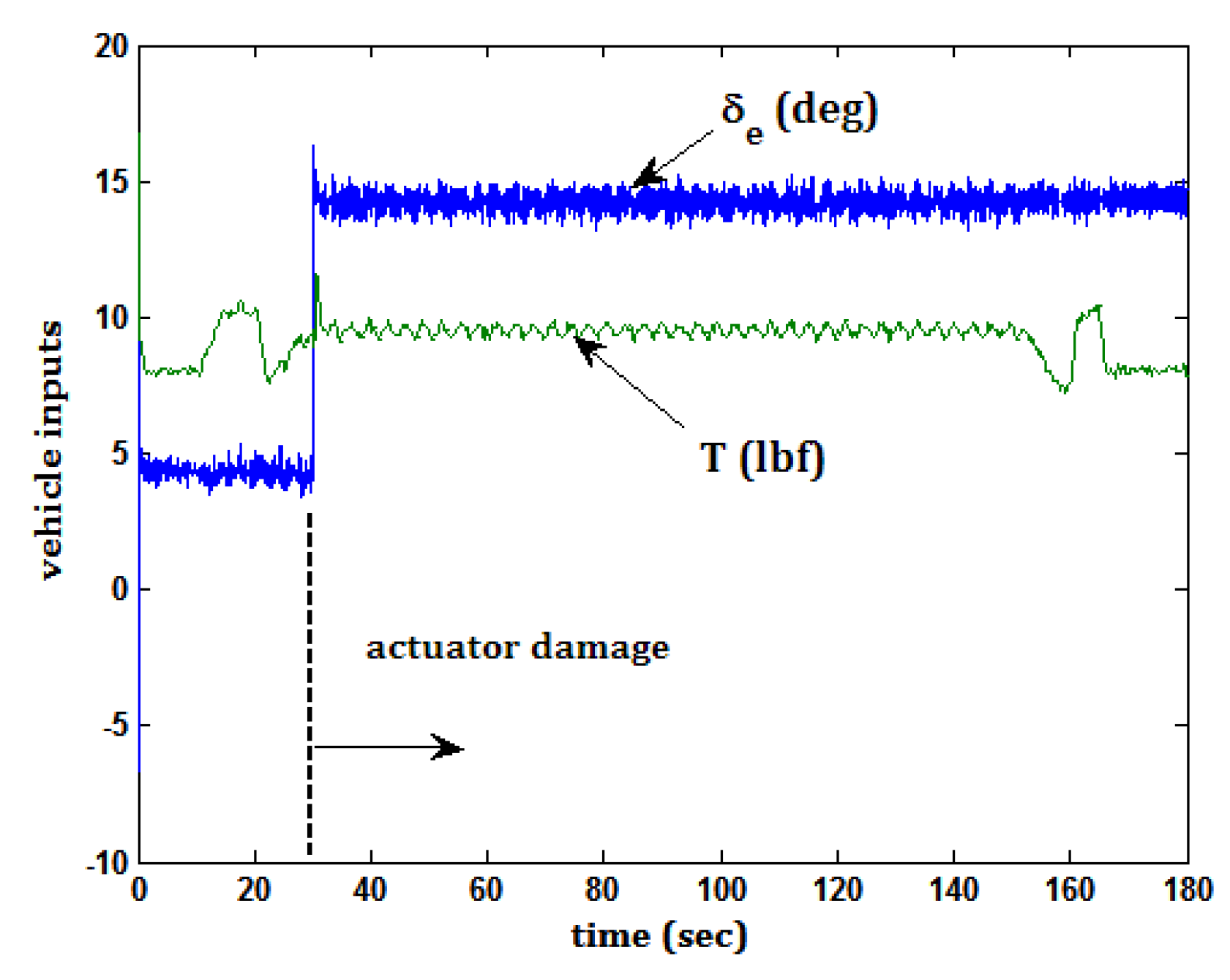
6. Discussion

Quoting from the Introduction: The philosophy behind the approach espoused herein is that the preservation of fundamental pilot input—system response characteristics throughout the flight envelope is important, indeed vital, in preventing LOC events. The computer simulations of Section 5 were intended to provide limited evidence that the SMC design approach has allowed preservation of the fundamental system response characteristics for a number of challenging flight tasks including actuator damage.

With two exceptions, the compensation elements that have been employed in the design were, at most, PI controllers or first-order bandwidth limited rate controllers. The two exceptions were the “hedge dynamics” for the pitch-rate and roll-rate loops. The form of these latter elements, however, is explicitly called out in the design Step (8) of Section 3. The only system “adaptation” that is needed is the scheduling of the observer with flight condition, i.e., altitude and airspeed (Mach No.). This would imply that civil certification of such a design may be considerably less involved than that for a truly adaptive system. As in previous applications of the methodology, control activity is the price to be paid for the robustness that has been demonstrated in the computer simulations. Sensor noise is the primary source of this increased control activity.

7. Conclusions

Based upon the study summarized herein, the following conclusions can be drawn:

(1)

The frequency-domain based pseudo-sliding mode design procedure introduced previously in the literature can be successfully applied to the design of a highly nonlinear model of the GTM aircraft.

(2)

The sliding-mode design can be limited to the inner-most loops of a square control architecture in which nested control loops are closed in sequential fashion.

(3)

Simple loop-shaping principles are used in each of the loop closures.

(4)

The majority of the compensators obtained in the design are simple in form, i.e., PI controllers.

(5)

Computer simulations of the vehicle and control system exhibited stability and performance robustness in different flight conditions and including simulated actuator damage.

(6)

The overall goal of the study, to demonstrate that fundamental pilot input—system response characteristics could be preserved, with significant variations in flight condition and actuator characteristics, was met.