Following model performance evaluation, correlations between observed temperature and surface physical properties were evaluated. In this case, two surface properties of interest were examined: neighborhood-scale albedo and vegetation canopy cover. The relationships between observed air temperature (dependent variable, or “predictand”) and either albedo and/or canopy cover (independent variables, or “predictors”) were examined in three manners: (1) simple linear regression, (2) multiple regression, and (3) CART analysis.
3.3.1. Simple Linear Regression
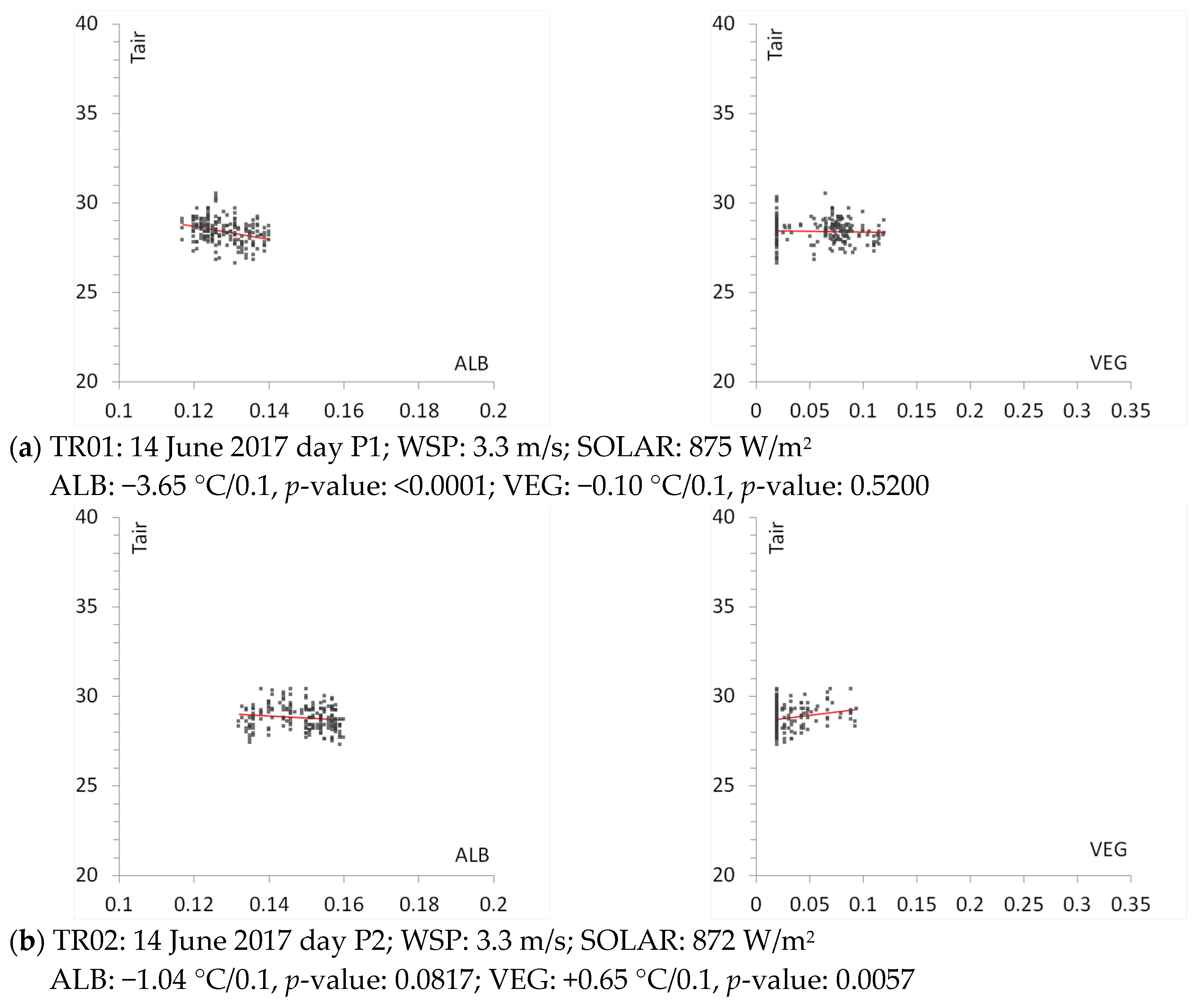
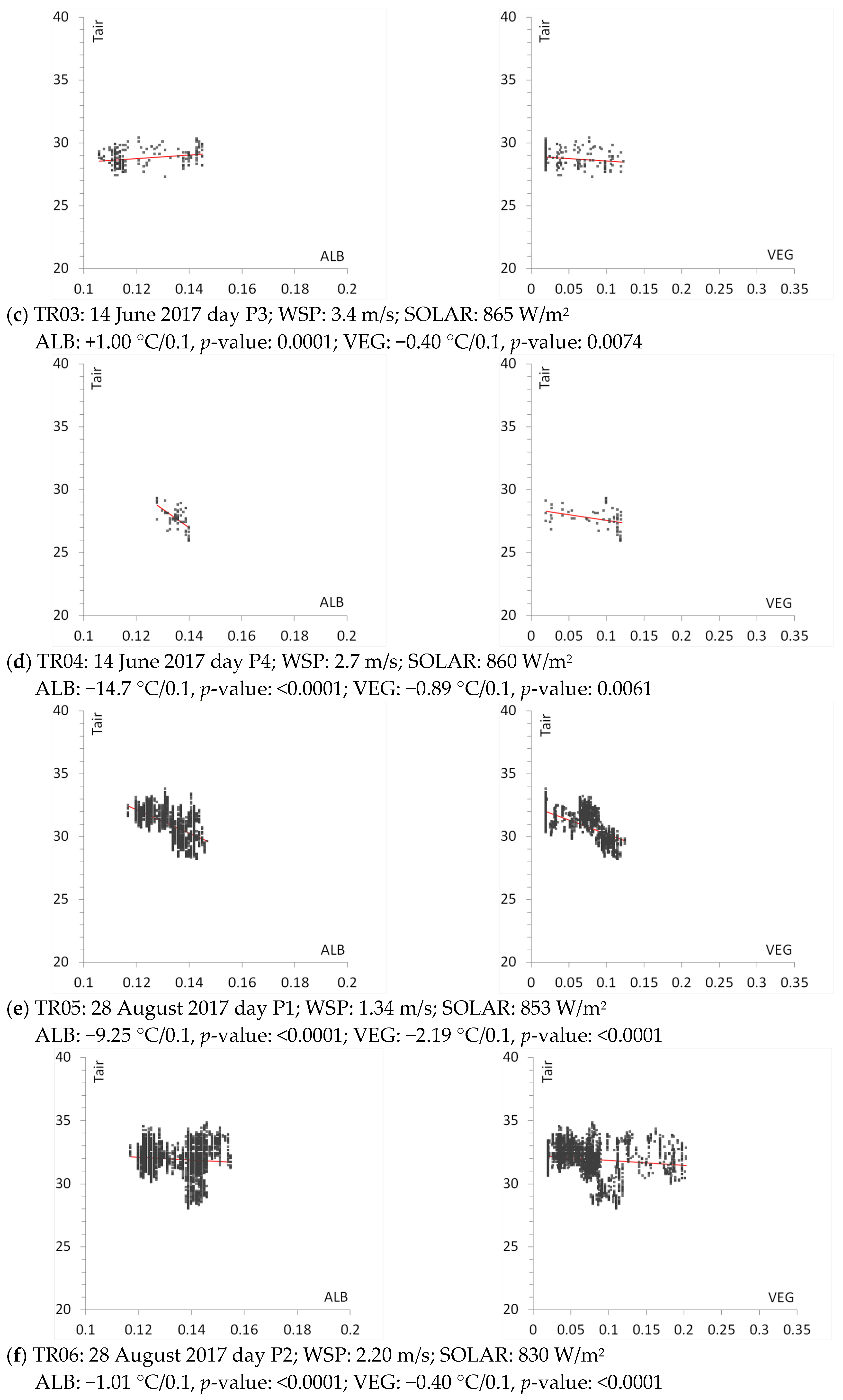
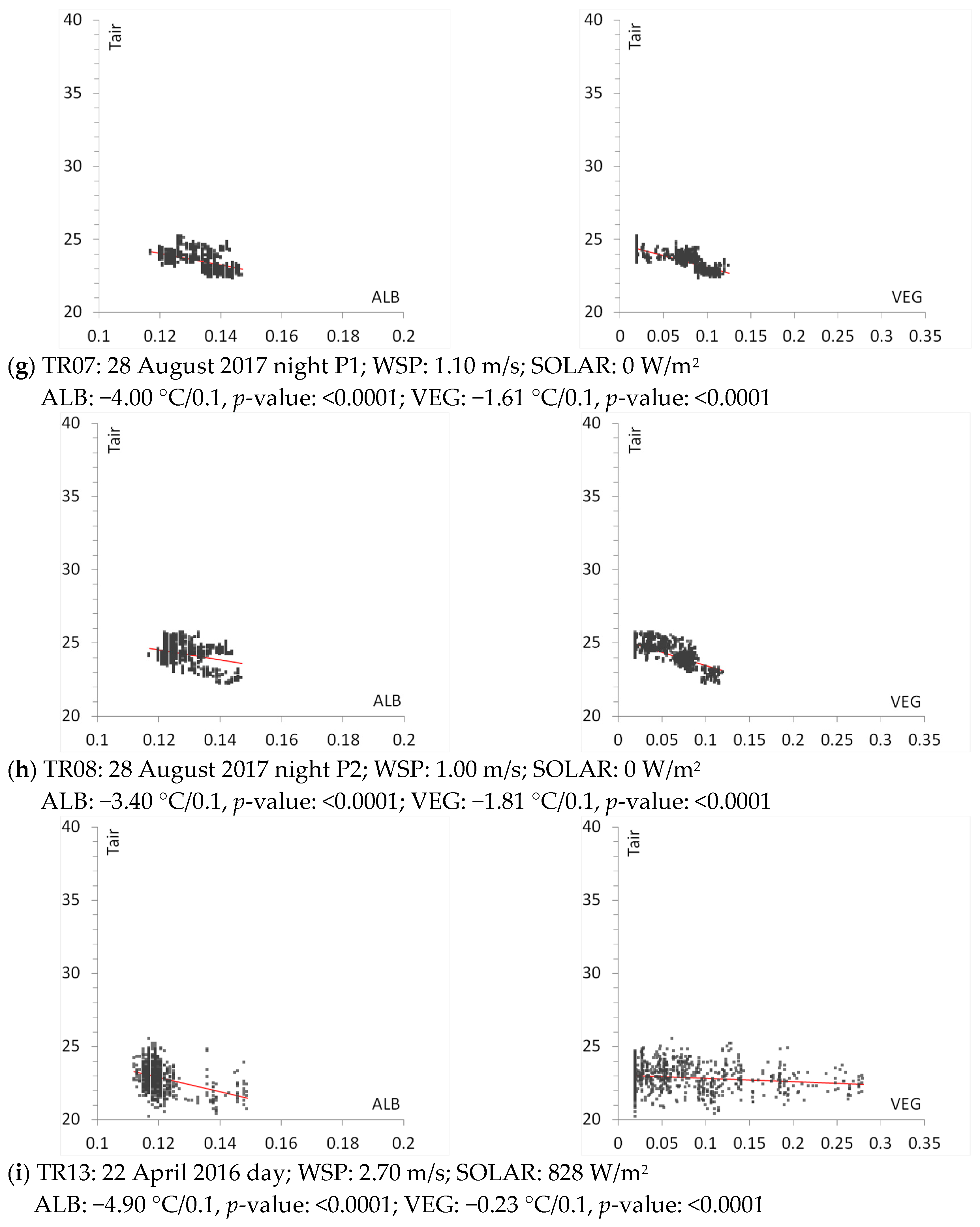
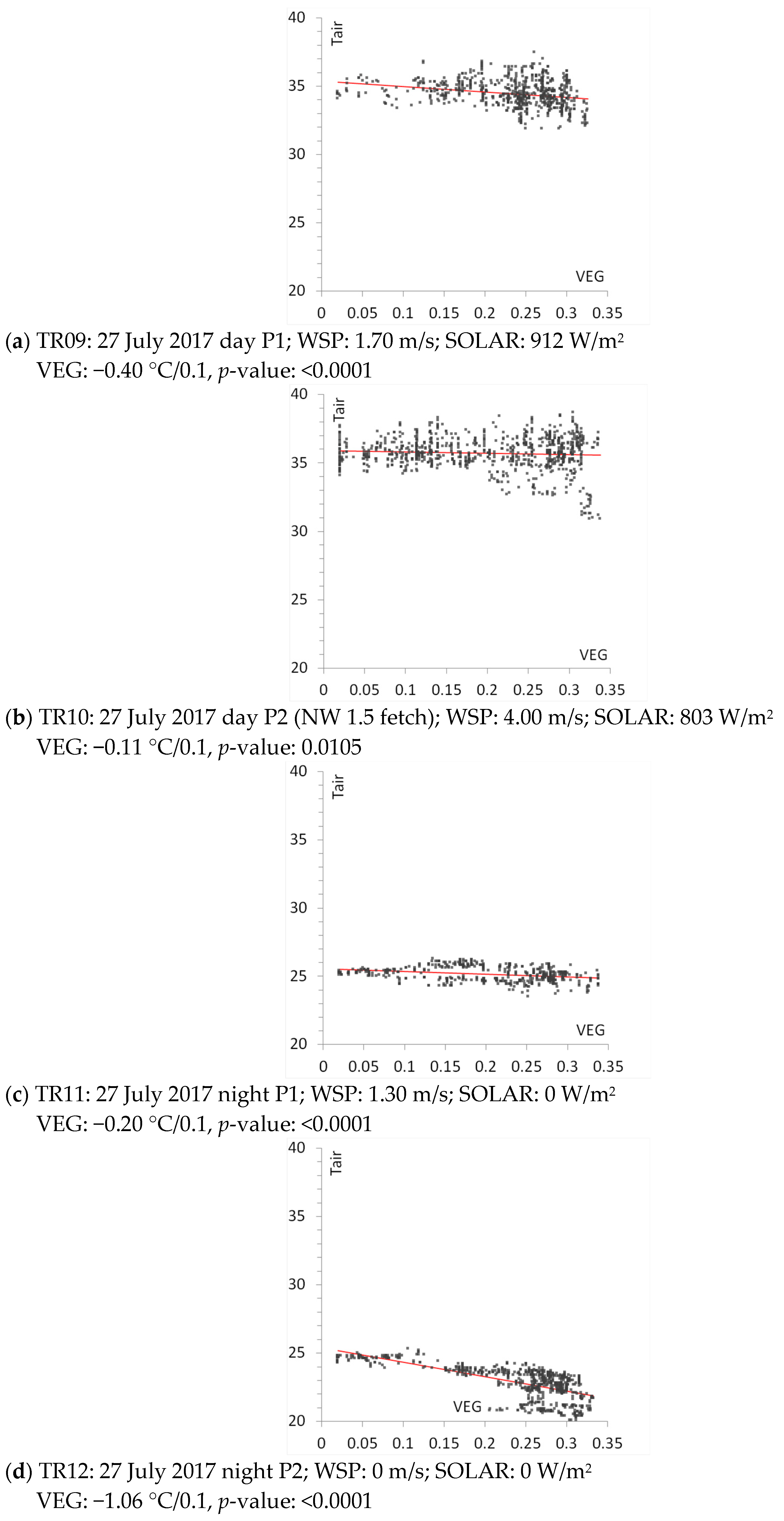
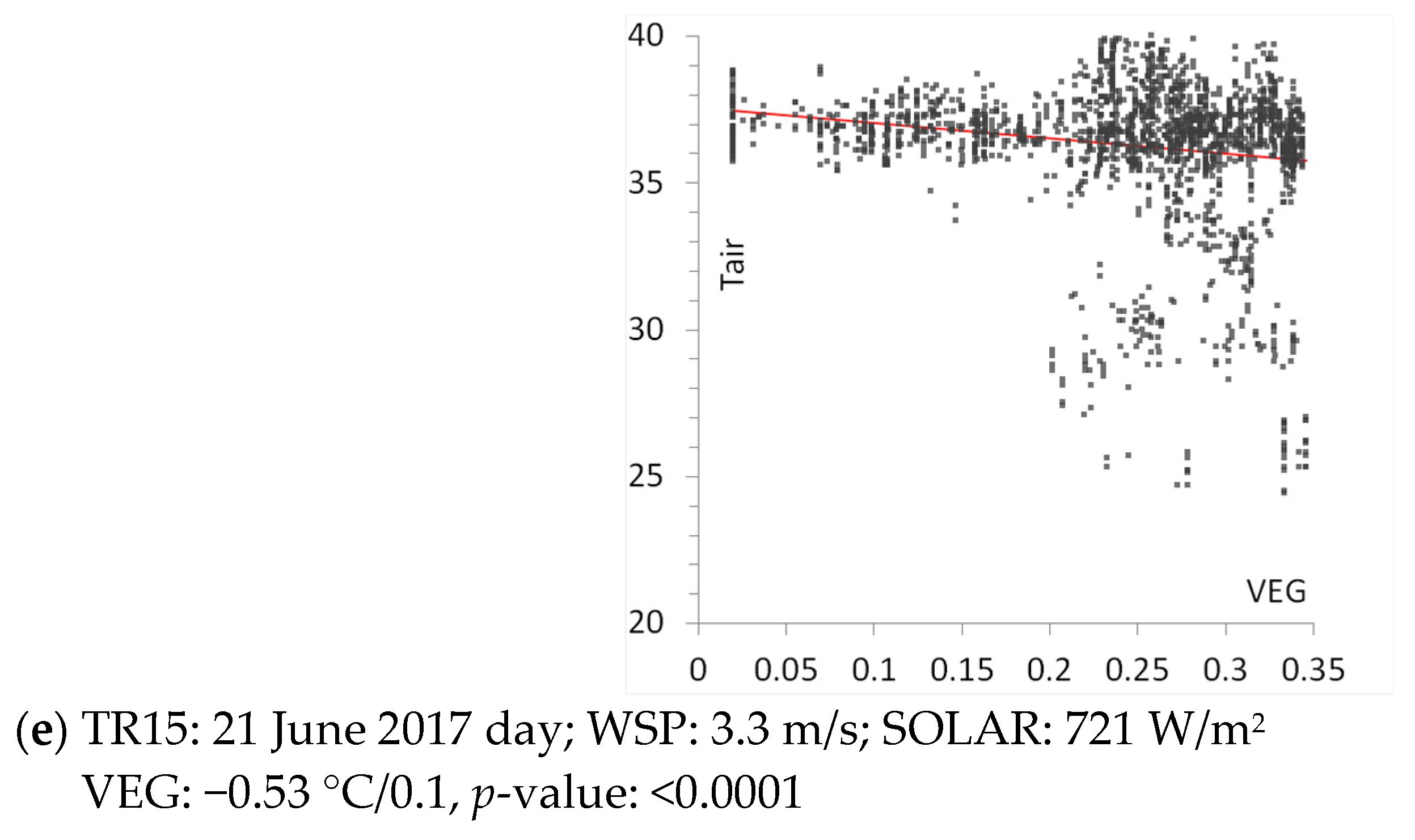
In
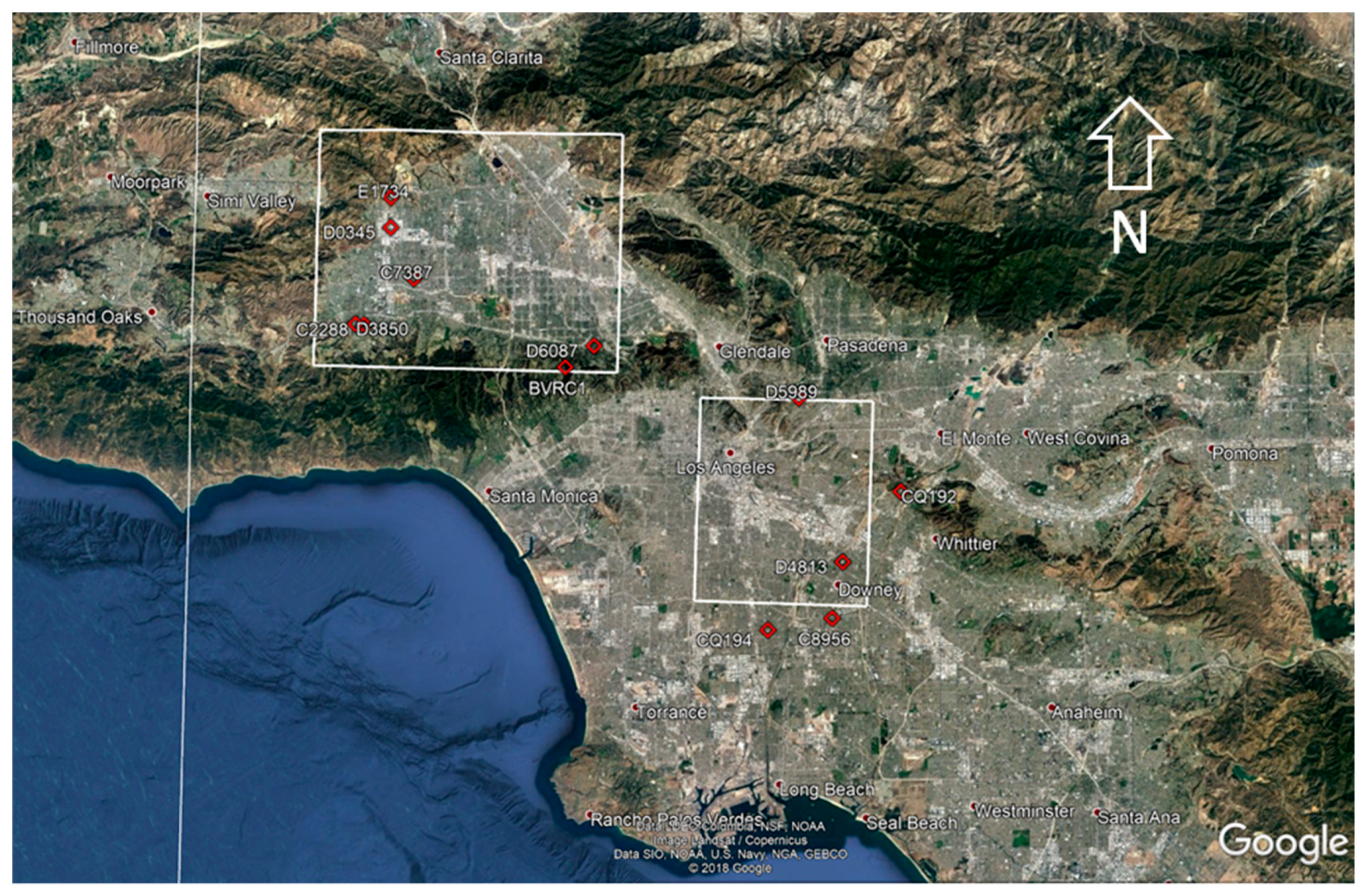
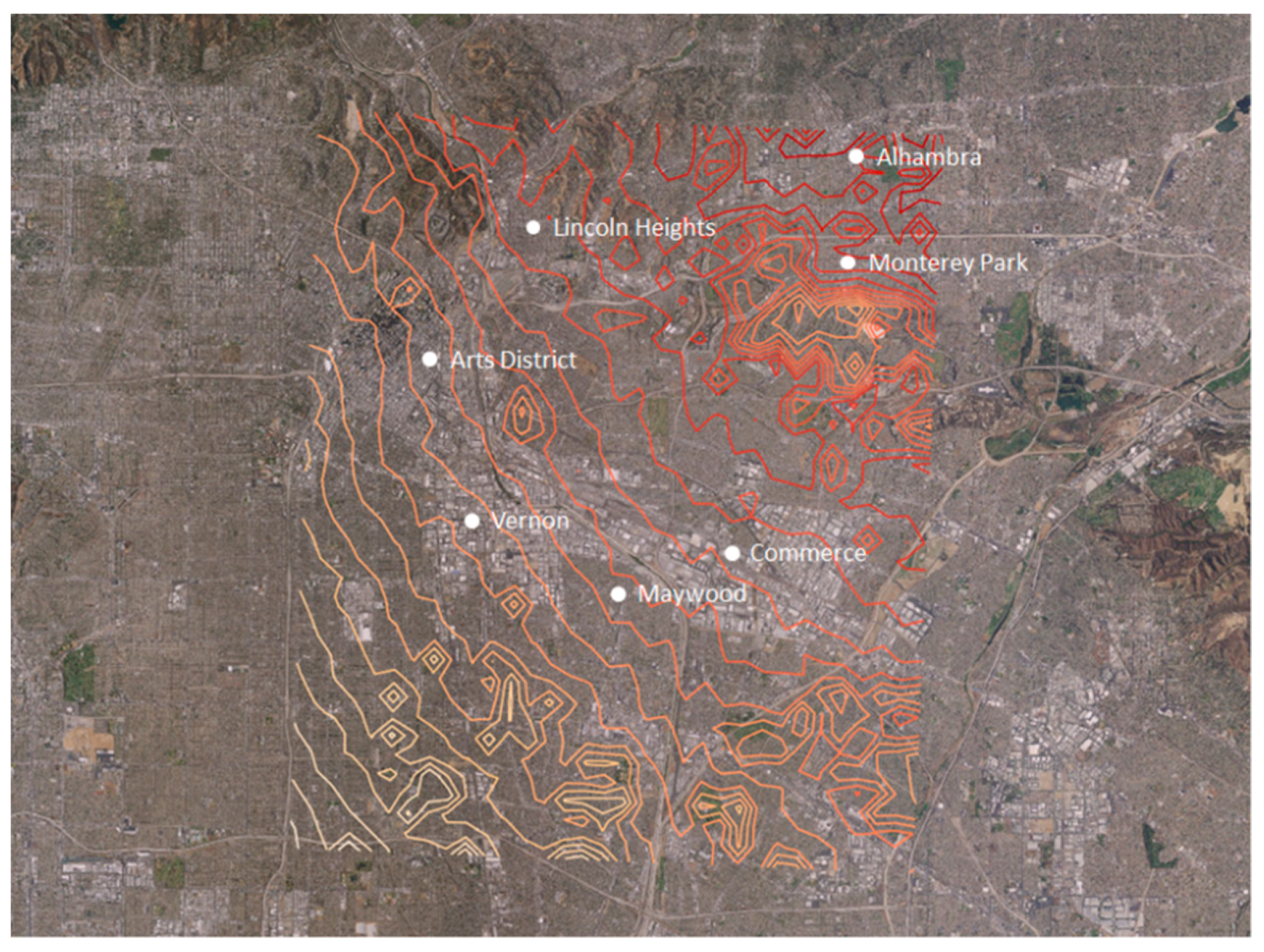
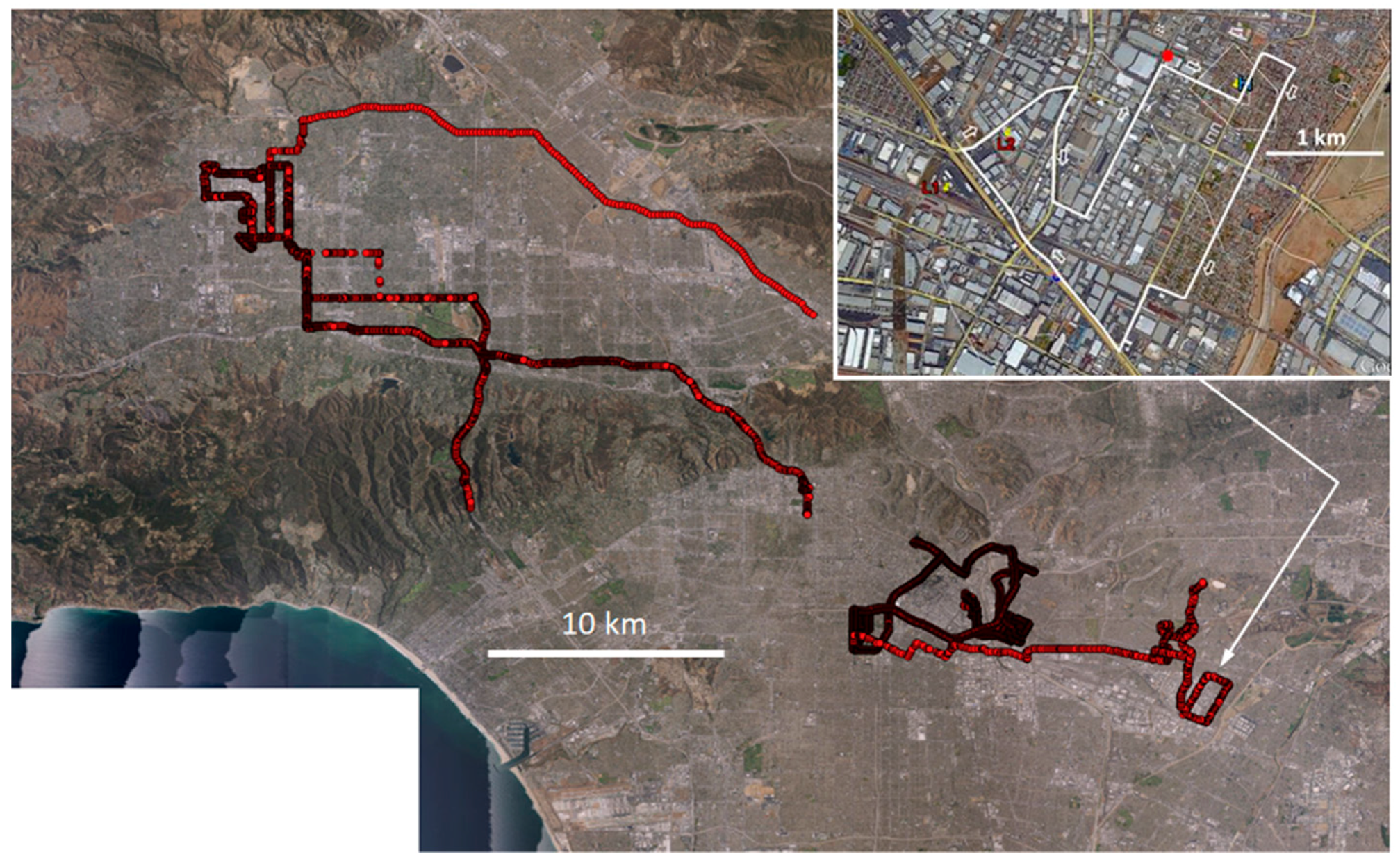
Figure 9a–i, observed air temperature (°C) from mobile transects is plotted on the vertical axis against grid-level (neighborhood-scale) albedo (ALB) or canopy cover (VEG), where ALB and VEG are each computed via Equations (1) and (2). This analysis is for the downtown area defined by the rectangle on the right in
Figure 1. For the San Fernando Valley (domain defined by white rectangle on the left in
Figure 1), the observed temperature in
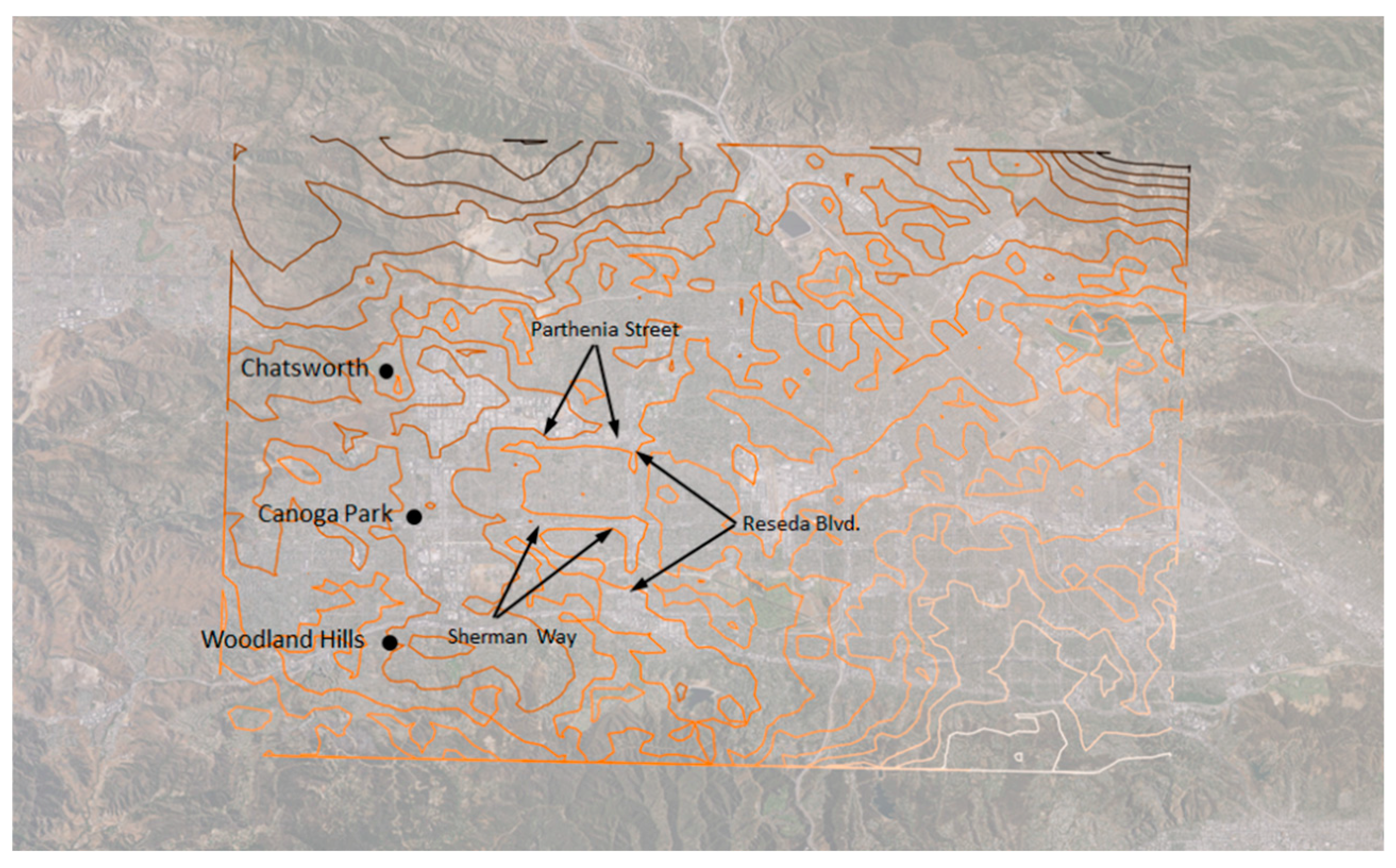
Figure 10a–e is plotted against canopy cover only (as predictor) because albedo has a smaller variability in this domain.
The analysis in
Figure 9 and
Figure 10 provides information for each transect segment including dates, slopes computed as temperature change per 0.1 increase in albedo or canopy cover (to normalize and facilitate inter-comparisons of effects across various transects), corresponding
p-values (probability values), wind speed (WSP), and solar radiation (SOLRAD) at the time of the transect. The latter two were obtained from the NOAA/MADIS mesonet monitors closest to each mobile transect at the time it was conducted. In this analysis, a significance level of 0.05 was selected and, as such, a
p-value < 0.05 represents a statistically significant correlation between observed temperature (from the transect) and surface properties (albedo and canopy cover).
The analysis in
Figure 9 and
Figure 10 was based on the Cressman-weighting scheme discussed above and a radius of influence of 1 km. The fifteen transects are identified as TR01 through TR15 and if a transect is made up of parts carried out at different times, these will be indicated as P1, P2, etc. One transect (TR14) is not shown in this analysis because of missing data.
Table 4 summarizes the main takeaways from the analysis in
Figure 9 and
Figure 10. It shows the response of observed air temperature (°C) to a 0.1 increase in neighborhood-scale albedo, symbolically written as Δ
T/(0.1Δ
a), or in canopy cover, written as Δ
T/(0.1Δ
η), in columns 2 and 6, along with the corresponding
p-value for each transect (in columns 3 and 7, respectively). Again, the reason for selecting a denominator of 0.1 is simply to normalize the temperature sensitivity and facilitate inter-comparisons of the effects across various transects. Also, an increase of 0.1 in neighborhood-scale albedo and/or canopy cover is one assumption often made as a mitigation scenario in UHI studies. Hence, it is used here as an indicator to what the real-world impact might be on air temperature.
Except for two entries (contribution of canopy cover to air temperature in transect TR01 and contribution of albedo to air temperature in transect TR02, as seen in columns 7 and 3, respectively), all other entries are statistically significant. For these two transects, the p-values suggest that in TR01, albedo is the main driver of air temperature and in TR02, canopy cover is the main driver.
In addition, all correlations are negative (i.e., when albedo and/or canopy cover increase, temperature decreases) except for transects TR02 (for canopy cover, column 6) and TR03 (for albedo, column 2). As will be discussed next, these two transects were among those carried out during periods of higher wind speeds, which can weaken the correlations. In transects TR04 and TR05, the large temperature response (sensitivity) to albedo change is likely caused by the extensive freeway and roof cover in these areas (>95%).
Columns 4 and 8 show the actual range of albedo and canopy cover, respectively, associated with each specific transect instead of a hypothetical range of 0.1 as used in columns 2 and 6. In other words, the ranges of albedo and canopy cover in columns 4 and 8 are “bounded” by the values encountered in the real world at each of these transects.
Columns 5 and 9 are temperature changes (°C) computed by multiplying the corresponding actual range (from columns 4 or 8, respectively) by the slope given in columns 2 or 6 and dividing by 0.1. Thus the bounded temperature variations in columns 5 and 9 represent the maximum changes that can be expected in each specific transect (per its actual albedo or canopy-cover range) rather than the unbounded values in columns 2 and 6. By doing so, some of the unreasonably large slopes (unbounded) in column 2, e.g., for TR04 and TR05, become much more reasonable when bounded, as in column 5.
Thus, columns 5 and 9 represent the changes in temperature that one can expect as a result of increasing albedo and/or canopy cover by the amounts already encountered in the real world and that are achievable via current practices in building and planning. On the other hand, columns 2 and 6 represent the potential cooling effects that would result from implementations of high-albedo measures (cool roofs and cool pavements) and/or urban forestation, where each would be increased by 0.1.
Next, the correlations between mobile-observed temperature and albedo and/or canopy cover are re-examined but with a smaller radius of influence (<500 m). The goal is to evaluate whether a length-scale effect exists in these correlations. This analysis is done by comparing observations directly to surface properties at grid points, that is, without the Cressman analysis discussed above.
This analysis shows that the correlations between observed temperature and neighborhood-scale albedo and/or canopy cover are negative and statically significant at
R < 500 m when wind speed is under 3 m/s locally—compare the
p-values of rows 1, 3, 5, 7, and 9 in the right half of
Table 5 with all the rows in the left half, suggesting weaker correlation between temperature and surface properties within 500 m at wind speeds exceeding 3 m/s. That is, when wind speed exceeds 3 m/s, the correlations either become weaker (for one of the predictors or the other) or statistically insignificant (see TR01, TR02, TR03, TR10, and TR15). For these cases, the analysis was repeated once more by (1) increasing the radius of influence from 500 m to 1 km and (2) restricting the correlations to upwind model points.
In this repeated analysis, the correlations improved further, i.e., some positive or weak correlations converted into negative or stronger ones as seen in
Table 5 (compare TR01-SE to TR01, TR02-NW to TR02, TR03-NE to TR03, TR10-NW to TR10, and TR15-NE to TR10). In these cases, the
p-values and slopes improved after increasing the upwind fetch (from 500 m to 1 km) and including only grid points within the wind approach direction. This also explains why these adjusted correlations are better than the corresponding ones in
Table 4 (in some cases) for one or the other predictors, since the correlations in
Table 4 were not limited to upwind points. For example, comparing TR01-SE from
Table 5 to TR01 from
Table 4, we can see that whereas the albedo-temperature correlation becomes a little weaker, the canopy-temperature correlation becomes much more significant (
p-value changes from 0.53 to 0.0087). Comparing TR02-NW (
Table 5) to TR02 (
Table 4) shows a slight improvement in the significance of the albedo-temperature correlation and also a change in sign (from 0.65 to −0.11) for canopy-temperature correlation, albeit at a larger
p-value. In this case, therefore, the temperature is driven by the albedo effect mainly. For TR03-NE there are mixed effects: whilst TR03-NE is improved relative to TR03 (in
Table 5), it is not as good as the correlation for TR03 in
Table 4 (this transect appears to be an exception). Finally, for TR10-NW and TR15-NW (in
Table 5 relative to
Table 4), the correlations do not change much.
Thus the results from this analysis suggest that when wind speed is less than 3 m/s, the observed temperature is influenced by the physical properties of the immediate surroundings (less than 500 m radius). At wind speeds exceeding 3 m/s, temperature is influenced by surface properties in a longer fetch (~1 km) in the upwind direction. Physically, this is because advective effects are smaller than the localized convective effects when wind speed is lower. At higher wind speed, in this case >3 m/s, temperature is influenced more by advective than localized effects. To provide context, the monthly average wind speeds in the study areas (from climatology) for January–December are 3.7, 3.5, 3.3, 3.1, 3.1, 2.6, 2.3, 2.2, 2.6, 2.6, 3.1, and 4.0 m/s, respectively. Thus the 3.3–4.0 m/s winds that were observed during some of the transects are relatively uncommon in this area and time of year, i.e., July and August, where 2.2–2.6 m/s is a more typical range. Of note, while there likely is a smooth transition around the 3-m/s threshold, we do not have observational values slightly under or over 3 m/s that can be used to evaluate this transition. Thus the suggested threshold of 3 m/s, while not a hard cutoff, is the most representative value that we determined based on the statistical analysis discussed above.
3.3.2. Multiple Regression
Multiple regression was carried out for albedo and canopy cover as predictors to observed air temperature from the transects. This analysis applies only to the downtown area since the San Fernando Valley analysis involved only variations in one predictor, canopy cover.
Here, the form of the correlation is given by Equation (3) where
a is albedo and
η is canopy cover. The coefficients (
C1,
C2,
C3) and corresponding
p-values (
p1,
p2,
p3) are given in
Table 6 and
Table 7. Coefficients
C1,
C2, and
C3 are in °C, and the “0.1” denominator simply indicates that the changes in temperature (
C2 and
C3) correspond to a 0.1 increase in surface albedo or a 0.1 increase in canopy cover. This was done for reasons explained in
Section 3.3.1.
Following the structure of the discussion above, results from the multiple-regression analysis are presented in two parts;
Table 6 summarizes the analysis at a 1-km radius of influence using the Cressman-type weighting discussed earlier, while
Table 7 summarizes the 500-m analysis without weighting. The results in
Table 6 show that the correlations are overwhelmingly negative (as albedo and canopy cover increase, temperature decreases) and statistically significant except for three situations. These are in transect TR01, where the role of the canopy cover is insignificant, and in transects TR02 and TR03, where the role of albedo is insignificant. This was already discussed in
Section 3.3.1, as were the large slopes in TR04 and TR05.
In
Table 7, and as introduced in
Section 3.3.1, the sign of some correlations change to negative or significance improves (smaller
p-values) when the radius of influence is increased and wind from a specific direction is accounted for rather than an average from several directions (e.g., TR01-SE and TR02-NW). In other words, at wind speeds exceeding 3 m/s, extending the upwind fetch from 500 m to 1 km and accounting for LULC properties only in the wind-approach direction improves the
p-values and/or the coefficients for albedo and/or canopy cover changes. This is similar to what was found in
Section 3.3.1.
The values listed in
Table 6 and
Table 7 are relative to changes of 0.1 in albedo or vegetation cover and, thus, are unbounded. These can be converted into transect-specific bounded values as was done in
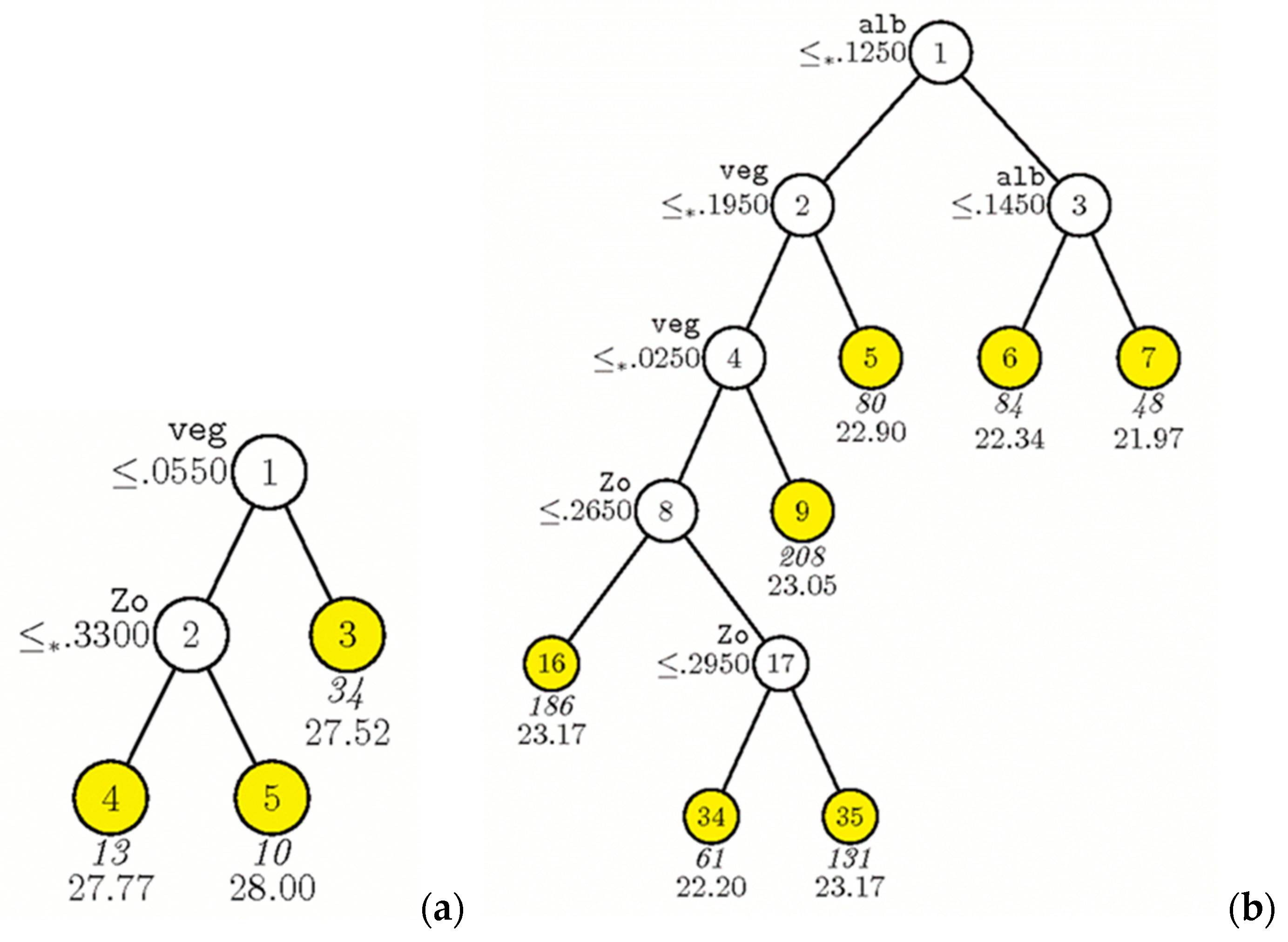
Table 4. Two examples are demonstrated here that will be referred to in the following discussion of example CART for transects TR04 and TR13 in
Section 3.3.3. The first example is the coefficient
C3 (for canopy cover) in
Table 7, corresponding to transect TR04 with a value of −0.417 °C. If this is multiplied by the actual canopy-cover range of 0.1 (from
Table 4, TR04 under column 8) and divided by 0.1, we obtain a bounded value of −0.41 °C. The second example is the coefficient
C2 (for albedo) in
Table 7, corresponding to transect TR13 (value of −2.088 °C). If this is multiplied by the actual albedo range of 0.037 (
Table 4, transect TR13, under column 4), and divided by 0.1, we obtain a bounded value of −0.77 °C.